2019届秋季上学期高二语文8月月考试题(含解析) (198)
2019届秋季上学期高二语文8月月考试题(含解析) (807)

专题十三复合句1.[2018河南,33]Anyone who is a server or has been one knows that customers always come first.A. whomB. whatC. whoD. which2.[2018河南,34]—Excuse me.Do you know ?—Sorry, I don't know, either.A. how to check out a bookB. when will the concert beginC. that there is a bank near hereD. how long the meeting would last3.[2017河南,33]I hate the dogs live in the next house. They make loud noises all night.A. whoB. thatC. whatD. whom4.[2016河南,32]Theaters may have a brighter future if they can provide a movie experience people cannot get at home.A. thatB. whoC. whomD. what5.[2016河南,35]—What did Tom say to you just now, John?—He asked .A. why I am so happy todayB. what will I do for the weekendC. who did I play football with after schoolD. if I could go to the movies with him tonight6.[2015河南,33]—Why don't you like fishing?—Fishing is a hobby needs much patience,but I'm not patient at all.A. whoB. thatC. itD. what7.[2015河南,35]—Hi,Tony!Do you know ?—Yes,there is a coffee shop at the corner of the street.A. when I can get a cup of coffeeB. when can I get a cup of coffeeC. where I can get a cup of coffeeD. where can I get a cup of coffee8.[2014河南,30]"Underground" is the only word in the English languagebegins and ends with the letters "und".A. whatB. thatC. whoD. whom9.[2014河南,35]—Excuse me, can you tell me ?—Sorry, I don't know. You can go to the information desk.A. that there is a trainB. when the train leavesC. which train can I takeD. where does the train go10.[2013河南,32]A friend is someone says, "What! You too? I thought I was the only one!"A. whoB. whichC. whatD. whose11.[2013河南,35]—Miss Lee, I didn't catch what you said. Could you tell me again?—OK.A. what should we takeB. where shall we meetC. when we would startD. how we will get there12.[2012河南,33]Success will belong to those never say "impossible".A. whomB. whatC. whoD. which13.[2012河南,35]My pen pal from America is coming to visit me. I'm thinking about .A. what present did I give herB. how I will give her a surpriseC. where will we have a big mealD. whether I planned a trip for her14.[2011河南,32]Tony, tell me the result of the discussion you had with your dad yesterday.A. whatB. whichC. whenD. who15.[2011河南,35]I didn't see Laura at the party last night. Do you know ?A. why didn't she comeB. what happenedC. when would she arriveD. where she has been16.[2010河南,33]Friends are those make you smile, always open their hearts to you and encourage you to succeed.A. whichB. whatC. whomD. who17.[2010河南,35]Some of my friends are interested in science,but none of them can tell .A. when UFOs will appear next timeB. why do horses know the wayC. where was this kind of plant foundD. how do elephants communicate18.[2009河南,31]It's time to say goodbye to my school. I'll always remember the people have helped me.A. whoB. whatC. whichD. where19.[2009河南,35]—What time will Mr. Brown be back to China?—Sorry. I don't know .A. when did he go abroadB. why he is going abroadC. how soon will he be backD. how long he will stay abroad【参考答案】1—5 CABAD 6—10 BCBBA 11—15 DCBBB 16—19 DAAD。
2019届秋季上学期高二语文8月月考试题(含解析) (956)
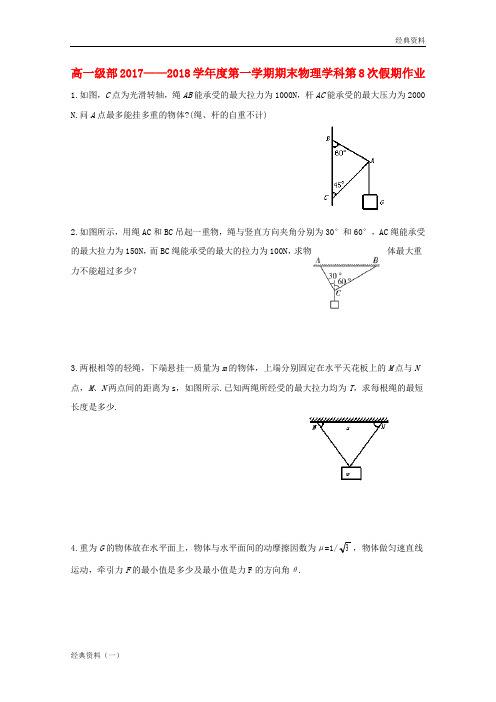
高一级部2017——2018学年度第一学期期末物理学科第8次假期作业1.如图,C点为光滑转轴,绳AB能承受的最大拉力为1000N,杆AC能承受的最大压力为2000 N.问A点最多能挂多重的物体?(绳、杆的自重不计)2.如图所示,用绳AC和BC吊起一重物,绳与竖直方向夹角分别为30°和60°,AC绳能承受的最大拉力为150N,而BC绳能承受的最大的拉力为100N,求物体最大重力不能超过多少?3.两根相等的轻绳,下端悬挂一质量为m的物体,上端分别固定在水平天花板上的M点与N 点,M、N两点间的距离为s,如图所示.已知两绳所经受的最大拉力均为T,求每根绳的最短长度是多少.4.重为G的物体放在水平面上,物体与水平面间的动摩擦因数为μ=1/3,物体做匀速直线运动,牵引力F的最小值是多少及最小值是力F的方向角θ.5.如图3,用力F推质量为M的物体,物体与地面间的摩擦因数为μ,求外力F与水平方向交角θ最小为多大时,无论外力F多么大均不能使物体前进?6.一个弹簧台秤的秤盘和弹簧的质量都不计,盘内放一个物体P处于静止状态,如图所示,P 的质量为m=10kg,弹簧的劲度系数k=500N/m,现给P施加一个竖直向上的力F,使P由静止开始向上做匀加速直线运动.已知在最初0.2 s内F是变力.在0.2 s以后是恒力.则F的范围.7.如图所示,一根弹性细绳原长为l,劲度系数为k,将其一端穿过一个光滑小孔O(其在水平地面上的投影点为O′),系在一个质量为m的滑块A上,A放在水平地面上.小孔O离绳固定端的竖直距离为l,离水平地面高度为h(h<mg/k),滑块A与水平地面间的最大静摩擦力为正压力的μ倍.问:(1)当滑块与O′点距离为r时,弹性细绳对滑块A的拉力为多大?(2)滑块处于怎样的区域内时可以保持静止状态?8.如图所示,一球A夹在竖直墙与三角劈B的斜面之间,三角劈的重力为G,劈的底部与水平地面间的动摩擦因数为μ,劈的斜面与竖直墙面是光滑的。
2019届秋季上学期高二语文8月月考试题(含解析) (632)

全等三角形课后作业题十三1.如图,AC是△ABC和△ADC的公共边,下列条件中不能判定△ABC≌△ADC的是()A.AB=AD,∠2=∠1B.AB=AD,∠3=∠4C.∠2=∠1,∠3=∠4D.∠2=∠1,∠B=∠D2.如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是()A. 50B. 62C. 65D. 683.如图,在Rt△ABC中,∠ACB=90°,AC=BC,CD⊥AB于D点,M,N是AC,BC上的动点,且∠MDN=90°,下列结论:①AM=CN;②四边形MDNC的面积为定值;③AM2+BN2=MN2;④MN平分∠CND.其中正确的是()A.①②③ B.①②④ C.①③④ D.①②③④4.已知△ABC≌△DEF,∠A=80°,∠E=50°,则∠F的度数为()A.30° B.50° C.80° D.100°5.如图,已知△ABC,按如下步骤作图:(1)以A圆心,AB长为半径画弧;(2)以C为圆心,CB长为半径画弧,两弧相交于点D;(3)连接BD,与AC交于点E,连接AD,CD.①四边形ABCD是中心对称图形;②△ABC≌△ADC;③AC⊥BD且BE=DE;④BD平分∠ABC.其中正确的是()A.①② B.②③ C.①③ D.③④6.如图,已知AB=AC,AD=AE,若要得到“△ABD≌△ACE”,必须添加一个条件,则下列所添条件不恰当的是()A.BD=CE B.∠ABD=∠ACE C.∠BAD=∠CAE D.∠BAC=∠DAE7.(2015秋•常州期末)如图,下列条件中,不能证明△ABC≌△DCB的是()A.AB=CD,AC=BDB.AB=CD,∠ABC=∠BCDC.∠ABC=∠DCB,∠A=∠DD.AB=CD,∠A=∠D8.如图,由∠1=∠2,BC=DC、AC=EC,最后推出△ABC≌△EDC的根据是()A. SAS B.ASA C.AAS D.SSS9.(2015春•南京校级期末)下列说法中:①如果两个三角形可以依据“AAS”来判定全等,那么一定也可以依据“ASA”来判定它们全等;②如果两个三角形都和第三个三角形不全等,那么这两个三角形也一定不全等;③要判断两个三角形全等,给出的条件中至少要有一对边对应相等.正确的是()A.①和② B.②和③ C.①和③ D.①②③10.如图,△ABC≌△BDE,点B、C、D在一条直线上,AC、BE交于点O,若∠AOE=95°,则∠BDE= °.11.已知:如图,△ABC≌△DFE,若∠A=60°,∠E=90°,DE=6cm,则AB= cm.12.如图,△OAD≌△OBC,且∠O=60°,∠C=20°,则∠OAD= °.13.如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是30cm2,AB=8cm,BC=7cm,则DE= cm.14.如图,AC⊥BC于C ,DE⊥AC于E ,A D⊥AB于A , BC=AE.若AB=5 ,则AD=___________.15.AD是△ABC的边BC上的中线,AB=12,AC=8,则边BC的取值范围是;中线AD的取值范围是.16.如图,已知AC=BD,∠A=∠D,请你添一个直接条件,,使△AFC≌△DEB.(写出一种答案即可)17.如图,在Rt△ABC中,∠C=90°,AM、BN分别平分∠CAB、∠ABC,AM与BN相交于点O,OD⊥AB,AB=10,AC=8,BC=6,则OD=____________.18.已知图中的两个三角形全等,则∠1等于度.19.如图,△ABC中,∠C为直角,射线AD平分∠BAC交BC于点D,BD∶DC=2∶1,BC=3.6cm,则点D到AB 边的距离为 cm。
2019届秋季上学期高二语文8月月考试题(含解析) (502)

河南省滑县2019届高三数学第二次联考试题文(扫描版)2018—2019学年高三年级调研考试(二)数学(文科)参考答案1.【答案】B【解析】依题意,{}{}232,1,0,1,2Z A x x =∈-≤<=--,故{}0,2A B =,故选B.2.【答案】A 【解析】依题意,()()()()24i 13i 24i 26i 4i 121010i1i 13i 13i 13i 1010--------====--++-,故选A. 3.【答案】D【解析】依题意,131********n n ⎡⎤⎛⎫-⎢⎥⎪⎝⎭-⎢⎥⎣⎦=--,化简可得2log 6n =,故[]2n =,则第2日蒲生长的长度为D. 4.【答案】C【解析】运行该程序,第一次,999,2S k ==;第二次,995,4S k ==;第三次,979,6S k ==;第四次,915,8S k ==;第五次,659,10S k ==,第六次365,12S k =-=,此时0S <,故输出的k 的值为12,故选C. 5.【答案】B【解析】A 班学生的分数多集中在[70,80]之间,B 班学生的分数集中在[50,70]之间,故A B x x >;相对两个班级的成绩分布来说,A 班学生的分数更加集中,B 班学生的分数更加离散,故22A B s s <,故选B.6.【答案】A【解析】依题意,()()()()55255550550mn m n m n n m n ->-⇔--->⇔-->5,5,5,5,m m n n ><⎧⎧⇔⎨⎨><⎩⎩或故“2216m n +<”⇒“5525mn m n ->-”,反之不成立,例如6m n ==;故“2216m n +<”是“5525mn m n ->-”的充分不必要条件,故选A. 7.【答案】C【解析】作出该几何体1111ABCD A B C D -的直观图,旋转一定的角度后,得到的图形如下图所示,观察可知,1CA =1A D =,1A B = C.8.【答案】B【解析】依题意,不妨设点M (x,y )在第一象限,联立225,,x y by x a ⎧+=⎪⎨=⎪⎩解得,x c y ⎧=⎪⎪⎨⎪=⎪⎩(其中222b a c +=),可知四边形MNPQ为矩形,且根据双曲线的对称性,2c c ⋅=,即225c ab =,解得12b a =(2b a=舍去),故所求渐近线方程为12y x =±,故选B. 9.【答案】D【解析】依题意,函数()f x 为偶函数,故1k =-,则()()320g k x g x ++-+=即为()()132g x g x -++-=-,故函数()g x 的图象的对称中心为()1,1-,故选D.10.【答案】A【解析】依题意,()()()3sin 32sin 33f x x x x πϕϕϕ⎛⎫=-+-=-+ ⎪⎝⎭,则()333Z k k ππϕπ⨯-+=∈,则()43Z k k πϕπ=-∈;因为2πϕ<,故3πϕ=,故()2sin 3f x x =,则将函数()f x 的图象向右平移6π个单位长度 后得到函数()2cos3g x x =-的图象,故选A. 11.【答案】B【解析】依题意,当0x ≥时,()()2'1212121f x x x x x =-=-,故当()0,1x ∈时,()'0f x <,当()1,x ∈+∞时,()'0f x >,且()11f =-,作出函数()f x 的大致图象如下所示;令()()()22320g x f x f x =--=⎡⎤⎣⎦,解得()()122f x f x ==-或,观察可知,函数()g x 共有3个零点,故选B.12.【答案】A【解析】设()00,M x y ,()11,N x y ,则直线MA 1的斜率为1003MA y k x -=,由11NA MA ⊥,所以直线NA 1的斜率为1003NA x k y =--.于是直线NA 1的方程为:0033x y x y =-+-.同理,NA 2的方程为:0033x y x y =--+.联立两直线方程,消去y ,得20109y x x -=. 因为()00,M x y 在椭圆221189y x +=上,所以22001189x y +=,从而2292x y -=-.所以012x x =-. 所以1212012MA A NA A S x S x ∆∆==,故选A. 13.【答案】322-或【解析】依题意,()4212m m +⋅=,解得322m =-或. 14.【答案】5【解析】作出不等式组所表示的平面区域如下图阴影部分所示,观察可知,当直线2z x y =-过点55,33A ⎛⎫- ⎪⎝⎭时,2z x y =-取最大值,最大值为5.15.【答案】108【解析】依题意,不妨设2AB =,故所求概率22224P ππ⨯⨯+⨯⨯==.16.【解析】因为()sin sin 4sin sin ABC b a A b B B S bc C ∆+=⋅+,故2sin sin 4sin sin ABC ab A b B B S bc C ∆+=⋅+,即222sin sin 4sin sin ABC a B b B B S c B ∆+=⋅+,即2224ABC a b c S ∆+-=,故cos sin ab C ab C =,故4C π=,则△ABC的外接圆半径为2sin c C ==.17.【解析】(1)依题意,设BD x =,则AD =,3BC x =,又,43B AB π==.在△ABD 中,由余弦定理得3cos4216322π⋅⋅-+=x x x ,即2280x x +-=,解得2x =,或4-=x (舍去). 则36BC x ==;(5分)(2) 在△ ABC 中,设A,B,C 所对的边分别为a,b,c , 由正弦定理sin sin b c B C=,得sin sin c B C b ==又AC b AB c =>=,所以B C >,则C为锐角,所以cos 3C =则()1sin sin sin cos cos sin 2BAC B C B C B C ∠=+=++=.(10分) 18.【解析】(1)依题意,设等差数列{}n a 的公差为d ,则4224d a a =-=,解得2d =,故11a =,21n a n =-,而236m mS S +=+,则214436m m a a m +++=+=,解得8m =,故32424232425762m S S ⨯==+⨯=;(6分)(2)因为21n a n =-,故()()+1211111212322123n n a a n n n n +⎛⎫==- ⎪++++⎝⎭,故()111111111...23557792123323n nT n n n ⎛⎫=-+-+-++-= ⎪+++⎝⎭.(12分) 19.【解析】(1)依题意 ,所求平均数为20.260.36100.28140.12180.04⨯+⨯+⨯+⨯+⨯ 0.4 2.16 2.8 1.680.727.76=++++=;(3分) (2)依题意,完善表中的数据如下所示:故()222000800600200400333.3310.828100010001200800K ⨯⨯-⨯=≈>⨯⨯⨯;故有99.9%的把握认为“愿意购买该款电视机”与“市民的年龄”有关;(7分)(3)依题意,使用时间在[)0,4内的有1台,记为A ,使用时间在[]4,20内的有4台,记为a,b,c,d ,则随机抽取2台,所有的情况为(A ,a ),(A ,b ),(A ,c ),(A ,d ),(a ,b ),(a ,c ),(a ,d ),(b ,c ),(b ,d ),(c ,d ),共10种,其中满足条件的为(a ,b ),(a ,c ),(a ,d ),(b ,c ),(b ,d ),(c ,d ),共6种,故所求概率63105P==.(12分)20.【解析】(1)作出平面EFG 的图形如下所示,点G 为线段SB 上靠近B 点的三等分点;C(5分)(2)依题意, 因为0090,45SDA SAD ∠=∠=,故SD AD ==而2SA SB ==,所以222SB SD BD =+, 所以SD BD ⊥,又因为DADB D =,所以SD ABCD ⊥平面;因为SD ⊂平面SCD,所以平面SCD ABCD ⊥平面. 作'EE CD ⊥于'E ,因为平面=SCDABCD CD 平面,所以'EE ⊥平面SCD ;又因为//EF SCD 平面,所以'EE 即为F 到平面SCD 的距离.在△ABD 中,设AB 边上的高为h ,则h =,因为23ED EC BD AC ==,所以2'3EE h ==,即F 到平面SCD(12分)21.【解析】(1)依题意,直线l :28y x =+,联立22,28,x y y x ⎧=⎨=+⎩故24160x x --=,设11(,)M x y ,22(,)N x y ,则124x x +=,1216x x =-,故1220MN x =-==;(5分)(2)联立0,40,x y x y -=⎧⎨+-=⎩解得2x y ==,故()2,2A ,设直线l 的方程为:4(2)y k x -=+,11(,)M x y ,22(,)N x y , 则11112(2)222AM y k x k x x -++==--,22222(2)222AN y k x k x x -++==--, 212121212121212[(2)2][(2)2][2()4]2(4)4(2)(2)2()4AM ANk x k x k x x x x k x x k k x x x x x x +++++++++++==---++, 联立抛物线22x y =与直线4(2)y k x -=+的方程消去y 得22480x kx k ---=,可得122x x k +=,1248x x k =--,代入AM AN k k ⋅可得1AM AN k k ⋅=-.(12分)22.【解析】(1)依题意,()0,x ∈+∞,()221'222x mx f x x m x x++=++=⋅,若22m -≤≤,则210x mx ++≥,故()'0f x ≥,故函数()f x 在()0,+∞上单调递增;当22m m <->或时,令210x mx ++=,解得12xx ; 若2m >0<0<,故函数()f x 在()0,+∞上单调递增; 若2m <-,则当x ⎛∈⎝⎭时,()'0f x >,当x ∈⎝⎭时,()'0f x <,经典资料经典资料(一)当x ⎫∈+∞⎪⎝⎭时,()'0f x >; 综上所述;当2m ≥-时,函数()f x 在()0,+∞上单调递增;当2m <-时,函数()f x在⎛ ⎝⎭和⎫+∞⎪⎝⎭上单调递增,在⎝⎭上单调递减;(6分) (2)题中不等式等价于2222ln 2e 3x x mx x x ++≤+,即2e ln x x x mx -+≥, 因此2e ln x x x m x -+≥,设()2e ln x x x h x x-+=,∴ ()'10h =,当)1,0(∈x 时,()2e 1ln 10x x x x -++-<,即0)('<x h ,)(x h 单调递减; 当),1(+∞∈x 时,()2e 1ln 10x x x x -++->,即0)('>x h ,)(x h 单调递增; 因此1=x 为)(x h 的极小值点,即1)1()(+=≥e h x h ,故e 1m ≤+, 故实数m 的取值范围为(],e 1-∞+.(12分)。
2019届秋季上学期高二语文8月月考试题(含解析) (842)

第一节统计1.[2014河南,5]涉及考点:调查方式、事件的概率下列说法中,正确的是( )A.“打开电视,正在播放河南新闻节目”是必然事件B.某种彩票中奖概率为10%是指买十张一定有一张中奖C.神舟飞船发射前需要对零部件进行抽样检查D.了解某种节能灯的使用寿命适合抽样调查2.[2009河南,3]涉及考点:调查方式下列调查适合普查的是( )A.调查2009年6月份市场上某品牌饮料的质量B.了解中央电视台直播北京奥运会开幕式的全国收视率情况C.环保部门调查5月份黄河某段水域的水质情况D.了解全班同学本周末参加社区活动的时间3.[2018河南,5]涉及考点:中位数、众数、平均数、方差河南省旅游资源丰富,2013~2017年旅游收入不断增长,同比增速分别为15.3%,12.7%,15.3%,14.5%,17.1%.关于这组数据,下列说法正确的是( )A.中位数是12.7%B.众数是15.3%C.平均数是15.98%D.方差是04.[2017河南,5]涉及考点:众数、中位数八年级某同学6次数学小测验的成绩分别为80分,85分,95分,95分,95分,100分,则该同学这6次成绩的众数和中位数分别是( )A.95分,95分B.95分,90分C.90分,95分D.95分,85分5.[2016河南,7]涉及考点:平均数、方差:根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )A.甲B.乙C.丙D.丁6.[2015河南,6]涉及考点:加权平均数小王参加某企业的招聘测试,他的笔试、面试、技能操作得分分别为85分,80分,90分,若依次按照2∶3∶5的比例确定成绩,则小王的成绩是( )A.255分B.84分C.84.5分D.86分7.[2013河南,4]涉及考点:中位数在一次体育测试中,小芳所在小组8人的成绩(单位:分)分别是46,47,48,48,49,49,49,50,则这8人体育成绩的中位数是( )A.47B.48C.48.5D.498.[2012河南,4]涉及考点:中位数、众数、极差、平均数某校九年级8位同学一分钟跳绳的次数排序后如下:150,164,168,168,172,176,183,185.则由这组数据得到的结论中错误的是 ( )A.中位数为170B.众数为168C.极差为35D.平均数为1709.[2011河南,5]涉及考点:平均数、方差某农科所对甲、乙两种小麦各选用10块面积相同的试验田进行种植试验,它们的平均亩产量分别是=610千克,=608千克,亩产量的方差分别是=29.6,=2.7,则关于两种小麦推广种植的合理决策是( )A.甲的平均亩产量较高,应推广甲B.甲、乙的平均亩产量相差不多,均可推广C.甲的平均亩产量较高,且亩产量比较稳定,应推广甲D.甲、乙的平均亩产量相差不多,但乙的亩产量比较稳定,应推广乙10.[2010河南,3]涉及考点:众数、极差在某次体育测试中,九年级(3)班6位同学的立定跳远成绩(单位:m)分别为1.71,1.85,1.85,1.96,2.10,2.31,则这组数据的众数和极差分别为( )A.1.85和0.21B.2.31和0.46C.1.85和0.60D.2.31和0.6011.[2018河南,17]涉及考点:扇形统计图、条形统计图每到春夏交替时节,雌性杨树会以满天飞絮的方式来传播下一代,漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等,给人们造成困扰.为了解市民对治理杨絮方法的赞同情况,某课题小组随机调查了部分市民(问卷调查的内容如图(1)所示),并根据调查结果绘制了如图(2)所示的图(1)图(2)根据以上统计图,解答下列问题:(1)本次接受调查的市民共有人;(2)扇形统计图中,E所在扇形的圆心角度数是;(3)请补全条形统计图;(4)若该市约有90万人,请估计赞同“选育无絮杨品种,并推广种植”的人数.12.[2017河南,17]涉及考点:统计表、扇形统计图为了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下尚不完整的统计图表.调查结果统计表调查结果扇形统计图请根据以上图表,解答下列问题:(1)填空:这次被调查的同学共有人,a+b= ,m= ;(2)求扇形统计图中扇形C的圆心角度数;(3)该校共有学生1 000人,请估计每月零花钱的数额x在60≤x<120范围的人数.13.[2016河南,17]涉及考点:频数分布表、频数分布直方图在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:5 6406 430 6 520 6 7987 3258 430 8 215 7 453 7 446 6 7547 638 6 834 7 326 6 830 8 6488 753 9 450 9 865 7 290 7 850对这20个数据按组距1 000进行分组,并统计整理,绘制了如下尚不完整的统计图表:频数分布直方图请根据以上信息解答下列问题:(1)填空:m= ,n= ;(2)补全频数分布直方图;(3)这20名“健步走运动”团队成员一天行走步数的中位数落在组;(4)若该团队共有120人,请估计其中一天行走步数不少于7 500步的人数.14.[2015河南,18]涉及考点:扇形统计图、条形统计图为了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图.根据以上信息解答下列问题:(1)这次接受调查的市民总人数是;(2)扇形统计图中,“电视”所对应的圆心角的度数是;(3)请补全条形统计图;(4)若该市约有80万人,请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.15.[2014河南,18]涉及考点:扇形统计图、条形统计图某兴趣小组为了解本校男生参加课外体育锻炼的情况,随机抽取本校300名男生进行了问卷调查,统计整理并绘制了如下两幅尚不完整的统计图.请根据以上信息解答下列问题:(1)课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为;(2)请补全条形统计图;(3)该校共有1 200名男生,请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数;(4)小明认为“全校所有男生中,课外最喜欢参加的运动项目是乒乓球的人数约为 1 200×=108.”请你判断这种说法是否正确,并说明理由.16.[2012河南,17]涉及考点:条形统计图、扇形统计图5月31日是世界无烟日.某市卫生机构为了解“导致吸烟人口比例高的最主要原因”,随机抽样调查了该市部分18~65岁的市民.下图是根据调查结果绘制的统计图,根据图中信息解答下列问题:图(1) 图(2)(1)这次接受随机抽样调查的市民总人数为;(2)图(1)中m的值是;(3)求图(2)中认为“烟民戒烟的毅力弱”所对应扇形的圆心角的度数;(4)若该市18~65岁的市民约有200万人,请你估算其中认为导致吸烟人口比例高的最主要原因是“对吸烟危害健康认识不足”的人数.17.[2009河南,18]涉及考点:频数分布表、扇形统计图2008年北京奥运会后,同学们参与体育锻炼的热情高涨.为了解他们平均每周的锻炼时间情况,小明同学在校内随机调查了.根据上述信息解答下列问题:(1)m= ,n= ;(2)在扇形统计图中,D组所对应圆心角的度数是;(3)全校共有3 000名学生,该校平均每周体育锻炼时间不少于6小时的学生约有多少名?第二节概率1.[2018河南,8]现有4张卡片,其中3张卡片正面上的图案是“ ,1张卡片正面上的图案是“♣”,它们除此之外完全相同.把这4张卡片背面朝上洗匀,从中随机抽取2张,则这2张卡片正面上的图案相同的概率是( )A. B. C. D.2.[2017河南,8]如图是一次数学活动课制作的一个转盘,盘面被等分成四个扇形区域,并分别标有数字-1,0,1,2.若转动转盘两次,每次转盘停止后记录指针所指区域的数字(当指针恰好指在分界线上时,不记,重转),则记录的两个数字都是正数的概率为( )A. B. C. D.3.[2016河南,12]在“阳光体育”活动时间,班主任将全班同学随机分成了4组进行活动,该班小明和小亮同学被分在同一组的概率是.4.[2015河南,13]现有四张分别标有数字1,2,2,3的卡片,它们除数字外完全相同.把卡片背面朝上洗匀,从中随机抽出一张后放回,再背面朝上洗匀,从中随机抽出一张,则两次抽出的卡片所标数字不同的概率是.5.[2014河南,13]一个不透明的袋子中装有仅颜色不同的2个红球和 2个白球.两个人依次从袋子中随机摸出一个小球不放回,则第一个人摸到红球且第二个人摸到白球的概率是.6.[2013河南,13]现有四张完全相同的卡片,上面分别标有数字-1,-2,3,4.把卡片背面朝上洗匀,然后从中随机抽取两张,则这两张卡片上的数字之积为负数的概率是.7.[2012河南,12]一个不透明的袋子中装有三个小球,它们除分别标有的数字1,3,5不同外,其他完全相同.任意从袋子中摸出一球后放回,再任意摸出一球,则两次摸出的球所标数字之和为6的概率是.8.[2011河南,12]现有两个不透明的袋子,其中一个装有标号分别为1,2的两个小球,另一个装有标号分别为2,3,4的三个小球,小球除标号外其他均相同.从两个袋子中各随机摸出1个小球,两球标号恰好相同的概率是.9.[2010河南,12]现有点数为2,3,4,5的四张扑克牌,背面朝上洗匀,然后从中任意抽取两张,这两张牌上的数字之和为偶数的概率是.10.[2009河南,13]在一个不透明的袋子中有2个黑球、3个白球,它们除颜色外,其他均相同,充分摇匀后,先摸出1个球不放回,再摸出1个球,那么两个球都是黑球的概率为.11.[2013河南,17]从2013年1月7日起,中国中东部大部分地区持续出现雾霾天气.某市记者为了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制请根据图表中提供的信息解答下列问题:(1)填空:m= ,n= ,扇形统计图中E组所占的百分比为%;(2)若该市人口约有100万人,请你估计其中持D组“观点”的市民人数;(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?12.[2011河南,18]为更好地宣传“开车不喝酒,喝酒不开车”的驾车理念,某市一家报社设计了如下的调查问卷(单选).在随机调查了本市全部5 000名司机中的部分司机后,统计整理并制成了如下的统计图:根据以上信息解答下列问题:(1)补全条形统计图,并计算扇形统计图中m= ;(2)该市支持选项B的司机大约有多少名?(3)若要从该市支持选项B的司机中随机选择100名,给他们发放“请勿酒驾”的提醒标志,则支持该选项的司机小李被选中的概率是多少?13.[2010河南,18]“校园手机”现象越来越受到社会的关注.“五一”期间,小记者刘凯随机调查了城区若干名学生和家长对中学生带手机现象的看法,统计整理并制成了如下的统计图:图(1)图(2)(1)求这次调查的家长人数,并补全图(1);(2)求图(2)中表示家长“赞成”的圆心角的度数;(3)从这次接受调查的学生中,随机抽查一个,恰好是持“无所谓”态度的学生的概率是多少?参考答案第一节统计1.D 打开电视,正在播放河南新闻节目可能发生,也可能不发生,是随机事件,故A中的说法不正确;某种彩票中奖概率为10%,但买十张不一定中奖,故B中的说法不正确;为了保证神舟飞船发射成功,发射前需要对零部件进行全面检查,故C中的说法不正确;由于检查节能灯的使用寿命具有破坏性,因此不适合全面检查,应采用抽样调查,故D中的说法正确.2.D 选项A中,因市场上该品牌饮料的数量比较多,普查工作量大,且带有破坏性,所以不宜普查,宜抽样调查;选项B,C中的事件在普查时工作量都非常大,易造成资源的浪费,都不适合普查,适合抽样调查;选项D中,因一个班级中人数较少且集中,适合普查.3.B 把这组数据按从小到大的顺序排列为12.7%,14.5%,15.3%,15.3%,17.1%,故中位数是15.3%;数据15.3%出现了2次,出现的次数最多,故众数是15.3%;这组数据的平均数为=14.98%;易得这组数据的方差不为0.故选B.4.A 由题意可得,95分出现了3次,出现的次数最多,所以这组数据的众数是95分;这组数据是按从小到大的顺序排列的,中间的两个数据都是95分,所以这组数据的中位数是95分.故选A.5.A 由题中表格可以看出,成绩较好的是甲与丙.因为甲成绩的方差比丙成绩的方差小,所以甲的成绩较好且比较稳定,所以应当选择甲.故选A.6.D 根据加权平均数的定义,可得小王的成绩为85×20%+80×30%+90×50%=86(分).7.C 在这8个数据中,最中间的2个数据是48和49,它们的平均数48.5即是这组数据的中位数.8.D 这组数据的平均数为(150+164+168+168+172+176+183+185)÷8=170.75,故D选项中的结论错误.9.D 当两组数据的平均数相差不大或相等时,我们一般都是从反映数据离散程度的量——方差或极差来分析问题,方差或极差越小,数据越稳定.10.C这组数据中,1.85出现了2次,出现的次数最多,故众数为 1.85;极差为2.31-1.71=0.60.11~17.略第二节概率1.D 设正面上的图案是“ 的3张卡片分别为A1,A2,A3,正面上的图案是“♣”的1张卡片为B,则抽取的2张卡片的所有等可能的情况为(A1,A2),(A1,A3),(A1,B),(A2,A3),(A2,B),(A3,B),共6种,其中卡片正面上的图案相同的情况为(A1,A2),(A1,A3),(A2,A3),有3种,故所求概率为=.2.C 由题意列表如下由上表可得,一共有16种等可能的结果,其中两个数字都是正数的结果有4种,故所求概率为=,故选C.3.由题意画树状图如图,由树状图可以看出,一共有16种等可能的情况,其中两人被分到同一组的情况有4种,故所求概率是=.4.根据题意列表如下:根据上表可知,共有16种等可能的结果,其中两次抽出的卡片所标数字不同的结果有10种,故所求概率是=.5. 根据题意列表如下:由上表可知,共有12种等可能的结果,其中第一个人摸到红球且第二个人摸到白球的结果有4种,故所求概率为=.6.由题意得,所有等可能的结果为(-1,-2),(-1,3),(-1,4),(-2,3),(-2,4),(3,4),共6种,其中两张卡片上的数字之积为负数的结果有4种,故所求概率为=.7.由题意列表如下:由上表可知,共有9种等可能的结果,其中数字之和为6的有3种,故所求概率为=.8.由题意可知,摸出的两球标号共有(1,2),(1,3),(1,4),(2,2),(2,3),(2,4)6种等可能的结果,其中两球标号恰好相同的结果有1种,故所求概率为.9.由题意得,任意抽取两张,这两张牌上的数字所有等可能的结果为(2,3),(2,4),(2,5),(3,4),(3,5),(4,5),共6种,其中两张牌上的数字之和为偶数的结果有2种,故所求概率为=.10.由题意画树状图如下:由上图可知,一共有20种等可能的结果,其中摸出的两个球都是黑球的结果有2种,故所求概率为=.11.(1)40 100 15(2)80÷20%=400(人),100×=30(万人).答:持D组“观点”的市民人数约为30万人.(3)持C组“观点”的概率为=.12.(1)C选项的频数为90,补全条形统计图略.20(2)5 000×23%=1 150(名).故该市支持选项B的司机大约有1 150名.(3)司机小李被选中的概率是=.13.(1)家长人数为80÷20%=400(人).补全题图(1)略.(2)表示家长“赞成”的圆心角的度数为×360°=36°.(3)学生恰好持“无所谓”态度的概率是=0.15.。
2019届秋季上学期高二语文8月月考试题(含解析) (476)

河南省周口市淮阳县第一高级中学2018-2019学年高二上学期理数月考试卷一、选择题(本大题共12小题,每小题5分,共60分,每小题只有一个选项符合题意) 1.曲线2122y x x =-在点3(1,)2-处的切线的倾斜角为( ) A .135-︒ B .45︒C .45-︒D .135︒2.下列求导运算正确的是( ) A .(cos )sin x x '= B .1(ln 2)x x'=C .3(3)3log x xe '= D .2()2x x x e xe '=3.若函数2()f x ax bx c =++的图象的顶点在第四象限且开口向上,则函数()f x '的图象是( )4.函数3()1f x ax x =++有极值的充要条件是( ) A .0a >B .0a ≥C .0a <D .0a ≤5.已知函数3()f x x =,则()f x 与y x =围成的封闭图形的面积为( )A .13B .14C .12D .16.设(),()f x g x 分别是定义在R 上的奇函数和偶函数,当0x <时,()()f x g x '+()()f x g x '0>,且(3)0g -=,则不等式()()0f x g x <的解集是( )A .(3,0)(3,)-+∞B .(3,0)(0,3)-C .(,3)(3,)-∞-+∞D .(,3)(0,3)-∞-7.已知32()(6)1f x x ax a x =++++有极大值和极小值,则a 的取值范围为( ) A . (1,2)- B .(3,6)-C .(,1)(2,)-∞-+∞D .(,3)(6,)-∞-+∞8.若sin 0bxdx =⎰,则cos()a b +=( )A .0B .12C .1D .以上均不对9.设函数()f x 的导函数为()f x ',且2()2(1)f x x xf '=+,则(0)f '=( ) A .0B .4-C .2-D .210.已知,(0,)a b e ∈,且a b <,则下列式子中正确的是( ) A .ln ln a b b a <B .ln ln a b b a >C .ln ln a a b b >D .ln ln a a b b <11.若函数2()2ln f x x x =-在其定义域内的一个子区间(1,1)k k -+内不是单调函数,则实数k 的取值范围是( ) A .[1,)+∞B .31,2⎡⎫⎪⎢⎣⎭C .[)1,2D .3,22⎡⎫⎪⎢⎣⎭12.已知函数1()ln ln f x x x=+,则下列结论正确的是( ) A .若1212,()x x x x <是()f x 的极值点,则()f x 在区间12(,)x x 内是增函数 B .若1212,()x x x x <是()f x 的极值点,则()f x 在区间12(,)x x 内是减函数 C .0x ∀>,且1,()2x f x ≠≥ D .00,()x f x ∃>在0(,)x +∞上是增函数二、填空题(本大题共4小题,每小题5分,共20分,把答案填在题中横线上) 13.已知函数1()sin ,(0,)2f x x x x π=-∈,则()f x 的最小值为 . 14.1(1ln )ex dx +=⎰.15.已知函数()xf x xe c =+有两个零点,则c 的取值范围是 .16.已知函数2()1(0),()43,xf x e x xg x x x =--≥=-+-若有()()f a g b =,则b 的最大值为 .三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤) 17.(10分)已知函数()ln x mf x x e +=-在1x =处有极值,求m 的值及()f x 的单调区间.18.(12分)设函数3()(0)f x ax bx c a =++≠为奇函数,其图象在点(1,(1))f 处的切线与直线670x y --=垂直,导函数()f x '的最小值为12-(1)求,,a b c 的值;(2)求函数()f x 的单调递增区间,并求函数()f x 在[1,3]-上的最大值和最小值。
2019届秋季上学期高二语文8月月考试题(含解析) (819)
第一节实数考点1 实数的分类1.[2018贵州遵义]如果电梯上升5层记为+5,那么电梯下降2层应记为( )A.+2B.-2C.+5D.-52.[2018南阳地区模拟]一种面粉包装袋上的质量标识为“25±0.20千克”,下列各袋面粉中质量合格的是( )A.25.30千克B.24.70千克C.25.51千克D.24.82千克3.[2018辽宁沈阳]下列各数中是有理数的是( )A.πB.0C.D.4.[2018驻马店一模]下列各数中:,-,,-π,,-0.101 001 000 1,无理数有( )A.2个B.3个C.4个D.5个考点2 实数的相关概念5.[2017三门峡一模]的倒数是( )A.-B.C.D.6.[2018四川眉山]绝对值为1的实数共有( )A.0个B.1个C.2个D.4个7.[2017商丘地区模拟]下列各组数中,互为相反数的是( )A.和-B.|5|和|-5|C.2和D.42和(-4)28.[2018贵州贵阳]如图,数轴上有三个点A,B,C,若点A,B表示的数互为相反数,则图中点C 对应的数是( )A.-2B.0C.1D.49.[2018江苏南京]写出一个数,使这个数的绝对值等于它的相反数: .考点3 科学记数法10.[2019原创]据对全国规模以上文化及相关产业5.9万家企业调查,2018年上半年,上述企业实现营业收入42 227亿元,比上年同期增长9.9%,继续保持较快增长.其中42 227亿用科学记数法可表示为( )A.42 227×108B.42.227×1011C.4.222 7×1012D.0.422 27×101311.[2018广西桂林]2018年5月3日,中国科学院在上海发布了中国首款人工智能芯片:寒武纪(MLU100),该芯片在平衡模式下的等效理论峰值速度达每秒128 000 000 000 000次定点运算,将数128 000 000 000 000用科学记数法表示为( )A.1.28×1014B.1.28×10-14C.128×1012D.0.128×101112.[2018河北]若一个整数用科学记数法表示为8.155 5×1010,则原数中“0”的个数为( )A.4B.6C.7D.1013.[2018湖南张家界]目前世界上能制造的芯片最小工艺水平是5 nm,而我国能制造芯片的最小工艺水平是16 nm,已知1 nm=10-9 m,用科学记数法将16 nm表示为m.考点4 实数的大小比较14.[2018四川南充]下列实数中, 最小的数是( )A.-B.0C.1D.15.[2018南阳一模]下列各数的相反数中,比1大的是( )A.-B.0C.-1D.416.[2018北京]实数a,b,c在数轴上的对应点的位置如图所示,则正确的结论是( )A.|a|>4B.c-b>0C.ac>0D.a+c>017.[2018海南]比较实数的大小: 3 (填“>”、“<”或“=”).考点5 平方根、算术平方根、立方根18.[2018南阳地区模拟](-3)-2的平方根是( )A.±B.±C.D.±319.[2018郑州外国语模拟]的算术平方根为( )A.9B.±9C.3D.±320.[2019原创]计算:= .21.[2018广东]已知+|b-1|=0,则a+1= .考点6 实数的运算22.[2018南阳地区模拟]计算2-(-3)×4的结果是.23.[2018洛阳二模]计算:-(-2)3= .24.[2018南阳一模]计算:(π-3)0+(-)-1= .25.[2018开封二模]计算:sin 45°-(-2)0= .26.[2018平顶山二模]-|-1|= .27.[2018湖南湘西州]按照如图所示的操作步骤,若输入x的值为2,则输出的值是.(用科学计算器计算或笔算)第二节整式考点1 列代数式及求值1.[2018山东枣庄]如图,将边长为3a的正方形沿虚线剪成两块正方形和两块长方形.若拿掉边长为2b的小正方形后,再将剩下的三块拼成一块矩形,则这块矩形较长的边长为( )A.3a+2bB.3a+4bC.6a+2bD.6a+4b2.[2018安徽]据省统计局发布,2017年我省有效发明专利数比2016年增长22.1%.假定2018年的年增长率保持不变,2016年和2018年我省有效发明专利分别为a万件和b万件,则( )A.b=(1+22.1%×2)aB.b=(1+22.1%)2aC.b=(1+22.1%)×2aD.b=22.1%×2a3.[2018重庆A卷]按如图所示的运算程序,能使输出的结果为12的是( )A.x=3,y=3B.x=-4,y=-2C.x=2,y=4D.x=4,y=24.[2017洛阳地区模拟]已知a+b=1,则代数式5-2a-2b的值是.5.[2017江苏镇江]已知实数m满足m2-3m+1=0,则代数式m2+的值等于.考点2 整式的运算及化简求值6.[2018浙江金华]计算(-a)3÷a结果正确的是( )A.a2B.-a2C.-a3D.-a47.[2018新疆]下列计算正确的是( )A.a2·a3=a6B.(a+b)(a-2b)=a2-2b2C.(ab3)2=a2b6D.5a-2a=38.[2018山东临沂]已知m+n=mn,则(m-1)(n-1)= .9.[2018四川达州]已知a m=3,a n=2,则a2m-n的值为.10.[2018南阳卧龙区模拟]若x2+2(m-3)x+16是关于x的完全平方式,则m= .11.(8分)[2018信阳七中模拟]某同学化简a(a+2b)-(a+b)(a-b)时出现了错误,解答过程如下:原式=a2+2ab-(a2-b2) (第一步)=a2+2ab-a2-b2(第二步)=2ab-b2. (第三步)(1)该同学解答过程从第步开始出错,错误原因是;(2)写出此题正确的解答过程.12.(8分)[2018湖北襄阳]先化简,再求值:(x+y)(x-y)+y(x+2y)-(x-y)2,其中x=2+,y=2-.13.(8分)[2019原创]先化简,再求值:-a2b+(3ab2-a2b)-2(2ab2-a2b),其中 a=-1,b=-2.14.(8分)[2018四川乐山]先化简,再求值:(2m+1)(2m-1)-(m-1)2+(2m)3÷(-8m),其中m是方程x2+x-2=0的根.考点3 因式分解15.[2017安阳一模]多项式m2-m与2m2-4m+2的公因式是( )A.m-1B.m+1C.m2-1D.(m-1)216.[2018安徽]下列分解因式正确的是( )A.-x2+4x=-x(x+4)B.x2+xy+x=x(x+y)C.x(x-y)+y(y-x)=(x-y)2D.x2-4x+4=(x+2)(x-2)17.[2018山东潍坊]因式分解:(x+2)x-x-2= .18.[2018三门峡二模]因式分解:9a3b-ab= .19.[2018山东威海]分解因式:-a2+2a-2= .20.(8分)[2018浙江衢州]有一张边长为a厘米的正方形桌面,因为实际需要,需将正方形边长增加b厘米,木工师傅设计了如图所示的三种方案:小明发现这三种方案都能验证公式:a2+2ab+b2=(a+b)2,对于方案一,小明是这样验证的:a2+ab+ab+b2=a2+2ab+b2=(a+b)2.请你根据方案二、方案三,写出公式的验证过程.方案二:方案三:考点4 数字、图形规律探索题21.[2018重庆B卷]第①个图中有3张黑色正方形纸片,第②个图中有5张黑色正方形纸片,第③个图中有7张黑色正方形纸片……按此规律排列下去,第⑥个图中黑色正方形纸片的张数为( )A.11B.13C.15D.1722.[2018广西梧州]按一定规律排列的一列数依次为:2,3,10,15,26,35,…,按此规律排列下去,则这列数中的第100个数是( )A.9 999B.10 000C.10 001D.10 00223.[2018内蒙古赤峰]观察下列一组由★排列的“星阵”,按图中规律,第(n)个“星阵”中★的个数是.24.(9分)[2017云南]观察下列各个等式的规律.第1个等式:=1,第2个等式:=2,第3个等式:=3,…请用上述等式反映出的规律解决下列问题:(1)直接写出第4个等式;(2)猜想第n个等式(用含n的代数式表示,n为正整数),并证明你猜想的等式是正确的.第三节分式考点1 分式的有关概念和性质1.[2018南阳卧龙区模拟]使分式有意义的x的取值范围为( )A.x>-3B.x≠3C.x≠-3D.x<32.[2018辽宁葫芦岛]若分式的值为0,则x的值为( )A.0B.1C.-1D.±13.[2018山东莱芜]若x,y的值均扩大为原来的3倍,则下列分式的值保持不变的是( )A. B.C. D.考点2 分式的化简及求值4.[2018山东淄博]化简-的结果为( )A. B.a-1C.aD.15.[2018云南]已知x+=6,则x2+=( )A.38B.36C.34D.326.[2018四川南充]已知-=3,则代数式的值是( )A.-B.-C. D.7.[2018河北]老师设计了接力游戏,用合作的方式完成分式化简.规则:每人只能看到前一人给的式子,并进行一步计算,再将结果传递给下一人,最后完成化简.过程如图所示:÷···接力中,自己负责的一步出现错误的是( )A.只有乙B.甲和丁C.乙和丙D.乙和丁8.[2018洛阳一模]计算:+= .9.[2018黑龙江大庆]已知=+,则实数A= .10.(8分)[2018山西]计算:·-.11.(8分)[2018新乡地区模拟]小林化简(-)÷后说:“在原分式有意义的前提下,分式的值一定是正数.”你同意小林的说法吗?请说明理由.12.(8分)[2018辽宁葫芦岛]先化简,再求值:(-)÷,其中a=3-1+2sin 30°.13.(8分)[2018平顶山二模]先化简,再求值:(-)÷,其中a=+1,b=-1.14.(8分)[2018安阳二模]先化简÷(-x+2),再从-<x<的范围内选取一个合适的整数作为x的值代入求值.15.(8分)[2018信阳二模]先化简,再求值:÷(m+2-),其中m是方程x2+2x-3=0的根.16.(8分)[2016河南B卷]先化简,再求值:÷(x-),其中x的值从不等式组的整数解中选取.17.(8分)[2018郑州二模]已知关于x的方程x2-2ax+a=0有两个相等的实数根,请先化简代数式(-)÷,再求出该代数式的值.第四节二次根式考点1 二次根式的有关概念和性质1.[2019原创]代数式+中x的取值范围在数轴上表示为( )2.[2018云南曲靖]下列二次根式中能与2合并的是( )A. B. C. D.3.[2018广西柳州柳北区三模]下列根式中,不是最简二次根式的是( )A. B. C. D.4.[2018四川巴中]已知|sin A-|+=0,那么∠A+∠B=.考点2 二次根式的运算5.[2018四川绵阳]等式=成立的x的取值范围在数轴上可表示为( )A B C D6.[2018江苏泰州]下列运算正确的是( )A.+=B.=2C.×=D.÷=27.[2018商丘地区模拟]下列计算错误的是( )A.=B.×=3C.-=D.=-28.[2018南阳地区模拟]计算(-2)÷(-)的结果为.9.(6分)[2018郑州高新区模拟]计算:(-1)2++()-1.10.(8分)[2018四川南充]计算:-(1-)0+sin 45°+()-1.考点3 二次根式的估值11.[2018山东潍坊]|1-|=( )A.1-B.-1C.1+D.-1-12.[2018山东淄博]与最接近的整数是( )A.5B.6C.7D.813.[2018江苏南通]如图,数轴上的点A,B,O,C,D分别表示数-2,-1,0,1,2,则表示数2-的点P应落在( )A.线段AB上B.线段BO上C.线段OC上D.线段CD上考点4 二次根式的应用14.[2018山东枣庄]我国南宋著名数学家秦九韶在他的著作《数书九章》一书中,给出了著名的秦九韶公式,也叫三斜求积公式,即如果一个三角形的三边长分别为a,b,c,那么该三角形的面积S=.现已知△ABC的三边长分别为1,2,,则△ABC的面积为.15.[2018山东莱芜]如图,正三角形和矩形具有一条公共边,矩形内有一个正方形,其四个顶点都在矩形的边上,正三角形和正方形的面积分别是2和2,则图中阴影部分的面积是.参考答案第一节实数1.B2.D 设一袋合格面粉的质量为a千克,则25-0.20≤a≤25+0.20,即24.80≤a≤25.20.故选D.3.B4.B ,-,-π是无理数,,,-0.101 001 000 1是有理数,故选B.5.C 因×=1,故的倒数是,故选C.6.C 在数轴上表示一个数的点到原点的距离叫做这个数的绝对值,在原点两侧各有一个点到原点的距离为1,故选C.7.A 只有符号不同的两个数互为相反数.故选A.8.C 因为点A,B表示的数互为相反数,所以原点在线段AB的中点处,所以点C对应的数是1,故选C.9.-1(答案不唯一) 所有非正数的绝对值均等于它的相反数.10.C 42 227亿=42 227×108=4.222 7×1012,故选C.11.A 128 000 000 000 000=1.28×1014.故选A.12.B 8.155 5×1010=81 555 000 000,故原数中有6个“0”.13.1.6×10-8因为1 nm=10-9 m,所以16 nm=16×10-9m=1.6×10-8 m.14.A 负数小于0和一切正数,故选A.15.A -,0,-1,4的相反数分别是,0,1,-4,且-4<0<1<,故选A.16.B∵-4<a<-3,∴3<|a|<4;∵b<0,c>0,∴c-b>0;∵a<0,c>0,∴ac<0;∵a<-3,2<c<3,∴a+c<0.故选B.17.> 3=>.18.A (-3)-2==,故(-3)-2的平方根是±.故选A.19.C ∵=9,=3,∴的算术平方根为3.故选C.20.-621.2 根据算术平方根和绝对值的非负性可得解得故a+1=2.22.14 原式=2-(-12)=2+12=14.23.11 原式=3-(-8)=11.24.-2 原式=1+(-3)=-2.25.0 原式=×-1=1-1=0.26.2 原式=3-1=2.27.2 将x=2输入,得22×3-10=12-10=2.第二节整式1.A2.B 由题意可知,2017年我省有效发明专利为(1+22.1%)a万件,因为2018年我省有效发明专利数比2017年增长22.1%,所以2018年我省有效发明专利为(1+22.1%)2a万件,即b=(1+22.1%)2a,故选B.3.C A选项中,输出结果为15;B选项中,输出结果为20;C选项中,输出结果为12;D选项中,输出结果为20.故选C.4.3 ∵a+b=1,∴原式=5-2(a+b)=5-2=3.5.9∵m2-3m+1=0,∴m2=3m-1,∴m2+=3m-1+=3m-1+=====9.6.B (-a)3÷a=(-1)3·a3÷a=-a3÷a=-a3-1=-a2,故选B.7.C a2·a3=a2+3=a5,故A项中的计算错误;(a+b)(a-2b)=a2-2ab+ab-2b2=a2-ab-2b2,故B项中的计算错误;(ab3)2=a2(b3)2=a2b6,故C项中的计算正确;5a-2a=(5-2)a=3a,故D项中的计算错误.故选C.8.1 ∵m+n=mn,∴(m-1)(n-1)=mn-m-n+1=mn-(m+n)+1=mn-mn+1=1.9.∵a m=3,a n=2,∴a2m-n=(a m)2÷a n=32÷2=.10.-1或7 ∵x2+2(m-3)x+16是关于x的完全平方式,∴2(m-3)=±8,解得m=-1或7.11.(1)二去括号时没有变号 (4分)(2)原式=a2+2ab-(a2-b2)=a2+2ab-a2+b2=2ab+b2.(8分)12.原式=x2-y2+xy+2y2-(x2-2xy+y2)=3xy.(5分)∵x=2+,y=2-,∴原式=3×(2+)(2-)=3.(8分)13.原式=-a2b+3ab2-a2b-4ab2+2a2b=-ab2,(5分)∵a=-1,b=-2,∴原式=-(-1)×(-2)2=1×4=4.(8分)14.原式=4m2-1-(m2-2m+1)+8m3÷(-8m)=4m2-1-m2+2m-1-m2=2m2+2m-2=2(m2+m-1),(5分)∵m是方程x2+x-2=0的根,∴m2+m-2=0,即m2+m=2,故原式=2×(2-1)=2.(8分)15.A m2-m=m(m-1),2m2-4m+2=2(m-1)2,故多项式m2-m与2m2-4m+2的公因式是m-1,故选A.16.C-x2+4x=-x(x-4);x2+xy+x=x(x+y+1);x(x-y)+y(y-x)=x(x-y)-y(x-y)=(x-y)2;x2-4x+4=(x-2)2.故选C.17.(x+2)(x-1) (x+2)x-x-2=(x+2)x-(x+2)=(x+2)(x-1).18.ab(3a+1)(3a-1) 原式=ab(9a2-1)=ab(3a+1)(3a-1).19.-(a-2)2原式=-(a2-4a+4)=-(a-2)2.20.方案二:a2+ab+(a+b)b=a2+ab+ab+b2=a2+2ab+b2=(a+b)2.(4分)方案三:a2++=a2+ab+b2+ab+b2=a2+2ab+b2=(a+b)2.(8分)21.B 观察图形可知,第①个图中正方形纸片的张数为3,第②个图中正方形纸片的张数为3+2×1=5,第③个图中正方形纸片的张数为3+2×2=7……第⑥个图中正方形纸片的张数为3+2×5=13,故选B.22.A 分析题意可知,2=12+1,3=22-1,10=32+1,15=42-1,26=52+1,35=62-1,…,∴第100个数是1002-1=9 999,故选A.23.n2+n+2 第(1)个“星阵”中★的个数是2+1×2=4,第(2)个“星阵”中★的个数是2+2×3=8,第(3)个“星阵”中★的个数是2+3×4=14,第(4)个“星阵”中★的个数是2+4×5=22……故第(n)个“星阵”中★的个数是2+n×(n+1)=n2+n+2.24.(1)第4个等式是=4.(2分)(2)第n个等式是=n.(4分)证明:====n.(9分)第三节分式1.B 根据题意,得3-x≠0,即x≠3.故选B.2.B 因为分式的值为0,所以解得x=1.故选B.3.D 根据分式的基本性质,可知若x,y的值均扩大为原来的3倍,则A中,≠;B中,≠;C中,≠;D中,=.故选D.4.B 原式=+==a-1,故选B.5.C 把x+=6的两边同时平方,得(x+)2=x2++2=36,则x2+=34,故选C.6.D ∵-=3,∴=3,∴x-y=-3xy,∴====.故选D.7.D ÷=·=·,故甲负责的一步没有出现错误,乙负责的一步出现错误.·=·=,故丙负责的一步没有出现错误,丁负责的一步出现错误.8.0 原式=-=-=0.9.1+=+=.∵=+,∴解得10.原式=·-(3分)=-(5分)=.(8分)11.同意小林的说法.理由:原式=[-]·=·=·=.(6分)∵原分式有意义,即a≠0,a≠2且a≠4,∴>0,故小林的说法是正确的.(8分)12.原式=[-]·=(-)·=·=.(5分)∵a=3-1+2sin 30°=+2×=,∴原式==7.(8分)13.原式=·(4分) =·=. (5分)∵a=+1,b=-1,∴原式==.(8分) 14.原式=÷(4分) =×=-.(5分)∵(x+2)(x-2)≠0,x+2≠0且x(x-2)≠0,∴x≠0,±2,又∵-<x<,且x为整数,∴x可取±1,(7分)当x=1时,原式=-=-1.(8分)(或当x=-1时,原式=-=1.(8分)) 15.原式=÷=·=.(5分)解方程x2+2x-3=0,得x1=-3,x2=1,∵m=-3时,原分式无意义,∴m=1,(7分)故原式==.(8分)16.原式=÷=÷=·=.(4分)解不等式组得-2≤x<2.∵x是整数,∴x=-2,-1,0或1.若使原分式有意义,x只能取0,(6分)∴原式==-.(8分)17.∵关于x的方程x2-2ax+a=0有两个相等的实数根,∴(-2a)2-4a=0,解得a1=0,a2=1. (3分)(-)÷=·=.(6分)∵a-1≠0,∴取a=0,(7分)∴原式==-1.(8分)第四节二次根式1.A 由题意,得3-x≥0且x-1≠0,解得x≤3且x≠1,在数轴上表示如图所示,故选A.2.B =2,不能与2合并;=,能与2合并;=3,不能与2合并;=3,不能与2合并.故选B.3.A =2,不是最简二次根式;,,均是最简二次根式.故选A.4.90°由题意可知,sin A=,tan B=,∴∠A=30°,∠B=60°,∴∠A+∠B=90°.5.B 根据题意可得,等式成立的条件是解得x≥3,故选项B符合题意.6.D 与不能合并,故A项中的运算错误;=3,故B项中的运算错误;×==,故C项中的运算错误;÷==2,故D项中的运算正确.故选D.7.D =,故A项中的计算正确;×=3,故B项中的计算正确;-=3-2=,故C项中的计算正确;==3,故D项中的计算错误.故选D.8.5 原式=(-6)÷(-)=5.9.原式=3-2+1+2+2(4分)=6.(6分)10.原式=-1-1++2(6分)=.(8分)11.B 根据一个负数的绝对值等于它的相反数,可得|1-|=-1.12.B ∵36<37<49,∴<<,即6<<7,又∵37与36更接近,∴与最接近的整数是6,故选B.13.B ∵2<<3,∴-1<2-<0,∴表示数2-的点P应落在线段BO上,故选B.14.1 由题意得△ABC的面积为=1.15.2 设正三角形的边长为a(a>0),则a2×=2,解得a=2,则阴影部分的面积为2×-2=2.。
2019届秋季上学期高二语文8月月考试题(含解析) (826)
第一节角、相交线与平行线1.命题角度1[2018平顶山模拟改编]如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠BOD=76°,则∠BOM等于( )A.38°B.104°C.142°D.144°(第1题) (第2题)2.命题角度2[2018新疆乌鲁木齐]如图,把一个直角三角尺的直角顶点放在直尺的一边上,若∠1=50°,则∠2=()A.20°B.30°C.40°D.50°3.命题角度2[2018山东聊城] 如图,直线AB∥EF,点C是直线AB上一点,点D是直线AB外一点,若∠BCD=95°,∠CDE=25°,则∠DEF的度数是( )A.110°B.115°C.120°D.125°(第3题) (第4题)4.[2018浙江衢州]如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB边上的点E 处,若∠AGE=32°,则∠GHC等于( )A.112°B.110°C.108°D.106°5.命题角度1[2018云南昆明]如图,过直线AB上一点O作射线OC,∠BOC=29°18',则∠AOC 的度数为.(第5题) (第6题)6.如图所示,将一副三角板的直角顶点重合摆放在桌面上,若∠AOD=145°,则∠BOC=°.第二节三角形及其性质1.命题角度1[2017甘肃白银]已知a,b,c是△ABC的三条边长,化简|a+b-c|-|c-a-b|的结果为( )A.2a+2b-2cB.2a+2bC.2cD.02.命题角度2[2018云南昆明]在△AOC中,OB交AC于点D,量角器的摆放如图所示,则∠CDO 的度数为( )A.90°B.95°C.100°D.120°3.命题角度2[2018山东聊城]如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE.如果∠A=α,∠CEA'=β,∠BDA'=γ,那么下列式子中正确的是( )A.γ=2α+βB.γ=α+2βC.γ=α+βD.γ=180°-α-β4.命题角度3[2018湖北黄石]如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC,∠ABC 的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=()A.75°B.80°C.85°D.90°5.命题角度3[2017贵州毕节]如图,Rt△ABC中,∠ACB=90°,斜边AB=9,点D为AB的中点,点F为CD上一点,且CF=CD,过点B作BE∥DC交AF的延长线于点E,则BE的长为( )A.6B.4C.7D.126.[2018福建A]如图,等边三角形ABC中,AD⊥BC,垂足为点D,点E在线段AD上,∠EBC=45°,则∠ACE等于( )A.15°B.30°C.45°D.60°7.[2018广西玉林]如图,∠AOB=60°,OA=OB,动点C从点O出发,沿射线OB移动,以AC为边在右侧作等边三角形ACD,连接BD,则BD所在直线与OA所在直线的位置关系是( )A.平行B.相交C.垂直D.平行、相交或垂直(第7题) (第8题)8.命题角度4[2017湖北武汉]如图,在Rt△ABC中,∠C=90°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点在△ABC的其他边上,则可以画出的不同的等腰三角形的个数最多为( )A.4B.5C.6D.79.命题角度5[2018山东淄博]如图,在Rt△ABC中,CM平分∠ACB交AB于点M,过点M作MN∥BC 交AC于点N,且MN平分∠AMC,若AN=1,则BC的长为( )A.4B.6C.4D.810.命题角度1[2018江苏泰州]已知三角形两边的长分别为1,5,第三边长为整数,则第三边的长为.11.[2018湖南娄底]如图,在△ABC中,AB=AC,AD⊥BC于点D,DE⊥AB于点E,BF⊥AC于点F,DE=3 cm,则BF= cm.12.命题角度4[2017黑龙江绥化]在等腰三角形ABC中,AD⊥BC交直线BC于点D,若AD=BC,则△ABC的顶角的度数为.13.命题角度5[2018福建A]把两个同样大小的含45°角的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个的直角顶点重合于点A,且另外三个锐角顶点B,C,D在同一直线上.若AB=,则CD= .(第13题) (第14题)14.[2018广西玉林]如图,在四边形ABCD中,∠B=∠D=90°,∠A=60°,AB=4,则AD的取值范围是.15.命题角度6[2017河南B卷]如图,在等边三角形ABC中,AB=2 cm,点M为边BC的中点,点N为边AB上的任意一点(不与点A,B重合),若点B关于直线MN的对称点B'恰好落在等边三角形ABC的边上,则BN的长为cm.16.[2018黑龙江龙东地区]在Rt△ABC中,∠ABC=90°,AB=3,BC=4,过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是.第三节全等三角形1.命题角度1[2018江苏南京]如图,AB⊥CD,且AB=CD.E,F是AD上两点,C E⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )A.a+cB.b+cC.a-b+cD.a+b-c2.命题角度1如图,在四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为( )A.15B.12.5C.14.5D.17(第2题) (第4题)3.只给定三角形的两个元素,画出的三角形的形状和大小是不确定的,在下列给定的两个条件上增加一个“AB=5 cm”的条件后,所画出的三角形的形状和大小仍不能完全确定的是( )A.∠A=30°,BC=3 cmB.∠A=30°,AC=6 cmC.∠A=30°,∠C=50°D.BC=3 cm,AC=6 cm4.命题角度1[2017湖南怀化]如图,AC=DC,BC=EC,请你添加一个适当的条件: ,使得△ABC≌△DEC.5.[2018黑龙江哈尔滨]已知:在四边形ABCD中,对角线AC,BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点G,∠BGE=∠ADE.(1)如图(1),求证:AD=CD;(2)如图(2),BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图(2)中4个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.图(1) 图(2)6.命题角度2[2018山东滨州]已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.(1)如图(1),若点E,F分别为AB,AC上的点,且DE⊥DF,求证:BE=AF;(2)若点E,F分别为AB延长线,CA延长线上的点,且DE⊥DF,则BE=AF成立吗?请利用图(2)说明理由.图(1) 图(2)第四节相似三角形1.命题角度1[2018四川乐山]如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是( )A.EG=4GCB.EG=3GCC.EG=GCD.EG=2GC2.命题角度3[2017重庆十一中模拟]两个相似三角形的最短边长分别是5 cm和3 cm,它们的周长之差为12 cm,那么小三角形的周长为( )A.14 cmB.16 cmC.18 cmD.30 cm3.命题角度2[2018安徽十校联考四模]如图,在四边形ABCD中,如果∠ADC=∠BAC,那么下列条件中不能判定△ADC和△BAC相似的是( )A.∠DAC=∠ABCB.AC是∠BCD的平分线C.AC2=BC·CDD.AD·AB=DC·AC4.[2018四川达州]如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF=AC.连接DE,DF 并延长,分别交AB,BC于点G,H,连接GH,则的值为( )A. B. C. D.15.命题角度1[2018南阳一模]如图,EF∥BC,若AE∶EB=2∶1,EM=1,MF=2,则BN∶NC=.6.命题角度3[2017安徽合肥十九中模拟]如图,在平面直角坐标系中,已知点A(4,0),B(0,2),如果点C在x轴上(点C与点A不重合),当点C的坐标为时,使以点B,O,C为顶点的三角形与△AOB相似(至少找出两个满足条件的点).7.命题角度3[2016辽宁本溪]如图,在△ABC中,AC=6,AB=4,点D与点A在直线BC的同侧,且∠ACD=∠ABC,CD=2,点E是线段BC延长线上的动点,当△DCE和△ABC相似时,线段CE的长为.8.命题角度3[2018江苏常州]如图,在△ABC纸板中,AC=4,BC=2,AB=5,点P是AC上一点,过点P沿直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么AP长的取值范围是.9.命题角度4[2018湖北黄石中考改编]在△ABC中,E,F分别为线段AB,AC上的点(不与点A,B,C重合).(1)如图(1),若EF∥BC,求证:=;(2)如图(2),若EF不与BC平行,(1)中的结论是否仍然成立?请说明理由.图(1) 图(2)第五节锐角三角函数及其应用1.[2018湖南邵阳]某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯.如图,已知原阶梯式自动扶梯AB长为10 m,坡角∠ABD为30°;改造后的斜坡式自动扶梯的坡角∠ACB为15°,请你计算改造后的斜坡式自动扶梯AC的长度.(结果精确到0.1 m.温馨提示:sin 15°≈0.26, cos 15°≈0.97,tan 15°≈0.27)2.[2018安徽]为了测量竖直旗杆AB的高度,某综合实践小组在地面D处竖直放置标杆CD,并在地面上水平放置一个平面镜E,使得B,E,D在同一水平线上,如图所示.该小组在标杆的F 处通过平面镜E恰好观测到旗杆顶A(此时∠AEB=∠FED).在F处测得旗杆顶A的仰角为39.3°,平面镜E的俯角为45°,FD=1.8米,问旗杆AB的高度约为多少米.(结果保留整数,参考数据:tan 39.3°≈0.82,tan 84.3°≈10.02)3.[2018山东青岛]某区域平面示意图如图所示,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲勘测员在A处测得点O位于北偏东45°,乙勘测员在B处测得点O位于南偏西73.7°,且AC=840 m,BC=500 m.请求出点O到BC的距离.参考数据:sin 73.7°≈,cos 73.7°≈,tan 73.7°≈.参考答案第一节角、相交线与平行线1.C∵∠BOD=76°,∴∠AOC=76°.∵射线OM平分∠AOC,∴∠AOM=∠AOC=×76°=38°,∴∠BOM=180°-∠AOM=180°-38°=142°.故选C.2.C 如图,∵直尺的对边互相平行,∴∠3=∠1=50°,∴∠2=180°-50°-90°=40°.故选C.3.C如图,延长FE,交DC于点N,∵直线AB∥EF,∴∠DNF=∠BCD=95°.∵∠CDE=25°,∴∠DEF=95°+25°=120°.故选C.4.D∵∠AGE=32°,∴∠DGE=148°.由折叠可得,∠DGH=∠DGE=74°.∵AD∥BC,∴∠GHC=180°-∠DGH=106°,故选D.5.150°42'∵∠BOC=29°18',∴∠AOC=180°-29°18'=150°42'.6.35∵∠AOD=145°,∠AOB=90°,∴∠BOD=∠AOD-∠AOB=145°-90°=55°,∴∠BOC=∠COD-∠BO D=90°-55°=35°.第二节三角形及其性质1.D∵a,b,c为△ABC的三条边长,∴a+b>c,∴a+b-c>0,c-a-b<0,故原式=a+b-c+(c-a-b)=a+b-c+c-a-b=0,故选D.2.B∵CO=AO,∠AOC=130°,∴∠CAO=25°,又∵∠AOB=70°,∴∠CDO=∠CAO+∠AOB=25°+70°=95°,故选B.3.A由折叠的性质可得∠A'=∠A=α.设AC交DA'于点F,∵∠BDA'=∠A+∠AFD,∠AFD=∠A'+∠CEA',∴∠BDA'=γ=α+α+β=2α+β.故选A.4.A 易得∠ACD=180°-(∠BAC+∠ABC)=70°,∴∠CAD=90°-∠ACD=20°.∵AE是∠BAC的平分线,∴∠CAE=∠BAC=25°,∴∠EAD=∠CAE-∠CAD=25°-20°=5°,∴∠EAD+∠ACD=5°+70°=75°.5.A∵在Rt△ABC中,∠ACB=90°,AB=9,点D为AB的中点,∴CD=AB=.∵CF=CD,∴DF=CD=×=3.∵BE∥DC,∴DF是△ABE的中位线,∴BE=2DF=6.故选A.6.A∵△ABC是等边三角形,∴∠ACB=60°.∵AD⊥BC,∴BD=CD,∴AD垂直平分BC,∴EB=EC,∴∠ECB=∠EBC=45°,∴∠ACE=∠ACB-∠ECB=60°-45°=15°.7.A ∵∠AOB=60°,OA=OB,∴△OAB是等边三角形,∴OA=AB,∠OAB=∠ABO=60°.①当点C在线段OB上时,如图(1),∵△ACD是等边三角形,∴AC=AD,∠CAD=60°,∴∠OAC=∠BAD,∴△AOC≌△ABD,∴∠ABD=∠AOC=60°,∴∠DBE=1 80°-∠ABO-∠ABD=60°=∠AOB,∴BD∥OA.②当点C在OB的延长线上时,如图(2),同①的方法可得出BD∥OA.故选A.图(1) 图(2)8.D 符合题意的等腰三角形有如图所示的7种情况.9.B由题意可得,∠AMN=∠NMC=∠B,∠NCM=∠BCM=∠NMC,∴∠ACB=2∠B,NM=NC,∴∠AMN=∠B=30°.∵AN=1 ,∴MN=2,∴AC=AN+NC=3,∴BC=6,故选B.10.5 设第三边的长为a,根据三角形的三边关系,得5-1<a<5+1,即4<a<6.因为第三边长为整数,所以第三边的长是5.11.6 过点D作DG⊥AC于点G.在△ABC中,AB=AC,AD⊥BC,∴∠BAD=∠CAD,BD=CD,∴DG=DE=3 cm.∵BF⊥AC,∴DG∥BF,又BD=CD,∴DG是△CBF的中位线,∴BF=2DG=6 cm.12.30°,150°或90°分两种情况讨论.①BC为腰,∵AD⊥BC,AD=BC,∴∠ACD=30°,如图(1),AD在△ABC内部时,顶角∠C=30°;如图(2),AD在△ABC外部时,顶角∠ACB=180°-30°=150°.②BC为底,如图(3),∵AD⊥BC,AD=BC,AB=AC,∴AD=BD=CD,∴∠BAD=∠CAD=45°,∴∠BAC=90°.综上所述,等腰三角形ABC的顶角度数为30°,150°或90°.图(1) 图(2) 图(3)13.-1如图,过点A作AF⊥BC于点 F.在Rt△ABC中,AC=AB=,∠B=45°,∴BC=AB=2.∵AF⊥BC,∴AF=BF=CF=1.在Rt△AFD 中,AF=1,AD=BC=2,∴DF==,∴CD=DF-FC=-1.14.2<AD<8如图,延长BC交AD的延长线于点E,作BF⊥AD于点 F.在Rt△ABE 中,∵∠E=90°-60°=30°,AB=4,∴AE=2AB=8.在Rt△ABF中,AF=AB=2.故AD的取值范围为2<AD<8.15.或在等边三角形ABC中,BC=AB=2 cm,点M为BC的中点,∴BM= cm.分两种情况讨论.①如图(1),当点B'落在AB上时,∵点B与点B'关于直线MN对称,∴∠BNM=90°,又∵∠B=60°,∴BN=BM=cm.②如图(2),当点B'落在AC上时,连接B'M,∵点B与点B'关于直线MN对称,∴B'M=BM=MC,∠BMN=∠B'MN.又∵∠C=60°,∴△B'MC是等边三角形,∴∠B'MC=60°,∴∠BMB'=120°,∴∠BMN=60°.又∵∠B=60°,∴△BMN是等边三角形,∴BN=BM= cm.综上所述,BN的长为或 cm.图(1) 图(2)16.3.6,4.32或 4.8在Rt△ABC中,∠ABC=90°,AB=3,BC=4,∴AC==5,S△ABC=AB·BC=6.沿过点B的直线把△ABC分割成两个三角形,使其中只有一个是等腰三角形,有三种情况:①当AP=AB=3时,如图(1)所示,S等腰三角形ABP=S△ABC=×6=3.6;②当BP=AB=3,且点P在AC上时,如图(2)所示,作△ABC的高BD,则BD===2.4,∴AD=DP==1.8,∴AP=2AD=3.6,∴S等腰三角形ABP=S△ABC=×6=4.32;③当CP=CB=4时,如图(3)所示,S等腰三角形BCP=S△ABC=×6=4.8.综上所述,等腰三角形的面积为3.6,4.32或4.8.图(1) 图(2) 图(3)第三节全等三角形1.D设BF交CD于点M,则∠BMC=∠DMF,∴∠B=∠D.在△ABF和△CDE中,∴△ABF≌△CDE,∴AF=CE=a,DE=BF=b,∴DF=DE-EF=b-c, ∴AD=AF+FD=a+b-c.2.B如图,过点A作AE⊥AC,交CB的延长线于点E.∵∠DAB=∠DCB=90°,∴∠D+∠ABC=180°=∠ABE+∠ABC,∴∠D=∠ABE,又∵∠DAB=∠CAE=90°,∴∠CAD=∠EAB,又∵AD=AB,∴△ACD≌△AEB,∴AC=AE,即△ACE是等腰直角三角形,∴四边形ABCD的面积与△ACE的面积相等.∵S△ACE=×5×5=12.5,∴四边形ABCD的面积为12.5,故选B.3.A A项中,∠A=30°,BC=3 cm,AB=5 cm,不能确定三角形的形状和大小;B项中,∠A=30°,AC=6 cm,AB=5 cm,能确定三角形的形状和大小;C项中,∠A=30°,∠C=50°,AB=5 c m,能确定三角形的形状和大小;D项中,BC=3 cm,AC=6 cm,AB=5 cm,能确定三角形的形状和大小.故选A.4.答案不唯一,如AB=DE等. 在△ABC与△DEC中,AC=DC,BC=EC.若利用SSS证明,则可添加AB=DE;若利用SAS证明,则可添加∠ACB=∠DCE或∠ACD=∠BCE.5.(1)证明:∵AC⊥BD,∴∠AED=∠BEG=90°,∠GBE+∠BGE=90°.又∵∠BGE=∠ADE,∴∠DAE=∠GBE.∵BF⊥CD,∴∠GBE+∠CDE=90°,∴∠ADE=∠CDE,又∵DE=DE,∠AED=∠DEC=90°,∴△ADE≌△CDE,∴AD=CD.(2)△ACD,△ABE,△BCE,△GBH.6.(1)证明:连接AD,如图(1)所示.∵∠BAC=90°,AB=AC,∴△ABC为等腰直角三角形,∠EBD=45°.∵点D为BC的中点,∴AD=BC=BD,∠FAD=45°.∵∠BDE+∠EDA=90°,∠EDA+∠ADF=90°,∴∠BDE=∠ADF.在△BDE和△ADF中,∴△BDE≌△ADF,∴BE=AF.(2)成立.理由:连接AD,如图(2)所示.∵∠ABD=∠CAD=45°,∴∠EBD=∠FAD=135°.∵∠EDB+∠BDF=90°,∠BDF+∠FDA=90°,∴∠EDB=∠FDA.在△EDB和△FDA中,∴△EDB≌△FDA,∴BE=AF.第四节相似三角形1.B ∵DB=4FB,∴DF=3FB,又∵DE∥FG∥BC,∴===3.故选B.2.C 根据题意得两三角形的周长的比为5∶3,设两三角形的周长分别为5x cm,3x cm,则5x-3x=12,解得x=6,所以3x=18,即小三角形的周长为18 cm.故选C.3.C 在△ADC和△BAC中,∠ADC=∠BAC.若添加A或B中条件,可利用“两角分别相等的两个三角形相似”,得到△ADC与△BAC相似;若添加C中条件,不能得到△ADC与△BAC相似;若添加D中条件,可利用“两边成比例且夹角相等的两个三角形相似”,得到△ADC∽△CAB.故选C.4.C 连接BD,设S平行四边形ABCD=1.∵AE=CF=AC,∴==.∵四边形ABCD是平行四边形,∴BC∥AD,AB∥CD,∴===,===,∴S△ADG=S△ABD=,△BGH∽△BAC,∴=()2=,∴S△BGH=,∴==.故选C.5.1∶2∵AE∶EB=2∶1,∴AE∶AB=2∶3.∵EF∥BC,∴===,即===,∴BN=1.5,NC=3,∴BN∶NC=1∶2.6.答案不唯一,如(-1,0)或(1,0). ∵点C在x轴上,∴点C的纵坐标是0,且∠BOC=90°.分两种情况:①当△AOB∽△COB时,=,∴OC=OA=4,∴C(-4,0);②当△AOB∽△BOC 时,=,∴OC=1,∴C(-1,0)或(1,0).综上可知,点C的坐标为(-1,0),(1,0)或(-4,0).7.或 3 ∵∠ACD=∠ABC,∠ACD+∠ACB+∠DCE=180°,∠ABC+∠ACB+∠A=180°,∴∠A=∠DCE.当△DCE∽△CAB时,=,即=,∴CE=.当△DCE∽△BAC时,=,即=,∴CE=3.8.3≤AP<4如图(1)所示,过点P作PD∥AB交BC于点D,过点P作PE∥BC交AB于点E,则△PCD∽△ACB,△APE∽△ACB,此时0<AP<4.如图(2)所示,过点P作∠APF=∠B交AB于点F,则△APF∽△ABC,此时0<AP≤4.如图(3)所示,过点P作∠CPG=∠CBA交BC于点G,则△CPG∽△CBA,当点G与点B重合时,如图(4),此时CB2=CP×CA,即22=CP×4,∴CP=1,AP=3,此时3≤AP<4.综上所述,AP长的取值范围是3≤AP<4.9.(1)证明:∵EF∥BC,∴△AEF∽△ABC,∴=,∴==.(2)成立.理由如下:分别过点F,C作AB的垂线,垂足分别为点N,H.∵FN⊥AB,CH⊥AB,∴FN∥CH,∴△AFN∽△ACH,∴=,∴==.第五节锐角三角函数及其应用1.在Rt△ABD中,∠ABD=30°,AB=10 m,∴AD=AB·sin∠ABD=10×sin 30°=5(m),在Rt△ACD中,∠ACD=15°,sin∠ACD=,∴AC==≈≈19.2(m).答:改造后的斜坡式自动扶梯AC的长度约为19.2 m.2.如图,过点F作FG⊥AB于点G,则AG=AB-GB=AB-FD=AB-1.8.由题意知:△ABE和△FDE均为等腰直角三角形,∴AB=BE,DE=FD=1.8,∴FG=DB=DE+BE=AB+1.8.在Rt△AFG中,AG=FG·tan∠AFG,∴AB-1.8≈0.82(AB+1.8),解得AB=18.2≈18.答:旗杆AB的高度约为18米.3.如图,过点O分别作OM⊥BC于点M,ON⊥AC于点N,则四边形ONCM为矩形,∴ON=MC,OM=NC.设OM=x m,则NC=x m,AN=(840-x)m. 在Rt△ANO中,∠OAN=45°,∴ON=AN=(840-x)m,∴MC=ON=(840-x)m.在Rt△BOM中,BM=≈x m, ∴840-x+x=500,解得x=480.答:点O到BC的距离约为480 m.。
2019届秋季上学期高二语文8月月考试题(含解析) (766)
24.mouse(n.)→(pl.)老鼠;耗子
25.fly(v.)→(过去式)→(过去分词)飞
26.wake(v.)→(过去式)→(过去分词)弄醒;醒→(adj.)醒着的
短语归纳
1.中等身高
2.一点儿;少量
3.in the end
12.luck(n.)→(adj.)幸运的→(adv.)幸运地;好运地→(adj.)不幸的
13.feed(v.)→(过去式/过去分词)喂养;饲养
14.farm(v.& n.)→(n.)农民;农场主
15.grow(v.)→(过去式)→(过去分词)种植;生长;发育
16.paint(v.)→(n.)油漆匠;画家→(n.)油画;绘画
5.May I take your order
6.How was your school trip
7.What did you do last weekend
8.Where did she go last weekend
语法回顾
1.选择疑问句
2.would like的用法
3.some与any
4.一般过去时的用法和句式变化
5.what, how, who引导的特殊疑问句
【参考答案】
【词汇拓展】
1.height2.thinner; thinnest3.heavily4.less; least5.glasses6.actor; actress; action7.personal8.put9.differently; difference10.potatoes11.blew; blown12.lucky; luckily; unlucky13.fed14.farmer 15.grew; grown16.painter; painting
2019届秋季上学期高二语文8月月考试题(含解析) (462)
河南省辉县市高级中学2018-2019学年高二化学上学期第一次月考试题可能用到的元素相对原子质量:H : 1 C :12 O :16 Na :23 Al :27 Cl:35.5Fe: 56 Cu: 64 Mn :55 S:32 Mg:24第I 卷(选择题共48分)一、选择题:(本题包括16小题,每小题3分,每小题只有一个选项符合题意)1.能源分类相关图如图所示,下列四个选项中,全部符合图中阴影部分的能源是A .煤炭、石油、沼气B .水能、生物质能、天然气C .太阳能、风能、潮汐能D .地热能、海洋能、核能 2.下列物质间的反应,其能量变化符合右图的是( ) A .由Zn 和稀H 2SO 4制氢气B .灼热的炭粉与二氧化碳反应C .Ba(OH)2·8H 2O 晶体和NH 4Cl 晶体混合D .碳酸钙的分解3.下列说法或表示方法不正确的是( ) A .盖斯定律实质上是能量守恒定律的体现B .在稀溶液中:H +(aq)+OH -(aq)===H 2O(l) ΔH = -57.3 kJ/mol ,含0.5 mol H 2SO 4的浓硫酸与含1 mol NaOH 的溶液混合,放出的热量大于57.3 kJC .由C(石墨)―→C(金刚石) ΔH =+73 kJ/mol ,可知石墨比金刚石稳定D .在101 kPa 时,2 g H 2完全燃烧生成液态水,放出285.8 kJ 热量,氢气燃烧的热化学方程式表示为:2H 2(g)+O 2(g)===2H 2O(l) ΔH =-285.8 kJ/mol 4.已知①H 2(g)+12O 2(g)===H 2O(g)ΔH 1=a kJ/mol ②2H 2(g)+O 2(g)===2H 2O(g)ΔH 2=b kJ/mol③H 2(g)+12O 2(g)===H 2O(l)ΔH 3=c kJ/mol ④2H 2(g)+O 2(g)===2H 2O(l)ΔH 4=d kJ/mol下列关系式正确的是( )A .a <c <0B .b >d >0C .2a =b <0D .2c =d >0 5.已知白磷转变成红磷时放出热量和下列两个热化学方程式:4P(白,s)+5O 2(g)===2P 2O 5(s)ΔH 1,4P(红,s)+5O 2(g)===2P 2O 5(s)ΔH 2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
经典资料 经典资料(一) 河北辛集中学2018-2019学年度第一学期第一次阶段考试 高二数学试卷
第Ⅰ卷(选择题 共80分) 一.选择题(每小题5分,共80分。下列每小题所给选项只有一项符合题意,请将正确答案 的序号填涂在答题卡上) 1.命题“20,0xxx”的否定是( ) A. 20000,0xxx B. 20000,0xxx C. 20,0xxx D. 20,0xxx
2. 分别在区间[1,6]和[1,4]内任取一个实数,依次记为m和n,则m>n的概率为( ) A.710 B.310 C.35 D.25
3.如图所示,样本A和B分别取自两个不同的总体,它们的样本平均数分别为xA和xB,样本标准差分别为sA和sB,则( ) A.xA>xB,sA>sB B.xA<xB,sA>sB
C.xA>xB,sA<sB D.xA<xB,sA<sB 4.由辗转相除法可以得到390,455,546三个数的最大公约数是( ) A.65 B.91 C.26 D.13 5.某单位青年、中年、老年职员的人数之比为10∶8∶7,从中抽取200名职员作为样本,若每人被抽取的概率是0.2,则该单位青年职员的人数为( ) A.280 B.320 C.400 D.1000 6. 设,abR,则“1a,且1b”是“2ab”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 7. {}na是首项为正数的等比数列,公比为q,则“0q”是“对任意的正整数n,
2120nnaa-+<”
A.充分而不必要条件 B.必要而不充分条件C.充要条件 D.既不充分也不必要条件 经典资料 经典资料(一) 8.下列命题中,不是真命题的是( ) A. 命题“若22ambm,则ab”的逆命题.B. “1ab”是“1a且1b”的必要条件. C. 命题“若29x,则3x”的否命题.D. “1x”是“11x”的充分不必要条件. 9.某品牌产品在男士中有10%的人使用过,在女士中有40%的人使用过,若从男女人数相等的人群中任取一人,此人恰好使用过该产品,则此人是位女士的概率是( ) A.15 B.25 C.35 D.45 10.经过椭圆2222xy的一个焦点作倾斜角为的直线l,交椭圆于M,N两点,设O为坐标原点,则OMON等于 A. 3 B. 13 C. 13 D. 12 11.某中学高三年级从甲、乙两个班级各选出8名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的平均分是86,乙班学生成绩的中位数是83,则xy的值为( ) A. 9 B. 10 C. 11 D. 13 12.过圆x2+y2-4x=0外一点(m,n)作圆的两条切线,当这两条切线相互垂直时,m、n满足的关系式是( ) A.(m-2)2+n2=4 B.(m+2)2+n2=4 C.(m-2)2+n2=8 D.(m+2)2+n2=8
13.已知直线360xy经过椭圆22221(0)xyabab的左焦点F1,且与椭圆在第二象限的交点为M,与y轴的交点为N,F2是椭圆的右焦点,且|MN|=|MF2|,则椭圆的方程为( ) A.221404xy B. 2215xy C. 22110xy D. 221106xy 14.从1,2,…,10这十个数中任意取出两个,假设两个数的和是偶数的概率为p,两个数的积是偶数的概率为q.给出下列说法:①p+q=1;②p=q;③|p-q|≤110;④p≤12.其中说法正确的有( ) A.1个 B.2个 C.3个 D.4个 15.利用秦九韶算法求1)(235xxxxxf当3x时的值为 A.121 B.321 C.283 D.239 经典资料 经典资料(一) 16. 设椭圆22195xy的左、右焦点分别为F1,F2,过焦点F1的直线交椭圆于A(x1,y1),B(x2,y2)两点,若△ABF2的内切圆的面积为π,则|y1-y2|= ( ) A.3 B.6 C.9 D.12 第 Ⅱ 卷 二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上 17.从一箱苹果中任取一个,如果其重量小于200克的概率为0.2,重量在200,300内的概
率为0.5,那么重量超过300克的概率为________.
18.命题“2000(1,2),+m40xxx满足不等式”是假命题,则m的取值范围为 。 19.若直线l:220(0,0)axbyab与x轴相交于点A,与y轴相交于B,被圆222410xyxy截得的弦长为4,则||||OAOB(O为坐标原点)的最小值为
______. 20.下列关于概率和统计的几种说法: ①10名工人某天生产同一种零件,生产的件数分别是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则a,b,c的大小关系为c>a>b; ②样本4,2,1,0,-2的标准差是2; ③在面积为S的△ABC内任选一点P,则随机事件“△PBC的面积小于S3”的概率为13; ④从写有0,1,2,…,9的十张卡片中,有放回地每次抽一张,连抽两次,则两张卡片上的数字各不相同的概率是910. 其中正确说法的序号有________. 三、解答题(本大题共4小题,共计50分) 21.(12分)已知102:xp,q:x2-2x+1-m2£0(m>0),且p是Øq
的必要不充
分条件,求实数m的取值范围.
22.(12分)某大学为调查来自南方和北方的同龄大学生的身高差异,从2016级的年龄在18~19岁之间的大学生中随机抽取了来自南方和北方的大学生各10名,测量他们的身高,量出的身高如下(单位:cm): 经典资料 经典资料(一) 南方:158,170,166,169,180,175,171,176,162,163. 北方:183,173,169,163,179,171,157,175,184,166. (1)根据抽测结果,画出茎叶图,对来自南方和北方的大学生的身高作比较,写出统计结论.
(2)设抽测的10名南方大学生的平均身高为xcm,将10名南方大学生的身高依次输入如图所示的程序框图进行运算,问输出的s大小为多少?并说明s的统计学意义.
23.(12分)在平面直角坐标系xOy中,点A(0,3),直线l:y=2x-4. 设圆C的半径为1,圆心在l上. (1)若圆心C也在直线y=x-1上,过点A作圆C的切线,求切线的方程;
(2)若圆C上存在点M,使MA=2MO,求圆心C的横坐标a的取值范围.
24.(14分) 2013年1月,北京经历了59年来雾霾天气最多的一个月.据气象局统计,北京市2013年1月1日至1月30日这30天里有26天出现雾霾天气,《环境空气质量指数(AQI)技术规定(试行)》如表1: 表1 空气质量指数AQI分组表 AQI指数M 0~50 51~100 101~150 151~200 201~300 >300 级别 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ 状况 优 良 轻度污染 中度污染 重度污染 严重污染 表2是某气象观测点记录的连续4天里AQI指数M与当天的空气水平可见度y(km)的情况,表3是某气象观测点记录的北京市2013年1月1日至1月30日的AQI指数频数分布表.
表2 AQI指数M与当天的空气水平可见度y(km)的情况 AQI指数M 900 700 300 100 空气水平可见度y(km) 0.5 3.5 6.5 9.5 表3 北京市2013年1月1日至1月30日AQI指数频数分布表 AQI指数M [0,200) [200,400) [400,600) [600,800) [800,1000] 频数 3 6 12 6 3 (1) 设x=M100,根据表2的数据,求出y关于x的线性回归方程. 经典资料 经典资料(一) (参考公式:1122211()()()nniiiiiinniiiixxyyxynxybxxxnx,aybx.) (2)小王在北京开了一家洗车店,经小王统计:当AQI指数低于200时,洗车店平均每天亏损约2000元;当AQI指数在200至400时,洗车店平均每天收入约4000元;当AQI指数不低于400时,洗车店平均每天收入约7000元. ①估计小王的洗车店在2013年1月份平均每天的收入; ②从AQI指数在[0,200)和[800,1000]内的这6天中抽取2天,求这2天的收入之和不低于5000元的概率.
附加题(10分)
已知椭圆2222:1(0)xyCabab经过点135(,)24A,且两个焦点12,FF的坐标依次为(1,0)和(1,0). (1)求椭圆的标准方程; (2)设E,F是椭圆C上的两个动点,O为坐标原点,直线OE的斜率为1k,直线OF的斜率为2k,若121kk,证明:直线与以原点为圆心的定圆相切,并写出此定圆的标准方程. 经典资料
经典资料(一) 高二数学第一次月考试题答案 1-5 BABDC 6-10 ABADC 11-16 DCDACA
17. 0.3 18.5m 19. 20.②④ 21.已知:210px,q:x2-2x+1-m2£0(m>0),且p是Øq
的必要不充分条件,
求实数m的取值范围.
22解:(1)茎叶图如图所示.统计结论(给出下述四个结论供参考):①北方大学生的平均身高大于南方大学生的平均身高;②南方大学生的身高比北方大学生的身高更整齐;③南方大学生的身高的中位数为169.5 cm,北方大学生的身高的中位数是172 cm;④南方大学生的身高基本上是对称的,而且大多数集中在均值附近,北方大学生的身高分布较为分散.
(2)s=42.6,s表示10位南方大学生身高的方差,是描述身高的离散程度的量.s值越小,表示身高越整齐,s值越大,表示身高越参差不齐. 23. (1)由题设,圆心C是直线y=2x-4和y=x-1的交点,解得点C(3,2), 于是切线的斜率必存在.设过A(0,3)的圆C的切线方程为y=kx+3,
由题意,得|3k+1|k2+1=1,解得k=0或k=-34, 故所求切线方程为y=3或3x+4y-12=0. (2)因为圆心在直线y=2x-4上,所以圆C的方程为(x-a)2+[y-2(a-2)]2=1.
设点M(x,y),因为MA=2MO,所以223xy=2x2+y2,
