高联二试难度几何100题(带图、已精排适合打印、预留做题空间)
2021届高考数学文全国版二轮复习参考专题检测(十) 空间几何体、三视图、表面积与体积

专题检测(十) 空间几何体、三视图、表面积与体积A 组——“12+4”满分练一、选择题1.(2019·福州市第一学期抽测)如图,为一圆柱切削后的几何体及其正视图,则相应的侧视图可以是( )解析:选B 由题意,根据切削后的几何体及其正视图,可得相应的侧视图的切口为椭圆,故选B.2.如图,在正方体ABCD -A 1B 1C 1D 1中,P 为BD 1的中点,则△P AC 在该正方体各个面上的正投影可能是( )A.①②B.①④C.②③D.②④解析:选B 连接A 1C 1,则点P 在上、下底面的正投影落在A 1C 1或AC 上,所以△P AC 在上底面或下底面的正投影为①,在前面、后面、左面、右面的正投影为④.故选B.3.(2019·武汉市调研测试)如图,在棱长为1的正方体ABCD -A 1B 1C 1D 1中,M 为CD 的中点,则三棱锥A BC 1M 的体积VA BC 1M =( )A.12B.14C.16D.112解析:选C VA BC 1M =VC 1ABM =13S △ABM ·C 1C =13×12AB ×AD ×C 1C =16.故选C.4.设一个球形西瓜,切下一刀后所得切面圆的半径为4,球心到切面圆心的距离为3,则该西瓜的体积为( )A.100πB.2563πC.4003π D.5003π 解析:选D 因为切面圆的半径r =4,球心到切面的距离d =3,所以球的半径R =r 2+d 2=42+32=5,故球的体积V =43πR 3=43π×53=5003π,即该西瓜的体积为5003π.故选D.5.(2019届高三·开封高三定位考试)某几何体的三视图如图所示,其中俯视图为扇形,则该几何体的体积为( )A.4πB.2πC.4π3D.π解析:选B 由题意知该几何体的直观图如图所示,该几何体为圆柱的一部分,设底面扇形的圆心角为α,由tan α=31=3,得α=π3,故底面面积为12×π3×22=2π3,则该几何体的体积为2π3×3=2π.故选B.6.某圆锥的侧面展开图是面积为3π且圆心角为2π3的扇形,此圆锥的体积为( )A.πB.22π3C.2πD.22π解析:选B 设圆锥的母线为R ,底面圆的半径为r ,扇形的圆心角为α,则S =12αR 2=12×2π3×R 2=3π,解得R =3,底面圆的半径r 满足rR =2π32π,解得r =1,所以这个圆锥的高h =32-12=22,故圆锥的体积V =13πr 2h =22π3.故选B.7.已知矩形ABCD ,AB =2BC ,把这个矩形分别以AB ,BC 所在直线为轴旋转一周,所成几何体的侧面积分别记为S 1,S 2,则S 1与S 2的比值等于( )A.12 B.1 C.2D.4解析:选B 设BC =a ,AB =2a ,所以S 1=2π·a ·2a =4πa 2,S 2=2π·2a ·a =4πa 2,S 1∶S 2=1.故选B.8.(2019·广东省七校联考)某几何体的三视图如图所示,则该几何体的表面积和体积分别是( )A.24+62和40B.24+62和72C.64+62和40D.64+62和72解析:选C 把三视图还原成几何体,如图所示.由题意知S 四边形ABCD =12,S 四边形BCC 1B 1=8,S 四边形ABB 1A 1=6,S 四边形ADSA 1=(2+6)×4×12=16,S 四边形DCC 1S =(2+6)×3×12=12.易得B 1A 1⊥SA 1,B 1C 1⊥SC 1,且SA 1=42,SC 1=5,所以S △SA 1B 1=3×42×12=62,S △SB 1C 1=4×5×12=10,所以该几何体的表面积为12+8+6+16+12+62+10=64+6 2.在棱SD 上取一点D 1,使得DD 1=2,连接A 1D 1,C 1D 1,则该几何体的体积V =V S -A 1B 1C 1D 1+V ABCD -A 1B 1C 1D 1=13×12×4+12×2=40.故选C. 9.(2019·蓉城名校第一次联考)已知一个几何体的正视图和侧视图如图1所示,其俯视图用斜二测画法所画出的水平放置的直观图是一个直角边长为1的等腰直角三角形(如图2所示),则此几何体的体积为( )A.1B. 2C.2D.2 2解析:选B 根据直观图可得该几何体的俯视图是一个直角边长分别是2和2的直角三角形(如图所示),根据三视图可知该几何体是一个三棱锥,且三棱锥的高为3,所以体积V =13×⎝⎛⎭⎫12×2×2×3= 2.故选B. 10.《九章算术》是我国古代内容极为丰富的数学名著,书中提到了一种名为“刍甍”的五面体,如图所示,四边形ABCD 为矩形,棱EF ∥AB .若此几何体中,AB =4,EF =2,△ADE 和△BCF 都是边长为2的等边三角形,则该几何体的表面积为( )A.8 3B.8+8 3C.62+2 3D.8+62+2 3解析:选B 如图所示,取BC 的中点P ,连接PF ,则PF ⊥BC ,过F 作FQ ⊥AB ,垂足为Q .因为△ADE 和△BCF 都是边长为2的等边三角形,且EF ∥AB , 所以四边形ABFE 为等腰梯形,FP =3, 则BQ =12(AB -EF )=1,FQ =BF 2-BQ 2=3,所以S 梯形EFBA =S 梯形EFCD =12×(2+4)×3=33,又S △ADE =S △BCF =12×2×3=3,S 矩形ABCD =4×2=8,所以该几何体的表面积S =33×2+3×2+8=8+8 3.故选B.11.古人采取“用臼舂米”的方法脱去稻谷的外壳,获得可供食用的大米,用于舂米的“臼”多用石头或木头制成.一个“臼”的三视图如图所示,则凿去部分(看成一个简单的组合体)的体积为( )A.63πB.72πC.79πD.99π解析:选A 由三视图得凿去部分是圆柱与半球的组合体,其中圆柱的高为5,底面圆的半径为3,半球的半径为3,所以组合体的体积为π×32×5+12×43π×33=63π.故选A.12.已知三棱锥P -ABC 的四个顶点都在球O 的表面上,P A ⊥平面ABC ,AB ⊥BC ,且P A =8.若平面ABC 截球O 所得截面的面积为9π,则球O 的表面积为( )A.10πB.25πC.50πD.100π解析:选D 设球O 的半径为R ,由平面ABC 截球O 所得截面的面积为9π,得△ABC 的外接圆的半径为3.设该外接圆的圆心为D ,因为AB ⊥BC ,所以点D 为AC 的中点,所以DC =3.因为P A ⊥平面ABC ,易证PB ⊥BC ,所以PC 为球O 的直径.又P A =8,所以OD =12P A=4,所以R =OC =42+32=5,所以球O 的表面积为S =4πR 2=100π.故选D. 二、填空题13.(2019·长春市质量监测一)已知一所有棱长都是2的三棱锥,则该三棱锥的体积为________.解析:记所有棱长都是2的三棱锥为P -ABC ,如图所示,取BC 的中点D ,连接AD ,PD ,作PO ⊥AD 于点O ,则PO ⊥平面ABC ,且OP =63×2=233,故三棱锥P -ABC 的体积V =13S △ABC ·OP =13×34×(2)2×233=13. 答案:1314.如图,在正三棱柱ABC -A 1B 1C 1中,D 为棱AA 1的中点.若AA 1=4,AB =2,则四棱锥B -ACC 1D 的体积为________.解析:取AC 的中点O ,连接BO (图略),则BO ⊥AC , 所以BO ⊥平面ACC 1D . 因为AB =2,所以BO = 3.因为D 为棱AA 1的中点,AA 1=4,所以AD =2, 所以S 梯形ACC 1D =12×(2+4)×2=6,所以四棱锥B -ACC 1D 的体积为13×6×3=2 3.答案:2 315.如图,半径为4的球O 中有一内接圆柱,则圆柱的侧面积最大值是________.解析:设圆柱的上底面半径为r ,球的半径与上底面夹角为α,则r =4cosα,圆柱的高为8sin α.所以圆柱的侧面积为32πsin 2α.当且仅当α=π4时,sin 2α=1,圆柱的侧面积最大,所以圆柱的侧面积的最大值为32π. 答案:32π16.(2019·江西省五校协作体试题)某几何体的三视图如图所示,正视图是一个上底为2,下底为4的直角梯形,俯视图是一个边长为4的等边三角形,则该几何体的体积为________.解析:把三视图还原成几何体ABC -DEF ,如图所示,在AD 上取点G ,使得AG =2,连接GE ,GF ,则把几何体ABC -DEF 分割成三棱柱ABC -GEF 和三棱锥D -GEF ,所以V ABC -DEF =V ABC -GEF +V D -GEF =43×2+13×43×2=3233. 答案:3233B 组——“5+3”提速练1.(2019·福州市质量检测)棱长为1的正方体ABCD -A 1B 1C 1D 1木块的直观图如图所示,平面α过点D 且平行于平面ACD 1,则该木块在平面α内的正投影面积是( )A.3B.32 3 C. 2D.1解析:选A 棱长为1的正方体ABCD -A 1B 1C 1D 1木块在平面α内的正投影是三个全等的菱形,如图,正投影可以看成两个边长为2的等边三角形,所以木块在平面α内的正投影面积是2×12×2×2×32= 3.故选A.2.在棱长为3的正方体ABCD -A 1B 1C 1D 1中,P 在线段BD 1上,且BP PD 1=12,M 为线段B 1C 1上的动点,则三棱锥M -PBC 的体积为( )A.1B.32C.92D.与M 点的位置有关解析:选B ∵BP PD 1=12,∴点P 到平面BCC 1B 1的距离是D 1到平面BCC 1B 1距离的13,即为D 1C 13=1.M 为线段B 1C 1上的点,∴S △MBC =12×3×3=92, ∴V M PBC =V P MBC =13×92×1=32.故选B.3.(2019·重庆市学业质量调研)三棱锥S -ABC 中,SA ,SB ,SC 两两垂直,已知SA =a ,SB =b ,SC =2,且2a +b =52,则此三棱锥的外接球的表面积的最小值为( )A.21π4B.17π4C.4πD.6π解析:选A 由题意,设三棱锥的外接球的半径为R ,因为SA ,SB ,SC 两两垂直,所以以SA ,SB ,SC 为棱构造长方体,其体对角线即三棱锥的外接球的直径,因为SA =a ,SB =b ,SC =2,所以4R 2=a 2+b 2+4=a 2+⎝⎛⎭⎫52-2a 2+4=5(a -1)2+214,所以a =1时,(4R 2)min =214,所以三棱锥的外接球的表面积的最小值为21π4.故选A.4.(2019·洛阳尖子生第二次联考)已知正三角形ABC 的三个项点都在半径为2的球面上,球心O 到平面ABC 的距离为1,点E 是线段AB 的中点,过点E 作球O 的截面,则截面圆面积的最小值是( )A.7π4B.2πC.9π4D.3π解析:选C 设正三角形ABC 的中心为O 1,连接OO 1,OA ,O 1A , 由题意得O 1O ⊥平面ABC ,O 1O =1,OA =2,∴在Rt △O 1OA 中,O 1A =3,∴AB =3.∵E 为AB 的中点,∴AE =32.连接OE ,则OE ⊥AB .过点E 作球O 的截面,当截面与OE 垂直时,截面圆的面积最小,此时截面圆的半径r =32,可得截面圆面积的最小值为πr 2=9π4.故选C.5.(2019·全国卷Ⅰ)已知三棱锥P -ABC 的四个顶点在球O 的球面上,P A =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是P A ,AB 的中点,∠CEF =90°,则球O 的体积为( )A.86πB.46πC.26πD.6π解析:选D 设P A =PB =PC =2a ,则EF =a ,FC =3,∴EC 2=3-a 2.在△PEC 中,cos ∠PEC =a 2+3-a 2-(2a )22a 3-a 2.在△AEC 中,cos ∠AEC =a 2+3-a 2-42a 3-a 2.∵∠PEC 与∠AEC 互补,∴3-4a 2=1,a =22, 故P A =PB =PC = 2.又∵AB =BC =AC =2,∴P A ⊥PB ⊥PC , ∴外接球的直径2R =(2)2+(2)2+(2)2=6,∴R =62,∴V =43πR 3=43π×⎝⎛⎭⎫623=6π.故选D.6.(2019·全国卷Ⅰ)已知∠ACB =90°,P 为平面ABC 外一点,PC =2,点P 到∠ACB 两边AC ,BC 的距离均为3,那么P 到平面ABC 的距离为________.解析:如图,过点P 作PO ⊥平面ABC 于O ,则PO 为P 到平面ABC 的距离.再过O 作OE ⊥AC 于E ,OF ⊥BC 于F ,连接PC ,PE ,PF ,则PE ⊥AC ,PF ⊥BC .又PE =PF =3,所以OE =OF , 所以CO 为∠ACB 的平分线,即∠ACO =45°.在Rt △PEC 中,PC =2,PE =3,所以CE =1,所以OE =1,所以PO =PE 2-OE 2=(3)2-12= 2.答案: 27.(2019·河南八市重点高中联盟测评改编)已知一个高为1的三棱锥,各侧棱长都相等,底面是边长为2的等边三角形,则三棱锥的表面积为________,若三棱锥内有一个体积为V 的球,则V 的最大值为________.解析:该三棱锥侧面的斜高为⎝⎛⎭⎫13×32+12=233,则S 侧=3×12×2×233=23,S底=12×3×2=3,所以三棱锥的表面积S 表=23+3=3 3.由题意知,当球与三棱锥的四个面都相切时,其体积最大.设三棱锥的内切球的半径为r ,则三棱锥的体积V 锥=13S 表·r =13S底·1,所以33r =3,所以r =13,所以三棱锥的内切球的体积最大为V max =43πr 3=4π81.答案:334π818.已知在正四棱锥S -ABCD 中,SA =63,那么当该棱锥的体积最大时,它的高为________. 解析:设正四棱锥的底面正方形的边长为a ,高为h ,因为在正四棱锥S -ABCD 中,SA =63,所以a 22+h 2=108,即a 2=216-2h 2,所以正四棱锥的体积V S -ABCD =13a 2h =72h -23h 3,令y =72h -23h 3,则y ′=72-2h 2,令y ′>0,得0<h <6,令y ′<0,得h >6,所以当该棱锥的体积最大时,它的高为6.答案:6。
高联二试概率题

高联二试概率题
(原创版)
目录
1.高联二试概率题概述
2.高联二试概率题的解题方法
3.高联二试概率题的技巧和策略
正文
【高联二试概率题概述】
高联二试概率题是高联考试中的一种题型,主要考察考生对概率论知识的掌握程度,以及运用概率论知识解决实际问题的能力。
在高联二试中,概率题通常难度较大,需要考生具备一定的数学基础和逻辑思维能力。
【高联二试概率题的解题方法】
解决高联二试概率题,一般可以采用以下几种方法:
1.概率基本公式法:根据概率的基本公式,即概率=事件发生的次数/总的可能性的次数,计算出事件发生的概率。
2.条件概率法:根据条件概率的定义,即 P(A|B)=P(A∩B)/P(B),计算出给定某个条件时,事件发生的概率。
3.独立事件概率法:根据独立事件的定义,即事件之间的发生不会互相影响,计算出多个独立事件同时发生的概率。
4.全概率公式法:根据全概率公式,即
P(A)=P(A|B1)P(B1)+P(A|B2)P(B2)+…+P(A|Bn)P(Bn),计算出事件发生的概率。
【高联二试概率题的技巧和策略】
在解决高联二试概率题时,除了掌握基本的解题方法外,还需要注意
以下几点:
1.仔细阅读题目,理解题意,找出题目中的关键信息。
2.在解题过程中,要充分利用题目中给出的条件,合理运用概率论知识,进行逻辑推理和计算。
3.注意分类讨论,对于复杂的题目,需要根据不同的情况进行分类讨论,避免遗漏。
4.在计算概率时,要保证计算过程的准确性,避免出现计算错误。
5.在解题过程中,要保持冷静,不要因为遇到困难而慌乱,要有信心,相信自己能够解决问题。
2023年江西省初中名校联盟九年级第二次学习效果检测数学试题(二模)

2023年江西省初中名校联盟九年级第二次学习效果检测数学
试题(二模)
学校:___________姓名:___________班级:___________考号:___________
A.B.
C.D.
二、填空题
11.如图,图①,图②,图③,……是用围棋棋子摆成的一列具有一定规律的“山”字,则第n个“山”字中的棋子个数是__________.
12.已知正方形ABCD的边长为4,点P是射线BC上的点,将ABP
V沿AP折叠得到V为等腰三角形,则点E到BC的距离可能是__________.
△,若CDE
AEP
三、解答题
2
---
122
x x x x
b
23.观察发现 (1)如图1,在ABC V 中,AB AC =,120CAB ∠=︒,将ABC V 绕着点B 逆时针旋转α角度得到BDE △,连接CD ,AE .
①若120α=︒,1AB =,求DC 的长及CDB ∠的度数;
②如图2,若90α=︒,F 是AE 的中点,判断CD 与BF 之间的数量关系及位置关系,并证明.
拓展应用
(2)如图3,在ABC V 中,90CBA ∠=︒,30A ∠=︒,将BA 绕着点B 逆时针旋转60︒得到BE ,3EB =,连接CE ,
①点F 是CE 中点,连接BF ,求BF 的长;
②若CE 与AB 交于点N ,直接写出sin ENA ∠的值.。
高联二试概率题

高联二试概率题(原创实用版)目录1.高联二试概率题概述2.高联二试概率题的解题方法与技巧3.高联二试概率题的典型例题解析4.如何准备高联二试概率题正文一、高联二试概率题概述高联二试是指高校联合招生考试的第二次考试,通常在每年的 3 月至 4 月进行。
高联二试是选拔高中毕业生的重要手段之一,其目的是评估学生的学科知识和能力,为高校招生提供依据。
在高联二试中,概率题是数学科目中的一个重要部分,主要考察学生对概率知识的掌握程度和运用能力。
二、高联二试概率题的解题方法与技巧1.理解概率的基本概念:概率是反映事件发生机会的大小的概念,它的取值范围在 0 和 1 之间。
理解概率的基本概念有助于正确解决概率题。
2.熟悉概率的计算方法:概率的计算方法包括古典概率和条件概率。
古典概率主要用于计算具有等可能性的事件的概率,而条件概率则用于计算在已知某些条件下事件发生的概率。
3.掌握概率分布和统计量:概率分布是用来描述随机变量取值范围和取值机会的工具,而统计量则是用来衡量数据的中心趋势和离散程度。
掌握概率分布和统计量有助于解决复杂的概率题。
4.善于运用数理统计方法:数理统计方法是研究随机现象的一般规律和总结经验的方法,包括描述性统计、推断性统计和假设检验等。
在解决概率题时,可以灵活运用数理统计方法,提高解题效率。
三、高联二试概率题的典型例题解析例题:某袋中有 3 个红球、2 个蓝球和 5 个黄球,现从袋中随机抽取 2 个球,求抽到的球为红色或蓝色的概率。
解:根据组合数学知识,从 n 个不同元素中抽取 m 个元素的组合数为 C(n,m),即从 n 个元素中任意抽取 m 个元素的方案数。
本题中,从7 个球中抽取 2 个球的组合数为 C(7,2)=21。
而抽到的球为红色或蓝色的组合数为 C(3,2)+C(2,2)=3+1=4。
因此,抽到的球为红色或蓝色的概率为 4/21=2/7。
四、如何准备高联二试概率题1.扎实掌握概率基础知识:要解决高联二试概率题,首先要扎实掌握概率的基本概念、计算方法和概率分布等基础知识。
2023版高中数学新同步精讲精炼(必修第二册) 第八章 立体几何初步 章末测试(提升)(学生版)

第八章 立体几何初步 章末测试(提升)一、单选题(每题只有一个选项为正确答案,每题5分,8题共40分)1.(2021·上海市控江中学高二期中)已知圆柱的上、下底面的中心分别为1O 、2O ,过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的侧面积为( )A .8πB .C .12πD .2.(2021·天津市南开区南大奥宇培训学校 )a ,b 为两条直线,α,β为两个平面,则下列四个命题中,正确的命题是( )A .若a α⊥,b β⊥,a b ⊥,则αβ⊥B .若//a α,//b β,//αβ,则//a bC .若a α⊂,b β⊂,//a b ,则//αβD .若//a α,αβ⊥,则a β⊥3.(2021·广东顺德·一模)如图,正方体1111ABCD A B C D -的棱长为1,线段11B D 上有两个动点E ,F ,且EF 则三棱锥A BEF -的体积为( )A .112 B .14 C D .不确定4.(2021·湖北·大冶市第一中学 )在空间四边形ABCD 中,,,,E F G H 分别是AB ,BC ,CD ,DA 的中点.若AC BD a ==,且AC 与BD 所成的角为60︒,则EG 的长为( )A .aB .2aC .aD .2a5.(2021·湖北·武汉外国语学校(武汉实验外国语学校)高二月考)在正四面体P ABC -中,D ,E ,F 侧棱AB ,BC ,CA 的中点,下列说法不正确的( )A .//BC 面PDFB .面PDE ⊥面ABC C .面PDF ⊥面PAED .DF ⊥面PAE6.(2021·贵州·贵阳一中 )如图,在棱长为a 的正方体1111ABCD A B C D -中,P 在线段1BD 上,且12BP PD =,M 为线段11B C 上的动点,则三棱锥M PBC -的体积为( )A .319aB .332aC .313aD .与点M 的位置有关7.(2021·浙江宁波 )如图一,矩形ABCD 中,2BC AB =,AM BD ⊥交对角线BD 于点O ,交BC 于点M .现将ABD △沿BD 翻折至A BD '的位置,如图二,点N 为棱A D '的中点,则下列判断一定成立的是( )A .BD CN ⊥B .AO '⊥平面BCDC .//CN 平面A OM 'D .平面A OM '⊥平面BCD8.(2021·四川省峨眉第二中学校 )在三棱锥A BCD -中,AB CD a ==,截面MNPQ 与AB ,CD 都平行,则截面MNPQ 的周长等于( )A .2aB .4aC .aD .无法确定二、多选题(每题至少有2个选项为正确答案,每题5分,4题共20分)9.(2021·全国 )已知直线l 、m ,平面,,l m αβαβ⊂⊂、,则下列说法中正确的是( )A .若//l m ,则必有//αβB .若l m ⊥,则必有αβ⊥C .若l β⊥,则必有αβ⊥D .若//αβ,则必有l β//10.(2021·福建·永安市第三中学高中校 )如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,3DAB π∠=,22AB AD PD ==,PD ⊥底面ABCD ,则( )A .PA BD ⊥B .BC ⊥平面PBD .C .异面直线AB 与PCD .PB 与平面ABCD 所成角为π3 11.(2021·全国·模拟预测)如图,点A ,B ,C ,M ,N 是正方体的顶点或所在棱的中点,则满足//MN平面ABC 的有( )A .B .C .D .12.(2021·江苏省苏州第十中学校 )矩形ABCD 中,2AB =,1BC =,将此矩形沿着对角线BD 折成一个三棱锥C BDA -,则以下说法正确的有( )A .三棱锥C BDA -B .当二面角C BD A --为直二面角时,三棱锥C BDA -C .当二面角C BD A --为直二面角时,三棱锥C BDA -的外接球的表面积为5πD .当二面角C BD A --不是直二面角时,三棱锥C BDA -的外接球的表面积小于5π三、填空题(每题5分,共20分)13.(2021·上海·华东师范大学第三附属中学)如图,OABC 是边长为1的正方形,AC 是四分之一圆弧,则图中阴影部分绕轴OC 旋转一周得到的旋转体的表面积为________________.14.(2021·上海外国语大学闵行外国语中学 )如图已知A 是BCD △所在平面外一点,AD BC =,E 、F 分别是AB CD 、的中点,若异面直线AD 与BC 所成角的大小为3π,则AD 与EF 所成角的大小为___________.15.(2021·河南 )2021年7月,某学校的学生到农村参加劳动实践,一部分学生学习编斗笠,一种用竹篾或苇蒿等材料制作外形为圆锥形的斗笠,称为“灯罩斗笠”(如图),一部分学生学习制作泥塑几何体,现有一个棱长为6的正方体形状泥块,其各面的中心分别为点E ,F ,G ,H ,M ,N ,将正方体削成正八面体形状泥块G EMHF N --,若用正视图为正三角形的一个“灯罩斗笠”罩住该正八面体形状泥块G EMHF N --,使得正八面体形状泥块G EMHF N --可以在“灯罩斗笠”中任意转动,则该有底的“灯罩斗笠”的表面积的最小值为___________.16.(2021·湖南·临澧县第一中学 )在三棱锥S ABC -中,2SB SC AB BC AC =====,二面角S BC A --为120︒,则三棱锥S ABC -的外接球的表面积为______________.四、解答题(17题10分,其余每题12分,共70分)17.(2021·上海市甘泉外国语中学)已知正方体ABCD ﹣A 1B 1C 1D 1.(1)求证:1//AD 平面C 1BD ;(2)求证:1AD ⊥平面A 1D C .18.(2021·上海市控江中学 )如图,AD ⊥平面ABC ,CE ⊥平面ABC ,AD 与CE 不相等,1AC AD AB ===,BC =B ACED -的体积为12,F 为BC 的中点.(1)求CE的长度;AF平面BDE;(2)求证://(3)求证:平面BDE 平面BCE.19.(2021·广东·普宁市华侨中学 )如图,在四棱锥PABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD(1)求证:PD ⊥平面PAB ;(2)求直线PB 与平面PCD 所成角的正弦值;(3)在棱PA 上是否存在点M ,使得BM ∥平面PCD ?若存在,求AM AP的值;若不存在,说明理由.20.(2021·广东· )如图所示的几何体由三棱锥P ADQ -和正四棱锥P ABCD -拼接而成,PQ ⊥平面ADQ ,//AB PQ ,1PQ =,2AB =,AQ =O 为四边形ABCD 对角线的交点.(1)求证://OP 平面ADQ ;(2)求二面角O AP D --的正弦值.21.(2021·上海市洋泾中学 )如左图所示,在直角梯形ABCD 中,//BC AD ,AD CD ⊥,2BC =,3AD =,CD =AD 上一点E 满足1DE =.现将ABE △沿BE 折起到1A BE 的位置,使平面1A BE ⊥平面BCDE ,如右图所示.(1)求证:1A C BE ⊥;(2)求异面直线1A C 与BE 的距离;(3)求平面1A BE 与平面1A CD 所成锐二面角的余弦值.22.(2021·天津市武清区杨村第一中学 )如图,在直三棱柱111ABC A B C -中,侧棱11BB =,23ABC π∠=,且M ,N 分别为1BB ,AC 的中点.(1)证明://MN 平面11AB C ;(2)若2BA BC ==,求二面角11A B C B --的大小.。
高一下数学期末专题练习(必修2立体几何)
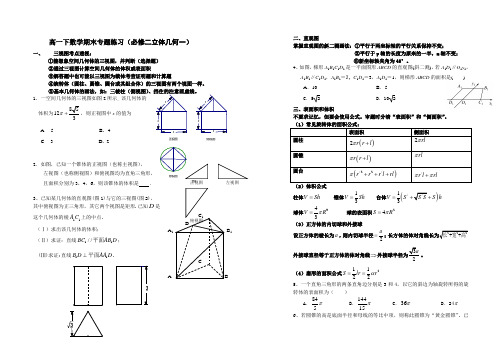
图2侧视图正视图高一下数学期末专题练习(必修二立体几何一)一、三视图考点透视:①能想象空间几何体的三视图,并判断(选择题) ②通过三视图计算空间几何体的体积或表面积③解答题中也可能以三视图为载体考查证明题和计算题④旋转体(圆柱、圆锥、圆台或其组合体)的三视图有两个视图一样。
⑤基本几何体的画法,如:三棱柱(侧视图)1. 一空间几何体的三视图如图2所示, 该几何体的体积为123π+,则正视图中x 的值为A. 5 B . 4 C. 3 D . 22.如图,已知一个锥体的正视图(也称主视图),左视图(也称侧视图)和俯视图均为直角三角形,且面积分别为3,4,6,则该锥体的体积是 .3、已知某几何体的直观图(图1)与它的三视图(图2), 其中俯视图为正三角形,其它两个视图是矩形.已知D 是 这个几何体的棱11C A 上的中点。
(Ⅰ)求出该几何体的体积;(Ⅱ)求证:直线11//BC AB D 平面; (Ⅲ)求证:直线11B D AA D ⊥平面.二、直观图掌握直观图的斜二测画法:①平行于两坐标轴的平行关系保持不变;②平行于y 轴的长度为原来的一半,x 轴不变;③新坐标轴夹角为45°。
4、如图,梯形A 1B 1C 1D 1是一平面图形ABCD 的直观图(斜二测),若A 1D 1∥O 1y 1,A 1B 1∥C 1D 1,A 1B 1=2,C 1D 1=3,A 1D 1=1,则梯形ABCD 的面积是( ) A .10 B .5 C .5 2D .102三、表面积和体积不要求记忆,但要会使用公式。
审题时分清“表面积”和“侧面积”。
(1)常见旋转体的面积公式:柱体V Sh = 锥体13V Sh =台体()/13V S S h = 球体343V R π=球的表面积24S R π= (3)正方体的内切球和外接球 设正方体的棱长为a ,则内切球半径=2a ;外接球直径等于正方体的体对角线⇒。
(4)扇形的面积公式21122S lr r α== 5、一个直角三角形的两条直角边分别是3和4,以它的斜边为轴旋转所得的旋转体的表面积为( )A .845π B .14415π C .36π D .24π6、若圆锥的高是底面半径和母线的等比中项,则称此圆锥为“黄金圆锥”。
高中同步测试卷人教B数学必修2高中同步测试卷十含答案

高中同步测试卷(十)空间几何体微专题(时刻:100分钟,总分值:120分)一、选择题(本大题共10小题,每题4分,共40分.在每题给出的四个选项中,只有一项为哪一项符合题目要求的)1.如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,若是不计容器厚度,那么球的体积为( )cm3cm3cm3cm32.假设某几何体的三视图如下图,那么那个几何体的直观图能够是( )3.已知直三棱柱ABCA1B1C1的6个极点都在球O的球面上.假设AB=3,AC=4,AB⊥AC,AA=12,那么球O的半径为( )1B.210D.3104.某几何体的三视图如下图,那么该几何体的体积为()A.16+8πB.8+8πC.16+16πD.8+16π4题图5题图5.一个空间几何体的三视图如下图,那么该几何体的表面积为()A.48 B.32+817C.48+817 D.806.已知球的直径SC=4,A,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,那么棱锥S-ABC的体积为()7.某四棱台的三视图如下图,那么该四棱台的体积是()A.4D.67题图8题图8.某三棱锥的三视图如下图,该三棱锥的表面积是()A.28+6 5 B.30+6 5C.56+12 5 D.60+12 59.设球的体积为V1,它的内接正方体的体积为V2,以下说法中最适合的是()A.V1比V2大约多一半B.V1比V2大约多两倍半C.V1比V2大约多一倍D.V1比V2大约多一倍半10.一个几何体的三视图如下图,该几何体从上到下由四个简单几何体组成,其体积别离记为V1,V2,V3,V4,上面两个简单几何体均为旋转体,下面两个简单几何体均为多面体,那么有()A.V1<V2<V4<V3 B. V1<V3<V2<V4C.V2<V1<V3<V4D.V2<V3<V1<V4题号 1 2 3 4 5 6 7 8 9 10 答案二、填空题(本大题共4小题,每题5分,共20分.把答案填在题中横线上)11.如图,正方体ABCD-A1B1C1D1的棱长为1,E,F别离为线段AA1,B1C上的点,那么三棱锥D1EDF的体积为____________.12.如图,在三棱柱A1B1C1ABC中,D,E,F别离是AB,AC,AA1的中点.设三棱锥F-ADE的体积为V1,三棱柱A1B1C1ABC的体积为V2,则V1∶V2=________.13.已知某一多面体内接于球组成一个简单组合体,若是该组合体的正视图、侧视图、俯视图均如下图,且图中的四边形是边长为2的正方形,那么该球的表面积是________.14.已知矩形ABCD的极点都在半径为4的球O的球面上,且AB=6,BC=23,那么棱锥O-ABCD的体积为________.三、解答题(本大题共6小题,共60分.解许诺写出文字说明,证明进程或演算步骤)15.(本小题总分值10分)如图,在长方体ABCD-A1B1C1D1中,AB=AD=3 cm,AA1=2 cm,求四棱锥A-BB1D1D的体积.16.(本小题总分值10分)已知三棱锥S-ABC的所有极点都在球O的球面上,△ABC是边长为1的正三角形,SC为球O的直径,且SC=2,求此棱锥的体积.17.(本小题总分值10分) 某四面体的三视图如下图,求该几何体的表面积.18.(本小题总分值10分)某高速公路收费站入口处的平安标识墩如图甲所示.墩的上半部份是正四棱锥P-EFGH,下半部份是长方体ABCD-EFGH.图乙、图丙别离是该标识墩的正视图和俯视图.(1)请画出该平安标识墩的侧视图; (2)求该平安标识墩的体积. 附加题19.(本小题总分值10分)如下图,圆柱OO ′的底面半径为2 cm ,高为4 cm ,点P 为母线B ′B 的中点,∠AOB =23π,试求一蚂蚁从A 点沿圆柱表面爬到P 点的最小路程.20.(本小题总分值10分)已知正三棱锥的高为1,底面边长为26,其内有一个球和该三棱锥的四个面都相切.求:(1)棱锥的全面积; (2)球的半径R .参考答案与解析1.[导学号] 【解析】选A.设球的半径为R cm ,那么球的截面圆的半径是4 cm ,且球心到该截面的距离是(R -2) cm ,故R 2=(R -2)2+42,得R =5,∴V =43πR 3=500π3(cm 3).2.[导学号] 【解析】选B.由三视图能够直接得出B 正确.3.[导学号] 【解析】选C.因为直三棱柱中AB =3,AC =4,AA 1=12,AB ⊥AC ,因此BC =5,且BC 为过底面ABC 的截面圆的直径.取BC 的中点D ,则OD ⊥底面ABC ,则O 在侧面BCC 1B 1内,矩形BCC 1B 1的对角线长即球的直径,因此2R =122+52=13,即R =132.4.[导学号] 【解析】选A.由三视图可知该组合体下半部份是一个半圆柱,上半部份是一个长方体,故体积为V =2×2×4+12×π×22×4=16+8π.5.[导学号]【解析】选C.由三视图知该几何体的直观图如下图,该几何体的下底面是边长为4的正方形;上底面是长为4、宽为2的矩形;两个梯形侧面垂直于底面,上底长为2,下底长为4,高为4;另两个侧面是矩形,宽为4,长为42+12=17.因此S表=42+2×4+12×(2+4)×4×2+4×17×2=48+817.6.[导学号]【解析】选C.如下图,连接OA、OB(O为球心).∵AB=2,SC=4,∴△OAB为正三角形.又∵△ASC与△BSC均为等腰直角三角形.∴BO⊥SC,AO⊥SC.又∵AO∩BO=O,∴SC⊥面ABO.∴V SABC=V COAB+V SOAB=13·S△OAB·(SO+OC)=13×12×2×3×4=433,应选C.7.[导学号]【解析】选B.由三视图可还原出四棱台的直观图如下图,其上底和下底都是正方形,边长别离是1和2,与底面垂直的棱为棱台的高,长度为2,故其体积为V=13×(12+1×4+22)×2=143,应选B.8.[导学号]【解析】选B.由三视图可知,三棱锥如下图,其中△ABC、△DBC为直角三角形,AE⊥底面DBC.通过图中数据可求得AC=CD=41,AD=25,三角形ADC中AD边上的高为6.因此三棱锥的表面积S=S△ADB+S△ABC+S△DBC+S△ADC=12×5×4+12×5×4+12×5×4+12×25×6=30+65,应选B.9.[导学号]【解析】选D.设正方体的棱长为a,那么球的半径32a,正方体的体积V2=a3,球的体积V1=32πa3,则V1-V2=32πa3-a3=⎝⎛⎭⎫32π-1a3≈,应选D.10.[导学号]【解析】选C.由三视图可知,四个几何体自上而下依次是:圆台、圆柱、正方体、棱台,其体积别离为V1=13×1×(π+2π+4π)=73π,V2=π×12×2=2π,V3=23=8,V4=13×1×(4+8+16)=283,于是有V2<V1<V3<V4.11.[导学号]【解析】VD1EDF=VFDD1E=13S△D1DE·AB=13×12×1×1×1=16.【答案】1 612.[导学号]【解析】设三棱柱的底面ABC的面积为S,高为h,那么其体积为V2=Sh.因为D,E别离为AB,AC的中点,因此△ADE的面积等于14S.又因为F为AA1的中点,因此三棱锥F-ADE的高等于12h,于是三棱锥F-ADE的体积V1=13×14S·12h=124Sh=124V2,故V1∶V2=1∶24.【答案】1∶2413.[导学号]【解析】由三视图知组合体为球内接正方体,正方体的棱长为2,假设球半径为R,那么2R=23,∴R=3,∴S球表=4πR2=4π×3=12π.【答案】12π14.[导学号]【解析】依题意棱锥O-ABCD的四条侧棱长相等且均为球O的半径,如图连接AC,取AC中点O′,连接OO′.易知AC=AB2+BC2=43,故AO′=2 3.在Rt△OAO′中,OA=4,从而OO′=42-12=2.因此V OABCD=13×2×6×23=8 3.【答案】8 315.[导学号]【解】由题意知,四边形ABCD为正方形,连接AC,交BD于O(图略),则AC⊥BD,则AO⊥平面BB1D1D,且OA=322cm.四棱锥底面BB1D1D的面积为32×2=62(cm2),则VABB1D1D=13×OA×SBB1D1D=13×62×322=6(cm3).16.[导学号]【解】由于三棱锥S-ABC与三棱锥OABC底面都是△ABC,O是SC的中点,因此三棱锥S-ABC 的高是三棱锥O-ABC高的2倍,因此三棱锥S-ABC的体积也是三棱锥O-ABC体积的2倍.在三棱锥O-ABC中,其棱长都是1,如下图,S△ABC=34×AB2=34,高OD=12-(33)2=63,∴V SABC=2V OABC=2×13×34×63=26.17.[导学号]【解】由三视图可知该几何体是一个四面体,可得其直观图如下图,其中SA⊥AC,SA⊥AB,AB⊥BC,则△SAB,△SAC,△SBC,和△ABC都为直角三角形.由已知得SA=4,AB=4,BC=3,则AC=5,SB=SA2+AB2=42+42=4 2.故四面体的表面积为S=S△SAB+S△SAC+S△SBC+S△ABC=12×4×4+12×4×5+12×42×3+12×4×3=8+10+62+6 =24+6 2.18.[导学号]【解】(1)该平安标识墩的侧视图如下图.(2)该平安标识墩的体积V=V PEFGH+V ABCDEFGH=13×40×40×60+40×40×20=64 000(cm3).19.[导学号]【解】将圆柱侧面沿母线A′A剪开展平为平面图,如下图.那么易知最短路程为平面图中线段AP的长.在Rt△ABP中,AB=23π×2=43πcm,PB=2 cm,∴AP=AB2+BP2=234π2+9(cm),即蚂蚁爬的最小路程为234π2+9 cm.20.[导学号]【解】(1)如下图正三棱锥A-BCD.由题可知AE=1,CD=26,EF=13×32×CD=2,∴侧面的高AF=AE2+EF2=3,∴S全=3×12×26×3+12×26×26×32=92+6 3.(2)由题可得1-R3=R2,∴R=6-2.。
天一大联考齐鲁名校联盟2024-2025学年高三上学期第二次联考(10月)数学试题

“天一大联考·齐鲁名校联盟”2024—2025学年高三年级第二次联考数学一、单项选择题:本题共8小题,每小题5分,共40分.1.已知集合{}1,2,3,4,5,6U =,{}13,5A =,,{}1,2,3B =,则()U A B =ð()A.{}2,4,5,6 B.{}4,6 C.{}2,4,6 D.{}2,5,62.已知0,0m n >>,且3m n +=,则21m n +++的最大值为()A.8B.23C.22D.572+3.函数)()(e e x x f x x -=-的图象大致为()A. B. C. D.4.一块扇形薄铁板的半径是30,圆心角是120 ,把这块铁板截去一个半径为15的小扇形后,剩余铁板恰好可作为一个圆台的侧面,则该圆台的体积为()A.17502π9B.1750π9C.17502π3D.17502π5.设等比数列{}n a 的前n 项和为n S ,则“数列{}n S 为递增数列”是“321a a a >>”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件6.函数221,2()2,2x x f x x x ⎧-<-=⎨-≥-⎩的最小值为()A .4- B.2- C.3D.57.已知数列{}n a 满足:11a =,点()1,n n n a a ++在函数1y kx =+的图象上,其中k 为常数()0k ≠,且124,,a a a 成等比数列,则k 的值为()A.2B.3C.4D.58.已知定义在R 上的函数()f x 满足()1(1)f x f x =--,若函数442x xy =+与函数()y f x =的图象的交点为112220252025(),),(,),,(,x y x y x y ,则20251)(i i i x y =+=∑()A.0B.20252C.2025D.60752二、多项选择题:本题共3小题,每小题6分,共18分.9.下列说法正确的是()A.若,a b c >∈R ,则22ac bc >B.若22,a b c cc >∈R ,则a b >C.若a b >,则22a b >D.函数2sin sin y x x=+的最小值为2210.如图,有一列曲线012,,, P P P ,已知0P 所围成的图形是面积为1的等边三角形,1(0,1,2,3,)k P k += 是对k P 进行如下操作得到的:将k P 的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉,记k S 为曲线k P 所围成图形的面积,则()A.3P 的边数为128B.24027S =C.n P 的边数为34n⨯ D.834()559nn S =-⋅11.已知函数()32,f x x ax a =-+∈R ,则()A.()f x 的图象关于点()0,2对称B.(),a f x ∃∈R 仅有一个极值点C.当1a =时,()f x 图象的一条切线方程为240x y -+=D.当3a <时,()f x 有唯一的零点三、填空题:本题共3小题,每小题5分,共15分.12.已知集合*2{13,{|(2)20}|}A x x B x ax a x =∈≤<=-++=N ,若“x B ∈”是“x A ∈”的充分不必要条件,则实数a 的所有取值组成的集合是______.13.蜜蜂被举为“天才的建筑师”,蜂巢结构是一种在一定条件下建筑用材最少的结构.如图是一个蜂房的立体模型,底面ABCDEF 是正六边形,棱,,,,,AG BH CI DJ EK FL 均垂直于底面ABCDEF ,上顶由三个全等的菱形,,PGHI PIJK PKLG 构成,10928GPI IPK KPG θ'∠=∠=∠=≈ ,设1BC =,则上顶的面积为______.(参考数据:1cos ,tan232θθ=-=)14.已知函数()ln f x x x =,则()f x 的最小值为______;设函数()()2g x x af x =-,若()g x 在()0,∞+上单调递增,则实数a 的取值范围是______.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.已知数列{}n a 满足()2*112,1n n n a a a a n +==-+∈N.(1)比较20242026,a a 的大小,并写出过程;(2)设数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和为n S ,证明:1n S <.16.已知函数()f x 与其导函数()f x '的定义域均为R ,且()f x 为奇函数,当0x >时,()()()2,10f x f x f ->='.(1)判断()y f x '=的奇偶性;(2)解不等式()0f x >.17.如图,在四棱锥P ABCD -中,侧棱PA ⊥底面,ABCD AB BC ⊥,且2,2,5PA AB BC AD CD =====.(1)证明:BD ⊥平面PAC ;(2)求平面PBC 与平面PAD 夹角的正弦值.18.设函数()ln(1)(0)f x x k x k =+-≠.(1)讨论()f x 的单调区间.(2)已知直线l 是曲线()y f x =在点(,())(2)t f t t >处的切线.(i )求直线l 的方程;(ii )判断直线l 是否经过点(2,2).19.设数阵111202122x x X x x ⎛⎫=⎪⎝⎭,其中{}11122122,,,1,2,3,4,5,6x x x x ∈.设{}{}12,,,1,2,3,4,5,6k B n n n =⊆ ,其中*12,k n n n k <<<∈N 且6k ≤.定义变换t M 为“对于数阵的每一列,若其中有t 或t -,则将这一列中所有数均保持不变;若其中没有t 且没有t -,则这一列中每个数都乘以()121,,,k t n n n -= ”,()0B M X 表示“将0X 经过1n M 变换得到1X ,再将1X 经过2n M 变换得到2,X ,以此类推,最后将1k X -经过k n M 变换得到k X ”.记数阵k X 中四个数的和为()0B T X .(1)若{}021,2,534X B ⎛⎫==⎪⎝⎭,写出0X 经过2M 变换后得到的数阵1X ,并求()0B T X 的值;(2)若{}012321,,,34X B n n n ⎛⎫== ⎪⎝⎭,求所有()0B T X 取值的和;(3)对任意确定的一个数阵0X ,证明:所有()0B T X 取值的和不大于8-;(4)如果01336X ⎛⎫=⎪⎝⎭,其他条件不变,你研究(1)后得出什么结论?“天一大联考·齐鲁名校联盟”2024—2025学年高三年级第二次联考数学一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的1.已知集合{}1,2,3,4,5,6U =,{}13,5A =,,{}1,2,3B =,则()U A B =ð()A.{}2,4,5,6 B.{}4,6 C.{}2,4,6 D.{}2,5,6【答案】A 【解析】【分析】由集合的交集运算、补集运算即可求解.【详解】由题意集合{}1,2,3,4,5,6U=,{}13,5A =,,{}1,2,3B =,则{}1,3A B = ,(){}2,4,5,6U A B = ð.故选:A.2.已知0,0mn >>,且3m n +=,则21m n +++的最大值为()A.8B.23C.22D.572+【答案】B 【解析】【分析】根据给定条件,利用配凑法及基本不等式求出最大值.【详解】由0,0mn >>,3m n +=,得6(2)(1)2(2)(1)m n m n =+++≥++,当且仅当213m n +=+=,即1,2m n ==时取等号,因此221(21)62(2)(1)23m n m n m n +++=+++=+++≤,所以21m n +++的最大值为23.故选:B3.函数)()(e e x x f x x -=-的图象大致为()A. B. C. D.【答案】B 【解析】【分析】利用函数()f x 奇偶性排除两个选项,再利用0x >时,函数值的正负判断即可.【详解】函数)()(e e x x f x x -=-的定义域为R ,()()(e )e x x f x x f x -=-=--,因此函数()f x 是偶函数,其图象关于y 轴对称,排除AC ;当0x >时,0e e 1x x -<<<,则()0f x <,排除D ,选项B 符合题意.故选:B4.一块扇形薄铁板的半径是30,圆心角是120 ,把这块铁板截去一个半径为15的小扇形后,剩余铁板恰好可作为一个圆台的侧面,则该圆台的体积为()A.2π9B.1750π9C.2π3D.17502π【答案】C 【解析】【分析】根据给定条件,求出原扇形及截去的小扇形围成的圆锥体积,再利用圆台的定义求出圆台体积.【详解】半径为30,圆心角为120 的扇形围成圆锥的底面圆半径r ,则2π2π303r =⋅,解得10r =,该圆锥的高h=2211ππ10π333V r h ==⋅⋅=,截去半径为15的小扇形围成圆锥的底面圆半径0r,则02π2π153r =⋅,解得05r =,该圆锥的高0h==2200011ππ5π333V r h ==⋅⋅=,所以该圆台的体积为0π27π31π33VV -=-=.故选:C5.设等比数列{}n a 的前n 项和为n S ,则“数列{}n S 为递增数列”是“321a a a >>”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【答案】D 【解析】【分析】由321a a a >>可得10,01a q <<<或10,1a q >>,由{}n S 递增得出0n a >恒成立,再由充分条件、必要条件的定义判断即可.【详解】令等比数列{}n a 的公比为q ,由321a a a >>,得1112a a a q q >>,则10,01a q <<<或10,1a q >>,由数列{}n S 为递增数列,得110n n n a S S ++=->,即N n *∀∈,10n a q >,因此10,0a q >>,所以“数列{}n S 为递增数列”是“321a a a >>”的既不充分也不必要条件.故选:D6.函数221,2()2,2x x f x x x ⎧-<-=⎨-≥-⎩的最小值为()A.4- B.2- C.3 D.5【答案】B 【解析】【分析】根据给定条件,分段探讨函数()f x 的单调性,进而求出最小值.【详解】当2x <-时,函数()21x f x =-在(,2)-∞-上单调递增,31()4f x -<<-;当2x ≤-时,函数2()2f x x =-在[2,0]-上单调递减,在[0,)+∞上单调递增,()(0)2f x f ≥=-,所以当0x =时,min ()2f x =-.故选:B7.已知数列{}n a 满足:11a =,点()1,n n n a a ++在函数1y kx =+的图象上,其中k 为常数()0k ≠,且124,,a a a 成等比数列,则k 的值为()A.2B.3C.4D.5【答案】A 【解析】【分析】根据递推公式求出2a ,4a ,再根据124,,a a a 成等比数列,可求k 的值.【详解】因为点()1,n n n a a ++在函数1y kx =+的图象上,所以11n n a a kn ++=+⇒11n n kn a a +=+-,所以11a =,211k ka a =+-=,32211a k k a =+-=+,43312k k a a =+-=,因为124,,a a a 成等比数列,所以212k k =⨯⇒2k =或0k =(舍去).故选:A8.已知定义在R 上的函数()f x 满足()1(1)f x f x =--,若函数442x x y =+与函数()y f x =的图象的交点为112220252025(),),(,),,(,x y x y x y ,则20251)(i i i x y =+=∑()A.0B.20252C.2025D.60752【答案】C 【解析】【分析】根据给定条件,求出函数()f x 及442x xy =+的图象的对称中心,再结合中心对称图形的性质计算即得.【详解】依题意,由()1(1)f x f x =--,得()(1)1f x f x +-=,则函数()y f x =的图象关于点11(,)22对称,令4()42xxg x =+,则114444()(1)1424242424x x x x x x x g x g x --+-=+=+=++++⋅,因此函数()y g x =的图象关于点11(,)22对称,显然函数()y f x =与()y g x =的图象对称中心相同,则函数()y f x =与()y g x =的图象的交点关于点11(,22对称,不妨令点(,)i i x y 与20262026(,)(1,2,3,,2025)i i x y i --= 关于点11(,)22对称,则202620261,1i i i i x x y y --+=+=,20262026()()2i i i i x y x y --+++=,所以202512(202520252)i i i x y =+=⨯=∑.故选:C 【点睛】结论点睛:函数()y f x =的定义域为D ,x D ∀∈,①存在常数a ,b 使得()(2)2()()2f x f a x b f a x f a x b +-=⇔++-=,则函数()y f x =图象关于点(,)a b 对称.②存在常数a 使得()(2)()()f x f a x f a x f a x =-⇔+=-,则函数()y f x =图象关于直线x a =对称.二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.9.下列说法正确的是()A.若,a b c >∈R ,则22ac bc >B.若22,a bc c c>∈R ,则a b >C.若ab >,则22a b > D.函数2sin sin y x x=+的最小值为【答案】BC 【解析】【分析】对A 举反例即可;对B 根据不等式性质即可判断;对C ,利用指数函数单调性即可判断;对D 举反例即可.【详解】对A ,当0c=时,22ac bc =,故A 错误;对B ,当22a b c c >,则20c >,则a b >,故B 正确;对C ,根据指数函数2x y =在R 上单调递增,且a b >,则22a b >,故C 正确;对D ,当sin 1x =-时,2sin 3sin y x x=+=-<D 错误.故选:BC.10.如图,有一列曲线012,,,P P P ,已知0P 所围成的图形是面积为1的等边三角形,1(0,1,2,3,)k P k += 是对k P 进行如下操作得到的:将k P 的每条边三等分,以每边中间部分的线段为边,向外作等边三角形,再将中间部分的线段去掉,记k S 为曲线kP 所围成图形的面积,则()A.3P 的边数为128 B.24027S =C.n P 的边数为34n⨯ D.834()559n n S =-⋅【答案】BCD 【解析】【分析】根据给定信息,归纳可得n P 的边数判断AC ;依次计算归纳得n P 所围图形的面积判断BD.【详解】依题意,令0P 图形的边长为a ,2314a =,边数是3;根据图形规律,1P 图形边长为3a,边数为0P 边数的4倍,即34⨯;2P 图形边长为23a,边数为234⨯;依此类推,n P 图形边长为3n a ,边数为34n ⨯,C 正确;3P 的边数为334192⨯=,A 错误;由图形规律知曲线n P 所围图形的面积n S 等于曲线1n P -所围面积加上每一条边增加的小等边三角形的面积,而每一个边增加的小等边三角形面积为23()43n a ⨯,则1213(34)()43n nn n a SS --=+⨯⨯,整理得1114()39n n n S S ---=⨯,数列1{}nn S S --是等比数列,1P 图形的面积213413()433a S =+⨯⨯=,121321144[1(]4183499()433559()9()()1n n n n n S S S S S S S S ---=+⨯-=+-+--⨯++=- ,D 正确;2831640558127S =-⨯=,B 正确.故选:BCD 11.已知函数()32,f x x ax a =-+∈R ,则()A.()f x 的图象关于点()0,2对称B.(),a f x ∃∈R 仅有一个极值点C.当1a=时,()f x 图象的一条切线方程为240x y -+= D.当3a <时,()f x 有唯一的零点【答案】ACD 【解析】【分析】根据函数的奇偶性判断A ,根据三次函数的性质判断B ,根据导数的意义求切线判断C ,利用极值点的符号判断D.【详解】对A :设()3g x x ax =-,则函数()g x 为奇函数,图象关于原点()0,0对称,将()3g x x ax =-的图象向上平移2个单位,得函数()32f x x ax =-+的图象,故函数()f x 的图象关于点()0,2对称,A 正确;对B :由三次函数的性质可知,函数()f x 要么有2个极值点,要么没有极值点,所以B 错误;对C :当1a=时,()32f x x x =-+,()231f x x '=-.由()2f x '=⇒2312x -=⇒1x =或1x =-.若1x =,则2y =,所以()f x 在1x =处的切线方程为:即2y x =;若1x =-,则2y =,所以()f x 在1x =-处的切线方程为:()221y x -=+即240x y -+=.故C 正确;对D :因为()23f x x a '=-,若0a ≤,则()0f x '≥在(),-∞+∞上恒成立,则()f x 在(),-∞+∞上单调递增,由三次函数的性质可知,此时函数()f x 只有一个零点;若0a >,由()0f x '<⇒3333x -<<,由()0f x '>⇒33x <-或33x >.所以函数()f x 在3,3⎛-∞-⎝⎭和3,3⎛⎫+∞ ⎪ ⎪⎝⎭上单调递增,在,33⎛⎫- ⎪ ⎪⎝⎭上单调递减,要使函数()f x 只有1个零点,须有03f ⎛⎫> ⎪ ⎪⎝⎭(因为()02f =,所以03f ⎛⎫-< ⎪ ⎪⎝⎭不成立),即3332033a ⎛⎫-⋅+> ⎪ ⎪⎝⎭⇒3a <,得0<<3a .综上可知:当3a <时,函数()f x 有唯一的零点,故D 正确.故选:ACD 【点睛】方法点睛:本题可以结合三次函数的图象和性质进行分析.三、填空题:本题共3小题,每小题5分,共15分.12.已知集合*2{13,{|(2)20}|}A x x B x ax a x =∈≤<=-++=N ,若“x B ∈”是“x A ∈”的充分不必要条件,则实数a 的所有取值组成的集合是______.【答案】{0,2}【解析】【分析】用列举法表示集合A ,利用充分不必要条件的定义,借助集合的包含关系分类求解即得.【详解】依题意,{1,2}A =,{|(2)(1)0}B x ax x =--=,显然B ≠∅,由“x B ∈”是“x A ∈”的充分不必要条件,得BA ,当0a=时,{1}B =,符合题意,当0a ≠时,方程2(2)20ax a x -++=的根为1和2a,显然22a ≠,否则B A =,不符合题意,因此21a=,解得2a =,此时{1}B =,符合题意,所以实数a 的所有取值组成的集合是{0,2}.故答案为:{0,2}13.蜜蜂被举为“天才的建筑师”,蜂巢结构是一种在一定条件下建筑用材最少的结构.如图是一个蜂房的立体模型,底面ABCDEF 是正六边形,棱,,,,,AG BH CI DJ EK FL 均垂直于底面ABCDEF ,上顶由三个全等的菱形,,PGHI PIJK PKLG 构成,10928GPI IPK KPG θ'∠=∠=∠=≈ ,设1BC =,则上顶的面积为______.(参考数据:1cos ,tan 232θθ=-=)【答案】924【解析】【分析】根据蜂房的结构特征,即可根据锐角三角函数以及三角形面积公式求解.【详解】依题意,由10928GPIIPK KPG θ'∠=∠=∠=≈ ,得10928GHI θ'∠=≈ ,在菱形PGHI 中,连接G I 并取其中点O,连接OH ,则2224tan2GOOH GO GI θ===,由正六边形ABCDEF 的边长1BC =,得2sin 603AC AB == ,由蜂巢结构特征知,AG CI =,又,AG CI都垂直于平面ABCDEF ,则//AG CI ,于是四边形ACIG 是平行四边形,有=3GI AC =,则26=44OH GI =,因此一个菱形的面积为1632223244GHISGI OH =⋅⋅=⨯=,所以上顶的面积为3292344⨯=.故答案为:92414.已知函数()ln f x x x =,则()f x 的最小值为______;设函数()()2g x x af x =-,若()g x 在()0,∞+上单调递增,则实数a 的取值范围是______.【答案】①.1e-②.[]0,2【解析】【分析】空1,直接求导利用()f x 的单调性去求其最小值即可;空2,利用导数与单调性的关系建立不等式,利用不等式的恒成立解决参数范围即可.【详解】由题可知()ln f x x x =定义域为()0,∞+()ln 1f x x ='-显然,当10,e x ⎛⎫∈ ⎪⎝⎭时,′<0,()f x 单调递减;当1,+e x ∞⎛⎫∈ ⎪⎝⎭时,′>0,()f x 单调递增;所以()f x 的最小值为11e e f ⎛⎫=- ⎪⎝⎭;由题可知,()()22ln g x x af x x ax x=-=-所以()2ln g x x a x a =--'由题可知()2ln 0g x x a x a '=--≥恒成立,当0a <,显然当0x →时,()g x ∞'→-,故不成立;当0a=时,()2g x x '=,因为∈0,+∞,所以()20g x x '=>,故成立;当0a >时,由2ln 0x a x a --≥恒成立,得21ln xax +≥恒成立,即max 21ln x a x +⎛⎫≥ ⎪⎝⎭不妨令()1ln x h x x +=,所以()2ln xh x x -='所以显然当∈0,1时,ℎ′>0,ℎ单调递增;当()1,+x ∞∈时,ℎ′<0,ℎ单调递减;所以()()max 11h x h ==,即2102a a ≥⇒<≤综上所述:[]0,2a ∈故答案为:1e-;0,2【点睛】关键点点睛,当不等式化简时,不要在不等式两边去随意乘或者除以一个未知数,要保证知道其正或负,再去作乘除计算.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.已知数列{}n a 满足()2*112,1n n n a a a a n +==-+∈N .(1)比较20242026,a a 的大小,并写出过程;(2)设数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和为n S ,证明:1n S <.【答案】(1)20242026a a <(2)证明见解析.【解析】【分析】(1)证明数列的单调性,可比较给出的两项的大小.(2)先根据统计得到111111n n n a a a +=---,再求n S 进行判断即可.【小问1详解】因为211n n n a a a +=-+⇒()2212110n n n n n a a a a a +-=-+=-≥,所以1n n a a +≥.若1n n a a +=,则211n n n n a a a a +=-+=⇒1n a =,这与12a =矛盾.所以1n n a a +>.故20242026a a <.【小问2详解】由211n n n a a a +=-+⇒()2111n nn n n a a a a a +-=-=-,所以()11111111n n n n n a a a a a +==----⇒111111n n n a a a +=---.所以11111111nnn i i i i i S a a a ==+⎛⎫==- ⎪--⎝⎭∑∑1111111111n n a a a ++=-=----.由(1)可知:12n a +>,所以1n S <.16.已知函数()f x 与其导函数()f x '的定义域均为R ,且()f x 为奇函数,当0x >时,()()()2,10f x f x f ->='.(1)判断()y f x '=的奇偶性;(2)解不等式()0f x >.【答案】(1)偶函数,理由见解析(2)(1,0)(1,)-+∞ 【解析】【分析】(1)对()()f x f x -=-两边同时求导即可证明;(2)构造函数2()()ex f x h x =,求导得到其单调性即可得到()f x 在(1,)+∞上大于零,在(0,1)上小于零,再根据其为奇函数即可得到答案.【小问1详解】因为()f x 为奇函数,定义域为R ,所以()()f x f x -=-,两边同时求导可得()()f x f x ''--=-,即()()f x f x ''-=,所以()y f x '=为偶函数.【小问2详解】因为当0x >时,()2()f x f x '->,所以()2()f x f x '>.构造函数2()()e x f x h x =,则2()2()()e xf x f x h x '-'=,所以当0x >时,()0,()h x h x >'在(0,)+∞上单调递增,又因为(1)0f =,所以(1)0,()h h x =在(1,)+∞上大于零,在(0,1)上小于零,又因为2e 0x>,所以()f x 在(1,)+∞上大于零,在(0,1)上小于零,因为()f x 是定义域为R 的奇函数,所以(0)0,()f f x =在(,1)∞--上小于零,在(1,0)-上大于零,综上所述,()0f x >的解集为(1,0)(1,)-+∞ .17.如图,在四棱锥P ABCD -中,侧棱PA ⊥底面,ABCD AB BC ⊥,且2,2,5PA AB BC AD CD =====.(1)证明:BD ⊥平面PAC ;(2)求平面PBC与平面PAD 夹角的正弦值.【答案】(1)证明见解析(2)105【解析】【分析】(1)首先证明AC BD ⊥,再利用线面垂直的性质得PA BD ⊥,最后线面垂直的判定即可证明;(2)建立合适的空间直角坐标系,求出相关平面的法向量,最后根据面面角的空间向量求法即可得到答案.【小问1详解】记AC BD O = ,如图.因为,AB BC AD CD ==,BD BD =,所以ABD CBD ≅ ,所以ADOCDO ∠=∠,由等腰三角形三线合一知90AOD COD ︒∠=∠=,即AC BD ⊥,又PA ⊥底面,ABCD BD ⊂平面ABCD ,所以PA BD ⊥,因为AC PA A ⋂=,且AC ⊂平面,PAC PA ⊂平面PAC ,所以BD ⊥平面PAC .【小问2详解】取PC 的中点M,连接OM ,则//OM PA ,所以OM ⊥平面ABCD ,所以,,OC OD OM 三条直线两两互相垂直,以,,OC OD OM 所在的直线分别为x ,y ,z 轴建立如图所示的空间直角坐标系Oxyz ,由题意及(1)知1,2OAOD ==,则(1,0,0),(0,1,0),(1,0,0),(0,2,0),(1,0,2)A B C D P ---,所以(1,2,2),(1,2,0),(1,1,2),(1,1,0)PD AD PB BC =-==--=,设平面PAD 的法向量为()111,,m x y z =,同理设平面PBC的法向量为()222,,n x y z =,则2222220n PB x y z n BC x y ⎧⋅=--=⎪⎨⋅=+=⎪⎩,可取(1,1,1)n =- .所以15cos ,553m n m n m n ⋅===-⋅⨯,所以平面PBC 与平面PAD 夹角的余弦值为155,所以平面PBC 与平面PAD 夹角的正弦值为105.【点睛】18.设函数()ln(1)(0)f x x k x k =+-≠.(1)讨论()f x 的单调区间.(2)已知直线l 是曲线()y f x =在点(,())(2)t f t t >处的切线.(i )求直线l 的方程;(ii )判断直线l 是否经过点(2,2).【答案】(1)答案见解析;(2)(i )(1)ln(1)11k kty x k t t t =++----;(ii )不经过.【解析】【分析】(1)求出函数()f x 的导数,再按0k <和0k >分类求出()f x 的单调区间.(2)(i )由(1)结合导数的几何意义求出切线l 的方程;(ii )令2x =,求出y 的值并判断与2的大小.【小问1详解】函数()ln(1)f x x k x =+-的定义域为(1,)+∞,求导得(1)()111kx k f x x x --'=+=--,当0k <时,11k ->,由()0f x '<,得11x k <<-;由()0f x '>,得1x k >-,函数()f x 在(1,1)k -上单调递减,在(1,)k -+∞上单调递增,当0k>时,11k -<,则恒有()0f x '>,函数()f x 在(1,)+∞上单调递增,所以当0k <时,函数()f x 的单调递减区间是(1,1)k -,单调递增区间是(1,)k -+∞;当0k>时,函数()f x 的单调递增区间是(1,)+∞,无递减区间.【小问2详解】(i )由(1)知,()11kf t t '=+-,而()ln(1)f t t k t =+-,则直线l 的方程为ln(1)](1))1[(y kt k t x t t +--=+--,即(1ln(1)11k kt y x k t t t =++----.(ii )由(i )知,直线l 的方程为(1)ln(1)11kkt y x k t t t =++----,当2x =时,22(1)ln(1)2[ln(1)]111k ktt y k t k t t t t -=++--=++----,令21()ln(1)1ln(1)11t g t t t t t -=+-=-+---,而2t >,求导得22112()0(1)1(1)t g t t t t -'=-+=>---,函数()g t 在(2,)+∞上单调递增,因此()(2)0g t g >=,即2t ∀>,()0g t ≠,而0k ≠,于是22[ln(1)]21tk t t -++-≠-,所以直线l 不经过点(2,2).19.设数阵111202122x x X x x ⎛⎫= ⎪⎝⎭,其中{}11122122,,,1,2,3,4,5,6x x x x ∈.设{}{}12,,,1,2,3,4,5,6k B n n n =⊆ ,其中*12,k n n n k <<<∈N 且6k ≤.定义变换t M 为“对于数阵的每一列,若其中有t 或t -,则将这一列中所有数均保持不变;若其中没有t 且没有t -,则这一列中每个数都乘以()121,,,k t n n n -= ”,()0B M X 表示“将0X 经过1n M 变换得到1X ,再将1X 经过2n M 变换得到2,X ,以此类推,最后将1k X -经过k n M 变换得到k X ”.记数阵k X 中四个数的和为()0B T X .(1)若{}021,2,534X B ⎛⎫== ⎪⎝⎭,写出0X 经过2M 变换后得到的数阵1X ,并求()0B T X 的值;(2)若{}012321,,,34X B n n n ⎛⎫== ⎪⎝⎭,求所有()0B T X 取值的和;(3)对任意确定的一个数阵0X ,证明:所有()0B T X 取值的和不大于8-;(4)如果01336X ⎛⎫= ⎪⎝⎭,其他条件不变,你研究(1)后得出什么结论?【答案】(1)0(2)40(3)证明见解析(4)()013BTX =【解析】【分析】(1)先写出12134X -⎛⎫= ⎪-⎝⎭,再计算得22134X -⎛⎫= ⎪-⎝⎭,最后相加即可;(2)分{1,2,3,4}B ⊆和{}32,3,B n =或{}331,4,,{5,6}B n n =∈以及{}11,5,6,{1,2,3,4}B n n =∈讨论即可;(3)分若1121x x ≠和1121x x =两大类讨论即可;(4)直接代入计算得11336X --⎛⎫= ⎪--⎝⎭,21336X ⎛⎫= ⎪⎝⎭即可得到答案.【小问1详解】因为021,{2,5}34X B ⎛⎫== ⎪⎝⎭,0X 经过2M 变换后得到数阵12134X -⎛⎫= ⎪-⎝⎭,1X 经过5M变换后得到数阵22134X -⎛⎫= ⎪-⎝⎭,所以()021340B T X =-+-+=.【小问2详解】若{1,2,3,4}B ⊆,则32134X -⎛⎫= ⎪-⎝⎭或32134X -⎛⎫= ⎪-⎝⎭,可得()00,4B T X =种情况;若{}32,3,B n =或{}331,4,,{5,6}B n n =∈,则32134X --⎛⎫= ⎪--⎝⎭,可得()010,4B T X =-种情况;若{}123,,B n n n =,从{1,4}和{2,3}中各取出一个元素a ,b ,12min{,},max{,},{5,6}n a b n a b n ==∈,则32134X ⎛⎫= ⎪⎝⎭,可得()010,8BT X =种情况;若{}11,5,6,{1,2,3,4}B n n =∈,则32134X -⎛⎫= ⎪-⎝⎭或32134X -⎛⎫= ⎪-⎝⎭,可得()00,4B T X =种情况.综上,所有()0BT X 取值的和为404(10)8104040⨯+⨯-+⨯+⨯=.【小问3详解】若1121x x ≠,在{1,2,3,4,5,6}的所有非空子集中,①含有11x且不含21x 的子集共42个,其中含有奇数个元素的集合有8个,经过变换后第一列均仍为1121,x x ,其中含有偶数个元素的集合有8个,经过变换后第一列均变为1121,x x --;②含有21x 且不含11x 的子集共42个,其中含有奇数个元素的集合有8个,经过变换后第一列均仍为1121,x x ,其中含有偶数个元素的集合有8个,经过变换后第一列均变为1121,x x --;③同时含有11x和21x 的子集共42个,其中含有奇数个元素的集合有8个,经过变换后第一列均变为1121,x x --,其中含有偶数个元素的集合有8个,经过变换后第一列均仍为1121,x x ;④不含11x也不含21x 的子集共421-个,其中含有奇数个元素的集合有8个,经过变换后第一列均变为1121,x x --,其中含有偶数个元素的集合有7个,经过变换后第一列均仍为1121,x x .若1121x x =,在{1,2,3,4,5,6}的所有非空子集中,①含有11x的子集共52个,其中含有奇数个元素的集合有16个,经过变换后第一列均仍为1121,x x ,其中含有偶数个元素的集合有16个,经过变换后第一列均变为1121,x x --;②不含11x的子集共521-个,其中含有奇数个元素的集合有16个,经过变换后第一列均变为1121,x x --,其中含有偶数个元素的集合有15个,经过变换后第一列均仍为1121,x x ;综上,经过变换后,所有k X 的第一列数的和为()()()112111211121(88881616)(88871615)2x x x x x x +++++--+++++++=--同理,经过变换后所有k X 的第二列数的和为()12222x x --.所以所有()0BT X 取值的和为()112112222x x x x ----,又因为11122122,,,{1,2,3,4,5,6}x x x x ∈,所以所有()0B T X 取值的和不超过8-.【小问4详解】如果01336X ⎛⎫= ⎪⎝⎭,其他条件不变,0X 经过2M 变换后得到数阵11336X --⎛⎫= ⎪--⎝⎭,1X 经过5M 变换后得到数阵21336X ⎛⎫=⎪⎝⎭,则(1)中()013B T X =.【点睛】关键点点睛:本题第三问的关键是利用分类讨论的思想,分1121x x ≠和1121x x =讨论即可.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高联难度平面几何100题二〇一七年八月目录第一题:证明角平分 (5)第二题:证明四点共圆 (6)第三题:证明角的倍数关系 (7)第四题:证明线与圆相切 (8)第五题:证明垂直 (9)第六题:证明线段相等 (10)第七题:证明线段为比例中项 (11)第八题:证明垂直 (12)第九题:证明线段相等 (13)第十题:证明角平分 (14)第十一题:证明垂直 (15)第十二题:证明线段相等 (16)第十三题:证明角相等 (17)第十四题:证明中点 (18)第十五题:证明线段的二次等式 (19)第十六题:证明角平分 (20)第十七题:证明中点 (21)第十八题:证明角相等 (22)第十九题:证明中点 (23)第二十题:证明线段相等 (24)第二十一题:证明垂直 (25)第二十二题:证明角相等 (26)第二十三题:证明四点共圆 (27)第二十四题:证明两圆相切 (28)第二十五题:证明线段相等 (29)第二十六题:证明四条线段相等 (30)第二十七题:证明线段比例等式 (31)第二十八题:证明角的倍数关系 (32)第二十九题:证明三线共点 (33)第三十题:证明平行 (34)第三十一题:证明线段相等 (35)第三十二题:证明四点共圆 (36)第三十三题:证明三角形相似 (37)第三十四题:证明角相等 (38)第三十五题:证明内心 (39)第三十六题:证明角平分 (40)第三十七题:证明垂直 (41)第三十八题:证明面积等式 (42)第三十九题:证明角平分 (43)第四十题:证明角相等 (44)第四十一题:证明中点 (45)第四十二题:证明中点 (46)第四十三题:证明角相等 (47)第四十七题:证明四点共圆 (51)第四十八题:证明四点共圆 (52)第四十九题:证明四点共圆 (53)第五十题:证明角平分 (54)第五十一题:证明线段相等 (55)第五十二题:证明两圆外切 (56)第五十三题:证明垂直 (57)第五十四题:证明垂直 (58)第五十五题:证明垂直 (59)第五十六题:证明垂直 (60)第五十七题:证中点 (61)第五十八题:证明角相等 (62)第五十九题:证明角相等 (63)第六十题:证明四点共圆 (64)第六十一题:证明四点共圆 (65)第六十二题:证明四点共圆 (66)第六十三题:证明角相等 (67)第六十四题:证明角的倍数关系 (68)第六十五题:证明中点 (69)第六十六题:伪旁切圆 (70)第六十七题:证明垂直 (71)第六十八题:证明平行 (72)第六十九题:证明圆心在某线上 (73)第七十题:证明三线共点 (74)第七十一题:证明垂直 (75)第七十二题:证明垂直 (76)第七十三题:证明中点 (77)第七十四题:证明垂直 (78)第七十五题:证明垂直 (79)第七十六题:证明三线共点 (80)第七十七题:证明平行 (81)第七十八题:证明平行 (82)第七十九题:证明三线共点、证明垂直 (83)第八十题:证明三点共线(牛顿定理) (84)第八十一题:证明角平分 (85)第八十二题:证明角相等 (86)第八十三题:证明三点共线 (87)第八十四题:证明四圆共点 (88)第八十五题:证明角平分 (89)第八十六题:证明线段相等 (90)第八十七题:证明角相等 (91)第八十八题:证明线段相等 (92)第八十九题:证明线段相等 (93)第九十三题:证明西姆松定理及逆定理 (97)第九十四题:证明线段的和差关系等式 (98)第九十五题:证明角相等 (99)第九十六题:证明托勒密定理及逆定理 (100)第九十七题:证明线段的和差关系等式 (101)第九十八题:证明角相等 (102)第九十九题:证明四点共圆 (103)第一百题:证明两三角形共内心 (104)第一题:证明角平分已知PE 、PF 是⊙O 的切线,A 、B 是一组对径点,PB 交⊙O 于另一点C ,直线AF 、BE 交于D 点。
求证:PCE PCD ∠=∠。
C DAFEOP B第二题:证明四点共圆如图,AB 是⊙O 的直径,C ,D 是圆上异于A 、B ,且在AB 同侧的两点,分别过C 、D 作⊙的O 切线,它们交于点E ,线段AD 与BC 的交点为F , 线段AB 与EF 的交点为M ,求证:E 、C 、M 、D 四点共圆。
M FD CA O EB第三题:证明角的倍数关系如图,PE 、PF 是以AB 为直径圆的切线E 、F 是切点,PB 交圆于C 点,AF 、BE 交于D 点,AB 是直径。
求证:ACD DPE ∠=∠2。
CDF EA O PB第四题:证明线与圆相切已知:ABC ∆中,︒=∠90A ,AD 切⊙ABC ,AD 交BC 延长线于D ,E 是A 关于BC 的对称点,BE AY ⊥于Y ,X 是AY 中点,延长BX 交⊙ABC 于J ,求证:BD 切AJD ∆外接圆。
F JXYEDB OC A第五题:证明垂直已知四边形ABCD 内接于以BD 为直径的圆,设'A 为A 关于BD 为对称点,'B 是B 关于AC 对称点,直线AC 交'DB 于Q ,直线DB 交'CA 于P 。
求证:AC PQ 。
P QB'A'D O B AC第六题:证明线段相等已知:BC 、BD 是⊙O 切线,C 、D 是切点,BJA 是割线,A 、J 在圆上,J 离B 较近, AO DE ⊥于E ,交AB 于F ,AC 交DE 于G ,求证:FG DF =。
G FEJD C O BA第七题:证明线段为比例中项已知ABC ∆中,BC AC =,M 是AB 的中点,FG 经过点M ,且CFG ∆与ABC ∆有相同的内心。
求证:GM FM AM ⨯=2。
GMBACF第八题:证明垂直已知:ABC ∆为非直角三角形,AD 平分BAC ∠,D 在BC 上,AC DF ⊥于F ,AB DE ⊥于E ,CE 交BF 于P 。
求证:BC AP ⊥。
HPFED ABC第九题:证明线段相等过圆O 外一点P 作圆O 的两条切线PC 、PD ,切点分别为C 、D ,过劣弧CD 上一点E 作圆O 的另一条切线分别交PC 、PD 于A 、B ,连结OE 交CD 于点N ,连结PN 交AB 于点M 。
求证:MB MA 。
MNB ACDOPE已知PA 、PB 是⊙O 切线,DE 是过C 的切线,D 、E 分别在AP 、PB 上,AB CF ⊥于F ,连接DF 、EF 。
求证:EFC DFC ∠=∠FED BAOPC设PAB 是圆O 的割线,PC 是切线,CD 是圆O 的直径,DB 、OP 相交于E 。
求证:CE AC 。
EADOBCP第十二题:证明线段相等设C、D是以O为圆心AB为直径的半圆上两点,过B做圆O的切线交CD于P,直线PO交直线CA、AD分别于E、F。
求证: OFOE 。
EFPA O BDC第十三题:证明角相等如图,ABC ∆中,D 、E 分别为AB 、AC 上一点,且BC DE //,BE 、CD 交于点F ,BDF ∆的外接圆⊙O ,与CEF ∆的外接圆⊙P 交于点G ,求证:CAG BAF ∠=∠。
GPOFEABCD第十四题:证明中点如图,⊙O 、⊙P 交于A 、B 两点,BO 、PA 延长线交于点C ,CD 、CE 分别切⊙O 、⊙P 于D 、E ,连接DE 交AB 于F ,求证:F 为DE 中点。
FEDCBA OP第十五题:证明线段的二次等式如图,半径不相等的两圆⊙O 、⊙P 交于A 、B 两点,过A 的直线CD 分别交⊙O 、⊙P 于C 、D ,CB 延长线交⊙P 于F ,DB 延长线交⊙O 于E ,过A 作CD 垂线交EF 中垂线于G ,求证:AD AC EG AG ⋅+=22GEFDB AOPC第十六题:证明角平分如图,ABC ∆内接于⊙O ,D 为BC 中点,AD 交⊙O 于E ,过E 作BC EF //,交⊙O 于F ,过C 作AC CG ⊥,交AE 于G 。
求证:FGC AGC ∠=∠。
G FEDOABC第十七题:证明中点如图,ABC 内切圆⊙I 切BC 于D ,过I 作AD IE //交BC 于E ,过E 作⊙I 切线,分别交AB 、AC 于F 、G 。
求证:E 为FG 中点。
G FECA BID第十八题:证明角相等如图,如图,⊙P 、⊙Q 交于A 、B 两点,它们的外公切线CD 分别切⊙P 、⊙Q 于C 、D ,E 为BA 延长线上一点,EC 交⊙P 于F ,ED 交⊙Q 于G ,AH 平分F A G ∠交FG 于H 。
求证:GDH FCH ∠=∠。
HGF B AQD CPE第十九题:证明中点如图,⊙O 为ABC ∆外接圆,I 、E 分别为ABC ∆的内心和一个旁心,BAC ∠的外角平分线交BC 延长线于D ,DE IF ⊥于F ,交⊙O 于G 。
求证:G 为IF 中点。
G FE I DOB CA第二十题:证明线段相等如图,在锐角ABC ∆中,C B ∠>∠,F 是BC 的中点,BE 、CD 是高。
G 、H 分别是FD 、FE 的中点,若过A 且平行于BC 的直线交GH 于I 。
求证:IF IA =IHGDEF B AC第二十一题:证明垂直如图,D 是ABC ∆边BC 上一点,ABD DAC ∠=∠,⊙O 过点B 、D 分别交AB 、AD 于E 、F ,直线BF 交DE 于G ,M 是AG 中点。
求证:AO CM ⊥。
MGFOAB CD E第二十二题:证明角相等如图,如图,CD 为⊙O 直径,PC 、PE 分别切⊙O 于C 、E ,割线PBA 交⊙O 于A 、B ,AC 、BD 交于点F ,DE 交AB 于G ,求证:ADE GFE ∠=∠。
GFBED OC PA如图,O 为ABC ∆外心,D 、E 分别为AB 、AC 上一点,DE OF ⊥于F ,L 、M 、N 分别为DE 、BE 、CD 中点。
求证:F 、L 、M 、N 四点共圆。
F NM LOABC D E如图,ABC ∆内切圆⊙I 切BC 于D ,BC AE ⊥于E ,F 为AE 中点,DF 交⊙I 于G ,作BCG ∆的外接圆⊙O ,求证:⊙O 、⊙I 相切于点G 。
OGFE D IAB C如图,ABC ∆内接于⊙O ,内切圆⊙I 分别切AB 、AC 于J 、K ,AO 交⊙O 于D ,连接DI ,延长CA 到F ,使得BJ AF =,过F 作DI 的垂线交BA 延长线于G ,求证:CK AG =。
GD OJKI AB CF第二十六题:证明四条线段相等如图,⊙O 为ABC ∆外接圆,AD 平分BAC ∠交⊙O 于D ,BD OE //交AB 于E ,CD OF //交AC 于F ,H 为ABC ∆垂心,AD HG //交BC 于G ,求证:CF GF GE BE ===。
