C03【数学】2010年高考数学计算试题分类汇编——函数
十年真题(2010_2019)高考数学真题分类汇编专题03函数概念与基本初等函数理(含解析)

专题03函数概念与基本初等函数历年考题细目表题型年份考点试题位置单选题2019 对数函数2019年新课标1理科03单选题2018 分段函数2018年新课标1理科09单选题2017 函数的奇偶性2017年新课标1理科05单选题2017 指数函数2017年新课标1理科11单选题2016 指数函数2016年新课标1理科08单选题2014 函数的奇偶性2014年新课标1理科03单选题2014 函数模型2014年新课标1理科06单选题2013 分段函数2013年新课标1理科11单选题2011 函数的奇偶性2011年新课标1理科02单选题2011 函数的对称性2011年新课标1理科12单选题2010 函数模型2010年新课标1理科04单选题2010 函数的奇偶性2010年新课标1理科08单选题2010 分段函数2010年新课标1理科11填空题2015 函数的奇偶性2015年新课标1理科13历年高考真题汇编1.【2019年新课标1理科03】已知a=log20.2,b=20.2,c=0.20.3,则()A.a<b<c B.a<c<b C.c<a<b D.b<c<a【解答】解:a=log20.2<log21=0,b=20.2>20=1,∵0<0.20.3<0.20=1,∴c=0.20.3∈(0,1),∴a<c<b,故选:B.2.【2018年新课标1理科09】已知函数f(x),g(x)=f(x)+x+a.若g(x)存在2个零点,则a的取值范围是()A.[﹣1,0)B.[0,+∞)C.[﹣1,+∞)D.[1,+∞)【解答】解:由g(x)=0得f(x)=﹣x﹣a,作出函数f(x)和y=﹣x﹣a的图象如图:当直线y=﹣x﹣a的截距﹣a≤1,即a≥﹣1时,两个函数的图象都有2个交点,即函数g(x)存在2个零点,故实数a的取值范围是[﹣1,+∞),故选:C.3.【2017年新课标1理科05】函数f(x)在(﹣∞,+∞)单调递减,且为奇函数.若f(1)=﹣1,则满足﹣1≤f(x﹣2)≤1的x的取值范围是()A.[﹣2,2] B.[﹣1,1] C.[0,4] D.[1,3]【解答】解:∵函数f(x)为奇函数.若f(1)=﹣1,则f(﹣1)=1,又∵函数f(x)在(﹣∞,+∞)单调递减,﹣1≤f(x﹣2)≤1,∴f(1)≤f(x﹣2)≤f(﹣1),∴﹣1≤x﹣2≤1,解得:x∈[1,3],故选:D.4.【2017年新课标1理科11】设x、y、z为正数,且2x=3y=5z,则()A.2x<3y<5z B.5z<2x<3y C.3y<5z<2x D.3y<2x<5z【解答】解:x、y、z为正数,令2x=3y=5z=k>1.lgk>0.则x,y,z.∴3y,2x,5z.∵,.∴lg0.∴3y<2x<5z.另解:x、y、z为正数,令2x=3y=5z=k>1.lgk>0.则x,y,z.∴1,可得2x>3y,1.可得5z>2x.综上可得:5z>2x>3y.解法三:对k取特殊值,也可以比较出大小关系.故选:D.5.【2016年新课标1理科08】若a>b>1,0<c<1,则()A.a c<b c B.ab c<ba cC.a log b c<b log a c D.log a c<log b c【解答】解:∵a>b>1,0<c<1,∴函数f(x)=x c在(0,+∞)上为增函数,故a c>b c,故A错误;函数f(x)=x c﹣1在(0,+∞)上为减函数,故a c﹣1<b c﹣1,故ba c<ab c,即ab c>ba c;故B错误;log a c<0,且log b c<0,log a b<1,即1,即log a c>log b c.故D错误;0<﹣log a c<﹣log b c,故﹣b log a c<﹣a log b c,即b log a c>a log b c,即a log b c<b log a c,故C正确;故选:C.6.【2014年新课标1理科03】设函数f(x),g(x)的定义域都为R,且f(x)是奇函数,g(x)是偶函数,则下列结论正确的是()A.f(x)•g(x)是偶函数B.|f(x)|•g(x)是奇函数C.f(x)•|g(x)|是奇函数D.|f(x)•g(x)|是奇函数【解答】解:∵f(x)是奇函数,g(x)是偶函数,∴f(﹣x)=﹣f(x),g(﹣x)=g(x),f(﹣x)•g(﹣x)=﹣f(x)•g(x),故函数是奇函数,故A错误,|f(﹣x)|•g(﹣x)=|f(x)|•g(x)为偶函数,故B错误,f(﹣x)•|g(﹣x)|=﹣f(x)•|g(x)|是奇函数,故C正确.|f(﹣x)•g(﹣x)|=|f(x)•g(x)|为偶函数,故D错误,故选:C.7.【2014年新课标1理科06】如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P作直线OA的垂线,垂足为M,将点M到直线OP的距离表示为x的函数f(x),则y=f(x)在[0,π]的图象大致为()A.B.C.D.【解答】解:在直角三角形OMP中,OP=1,∠POM=x,则OM=|cos x|,∴点M到直线OP的距离表示为x的函数f(x)=OM|sin x|=|cos x|•|sin x||sin2x|,其周期为T,最大值为,最小值为0,故选:C.8.【2013年新课标1理科11】已知函数f(x),若|f(x)|≥ax,则a的取值范围是()A.(﹣∞,0] B.(﹣∞,1] C.[﹣2,1] D.[﹣2,0]【解答】解:由题意可作出函数y=|f(x)|的图象,和函数y=ax的图象,由图象可知:函数y=ax的图象为过原点的直线,当直线介于l和x轴之间符合题意,直线l为曲线的切线,且此时函数y=|f(x)|在第二象限的部分解析式为y=x2﹣2x,求其导数可得y′=2x﹣2,因为x≤0,故y′≤﹣2,故直线l的斜率为﹣2,故只需直线y=ax的斜率a介于﹣2与0之间即可,即a∈[﹣2,0]故选:D.9.【2011年新课标1理科02】下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是()A.y=2x3B.y=|x|+1 C.y=﹣x2+4 D.y=2﹣|x|【解答】解:对于A.y=2x3,由f(﹣x)=﹣2x3=﹣f(x),为奇函数,故排除A;对于B.y=|x|+1,由f(﹣x)=|﹣x|+1=f(x),为偶函数,当x>0时,y=x+1,是增函数,故B正确;对于C.y=﹣x2+4,有f(﹣x)=f(x),是偶函数,但x>0时为减函数,故排除C;对于D.y=2﹣|x|,有f(﹣x)=f(x),是偶函数,当x>0时,y=2﹣x,为减函数,故排除D.故选:B.10.【2011年新课标1理科12】函数y的图象与函数y=2sinπx,(﹣2≤x≤4)的图象所有交点的横坐标之和等于()A.8 B.6 C.4 D.2【解答】解:函数y1,y2=2sinπx的图象有公共的对称中心(1,0),作出两个函数的图象,如图,当1<x≤4时,y1<0而函数y2在(1,4)上出现1.5个周期的图象,在(1,)和(,)上是减函数;在(,)和(,4)上是增函数.∴函数y1在(1,4)上函数值为负数,且与y2的图象有四个交点E、F、G、H相应地,y1在(﹣2,1)上函数值为正数,且与y2的图象有四个交点A、B、C、D且:x A+x H=x B+x G=x C+x F=x D+x E=2,故所求的横坐标之和为8.故选:A.11.【2010年新课标1理科04】如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P0(,),角速度为1,那么点P到x轴距离d关于时间t的函数图象大致为()A.B.C.D.【解答】解:通过分析可知当t=0时,点P到x轴距离d为,于是可以排除答案A,D,再根据当时,可知点P在x轴上此时点P到x轴距离d为0,排除答案B,故选:C.12.【2010年新课标1理科08】设偶函数f(x)满足f(x)=2x﹣4(x≥0),则{x|f(x﹣2)>0}=()A.{x|x<﹣2或x>4} B.{x|x<0或x>4} C.{x|x<0或x>6} D.{x|x<﹣2或x>2}【解答】解:由偶函数f(x)满足f(x)=2x﹣4(x≥0),可得f(x)=f(|x|)=2|x|﹣4,则f(x﹣2)=f(|x﹣2|)=2|x﹣2|﹣4,要使f(|x﹣2|)>0,只需2|x﹣2|﹣4>0,|x﹣2|>2解得x>4,或x<0.应选:B.13.【2010年新课标1理科11】已知函数,若a,b,c互不相等,且f(a)=f (b)=f(c),则abc的取值范围是()A.(1,10)B.(5,6)C.(10,12)D.(20,24)【解答】解:作出函数f(x)的图象如图,不妨设a<b<c,则ab=1,则abc=c∈(10,12).故选:C.14.【2015年新课标1理科13】若函数f(x)=xln(x)为偶函数,则a=.【解答】解:∵f(x)=xln(x)为偶函数,∴f(﹣x)=f(x),∴(﹣x)ln(﹣x)=xln(x),∴﹣ln(﹣x)=ln(x),∴ln(﹣x)+ln(x)=0,∴ln(x)(x)=0,∴lna=0,∴a=1.故答案为:1.考题分析与复习建议本专题考查的知识点为:函数,函数的单调性与最值,函数的奇偶性与周期性,幂函数与二次函数,指数函数,对数函数,分段函数,函数的图象,函数与方程等.历年考题主要以选择填空题型出现,重点考查的知识点为:函数的单调性与最值,函数的奇偶性与周期性,指数函数,对数函数,分段函数,函数的图象,函数与方程等.预测明年本考点题目会比较稳定,备考方向以知识点函数的单调性与最值,函数的奇偶性与周期性,指数函数,对数函数,分段函数,函数的图象,函数与方程等为重点较佳.最新高考模拟试题1.已知()21f x ax bx =-+是定义域为[a ,a +1]的偶函数,则2b a a -=( )A .0B .34C D .4【答案】B 【解析】∵f (x )在[a ,a +1]上是偶函数, ∴﹣a =a +1⇒a 12=-, 所以f (x )的定义域为[12-,12], 故:f (x )12=-x 2﹣bx +1, ∵f (x )在区间[12-,12]上是偶函数,有f (12-)=f (12),代入解析式可解得:b =0;∴2b a a -13144=-=.故选:B .2.已知函数()y f x =的定义域为R ,)1(+x f 为偶函数,且对121x x ∀<≤,满足()()01212<--x x x f x f .若(3)1f =,则不等式()2log 1f x <的解集为( )A .1,82⎛⎫ ⎪⎝⎭B .)8,1(C .10,(8,)2⎛⎫⋃+∞ ⎪⎝⎭D .(,1)(8,)-∞⋃+∞【答案】A 【解析】因为对121x x ∀<≤,满足()()01212<--x x x f x f ,所以()y f x =当1≤x 时,是单调递减函数,又因为)1(+x f 为偶函数,所以()y f x =关于1x =对称,所以函数()y f x =当1>x 时,是增函数,又因为(3)1f =,所以有1)1(=-f ,当2log 1x ≤时,即当02x <≤时,()()222log 1log (11log 2221)1f x f x x x x f <⇒<-⇒>-⇒>∴<≤当2log 1x >时,即当2x >时,()()222log 1log (3)log 3828x x f x f x f x <⇒<⇒∴<<⇒<<,综上所述:不等式()2log 1f x <的解集为1,82⎛⎫ ⎪⎝⎭,故本题选A.3.函数22()log (34)f x x x =--的单调减区间为( )A .(,1)-∞-B .3(,)2-∞-C .3(,)2+∞D .(4,)+∞【答案】A 【解析】函数()()22log 34f x x x =--,所以 2340(4)(1)04x x x x x -->⇒-+>⇒>或1x <-,所以函数()f x 的定义域为4x >或1x <-,234y x x =--当3(,)2-∞时,函数是单调递减,而1x <-,所以函数()()22log 34f x x x =--的单调减区间为(),1-∞-,故本题选A 。
2010年高考数学真题分类汇编(老人教)考点4 函数的性质

考点4 函数的性质1.(2010·湖北高考文科·T5)函数y =的定义域为 A.( 34,1) B(34,+∞) C (1,+∞) D. ( 34,1)∪(1,+∞) 【命题立意】本题主要考查函数定义域的求法及对数函数单调性的应用,考查考生的运算求解能力.【思路点拨】分母不为0且被开方数大于或等于0⇒0.5log (43)0x ->⇒043x <-<1解该不等式即可。
【规范解答】选A ,由0.5log (43)0x ->得043x <-<1解得34x <<1。
【方法技巧】1、已知解析式的函数求定义域时要注意:(1)、分式的分母不为0;(2)、开偶次方根式被开方数要非负;(3)、对数的真数要为正,对数的底数须大于零且不为1。
2、已知函数[()]y f g x =的定义域求函数[()]y f h x =的定义域:[()]y f g x =的定义域()x g x −−−−−−−−−→已知的范围求的取值范围()y f x =的定义域()h x x −−−−−−−−−→已知的取值范围求的范围[()]y f h x =的定义域。
2.(2010·全国Ⅰ文科·T7)已知函数()|lg |f x x =.若a b ≠,且()()f a f b =,则a b +的取值范围是(A)(1,)+∞ (B)[1,)+∞(C) (2,)+∞ (D) [2,)+∞【命题立意】本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a 的取值范围,而利用均值不等式求得a+b=12a a +≥,从而错选D,这也是命题者的用心良苦之处. 【思路点拨】根据题意运用两种思路解答:思路1:运用“对勾”函数求解;思路2:运用将a b +看成目标函数,运用线性规划求解.【规范解答】因为 f(a)=f(b),所以|lga|=|lgb|,所以a=b(舍去),或1b a =,所以a+b=1a a + 又0<a<b,所以0<a<1<b ,令2()f a =1a a+由“对勾”函数的性质知函数()f a 在a ∈(0,1)上为减函数,所以f(a)>f(1)=1+1=2,即a+b 的取值范围是(2,+∞).【解析2】由0<a<b,且f (a )=f (b )得:0111a b ab <<⎧⎪<⎨⎪=⎩,利用线性规划得:0111x y xy <<⎧⎪<⎨⎪=⎩,化为求z x y =+的取值范围问题,z x y y x z =+⇒=-+,2111y y x x'=⇒=-<-⇒过点()1,1时z 最小为2,∴(C) (2,)+∞3.(2010·全国Ⅰ理科·T10)已知函数()|lg |f x x =,若b a <<0,且)()(b f a f =,则b a 2+的取值范围是( )(A))+∞(B))+∞ (C)(3,)+∞ (D)[3,)+∞【命题立意】本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a 的取值范围,而利用均值不等式求得a+2b 2a a=+>,从而错选A,这也是命题者的用心良苦之处. 【思路点拨】根据题意运用两种思路解答:思路1:运用“对勾”函数求解;思路2:运用将b a 2+看成目标函数,运用线性规划求解.【规范解答】选C.【解析1】因为 f(a)=f(b),所以|lga|=|lgb|,所以a=b(舍去),或1b a =,所以a+2b=2a a + 又0<a<b,所以0<a<1<b ,令2()f a a a =+,由“对勾”函数的性质知函数()f a 在a ∈(0,1)上为减函数,所以f(a)>f(1)=1+21=3,即a+2b 的取值范围是(3,+∞). 【解析2】由0<a<b,且f (a )=f (b )得:0111a b ab <<⎧⎪<⎨⎪=⎩,利用线性规划得:0111x y xy <<⎧⎪<⎨⎪=⎩,求2z x y =+的取值范围问题,11222z x y y x z =+⇒=-+,2111y y x x'=⇒=-<-⇒过点()1,1时z 最小为3,∴(C)(3,)+∞4.(2010·重庆高考理科·T15)已知函数()f x 满足:()114f =,()()()()4f x f y f x y f x y =++-(),x y R ∈,则()2010f =_____________. 【命题立意】本小题考查函数的有关性质,考查赋值运算求解的能力,考查探究规律、归纳概括的能力.【思路点拨】赋予x ,y 特殊值,分别求出(0)f ,(2),(3),(4),(5)f f f f ,(6)f ,(7),(8)f f ,……等值,归纳概括找出规律,最后求出()2010f 的值;或根据已知条件推导出函数具有周期性. 【规范解答】12 (方法一)令1,0x y ==,则4(1)(0)(1)(1)f f f f =+,所以1(0)2f =; 令1x y ==,则4(1)(1)(2)(0)f f f f =+,所以1(2)4f =-;令2,1x y ==,则4(2)(1)(3)(1)f f f f =+,所以1(3)2f =-; 令2x y ==,则4(2)(2)(4)(0)f f f f =+,所以1(4)4f =-; 令4,1x y ==,则4(4)(1)(5)(3)f f f f =+,所以1(5)4f =; 令3x y ==,则4(3)(3)(6)(0)f f f f =+,所以1(6)2f =; 令6,1x y ==,则4(6)(1)(7)(5)f f f f =+,所以1(7)4f =; ……函数值以6为周期循环出现,又因为20103356=,所以1(2010)(3356)2f f =⨯=. (方法二)令1y =,则4()(1)(1)(1)f x f f x f x =++-,所以()(1)(1)f x f x f x =++-,所以(1)()(2)(1)(1)(2)f x f x f x f x f x f x +=++=++-++,所以(1)(2)f x f x -=-+,即()(3)f x f x =-+,所以(6)()f x f x +=,即函数()f x 是周期为6的函数,有1(0)2f =,所以1(2010)(33560)(0)2f f f =⨯+==. 【方法技巧】方法一是应用归纳得出的结论求值,需要求出多个函数值才发现规律;方法二是巧妙推导出周期函数的结论,减少了运算.5.(2010·湖北高考理科·T17)为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C (单位:万元)与隔热层厚度x (单位:cm )满足关系:()()01035k C x x x =≤≤+,若不建隔热层,每年能源消耗费用为8万元.设()f x 为隔热层建造费用与20年的能源消耗费用之和.(Ⅰ)求k 的值及()f x 的表达式;(Ⅱ)隔热层修建多厚时,总费用()f x 达到最小,并求最小值.【命题立意】本题主要考查由实际问题求函数解析式、利用导数求函数最值,考查考生的阅读理解及运算求解能力.【思路点拨】(0)8C =⇒k 的值20−−−−−−−−−−−−→隔热层建造费用与年的能源消耗费用相加()f x 的表达式−−−−→利用导数()f x 的最小值 【规范解答】(Ⅰ)设隔热层厚度x cm ,由题意建筑物每年的能源消耗费用为()()01035k C x x x =≤≤+,再由(0)8C =得40k =,故()()4001035C x x x =≤≤+;又x 厘米厚的隔热层建造费用为6x ,所以由题意()f x =402035x ⨯++6x =80035x ++6x ()010x ≤≤。
2010全国各地高考数学理科试题分类汇编函数

2010全国各地高考数学理科试题分类汇编函数与导数1安徽17、(本小题满分12分)设a 为实数,函数()22,xf x e x a x =-+∈R 。
(Ⅰ)求()f x 的单调区间与极值;(Ⅱ)求证:当ln 21a >-且0x >时,221x e x ax >-+。
2福建20.(本小题满分14分)(Ⅰ)已知函数3(x)=x -x f ,其图象记为曲线C 。
(i )求函数(x)f 的单调区间;(ii )证明:若对于任意非零实数1x ,曲线C 与其在点111P (x ,f(x ))处的切线交于另一点222P (x ,f(x )),曲线C 与其在点222P (x ,f(x ))处的切线交于另一点333P (x ,f(x )),线段11223122P P ,P P ,S ,S C S 与曲线所围成封闭图形的面积分别记为S 则为定值;(Ⅱ)对于一般的三次函数32g(x)=ax +bx +cx+d(a 0),≠请给出类似于(Ⅰ)(ii )的正确命题,并予以证明。
3新课标全国卷(21)(本小题满分12分)设函数2()1x f x e x ax =---。
(1) 若0a =,求()f x 的单调区间; (2) 若当0x ≥时()0f x ≥,求a 的取值范围4 北京(18)(本小题共13分)已知函数2()ln(1)(0)2k f x x x x k =+-+≥(Ⅰ)当k =2时,求曲线y =f (x )在点(1,(1)f )处的切线方程; (Ⅱ)求f (x )的单调区间。
5浙江2222)(本题满分14分)已知a 是给定的实常数,设函数22()()()f x x a x b e =-+,b R ∈, x a =是()f x 的一个极大值点.(Ⅰ)求b 的取值范围;(Ⅱ)设123,,x x x 是()f x 的3个极值点,问是否存在实数b ,可找到4x R ∈,使得1234,,,x x x x的某种排列1234,,,i i i i x x x x (其中{}1234,,,i i i i ={}1,2,3,4)依次成等差数列?若存在,求所有的b及相应的4x ;若不存在,说明理由.6辽宁21)(本小题满分12分)已知函数1ln )1()(2+++=ax x a x f (I )讨论函数)(x f 的单调性;(II )设1-<a .如果对任意),0(,21+∞∈x x ,||4)()(|2121x x x f x f -≥-,求a 的取值范围。
十年高考真题分类汇编2010-2019数学专题03函数Word版含解析

【解析】∵f(x+1)=2f(x),∴f(x)=2f(x-1).
∵当 x∈(0,1]时,f(x)=x(x-1),
∴f(x)的图象如图所示.
∵当 2<x≤3 时,f(x)=4f(x-2)=4(x-2)(x-3),
∴令 4(x-2)(x-3)=- , 整理得 9x2-45x+56=0,
即(3x-7)(3x-8)=0,
转 后与原图像重合,则在以下各项中,f(1)的可能取值只能是( )
6
A. 3
B. 3
2
【答案】B
C. 3
D.0
3
【解析】若 f(1)= 3,则 f( 3)=1,f(1)=- 3,与函数的定义矛盾,舍去;
若 f(1)= 3,则 f 2 3 =0,f(1)=- 3,与函数的定义矛盾,舍去;
3
3
3
若 f(1)=0,则 f 1
(a
+
1)x2
+
ax,x
≥
0.若函数
y=f(x)-ax-b
恰有
3
个零点,
则( )
A.a<-1,b<0 B.a<-1,b>0
C.a>-1,b<0 D.a>-1,b>0
【答案】C
【解析】当 x<0 时,由 x=ax+b,得 x= b ,最多一个零点 取决于 x= b 与 0 的大小 ,所以关键研究当 x≥0 时,
A.f
log3
1 4
>f(2-
32)>f(2-
2 3
)
B.f
log3
1 4
>f(2-
23)>f(2-
2010年高考数学真题分类汇编(老人教)考点4 函数的性质

考点4 函数的性质1.(2010·湖北高考文科·T5)函数y =的定义域为 A.( 34,1) B(34,+∞) C (1,+∞) D. ( 34,1)∪(1,+∞) 【命题立意】本题主要考查函数定义域的求法及对数函数单调性的应用,考查考生的运算求解能力.【思路点拨】分母不为0且被开方数大于或等于0⇒0.5log (43)0x ->⇒043x <-<1解该不等式即可。
【规范解答】选A ,由0.5log (43)0x ->得043x <-<1解得34x <<1。
【方法技巧】1、已知解析式的函数求定义域时要注意:(1)、分式的分母不为0;(2)、开偶次方根式被开方数要非负;(3)、对数的真数要为正,对数的底数须大于零且不为1。
2、已知函数[()]y f g x =的定义域求函数[()]y f h x =的定义域:[()]y f g x =的定义域()x g x −−−−−−−−−→已知的范围求的取值范围()y f x =的定义域()h x x −−−−−−−−−→已知的取值范围求的范围[()]y f h x =的定义域。
2.(2010·全国Ⅰ文科·T7)已知函数()|lg |f x x =.若a b ≠,且()()f a f b =,则a b +的取值范围是(A)(1,)+∞ (B)[1,)+∞(C) (2,)+∞ (D) [2,)+∞【命题立意】本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a 的取值范围,而利用均值不等式求得a+b=12a a +≥,从而错选D,这也是命题者的用心良苦之处. 【思路点拨】根据题意运用两种思路解答:思路1:运用“对勾”函数求解;思路2:运用将a b +看成目标函数,运用线性规划求解.【规范解答】因为 f(a)=f(b),所以|lga|=|lgb|,所以a=b(舍去),或1b a =,所以a+b=1a a + 又0<a<b,所以0<a<1<b ,令()f a a=1a +由“对勾”函数的性质知函数()f a 在a ∈(0,1)上为减函数,所以f(a)>f(1)=1+1=2,即a+b 的取值范围是(2,+∞).【解析2】由0<a<b,且f (a )=f (b )得:0111a b ab <<⎧⎪<⎨⎪=⎩,利用线性规划得:0111x y xy <<⎧⎪<⎨⎪=⎩,化为求z x y =+的取值范围问题,z x y y x z =+⇒=-+,2111y y x x'=⇒=-<-⇒过点()1,1时z 最小为2,∴(C) (2,)+∞3.(2010·全国Ⅰ理科·T10)已知函数()|lg |f x x =,若b a <<0,且)()(b f a f =,则b a 2+的取值范围是( )(A))+∞(B))+∞ (C)(3,)+∞ (D)[3,)+∞【命题立意】本小题主要考查对数函数的性质、函数的单调性、函数的值域,考生在做本小题时极易忽视a 的取值范围,而利用均值不等式求得a+2b 2a a=+>,从而错选A,这也是命题者的用心良苦之处. 【思路点拨】根据题意运用两种思路解答:思路1:运用“对勾”函数求解;思路2:运用将b a 2+看成目标函数,运用线性规划求解.【规范解答】选C.【解析1】因为 f(a)=f(b),所以|lga|=|lgb|,所以a=b(舍去),或1b a =,所以a+2b=2a a + 又0<a<b,所以0<a<1<b ,令2()f a a a =+,由“对勾”函数的性质知函数()f a 在a ∈(0,1)上为减函数,所以f(a)>f(1)=1+21=3,即a+2b 的取值范围是(3,+∞). 【解析2】由0<a<b,且f (a )=f (b )得:0111a b ab <<⎧⎪<⎨⎪=⎩,利用线性规划得:0111x y xy <<⎧⎪<⎨⎪=⎩,求2z x y =+的取值范围问题,11222z x y y x z =+⇒=-+,2111y y x x'=⇒=-<-⇒过点()1,1时z 最小为3,∴(C)(3,)+∞ 4.(2010·重庆高考理科·T15)已知函数()f x 满足:()114f =,()()()()4f x f y f x y f x y =++-(),x y R ∈,则()2010f =_____________. 【命题立意】本小题考查函数的有关性质,考查赋值运算求解的能力,考查探究规律、归纳概括的能力.【思路点拨】赋予x ,y 特殊值,分别求出(0)f ,(2),(3),(4),(5)f f f f ,(6)f ,(7),(8)f f ,……等值,归纳概括找出规律,最后求出()2010f 的值;或根据已知条件推导出函数具有周期性. 【规范解答】12(方法一)令1,0x y ==,则4(1)(0)(1)(1)f f f f =+,所以1(0)2f =; 令1x y ==,则4(1)(1)(2)(0)f f f f =+,所以1(2)4f =-; 令2,1x y ==,则4(2)(1)(3)(1)f f f f =+,所以1(3)2f =-;令2x y ==,则4(2)(2)(4)(0)f f f f =+,所以1(4)4f =-; 令4,1x y ==,则4(4)(1)(5)(3)f f f f =+,所以1(5)4f =; 令3x y ==,则4(3)(3)(6)(0)f f f f =+,所以1(6)2f =; 令6,1x y ==,则4(6)(1)(7)(5)f f f f =+,所以1(7)4f =; ……函数值以6为周期循环出现,又因为20103356=,所以1(2010)(3356)2f f =⨯=. (方法二)令1y =,则4()(1)(1)(1)f x f f x f x =++-,所以()(1)(1)f x f x f x =++-,所以(1)()(2)(1)(1)(2)f x f x f x f x f x f x +=++=++-++,所以(1)(2)f x f x -=-+,即()(3)f x f x =-+,所以(6)()f x f x +=,即函数()f x 是周期为6的函数,有1(0)2f =,所以1(2010)(33560)(0)2f f f =⨯+==. 【方法技巧】方法一是应用归纳得出的结论求值,需要求出多个函数值才发现规律;方法二是巧妙推导出周期函数的结论,减少了运算.5.(2010·湖北高考理科·T17)为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C (单位:万元)与隔热层厚度x (单位:cm )满足关系:()()01035k C x x x =≤≤+,若不建隔热层,每年能源消耗费用为8万元.设()f x 为隔热层建造费用与20年的能源消耗费用之和. (Ⅰ)求k 的值及()f x 的表达式;(Ⅱ)隔热层修建多厚时,总费用()f x 达到最小,并求最小值.【命题立意】本题主要考查由实际问题求函数解析式、利用导数求函数最值,考查考生的阅读理解及运算求解能力.【思路点拨】(0)8C =⇒k 的值20−−−−−−−−−−−−→隔热层建造费用与年的能源消耗费用相加()f x 的表达式−−−−→利用导数()f x 的最小值 【规范解答】(Ⅰ)设隔热层厚度x cm ,由题意建筑物每年的能源消耗费用为()()01035k C x x x =≤≤+,再由(0)8C =得40k =,故()()4001035C x x x =≤≤+;又x 厘米厚的隔热层建造费用为6x ,所以由题意()f x =402035x ⨯++6x =80035x ++6x ()010x ≤≤。
2010年高考分类汇编之函数的概念及基本性质

函数的概念及基本性质◆2010年高考一、选择题2. (2010重庆,4)函数164xy =-的值域是 (A )[0,)+∞ (B )[0,4] (C )[0,4) (D )(0,4)3.(2010山东,5)设()f x 为定义在R 上的奇函数,当0x ≥时,()22xf x x b =++(b 为常数),则(1)f -=(A )-3 (B )-1 (C )1 (D)34.(2010广东,3)若函数f (x )=3x +3-x 与g (x )=3x -3-x 的定义域均为R ,则A .f (x )与g (x )均为偶函数 B. f (x )为偶函数,g (x )为奇函数C .f (x )与g (x )均为奇函数 D. f (x )为奇函数,g (x )为偶函数13. (2010辽宁,10)设25a b m ==,且112a b +=,则m = (A )10 (B )10 (C )20 (D )100 ★福建5年高考:15.(2009福建,2)下列函数中,与函数1y x =有相同定义域的是 A ()ln f x x = B 1()f x x = C ()||f x x = D ()x f x e =16.(2008福建,4)函数f (x )=x 3+sin x +1(x ∈R),若f (a )=2,则f (-a )的值为A.3B.0C.-1D.-218.(2006福建,12)已知()f x 是R 上的减函数,则满足1()(1)f f x >的实数x 的取值范围是( ) A .(,1)-∞ B .(1,)+∞ C .(,0)(0,1)-∞ D .(,0)(1,)-∞+∞二、填空题19. (2010陕西,13)已知函数f (x )=232,1,,1,x x x ax x +<⎧⎨+≥⎩若f (f (0))=4a ,则实数a = .三、计算题22.(08福建,21)(本小题满分12分)已知函数32()2f x x m x nx =++-的图象过点(-1,-6),且函数()()6g x f x x '=+的图象关于y 轴对称. (Ⅰ)求m 、n 的值及函数y =f (x )的单调区间;(Ⅱ)若a >0,求函数y =f (x )在区间(a -1,a +1)内的极值.。
2010年高考数学填空题试题分类汇编——三角函数

sin2 (2x
) 的最小正周期是 4
。
答案: 2
(2010山东文数)(15) 在 ABC 中,角 A,B,C 所对的边分别为 a,b,c,若 a 2 ,
b 2 , sin B cos B 2 ,则角 A 的大小为
.
答案:
( 2010北 京 文 数 )( 10) 在 ABC 中 。 若 b 1, c
m
1280cos 8 a +
1120cos 6 a +
n cos4 a +
p cos
a-
1.
可以推测,m – n + p =
.
2
【答案】962
【解析】因为 2 21, 8 23, 32 25, 128 27 , 所以 m 29 512 ;观察可得 n 400,
p 50,所以 m – n + p =962。
2010年高考数学填空题试题分类汇编——三角函数
(2010浙江理数)(11)函数 f (x)
sin(2x
) 4
2 2 sin2 x 的最小正周期是
__________________ .
fx
解析:
2 sin 2x
2
4
相关公式,属中档题
2 故最小正周期为π,本题主要考察了三角恒等变换及
( 2010全 国 卷 2 理 数 )( 13) 已 知 a 是 第 二 象 限 的 角 , tan( 2a)
【解析】因为 为第二象限的角,又 sin
3 , 所以 cos 5
4 , tan sin
5
cos
tan(2 ) 12 ttaann2
24 7
3 ,所 4
-3-
( 2010全 国 卷 1 理 数 ) (14)已 知 为 第 三 象 限 的 角 , cos 2
十年真题(2010-近年)高考数学真题分类汇编专题03函数概念与基本初等函数文(含解析)(最新整理)
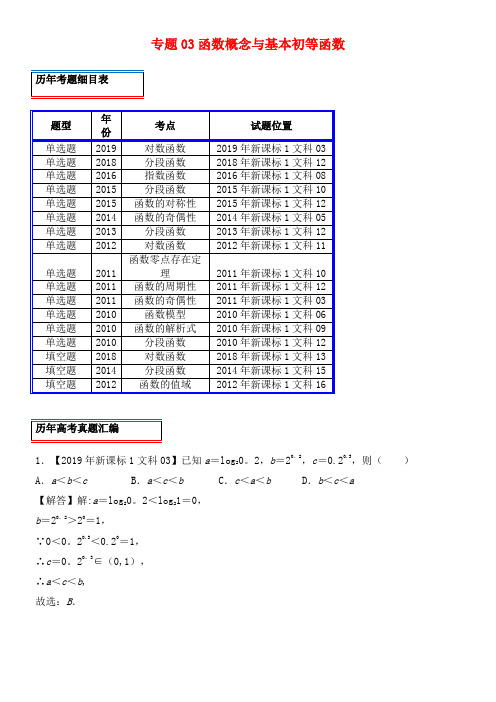
专题03函数概念与基本初等函数1.【2019年新课标1文科03】已知a=log20。
2,b=20。
2,c=0.20.3,则()A.a<b<c B.a<c<b C.c<a<b D.b<c<a【解答】解:a=log20。
2<log21=0,b=20。
2>20=1,∵0<0。
20.3<0.20=1,∴c=0。
20。
3∈(0,1),∴a<c<b,故选:B.2.【2018年新课标1文科12】设函数f(x),则满足f(x+1)<f(2x)的x的取值范围是()A.(﹣∞,﹣1]B.(0,+∞)C.(﹣1,0)D.(﹣∞,0)【解答】解:函数f(x),的图象如图:满足f(x+1)<f(2x),可得:2x<0<x+1或2x<x+1≤0,解得x∈(﹣∞,0).故选:D.3.【2016年新课标1文科08】若a>b>0,0<c<1,则()A.log a c<log b c B.log c a<log c bC.a c<b c D.c a>c b【解答】解:∵a>b>0,0<c<1,∴log c a<log c b,故B正确;∴当a>b>1时,0>log a c>log b c,故A错误;a c>b c,故C错误;c a<c b,故D错误;故选:B.4.【2015年新课标1文科10】已知函数f(x),且f(a)=﹣3,则f (6﹣a)=()A.B.C.D.【解答】解:由题意,a≤1时,2α﹣1﹣2=﹣3,无解;a>1时,﹣log(a+1)=﹣3,∴α=7,2∴f(6﹣a)=f(﹣1)=2﹣1﹣1﹣2.故选:A.5.【2015年新课标1文科12】设函数y=f(x)的图象与y=2x+a的图象关于y=﹣x对称,且f(﹣2)+f(﹣4)=1,则a=()A.﹣1 B.1 C.2 D.4【解答】解:∵与y=2x+a的图象关于y=x对称的图象是y=2x+a的反函数,x﹣a(x>0),y=log2即g(x)=log2x﹣a,(x>0).∵函数y=f(x)的图象与y=2x+a的图象关于y=﹣x对称,∴f(x)=﹣g(﹣x)=﹣log2(﹣x)+a,x<0,∵f(﹣2)+f(﹣4)=1,∴﹣log22+a﹣log24+a=1,解得,a=2,故选:C.6.【2014年新课标1文科05】设函数f(x),g(x)的定义域都为R,且f(x)是奇函数,g(x)是偶函数,则下列结论正确的是( )A.f(x)•g(x)是偶函数B.|f(x)|•g(x)是奇函数C.f(x)•|g(x)|是奇函数D.|f(x)•g(x)|是奇函数【解答】解:∵f(x)是奇函数,g(x)是偶函数,∴f(﹣x)=﹣f(x),g(﹣x)=g(x),f(﹣x)•g(﹣x)=﹣f(x)•g(x),故函数是奇函数,故A错误,|f(﹣x)|•g(﹣x)=|f(x)|•g(x)为偶函数,故B错误,f(﹣x)•|g(﹣x)|=﹣f(x)•|g(x)|是奇函数,故C正确.|f(﹣x)•g(﹣x)|=|f(x)•g(x)|为偶函数,故D错误,故选:C.7.【2013年新课标1文科12】已知函数f(x),若|f(x)|≥ax,则a 的取值范围是( )A.(﹣∞,0]B.(﹣∞,1] C.[﹣2,1] D.[﹣2,0]【解答】解:由题意可作出函数y=|f(x)|的图象,和函数y=ax的图象,由图象可知:函数y=ax的图象为过原点的直线,当直线介于l和x轴之间符合题意,直线l 为曲线的切线,且此时函数y=|f(x)|在第二象限的部分解析式为y=x2﹣2x,求其导数可得y′=2x﹣2,因为x≤0,故y′≤﹣2,故直线l的斜率为﹣2,故只需直线y=ax的斜率a介于﹣2与0之间即可,即a∈[﹣2,0]故选:D.8.【2012年新课标1文科11】当0<x时,4x<log a x,则a的取值范围是() A.(0,)B.(,1)C.(1,)D.(,2)【解答】解:∵0<x时,1<4x≤2要使4x<log a x,由对数函数的性质可得0<a<1,数形结合可知只需2<log a x,∴即对0<x时恒成立∴解得a<1故选:B.9.【2011年新课标1文科10】在下列区间中,函数f(x)=e x+4x﹣3的零点所在的区间为()A.(,)B.(,0)C.(0,)D.(,)【解答】解:∵函数f(x)=e x+4x﹣3∴f′(x)=e x+4当x>0时,f′(x)=e x+4>0∴函数f(x)=e x+4x﹣3在(﹣∞,+∞)上为f(0)=e0﹣3=﹣2<0f()1>0f()20∵f()•f()<0,∴函数f(x)=e x+4x﹣3的零点所在的区间为(,)故选:A.10.【2011年新课标1文科12】已知函数y=f(x)的周期为2,当x∈[﹣1,1]时f(x)=x2,那么函数y=f(x)的图象与函数y=|lgx|的图象的交点共有()A.10个B.9个C.8个D.1个【解答】解:作出两个函数的图象如上∵函数y=f(x)的周期为2,在[﹣1,0]上为减函数,在[0,1]上为增函数∴函数y=f(x)在区间[0,10]上有5次周期性变化,在[0,1]、[2,3]、[4,5]、[6,7]、[8,9]上为增函数,在[1,2]、[3,4]、[5,6]、[7,8]、[9,10]上为减函数,且函数在每个单调区间的取值都为[0,1],再看函数y=|lgx|,在区间(0,1]上为减函数,在区间[1,+∞)上为增函数,且当x=1时y=0;x=10时y=1,再结合两个函数的草图,可得两图象的交点一共有10个,故选:A.11.【2011年新课标1文科03】下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是()A.y=2x3B.y=|x|+1 C.y=﹣x2+4 D.y=2﹣|x|【解答】解:对于A.y=2x3,由f(﹣x)=﹣2x3=﹣f(x),为奇函数,故排除A;对于B.y=|x|+1,由f(﹣x)=|﹣x|+1=f(x),为偶函数,当x>0时,y=x+1,是增函数,故B正确;对于C.y=﹣x2+4,有f(﹣x)=f(x),是偶函数,但x>0时为减函数,故排除C;对于D.y=2﹣|x|,有f(﹣x)=f(x),是偶函数,当x>0时,y=2﹣x,为减函数,故排除D.故选:B.12.【2010年新课标1文科06】如图,质点P在半径为2的圆周上逆时针运动,其初始位置为P(,),角速度为1,那么点P到x轴距离d关于时间t的函数图象大致为()0A.B.C.D.【解答】解:通过分析可知当t=0时,点P到x轴距离d为,于是可以排除答案A,D,再根据当时,可知点P在x轴上此时点P到x轴距离d为0,排除答案B,故选:C.13.【2010年新课标1文科09】设偶函数f(x)满足f(x)=2x﹣4(x≥0),则{x|f(x ﹣2)>0}=()A.{x|x<﹣2或x>4} B.{x|x<0或x>4}C.{x|x<0或x>6}D.{x|x<﹣2或x>2}【解答】解:由偶函数f(x)满足f(x)=2x﹣4(x≥0),可得f(x)=f(|x|)=2|x|﹣4,则f(x﹣2)=f(|x﹣2|)=2|x﹣2|﹣4,要使f(|x﹣2|)>0,只需2|x﹣2|﹣4>0,|x﹣2|>2解得x>4,或x<0.应选:B.14.【2010年新课标1文科12】已知函数,若a,b,c互不相等,且f(a)=f(b)=f(c),则abc的取值范围是()A.(1,10)B.(5,6) C.(10,12) D.(20,24)【解答】解:作出函数f(x)的图象如图,不妨设a<b<c,则ab=1,则abc=c∈(10,12).故选:C.15.【2018年新课标1文科13】已知函数f(x)=log2(x2+a),若f(3)=1,则a =.【解答】解:函数f(x)=log2(x2+a),若f(3)=1,可得:log2(9+a)=1,可得a=﹣7.故答案为:﹣7.16.【2014年新课标1文科15】设函数f(x),则使得f(x)≤2成立的x的取值范围是.【解答】解:x<1时,e x﹣1≤2,∴x≤ln2+1,∴x<1;x≥1时,2,∴x≤8,∴1≤x≤8,综上,使得f (x )≤2成立的x 的取值范围是x ≤8. 故答案为:x ≤8.17.【2012年新课标1文科16】设函数f (x )的最大值为M ,最小值为m ,则M +m= .【解答】解:函数可化为f (x ),令,则为奇函数,∴的最大值与最小值的和为0.∴函数f (x )的最大值与最小值的和为1+1+0=2.即M +m =2. 故答案为:2.本专题考查的知识点为:函数,函数的单调性与最值,函数的奇偶性与周期性,幂函数与二次函数,指数函数,对数函数,分段函数,函数的图象,函数与方程等.历年考题主要以选择填空题型出现,重点考查的知识点为:函数的单调性与最值,函数的奇偶性与周期性,指数函数,对数函数,分段函数,函数的图象,函数与方程等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2010年高考数学试题分类汇编——函数 (2010上海文数)22.(本题满分16分)本题共有3个小题,第1小题满分3分,第2小题满分5分,第3小题满分8分。
若实数x、y、m满足xmym,则称x比y接近m.
(1)若21x比3接近0,求x的取值范围; (2)对任意两个不相等的正数a、b,证明:22abab比33ab接近2abab; (3)已知函数()fx的定义域,,DxxkkZxR.任取xD,()fx等于1sinx和1sinx中接近0的那个值.写出函数()fx的解析式,并指出它的奇偶性、最小正周期、最小值和单调性(结论不要求证明). 解析:(1) x(2,2);
(2) 对任意两个不相等的正数a、b,有222abababab,332ababab,
因为22332|2||2|()()0ababababababababab, 所以2233|2||2|ababababababab,即a2bab2比a3b3接近2abab;
(3) 1sin,(2,2)()1|sin|,1sin,(2,2)xxkkfxxxkxxkk,kZ, f(x)是偶函数,f(x)是周期函数,最小正周期T,函数f(x)的最小值为0, 函数f(x)在区间[,)2kk单调递增,在区间(,]2kk单调递减,kZ.
(2010湖南文数)21.(本小题满分13分) 已知函数()(1)ln15,afxxaxax其中a<0,且a≠-1.
(Ⅰ)讨论函数()fx的单调性;
(Ⅱ)设函数332(23646),1(),1(){xxaxaxaaexefxxgx
(e是自然数的底数)。是
否存在a,使()gx在[a,-a]上为减函数?若存在,求a的取值范围;若不存在,请说明理由。 (2010浙江理数) (22)(本题满分14分)已知a是给定的实常数,设函数22()()()fxxaxbe,bR,
xa是()fx的一个极大值点.
(Ⅰ)求b的取值范围; (Ⅱ)设123,,xxx是()fx的3个极值点,问是否存在实数b,可找到4xR,使得
1234,,,xxxx的某种排列1234,,,iiiixxxx(其中1234,,,iiii=1,2,3,4)依次成等差数列?若存
在,求所有的b及相应的4x;若不存在,说明理由. 解析:本题主要考查函数极值的概念、导数运算法则、导数应用及等差数列等基础知识,同时考查推理论证能力、分类讨论等综合解题能力和创新意识。 (Ⅰ)解:f’(x)=ex(x-a) 2(3)2,xabxbaba
令222()(3)2,=(3-a+b)4(2)(1)80,gxxabxbabababaab则 于是,假设1212,()0.xxgxxx是的两个实根,且 (1) 当x1=a 或x2=a时,则x=a不是f(x)的极值点,此时不合题意。 (2) 当x1a且x2a时,由于x=a是f(x)的极大值点,故x1即()0gx
即2(3)20aabababa 所以b<-a 所以b的取值范围是(-∞,-a)
此时4223xxaab2(1)826abaa 或4223xxaab2(1)826abaa (2)当21xaax时,则212()xaax或12()2()axxa 于是1ab9132 此时42(3)3(3)1133242axaababxba 综上所述,存在b满足题意, 当b=-a-3时,426xa
7132ba时,41132xa
7132ba时,41132xa
(2010全国卷2理数)(22)(本小题满分12分) 设函数1xfxe. (Ⅰ)证明:当x>-1时,1xfxx; (Ⅱ)设当0x时,1xfxax,求a的取值范围. 【命题意图】本题主要考查导数的应用和利用导数证明不等式,考查考生综合运用知识的能力及分类讨论的思想,考查考生的计算能力及分析问题、解决问题的能力. 【参考答案】 【点评】导数常作为高考的压轴题,对考生的能力要求非常高,它不仅要求考生牢固掌握基础知识、基本技能,还要求考生具有较强的分析能力和计算能力.估计以后对导数的考查力度不会减弱。作为压轴题,主要是涉及利用导数求最值解决恒成立问题,利用导数证明不等式等,常伴随对参数的讨论,这也是难点之所在.
(2010陕西文数)21、(本小题满分14分) 已知函数f(x)=x,g(x)=alnx,aR。 (1) 若曲线y=f(x)与曲线y=g(x)相交,且在交点处有相同的切线,求a的值及该切线的方程; (2) 设函数h(x)=f(x)- g(x),当h(x)存在最小之时,求其最小值(a)的解析式; (3) 对(2)中的(a),证明:当a(0,+)时, (a)1.
解 (1)f’(x)=12x,g’(x)=ax(x>0),
由已知得 x=alnx, 12x=ax, 解德a=2e,x=e2,
两条曲线交点的坐标为(e2,e) 切线的斜率为k=f’(e2)= 12e, 切线的方程为y-e=12e(x- e2).
(2)由条件知 Ⅰ 当a.>0时,令h '(x)=0,解得x=24a, 所以当0 < x< 24a时 h '(x)<0,h(x)在(0,24a)上递减; 当x>24a时,h '(x)>0,h(x)在(0,24a)上递增。 所以x>24a是h(x)在(0, +∞ )上的唯一极致点,且是极小值点,从而也是h(x)的最小值点。 所以Φ (a)=h(24a)= 2a-aln24a=2 Ⅱ当a ≤ 0时,h(x)=(1/2-2a) /2x>0,h(x)在(0,+∞)递增,无最小值。 故 h(x) 的最小值Φ (a)的解析式为2a(1-ln2a) (a>o) (3)由(2)知Φ (a)=2a(1-ln2a) 则 Φ 1(a )=-2ln2a,令Φ 1(a )=0 解得 a =1/2 当 00,所以Φ (a ) 在(0,1/2) 上递增 当 a>1/2 时, Φ 1(a )<0,所以Φ(a ) 在 (1/2, +∞)上递减。 所以Φ(a )在(0, +∞)处取得极大值Φ(1/2 )=1 因为Φ(a )在(0, +∞)上有且只有一个极致点,所以Φ(1/2)=1也是Φ(a)的最大值 所当a属于 (0, +∞)时,总有Φ(a) ≤ 1
(2010辽宁文数)(21)(本小题满分12分) 已知函数2()(1)ln1fxaxax.
(Ⅰ)讨论函数()fx的单调性; (Ⅱ)设2a,证明:对任意12,(0,)xx,1212|()()|4||fxfxxx.
解:(Ⅰ) f(x)的定义域为(0,+),2121()2aaxafxaxxx. 当a≥0时,()fx>0,故f(x)在(0,+)单调增加; 当a≤-1时,()fx<0, 故f(x)在(0,+)单调减少;
当-1<a<0时,令()fx=0,解得x=12aa.当x∈(0, 12aa)时, ()fx>0; x∈(12aa,+)时,()fx<0, 故f(x)在(0, 12aa)单调增加,在(12aa,+)单调减少. (Ⅱ)不妨假设x1≥x2.由于a≤-2,故f(x)在(0,+)单调减少. 所以1212()()4fxfxxx等价于 12()()fxfx≥4x1-4x2,
即f(x2)+ 4x2≥f(x1)+ 4x1. 令g(x)=f(x)+4x,则 1()2agxaxx
+4
=2241axxax. 于是()gx≤2441xxx=2(21)xx≤0. 从而g(x)在(0,+)单调减少,故g(x1) ≤g(x2), 即 f(x1)+ 4x1≤f(x2)+ 4x2,故对任意x1,x2∈(0,+) ,1212()()4fxfxxx.
(2010辽宁理数)(21)(本小题满分12分) 已知函数1ln)1()(2axxaxf
(I)讨论函数)(xf的单调性; (II)设1a.如果对任意),0(,21xx,||4)()(|2121xxxfxf,求a的取值范围。 解:
(Ⅰ)()fx的定义域为(0,+∞). 2121'()2aaxafxaxxx. 当0a时,'()fx>0,故()fx在(0,+∞)单调增加; 当1a时,'()fx<0,故()fx在(0,+∞)单调减少;
当-1<a<0时,令'()fx=0,解得12axa. 则当1(0,)2axa时,'()fx>0;1(,)2axa时,'()fx<0. 故()fx在1(0,)2aa单调增加,在1(,)2aa单调减少. (Ⅱ)不妨假设12xx,而a<-1,由(Ⅰ)知在(0,+∞)单调减少,从而
