最新新课标2013年全国高考理科数学试题分类汇编2:函数
2013年高考新课标II全国卷理科数学试题及答案

2013年普通高等学校招生全国统一考试(全国卷)数 学 试 题(必试部分)注意事项:考生在答题前请认真阅读本注意事项及各题答题要求 1.本试卷共4页,包含填空题(第1题——第14题)、解答题(第15题——第20题).本卷满分160分,考试时间为120分钟.考试结束后,请将答题卡交回. 2.答题前,请您务必将自己的姓名、班级写在答题卡的规定位置.3.请在答题卡上按照顺序在对应的答题区域内作答,在其他位置作答一律无效.作答必须用0.5毫米黑色墨水的签字笔.请注意字体工整,笔迹清楚. 4.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗. 5.请保持答题卡卡面清洁,不要折叠、破损. 一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置....上.. 1.设复数z 满足()(1)1i i i z ++=-(i 是虚数单位),则复数z 的模z =__ __. 2.已知tan 2α=,则sin()cos()sin()cos()παπααα++-=-+-_______.3.抛物线y 2= 8x 的焦点到双曲线x 212 – y 24= 1的渐近线的距离为___ ___.4.阅读下列算法语句:Read S ←1For I from 1 to 5 step 2 S ←S+IEnd for Print SEnd输出的结果是 .5.设集合11{3{0}3x x A xB x x-=<<=<,则A B =___________. 6.设等比数列{a n }的公比q = 12,前n 项和为S n ,则 S 4a 4= ___________.7.在区间[5,5]-内随机地取出一个数a ,则恰好使1是关于x 的不等式2220x ax a +-<的一个解的概率大小为_______. 8.已知向量)1-b =,2=a ,则2-a b 的最大值为 .9.已知A (2,4),B (–1,2),C (1,0),点P (x ,y )在△ABC 内部及边界上运动,则z = x – y 的最大值与最小值的和为_____10.设,b c 表示两条直线,,αβ表示两个平面,现给出下列命题:① 若,//b c αα⊂,则//b c ; ② 若,//b b c α⊂,则//c α; ③ 若//,c ααβ⊥,则c β⊥; ④ 若//,c c αβ⊥,则αβ⊥. 其中正确的命题是_________.(写出所有正确命题的序号)11.设函数22,0,()log ,0x x f x x x ⎧≤=⎨>⎩,若关于x 的方程2()()0f x af x -=恰有三个不同的实数解,则实数a 的取值范围为________.12.函数()()g x y f x =在求导数时,可以运用对数法:在函数解析式两边求对数得()()ln ln y g x f x =,两边求导数()()()()()ln f x y g x f x g x y f x '''=+,于是()()g x y f x '= ()()()()()ln f x g x f x g x f x '⎡⎤'+⎢⎥⎢⎥⎣⎦.运用此方法可以探求得知()10x y x x =>的一个单调增区间为_________.13.已知椭圆22134x y +=的上焦点为F ,直线10x y ++=和10x y +-=与椭圆相交于点A ,B ,C ,D ,则AF BF CF DF +++= .14.已知定义在R 上的函数()f x 满足()12f =,()1f x '<,则不等式()221f x x <+的解集为_ __.二、解答题:本大题共6小题,共计90分,请在答题卡指定区域.......内作答,解答时应写出文字说明、证明或演算步骤.PA CBA B C D EF 15.(本小题满分14分)如图,点B 在以P A 为直径的圆周上,点C 在线段AB 上,已知5,3,P A P B P ==,设,APB APC αβ∠=∠=,,αβ均为锐角. (1)求β;(2)求两条向量,AC PC的数量积AC PC ⋅ 的值.16. (本小题满分14分)如图,已知AB ⊥平面ACD ,DE //AB ,△ACD 是正三角形,AD = DE = 2AB ,且F 是CD 的中点.(1)求证:AF //平面BCE ;(2)求证:平面BCE ⊥平面CDE .17.(本大题满分14分)2010年上海世博会组委会为保证游客参观的顺利进行,对每天在各时间段进入园区和离开园区的人数(以百人..为计数单位)作了一个模拟预测.为了方便起见,以10分钟为一个计算单位,上午9点10分作为第一个计数人数的时间,即1n =;9点20分作为第二个计数人数的时间,即2n =;依此类推 ,把一天内从上午9点到晚上24点分成了90个计数单位.第n 个时刻进入园区的人数()f n 和时间n (n *∈N )满足以下关系: ()()()()()24123612436325363216377207390n n n f n n n n -≤≤⎧⎪⎪⎪⋅≤≤=⎨⎪-+≤≤⎪≤≤⎪⎩,n *∈N第n 个时刻离开园区的人数()g n 和时间()n n *∈N 满足以下关系:()()()()012451202572,507390n g n n n n n *≤≤⎧⎪=-≤≤∈⎨⎪≤≤⎩N . (1)试计算在当天下午3点整(即15点整)时,世博园区内共有游客多少百人?(提示: 1.1,结果仅保留整数)(2)问:当天什么时刻世博园区内游客总人数最多? 18.(本小题满分16分)设圆221:106320C x y x y +--+=,动圆222:22(8)4120 C x y ax a y a +---++=,(1)求证:圆1C 、圆2C 相交于两个定点;(2)设点P 是椭圆2214x y +=上的点,过点P 作圆1C 的一条切线,切点为1T ,过点P 作圆2C 的一条切线,切点为2T ,问:是否存在点P ,使无穷多个圆2C ,满足12PT PT =?如果存在,求出所有这样的点P ;如果不存在,说明理由.19. (本小题满分16分)已知数列{a n }的通项公式为a n = 2⨯3n + 23n – 1(n ∈N *).(1)求数列{a n }的最大项; (2)设b n =a n + pa n – 2,试确定实常数p ,使得{b n }为等比数列; (3)设*,,,N mn p m n p∈<<,问:数列{a n }中是否存在三项m a ,n a ,p a ,使数列m a ,n a ,p a 是等差数列?如果存在,求出这三项;如果不存在,说明理由.20.(本大题满分16分)已知函数()()||20,1x xf x aa a a=+>≠,(1)若1a >,且关于x 的方程()f x m =有两个不同的正数解,求实数m 的取值范围;BC ED A (2)设函数()()[),2,g x f x x =-∈-+∞,()g x 满足如下性质:若存在最大(小)值,则最大(小)值与a 无关.试求a 的取值范围.(加试部分)21.【选做题】在A 、B 、C 、D 四小题中只能选做两题....,每小题l0分,共计20分.请在答.题.卡.指.定.区.域.内作答,解答时应写出文字说明、证明过程或演算步骤. A .选修4 – 1几何证明选讲如图,△ABC 的外接圆的切线AE 与BC 的延长线相交于点E ,∠BAC 的平分线与BC 交于点D .求证:ED 2= EB ·EC .B .矩阵与变换 已知矩阵2143-⎡⎤=⎢⎥-⎣⎦A ,4131-⎡⎤=⎢⎥-⎣⎦B ,求满足=AX B 的二阶矩阵X .C .选修4 – 4 参数方程与极坐标若两条曲线的极坐标方程分别为ρ = 1与ρ = 2cos ( +3),它们相交于A ,B 两点,求线段AB 的长.P BDAMD .选修4 – 5 不等式证明选讲 设a ,b ,c 为正实数,求证:a 3 + b 3 + c 3 + 1abc≥23.【必做题】第22题、第23题,每题10分,共20分.请在答题..卡.指.定.区.域.内作答,解答时应写出文字说明、证明过程或演算步骤. 22. (本小题满分10分)如图,在四棱锥P – ABCD 中,底面ABCD 是边长为1的正方形,P A ⊥底面ABCD ,点M 是棱PC 的中点,AM ⊥平面PBD . (1)求P A 的长;(2)求棱PC 与平面AMD 所成角的正弦值.23.(本小题满分10分)用,,,a b c d 四个不同字母组成一个含1+n *)(N n ∈个字母的字符串,要求由a 开始,相邻两个字母不同. 例如1=n 时,排出的字符串是,,ab ac ad ;2=n 时排出的字符串是,,,,,,,,aba abc abd aca acb acd ada adb adc ,……, 如图所示.记这含1+n 个字母的所有字符串中,排在最后一个的字母仍是a 的字符串的种数为n a .ab d n=1abcd n=2ad a b d a b c(1)试用数学归纳法证明:*33(1)(,1)4N n nn a n n +-=∈≥; (2)现从,,,a b c d 四个字母组成的含*1(,2)N n n n +∈≥个字母的所有字符串中随机抽取一个字符串,字符串最后一个的字母恰好是a 的概率为P ,求证:2193P ≤≤.参考答案1.22.33.1 4.10 5.102x x ⎧⎫<<⎨⎬⎩⎭6.157.0.78.49.-210.④11.{}01a a << 12.()0,eA BC DEFP 13.814.()(),11,-∞-+∞15.解(1):因为点B 在以P A 为直径的圆周上,所以90ABP ∠=,所以34cos ,sin 55PB PA αα===.所以4tan 3α=,…………………………………2分cos cos()7PB CPB PC αβ∠=-===sin()10αβ-=, 所以1tan()7αβ-=,………………………………………………………………4分 tan tan()tan tan[()]11tan tan()ααββααβααβ--=--==+-,…………………………6分又(0,)2πβ∈,所以4πβ=.………………………………………………………8分(2)2()AC PC PC PA PC PC PA PC ⋅=-⋅=-⋅…………………………11分275(577249=-⨯⨯=-……………………………………………14分16.⑴解:取CE 中点P ,连结FP ,BP ,因为F 为CD 的中点,所以FP //DE ,且FP = 12DE , …2分又AB //DE ,且AB =12DE ,所以AB //FP ,且AB = FP ,所以四边形ABPF 为平行四边形,所以AF //BP . ………………4分 又因为AF ⊂/平面BCE ,BP ⊂平面BCE , 所以AF //平面BCE . ……7分 (该逻辑段缺1个条件扣1分)⑵因为△ACD 为正三角形,所以AF ⊥CD . 因为AB ⊥平面ACD ,DE //AB ,所以DE ⊥平面ACD ,又AF ⊂平面ACD ,所以DE ⊥AF . ……………………………………9分 又AF ⊥CD ,CD ∩DE = D ,所以AF ⊥平面CDE .又BP //AF ,所以BP ⊥平面CDE . ……………………………12分 又因为BP ⊂平面BCE ,所以平面BCE ⊥平面CDE . ………………………………………14分17.解:(1)当024n ≤≤且n *∈N 时,()36f n =,当3625≤≤n 且n *∈N 时,2412()363n f n -=⋅所以[]36(1)(2)(3)(24)S f f f f =+++++ …[])36()26()25(f f f ++++=36×24+36×1⎡⎤-=864+792=1656;…………………………2分另一方面,已经离开的游客总人数是:12(25)(26)(36)T g g g =+++ 12=×5121152⨯+⨯390=;…………………4分 所以361216563901266S S T =-=-=(百人)故当天下午3点整(即15点整)时,世博园区内共有游客1266百人. ……………6分 (2)当0)()(≥-n g n f 时园内游客人数递增;当0)()(<-n g n f 时园内游客人数递减. (i )当241≤≤n 时,园区人数越来越多,人数不是最多的时间;……………………8分 (ii )当3625≤≤n 时,令512036n -≤,得出31≤n ,即当3125≤≤n 时,进入园区人数多于离开人数,总人数越来越多;……………10分 (iii )当3632≤≤n 时,24123635120n n -⋅>-,进入园区人数多于离开人数,总人数越来越多;……………………………………………………………………12分 (Ⅳ)当7237≤≤n 时, 令32165120n n -+=-时,42n =, 即在下午4点整时,园区人数达到最多.此后离开人数越来越多,故园区内人数最多的时间是下午4点整. ………………14分 答:(1)当天下午3点整(即15点整)时,世博园区内共有游客1266百人; (2)在下午4点整时,园区人数达到最多.18.解(1)将方程2222(8)4120 x y ax a y a +---++=化为221612(224)0x y y x y a +-++-++=,令22161202240x y y x y ⎧+-+=⎨-++=⎩得42x y =⎧⎨=⎩或64x y =⎧⎨=⎩,所以圆2C 过定点(4,2)和(6,4),4分将42x y =⎧⎨=⎩代入22106320x y x y +--+=,左边=1644012320+--+==右边,故点(4,2)在圆1C 上,同理可得点(6,4)也在圆1C 上,所以圆1C 、圆2C 相交于两个定点(4,2)和(6,4);……………6分(2)设00(,)P x y,则1PT =8分2PT =, ………………………………10分12PT PT =即00001063222(8)412x y ax a y a --+=---++,整理得00(2)(5)0x y a ---=(*)…………………………………………………12分存在无穷多个圆2C ,满足12PT PT =的充要条件为0022002014x y x y --=⎧⎪⎨+=⎪⎩有解,解此方程组得0020x y =⎧⎨=⎩或006545x y ⎧=⎪⎪⎨⎪=-⎪⎩,………………………………………14分 故存在点P ,使无穷多个圆2C ,满足12PT PT =,点P 的坐标为64(2,0)(,)55或-.………………16分19.解 ⑴由题意a n = 2 + 43n– 1,随着n 的增大而减小,所以{a n }中的最大项为a 1 = 4. …4分⑵b n = 2 + 4n + p43n – 1= (2 + p )(3n – 1) + 44 = (2 + p )3n + (2 – p )4,若{b n }为等比数列,则b 2n +1 – b n b n +2= 0(n ∈N * )所以 [(2 + p )3n +1 + ( 2 – p )]2 – [{2 + p )3n + (2 – p )][(2 + p )3n +2 + (2 – p )] = 0(n ∈N *), 化简得(4 – p 2)(2·3n +1 – 3n +2 – 3n ) = 0即– (4 – p 2)·3n ·4 = 0,解得p = ±2. ……………………………7分反之,当p = 2时,b n = 3n ,{b n }是等比数列;当p = – 2时,b n = 1,{b n }也是等比数列.所以,当且仅当p = ±2时{b n }为等比数列. ………………………………………………10分 ⑶因为4231m m a =+-,4231n n a =+-,4231p pa =+-,若存在三项m a ,n a ,p a ,使数列m a ,n a ,p a 是等差数列,则2n m p a a a =+,所以42(2)31n +-=4231m +-4231p ++-,……………12分 化简得3(2331)1323n p n p m p m n m ----⨯--=+-⨯(*),因为*,,,N m n p m n p ∈<<,所以1p m p n -≥-+,1p m n m -≥-+,所以13333p mp npn--+-≥=⨯,13333p m n m n m --+-≥=⨯,(*)的左边3(23331)3(31)0n p n p n n p n ---≤⨯-⨯-=--<, 右边13323130n mn m n m ---≥+⨯-⨯=+>,所以(*)式不可能成立,故数列{a n }中不存在三项m a ,n a ,p a ,使数列m a ,n a ,p a 是等差数列. ………16分20.解:(1)令x a t =,0x >,因为1a >,所以1t >,所以关于x 的方程()f x m =有两个不同的正数解等价于关于t 的方程2t m t+=有相异的且均大于1的两根,即 关于t 的方程220t mt -+=有相异的且均大于1的两根,……………………2分所以2280,1,2120m m m ⎧∆=->⎪⎪>⎨⎪⎪-+>⎩,…………………………………………………………………4分解得3m <<,故实数m的取值范围为区间.………………………6分 (2)||()2,[2,)x x g x a a x =+∈-+∞①当1a >时,a )0x ≥时,1x a ≥,()3x g x a =,所以 ()[3,)g x ∈+∞,b )20x -≤<时,211xa a≤<()2x x g x a a -=+,所以 ()221'()ln 2ln ln x x x xa g x a a a a a a--=-+=……8分ⅰ当21a >1a <<(2,0)x ∀∈-,'()0g x >,所以 ()g x 在[2,0)-上递增, 所以 222()[,3)g x a a ∈+,综合a ) b )()g x 有最小值为222a a+与a 有关,不符10分ⅱ当21a ≤a ≥'()0g x =得1log 22ax =-,且当12log 22a x -<<-时,'()0g x <,当1log 202a x -<<时,'()0g x >,所以 ()g x 在1[2,log 2]2a --上递减,在1[log 2,0]2a -上递增,所以min 1()log 22a g x g ⎛⎫=-= ⎪⎝⎭a )b ) ()g x 有最小值为a 无关,符合要求.………12分②当01a <<时,a ) 0x ≥时,01x a <≤,()3x g x a =,所以 ()(0,3]g x ∈ b ) 20x -≤<时,211x a a<≤,()2x x g x a a -=+, 所以 ()221'()ln 2ln ln x x x xa g x a a a a a a --=-+= 0<,()g x 在[2,0)-上递减,所以 222()(3,]g x a a ∈+,综合a ) b ) ()g x 有最大值为222a a+与a 有关,不符14分 综上所述,实数a的取值范围是a ≥16分数学Ⅱ(附加题)21.【选做题】在A 、B 、C 、D 四小题中只能选做两题....,每小题l0分,共计20分.请在答.题.卡.指.定.区.域.内作答,解答时应写出文字说明、证明过程或演算步骤. A .选修4 – 1几何证明选讲证明: 因为EA 是圆的切线,AC 为过切点A 的弦,所以∠CAE = ∠CBA . 又因为AD 是∠BAC 的平分线,所以∠BAD = ∠CAD 所以∠DAE = ∠DAC + ∠EAC = ∠BAD + ∠CBA = ∠ADE所以,△EAD 是等腰三角形,所以EA = ED . …………………………6分 又EA 2 = EC ·EB ,所以ED 2 = EB ·EC . ……………………………………………………4分 B .矩阵与变换: 解:由题意得1312221-⎡⎤⎢⎥=⎢⎥⎣⎦A,…………………………………………………5分 =AX B ,1319411222312151-⎡⎤⎡⎤--⎡⎤⎢⎥⎢⎥∴===⎢⎥⎢⎥⎢⎥-⎣⎦-⎣⎦⎣⎦X A B ………………………………10分 B C EDAC .选修4 – 4 参数方程与极坐标若两条曲线的极坐标方程分别为ρ = 1与ρ = 2cos ( +3),它们相交于A ,B 两点,求线段AB 的长.解 首先将两曲线的极坐标方程化为直角坐标方程,得 x 2 + y 2 = 1与x 2 + y 2– x + 3y = 0……………………………………………………6分解方程组⎩⎨⎧x 2 + y 2= 1x 2 + y 2– x + 3y = 0 得两交点坐标(1,0),(–12, – 32)所以,线段AB 的长为(1 + 12)2 + (0 + 32)2= 3即AB = 3.………………………………………………………………………………10分D .选修4 – 5 不等式证明选讲 设a ,b ,c 为正实数,求证:a 3 + b 3 + c 3 +1abc≥23. 证明 因为a ,b ,c 为正实数,所以a 3 + b 3 + c 3≥33a 3b 3c 3 = 3abc >0………………………5分 又3abc +1abc≥23abc ·1abc= 23. 所以a 3 + b 3 + c 3 +1abc≥23.………………………………………………10分 【必做题】第22题、第23题,每题10分,共20分.请在答题..卡.指.定.区.域.内作答,解答时应写出文字说明、证明过程或演算步骤.22.解 如图,以A 为坐标原点,AB ,AD ,AP 分别为x ,y ,z 系,则A (0,0,0),B (1,0,0),C (1,1,0),D (0,1,0),P (0,0,a ).因为M 是PC 中点,所以M 点的坐标为(12,12,a 2),所以AM → =(12,12,a 2),BD → = (–1,1,0),BP → = ( – 1,0,a ). ⑴因为AM →⊥平面PBD ,所以AM →·BD → = AM →·BP →= 0.即– 12 + a22= 0,所以a = 1,即P A = 1. ………………………………………4分⑵由AD → = (0,1,0),M →= (12,12,12),可求得平面AMD 的一个法向量n = ( – 1,0,1).又CP → = ( – 1,–1,1).所以cos<n , CP →> = 错误! = 错误! = 错误!. 所以,PC 与平面AMD 所成角的正弦值为63.……………………………10分23.解(1):证明:(ⅰ)当1n =时,因为10a =,33(1)04+-=,所以等式正确. (ⅱ)假设n k =时,等式正确,即*33(1)(,1)4N k kk a k k +-=∈≥, 那么,1n k =+时,因为11133(1)4333(1)33(1)33444k k k k k k k kkk k a a ++++-⋅---+-=-=-==,这说明1n k =+时等式仍正确.据(ⅰ),(ⅱ)可知,*33(1)(,1)4N n nn a n n +-=∈≥正确. ……………………5分(2)易知133(1)13(1)[1]4343n n nn nP +--=⋅=+, ①当n 为奇数(3n ≥)时,13(1)43n P =-,因为327n ≥,所以132(1)4279P ≥-=,又131(1)434n P =-<,所以2194P ≤<;②当n 为偶数(2n ≥)时,13(1)43n P =+,因为39n≥,所以131(1)493P ≤+=,又131(1)434n P =+>,所以1143P <≤.综上所述,2193P ≤≤.…………………………………………………………………10分。
2013年全国高考理科数学试题分类汇编2:函数

2013年全国高考理科数学试题分类汇编2:函数一、选择题错误!未指定书签。
.(2013年高考江西卷(理))函数y=x ln(1-x)的定义域为A.(0,1)B.[0,1)C.(0,1]D.[0,1] 【答案】D错误!未指定书签。
.(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))若a b c <<,则函数()()()()()()()f x x a x b x b x c x c x a =--+--+--的两个零点分别位于区间( )A.(),a b 和(),b c 内B.(),a -∞和(),a b 内C.(),b c 和(),c +∞内D.(),a -∞和(),c +∞内【答案】A错误!未指定书签。
.(2013年上海市春季高考数学试卷(含答案))函数12()f x x -=的大致图像是( )【答案】A错误!未指定书签。
.(2013年高考四川卷(理))设函数()x f x e x a =+-(a R ∈,e 为自然对数的底数).若曲线sin y x =上存在00(,)x y 使得00(())f f y y =,则a 的取值范围是( )(A)[1,]e (B)1[,-11]e -, (C)[1,1]e + (D)1[-1,1]e e -+ 【答案】A错误!未指定书签。
.(2013年高考新课标1(理))已知函数()f x =22,0ln(1),0x x x x x ⎧-+≤⎨+>⎩,若|()f x |≥ax ,则a 的取值范围是 A.(,0]-∞B.(,1]-∞C.[2,1]-D.[2,0]-【答案】Dx yxyBA0 xyC0 x yD错误!未指定书签。
.(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))函数()()21=log 10f x x x ⎛⎫+> ⎪⎝⎭的反函数()1=f x -(A)()1021x x >- (B)()1021xx ≠- (C)()21x x R -∈ (D)()210xx ->【答案】A错误!未指定书签。
2013年全国高考理科数学试题分类汇编2:函数Word版含答案

2013 年全国高考理科数学试题分类汇编2:函数一、选择题1 .(2 013年高考江西卷(理))函数 y= x ln(1-x) 的定义域为A.(0,1)B.[0,1) C.(0,1] D.[0,1]【答案】 D 2 .( 2 013年普通高等学校招生统一考试重庆数学(理)试题(含答案))若a bc , 则函数f x x a x b x b x c x c x a 的两个零点分别位于区间( )A.a,b 和 b, c 内 B., a 和 a,b 内C. b,c 和 c, 内D. ,a 和 c, 内【答案】 A13 .( 2 013年上海市春季高考数学试卷(含答案 ))函数 f( x) x2的大致图像是 ( )y y y yA x 0Bx 0 x 0xC D【答案】 A 4 .( 2013年高考四川卷(理))设函数 f ( x)e x x a ( aR , e为自然对数的底数 ).若曲线y sin x 上存在( x , y) 使得 f ( f( y ))y,则a的取值范围是 ( ) 000 0(A ) [1,e](B)1 ,(C)[1, e1](D)1[ e,-11] [e -1, e 1]【答案】 A5 .( 2013年高考新课标 1(理))已知函数 f ( x) x22x, x 0, 若|f (x) | ≥ ax ,则 aln( x1),x 0的取值范围是A. ,0]B. ( ,1]C.D. [ 2,0]( [ 2,1] 【答案】 D6 .( 2013年普通高等学校招生统一考试大纲版数学(理)WORD版含答案(已校对))函数f x = log 2 1 1 x 0 的反函数f1x=x第 1 页共 7 页(A) 1 x 0 (B) 1 x 0 (C) 2x 1 x R (D) 2x 1 x 0 2x 1 2x 1【答案】 A7 .( 2 013 年普通高等学校招生统一考试浙江数学(理)试题(纯WORD版))已知 x, y为正实数 , 则A. 2lgxlgy 2lg x2lg y B.2lg( xy)2lgx 2lg yC. 2lgxlgy 2lg x2lg y D.2lg( xy)2lgx 2lg y【答案】 D8 .年普通高等学校招生统一考试山东数学(理)试题(含答案))已知函数f( x)为奇( 2013函数 , 且当 x 0时 , f( x) x21 , 则 f ( 1)x(A)2(B) 0 (C) 1 (D) 2【答案】 A9 .(2 013 年高考陕西卷(理))在如图所示的锐角三角形空地中,欲建一个面积不小于3002m的内接矩形花园 ( 阴影部分 ), 则其边长x( 单位) 的取值范围是mx40m40m(A) [15,20] (B) [12,25] (C) [10,30] (D) [20,30]【答案】 C10 .( 2013 年普通高等学校招生统一考试重庆数学(理)试题(含答案))y 3 a a 6 6 a 3 的最大值为( )A.9B.9C. 33 2 2 D.2 【答案】 B 11.( 2 013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))已知函数f x 的定义域为1,0, 则函数 f 2 x1 的定义域为(A) 1,1(B) 1, 1(C) -1,0 (D) 1 ,12 2第 2 页共 7 页【答案】 B 12.( 2 013年高考湖南卷(理))函数 f x2ln x 的图像与函数g x x24x 5 的图像的交点个数为A.3B.2C.1D.0 【答案】 B 13.( 2 013x2) 年高考四川卷(理))函数 y 的图象大致是(3x 1【答案】 C14.( 2 013 年普通高等学校招生统一考试辽宁数学(理)试题(WORD版))已知函数f x x2 2 a 2 x a2 ,g x x2 2 a 2 x a28. 设H1x max f x , g x , H 2x min f x , g x , max p, q表示 p,q 中的较大值 , min p,q 表示 p, q 中的较小值 , 记 H1x 得最小值为 A,H 2x 得最小值为 B ,则A B(A) a22a 16 (B) a22a 16 (C) 16 (D) 16【答案】 B15.( 20 13年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))定义域为R 的四个函数 y x3 ,y 2x , y x21, y 2sin x 中 , 奇函数的个数是 ( )A . 4 B. 3 C. 2 D. 1【答案】 C16.( 2013 年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))若函数f (x)=x3 +bx+c 有极值点 x1 , x2 , 且 f (x1)=x1 , 则关于 x 的方程 3(f (x1)) 2 +2f(x)+b=0 的不同实根个数是(A)3 (B)4 (C) 5 (D)6【答案】 A17 .( 2013 年普通高等学校招生统一考试天津数学(理)试题(含答案))函数第 3 页共 7 页f ( x) 2x | log 0.5x | 1的零点个数为(A) 1 (B) 2 (C)3 (D) 4【答案】 B18.( 2013年高考北京卷(理) ) 函数 f ( x) 的图象向右平移 1 个单位长度 , 所得图象与y=ex关于 y 轴对称 , 则 f( x)=A. e x 1B. e x 1C. e x 1D. e x 1【答案】 D19.( 2013 年上海市春季高考数学试卷(含答案 ))设 f -1( x) 为函数 f ( x) x 的反函数 ,下列结论正确的是( )(A)f 1(2) 2 (B) f 1(2) 4 (C) f 1(4) 2 (D) f 1(4)4【答案】 B20.( 2013 年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对) )若函 数 f x =x 2 ax 1 在 1 ,+ 是增函数 , 则 a 的取值范围是x 2(A) [-1,0] (B) [ 1, ) (C) [0,3] (D) [3, ) 【答案】 D 二、填空题21 .( 2013年 上 海 市 春 季 高 考 数 学 试 卷 ( 含 答案 ) ) 函 数 y log 2 x( 2)的 定 义 域是_______________【答案】 ( 2, )22.( 2013 年高考上海卷(理) )方程3x 31 3x1的实数解为 ________1 3 【答案】 x log3 4 .23(.2013 年高考上海卷(理))对区间 I 上有定义的函数g( x) , 记 g (I ){ y | y g( x), x I } ,已知定义域为[0,3]的函数y f ( x) 有反函数y f 1( x) , 且f 1 ([0,1)) [1,2), f 1 ((2,4]) [0,1), 若方程 f( x) x 0有解x0 ,则x0_____第 4 页共 7 页【答案】 x0 2 .24.( 2 013年高考新课标 1(理))若函数 f ( x) = (1 x2 )( x2ax b) 的图像关于直线x2对称 , 则 f ( x) 的最大值是______.【答案】 16.25.( 2 013年上海市春季高考数学试卷(含答案 ))方程 2x8 的解是_________________【答案】 3 26.( 2 013年高考湖南卷(理))设函数f ( x) a x b x c x , 其中 c a 0,c b 0.(1)记集合 M (a,b, c) a,b,c不能构成一个三角形的三条边长,且a=b , 则( a,b, c) M 所对应的 f ( x) 的零点的取值集合为____.(2)若 a,b, c是 ABC的三条边长,则下列结论正确的是 ______.( 写出所有正确结论的序号 )①x ,1 , f x 0;②x R,使 xa x ,b x , c x不能构成一个三角形的三条边长;③若 ABC为钝角三角形,则x 1,2 , 使 f x 0.【答案】 (1) (0,1](2) ①②③27.( 2 013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯 WORD版含附加题))已知 f ( x) 是定义在 R 上的奇函数 . 当x 0 时 , f ( x) x24x , 则不等式 f (x)x的解集用区间表示为 ___________. 【答案】5,0 5,28.( 2 013年高考上海卷(理))设 a为实常数 , yf ( x) 是定义在 R 上的奇函数 , 当 x 0时, f ( x)a27 , 若 f ( x) a 1对一切x0 成立 , 则 a 的取值范围为________9xx【答案】 a 8 . 7三、解答题29.( 2 013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))设函数第 5 页共 7 页f ( x) ax (1 a2 ) x2 , 其中 a 0 , 区间 I | x f (x)>0( Ⅰ) 求的长度 ( 注 : 区间 ( , ) 的长度定义为 ); ( Ⅱ) 给定常数 k (0,1) , 当时 , 求 l 长度的最小值 .【答案】解 : ( Ⅰ) f( x) x[ a (1 a 2 )x]( Ⅱ) 由( Ⅰ) 知 ,a 1 l2 11 aaa已知 k(0,1),0 1 - k a 1 k.令11 kg(a) a 1在 a 1 k时取最大值a0 x (0,a) . 所以区间长度为aa2.1 1 a2 1 - kk 20 11 - k恒成立 .1 k这时 l1 k 1 k(1 k )2 1 (1 k ) 211k所以当a1 k时, l取最小值1 (1 k )2 .30.( 2013 年上海市春季高考数学试卷 (含答案 ))本题共有 3 个小题 ,第 1 小题满分 5 分, 第 2 小题满分 7 分 , 第 3 小题满分 6 分 .已知真命题 : “函数y f ( x) 的图像关于点P(a、b) 成中心对称图形”的充要条件为“函数y f ( x a) b 是奇函数” .(1 ) 将函数g( x) x33x2的图像向左平移1 个单位 , 再向上平移2 个单位 , 求此时图像对应的函数解析式 , 并利用题设中的真命题求函数g (x) 图像对称中心的坐标 ;(2 ) 求函数h( x) log 22x图像对称中心的坐标 ;4 x(3)已知命题 : “函数y f ( x) 的图像关于某直线成轴对称图像”的充要条件为“存在实数 a 和 b, 使得函数 y f (x a) b 是偶函数” . 判断该命题的真假. 如果是真命题 ,请给予证明 ; 如果是假命题 , 请说明理由 , 并类比题设的真命题对它进行修改, 使之成为真命题( 不必证明 ).【答案】(1) 平移后图像对应的函数解析式为y (x 1)33(x 1)2 2 , 整理得 y x3 3x ,第 6 页共 7 页由于函数yx 3 3x 是奇函数 , 由题设真命题知 , 函数 g( x) 图像对称中心的坐标是(1, 2) . (2) 设 h( x) log 2 2x 的对称中心为 P(a ,b) , 由题设知函数 h(x a) b 是奇函数 .4 x设 f (x) h( x a) b, 2( x a) 2x 2a 则 f ( x) log 2 ( x a) b , 即 f (x) log 2 a b . 4 4 x 由不等式 2x 2a 0 的解集关于原点对称, 得 a 2 . 4 a x此时 f (x) lo g 2( x 2) , , . 2 x b x ( 2 2) 2 任取 x ( 2,2) , 由 f ( x) f (x) 0 , 得 b 1,所以函数 h(x)log 2 2x 图像对称中心的坐标是 (2,1) . 4 x (3) 此命题是假命题 .举反例说明 : 函数 f ( x) x 的图像关于直线 y x 成轴对称图像 , 但是对任意实数 a 和 b ,函数 y f (x a) b , 即 y x a b 总不是偶函数 .修改后的真命题 :“函数 y f ( x) 的图像关于直线 x a 成轴对称图像”的充要条件是“函数 y f ( x a)是偶函数” .第 7 页共 7 页。
2013年高考真题理科数学分类汇编(解析版):函数及答案

2013年高考真题理科数学分类汇编(解析版)函 数1、(2013年高考(安徽卷))函数=()y f x 的图像如图所示,在区间[],a b 上可找到(2)n n ≥ 个不同的数12,...,,n x x x 使得1212()()()==,n nf x f x f x x x x 则n 的取值范围是 (A ){}3,4 (B ){}2,3,4 (C ) {}3,4,5 (D ){}2,3【答案】B【解析】由题知,过原点的直线与曲线相交的个数即n 的取值.用尺规作图,交点可取2,3,4. 所以选B 2、(2013年高考(北京卷))函数f (x )的图象向右平移一个单位长度,所得图象与y =e x 关于y 轴对称,则f (x )= A.1ex + B. 1ex - C. 1ex -+ D. 1ex --3、(2013年高考(广东卷))定义域为R 的四个函数3y x =,2xy =,21y x =+,2sin y x =中,奇函数的个数是( )A . 4B .3C .2D .【解析】C ;考查基本初等函数和奇函数的概念,是奇函数的为3y x =与2sin y x =,故选C .4、(2013年高考(全国(广西)卷))已知函数()()()-1,021f x f x -的定义域为,则函数的定义域为(A )()1,1- (B )11,2⎛⎫- ⎪⎝⎭ (C )()-1,0 (D )1,12⎛⎫ ⎪⎝⎭【答案】B【解析】由题意可知 1210,x -<+<,则112x -<<-。
故选B5、(2013年高考(全国(广西)卷))函数()()1=log 10f x x x ⎛⎫+> ⎪⎝⎭的反函数()1=f x - (A )()1021x x >- (B )()1021xx ≠- (C )()21x x R -∈ (D )()210x x -> 【答案】A【解析】由题意知1112(0)21y y x y x +=⇒=<-, 因此,故选A6、(2013年高考(全国(广西)卷))若函数()211=,2f x x ax a x ⎛⎫++∞ ⎪⎝⎭在是增函数,则的取值范围是(A )[]-1,0 (B )[]-∞1, (C )[]0,3 (D )[]3∞,+7、(2013年高考(湖南卷))函数()2ln f x x =的图像与函数()245g x x x =-+的图像的交点个数为A .3B .2C .1D .0【答案】B【解析】画出两个函数的图象,可得交点数。
2013高考数学真题分类汇编---------函数模块

2013高考数学—三角函数分类汇编1.(2013山东卷理3)已知函数)(x f 为奇函数,当0>x 时,xx x f 1)(2+=,在=-)1(f .A 2- .B 0 .C 1 .D 22.(2013陕西卷理1)设全集为R ,函数21)(x x f -=的定义域为M ,则M C R 为.A ]1,1[- .B )1,1(-.C ),1[]1,(+∞--∞ .D ),1()1,(+∞--∞3.(2013陕西卷理12)设][x 表示不大于x 的最大整数,则对任意实数y x ,,有.A ][][x x -=- .B ][2]2[x x = .C ][][][y x y x +≤+ .D ][][][y x y x -≤-4.(2013新课标2卷理10)已知函数c bx ax x x f +++=23)(,下列结论错误的是.A R x ∈∃0,0)(0=x f .B 函数)(x f y =的图像是中心对称图形.C 若0x 是)(x f 的极小值点,则)(x f 在区间),(0x -∞单调递减 .D 若0x 是)(x f 的极值点,则0)(0'=x f5.(2013新课标1卷理11)已知函数⎩⎨⎧>+≤+-=)0(),1ln()0(,2)(2x x x x x x f ,若ax x f ≥)(,则a 的取值范围是.A ]0,(-∞ .B ]1,(-∞ .C ]1,2[- ]0,2.[-D6.(2013新课标1卷理16)若函数))(1()(22b ax x x x f ++-=的图像关于直线2-=x 对称,在)(x f 的最大值是7.(2013江西卷理2)函数)1ln(x x y -=的定义域为.A )1,0( .B )1,0[ .C ]1,0( .D ]1,0[8.(2013江西卷理10)如图,半径为1的半圆O 与等边三角形夹在两平行线21,l l 之间,1l ∥2l ,l 与半圆相交于G F ,两点,与三角形ABC 两边相交于D E ,两点,设弧FG 的长为x (π<<x 0),CD BC EB y ++=,若l 从1l 平移到2l ,则函数)(x f y =的图像大致是9.(2013广西卷理5)函数)(11(log )(2+=xx f 的反函数)(1x f-=.A 121-x )0(>x.B 121-x )0(≠x .C 12-x (R x ∈) .D 12-x )0(>x10.(2013辽宁卷理11)已知函数)(x f 满足22)2(2)(a x a x x f ++-=,8)2(2)(22+--+-=a x a x x g 。
2013年全国高考(理科)数学试题分类汇编:函数

全国高考理科数学试题分类汇编2:函数一、选择题1 (高考江西卷(理))函数的定义域为A.(0,1)B.[0,1)C.(0,1]D.[0,1]*D 2 (重庆数学(理)试题)若a b c<<,则函数()()()()()()()f x x a x b x b x c x c x a =--+--+--的两个零点分别位于区间( )A.(),a b 和(),b c 内B.(),a -∞和(),a b 内C.(),b c 和(),c +∞内D.(),a -∞和(),c +∞内*A3 (上海市春季高考数学试卷(含答案))函数12()f x x -=的大致图像是( )*A4 (高考四川卷(理))设函数()f x a R ∈,e 为自然对数的底数).若曲线sin y x =上存在00(,)x y 使得00(())f f y y =,则a 的取值范围是( )(A)[1,]e (B)1[,-11]e -, (C)[1,1]e + (D)1[-1,1]e e -+*A5 (高考新课标1(理))已知函数()f x =22,0ln(1),0x x x x x ⎧-+≤⎨+>⎩,若|()f x |≥ax ,则a 的取值范围是A.(,0]-∞B.(,1]-∞C.[2,1]-D.[2,0]-*D6 .(大纲版数学(理))函数()()21=log 10f x x x ⎛⎫+> ⎪⎝⎭的反函数()1=f x - (A)()1021x x >- (B)()1021xx ≠- (C)()21x x R -∈ (D)()210xx ->*A 7 (浙江数学(理)试题)已知y x ,为正实数,则A.y x yx lg lg lg lg 222+=+ B.y x y x lg lg )lg(222∙=+ C.y x yx lg lg lg lg 222+=∙ D.y x xy lg lg )lg(222∙=*D8 (山东数学(理)试题)已知函数()f x 为奇函数,且当0x >时,21()f x x x=+,则(1)f -=(A) 2- (B) 0 (C) 1 (D) 2*A9 (高考陕西卷(理))在如图所示的锐角三角形空地中, 欲建一个面积不小于300m 2的内接矩形花园(阴影部分), 则其边长x (单位m )的取值范围是(A) [15,20] (B) [12,25] (C) [10,30] (D) [20,30]*C 10(重庆数学(理)试题)y =()63a -≤≤的最大值为( )A.9B.92 C.3 B 11(大纲版数学(理))已知函数()f x 的定义域为()1,0-,则函数()21f x -的定义域为(A)()1,1- (B)11,2⎛⎫- ⎪⎝⎭(C)()-1,0 (D)1,12⎛⎫⎪⎝⎭*B12(高考湖南卷(理))函数()2ln f x x =的图像与函数()245g x x x =-+的图像的交点个数为A.3B.2C.1D.0 *B13(高考四川卷(理))函数231x x y =-的图象大致是( )*C14(辽宁数学(理)试题)已知函数()()()()222222,228.f x x a x a g x x a x a =-++=-+--+设()()(){}()()(){}{}()12max ,,min ,,max ,H x f x g x H x f x g x p q ==表示,p q 中的较大值,{}min ,p q 表示,p q 中的较小值,记()1H x 得最小值为,A ()2H x 得最小值为B ,则A B -=(A)2216a a -- (B)2216a a +- (C)16- (D)16*B15(广东省数学(理)卷)定义域为R 的四个函数3y x =,2x y =,21y x =+,2sin y x =中,奇函数的个数是( )A . 4 B.3C.2D.1*C16(安徽数学(理)试题)若函数3()=+b +f x x x c 有极值点1x ,2x ,且11()=f x x ,则关于x 的方程213(())+2()+=0f x f x b 的不同实根个数是 (A)3 (B)4 (C) 5 (D)6*A17(天津数学(理)试题)函数0.5()2|log |1x f x x =-的零点个数为(A) 1 (B) 2(C) 3(D) 4*B18(高考北京卷(理))函数f (x )的图象向右平移1个单位长度,所得图象与y =e x关于y 轴对称,则f (x )=A.1e x +B. 1e x -C. 1ex -+ D. 1ex --*D19(上海市春季高考数学试卷(含答案))设-1()f x 为函数()f x =,下列结论正确的是( )(A) 1(2)2f -= (B) 1(2)4f -= (C) 1(4)2f -= (D) 1(4)4f -=*B20(大纲版数学(理))若函数()21=f x x ax x ++在1,+2⎛⎫∞ ⎪⎝⎭是增函数,则a 的取值范围是 (A)[-1,0] (B)[1,)-+∞ (C)[0,3] (D)[3,)+∞*D二、填空题21(上海市春季高考数学试卷(含答案))函数2log (2)y x =+的定义域是_________*(2,)-+∞ 22(高考上海卷(理))方程1313313x x-+=-的实数解为________*3log 4x =. 23(高考上海卷(理))对区间I 上有定义的函数()g x ,记(){|(),}g I y y g x x I ==∈,已知定义域为[0,的函数()y f x =有反函数1()y f x -=,且11([0,1))[1,2),((2,4])[0,1)f f --==,若方程()0f x x -=有解0x ,则0_____x =*02x =.24(高考新课标1(理))若函数()f x =22(1)()xx ax b -++的图像关于直线2x =-对称,则()f x 的最大值是______.*16.25(上海市春季高考数学试卷(含答案))方程28x=的解是_______________*326(高考湖南卷(理))设函数(),0,0.x x x f x a b c c a c b =+->>>>其中(1)记集合{}(,,),,M a b c a b c a =不能构成一个三角形的三条边长,且=b ,则(,,)a b c M ∈所对应的()f x 的零点的取值集合为____.(2)若,,a b c ABC ∆是的三条边长,则下列结论正确的是______.(写出所有正确结论的序号)①()(),1,0;x f x ∀∈-∞>②,,,x x x x R xa b c ∃∈使不能构成一个三角形的三条边长; ③若()()1,2,0.ABC x f x ∆∃∈=为钝角三角形,则使*(1)]10(, (2)①②③27(江苏卷(数学))已知)(x f 是定义在R 上的奇函数.当0>x 时,x x x f 4)(2-=,则不等式x x f >)(的解集用区间表示为___________.*()()+∞-,50,528(高考上海卷(理))设a 为实常数,()y f x =是定义在R 上的奇函数,当0x <时,2()97a f x x x=++,若()1f x a ≥+对一切0x ≥成立,则a 的取值范围为_______*87a ≤-. 三、解答题29(安徽数学(理)试题)设函数22()(1)f x ax a x =-+,其中0a >,区间|()>0I x f x =(Ⅰ)求的长度(注:区间(,)αβ的长度定义为βα-); (Ⅱ)给定常数(0,1)k ∈,当时,求l 长度的最小值.*解: (Ⅰ))1,0(0])1([)(22aa x x a a x x f +∈⇒>+-=.所以区间长度为21a a+. (Ⅱ) 由(Ⅰ)知,aa aal 1112+=+=恒成立令已知k kk k k k a k k -1110-111.1-10),1,0(2>+∴>⇒>++≤≤<∈.22)1(11)1(1111)(k kk k l k a a a a g -+-=-+-≥⇒-=+=⇒这时时取最大值在 所以2)1(111k kl k a -+--=取最小值时,当. 30(上海市春季高考数学试卷(含答案))本题共有3个小题,第1小题满分5分,第2小题满分7分,第3小题满分6分.已知真命题:“函数()y f x =的图像关于点( )P a b 、成中心对称图形”的充要条件为“函数()y f x a b =+- 是奇函数”.(1)将函数32()3g x x x =-的图像向左平移1个单位,再向上平移2个单位,求此时图像对应的函数解析式,并利用题设中的真命题求函数()g x 图像对称中心的坐标; (2)求函数22()log 4xh x x=- 图像对称中心的坐标; (3)已知命题:“函数 ()y f x =的图像关于某直线成轴对称图像”的充要条件为“存在实数a 和b,使得函数()y f x a b =+- 是偶函数”.判断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).*(1)平移后图像对应的函数解析式为32(1)3(1)2y x x =+-++, 整理得33y x x =-, 由于函数33y x x =-是奇函数, 由题设真命题知,函数()g x 图像对称中心的坐标是(1 2)-,. (2)设22()log 4xh x x=-的对称中心为( )P a b ,,由题设知函数()h x a b +-是奇函数. 设()(),f x h x a b =+-则22()()log 4()x a f x b x a +=--+,即222()log 4x af x b a x +=---. 由不等式2204x aa x+>--的解集关于原点对称,得2a =. 此时22(2)()l o g (2 2)2x f x b x x+=-∈--,,. 任取(2,2)x ∈-,由()()0f x f x -+=,得1b =, 所以函数22()log 4xh x x=-图像对称中心的坐标是(2 1),. (3)此命题是假命题. 举反例说明:函数()f x x =的图像关于直线y x =-成轴对称图像,但是对任意实数a 和b ,函数()y f x a b =+-,即y x a b =+-总不是偶函数. 修改后的真命题: “函数()y f x =的图像关于直线x a =成轴对称图像”的充要条件是“函数()y f x a =+是偶函数”.。
2013年高考理科数学全国新课标卷2试题与答案word解析版
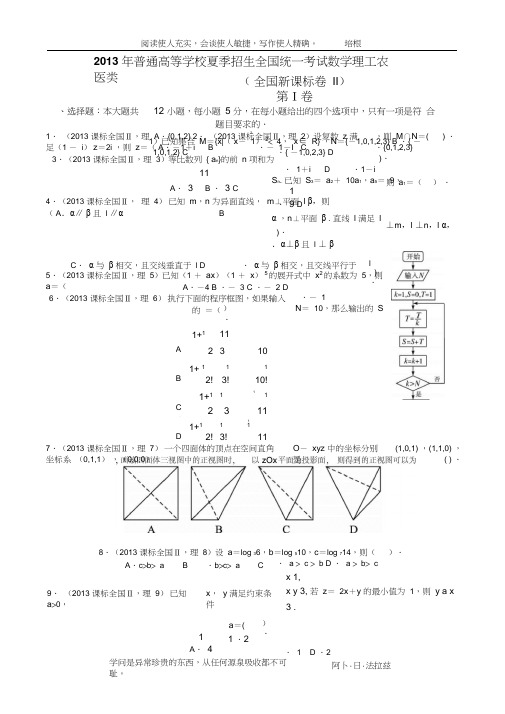
2013 年普通高等学校夏季招生全国统一考试数学理工农医类、选择题:本大题共 ( 全国新课标卷 II )第Ⅰ卷12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符 合题目要求的. 21)已知集合 M ={x |( x - 1) 2< 4, x ∈ R} ,N ={-1,0,1,2,3} B .{ -1,0,1,2} C .{ -1,0,2,3} D 1. (2013 课标全国Ⅱ,理 A .{0,1,2} 2. (2013 课标全国Ⅱ,理 2)设复数 z 满足(1 - i ) z =2i ,则 z =( A .-1+i B .- 1-I C3.(2013 课标全国Ⅱ,理 3)等比数列 { a n }的前 n 项和为 11A . 3B . 3C 4.(2013 课标全国Ⅱ, 理 4) 已知 m ,n 为异面直线, m ⊥平面 l β,则 ( A .α∥ β 且 l ∥α B,则 M ∩N =( ) . .{0,1,2,3} ). . 1+i D .1-i S n . 已知 S 3= a 2+ 10a 1,a 5= 9, 1. 9 D α ,n ⊥平面 β . 直线 l 满足 l )..α⊥β 且 l ⊥ β则 a 1=( ) .⊥m ,l ⊥n ,l α, C . α 与 β 相交,且交线垂直于 l D . α 与 β 相交,且交线平行于 5.(2013 课标全国Ⅱ,理 5)已知(1 + ax )(1 + x ) 5的展开式中 x 2的系数为 5,则a =( .- 1 N = 10,那么输出的 S A .-4 B .- 3 C .- 2 D6.(2013 课标全国Ⅱ,理 6) 执行下面的程序框图,如果输入的 =().A. 2 3 101+ 1 11B .2! 3!10!1+1 111C . 2 3111+1 1 1 1D 2! 3! 11 1+1 11 l ). 7.(2013 课标全国Ⅱ,理 7) 一个四面体的顶点在空间直角坐标系 (0,1,1) ,(0,0,0) O - xyz 中的坐标分别是 (1,0,1) ,(1,1,0) ,( ) .8.(2013 课标全国Ⅱ,理 8)设 a =log 36,b =log 510,c =log 714,则( ).. a > c > b D . a > b > cx 1,x y 3, 若 z = 2x +y 的最小值为 1,则 y a x 3 .A .c >b > aB .b >c > a C9. (2013 课标全国Ⅱ,理 9) 已知a >0,x , y 满足约束条件 a =( 1 .2). 1 A . 4 . 1 D .210.(2013 课标全国Ⅱ,理10)已知函数f(x) =x 3+ax2+bx+ c ,下列结论中错误的是( ).A.x0∈R,f(x0) =0B.函数y =f(x) 的图像是中心对称图形C.若x0 是f(x) 的极小值点,则f(x) 在区间( -∞,x0) 单调递减D.若x0 是f(x) 的极值点,则f′ (x0) =011.(2013 课标全国Ⅱ,理11)设抛物线C:y2=2px( p> 0)的焦点为F,点M在C上,| MF| =5,若以MF为直径的圆过点(0,2) ,则C的方程为( ) .A.y2 =4x 或y2=8x B .y2=2x 或y2=8xC.y2=4x 或y2=16x D .y2=2x 或y2=16x12.(2013 课标全国Ⅱ,理12)已知点A(-1,0) ,B(1,0) ,C(0,1) ,直线y=ax+b(a>0)将△ ABC分割为面积相等的两部分,则 b 的取值范围是( ) .12 , 11,12 ,11,1,1 A.(0,1) B.2 2 C . 2 3 D .3,2第Ⅱ卷本卷包括必考题和选考题两部分,第13题~第21 题为必考题,每个试题考生都必须做答。
2013年高考真题——理科数学(新课标Ⅱ卷)-Word版附答案

一、选择题:本大题共10小题。
每小题5分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合M={x|(x-1)2< 4,x ∈R },N={-1,0,1,2,3},则M ∩N =( ) (A ){0,1,2} (B ){-1,0,1,2} (C ){-1,0,2,3} (D ){0,1,2,3} (2)设复数z 满足(1-i )z=2 i ,则z =( ) (A )-1+i(B )-1-i(C )1+i(D )1-i(3)等比数列{a n }的前n 项和为S n ,已知S 3 = a 2 +10a 1 ,a 5 = 9,则a 1=( ) (A )13 (B )13- (C )19 (D )19- (4)已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β。
直线l 满足l ⊥m ,l ⊥n ,,l l αβ⊄⊄,则()(A )α∥β且l ∥α(B )α⊥β且l ⊥β(C )α与β相交,且交线垂直于l(D )α与β相交,且交线平行于l(5)已知(1+ɑx )(1+x )5的展开式中x 2的系数为5,则ɑ=( ) (A )-4(B )-3(C )-2(D )-1(6)执行右面的程序框图,如果输入的N=10,那么输出的S=(A )11112310++++(B )11112!3!10!++++(C )11112311++++ (D )11112!3!11!++++ (7)一个四面体的顶点在空间直角坐标系O-xyz 中的坐标分 别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四 面体三视图中的正视图时,以zOx 平面为投影面,则得到正视 图可以为(A) (B)(C)(D)(8)设a=log 36,b=log 510,c=log 714,则(A )c >b >a (B )b >c >a (C )a >c >b (D)a >b >c(9)已知a >0,x ,y 满足约束条件()133x x y y a x ⎧≥⎪+≤⎨⎪≥-⎩,若z=2x+y 的最小值为1,则a=(A)14(B)12(C)1 (D)2(10)已知函数f(x)=x 3+ax 2+bx+c ,下列结论中错误的是 (A )∃x α∈R,f(x α)=0(B )函数y=f(x)的图像是中心对称图形(C )若x α是f(x)的极小值点,则f(x)在区间(-∞,x α)单调递减(D )若x 0是f (x )的极值点,则()0'0f x =(11)设抛物线y 2=3px(p>0)的焦点为F ,点M 在C 上,|MF |=5,若以MF 为直径的圆过点(0,2),则C 的方程为(A )y 2=4x 或y 2=8x (B )y 2=2x 或y 2=8x(C )y 2=4x 或y 2=16x (D )y 2=2x 或y 2=16x(12)已知点A (-1,0);B (1,0);C (0,1),直线y=ax+b (a >0)将△ABC 分割为面积相等的两部分,则b 的取值范围是 (A )(0,1)(B)11,22⎛⎫-⎪ ⎪⎝⎭( C) 1123⎛⎤- ⎥ ⎦⎝(D) 11,32⎡⎫⎪⎢⎣⎭ 二、填空题:本大题共4小题,每小题5分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最新新课标2013年全国高考理科数学试题分类汇编2:函数一、选择题1 .(2013年高考江西卷(理))函数ln(1-x)的定义域为A.(0,1)B.[0,1)C.(0,1]D.[0,1] 【答案】D2 .(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))若a b c <<,则函数()()()()()()()f x x a x b x b x c x c x a =--+--+--的两个零点分别位于区间( )A.(),a b 和(),b c 内B.(),a -∞和(),a b 内C.(),b c 和(),c +∞内D.(),a -∞和(),c +∞内【答案】A3 .(2013年上海市春季高考数学试卷(含答案))函数12()f x x -=的大致图像是( )【答案】A4 .(2013年高考四川卷(理))设函数()f x =(a R ∈,e 为自然对数的底数).若曲线sin y x=上存在00(,)x y 使得00(())f f y y =,则a 的取值范围是( )(A)[1,]e (B)1[,-11]e -, (C)[1,1]e + (D)1[-1,1]e e -+【答案】A5 .(2013年高考新课标1(理))已知函数()f x =22,0ln(1),0x x x x x ⎧-+≤⎨+>⎩,若|()f x |≥ax ,则a 的取值范围是A.(,0]-∞B.(,1]-∞C.[2,1]-D.[2,0]-【答案】D6 .(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))函数()()21=log 10f x x x ⎛⎫+> ⎪⎝⎭的反函数()1=f x -(A)()1021x x >- (B)()1021xx ≠- (C)()21x x R -∈ (D)()210xx -> 【答案】A7 .(2013年普通高等学校招生统一考试浙江数学(理)试题(纯WORD 版))已知y x ,为正实数,则A.y x yx lg lg lg lg 222+=+ B.y x y x lg lg )lg(222∙=+ C.y x yx lg lg lg lg 222+=∙ D.y x xy lg lg )lg(222∙=【答案】D8 .(2013年普通高等学校招生统一考试山东数学(理)试题(含答案))已知函数()f x 为奇函数,且当0x >时,21()f x x x=+,则(1)f -= (A) 2- (B) 0 (C) 1 (D) 2【答案】A9 .(2013年高考陕西卷(理))在如图所示的锐角三角形空地中, 欲建一个面积不小于300m 2的内接矩形花园(阴影部分), 则其边长x (单位m )的取值范围是(A) [15,20] (B) [12,25] (C) [10,30] (D) [20,30] 【答案】C10.(2013年普通高等学校招生统一考试重庆数学(理)试题(含答案))y =()63a -≤≤的最大值为( ) A.9 B.92C.3【答案】B11.(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))已知函数()f x 的定义域为()1,0-,则函数()21f x -的定义域为 (A)()1,1- (B)11,2⎛⎫- ⎪⎝⎭ (C)()-1,0 (D)1,12⎛⎫⎪⎝⎭【答案】B12.(2013年高考湖南卷(理))函数()2ln f x x =的图像与函数()245g x x x =-+的图像的交点个数为A.3B.2C.1D.0【答案】B13.(2013年高考四川卷(理))函数231x x y =-的图象大致是( )【答案】C14.(2013年普通高等学校招生统一考试辽宁数学(理)试题(WORD 版))已知函数()()()()222222,228.f x x a x a g x x a x a =-++=-+--+设()()(){}()()(){}{}()12max ,,min ,,max ,H x f x g x H x f x g x p q ==表示,p q 中的较大值,{}min ,p q 表示,p q 中的较小值,记()1H x 得最小值为,A ()2H x 得最小值为B ,则A B -= (A)2216a a -- (B)2216a a +- (C)16- (D)16【答案】B 15.(2013年普通高等学校招生统一考试广东省数学(理)卷(纯WORD 版))定义域为R 的四个函数3y x =,2x y =,21y x =+,2sin y x =中,奇函数的个数是( )A . 4 B.3C.2D.【答案】C16.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))若函数3()=+b +f x x x c 有极值点1x ,2x ,且11()=f x x ,则关于x 的方程213(())+2()+=0f x f x b 的不同实根个数是(A)3 (B)4 (C) 5 (D)6 【答案】A17.(2013年普通高等学校招生统一考试天津数学(理)试题(含答案))函数0.5()2|log |1x f x x =-的零点个数为(A) 1 (B) 2 (C) 3 (D) 4 【答案】B18.(2013年高考北京卷(理))函数f (x )的图象向右平移1个单位长度,所得图象与y =e x关于y 轴对称,则f (x )=A.1e x +B. 1e x -C. 1e x -+D. 1e x --【答案】D19.(2013年上海市春季高考数学试卷(含答案))设-1()f x 为函数()f x =的反函数,下列结论正确的是( )(A) 1(2)2f-= (B) 1(2)4f -= (C) 1(4)2f-= (D) 1(4)4f -=【答案】B20.(2013年普通高等学校招生统一考试大纲版数学(理)WORD 版含答案(已校对))若函数()21=f x x ax x++在1,+2⎛⎫∞⎪⎝⎭是增函数,则a 的取值范围是 (A)[-1,0] (B)[1,)-+∞ (C)[0,3] (D)[3,)+∞【答案】D二、填空题21.(2013年上海市春季高考数学试卷(含答案))函数2log (2)y x =+的定义域是_______________【答案】(2,)-+∞22.(2013年高考上海卷(理))方程1313313x x-+=-的实数解为________ 【答案】3log 4x =.23.(2013年高考上海卷(理))对区间I 上有定义的函数()g x ,记(){|(),}g I y y g x x I ==∈,已知定义域为[0,3]的函数()y f x =有反函数1()y fx -=,且11([0,1))[1,2),((2,4])[0,1)f f --==,若方程()0f x x -=有解0x ,则0_____x =【答案】02x =.24.(2013年高考新课标1(理))若函数()f x =22(1)()xx ax b -++的图像关于直线2x =-对称,则()f x 的最大值是______. 【答案】16.25.(2013年上海市春季高考数学试卷(含答案))方程28x=的解是_________________ 【答案】326.(2013年高考湖南卷(理))设函数(),0,0.x x x f x a b c c a c b =+->>>>其中(1)记集合{}(,,),,M a b c a b c a =不能构成一个三角形的三条边长,且=b ,则(,,)a b c M ∈所对应的()f x 的零点的取值集合为____.(2)若,,a b c ABC ∆是的三条边长,则下列结论正确的是______.(写出所有正确结论的序号) ①()(),1,0;x f x ∀∈-∞>②,,,xxxx R xa b c ∃∈使不能构成一个三角形的三条边长; ③若()()1,2,0.ABC x f x ∆∃∈=为钝角三角形,则使【答案】(1)]10(, (2)①②③27.(2013年普通高等学校招生全国统一招生考试江苏卷(数学)(已校对纯WORD 版含附加题))已知)(x f 是定义在R 上的奇函数.当0>x 时,x x x f 4)(2-=,则不等式x x f >)(的解集用区间表示为___________.【答案】()()+∞-,50,528.(2013年高考上海卷(理))设a 为实常数,()y f x =是定义在R 上的奇函数,当0x <时,2()97a f x x x=++,若()1f x a ≥+对一切0x ≥成立,则a 的取值范围为________【答案】87a ≤-. 三、解答题29.(2013年普通高等学校招生统一考试安徽数学(理)试题(纯WORD 版))设函数22()(1)f x ax a x =-+,其中0a >,区间|()>0I x f x =(Ⅰ)求的长度(注:区间(,)αβ的长度定义为βα-); (Ⅱ)给定常数(0,1)k ∈,当时,求长度的最小值.【答案】解: (Ⅰ))1,0(0])1([)(22a a x x a a x x f +∈⇒>+-=.所以区间长度为21a a+. (Ⅱ) 由(Ⅰ)知,aa aal 1112+=+=恒成立令已知k kk k k k a k k -1110-111.1-10),1,0(2>+∴>⇒>++≤≤<∈. 22)1(11)1(1111)(k kk k l k a a a a g -+-=-+-≥⇒-=+=⇒这时时取最大值在所以2)1(111k kl k a -+--=取最小值时,当. 30.(2013年上海市春季高考数学试卷(含答案))本题共有3个小题,第1小题满分5分,第2小题满分7分,第3小题满分6分.已知真命题:“函数()y f x =的图像关于点( )P a b 、成中心对称图形”的充要条件为“函数()y f x a b =+- 是奇函数”.(1)将函数32()3g x x x =-的图像向左平移1个单位,再向上平移2个单位,求此时图像对应的函数解析式,并利用题设中的真命题求函数()g x 图像对称中心的坐标; (2)求函数22()log 4xh x x=- 图像对称中心的坐标; (3)已知命题:“函数 ()y f x =的图像关于某直线成轴对称图像”的充要条件为“存在实数a 和b,使得函数()y f x a b =+- 是偶函数”.判断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).【答案】(1)平移后图像对应的函数解析式为32(1)3(1)2yx x =+-++,整理得33y x x =-,由于函数33y x x =-是奇函数,由题设真命题知,函数()g x 图像对称中心的坐标是(1 2)-,. (2)设22()log 4xh x x=-的对称中心为( )P a b ,,由题设知函数()h x a b +-是奇函数. 设()(),f x h x a b =+-则22()()log 4()x a f x b x a +=--+,即222()log 4x af x b a x +=---.由不等式2204x aa x+>--的解集关于原点对称,得2a =.此时22(2)()log (2 2)2x f x b x x+=-∈--,,.任取(2,2)x ∈-,由()()0f x f x -+=,得1b =, 所以函数22()log 4xh x x=-图像对称中心的坐标是(2 1),. (3)此命题是假命题.举反例说明:函数()f x x =的图像关于直线y x =-成轴对称图像,但是对任意实数a 和b ,函数()y f x a b =+-,即y x a b =+-总不是偶函数.修改后的真命题:“函数()y f x =的图像关于直线x a =成轴对称图像”的充要条件是“函数()y f x a =+是偶函数”.。
