北京市各区县初三一模数学反比例函数汇编
最新北京市各城区中考一模数学——一次函数和反比例函数第17题汇总(学生完结)
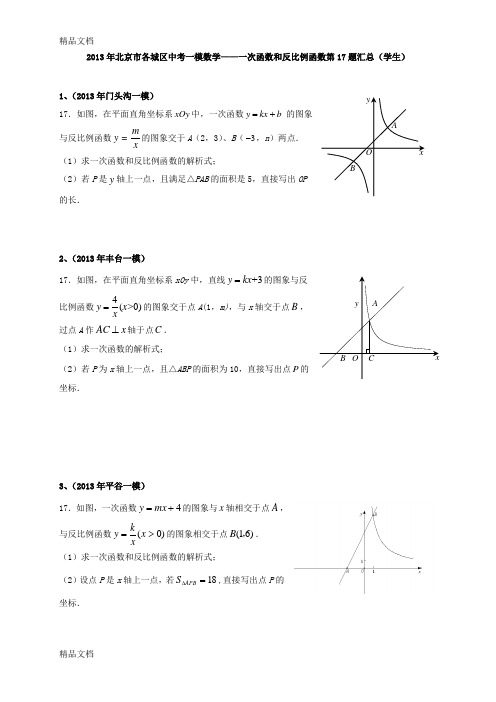
2013年北京市各城区中考一模数学——一次函数和反比例函数第17题汇总(学生)1、(2013年门头沟一模)17.如图,在平面直角坐标系xOy 中,一次函数y kx b =+的图象与反比例函数m y x=的图象交于A (2,3)、B (3-,n )两点.(1)求一次函数和反比例函数的解析式;(2)若P 是y 轴上一点,且满足△PAB 的面积是5,直接写出OP 的长.2、(2013年丰台一模)17.如图,在平面直角坐标系xOy 中,直线+3y kx =的图象与反比例函数4(>0)y x x=的图象交于点A (1,m),与x 轴交于点B ,过点A 作AC x ⊥轴于点C . (1)求一次函数的解析式;(2)若P 为x 轴上一点,且△ABP 的面积为10,直接写出点P 的坐标.3、(2013年平谷一模)17.如图,一次函数4+=mx y 的图象与x 轴相交于点A ,与反比例函数)0(>=x xky 的图象相交于点(16)B ,. (1)求一次函数和反比例函数的解析式;(2)设点P 是x 轴上一点,若18=∆APB S ,直接写出点P 的坐标. yxA BOAB O Cxy4、(2013年顺义一模)17.如图,已知(2,2)A --,(,4)B n 是一次函数y kx b =+的图象和反比例函数my x=的图象的两个交点. (1)求反比例函数和一次函数的解析式; (2)求AOB ∆的面积.5、(2013年石景山一模)17.已知:一次函数3+=x y 与反比例函数3m y x-=(0<x ,m 为常数)的图象交于点A (a ,2)、B 两点. (1)求m 的值和B 点坐标;(2)过A 点作y 轴的平行线,过B 点作x 轴的平行线,这两条直线交于点E ,若反比例函数ky x=的图象与△ABE 有公共点,请直接写出k 的取值范围.6、(2013年海淀一模)17. 如图,在平面直角坐标系xOy 中,反比例函数xy 2-=的图象与一次函数k kx y -=的图象的一个交点为(1,)A n -. (1)求这个一次函数的解析式;(2)若P 是x 轴上一点,且满足45APO ∠=︒,直接写出点P 的坐标. yxO7、(2013年西城一模)17.如图,在平面直角坐标系xOy 中,正比例函数32y x =-与反比例函数ky x=的图象在第二象限交于点A ,且点A 的横坐标为 -2 .(1) 求反比例函数的解析式;(2) 点B 的坐标为(-3,0),若点P 在y 轴上,且△AOB 的面积与△AOP 的面积相等,直接写出点P 的坐标.8、(2013年通州一模)17.已知(42)A -,,(24)B -,是一次函数y kx b =+的图象和反比例函数my x=图象的两个交点. (1)求反比例函数和一次函数的表达式;(2)将一次函数y kx b =+的图象沿y 轴向上平移n 个单位长度,交y 轴于点C ,若12ABC S =V ,求n 的值.9、(2013年东城一模)18.如图,平行四边形ABCD 放置在平面直角坐标系xOy 中,已知A (-2,0),B (2,0),D (0,3),反比例函数ky x=(x >0)的图象经过点C .(1)求此反比例函数的解析式;(2)问将平行四边形ABCD 向上平移多少个单位,能使点B 落在双曲线上.10、(2013年朝阳一模)17.如图,在平面直角坐标系xOy 中,一次函数y = -x 的图象与反比例函数()0ky x x=<的图象相交于点()4A m -,. (1)求反比例函数ky x=的解析式;(2)若点P 在x 轴上,AP =5,直接写出点P 的坐标.11、(2013年密云一模)17.如图,已知直线l 1经过点A (-1,0)与点B (2,3),另一条直线l 2经过点B ,且与x 轴交于点P (m ,0). (1)求直线l 1的解析式;(2)若△APB 的面积为3,求m 的值.12、(2013年延庆一模)17.(本题满分5分) 已知直线l 与直线y=2x 平行,且与直线y= -x+m 交于点(2,0), 求m 的值及直线的解析式.13、(2013年房山一模) 17.如图,反比例函数xy 3=的图象与一次函数b kx y +=的图象交于A (m,3)、B (-3,n)两点.(1)求一次函数的解析式及AOB ∆的面积;(2)若点P 是坐标轴上的一点,且满足PAB ∆的面积等于AOB ∆的面积的2倍,直接写出点P 的坐标. yxO-4AxByOA17. 将直线y x=沿y轴向下平移后,得到的直线与x轴交于点A(30,),与双曲线myx=(0x>)交于点B.(1)求直线AB的解析式;(2)设点B的纵坐标为a,求m的值(用含a的代数式表示).15、(2013年怀柔一模)17. 已知反比例函数y=8mx-(m为常数)的图象经过点A(-1,6).(1)求m的值;(2)如图,过点A作直线AC与函数y=8mx-的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.17.已知:关于x 的一元二次方程 2(2)(1)0x m x m -+++=. . (1)求证:方程有两个实数根;(2)设m<0,且方程的两个实数根分别为 , (其中 < ),若y 是关于m 的函数,且1214x x y -=,求这个函数的解析式.21,x x 1x 2x。
2019-2020年北京市中考数学各地区模拟试题分类(北京专版)(二)——反比例函数(含解析)

2019-2020年北京市中考数学各地区模拟试题分类(北京专版)(二)——反比例函数一.选择题1.(2019•城区模拟)如图,直线y=mx与双曲线y=交于A、B两点,过点A作AM⊥x 轴,垂足为M,连接BM,若S△ABM=2,则k的值是()A.2 B.m﹣2 C.m D.4 2.(2018•朝阳区模拟)如图,在平面直角坐标系xOy中,反比例函数y=的图象经过点T.下列各点P(4,6),Q(3,﹣8),M(2,﹣12),N(,48)中,在该函数图象上的点有()A.4个B.3个C.2个D.1个3.(2019•历城区二模)如图,反比例函数(x>0)的图象与一次函数y=ax+b的图象交于点A(1,6)和点B(3,2).当时,则x的取值范围是()A.1<x<3 B.x<1或x>3 C.0<x<1 D.0<x<1或x>34.(2020•西城区校级模拟)如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将平行四边形ABCO绕点A逆时针旋转得到平行四边形ADEF,AD经过点O,点F恰好落在x轴的正半轴上.若点D在反比例函数y=(x<0)的图象上,则k的值为()A.4B.12 C.8D.6 5.(2020•海淀区二模)在平面直角坐标系xOy中,对于点P(a,b),若ab>0,则称点P 为“同号点”.下列函数的图象中不存在“同号点”的是()A.y=﹣x+1 B.y=x2﹣2x C.y=﹣D.y=x2+ 6.(2020•海淀区校级模拟)在平面直角坐标系xOy中,函数y=(x<0)的图象与直线l:y=x+b(b<0)交于点A,与直线l2:x=b交于点B,直线l1与l2交于点C,记函1数y=(x<0)的图象在点A、B之间的部分与线段AC,线段BC围成的区域(不含边界)为W,当﹣≤x≤﹣时,区域W的整点个数为(提示:平面直角坐标系内,横坐标、纵坐标都是整数的点称为整点)()A.3个B.2个C.1个D.没有二.填空题7.(2020•海淀区校级模拟)在平面直角坐标系中,点A(a,b)在双曲线y=﹣上,点A 关于y轴的对称点B在双曲线y=上,则k﹣2的值为.8.(2020•丰台区三模)如图,在平面直角坐标系xOy中,已知函数y1=(x>0)和y2=﹣(x<0),点M为y轴正半轴上一点,N为x轴上一点,过M作y轴的垂线分别交y1,y2的图象于A,B两点,连接AN,BN,则△ABN的面积为.9.(2020•朝阳区校级模拟)如图,曲线AB是抛物线y=﹣4x2+8x+1的一部分(其中A是抛物线与y轴的交点,B是顶点),曲线BC是双曲线y=(k≠0)的一部分.曲线AB 与BC组成图形W.由点C开始不断重复图形W形成一组“波浪线”.若点P(2020,m),Q(x,n)在该“波浪线”上,则m的值为,n的最大值为.10.(2020•北京模拟)如图,在平面直角坐标系xOy中,射线l的端点为(0,1),l∥x 轴,请写出一个图象与射线l有公共点的反比例函数的表达式:.11.(2020•丰台区模拟)如图,已知正方形OABC的三个顶点坐标分别为A(2,0),B(2,2),C(0,2),若反比例函数y=(k>0)的图象与正方形OABC的边有交点,请写出一个符合条件的k值.12.(2020•西城区校级模拟)如图,在平面直角坐标系中,菱形ABCD的顶点A、B在反比例函数y=(k>0,x>0)的图象上,横坐标分别为1,4,对角线BD∥x轴.若菱形ABCD的面积为,则k的值为.13.(2020•西城区校级模拟)已知Rt△ABC位于第二象限,点A(﹣1,1),AB=BC=2,且两条直角边AB、BC分别平行于x轴、y轴,写出一个函数y=(k≠0),使它的图象与△ABC有两个公共点,这个函数的表达式为.14.(2020•昌平区模拟)如图,A、B是函数图象上两点,点C、D、E、F分别在坐标轴上,且与点A、B、O构成正方形和长方形.若正方形OCAD的面积为6,则长方形OEBF的面积为.三.解答题15.(2020•东城区二模)在平面直角坐标系xOy中,反比例函数y=(k≠0,x>0)的图象经过点A(1,﹣4),直线y=﹣2x+m与x轴交于点B(1,0).(1)求k,m的值;(2)已知点P(n,﹣2n)(n>0),过点P作平行于x轴的直线,交直线y=﹣2x+m 于点C,过点P作平行于y轴的直线交反比例函数y=(k≠0.x>0)的图象于点D,当PD=2PC时,结合函数的图象,求出n的值.16.(2020•北京二模)如图,在平面直角坐标系xOy中,直线l:y=mx+3与x轴交于点C,与反比例函数y=(k≠0)的图象交于点A(1,4)和点B.(1)求m,k的值及点C的坐标;(2)若点P是x轴上一点,且S△ABP=5,直接写出点P的坐标.17.(2020•丰台区二模)在平面直角坐标系xOy中,一次函数y=mx+n的图象与反比例函数y=(x>0)的图象交于点A(2,1)和点B,与y轴交于点C.(1)求k的值;(2)如果AC=2AB,求一次函数的表达式.18.(2020•海淀区二模)如图,在平面直角坐标系xOy中,函数y=(x>0)的图象与直线y=kx(k≠0)交于点P(1,p).M是函数y=(x>0)图象上一点,过M作x轴的平行线交直线y=kx(k≠0)于点N.(1)求k和p的值;(2)设点M的横坐标为m.①求点N的坐标;(用含m的代数式表示)②若△OMN的面积大于,结合图象直接写出m的取值范围.19.(2020•门头沟区一模)在平面直角坐标系xOy中,一次函数y=x+m(m≠0)的图象与y轴交于点A,过点B(0,2m)且平行于x轴的直线与一次函数y=x+m(m≠0)的图象,反比例函数y=的图象分别交于点C,D.(1)求点D的坐标(用含m的代数式表示);(2)当m=1时,用等式表示线段BD与CD长度之间的数量关系,并说明理由;(3)当BD≤CD时,直接写出m的取值范围.20.(2020•朝阳区一模)有这样一个问题:探究函数的图象与性质并解决问题.小明根据学习函数的经验,对问题进行了探究.下面是小明的探究过程,请补充完整:(1)函数的自变量x的取值范围是x≠2;(2)取几组y与x的对应值,填写在下表中.x…﹣4 ﹣2 ﹣1 0 1 1.2 1.25 2.75 2.8 3 4 5 6 8 …y… 1 1.5 2 3 6 7.5 8 8 7.5 6 3 m 1.5 1 …m的值为;(3)如图,在平面直角坐标系xOy中,描出补全后的表中各组对应值所对应的点,并画出该函数的图象;(4)获得性质,解决问题:①通过观察、分析、证明,可知函数的图象是轴对称图形,它的对称轴是;②过点P(﹣1,n)(0<n<2)作直线l∥x轴,与函数的图象交于点M,N(点M在点N的左侧),则PN﹣PM的值为.21.(2020•朝阳区一模)在平面直角坐标系xOy中,直线y=1与一次函数y=﹣x+m的图象交于点P,与反比例函数的图象交于点Q,点A(1,1)与点B关于y轴对称.(1)直接写出点B的坐标;(2)求点P,Q的坐标(用含m的式子表示);(3)若P,Q两点中只有一个点在线段AB上,直接写出m的取值范围.22.(2020•平谷区一模)在平面直角坐标系xOy中,反比例函数y=(x>0)的图象G 与直线l:y=2x﹣4交于点A(3,a).(1)求k的值;(2)已知点P(0,n)(n>0),过点P作平行于x轴的直线,与图象G交于点B,与直线l交于点C.横、纵坐标都是整数的点叫做整点.记图象G在点A,B之间的部分与线段AC,BC围成的区域(不含边界)为W.①当n=5时,直接写出区域W内的整点个数;②若区域W内的整点恰好为3个,结合函数图象,直接写出n的取值范围.23.(2020•密云区一模)如图,在平面直角坐标系xOy中,直线l:y=x﹣1的图象与反比例函数y=(x>0)的图象交于点A(3,m).(1)求m、k的值;(2)点P(x p,0)是x轴上的一点,过点P作x轴的垂线,交直线l于点M,交反比例函数y=(x>0)的图象于点N.横、纵坐标都是整数的点叫做整点.记y=(x>0)的图象在点A,N之间的部分与线段AM,MN围成的区域(不含边界)为W.①当x p=5时,直接写出区域W内的整点的坐标为;②若区域W内恰有6个整点,结合函数图象,求出x p的取值范围.参考答案一.选择题1.解:设A(x,y),∵直线y=mx与双曲线y=交于A、B两点,∴B(﹣x,﹣y),∴S△BOM=|xy|,S△AOM=|xy|,∴S△BOM=S△AOM,∴S△ABM=S△AOM+S△BOM=2S△AOM=2,S△AOM=|k|=1,则k=±2.又由于反比例函数位于一三象限,k>0,故k=2.故选:A.2.解:∵反比例函数y=的图象经过点T(3,8),∴k=3×8=24,将P(4,6),Q(3,﹣8),M(2,﹣12),N(,48)分别代入反比例函数y=,可得Q(3,﹣8),M(2,﹣12)不满足反比例函数y=,∴在该函数图象上的点有2个,故选:C.3.解:由两函数图象交点可知,当x=1或3时,ax+b=,当0<x<1或x>3时,ax+b<.故选:D.4.解:由题意可得,OA=2,AF=2,∴∠AFO=∠AOF,∵AB∥OF,∠BAO=∠OAF,∴∠BAO=∠AOF,∠BAF+∠AFO=180°,解得,∠BAO=60°,∴∠DOC=60°,∵AO=2,AD=6,∴OD=4,∴点D的横坐标是:﹣4×cos60°=﹣2,纵坐标为:﹣4×sin60°=﹣2,∴点D的坐标为(﹣2,﹣2),∵D在反比例函数y=(x<0)的图象上,∴﹣2=,得k=4,故选:A.5.解:由题意,图象经过第一和第三象限的函数都是满足条件的,函数y=﹣的图象在二四象限,不满足条件,故选:C.6.解:∵y=(x<0),过整点(﹣1,﹣2)、(﹣2,﹣1),当b=﹣时,函数两个函数图象,如图1,从图1看,区域W内没有整点;当b=﹣时,同样画出如图2的图象,区域W内没有整点,∴当﹣≤x≤﹣时,区域W的整点个数为0,故选:D.二.填空题(共8小题)7.解:∵点A(a,b)在双曲线y=﹣上,∴ab=﹣2,又∵点A与点B关于y轴的对称,∴B(﹣a,b),∵点B在双曲线y=上,∴k=﹣ab=2,∴k﹣2的值为0.故答案为0.8.解:过点B作BE⊥x轴于点E,过点A作AF⊥x轴于点F,由题意可得,四边形BEFA是矩形,∵函数y1=(x>0)和y2=﹣(x<0),∴矩形BEOM面积为:1,矩形MOFA面积为:3,则矩形BEFA的面积为4,则△ABN的面积为:S矩形BEFA=2.故答案为:2.9.解:∵y=﹣4x2+8x+1=﹣4(x﹣1)2+5,∴当x=0时,y=1,∴点A的坐标为(0,1),点B的坐标为(1,5),∵点B(1,5)在y=(k≠0)的图象上,∴k=5,∵点C在y=的图象上,点C的横坐标为5,∴点C的纵坐标是1,∴点C的坐标为(5,1),∵2020÷5=404,∴P(2020,m)在抛物线y=﹣4x2+8x+1的图象上,m=﹣4×0+8×0+1=1,∵点Q(x,n)在该“波浪线”上,∴n的最大值是5,故答案为:1,5.10.解:∵射线l的端点为(0,1),l∥x轴,∴写出一个图象与射线l有公共点的反比例函数的表达式:答案不唯一,如y=.故答案为:答案不唯一,如y=.11.解:∵反比例函数y=(k>0)的图象与正方形OABC的边有交点,∴把B(2,2)代入y=得,k=4,∴满足条件的k值的范围是0<k≤4,故k=1(答案不唯一),故答案为:k=1(满足条件的k值的范围是0<k≤4).12.解:连接AC分别交BD、x轴于点E、F.由已知,A、B横坐标分别为1,4,∴BE=3,∵四边形ABCD为菱形,AC、BD为对角线∴S菱形ABCD=4×AE•BE=,∴AE=,设点B的坐标为(4,y),则A点坐标为(1,y+)∵点A、B同在y=图象上∴4y=1•(y+)∴y=,∴B点坐标为(4,)∴k=5故答案为5.13.解:B的坐标是(﹣3,1),C的坐标是(﹣3,3).则这个函数的解析式可以是:y=﹣.(答案不唯一).故答案是:y=﹣.14.解:∵S正方形OCAD=OD•OC=|x A•y A|=|k|=6,∴S长方形OCAD=OE•OF=|x B•y B|=|k|=6.故答案为6.三.解答题(共9小题)15.解:(1)把A(1,﹣4)代入y=得k=1×(﹣4)=﹣4;把B(1,0)代入y=﹣2x+m得﹣2+m=0,解得m=2;(2)反比例函数解析式为y=﹣(x>0),一次函数解析式为y=﹣2x+2,如图,当y=﹣2n时,﹣2x+2=﹣2n,解得x=n+1,则C(n+1,﹣2n),∴PC=n+1﹣n=1,当y=﹣2n时,y=﹣=,∴D(n,﹣),∴PD=|﹣2n+|,∵PD=2PC,∴|﹣2n+|=2,当﹣2n+=2时,解得n1=﹣2(舍去),n2=1,当﹣2n+=﹣2时,解得n1=﹣1(舍去),n2=2,综上所述,当PD=2PC时,n=1或n=2.16.解:(1)将点A(1,4)的坐标代入y=mx+3中得4=m×1+3,解得m=1;∴一次函数解析式为y=x+3,当y=0,x+3=0,解得x=﹣3,∴点C的坐标为(﹣3,0).将点A(1,4)的坐标代入中得k=1×4=4;(2)设P(t,0),解方程组得或,∴B(﹣4,﹣1),∵S△ABP=5,∴×|t+3|×4+×|t+3|×1=5,即|t+3|=2,∴t=﹣1或﹣5,∴P(﹣5,0)或P(﹣1,0).17.解:(1)把点A(2,1)代入y=(x>0)得,1=,∴k=2;(2)如图,由(1)知,反比例函数的解析式为y=,∵AC=2AB,∴AB=BC,∴B点的横坐标为1,∵点B在y=(x>0)的图象上,∴y=2,∴B(1,2),把A(2,1),B(1,2)代入y=mx+n得,,解得:,∴一次函数的表达式为y=﹣x+3.18.解:(1)将点P的坐标代入y=(x>0)得:2=1×p,解得:p=2,故点P(1,2);将点P的坐标代入y=kx得:2=k×1,解得:k=2;(2)①点M的横坐标为m,则点M(m,),∵MN∥x轴,故点N的纵坐标为,将点N的纵坐标代入直线y=2x得:=2x,解得:x=,故点N的坐标为(,);②△OMN的面积=×MN×y M=×|(﹣m)|×>(m>0),解得:m<或m,故0<m或m>.19.解:(1)∵过点B(0,2m)且平行于x轴的直线与反比例函数y=的图象交于点D,∴点D的纵坐标为2m,∴2m=,x=2,∴D(2,2m);(2)当m=1时,B(0,2),D(2,2),∵过点B(0,2m)且平行于x轴的直线与一次函数y=x+m(m≠0)的图象交于点C,∴2m=x+m,x=m,∴C(m,2m),∴C(1,2),∴BD==2,CD==1,∴BD=2CD;(3)∵B(0,2m),C(m,2m),D(2,2m),∴BD=2,CD=|m﹣2|,∵BD≤CD,∴|m﹣2|≥2,∴m≥4或m<0.20.解:(2)由题意x=5时,y==2,∴m=2,故答案为2.(3)函数图象如图所示:(4)①观察图象可知图象是轴对称图形,对称轴x=2.故答案为x=2.②由题意,M(﹣+2,n),N(+2,n),∴PN=+2+1=+3,PM=﹣1﹣(﹣+2)=﹣3,∴PN﹣PM=+3﹣(﹣3)=6,故答案为6.21.解:(1)∵点A(1,1)与点B关于y轴对称,∴点B的坐标是(﹣1,1);(2)把y=1代入y=﹣x+m,得1=﹣x+m,解得x=m﹣1,∴点P的坐标为(m﹣1,1);把y=1代入,得1=,解得x=m,∴点Q的坐标为(m,1);(3)∵点P的坐标为(m﹣1,1),点Q的坐标为(m,1),∴点P在点Q的左边.当P,Q两点中只有一个点在线段AB上时,分两种情况:①只有P点在线段AB上时,由题意,得,解得1<m≤2;②只有Q点在线段AB上时,由题意,得,解得﹣1≤m<0.综上可知,所求m的取值范围是﹣1≤m<0或1<m≤2.22.解:(1)反比例函数y=(x>0)的图象G与直线l:y=2x﹣4交于点A(3,a).∴a=2×3﹣4=2,∴A(3,2),∵反比例函数y=(x>0)的图象G经过A(3,2),∴k=3×2=6;(2)①当n=5时,则B为(,5),C(,5),∴在W区域内有3个整数点:(2,4),(3,3),(3,4);②由图1可知,若区域W内的整点恰好为3个,当P点在A点的上方时,则4<n≤5;当P点在A点的下方时,则0<n<1,综上所述,若区域W内恰有3个整点,n的取值范围为:4<n≤5或0<n<1 23.解:(1)∵直线l:y=x﹣1的图象与反比例函数y=(x>0)的图象交于点A(3,m).∴m=3﹣1=2,∴点A(3,2),∵反比例函数y=过点A,∴k=3×2=6;(2)①当x p=5时,M、N两点的坐标为M(5,4)、N(5,).∵A(3,2).∴区域W内的整点的坐标为(4,2).②当点P在点A左边时,如图1,结合函数图象可知,当0<x p<1时,区域W内有6个整点;当点P在点A右时,如图2,结合函数图象可知,当6<x P≤7时,区域W内有6个整点;综上所述:当0<x p<1或6<x P≤7时,区域W内有6个整点.。
北京市2019年中考数学一模分类汇编 反比例综合题
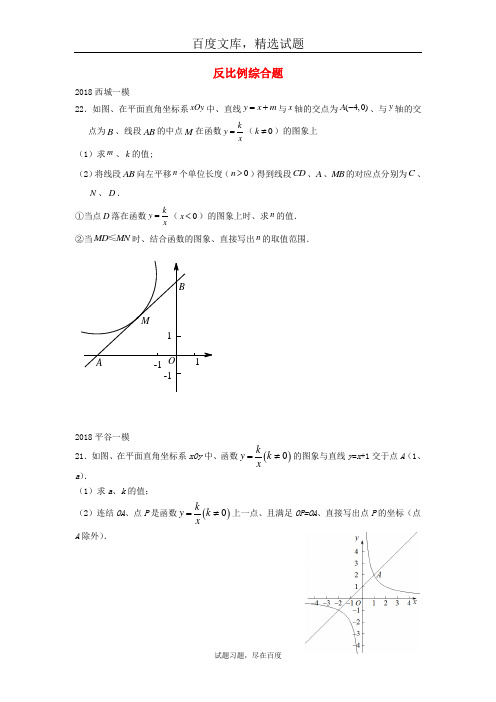
反比例综合题2018西城一模22.如图、在平面直角坐标系xOy 中、直线y x m =+与x 轴的交点为0()4,A -、与y 轴的交点为B 、线段AB 的中点M 在函数ky x=(0k ≠)的图象上 (1)求m 、k 的值;(2)将线段AB 向左平移n 个单位长度(0n >)得到线段CD 、A 、MB 的对应点分别为C 、N 、D .①当点D 落在函数ky x=(0x <)的图象上时、求n 的值. ②当MD MN ≤时、结合函数的图象、直接写出n 的取值范围.O -1-111BMA2018平谷一模21.如图、在平面直角坐标系xOy 中、函数()0ky k x=≠的图象与直线y =x +1交于点A (1、a ).(1)求a 、k 的值; (2)连结OA 、点P 是函数()0ky k x=≠上一点、且满足OP=OA 、直接写出点P 的坐标(点A 除外).2018石景山一模22.在平面直角坐标系xOy 中、函数a y x=(0x >)的图象与直线1l y x b =+:交于点(3,2)A a -. (1)求a 、b 的值;(2)直线2l y x m =-+:与x 轴交于点B 、与直线1l 交于点C 、若S △ABC 6≥、 求m 的取值范围.2018怀柔一模22.在平面直角坐标系xOy 中,一次函数y=kx+b 的图象与y 轴交于点B (0,1)、与反比例函数xmy =的图象交于点A(3、-2). (1)求反比例函数的表达式和一次函数表达式;(2)若点C 是y 轴上一点、且BC=BA 、直接写出点C 的坐标.2018海淀一模22.在平面直角坐标系xOy 中、已知点P (2、2)、Q (-1、2)、函数my x=. (1)当函数my x=的图象经过点P 时、求m 的值并画出直线y x m =+. (2)若P 、Q 两点中恰有一个点的坐标(x 、y )满足不等式组,m y xy x m⎧>⎪⎨⎪<+⎩(m >0)、求m 的取值范围.2018朝阳一模22. 如图、在平面直角坐标系xOy 中、直线AB 与x 轴、y 轴分别交于点A 、B 、与反比例函数xky =的图象在第四象限交于点C 、CD ⊥x 轴于点D 、tan ∠OAB =2、OA =2、OD =1. (1)求该反比例函数的表达式;(2)点M 是这个反比例函数图象上的点、过点M 作MN ⊥y 轴、垂足为点N 、连接OM 、AN 、如果S △ABN =2S △OMN 、直接写出点M 的坐标.yxPQ O2018东城一模22. 已知函数()30y x x=>的图象与一次函数()20y ax a =-≠的图象交于点()3,A n . (1)求实数a 的值;(2)设一次函数()20y ax a =-≠的图象与y 轴交于点B .若点C 在y 轴上、且=2ABC AOB S S △△、求点C 的坐标.2018丰台一模22.在平面直角坐标系xOy 中、反比例函数2y x=的图象与一次函数y kx b =+的图象的交点分别为P (m 、2)、Q (-2、n ). (1)求一次函数的表达式;(2)过点Q 作平行于y 轴的直线、点M 为此直线上的一点、当MQ = PQ 时、直接写出点M 的坐标.2018房山一模23. 如图、直线26y x =+与反比例函数()0ky x x=>的图象交于点()1,A m 、与x 轴交于点B 、与y 轴交于点D .(1)求m 的值和反比例函数的表达式;(2)在y 轴上有一动点P (0、n )()06n <<、过点P 作平行于x 轴的直线,交反比例函数的图象于点M 、交直线AB 于点N 、连接BM .若12BMN BOD S S ∆∆=、求n 的值.2018门头沟一模20. 如图、在平面直角坐标系xOy 中、一次函数y x =与反比例函数ky x=(k ≠0)的图象相交于点)A a . (1)求a 、k 的值;(2)直线x =b (0b >)分别与一次函数y x =、反比例函数ky x=的图象相交于点M 、N 、当MN =2时,画出示意图并直接写出b 的值.2018大兴一模22.如图、点A 是直线2y x =与反比例函数1m y x-=(m 为常数)的图象的交点.过点A 作x 轴的垂线、垂足为B 、且2OB =. (1)求点A 的坐标及m 的值;(2) 已知点()()0,08P n n <≤、过点P 作平行于x 轴的直线、交直线2y x =于点()11,C x y 、交反比例函数1m y x-=(m 为常数)的图象于点()22,D x y 、交垂线AB 于点()33,E x y .若231x x x <<、结合函数的图象、直接写出123x x x ++的取值范围.2018顺义一模22.如图、在平面直角坐标系xOy 中、直线24y x =+与双曲线ky x=(k ≠0)相交于 A (-3、a )、B 两点. (1)求k 的值;(2)过点P (0、m )作直线l 、使直线l 与y 轴垂直、直线l 与直线AB 交于点M 、与双曲线ky x=交于点N 、若点P 在点M 与点N 之间、直接写出m 的取值范围.2018通州一模19.如图、一次函数y kx b =+的图象与反比例函数ay x=的图象交于点()43A ,、与y 轴的负半轴交于点B 、连接OA 、且OA OB =. (1)求一次函数和反比例函数的表达式;(2)过点()0P k ,作平行于y 轴的直线、交一次函数2y x n =+于点M 、交反比例函数ay x=的图像于点N .若NM NP =、求n 的值.2018燕山一模24.如图、在平面直角坐标系中、直线l : y=kx+k (k ≠0)与x 轴,y 轴分别交于A,B 两点、且点B(0,2)、点P 在y 轴正半轴上运动、过点P 作平行于x 轴的直线y=t . (1)求 k 的值和点A 的坐标;(2)当t=4时、直线y=t 与直线l 交于点M 、反比例函数xny = (n ≠0)的图象经过点M 、求反比例函数的解析式;(3)当t<4时、若直线y=t 与直线l 和(2)反比例函数的图象分别交于点C 、D 、当CD 间距离大于等于2时、求t 的取值范围.。
九年级数学一模试题分类汇编——反比例函数综合及答案解析

九年级数学一模试题分类汇编——反比例函数综合及答案解析一、反比例函数1.已知反比例函数y= 的图象经过点A(﹣,1).(1)试确定此反比例函数的解析式;(2)点O是坐标原点,将线段OA绕O点顺时针旋转30°得到线段OB.判断点B是否在此反比例函数的图象上,并说明理由;(3)已知点P(m, m+6)也在此反比例函数的图象上(其中m<0),过P点作x轴的垂线,交x轴于点M.若线段PM上存在一点Q,使得△OQM的面积是,设Q点的纵坐标为n,求n2﹣2 n+9的值.【答案】(1)解:由题意得1= ,解得k=﹣,∴反比例函数的解析式为y=﹣(2)解:过点A作x轴的垂线交x轴于点C.在Rt△AOC中,OC= ,AC=1,∴OA= =2,∠AOC=30°,∵将线段OA绕O点顺时针旋转30°得到线段OB,∴∠AOB=30°,OB=OA=2,∴∠BOC=60°.过点B作x轴的垂线交x轴于点D.在Rt△BOD中,BD=OB•sin∠BOD= ,OD= OB=1,∴B点坐标为(﹣1,),将x=﹣1代入y=﹣中,得y= ,∴点B(﹣1,)在反比例函数y=﹣的图象上(3)解:由y=﹣得xy=﹣,∵点P(m, m+6)在反比例函数y=﹣的图象上,其中m<0,∴m( m+6)=﹣,∴m2+2 m+1=0,∵PQ⊥x轴,∴Q点的坐标为(m,n).∵△OQM的面积是,∴OM•QM= ,∵m<0,∴mn=﹣1,∴m2n2+2 mn2+n2=0,∴n2﹣2 n=﹣1,∴n2﹣2 n+9=8.【解析】【分析】(1)由于反比例函数y= 的图象经过点A(﹣,1),运用待定系数法即可求出此反比例函数的解析式;(2)首先由点A的坐标,可求出OA的长度,∠AOC的大小,然后根据旋转的性质得出∠AOB=30°,OB=OA,再求出点B的坐标,进而判断点B是否在此反比例函数的图象上;(3)把点P(m, m+6)代入反比例函数的解析式,得到关于m的一元二次方程;根据题意,可得Q点的坐标为(m,n),再由△OQM的面积是,根据三角形的面积公式及m<0,得出mn的值,最后将所求的代数式变形,把mn的值代入,即可求出n2﹣2 n+9的值.2.如图,在平面直角坐标系中,直线AB与x轴交于点B,与y轴交于点A,与反比例函数y= 的图象在第二象限交于点C,CE⊥x轴,垂足为点E,tan∠ABO= ,OB=4,OE=2.(1)求反比例函数的解析式;(2)若点D是反比例函数图象在第四象限上的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO,求点D的坐标.【答案】(1)解:∵OB=4,OE=2,∴BE=OB+OE=6.∵CE⊥x轴,∴∠CEB=90°.在Rt△BEC中,∠CEB=90°,BE=6,tan∠ABO= ,∴CE=BE•tan∠ABO=6× =3,结合函数图象可知点C的坐标为(﹣2,3).∵点C在反比例函数y= 的图象上,∴m=﹣2×3=﹣6,∴反比例函数的解析式为y=﹣(2)解:∵点D在反比例函数y=﹣第四象限的图象上,∴设点D的坐标为(n,﹣)(n>0).在Rt△AOB中,∠AOB=90°,OB=4,tan∠ABO= ,∴OA=OB•tan∠ABO=4× =2.∵S△BAF= AF•OB= (OA+OF)•OB= (2+ )×4=4+ .∵点D在反比例函数y=﹣第四象限的图象上,∴S△DFO= ×|﹣6|=3.∵S△BAF=4S△DFO,∴4+ =4×3,解得:n= ,经验证,n= 是分式方程4+ =4×3的解,∴点D的坐标为(,﹣4).【解析】【分析】(1)由边的关系可得出BE=6,通过解直角三角形可得出CE=3,结合函数图象即可得出点C的坐标,再根据点C的坐标利用反比例函数图象上点的坐标特征,即可求出反比例函数系数m,由此即可得出结论;(2)由点D在反比例函数在第四象限的图象上,设出点D的坐标为(n,﹣)(n>0).通过解直角三角形求出线段OA的长度,再利用三角形的面积公式利用含n的代数式表示出S△BAF,根据点D在反比例函数图形上利用反比例函数系数k的几何意义即可得出S△DFO的值,结合题意给出的两三角形的面积间的关系即可得出关于n的分式方程,解方程,即可得出n值,从而得出点D的坐标.3.如图,在平面直角坐标系中,△ABC的顶点A在x轴负半轴上,顶点在轴正半轴上,顶点B在第一象限,线段,的长是一元二次方程的两根,,.(1)直接写出点的坐标________点 C的坐标________;(2)若反比例函数的图象经过点,求k的值;(3)如图过点作轴于点;在轴上是否存在点,使以,,为顶点的三角形与以,,为顶点的三角形相似?若存在,直接写出满足条件的点的坐标;若不存在,请说明理由.【答案】(1);(2)解:如图,过点作,垂足为,∵,∴,设,∵ =12,∴EC=12-x,在RtΔBEC中,,∴整理得:,解得:(不合题意舍去),,∴,,∴,把代入,得(3)解:存在.如图2,若点P在OD上,若△PDB∽△AOP,则,即,解得:OP=2或OP=6,∴P(0,2)或P(0,6);如图3,若点P在OD上方,△PDB∽△AOP,则,即,解得:OP=12,∴P(0,12);如图4,若点P在OD上方,△BDP∽△AOP,则,即,解得:OP=4+2 或OP=4-2 (不合题意舍去),∴P(0,4+2 );如图5,若点P在y轴负半轴,△PDB∽△AOP,则,即,解得:OP=-4+2 或-4-2 (不合题意舍去),则P点坐标为(0,4-2 )故点的坐标为:或或或或【解析】【解答】解:(1)解一元二次方程,解得:,所以,所以,;【分析】(1)首先利用直接开平方法求出方程的两根,从而得出OA=OC=6,进而得出A,C两点的坐标;(2)如图,过点作,垂足为,根据等腰直角三角形的性质得出,设,EC=12-x,在RtΔBEC中利用勾股定理建立方程,求解并检验即可得出BE,OE 的长从而得出B点的坐标,然后利用待定系数法即可求出反比例函数的解析式;(3)存在.如图2,若点P在OD上,若△PDB∽△AOP,根据相似三角形对应边成比例得出,根据比例式列出方程,求解即可得出P点的坐标;如图3,若点P在OD上方,△PDB∽△AOP,根据相似三角形对应边成比例得出则根据比例式列出方程,求解并检验即可得出P点的坐标;如图4,若点P在OD上方,△PDB∽△AOP,根据相似三角形对应边成比例得出,根据比例式列出方程,求解并检验即可得出P 点的坐标;如图5,若点P在y轴负半轴,△PDB∽△AOP,根据相似三角形对应边成比例得出,根据比例式列出方程,求解并检验即可得出P点的坐标,综上所述即可得出答案。
初三数学一模试题分类汇编——反比例函数综合含详细答案
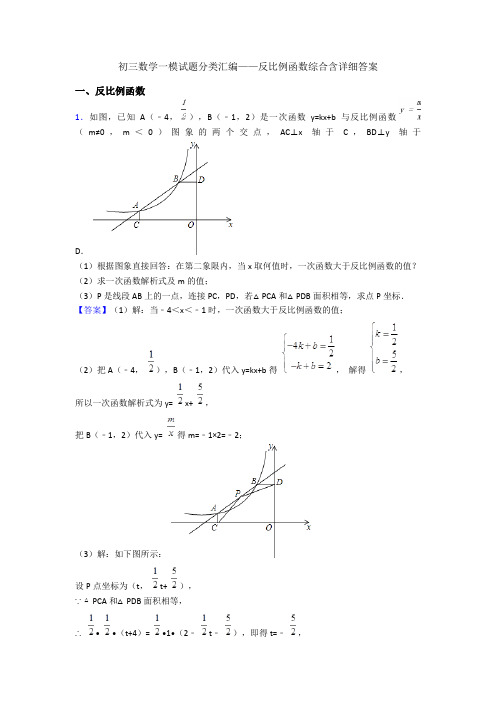
初三数学一模试题分类汇编——反比例函数综合含详细答案一、反比例函数1.如图,已知A(﹣4,),B(﹣1,2)是一次函数y=kx+b与反比例函数(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?(2)求一次函数解析式及m的值;(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.【答案】(1)解:当﹣4<x<﹣1时,一次函数大于反比例函数的值;(2)把A(﹣4,),B(﹣1,2)代入y=kx+b得,解得,所以一次函数解析式为y= x+ ,把B(﹣1,2)代入y= 得m=﹣1×2=﹣2;(3)解:如下图所示:设P点坐标为(t,t+ ),∵△PCA和△PDB面积相等,∴• •(t+4)= •1•(2﹣t﹣),即得t=﹣,∴P点坐标为(﹣,).【解析】【分析】(1)观察函数图象得到当﹣4<x<﹣1时,一次函数图象都在反比例函数图象上方;(2)先利用待定系数法求一次函数解析式,然后把B点坐标代入y= 可计算出m的值;(3)设P点坐标为(t, t+ ),利用三角形面积公式可得到• •(t+4)= •1•(2﹣ t﹣),解方程得到t=﹣,从而可确定P点坐标.2.如图,在平面直角坐标系中,反比例函数y= 的图象与一次函数y=ax+b的图象交于点A(﹣2,3)和点B(m,﹣2).(1)求反比例函数和一次函数的解析式;(2)直线x=1上有一点P,反比例函数图象上有一点Q,若以A、B、P、Q为顶点的四边形是以AB为边的平行四边形,直接写出点Q的坐标.【答案】(1)解:∵点A(﹣2,3)在反比例函数y= 的图形上,∴k=﹣2×3=﹣6,∴反比例函数的解析式为y=﹣,∵点B在反比例函数y=﹣的图形上,∴﹣2m=﹣6,∴m=3,∴B(3,﹣2),∵点A,B在直线y=ax+b的图象上,∴,∴,∴一次函数的解析式为y=﹣x+1(2)解:∵以A、B、P、Q为顶点的四边形是以AB为边的平行四边形,∴AB=PQ,AB∥PQ,设直线PQ的解析式为y=﹣x+c,设点Q(n,﹣),∴﹣ =﹣n+c,∴c=n﹣,∴直线PQ的解析式为y=﹣x+n﹣,∴P(1,n﹣﹣1),∴PQ2=(n﹣1)2+(n﹣﹣1+ )2=2(n﹣1)2,∵A(﹣2,3).B(3,﹣2),∴AB2=50,∵AB=PQ,∴50=2(n﹣1)2,∴n=﹣4或6,∴Q(﹣4. )或(6,﹣1)【解析】【分析】(1)先利用待定系数法求出反比例函数解析式,进而求出点B的坐标,再用待定系数法求出直线解析式;(2)先判断出AB=PQ,AB∥PQ,设出点Q的坐标,进而得出点P的坐标,即可求出PQ,最后用PQ=AB建立方程即可得出结论.3.心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化.开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y 随时间x(分钟)的变化规律如下图所示(其中AB、BC分别为线段,CD为双曲线的一部分):(1)开始上课后第五分钟时与第三十分钟时相比较,何时学生的注意力更集中?(2)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?【答案】(1)解:设线段AB所在的直线的解析式为y1=k1x+20,把B(10,40)代入得,k1=2,∴y1=2x+20.设C、D所在双曲线的解析式为y2= ,把C(25,40)代入得,k2=1000,∴当x1=5时,y1=2×5+20=30,当,∴y1<y2∴第30分钟注意力更集中.(2)解:令y1=36,∴36=2x+20,∴x1=8令y2=36,∴,∴∵27.8﹣8=19.8>19,∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.【解析】【分析】(1)根据一次函数和反比例函数的应用,用待定系数法求出线段AB所在的直线的解析式,和C、D所在双曲线的解析式;把x1=5时和进行比较得到y1<y2,得出第30分钟注意力更集中;(2)当y1=36时,得到x1=8,当y2=36,得到,由27.8﹣8=19.8>19,所以经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.4.已知点A,B分别是x轴、y轴上的动点,点C,D是某个函数图象上的点,当四边形ABCD(A,B,C,D各点依次排列)为正方形时,我们称这个正方形为此函数图象的“伴侣正方形”.例如:在图1中,正方形ABCD是一次函数y=x+1图象的其中一个“伴侣正方形”.(1)如图1,若某函数是一次函数y=x+1,求它的图象的所有“伴侣正方形”的边长;(2)如图2,若某函数是反比例函数(k>0),它的图象的“伴侣正方形”为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数的解析式;(3)如图3,若某函数是二次函数y=ax2+c(a≠0),它的图象的“伴侣正方形”为ABCD,C,D中的一个点坐标为(3,4),请你直接写出该二次函数的解析式.【答案】(1)解:(I)当点A在x轴正半轴、点B在y轴负半轴上时:正方形ABCD的边长为.(II)当点A在x轴负半轴、点B在y轴正半轴上时:设正方形边长为a,易得3a= ,解得a= ,此时正方形的边长为.∴所求“伴侣正方形”的边长为或(2)解:如图,作DE⊥x轴,CF⊥y轴,垂足分别为点E、F,易证△ADE≌△BAO≌△CBF.∵点D的坐标为(2,m),m<2,∴DE=OA=BF=m,∴OB=AE=CF=2﹣m.∴OF=BF+OB=2,∴点C的坐标为(2﹣m,2).∴2m=2(2﹣m),解得m=1.∴反比例函数的解析式为y=(3)解:实际情况是抛物线开口向上的两种情况中,另一个点都在(3,4)的左侧,而开口向下时,另一点都在(3,4)的右侧,与上述解析明显不符合a、当点A在x轴正半轴上,点B在y轴正半轴上,点C坐标为(3,4)时:另外一个顶点为(4,1),对应的函数解析式是y=﹣ x2+ ;b、当点A在x 轴正半轴上,点 B在 y轴正半轴上,点D 坐标为(3,4)时:不存在,c、当点A 在 x 轴正半轴上,点 B在 y轴负半轴上,点C 坐标为(3,4)时:不存在d、当点A在x 轴正半轴上,点B在y轴负半轴上,点D坐标为(3,4)时:另外一个顶点C为(﹣1,3),对应的函数的解析式是y= x2+ ;e、当点A在x轴负半轴上,点B在y轴负半轴上,点C坐标为(3,4)时,另一个顶点D的坐标是(7,﹣3)时,对应的函数解析式是y=﹣ x2+ ;f、当点A在x轴负半轴上,点B在y轴负半轴上,点C坐标为(3,4)时,另一个顶点D 的坐标是(﹣4,7)时,对应的抛物线为y= x2+ ;故二次函数的解析式分别为:y= x2+ 或y=﹣ x2+ 或y=﹣ x2+ 或y= x2+【解析】【分析】(1)先正确地画出图形,再利用正方形的性质确定相关点的坐标从而计算正方形的边长.(2)因为ABCD为正方形,所以可作垂线得到等腰直角三角形,利用点D(2,m)的坐标表示出点C的坐标,可求出m的值,即可得到反比例函数的解析式.(3)由抛物线开口既可能向上,也可能向下.当抛物线开口向上时,正方形的另一个顶点也是在抛物线上,这个点既可能在点(3,4)的左边,也可能在点(3,4)的右边,过点(3,4)向x轴作垂线,利用全等三角形确定线段的长即可确定抛物线上另一个点的坐标;当抛物线开口向下时也是一样地分为两种情况来讨论,即可得到所求的结论.5.如图1,经过原点的抛物线y=ax2+bx+c与x轴的另一个交点为点C;与双曲线y= 相交于点A,B;直线AB与分别与x轴、y轴交于点D,E.已知点A的坐标为(﹣1,4),点B在第四象限内且到x轴、y轴的距离相等.(1)求双曲线和抛物线的解析式;(2)计算△ABC的面积;(3)如图2,将抛物线平移至顶点在原点上时,直线AB随之平移,试判断:在y轴的负半轴上是否存在点P,使△PAB的内切圆的圆心在y轴上?若存在,求出点P的坐标;若不存在,请说明理由.【答案】(1)解:把点A的坐标代入双曲线的解析式得:k=﹣1×4=﹣4.所以双曲线的解析式为y=﹣.设点B的坐标为(m,﹣m).∵点B在双曲线上,∴﹣m2=﹣4,解得m=2或m=﹣2.∵点B在第四象限,∴m=2.∴B(2,﹣2).将点A、B、C的坐标代入得:,解得:.∴抛物线的解析式为y=x2﹣3x.(2)解:如图1,连接AC、BC.令y=0,则x2﹣3x=0,∴x=0或x=3,∴C(3,0),∵A(﹣1,4),B(2,﹣2),∴直线AB的解析式为y=﹣2x+2,∵点D是直线AB与x轴的交点,∴D(1,0),∴S△ABC=S△ADC+S△BDC= ×2×4+ ×2×2=6;(3)解:存在,理由:如图2,由原抛物线的解析式为y=x2﹣3x=(x﹣)2﹣,∴原抛物线的顶点坐标为(,﹣),∴抛物线向左平移个单位,再向上平移个单位,而平移前A(﹣1,4),B(2,﹣2),∴平移后点A(﹣,),B(,),∴点A关于y轴的对称点A'(,),连接A'B并延长交y轴于点P,连接AP,由对称性知,∠APE=∠BPE,∴△APB的内切圆的圆心在y轴上,∵B(,),A'(,),∴直线A'B的解析式为y=3x﹣,∴P(0,﹣).【解析】【分析】(1)首先将点A的坐标代入反比例函数的解析式求得k的值,然后再求得B的值,最后根据点A的坐标求出双曲线的解析式,进而得出点B的坐标,最后,将点A、B、O三点的坐标代入抛物线的解析式,求得a、b、c的值即可;(2)由点A和点B的坐标可求得直线AB的解析式,然后将y=0可求得点D的横坐标,最后用三角形的面积和求解即可;(3)先确定出平移后点A,B的坐标,进而求出点A关于y轴的对称点的坐标,求出直线BA'的解析式即可得出点P的坐标.6.函数学习中,自变量取值范围及相应的函数值范围问题是大家关注的重点之一,请解决下面的问题.(1)分别求出当2≤x≤4时,三个函数:y=2x+1,y= ,y=2(x﹣1)2+1的最大值和最小值;(2)若y= 的值不大于2,求符合条件的x的范围;(3)若y= ,当a≤x≤2时既无最大值,又无最小值,求a的取值范围;(4)y=2(x﹣m)2+m﹣2,当2≤x≤4时有最小值为1,求m的值.【答案】(1)解:y=2x+1中k=2>0,∴y随x的增大而增大,∴当x=2时,y最小=5;当x=4时,y最大=9.∵y= 中k=2>0,∴在2≤x≤4中,y随x的增大而减小,∴当x=2时,y最大=1;当x=4时,y最小= .∵y=2(x﹣1)2+1中a=2>0,且抛物线的对称轴为x=1,∴当x=1时,y最小=1;当x=4时,y最大=19(2)解:令y= ≤2,解得:x<0或x≥1.∴符合条件的x的范围为x<0或x≥1(3)解:①当k>0时,如图得当0<x≤2时,y= 无最大值,有最小值,同理当a<0时,且a≤x<0时,y≤ 有最大值,无最小值,②当k<0时,如图得当0<x≤2时,y=无最小值,有最大值,同理当a<0时,且a≤x<0时,y≤ 有最小值,无最大值,∴当k<0,a<0时,此时,y= 既无最大值,又无最小值,综上所述,a的取值范围是a<0(4)解:①当m<2时,有2(2﹣m)2+m﹣2=1,解得:m1=1,m2= (舍去);②当2≤m≤4时,有m﹣2=1,解得:m3=3;③当m>4时,有2(4﹣m)2+m﹣2=1,整理得:2m2﹣15m+29=0.∵△=(﹣15)2﹣4×2×29=﹣7,无解.∴m的值为1或3.①当k>0时,如图得当0<x≤2时,y= 无最大值,有最小值,同理当a<0时,且a≤x<0时,y≤ 有最大值,无最小值,②当k<0时,如图得当0<x≤2时,y= 无最小值,有最大值,同理当a<0时,且a≤x<0时,y≤ 有最小值,无最大值,∴当k<0,a<0时,此时,y= 既无最大值,又无最小值,综上所述,a的取值范围是a<0;【解析】【分析】(1)根据k=2>0结合一次函数的性质即可得出:当2≤x≤4时,y=2x+1的最大值和最小值;根据二次函数的解析式结合二次函数的性质即可得出:当2≤x≤4时,y=2(x﹣1)2+1的最大值和最小值;(2)令y= ≤2,解之即可得出x的取值范围;(3)①当k>0时,如图得当0<x≤2时,得到y= 无最大值,有最小值,同理当a<0时,且a≤x<0时,得到y≤ 有最大值,无最小值,②当k<0时,如图得当0<x≤2时,y=无最小值,有最大值,同理当a<0时,且a≤x<0时,y≤ 有最小值,无最大值,于是得到结论;(4)分m<2、2≤m≤4和m>4三种情况考虑,根据二次函数的性质结合当2≤x≤4时有最小值为1即可得出关于m的一元二次方程(一元一次方程),解之即可得出结论.7.如图,四边形ABCD的四个顶点分别在反比例函数与(x>0,0<m<n)的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为4.(1)当m=4,n=20时.①若点P的纵坐标为2,求直线AB的函数表达式.②若点P是BD的中点,试判断四边形ABCD的形状,并说明理由.(2)四边形ABCD能否成为正方形?若能,求此时m,n之间的数量关系;若不能,试说明理由.【答案】(1)①当x=4时,∴点B的坐标是(4,1)当y=2时,由得得x=2∴点A的坐标是(2,2)设直线AB的函数表达式为∴解得∴直线AB的函数表达式为②四边形ABCD为菱形,理由如下:如图,由①得点B(4,1),点D(4,5)∵点P为线段BD的中点∴点P的坐标为(4,3)当y=3时,由得,由得,∴PA= ,PC=∴PA=PC而PB=PD∴四边形ABCD为平行四边形又∵BD⊥AC∴四边形ABCD是菱形(2)四边形ABCD能成为正方形当四边形ABCD时正方形时,PA=PB=PC=PD(设为t,t≠0),当x=4时,∴点B的坐标是(4,)则点A的坐标是(4-t,)∴,化简得t=∴点D的纵坐标为则点D的坐标为(4,)所以,整理得m+n=32【解析】【分析】(1)①分别求出点A,B的坐标,运用待定系数法即可求出直线AB的表达示;②由特殊的四边形可知,对角线互相垂直的是菱形和正方形,则可猜测这个四边形是菱形或是正方形,先证明其为菱形先,则需要证明四边形ABCD是平行四边形,运用“对角线互相平分的四边形是平行四边形”的判定定理证明会更好些;再判断对角线是否相等,若不相等则不是正方形;(2)要使m,n有具体联系,根据A,B,C,D分别在两个函数图象,且由正方形的性质,可用只含m的代数式表示出点D或点C的坐标代入y= ,即可得到只关于m和n的等式.8.【阅读理解】对于任意正实数a、b,因为≥0,所以≥0,所以≥2 ,只有当时,等号成立.【获得结论】在≥2 (a、b均为正实数)中,若为定值,则≥2 ,只有当时,有最小值2 .(1)根据上述内容,回答下列问题:若 >0,只有当 =________时,有最小值________.(2)【探索应用】如图,已知A(-3,0),B(0,-4),P为双曲线(>0)上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.【答案】(1)1;2(2)解:设P(x,),则C(x,0),D(0,),∴CA=x+3,BD= +4,∴S四边形= CA×BD= (x+3)( +4),化简得:S=2(x+ )+12.∵x>0,>0,∴x+ ≥2 ABCD=6,只有当x= ,即x=3时,等号成立,∴S≥2×6+12=24,∴四边形ABCD的面积有最小值24,此时,P(3,4),C(3,0),D(0,4),AB=BC=CD=DA=5,∴四边形ABCD是菱形.【解析】【解答】解:(1)根据题目所给信息可知m+ ≥2 ,且当m= 时等号,∴当m=1时,m+ ≥2,即当m=1时,m+ 有最小值2.故答案为:1,2;【分析】(1)此题是一道阅读题,根据题中所给的信息可知:,只有当m=时等号成立,一个正数只有1和它的倒数相等,从而得出答案;(2)根据双曲线上点的坐标特点设出P点的坐标,根据垂直于坐标轴上的点的坐标特点表示出C,D两点的坐标,从而表示出AC,BD的长,根据对角线互相垂直的四边形的面积等于两对角线积的一半建立出S与x的函数关系式,根据题干提供的信息得出得出,只有在,即x=3时,等号成立,从而得出S的最小值,从而得出P,C,D三点的坐标,进而算出AB=BC=CD=DA=5,根据四边相等的四边形是菱形得出结论。
九年级数学一模试题分类汇编——反比例函数综合含答案解析

九年级数学一模试题分类汇编——反比例函数综合含答案解析一、反比例函数1.如图,一次函数y1=k1x+b与反比例函数y2= 的图象交于点A(4,m)和B(﹣8,﹣2),与y轴交于点C.(1)m=________,k1=________;(2)当x的取值是________时,k1x+b>;(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP 与线段AD交于点E,当S四边形ODAC:S△ODE=3:1时,求点P的坐标.【答案】(1)4;(2)﹣8<x<0或x>4(3)解:由(1)知,y1= x+2与反比例函数y2= ,∴点C的坐标是(0,2),点A 的坐标是(4,4).∴CO=2,AD=OD=4.∴S梯形ODAC= •OD= ×4=12,∵S四边形ODAC:S△ODE=3:1,∴S△ODE= S梯形ODAC= ×12=4,即OD•DE=4,∴DE=2.∴点E的坐标为(4,2).又点E在直线OP上,∴直线OP的解析式是y= x,∴直线OP与y2= 的图象在第一象限内的交点P的坐标为(4 ,2 ).【解析】【解答】解:(1)∵反比例函数y2= 的图象过点B(﹣8,﹣2),∴k2=(﹣8)×(﹣2)=16,即反比例函数解析式为y2= ,将点A(4,m)代入y2= ,得:m=4,即点A(4,4),将点A(4,4)、B(﹣8,﹣2)代入y1=k1x+b,得:,解得:,∴一次函数解析式为y1= x+2,故答案为:4,;(2)∵一次函数y1=k1x+2与反比例函数y2= 的图象交于点A(4,4)和B(﹣8,﹣2),∴当y1>y2时,x的取值范围是﹣8<x<0或x>4,故答案为:﹣8<x<0或x>4;【分析】(1)由A与B为一次函数与反比例函数的交点,将B坐标代入反比例函数解析式中,求出k2的值,确定出反比例解析式,再将A的坐标代入反比例解析式中求出m的值,确定出A的坐标,将B坐标代入一次函数解析式中即可求出k1的值;(2)由A与B 横坐标分别为4、﹣8,加上0,将x轴分为四个范围,由图象找出一次函数图象在反比例函数图象上方时x的范围即可;(3)先求出四边形ODAC的面积,由S四边形ODAC:S△ODE=3:1得到△ODE的面积,继而求得点E的坐标,从而得出直线OP的解析式,结合反比例函数解析式即可得.2.如图,已知A是双曲线y= (k>0)在第一象限内的一点,O为坐标原点,直线OA交双曲线于另一点C,当OA在第一象限的角平分线上时,将OA向上平移个单位后,与双曲线在第一象限交于点M,交y轴于点N,若 =2,(1)求直线MN的解析式;(2)求k的值.【答案】(1)解:∵OA在第一象限的角平分线上,∴直线OA的解析式为y=x,∴将OA向上平移个单位后,N(0,),可设直线MN的解析式为y=x+b,把N(0,)代入,可得b= ,∴直线MN的解析式为y=x+(2)解:如图所示,过A作AB⊥y轴于B,过M作MD⊥y轴于D,则∠MDN=∠ABO=90°,由平移可得,∠MND=∠AOB=45°,∴△MDN∽△ABO,∴ = =2,设A(a,a),则AB=a,∴MD= a=DN,∴DO= a+ ,∴M( a, a+ ),∵双曲线经过点A,M,∴k=a×a= a×( a+ ),解得a=1,∴k=1.【解析】【分析】(1)第一三象限角平分线为y=x,向上平移为y=x+b,可求出N点坐标,代入y=x+b,即可求出;(2)通过作垂线构造相似三角形,即△MDN∽△ABO,把A、M坐标代入解析式即可求出a,进而求出k.3.如图,反比例函数y= 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).(1)求反比例函数与一次函数的表达式;(2)点E为y轴上一个动点,若S△AEB=10,求点E的坐标.【答案】(1)解:把点A(2,6)代入y= ,得m=12,则y= .把点B(n,1)代入y= ,得n=12,则点B的坐标为(12,1).由直线y=kx+b过点A(2,6),点B(12,1)得,解得,则所求一次函数的表达式为y=﹣x+7(2)解:如图,直线AB与y轴的交点为P,设点E的坐标为(0,m),连接AE,BE,则点P的坐标为(0,7).∴PE=|m﹣7|.∵S△AEB=S△BEP﹣S△AEP=10,∴×|m﹣7|×(12﹣2)=10.∴|m﹣7|=2.∴m1=5,m2=9.∴点E的坐标为(0,5)或(0,9).【解析】【分析】(1)把点A的坐标代入反比例函数解析式,求出反比例函数的解析式,把点B的坐标代入已求出的反比例函数解析式,得出n的值,得出点B的坐标,再把A、B的坐标代入直线y=kx+b,求出k、b的值,从而得出一次函数的解析式;(2)设点E 的坐标为(0,m),连接AE,BE,先求出点P的坐标(0,7),得出PE=|m﹣7|,根据S△AEB=S△BEP﹣S△AEP=10,求出m的值,从而得出点E的坐标.4.已知一次函数y1=x+m的图象与反比例函数y2= 的图象交于A、B两点,已知当x>1时,y1>y2;当0<x<1时,y1<y2.(1)求一次函数的函数表达式;(2)已知反比例函数在第一象限的图象上有一点C到x轴的距离为2,求△ABC的面积.【答案】(1)解:∵当x>1时,y1>y2;当0<x<1时,y1<y2,∴点A的横坐标为1,代入反比例函数解析式,=y,解得y=6,∴点A的坐标为(1,6),又∵点A在一次函数图象上,∴1+m=6,解得m=5,∴一次函数的解析式为y1=x+5(2)解:∵第一象限内点C到x轴的距离为2,∴点C的纵坐标为2,∴2= ,解得x=3,∴点C的坐标为(3,2),过点C作CD∥x轴交直线AB于D,则点D的纵坐标为2,∴x+5=2,解得x=﹣3,∴点D的坐标为(﹣3,2),∴CD=3﹣(﹣3)=3+3=6,点A到CD的距离为6﹣2=4,联立,解得(舍去),,∴点B的坐标为(﹣6,﹣1),∴点B到CD的距离为2﹣(﹣1)=2+1=3,S△ABC=S△ACD+S△BCD= ×6×4+ ×6×3=12+9=21.【解析】【分析】(1)首先根据x>1时,y1>y2,0<x<1时,y1<y2确定点A的横坐标,然后代入反比例函数解析式求出点A的纵坐标,从而得到点A的坐标,再利用待定系数法求直线解析式解答;(2)根据点C到x轴的距离判断出点C的纵坐标,代入反比例函数解析式求出横坐标,从而得到点C的坐标,过点C作CD∥x轴交直线AB于D,求出点D 的坐标,然后得到CD的长度,再联立一次函数与双曲线解析式求出点B的坐标,然后△ABC的面积=△ACD的面积+△BCD的面积,列式进行计算即可得解.5.已知:如图,在平面直角坐标系xOy中,点A在x轴的正半轴上,点B、C在第一象限,且四边形OABC是平行四边形,OC=2 ,sin∠AOC= ,反比例函数y= 的图象经过点C以及边AB的中点D.(1)求这个反比例函数的解析式;(2)四边形OABC的面积.【答案】(1)解:过C作CM⊥x轴于M,则∠CMO=90°,∵OC=2 ,sin∠AOC= = ,∴MC=4,由勾股定理得:OM= =2,∴C的坐标为(2,4),代入y= 得:k=8,所以这个反比例函数的解析式是y=(2)解:过B作BE⊥x轴于E,则BE=CM=4,AE=OM=2,过D作DN⊥x轴于N,∵D为AB的中点,∴DN= =2,AN= =1,把y=2代入y= 得:x=4,即ON=4,∴OA=4﹣1=3,∴四边形OABC的面积为OA×CM=3×4=12【解析】【分析】(1)过C作CM⊥x轴于M,则∠CMO=90°,解直角三角形求出CM,根据勾股定理求出OM,求出C的坐标,即可求出答案;(2)根据D为中点求出DN的值,代入反比例函数解析式求出ON,求出OA,根据平行四边形的面积公式求出即可.6.如图,已知,A(0,4),B(﹣3,0),C(2,0),D为B点关于AC的对称点,反比例函数y= 的图象经过D点.(1)证明四边形ABCD为菱形;(2)求此反比例函数的解析式;(3)已知在y= 的图象(x>0)上一点N,y轴正半轴上一点M,且四边形ABMN是平行四边形,求M点的坐标.【答案】(1)解:∵A(0,4),B(﹣3,0),C(2,0),∴OA=4,OB=3,OC=2,∴AB= =5,BC=5,∴AB=BC,∵D为B点关于AC的对称点,∴AB=AD,CB=CD,∴AB=AD=CD=CB,∴四边形ABCD为菱形(2)解:∵四边形ABCD为菱形,∴D点的坐标为(5,4),反比例函数y= 的图象经过D点,∴4= ,∴k=20,∴反比例函数的解析式为:y=(3)解:∵四边形ABMN是平行四边形,∴AN∥BM,AN=BM,∴AN是BM经过平移得到的,∴首先BM向右平移了3个单位长度,∴N点的横坐标为3,代入y= ,得y= ,∴M点的纵坐标为:﹣4= ,∴M点的坐标为:(0,)【解析】【分析】(1)由A(0,4),B(﹣3,0),C(2,0),利用勾股定理可求得AB=5=BC,又由D为B点关于AC的对称点,可得AB=AD,BC=DC,即可证得AB=AD=CD=CB,继而证得四边形ABCD为菱形;(2)由四边形ABCD为菱形,可求得点D 的坐标,然后利用待定系数法,即可求得此反比例函数的解析式;(3)由四边形ABMN 是平行四边形,根据平移的性质,可求得点N的横坐标,代入反比例函数解析式,即可求得点N的坐标,继而求得M点的坐标.7.如图,在平面直角坐标系中,直线AB与x轴交于点B、与y轴交于点A,与反比例函数y= 的图象在第二象限交于C,CE⊥x轴,垂足为点E,tan∠ABO= ,OB=4,OE=2.(1)求反比例函数的解析式;(2)若点D是反比例函数图象在第四象限内的点,过点D作DF⊥y轴,垂足为点F,连接OD、BF.如果S△BAF=4S△DFO,求点D的坐标.(3)若动点D在反比例函数图象的第四象限上运动,当线段DC与线段DB之差达到最大时,求点D的坐标.【答案】(1)解:∵tan∠ABO= ,∴ = ,且OB=4,∴OA=2,∵CE⊥x轴,即CE∥AO,∴△AOB∽△CEB,∴ = ,即 = ,解得CE=3,∴C(﹣2,3),∴m=﹣2×3=﹣6,∴反比例函数解析式为y=﹣(2)解:设D(x,﹣),∵D在第四象限,∴DF=x,OF= ,∴S△DFO= DF•OF= x× =3,由(1)可知OA=2,∴AF=x+ ,∴S△BAF= AF•OB= (x+ )×4=2(x+ ),∵S△BAF=4S△DFO,∴2(x+ )=4×3,解得x=3+ 或x=3﹣,当x=3+ 时,﹣的值为3﹣,当x=3﹣时,﹣的值为3+ ,∵D在第四象限,∴x=3﹣不合题意,舍去,∴D(3+ ,3﹣)(3)解:∵D在第四象限,∴在△BCD中,由三角形三边关系可知CD﹣CB≤BC,即当B、C、D三点共线时,其差最大,设直线AB解析式为y=kx+b,由题意可得,解得,∴直线AB解析式为y=﹣ x+2,联立直线AB和反比例函数解析式可得,解得或(舍去),∴D(6,﹣1),即当线段DC与线段DB之差达到最大时求点D的坐标为(6,﹣1)【解析】【分析】(1)由条件可求得OA,由△AOB∽△CEB可求得CE,则可求得C点坐标,代入反比例函数解析式可求得m的值,可求得反比例函数解析式;(2)设出D的坐标,从而可分别表示出△BAF和△DFO的面积,由条件可列出方程,从而可求得D点坐标;(3)在△BCD中,由三角形三边关系可知CD﹣CB≤BC,当B、C、D三点共线时,其差最大,联立直线BC与反比例函数解析式可求得D点坐标.8.已知一次函数y=− x−12的图象分别交x轴,y轴于A,C两点。
初三数学一模试题分类汇编——反比例函数综合附详细答案
初三数学一模试题分类汇编——反比例函数综合附详细答案一、反比例函数1.如图,平行于y轴的直尺(一部分)与双曲线y= (k≠0)(x>0)相交于点A、C,与x轴相交于点B、D,连接AC.已知点A、B的刻度分别为5,2(单位:cm),直尺的宽度为2cm,OB=2cm.(1)求k的值;(2)求经过A、C两点的直线的解析式;(3)连接OA、OC,求△OAC的面积.【答案】(1)解:∵AB=5﹣2=3cm,OB=2cm,∴A的坐标是(2,3),代入y= 得3= ,解得:k=6(2)解:OD=2+2=4,在y= 中令x=4,解得y= .则C的坐标是(4,).设AC的解析式是y=mx+n,根据题意得:,解得:,则直线AC的解析式是y=﹣ x+(3)解:直角△AOB中,OB=2,AB=3,则S△AOB= OB•AB= ×2×3=3;直角△ODC中,OD=4,CD= ,则S△OCD= OD•CD= ×4× =3.在直角梯形ABDC中,BD=2,AB=3,CD= ,则S梯形ABDC= (AB+DC)•BD= (3+ )×2= .则S△OAC=S△AOB+S梯形ABDC﹣S△OCD=3+ ﹣3=【解析】【分析】(1)首先求得A的坐标,然后利用待定系数法求得函数的解析式;(2)首先求得C的坐标,然后利用待定系数法求得直线的解析式;(3)根据S△OAC=S△AOB+S梯形ABDC﹣S△OCD利用直角三角形和梯形的面积公式求解.2.如图,一次函数y=x+4的图象与反比例函数y= (k为常数,且k≠0)的图象交于A (﹣1,a),B(b,1)两点.(1)求反比例函数的表达式;(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标;(3)求△PAB的面积.【答案】(1)解:当x=﹣1时,a=x+4=3,∴点A的坐标为(﹣1,3).将点A(﹣1,3)代入y= 中,3= ,解得:k=﹣3,∴反比例函数的表达式为y=﹣(2)解:当y=b+4=1时,b=﹣3,∴点B的坐标为(﹣3,1).作点B关于x轴的对称点D,连接AD,交x轴于点P,此时PA+PB的值最小,如图所示.∵点B的坐标为(﹣3,1),∴点D的坐标为(﹣3,﹣1).设直线AD的函数表达式为y=mx+n,将点A(﹣1,3)、D(﹣3,﹣1)代入y=mx+n中,,解得:,∴直线AD的函数表达式为y=2x+5.当y=2x+5=0时,x=﹣,∴点P的坐标为(﹣,0)(3)解:S△PAB=S△ABD﹣S△BDP= ×2×2﹣ ×2× =【解析】【分析】(1)由一次函数图象上点的坐标特征可求出点A的坐标,根据点A的坐标利用待定系数法,即可求出反比例函数的表达式;(2)利用一次函数图象上点的坐标特征可求出点B的坐标,作点B关于x轴的对称点D,连接AD,交x轴于点P,此时PA+PB的值最小,由点B的坐标可得出点D的坐标,根据点A、D的坐标利用待定系数法,即可求出直线AB的函数表达式,再由一次函数图象上点的坐标特征即可求出点P的坐标;(3)根据三角形的面积公式结合S△PAB=S△ABD﹣S△BDP,即可得出结论.3.如图直角坐标系中,矩形ABCD的边BC在x轴上,点B,D的坐标分别为B(1,0),D(3,3).(1)点C的坐标________;(2)若反比例函数y= (k≠0)的图象经过直线AC上的点E,且点E的坐标为(2,m),求m的值及反比例函数的解析式;(3)若(2)中的反比例函数的图象与CD相交于点F,连接EF,在直线AB上找一点P,使得S△PEF= S△CEF,求点P的坐标.【答案】(1)(3,0)(2)解:∵AB=CD=3,OB=1,∴A的坐标为(1,3),又C(3,0),设直线AC的解析式为y=ax+b,则,解得:,∴直线AC的解析式为y=﹣ x+ .∵点E(2,m)在直线AC上,∴m=﹣ ×2+ = ,∴点E(2,).∵反比例函数y= 的图象经过点E,∴k=2× =3,∴反比例函数的解析式为y=(3)解:延长FC至M,使CM= CF,连接EM,则S△EFM= S△EFC, M(3,﹣0.5).在y= 中,当x=3时,y=1,∴F(3,1).过点M作直线MP∥EF交直线AB于P,则S△PEF=S△MEF.设直线EF的解析式为y=a'x+b',∴,解得,∴y=﹣ x+ .设直线PM的解析式为y=﹣ x+c,代入M(3,﹣0.5),得:c=1,∴y=﹣ x+1.当x=1时,y=0.5,∴点P(1,0.5).同理可得点P(1,3.5).∴点P坐标为(1,0.5)或(1,3.5).【解析】【解答】解:(1)∵D(3,3),∴OC=3,∴C(3,0).故答案为(3,0);【分析】(1)由D的横坐标为3,得到线段OC=3,即可确定出C的坐标;(2)由矩形的对边相等,得到AB=CD,由D的纵坐标确定出CD的长,即为AB的长,再由B的坐标确定出OB的长,再由A为第一象限角,确定出A的坐标,由A与C的坐标确定出直线AC的解析式,将E坐标代入直线AC解析式中,求出m的值,确定出E的坐标,代入反比例解析式中求出k的值,即可确定出反比例解析式;(3)延长FC至M,使CM=CF,连接EM,则S△EFM=S△EFC, M(3,﹣0.5).求出F(3,1),过点M作直线MP∥EF交直线AB于P,利用平行线间的距离处处相等得到高相等,再利用同底等高得到S△PEF=S△MEF.此时直线EF与直线PM的斜率相同,由F的横坐标与C横坐标相同求出F 的横坐标,代入反比例解析式中,确定出F坐标,由E与F坐标确定出直线EF斜率,即为直线PM的斜率,再由M坐标,确定出直线PM解析式,由P横坐标与B横坐标相同,将B横坐标代入直线PM解析式中求出y的值,即为P的纵坐标,进而确定出此时P的坐标.4.函数学习中,自变量取值范围及相应的函数值范围问题是大家关注的重点之一,请解决下面的问题.(1)分别求出当2≤x≤4时,三个函数:y=2x+1,y= ,y=2(x﹣1)2+1的最大值和最小值;(2)若y= 的值不大于2,求符合条件的x的范围;(3)若y= ,当a≤x≤2时既无最大值,又无最小值,求a的取值范围;(4)y=2(x﹣m)2+m﹣2,当2≤x≤4时有最小值为1,求m的值.【答案】(1)解:y=2x+1中k=2>0,∴y随x的增大而增大,∴当x=2时,y最小=5;当x=4时,y最大=9.∵y= 中k=2>0,∴在2≤x≤4中,y随x的增大而减小,∴当x=2时,y最大=1;当x=4时,y最小= .∵y=2(x﹣1)2+1中a=2>0,且抛物线的对称轴为x=1,∴当x=1时,y最小=1;当x=4时,y最大=19(2)解:令y= ≤2,解得:x<0或x≥1.∴符合条件的x的范围为x<0或x≥1(3)解:①当k>0时,如图得当0<x≤2时,y= 无最大值,有最小值,同理当a<0时,且a≤x<0时,y≤ 有最大值,无最小值,②当k<0时,如图得当0<x≤2时,y= 无最小值,有最大值,同理当a<0时,且a≤x<0时,y≤ 有最小值,无最大值,∴当k<0,a<0时,此时,y= 既无最大值,又无最小值,综上所述,a的取值范围是a<0(4)解:①当m<2时,有2(2﹣m)2+m﹣2=1,解得:m1=1,m2= (舍去);②当2≤m≤4时,有m﹣2=1,解得:m3=3;③当m>4时,有2(4﹣m)2+m﹣2=1,整理得:2m2﹣15m+29=0.∵△=(﹣15)2﹣4×2×29=﹣7,无解.∴m的值为1或3.①当k>0时,如图得当0<x≤2时,y= 无最大值,有最小值,同理当a<0时,且a≤x<0时,y≤ 有最大值,无最小值,②当k<0时,如图得当0<x≤2时,y= 无最小值,有最大值,同理当a<0时,且a≤x<0时,y≤ 有最小值,无最大值,∴当k<0,a<0时,此时,y= 既无最大值,又无最小值,综上所述,a的取值范围是a<0;【解析】【分析】(1)根据k=2>0结合一次函数的性质即可得出:当2≤x≤4时,y=2x+1的最大值和最小值;根据二次函数的解析式结合二次函数的性质即可得出:当2≤x≤4时,y=2(x﹣1)2+1的最大值和最小值;(2)令y= ≤2,解之即可得出x的取值范围;(3)①当k>0时,如图得当0<x≤2时,得到y= 无最大值,有最小值,同理当a<0时,且a≤x<0时,得到y≤ 有最大值,无最小值,②当k<0时,如图得当0<x≤2时,y=无最小值,有最大值,同理当a<0时,且a≤x<0时,y≤ 有最小值,无最大值,于是得到结论;(4)分m<2、2≤m≤4和m>4三种情况考虑,根据二次函数的性质结合当2≤x≤4时有最小值为1即可得出关于m的一元二次方程(一元一次方程),解之即可得出结论.5.如图,在平面直角坐标系中,矩形OADB的顶点A,B的坐标分别为A(﹣6,0),B (0,4).过点C(﹣6,1)的双曲线y= (k≠0)与矩形OADB的边BD交于点E.(1)填空:OA=________,k=________,点E的坐标为________;(2)当1≤t≤6时,经过点M(t﹣1,﹣ t2+5t﹣)与点N(﹣t﹣3,﹣ t2+3t﹣)的直线交y轴于点F,点P是过M,N两点的抛物线y=﹣ x2+bx+c的顶点.①当点P在双曲线y= 上时,求证:直线MN与双曲线y= 没有公共点;②当抛物线y=﹣ x2+bx+c与矩形OADB有且只有三个公共点,求t的值;③当点F和点P随着t的变化同时向上运动时,求t的取值范围,并求在运动过程中直线MN在四边形OAEB中扫过的面积.【答案】(1)6;-6;(﹣,4)(2)解:①设直线MN解析式为:y1=k1x+b1由题意得:解得∵抛物线y=﹣过点M、N∴解得∴抛物线解析式为:y=﹣ x2﹣x+5t﹣2∴顶点P坐标为(﹣1,5t﹣)∵P在双曲线y=﹣上∴(5t﹣)×(﹣1)=﹣6∴t=此时直线MN解析式为:联立∴8x2+35x+49=0∵△=352﹣4×8×48=1225﹣1536<0∴直线MN与双曲线y=﹣没有公共点.②当抛物线过点B,此时抛物线y=﹣ x2+bx+c与矩形OADB有且只有三个公共点∴4=5t﹣2,得t=当抛物线在线段DB上,此时抛物线与矩形OADB有且只有三个公共点∴,得t=∴t= 或t=③∵点P的坐标为(﹣1,5t﹣)∴y P=5t﹣当1≤t≤6时,y P随t的增大而增大此时,点P在直线x=﹣1上向上运动∵点F的坐标为(0,﹣)∴y F=﹣∴当1≤t≤4时,随者y F随t的增大而增大此时,随着t的增大,点F在y轴上向上运动∴1≤t≤4当t=1时,直线MN:y=x+3与x轴交于点G(﹣3,0),与y轴交于点H(0,3)当t=4﹣时,直线MN过点A.当1≤t≤4时,直线MN在四边形AEBO中扫过的面积为S=【解析】【解答】解:(1)∵A点坐标为(﹣6,0)∴OA=6∵过点C(﹣6,1)的双曲线y=∴k=﹣6y=4时,x=﹣∴点E的坐标为(﹣,4)故答案为:6,﹣6,(﹣,4)【分析】(1)根据A点的坐标即可得出OA的长,将C点的坐标代入双曲线y=,即可求出k的值,得出双曲线的解析式,根据平行于x轴的直线上的点的坐标特点得出点E的纵坐标为4,将y=4代入双曲线的解析式即可算出对应的自变量的值,从而得出E点的坐标;(2)①用待定系数法求出直线MN解析式,将M,N两点的坐标代入抛物线y=﹣x2+bx+c,得出关于b,c的方程组,求解得出b,c的值,根据顶点坐标公式表示出P点的坐标,再将P点的坐标代入双曲线即可求出t的值,从而得出直线MN解析式,解联立直线MN解析式与双曲线的解析式组成的方程组,根据根的判别式的值小于0,得出直线MN与双曲线没有公共点;②当抛物线过点B,此时抛物线y=﹣x2+bx+c与矩形OADB有且只有三个公共点,故4=5t﹣2,求解得出t的值,当抛物线在线段DB上,此时抛物线与矩形OADB有且只有三个公共点,故,求解得出t的值,综上所述得出答案;③根据P点的坐标判断出当1≤t≤6时,y P随t的增大而增大,此时,点P在直线x=﹣1上向上运动进而表示出F点的坐标,将F点的纵坐标配成顶点式,得出当1≤t≤4时,随者y F随t的增大而增大,此时,随着t的增大,点F在y轴上向上运动,故1≤t≤4,当t=1时,直线MN:y=x+3与x轴交于点G(﹣3,0),与y轴交于点H(0,3),当t=4﹣时,直线MN过点A.根据割补法算出当1≤t≤4时,直线MN在四边形AEBO中扫过的面积。
北京中考数学一模试卷函数题汇编
北京中考数学一模试卷函数题汇编Revised on July 13, 2021 at 16:25 pm2011年昌平区一摸 5. 函数y =中;自变量x 的取值范围是A .1x ≥B .1x ≤C .1x >D .1x ≠答案:A2011年昌平区一摸 12.如图;在函数象上;有点1P ;2P ;3P ;…;n P ;1n P +;若1P 的横坐标为a ;且以后 每点的横坐标与它前面一个点的横坐标的差都为过点1P ;2P ;3P ;…;n P ;1n P +分别作x 轴、y 轴的垂线段;构成若干个矩形如图所示;影部分的面积从左到右依次记为1S ;2S ;3S ;…;n S ;则1S = ; 1S +2S +3S +…+n S = .用n 的代数式表示答案:6;121nn +2011年昌平区一摸23. 已知二次函数22(1)(31)2y k x k x =---+. 1二次函数的顶点在x 轴上;求k 的值;2若二次函数与x 轴的两个交点A 、B 均为整数点坐标为整数的点;当k 为整数时;求A 、B 两点的坐标.答案:解:1方法一∵二次函数顶点在x 轴上;∴2-4=0b ac ;且0a ≠即()()22314210a k --⨯-=;且2-10k ≠2∵二次函数与x 轴有两个交点;∴2-40b ac >;且0a ≠.即2-30k ()>;且±k ≠1. 当3k ≠且1k ≠±时;即可行.∵A 、B 两点均为整数点;且k 为整数∴1222-1+-3-1+-3-42====-1-1-1+1k k k k k x k k k k (3)()342()2()2() 当=0k 时;可使1x ;2x 均为整数;∴当=0k 时;A 、B 两点坐标为(-10),和(20), 2011年朝阳区一摸 8.已知二次函数y=ax 2+bx 的图象经过点A -1;1;则ab 有A .最大值 1B .最大值2C .最小值0D .最小值41-答案:2011年朝阳区一摸 9.在函数21+=x y 中;自变量x 的取值范围是______.答案:2-≠x2011年朝阳区一摸16.如图;一次函数y=kx +2的图象与x 轴交于点B ;与反比例函数xmy =的图象的一个交 点为A 2;3.1分别求出反比例函数和一次函数的解析式;2过点A 作AC ⊥x 轴;垂足为C ;若点P 在反比例函数图象上;且△PBC 的面积等于18;求P 点的坐标.答案: 解:1把A2;3代入xmy =;∴m=6.∴xy 6=.把A2;3代入y=kx+2; ∴322=+k . ∴21=k . ∴.221+=x y 2令0221=+x ;解得x=-4;即B-4;0.∵AC ⊥x 轴;∴C2;0. ∴ BC=6.设Px;y;∵S △PBC=y BC ⋅⋅21=18;∴y 1=6或y 2=-6. 分别代入xy 6=中; 得x 1=1或x 2=-1. ∴P 11;6或P 2-1;-6答案: 1证明:∵()()()131422+⨯-⨯--=∆m m∴无论m 为任何实数;抛物线与x 轴总有交点. 2m <-1且m≠-4.3解:令()013)2(2=++-+-=m x m x y ; 解得x 1=m+1;x 2=-3.可求得顶点()⎪⎪⎭⎫⎝⎛+-44,222m m P .①当Am+1;0、B-3;0时; ∵ABC PAO S S ∆∆=;∴()()()()13421441212+⨯--=+⨯+m m m m 解得16-=m .∴45182---=x x y .②当A-3;0、Bm+1;0时;同理得()()()[]13421443212+-⨯+=+⨯⨯m m m . 解得58-=m .∴595182---=x x y . 2011年大兴区一摸 6.下列图形中;阴影部分面积为1的是答案:D2011年大兴区一摸8. 如图;已知点F 的坐标为3;0;点A 、B 分别是某函数图像与x 轴、y 轴的交点;点P 是此图像上的一动点;设点P 的横坐标为x;PF 的长为d;且d 与x 之间满足关系:d=5-35x0≤x≤5;则结论:① AF= 2 ② BF=4 ③ OA=5 ④ OB=3;正确结论的序号是 A .①②③ B ①③ C .①②④ D .③④答案:B2011年大兴区一摸 9.函数1-=x y 中;自变量x 的取值范围是 . 答案:1≥x2011年大兴区一摸 16.已知直线b x k y 1+=与双曲线xk y 2=相交于点A2;4;且与x 轴、y 轴分别交于B 、C 两点;AD 垂直平分OB;垂足为D;求直线和双曲线的解析式..答案:16.解法一:∵双曲线xky 2=经过点A 1;2∴22=k∴双曲线的解析式为xy 2=由题意;得OD=1;OB =2 ∴B 点坐标为2;0y xOPF BADA . 1 11;2 B . 1 C .1D .∵直线b x k y +=1经过点A 1;2;B 2;0∴⎩⎨⎧=+=+02211b k b k ∴⎩⎨⎧=-=421b k∴直线的解析式为42+-=x y解法二:同解法一;双曲线的解析式为xy 2=∵AD 垂直平分OB ;∴AD //CO ∴点A 是BC 的中点;∴CO =2AD =4 ∴点C 的坐标是0;4 ∵直线b x k y 1+=经过点A 1;2;C 0;4∴⎩⎨⎧==+421b b k ∴⎩⎨⎧=-=421b k ∴直线的解析式为42+-=x y2011年大兴区一摸 18.在平面直角坐标系中;点A 的坐标是0;6;点B 在一次函数y =-x +m 的图象上;且AB =OB =5.求一次函数的解析式. 答案:解:∵AB =OB ;点B 在线段OA 的垂直平分线BM 上;如图;当点B 在第一象限时;OM =3;OB =5. 在Rt △OBM 中; 2222534BM OB OM =-=-=. ∴ B 4;3.∵ 点B 在y =-x +m 上; ∴ m =7.∴ 一次函数的解析式为7y x =-+. 当点B 在第二象限时;根据对称性;B '-4;3 ∵ 点B'在y =-x +m 上; ∴ m =-1.∴ 一次函数的解析式为1y x =--.综上所述;一次函数的解析式为7y x =-+或1y x =--.2011年大兴区一摸 25.如图;在平面直角坐标系中;点A 的坐标为1;3 ;点B 在x 轴的负半轴上; ∠ABO=30°.1求过点A 、O 、B 的抛物线的解析式;2在1中抛物线的对称轴上是否存在点C;使AC+OC 的值最小 若存在;求出点C 的坐标;若不存在;请说明理由;3在1中x 轴下方的抛物线上是否存在一点P;过点P 作x 轴的垂线;交直线AB 于点D;线段OD 把△AOB 分成两个三角形.使其中一个三角形面积与四边形BPOD 面积比为2:3 若存在;求出点P 的坐标;若不存在;请说明理由.yxBAO答案 :解: 1过点A 作AF ⊥x 轴于点F ;∵∠ABO =30°;A 的坐标为1;3; ∴ BF =3 . ∵ OF =1 ; ∴ BO =2 . ∴ B -2;0.设抛物线的解析式为y=axx +2;代入点A 1; 3;得33a =; ∴232333y x x =+ 2存在点C .过点A 作AF 垂直于x 轴于点F ;抛物线的对称轴x = - 1交x 轴于点E . 当点C 位于对称轴与线段AB 的交点时;AC+OC 的值最小. ∵ △BCE ∽△BAF ; ∴AFCE BF BE = . ∴33=⋅=BF AF BE CE ∴C 1-;33 3存在.如图;连结AO ;设px;y ;直线AB 为y=kx+b ;则33,320.233k k b k b b ⎧=⎪⎧+=⎪⎪⎨⎨-+=⎪⎩⎪=⎪⎩解得;∴直线AB 为32333y x =+; BOD BPO BPOD ∆∆+=S S S 四 =12|OB||y P |+12|OB ||y D |=|y P |+|y D | =23323333x x --+. ∵S △AOD = S △AOB -S △BOD =3-21×2×∣33x +332∣=-33x +33.∴ODB OD S SP A 四∆=33233-33-33332++-x x x =32.∴x 1=-21; x 2=1舍去.∴p -21;-43 .又∵S △BOD =33x +332;∴ODB BOD S SP 四∆ =3323333332332+--+x x x =32. ∴x 1=-21; x 2=-2.P -2;0;不符合题意.∴ 存在;点P 坐标是-21;-43. 2011年东城区一摸 11. 已知A 、B 是抛物线y=x 2-4x +3上关于对称轴对称的两点;则A 、B 的坐标可能是 .写出一对即可答案:1;0;3;0或0;3;4;3等2011年东城区一摸21.在平面直角坐标系xOy 中;一次函数y=k 1x+b 与反比例函数y =xk 2的图象交于A 1;6;Ba ;3两点 . 1求k 1; k 2的值;2如图;点D 在x 轴上;在梯形OBCD中;BC ∥OD ;OB=DC ;过点C 作CE ⊥OD 于点E ;CE 和反比例函数的图象交于点P ;当梯形OBCD 的面积为18时;求PE :PC 的值.答案:解:1∵点A 1;6;Ba ;3在反比例函数y =xk 2的图象上; ∴ k 2=1×6=6. ∴ a ×3=6;a =2. ∴B 2;3.由点A 1;6;B 2;3也在直线y=k 1x+b 上;得⎩⎨⎧=+=+,32,611b k b k解得k 1=-3.∴k 1=-3; k 2=6. 2 设点P 的坐标为m;n.依题意;得 21×3m +2+m -2=18;m =6.∴ C 6;3;E 6;0.∵ 点P 在反比例函数y =x6的图象上;∴ n =1. ∴PE :PC =1:2 .2011年东城区一摸23. 已知关于x 的方程m -1x 2-2m-1x +2=0有两个正整数根. 1 确定整数m 值;2 在1的条件下;利用图象写出方程m -1x 2-2m -1x +2+xm=0的实数根的个数.答案:解: 由方程m -1x 2-2m -1x +2+xm=0可得=)1(2)32(12)1(2)32()12(2-+±-=--±-m m m m m m 111-=m x ;.22=x ∵21,x x 均为正整数;m 也是整数; ∴m =2.2由1知x 2-3x +2+x 2=0.∴x 2-3x +2= -x2.画出函数y = x 2-3x +2;y = -x2的图象;由图象可知;两个函数图象的交点个数是1.2011年东城区一摸25. 如图;已知二次函数y=ax 2+bx +8a ≠0的图像与x 轴交于点A -2;0;B ;与y 轴交于点C ;tan ∠ABC =2.1求抛物线的解析式及其顶点D 的坐标;2设直线CD 交x 轴于点E .在线段OB的垂直平分线上是否存在点P ;使Oxy得经过点P 的直线PM 垂直于直线CD ;且与直线OP 的夹角为75° 若存在;求出点P 的坐标;若不存在;请说明理由;3过点B 作x 轴的垂线;交直线CD 于点F ;将抛物线沿其对称轴向上平移;使抛物线与线段EF 总有公共点.试探究:抛物线最多可以向上平移多少个单位长度答案:解:1依题意;可知 C0;8;则B4;0将A-2;0;B4;0代入 y=ax 2+bx +8;⎩⎨⎧=++=+-.08416,0824b a b a 解得⎩⎨⎧=-=.2,1b a 配方得y2(1)9x =--+;顶点D1;9. 2假设满足条件的点P 存在;依题意设(2)P t ,; 由(08)(19)C D ,,,求得直线CD 的解析式为8y x =+; 它与x 轴的夹角为45. 过点P 作PN ⊥y 轴于点N. 依题意知;∠NPO=30°或∠NPO=60°. ∵PN=2;∴ON=332或23. ∴存在满足条件的点P ;P 的坐标为2;332 和2;23. 3由上求得(80)(412)E F -,,,.当抛物线向上平移时;可设解析式为228(0)y x x m m =-+++>. 当8x =-时;72y m =-+. 当4x =时;y m =.720m ∴-+≤或12m ≤.由题意可得m 的范围为072m ∴<≤. ∴ 抛物线最多可向上平移72个单位.2011年房山区一摸 8.如图;P 是边长为1的正方形ABCD 对角线AC 上一 动点P 与A 、C 不重合;点E 在射线BC 上;且PE =PB . 设AP =x ;△PBE 的面积为y . 则能够正确反映y 与x之间的函数关系的图象是201120115123P;点PM2;12∵2k=;∴23y x=-∴A32;0;B0;-3-3∵P、B两点在y轴上;∴点M到y轴的距离为2∵△MPB的面积为2;∴PB=2∵B0;-3∴点P的坐标为:1(0,1)P-;2(0,5)P-2011年房山区一摸23.本小题满分7分已知:关于x的一元二次方程2(32)220mx m x m--+-=.1若方程有两个不相等的实数根;求m的取值范围;2在1的条件下;求证:无论m取何值;抛物线y=2(32)22mx m x m--+-总过x轴上的一个固定点;3若m为正整数;且关于x的一元二次方程2(32)220mx m x m--+-=有两个不相等的整数根;把抛物线y=2(32)22mx m x m--+-向右平移4个单位长度;求平移后的抛物线的解析式.答案:解:1∵关于x的一元二次方程2(32)220mx m x m--+-=有两个不相等的实数根∴222[(32)]4(22)44(2)m m m m m m∆=----=-+=->0∴0≠m且m≠22证明:令0=y得;2(32)220mx m x m-+-+-=∴11x =;222m x m-=∴抛物线与x 轴的交点坐标为1,0;22,0m m-∴无论m 取何值;抛物线y=2(32)22mx m x m --+-总过x 轴上的定点1,03∵1x =是整数 ∴只需2222m m m-=-是整数.∵m 是正整数;且0,2m m ≠≠ ∴1m =.当1m =时;抛物线为2y x x =-把它的图象向右平移4个单位长度;得到的抛物线解析式为2011年房山区一摸 24.本小题满分8分如图;抛物线233y mx mx =+-m >0与y 轴交于点C;与x 轴交于A 、B 两点;点 A 在点B 的左侧;且1tan 3OCB ∠=.1求此抛物线的解析式;2如果点D 是线段AC 下方抛物线上的动点;设D 点的横坐标为x; △ACD 的面积为S;求S 与x 的关系式;并求当S 最大时点D 的坐标;3若点E 在x 轴上;点P 在抛物线上;是否存在以A 、C 、E 、P 为顶点的平行四边形 若存在求点P 坐标;若不存在;请说明理由.答案: 解:1由已知可得C0;-3;∵1tan 3OCB ∠=;∠COB=90°;∴13OB OC = ; ∴B1;0∵抛物线233y mx mx =+-m >0过点B;∴m+3m-3=0 ; ∴m=43∴抛物线的解析式为349432-+=x x y2如图1;∵抛物线对称轴为23-=x ;B1;0∴A-4;0 联结OD;∵点D 在抛物线349432-+=x x y 上∴设点Dx ;349432-+x x ;则=()2139114334324422x x x ⎛⎫⨯--++⨯--⨯⨯ ⎪⎝⎭ =2362x x -- ∴S=()23262x -++24题图备用图∴当x=-2时;△ACD 的面积S 有最大值为6.此时;点D 的坐标为-2;92-.3①如图2;当以AC 为边;CP 也是平行四边形的边时; CP ∥AE;点P 与点C 关于抛物线的对称轴对称;此时P-3;-3.②如图3;当以AC 为对角线;CP 为边时;此时P 点的坐标是-3;-3③如图4、图5;当以AC 为边;CP 是平行四边形的对角线时;点P 、C 到x 轴的距离相等;则349432-+x x =3;解得2413±-=x ;此时P 2413--;3如图4或2413+-;3如图5综上所述;存在三个点符合题意;分别是1P -3;-3;2P 2413--;3;3P 2413+-;3. -------------------------------------------------------- 8分2011年丰台区一摸 8. 一电工沿着如图所示的梯子NL 往上爬;当他爬到中点M 处时;由于地面太滑;梯子沿墙面与地面滑下;设点M 的坐标为x;yx>0;则y 与x 之间的函数关系用图象表示大致是A .B .C .D . 答案:C 2011年丰台区一摸10.在函数21-=x y 中;自变量x 的取值范围是 . 答案:2≠x2011年丰台区一摸18.如图;在平面直角坐标系中;一次函数121+-=x y 的图象与x 轴、y 轴分别 交于A 、B 两点.1求点A 、B 的坐标;2点C 在y 轴上;当2ABC AOB S S ∆∆=时;求点C 的坐标.答案:18.解:1令y=0;则0121=+-x ;∴x=2;点A2;0; ………………1’ 令x=0;则y=1;点B0;1;………2’2设点C 的坐标为0;y;2011年丰台区一摸23.已知: 反比例函数()y 0kk x=≠经过点B1;1 .1求该反比例函数解析式;2联结OB;再把点A2;0与点B 联结;将△OAB 绕点O 按顺时针方向旋转135°得到△O ''AB ;写出''AB 的中点P 的坐标;试判断点P 是否在此双曲线上;并说明理由;图2 图3 图4 图5xyOHGFE3若该反比例函数图象上有一点F m ;312m -其中m >0;在线段OF 上任取一点E;设E 点的纵坐标为n;过F 点作FM ⊥x 轴于点M;联结EM;使△OEM 的面积是22;求代数式2223n n +-的值. 答案:⑴反比例函数解析式:1y x=⑵∵已知B1;1;A2;0 ∴△OAB 是等腰直角三角形 ∵顺时针方向旋转135°;∴B’0;-2; A’-2;-2∴中点P 为-22; -2. ∵-22· -2=1 ∴点P 在此双曲线上. ⑶∵EH=n ; 0M=m∴S △OEM =EH OM ⋅21=mn 212∴m=2又∵31- 在函数图象上 ∴)123(-m m =1.将m 2代入上式;得2)2(23n 2=1∴2n 2n 3∴2n 2n 33-2011年丰台区一摸24.已知:如图;在□ EFGH 中;点F 的坐标是-2;-1;∠EFG=45°.1求点H 的坐标;2抛物线1C 经过点E 、G 、H ;现将1C 向左平移使之经过点F;得到抛物线2C ;求抛物线2C 的解析式;3若抛物线2C 与y 轴交于点A;点P 在抛物线2C 的对称轴上运动.请问:是否存在以AG 为腰的等腰三角形AGP 若存在;求出点P 的坐标;若不存在;请说明理由.答案: 解:1∵在□ABCD 中 ∴EH=FG=2 ;G0;-1即OG=1 ∵∠EFG=45°∴在Rt △HOG 中;∠EHG=45° 可得OH=1 ∴H1;02∵OE=EH-OH=1 ∴E -1;0; 设抛物线1C 解析式为1y =2ax +bx+c ∴代入E 、G 、H 三点; ∴a =1 ;b=0;;c=-1 ∴1y =2x -1依题意得;点F 为顶点;∴过F 点的抛物线2C 解析式是2y =2(+2x )-13∵抛物线2C 与y 轴交于点A ∴A0;3;∴AG=4 情况1:AP=AG=4过点A 作AB ⊥对称轴于B ∴AB=2在Rt △PAB 中;BP=∴1P -2;3+2P -2;3-情况2:PG=AG=4 同理可得:3P -2;-1+4P -2;-1-∴P 点坐标为 -2;3+-2;3--2;-1+-2;-1-2011年燕山区一摸 8.类比二次函数图象的平移;把双曲线y=x1向左平移2个单位;再向上平移1个单位;其对应的函数解析式变为A .2x 3x y ++=B .2x 1x y ++=C .2x 1x y -+=D .2x 1x y --=答案:A2011年燕山区一摸 9.函数y=12x -的自变量取值范围是 .答案:x ≥21 2011年燕山区一摸 18.如图;某一次函数y=kx+b 的图象与一个反比例函数的图象交于A 、B 两点;点A 和 点B 关于直线y=x 对称.1求出这个反比例函数的解析式; 2直接写出点B 的坐标; 3求k 和b 的值.答案:18. ⑴ 由题意;可认定点A 的坐标是-1; 2; 把x = -1; y=2代入y=xm ; 解得m= -2.∴ 反比例函数的解析式是y= -x2. ⑵ 点B 2; -1.⑶ 把点A -1;2、B 2; -1分别代入y=kx+b;得 ⎩⎨⎧-=+=+.122,b k -b k解得;k= -1;b=1.2011年燕山区一摸 23.已知在同一直角坐标系中;直线l :y=x-3k+6与y 轴交于点P;M 是抛物线C : y=x 2-2 k+2 x+8k 的顶点.1求证:当k ≠2时;抛物线C 与x 轴必定交于两点;2A 、B 是抛物线c 与x 轴的两交点;A 、B 在y 轴两侧;且A 在B 的左边;判断:直线l 能经过点B 吗 需写出判断的过程3在2的条件下;是否存在实数k;使△ABP 和△ABM 的面积相等 如果存在;请求出此时抛物线C 的解析式;若不存在;请说明理由.答案:⑴ 证明:在抛物线C 中; Δ=4 k+22-32k =4k 2-16k+16=4 k -22 . ∵当k ≠2时;4 k -22>0;∴方程x 2-2k+2 x+8k=0有两个不相等的实数根. ∴ 当k ≠2时;抛物线C 与x 轴必定交于两点. ⑵ 解方程x 2-2k+2 x+8k=0; 得 x 1=4;x 2=2k.∵点A 、B 在y 轴两侧;且A 在B 的左边; ∴k <0;点B4;0.把点B4;0代入y=x -3k+6; 得 k=310>0;与“k <0”不符. ∴ 直线l 不可能经过点B. ⑶ y=x 2-2k+2 x+8k =x-k+22-k-22;作MH ⊥x 轴于H;则MH=k-22. ∵k <0; ∴-3k+6>0.第17题图第8题图 ∴OP= -3k+6.由S △ABP =S △ABM ;得 -3k+6=k-22 解得 k 1= -1;k 2= 2舍去∴存在实数k= -1;使得S △ABP =S △ABM . 此时;抛物线C 的解析式是y=x 2-2x-8. 、、2011年延庆区一摸 8. 如图:已知P 是线段AB 上的动点P 不与B A ,重合;分别以AP 、PB 为边在线段AB 的同侧作等边A EP ∆和等 边PFB ∆;连结EF ;设EF 的中点为G ;点D C 、在线段AB 上且BD AC =;当点P 从点C 运动到点D 时;设点G 到直线AB 的距离为y ;则能表示y 与P 点移动的 时间x 之间函数关系的大致图象是答案:D 2011年延庆区一摸 9. 函数2y x =-中自变量x 的取值范围是 . 答案:2≥x2011年延庆区一摸10. 已知:a x x y +-=42的顶点纵坐标为b ;那么b a -的值是 . 答案:42011年延庆区一摸 17. 如图;M 点是正比例函数kx y =和反比例函数xm y =的图象的一个交点.1求这两个函数的解析式;2在反比例函数xmy =的图象上取一点P ;过点P 做A P 垂直于x 轴;垂足为A ;点Q 是直线MO 上一点;QB 垂直于y 轴;垂足为B ;直线MO 上是否存在这样的点Q ;使得 OBQ ∆的面积是OPA ∆的面积的2倍 如果存在;请求出点Q 的坐标;如果不存在;请说明理由; 答案:1由图可知;M 点的坐标为-1;2M 点是正比例函数kx y =和反比例函数xm y =的 图象的一个交点∴x y 2-=;xy 2-=2 ∵点P 在反比例函数xy 2-=的图象上;且2-=p x∴ 1=p yA .B .C .D .x x y 42+-=第24题图1第24题图2 设)2,(a a Q -由题意可知:OPA OBQ S S ∆∆=2 ∴12212221-⨯=-a a ∴22=a ∴2±=a∴点Q 的坐标22,2-或22,2-2011年延庆区一摸 24. 如图1;已知矩形ABCD 的顶点A 与点O 重合;AD 、AB 分别在x 轴、y 轴上;2=AD ;3=AB ;抛物线c bx x y ++-=2经过坐标原点O 和x 轴上另一点)0,4(E1当x 取何值时;该抛物线的最大值是多少2将矩形ABCD 以每秒1个单位长度的速度从图1所示的位置沿x 轴的正方向匀速平行移动;同时一动点P 也以相同的速度从点A 出发向B 匀速移动.设它们运动的时间为t 秒30≤≤t ;直线AB 与该抛物线的交点为N 如图2所示.① 当411=t 时;判断点P 是否在直线ME 上;并说明理由; ② 以D C N 、、、P 为顶点的多边形面积是否可能为5;若有可能;求出此时N 点的坐标;若无可能;请说明理由.答案:解:1因抛物线c bx x y ++-=2经过坐标原点O 0;0和点E4;0 故可得c=0;b=4所以抛物线的解析式为 由4)2(422+--=+-=x x x y得当x =2时;该抛物线的最大值是4.2① 点P 不在直线ME 上.已知M 点的坐标为2;4;E 点的坐标为4;0; 设直线ME 的关系式为y=kx +b .于是得⎩⎨⎧=+=+4204b k b k ;解得⎩⎨⎧=-=82b k所以直线ME 的关系式为y=-2x +8.由已知条件易得;当411=t 时;OA=AP=411; ∵ P 点的坐标不满足直线ME 的关系式y=-2x +8. ∴ 当411=t 时;点P 不在直线ME 上.②以P 、N 、C 、D 为顶点的多边形面积可能为5∵ 点A 在x 轴的非负半轴上;且N 在抛物线上; ∴ OA=AP=t .∴ 点P ;N 的坐标分别为t ;t 、t ;-t 2+4t ∴ AN=-t 2+4t 0≤t ≤3 ;∴ AN -AP=-t 2+4 t - t=-t 2+3 t=t 3-t ≥0 ; ∴ PN=-t 2+3 tⅰ当PN=0;即t=0或t =3时;以点P ;N ;C ;D 为顶点的多边形是三角形;此三角形的高为AD ;∴ S=21DC ·AD=21×3×2=3.ⅱ当PN ≠0时;以点P ;N ;C ;D 为顶点的多边形是四边形∵ PN ∥CD ;AD ⊥CD ;∴ S=21CD+PN ·AD=213+-t 2+3 t ×2=-t 2+3 t +3当-t 2+3 t +3=5时;解得t=1、2而1、2都在0≤t ≤3范围内;故以P 、N 、C 、D 为顶点的多边形面积为5综上所述;当t=1、2时;以点P ;N ;C ;D 为顶点的多边形面积为5; 当t=1时;此时N 点的坐标1;3 当t=2时;此时N 点的坐标2;42011年西城区一摸 11. 定义,,a b c 为函数2y ax bx c =++的特征数;下面给出特征数为2m ;14m -;21m - 的函数的一些结论:①当12m =时;函数图象的顶点坐标是11()24-,;②当1-=m 时;函数在1x >时;y 随x 的增大而减小;③无论m 取何值;函数图象都经过同一个点. 其中所有的正确结论有 .填写正确结论的序号 答案: ①③2011年西城区一摸15. 如图;在平面直角坐标系xOy 中;一条直线l 与x 轴相交于点A ;与y 轴相交于点(0,2)B ;与正比例函数 y =mxm ≠0的图象 相交于点(1,1)P .1求直线l 的解析式;2求△AOP 的面积. 答案:解:1如图1.设直线l 的解析式为y kx b =+k ;b 为常数且k ≠0.∵ 直线l 经过点(0,2)B ;点(1,1)P ;图1∴ 2, 1.b k b =⎧⎨+=⎩ 解得 1,2.k b =-⎧⎨=⎩∴ 直线l 的解析式为2y x =-+2∵ 直线l 的解析式为2y x =-+; ∴ 点A 的坐标为(2,0). ∵ 点P 的坐标为(1,1);∴ 12AOP P S OA y ∆=⨯⨯=12112⨯⨯=.2011年西城区一摸 23.抛物线2y ax bx c =++;a >0;c <0;2360a b c ++=.1求证:1023b a +>; 2抛物线经过点1(,)2P m ;Q (1,)n .① 判断mn 的符号;② 若抛物线与x 轴的两个交点分别为点A 1(,0)x ;点B 2(,0)x 点A 在点B左侧;请说明116x <;2112x <<.答案:23.1证明:∵ 2360a b c ++=;∴ 12362366b a b c c a a a a++==-=-. ∵ a >0;c <0;∴ 0c a <;0c a ->.∴ 1023b a +>. 2解:∵ 抛物线经过点P 1(,)2m ;点Q (1,)n ;∴ 11 ,42.a b c m a b c n ⎧++=⎪⎨⎪++=⎩ ① ∵ 2360a b c ++=;a >0;c <0;∴ 223a b c +=-;223ab c =--. ∴ 1112111()42424312b c m a b c a a a a +=++=+=+-=-<0图62(2)33a an a b c a c c c =++=+--+=->0. ∴ 0mn <.② 由a >0知抛物线2y ax bx c =++开口向上. ∵ 0m <;0n >;∴ 点P 1(,)2m 和点Q (1,)n 分别位于x 轴下方和x 轴上方. ∵ 点A ;B 的坐标分别为A 1(,0)x ;B 2(,0)x 点A 在点B 左侧; ∴ 由抛物线2y ax bx c =++的示意图可知;对称轴右侧的点B 的横坐标2x 满足2112x <<.如图6所示∵ 抛物线的对称轴为直线2bx a=-;由抛物线的对称性可1222x x b a +=-;由1知123b a -<; ∴ 12123x x +<.∴ 12221332x x <-<-;即116x <.2011年西城区一摸 24.如图1;平面直角坐标系xOy 中;A (23,2);B (4,0).将△OAB 绕点O 顺时针旋转 角0°< <90°得到△OCDO ;A ;B 的对应点分别为O ;C ;D ;将△OAB 沿x 轴负方向...平移m 个单位得到△EFGm >0;O ;A ;B 的对应点分别为E ;F ;G ; ;m 的值恰使点C ;D ;F 落在同一反比例函数ky x=k ≠0的图象上. 1∠AOB= °; = °;2求经过点A ;B ;F 的抛物线的解析式;3若2中抛物线的顶点为M ;抛物线与直线EF 的另一个交点为H ;抛物线上的点P 满足以P ;M ;F ;A 为顶点的四边形的面积与四边形MFAH 的面积相等点P 不与点H 重合;请直接写出满足条件的点P 的个数;并求位于直线EF绕点O 顺时针旋转 角得到△OCD ;74. AOB ∠.∴ 点C 与点A 关于x 轴对称;点C的坐标为2)-. ∵ 点C ;D ;F 落在同一反比例函数ky x=k ≠0的图象上; ∴C C k x y =⋅=-.∵ 点F 是由点A 沿x 轴负方向平移m 个单位得到; ∴ 2F y =;2F x -==-点F的坐标为(-. ∴ 点F 与点A 关于y 轴对称;可设经过点A ;B ;F 的抛物线的解析式为2y ax c =+.∴22,160.a c a c ⎧+=⎪⎨+=⎪⎩ 解得1 ,2 8.a c ⎧=-⎪⎨⎪=⎩ ∴ 所求抛物线的解析式为2182y x =-+. 3满足条件的点P 的个数为 5 .抛物线2182y x =-+的顶点为(0,8)M .∵ △EFG 是由△OAB 沿x 轴负方向平移m 个单位得到;∴m FA ==;E O x x m =-=-;∠FEG=∠AOB=30°. ∴ 点E的坐标为(-.可得直线EF的解析式为4y x +. ∵ 点H21482x +=-+的解;整理;得23240x +-=.解得123x x ==- ∴ 点H的坐标为16)3.由抛物线的对称性知符合题意的1P点的坐标为16()3. 可知△AFM 是等边三角形;∠MAF= 60°. 由A ;M 两点的坐标分别为A ;(0,8)M ; 可得直线AM的解析式为8y =+.过点H 作直线AM 的平行线l ;设其解析式为y b =+b ≠8.将点H 的坐标代入上式;得1643333b =-⨯+. 解得283b =;直线l 的解析式为2833y x =-+.∵ 直线l 与抛物线的交点的横坐标是方程 22813832x x -+=-+的解.整理;得236380x x -+=.解得124323,33x x ==. ∴ 点2P 2322(,)33满足HAM AM P S S ∆∆=2;四边形2P MFA 的面积与四边形MFAH 的面积相等.如图8点2P 关于y 轴的对称点3P 也符合题意;其坐标为3P 2322(,)33-. 综上所述;位于直线EF 上方的点P 的坐标分别为1P 4316(,)33-; 2P 2322(,)33;3P 2322(,)33-.2011年通州区一摸17.如图;直线2y x =-+与反比例函数ky x=的图象只有一个交点;求反比例函数的解析式. 答案:解: 直线2+-=x y 与xky =只有一个交点; ∴2+-=x xk且0=∆解之得:1=k∴反比例函数的解析式为:xy 1=2011年通州区一摸24.已知如图;ABC ∆中;AC BC =;BC 与x 轴平行;点A 在x 轴上;点C 在y 轴上;抛物线254y ax ax =-+经过ABC ∆ 的三个顶点;1求出该抛物线的解析式;2若直线7+=kx y 将四边形ACBD 面积平分;求此直线的解析式.3若直线b kx y +=将四边形ACBD 的周长和面积同时分成相等的两部分;请你确定b kx y +=中k 的取值范围.答案:解.1由题意可知;抛物线的对称轴为:2525=--=a a x ;与y 轴交点为)4,0(c把)0,3(-A 代入452+-=ax ax y 得:解之得:61-=a2直线7+=kx y 将四边形ACBD 面积平分;则直线一定经过OB 的中点P .根据题意可求P 点坐标为2,25把P 2,25代入7+=kx y 得:2-=k ;∴直线的解析式为:72+-=x y35454≥-≤k k 或2011年顺义区一摸 6. 如图;A 、B 是函数2y x=的图象上关于原点对称的任意两点;BC ∥x 轴;AC ∥y 轴;△ABC 的面积记为S ;则A . 2S =B . 4S =C . 24S <<D .4S > 答案:B2011年顺义区一摸8.如图;矩形ABCD 中;1AB =;2AD =;M 是CD 的中点;点P 在矩形的边上沿A B C M →→→运动;则APM △的面积y 与点P 经过的路程x 之间的函数关系用图象表示大致是下图中的答案: A 2011年顺义区一摸18. 已知:如图;在平面直角坐标系xOy 中;一次函数24y x =-+的图象分别与x y 、轴交于点A 、 B ;点P在x 轴上;若6ABP S ∆=;求直线PB 的函数解析式.答案: 解:令0y =;得 2x = ∴ A 点坐标为2 ;0 令0x =; 得 4y = ∴ B 点坐标为0 ;4- ∵ 6ABP S ∆=C .D . 11 2 3 3.5 x y 0 A . 1 1 2 3 3.5 xy 0 B .1 123 3.5 x y 0 11 2 3 3.5x y∴1462AP ⨯⨯= 即3AP =∴ P 点的坐标分别为1(1,0)P -或2(5,0)P 设直线PB 的函数解析式为y kx b =+∴ 04k b b -+=⎧⎨=⎩ 或 504k b b +=⎧⎨=⎩∴ 44k b =⎧⎨=⎩ 或 454k b ⎧=-⎪⎨⎪=⎩∴ 直线PB 的函数解析式为44y x =+或445y x =-+2011年顺义区一摸25. 已知:如图;抛物线22(0)y ax ax c a =-+≠与y 轴交于点(0,3)C ;与x 轴交于A 、B 两点;点A 的坐标为(1,0)-.1求抛物线的解析式及顶点D 的坐标;2设点P 是在第一象限内抛物线上的一个动点;求使与四边形ACDB 面积相等的四边形ACPB 的点P 的坐标; 3求APD ∆的面积.答案:解:1∵抛物线22(0)y ax ax c a =-+≠与y 轴交于点(0,3)C ;与x 轴交于A (1,0)-∴203a a c c ++=⎧⎨=⎩ 解得 13a c =-⎧⎨=⎩∴ 抛物线的解析式为223y x x =-++∵222(2)3(211)3(1)4y x x x x x =--+=--+-+=--+∴顶点D 的坐标为 1 ;42连结BC ;过点D 作DE x ⊥轴于点E . 令0y = 则2230x x -++= ∴ 11x =- ;23x = ∴ 点B 的坐标为3 ;0∴AOC EBD ACDB OEDC S S S S ∆∆=++四边形梯形∵14362ABC S ∆=⨯⨯=∴3BCD S ∆=∵点P 是在第一象限内抛物线上的一个动点;∴3BCP BCD S S ∆∆==∴ 点P 是过 D 且与直线BC 平行的直线和抛物线的交点 而直线BC 的函数解析式为3y x =-+∴设直线DP 的函数解析式为y x b =-+ ; 过点D1;4∴14b -+= ; 5b =∴直线DP 的函数解析式为5y x =-+把5y x =-+代入223y x x =-++中;解得11x =;22x = ∴点P 的坐标为2;33∵点P 与点C 关于DE 对称;点B 与点A 关于 DE 对称 ∴APD BCD ∆≅∆∴3APD BCD S S ∆∆==.源:学科网 2011年石景山区一摸 4.函数12y x =-的自变量x 的取值范围是 A .0x ≠ B .2x ≠C .2x ≥D .2x >答案:B2011年石景山区一摸9.将二次函数562++=x x y 配方为k h x y +-=2)(形式;则=h ____;=k ________. 答案:4,3--;2011年石景山区一摸17.已知:如图;一次函数3+=kx y 的图象与反比例函数xmy =0>x 的图象交于点P .x PA ⊥轴于点A ;y PB ⊥轴于点B .一次函数的图象分别交x 轴、y 轴于点C 、点D ;且27=DBP S △;21=CA OC .1求点D 的坐标;2求一次函数与反比例函数的解析式;3根据图象写出当x 取何值时;一次函数的值小于反比例函数的值答案:17.解:1根据题意;得:)3,0(D …………………………………1分 2在Rt △COD 和Rt △CAP 中; 21=CA OC ;3=OD ∴,6=AP 6=OB ∴9=DBRt △DBP 中;∴,272=⨯BPDB ∴6=BP ;)6,6(-P一次函数的解析式为: 323+-=x y反比例函数解析式为:xy 36-=3如图可得:6>x2011年石景山区一摸23.已知抛物线C :()112++-=x m x y 的顶点在坐标轴...上.1求m 的值;20>m 时;抛物线C 向下平移()0>n n 个单位后与抛物线1C :c bx ax y ++=2关于y 轴对称;且1C 过点()3,n ;求1C 的函数关系式;303<<-m 时;抛物线C 的顶点为M ;且过点()0,1y P .问在直线1-=x 上是否存在一点Q 使得△QPM 的周长最小;如果存在;求出点Q 的坐标; 如果不存在;请说明理由.答案:解:当抛物线C 的顶点在x 轴上时解得1=m 或3-=m 当抛物线C 的顶点在y 轴上时 ∴1-=m 综上1±=m 或3-=m . 2当0>m 时;1=m抛物线C 为122+-=x x y .向下平移()0>n n 个单位后得到n x x y -122+-=抛物线n x x y -122+-=与抛物线1C : c bx ax y ++=2关于y 轴对称 ∴1=a ;2=b ;n c -=1 ∴抛物线1C : n x x y -++=122 ∵1C 过点()3,n∴3122=-++n n n ;即022=-+n n解得2,121-==n n 由题意0>n ;舍去∴1=n ∴抛物线1C : x x y 22+=. 3当03<<-m 时1-=m抛物线C :12+=x y 顶点()1,0M ∵过点()0,1y P ∴2110=+=y∴()2,1P作点()1,0M 关于直线1-=x 的对称点()1,2'-M直线'PM 的解析式为3531+=x y∴⎪⎭⎫ ⎝⎛-34,1Q2011年平谷区一摸 9.在函数y =中;自变量x 的取值范围是 .答案:3x -≥2011年平谷区一摸23.已知二次函数)0a (23bx ax y 2≠-+=的图象经过点(10),;和(30)-,;反比例函数xk=1y x >0的图象经过点1;2.1求这两个二次函数的解析式;并在给定的直角坐标系中作出这两个函数的图象;2若反比例函数x k =1y 0x >的图象与二次函数)0a (23bx ax y 2≠-+=的图象在第一象限内交于点00()A x y ,;0x 落在两个相邻的正整数之间.请你观察图象写出这两个相邻的正整数; 3若反比例函数2k y x =00k x >>,的图象与二次函数)0a (23bx ax y 2≠-+=的图象在第一象限内的交点为A ;点A 的横坐标0x 满足023x <<;试求实数k 的取值范围.答案:解:1把(10),;和(30)-,分别代入 解方程组;得 .1b ,21a ==∴ 抛物线解析式为23212-+=x x y∵ 反比例函数x k=1y 的图象经过点1;2;∴ k =2. ∴ x2y 1=2正确的画出二次函数和反比例函数在第一象限内的图象 由图象可知;这两个相邻的正整数为1与2.3由函数图象或函数性质可知:当2<x <3时;对y=23212-+x x ;y 随着x 的增大而增大;对y 2=xkk >0;y 2随着x 的增大而减小.因为Ax 0;y 0为二次函数图象与反比例函数图象的交点;所以当x 0=2时;由反比例函数图象在二次函数的图象上方;得y 2>y. 即2k >2322212-+⨯;解得k >5.同理;当x 0=3时;由二次函数的图象在反比例函数图象上方的;得y >y 2; 即2333212-+⨯>3k;解得k <18. 所以k 的取值范围为5<k <18.2011年密云区一摸 3.在函数y=3x -中;自变量x 的取值范围是 A. x ≥3 B. x>3 C. x ≤3 D. x<3 答案:A2011年密云区一摸 11.二次函数223y x x =-+图像的顶点坐标为 . 答案:-1;22011年密云区一摸 18.已知:如图;在平面直角坐标系xOy 中;直线AB 与x 轴交于点A-2;0;与反比例函数在第一象限内的图象交于点B2;n;连接BO ;若S △AOB =4. 1求该反比例函数的解析式和直线AB 的解析式;2若直线AB 与y 轴的交点为C;求△OCB 的面积.答案:解:1由A-2;0;得OA=2. ∵点B2;n 在第一象限;S △AOB =4.∴.421=⋅n OA ∴4=n . ∴点B 的坐标是2;4.设该反比例函数的解析式为)0(≠=a x ay .将点B 的坐标代入;得,24a=∴8=a∴反比例函数的解析式为:xy 8=.设直线AB 的解析式为)0(≠+=k b kx y .将点A;B 的坐标分别代入;得⎩⎨⎧=+=+-.42,02b k b k解得⎩⎨⎧==.2,1b k∴直线AB 的解析式为.2+=x y2在2+=x y 中;令,0=x 得.2=y∴点C 的坐标是0;2.∴OC=2._x_ y _ O_ C _ A _ B _∴S △OCB =.2222121=⨯⨯=⋅B x OC甲型20台;获租金最高2011年密云区一摸 23.光华农机租赁公司共有50台联合收割机;其中甲型20台;乙型30台.现将这50台联合收割机派往A 、B 两地区收割小麦;其中30台派往A 地区;20台派往B 地区;两地区与该农机租赁公司商定每天的租赁价格见下表:1派往A 地区x 台乙型联合收割机;租赁公司这50台联合收割机一天获得的租金为y 元求x 与y 间的函数关系时;并写出x 的取值范围;2若使农机租菱公司这50台联合收割机一天的租金总额比低于79600元;说明有多少种分配方案;并将各种方案设计出来;3如果要使这50台联合收割机每天获得的租金最高;请你为光华农机租赁公司提出一条合理建议..答案:解:12007400....................1y x =+分x 的取值范围:1030.x ≤≤2由题意得200740079600x +≥;解得:28x ≥;由于1030.x ≤≤ x 取28;29;30.①派往A 地区甲型2台;乙型28台;派往B 地区甲型18台;乙型2台.②派往A 地区甲型1台;乙型29台;派往B 地区甲型19台;乙型1台.③派往A 地区乙型30台;派往B 地区甲型20台. …5分 3 60007400080000=+=最大当x=30时,y 元建议农机公司派往A 地区乙型30台;派往B 地区2011年门头沟区一摸 9. 在函数11y x =-中;自变量x 的取值范围是答案:1x ≠2011年门头沟区一摸 11.将二次函数246y x x =-+化为2()y x h k =-+的形式;则y = . 答案:2(-2)2x +B O D1xy1 1A .D2 2011年门头沟区一摸18.如图;正比例函数y mx 和反比例函数ny x 的图象 都过点A 1;a ;点B 2;1在反比例函数的图象上. 1求正比例函数和反比例函数的解析式; 2过A 点作直线AD 与x 轴交于点D ;且△AOD 的面积为3;求点D 的坐标.答案:解:1∵反比例函数n y x=的图象经过点B 2;1;∴2n =.∴反比例函数的解析式是2y x=.点A 1;a 在反比例函数2y x=的图象上;∴2a =. ∴(12)A ,. ∵正比例函数y mx 的图象经过点(12)A ,;∴ 2m =.∴正比例函数的解析式是2y x .2依题意;得1232OD ⨯⨯=.∴3OD =.∴ D 点坐标为1(3,0)D -或2(3,0)D .2011年门头沟区一摸 23.已知关于x 的一元二次方程2(2)210m x x +--=.1若此一元二次方程有实数根;求m 的取值范围;2若关于x 的二次函数21(2)21y m x x =+--和22(2)1y m x mx m =++++的图象都经过x 轴上的点n ;0;求m 的值;3在2的条件下;将二次函数21(2)21y m x x =+--的图象先沿x 轴翻折;再向下平移3个单位;得到一个新的二次函数3y 的图象.请你直接写出二次函数3y 的解析式;数3y 的值大于二次函数2y 的值.答案:解:1根据题意;得220,Δ(2)4(2)(1)0.m m +≠⎧⎨=--+⨯-≥⎩ 解得2,3.m m ≠-⎧⎨≥-⎩ ∴m 的取值范围是m ≥-3且m ≠-2.1 2 3 4 43 2 1xyO -1 -2 -3 -4 -4-3 -2 -1· A B Oxy 1 1。
2022初三一模--一次、反比例函数综合汇编(学生版)
一次、反比例函数函数与方程、不等式类问题解题思路:1.函数值:是指当自变量x 取一个确定值时,对应的y 的值称为函数值.也可以理解为函数上点的纵坐标;2. x m >时,对于x 的每一个值,函数1y 的值大于函数2y 的值,在函数图像表示为在x m =的右侧,函数1y 均高于函数2y .3.对于此类问题,需要利用数形结合的思想,先将已知函数画出,确定未知函数变化趋势,当未知函数是一次函数时(1)经过定点,但k 未知时,函数是绕着定点进行旋转运动的;(2)k 已知,b 未知时,函数是进行平移运动的。
最后通过临界值(极限值)找到符合题意的取值范围;(2022•海淀区一模)22.在平面直角坐标系xOy 中,一次函数(0)y kx b k =+≠的图象由函数12y x =的图象平移得到,且经过点(2,0)−. (1)求这个一次函数的解析式;(2)当x m >时,对于x 的每一个值,函数34y x =−的值大于一次函数y kx b =+的值,直接写出m 的取值范围.(2022•丰台区一模)22.在平面直角坐标系xOy 中,一次函数(0)y kx b k =+≠的图象由函数2y x =的图象平移得到,且经过点(2,1). (1)求这个一次函数的解析式;(2)当0x >时,对于x 的每一个值,函数(0)y mx m =≠的值大于一次函数y kx b =+的值,直接写出m 的取值范围.(2022•石景山区一模)23. 在平面直角坐标系xOy 中,直线11:2l y x b =+与直线2:2l y x =交于点(),A m n .(1)当2m =时,求n ,b 的值;(2)过动点(),0P t 且垂直于x 轴的直线与1l ,2l 的交点分别是C ,D .当1t ≤时,点C 位于点D 上方,直接写出b 的取值范围.(2022•房山区一模)23.一次函数4(0)y kx k k =+≠的图象与x 轴交于点A ,与y 轴交于点B ,且经过点(2,)C m .(1)当92m =时,求一次函数的解析式并求出点A 的坐标; (2)当1x >−时,对于x 的每一个值,函数y x =的值大于一次函数4(0)y kx k k =+≠的值,求k 的取值范围.(2022•门头沟区一模)22.如图,在平面直角坐标系xOy 中,点(1,4)A ,(3,)B m . (1)如果点A ,B 均在反比例函数1ky x=的图象上,求m 的值; (2)如果点A 、B 均在一次函数2y ax b =+的图象上, ①当2m =时,求该一次函数的表达式;②当3x 时,如果不等式1mx ax b −>+始终成立,结合函数图象,直接写出m 的取值范围.(2022•平谷区一模)21.在平面直角坐标系xOy 中,一次函数(0)y kx b k =+≠的图象经过点(1,0)−,(0,2).(1)求这个一次函数的表达式;(2)当2x >−时,对于x 的每一个值,函数(0)y mx m =≠的值小于一次函数(0)y kx b k =+≠的值,直接写出m 的取值范围.(2022•顺义区一模)22.在平面直角坐标系xOy 中,一次函数(0)y kx b k =+≠的图象平行于直线12y x =,且经过点(2,2)A . (1)求这个一次函数的表达式;(2)当2x <时,对于x 的每一个值,一次函数(0)y kx b k =+≠的值大于一次函数1(0)y mx m =−≠的值,直接写出m 的取值范围.(2022•燕山区一模)22.在平面直角坐标系xOy 中,一次函数(0)y kx b k =+≠的图象由函数12y x =的图象向上平移3个单位长度得到. (1)求这个一次函数的解析式;(2)当2x >时,对于x 的每一个值,函数(0)y mx m =≠的值大于一次函数y kx b =+的值,直接写出m 的取值范围.三角形面积类问题解题思路:1.三角形面积问题需要注意图形是否规则,能否比较轻松的找到底与高,如果不能则需要应用割补法;(2022•东城区一模)21. 在平面直角坐标系xOy 中,一次函数2y x =−的图象与x 轴交于点A ,与反比例函数(0)ky k x=≠的图象交于点(3,)B m ,点P 为反比例函数(0)ky k x=≠的图象上一点. (1)求m ,k 的值; (2)连接OP ,AP .当2OAPS =时,求点P 的坐标.整点个数类问题(2022•西城区一模)23.在平面直角坐标系xOy 中,直线1:l y kx b =+与坐标轴分别交于(2,0)A ,(0,4)B 两点.将直线1l 在x 轴上方的部分沿x 轴翻折,其余的部分保持不变,得到一个新的图形,这个图形与直线2:(4)(0)l y m x m =−≠分别交于点C ,D . (1)求k ,b 的值;(2)横、纵坐标都是整数的点叫做整点.记线段AC ,CD ,DA 围成的区域(不含边界)为W .①当1m =时,区域W 内有 1 个整点;②若区域W 内恰有3个整点,直接写出m 的取值范围.(2022•通州区一模)21.已知一次函数12y x m =+的图象与反比例函数2(0)ky k x=>的图象交于A ,B 两点.(1)当点A 的坐标为(2,1)时.①求m ,k 的值;②当2x >时,1y > 2y (填“>”“ =”或“<” ).(2)将一次函数12y x m =+的图象沿y 轴向下平移4个单位长度后,使得点A ,B 关于原点对称,求m 的值.一、一次函数1.一次函数的定义:一般地,形如y kx b =+(,是常数,)的函数,叫做一次函数.2.一次函数的系数与图像关系(1)一次函数y kx b =+(,,为常数)的图象是一条直线.(2)k 的符号决定直线倾斜方向:0k >,直线倾斜向上.0k <,直线倾斜向下;(3)k 决定直线倾斜程度:k 越大直线越倾斜,越趋近于平行y 轴。
北京市各区2020届九年级上学期期末数学试卷精选汇编:反比例函数专题(含答案)
反比例函数专题海淀24.在平面直角坐标系xOy 中,已知点A 是直线1322y x =+上一点,过点A 分别作x 轴,y 轴的垂线,垂足分别为点B 和点C ,反比例函数ky x=的图象经过点A . (1)若点A 是第一象限内的点,且AB AC =,求k 的值; (2)当AB AC >时,直接写出k 的取值范围.24. 解:(1)依题意,设点(,)A x y ,(,0)B x ,(0,)C y (0,0)x y >>.∴AB y =,AC x =. ∵AB AC =, ∴x y =. ∵点A 在直线1322y x =+上, ∴点A 的坐标为(3,3)A .∵点A 在函数ky x=(k ≠0)的图象上, ∴9k =.(2)190k k -<<≠且.东城22. 在平面直角坐标系xOy 中,反比例函数(0)ky x x =>的图象和ABC △都在第一象限内,52AB AC ==,//BC x 轴,且4BC =,点A 的坐标为(3,5). (1)若反比例函数(0)ky x x=>的图象经过点B ,求此反比例函数的解析式;(2)若将ABC △向下平移m (m>0)个单位长度,A ,C 两点的对应点同时落在反比例函数图象上,求m 的值.朝阳24.点A是反比例函数1(0)y xx=>的图象l1上一点,直线AB∥x轴,交反比例函数3(0)y xx=>的图象l2于点B,直线AC∥y轴,交l2于点C,直线CD∥x轴,交l1于点D.(1)若点A(1,1),求线段AB和CD的长度;(2)对于任意的点A(a,b),判断线段AB和CD的大小关系,并证明.石景山22.在平面直角坐标系xOy 中,函数(0)my x x=>的图象G 经过点(3,2)A , 直线:1(0)l y kx k =-≠与y 轴交于点B ,与图象G 交于点C . (1)求m 的值;(2)横、纵坐标都是整数的点叫做整点.记图象G 在点A ,C 之间的部分与线 段BA ,BC 围成的区域(不含边界)为W .①当直线l 过点(2,0)时,直接写出区域W 内的整点个数;②若区域W 内的整点不少于...4个,结合函数图象,求k 的取值范围.22.解:(1)∵函数(0)my x x=>的图象G 经过点(3,2)A , ∴6m =. ………………………… 1分 (2)① 1; ………………………… 2分 ②∵直线:1(0)l y kx k =-≠与y 轴交于点B , ∴点B 的坐标为(0,1)-,如图. (ⅰ)当直线1l 在BA 下方时, 若点(5,1)在直线1l 上, 则511k -=,解得25k =. 结合图象,可得205k <<.(ⅱ)当直线2l 在BA 上方时, 若点(1,3)在直线2l 上, 则13k -=,解得4k =. 结合图象,可得4k >. 综上所述,k 的取值范围是205k <<或4k >. ………………… 5分丰台20.在平面直角坐标系xOy 中,直线y x =与反比例函数ky x=的图象的两个交点分别为点P (m ,1)和点Q . (1)求k 的值和点Q 的坐标;(2)如果点A 为x 轴上的一点,且∠90PAQ =︒,直接写出点A 的坐标. 20. 解:(1)∵点P (m ,1)在直线y x =上, ∴1m =. ……1分 ∵点P (1,1)在k y x=上,∴1k =. ……2分∵点Q 为直线y x =与ky x=的交点, ∴点Q 坐标为(1-,1-).……3分 (2)1A,0) , 2A (0). ……5分顺义25. 已知:如图,在平面直角坐标系xOy 中,点A (0,2),正方形OABC 的顶点B 在函数x k y =(k ≠ 0,x <0) 的图象上,直线l :y x b =-+与函数xky =(k ≠ 0,x <0) 的图象交于点D ,与x 轴交于点E . (1)求k 的值;(2)横、纵坐标都是整数的点叫做整点.①当一次函数y x b =-+的图象经过点A 时,直接写出△DCE 内的整点的坐标;25.解:(1)依题意知:B (-2,2).………………………………………………… 1分∴反比例函数解析式为4y x-=. ∴k 的值为-4. …………………………………………………………… 2分 (2)①△DCE 内的整点的坐标为 (-1,1),(-1,2), (0,1) ;…… 5分 ② 当b =2时,△DCE 内有3个整点,当b =3时,△DCE 内有6个整点, ∴b 的取值范围是2<b ≤3.…………………………………………… 6分平谷22.如图,在平面直角坐标系xOy 中,曲线()0ky x x=>经过点A . (1)求曲线()0ky x x=>的表达式; (2)直线y=ax +3(a ≠0)与曲线()0ky x x=>围成的封闭区域为图象G .①当1a =-时,直接写出图象G 上的整数点个数是;(注:横,纵坐标均为整数的点称为整点,图象G 包含边界.) ②当图象G 内只有3个整数点时,直接写出a 的取值范围.22.解:(1)∵A (1,1),∴k =1. ······························· 1 ∴()10y x x=>. ················· 2 (2)①3; ·································· 3 ②213a -≤<-. (5)门头沟23.在平面直角坐标系xOy 中,直线y x =与双曲线()0ky k x=≠交于点A (2,a ). (1)求a 与k 的值;(2)画出双曲线()0ky k x=≠的示意图; (3)设点(),P m n 是双曲线()0ky k x=≠上一点(P 与A 不重合),直线PA 与y 轴交于点()0,B b ,当2AB BP =房山22.如图,在平面直角坐标系xOy 中,直线y =x +2与函数xky =(k ≠0)的图象交于A ,B 两点,且点A 的坐标为(1,a ). (1)求k 的值;(2)已知点P (m ,0),过点P 作平行于y 轴的直线,交直线y =x +2于点C ,交函数xky =(k ≠0)的图象于点D . ①当m =2时,求线段CD 的长;②若PC >PD ,结合函数的图象,直接写出m 的取值范围.密云23.在平面直角坐标系中,直线 y = x 与反比例函数的图象交于点A (2,m ).(1)求m 和k 的值;(2)点P (x P ,y P )是函数 图象上的任意一点,过点P 作平行于x 轴的直线,交直线y=x 于点B .① 当y P = 4时,求线段BP 的长;② 当3BP ≥时,结合函数图象,直接写出点P 的纵坐标y P 的取值范围.(0)k y x x=>(0)k y x x=>22.(1)把A (1,a )代入y =x +2得a =3…………1分把A (1,3)代入xky =得3=k …………2分 (2)① 当m =2时,C (2,4),D (2,23)…………3分⸫CD =25=23-4. …………4分② m< -3或m > 1 …………6分燕山23.如图,在平面直角坐标系xOy 中,函数ky x=(0x <)的图象经过点A (-1,6). (1) 求k 的值;(2) 已知点P (a ,-2a ) (0a <),过点P 作平行于x 轴的直线,交直线22y x =--于点M ,交函数ky x=(0x <)的图象于点N . ① 当a =-1时,求线段PM 和PN 的长;② 若PN ≥2PM ,结合函数的图象,直接写出a 的取值范围.23.解:(1) ∵函数ky x=(0x <)的图象经过点A (-1,6),∴k =-1×6=-6. ………………………1分(2)① 当a =-1时,点P 的坐标为(-1,2). ………………………2分 ∵直线22y x =--,反比例函数的解析式为6y x=-,PN ∥x 轴, ∴M (-2,2),N (-3,2),∴PM =1,PN =2. ………………………4分 ② a ≤-3,或-1≤a <0. ………………………6分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学习好资料 欢迎下载
2013年北京市中考数学一模反比例函数汇编
17.(13海淀) 如图,在平面直角坐标系xOy中,反比例函数
x
y2
的图象与一次函数kkxy的图象的一个交点为(1,)An.
(1)求这个一次函数的解析式;
(2)若P是x轴上一点,且满足45APO,直接写出点P的坐
标.
17.(13西)如图,在平面直角坐标系xOy中,正比例函数错误!未指定书签。32yx与
反比例函数kyx的图象在第二象限交于点A,且点A的横坐标为-2 .
(1) 求反比例函数的解析式;
(2) 点B的坐标为(-3,0),若点P在y轴上,
且△AOB的面积与△AOP的面积相等,
直接写出点P的坐标.
学习好资料 欢迎下载
18.(13东) 如图,平行四边形ABCD放置在平面直角坐标系xOy中,已知A(-2,0),B
(2,0),D(0,3),反比例函数kyx(x>0)的图象经过点C
.
(1)求此反比例函数的解析式;
(2)问将平行四边形ABCD向上平移多少个单位,能使点B落在双曲线上.
17.(13丰)如图,在平面直角坐标系xOy中,直线+3ykx的图象与反比例函数
4
(>0)yxx
的图象交于点A(1,m),与x轴交于点B,过点A作ACx轴于点C.
(1)求一次函数的解析式;
(2)若P为x轴上一点,且△ABP的面积为10,直接写出点P的坐标.
A
B O C
x
y
学习好资料 欢迎下载
17.(13朝)如图,在平面直角坐标系xOy中,一次函数y= -x的图象
与反比例函数0kyxx的图象相交于点4Am,.
(1)求反比例函数kyx的解析式;
(2)若点P在x轴上,AP=5,直接写出点P的坐标.
17.(13通)已知(42)A,,(24)B,是一次函数ykxb的图象和反比例函数myx图
象的两个交点.(1)求反比例函数和一次函数的表达式;
(2)将一次函数ykxb的图象沿y轴向上平移n个单位长度,交y轴于点C,
若12ABCSV,求n的值.
y
x
O
-4
A
学习好资料 欢迎下载
17.(13石)已知:一次函数3xy与反比例函数3myx(0x ,m为常数)的图象交
于点A(a,2)、B两点.
(1)求m的值和B点坐标;
(2)过A点作y轴的平行线,过B点作x轴的平行线,这两条直线交于点E,若反比例
函数kyx的图象与△ABE有公共点,请直接写出k的取值范围.
17.(13门)如图,在平面直角坐标系xOy中,一次函数ykxb
的图象与反比例函数myx=的图象交于A(2,3)、
B(3,n)两点.
(1)求一次函数和反比例函数的解析式;
(2)若P是y轴上一点,且满足△PAB的面积是5,
直接写出OP的长.
y
x
O
y
x
A
B
O
学习好资料 欢迎下载
17.(13顺)如图,已知(2,2)A,(,4)Bn是一次函数
ykxb
的图象和反比例函数myx的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求AOB的面积.
17.(13房)如图,反比例函数xy3的图象与一次函数bkxy的图象交于A(m,3)、B(-3,n)
两点.
(1)求一次函数的解析式及AOB的面积;
(2)若点P是坐标轴上的一点,且满足PAB的面积等于AOB的面积的2倍,直接写
出点P的坐标.
第17题图
学习好资料 欢迎下载
17.(13平)如图,一次函数4mxy的图象与x轴相交于点A,
与反比例函数)0(xxky的图象相交于点(16)B,.
(1)求一次函数和反比例函数的解析式;
(2)设点P是x轴上一点,若18APBS,直接写出点P的坐标.
17.(13密)如图,已知直线l1经过点A(-1,0)与点B(2,3),
另一条直线l2经过点B,且与x轴交于点P(m,0).
(1)求直线l1的解析式;
(2)若△APB的面积为3,求m的值.
17.(13延)(本题满分5分)
已知直线l 与直线y=2x平行,且与直线y= -x+m交于点(2,0), 求m的值及直线的
解析式.
x
B
y
O
A
学习好资料 欢迎下载
