无锡市洛社中学2020年秋八年级数学上册期中试题卷
2020-2021学年八年级上学期期中考试数学试题

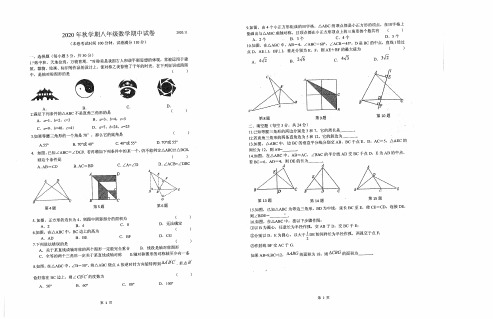
无锡市新吴区新一教育集团2020——2021学年第一学期八年级数学期中考试试卷总分:120分时间:100分钟命题人:核对人:一、选择题(本大题共10小题,每小题3分,共30分):1.下列图形中,是轴对称图形的是( )2.下列各式中,正确的是( )A.3±B.(-3)2=9 C.3-9=-3 D.(-2)2=-29±=3.一个等腰三角形的两边长分别是2cm和5cm,则它的周长为()A.9cm B.12cm C.7cm D.9cm或12cm4.下列各组数是勾股数的是()A.4,5,6 B.6,8,10 C.32,42,52D.7,12,135.如图,在下列条件中,不能..证明△ABD≌△ACD的条件是( )A.∠B=∠C,BD=DC B.∠ADB=∠ADC,BD=DCC.∠B=∠C,∠BAD=∠CAD D.BD=DC,AB=AC6.三角形中到三边距离相等的点是()A.三条边的垂直平分线的交点B.三条高的交点C.三条中线的交点D.三条角平分线的交点7.如图,将△ABC沿直线DE折叠后,使得点B与点A重合.已知AC=5cm,△ADC的周长为17cm,则BC的长为( )A.7cm B.10cm C.12cm D.22cm8.如图,底面周长为12,高为8的圆柱体上有一只小蚂蚁要从A 点爬到B 点,则蚂蚁爬行的最短距离是( ) A .4B .5C .8D .109.已知△ABC 中,AB =17,AC =10,BC 边上的高AH =8,则BC 的长是( ) A .21B .15C .21或15D .21或910.如图是由八个全等的直角三角形拼接而成的,记图中正方形ABCD 、正方形EFGH 、正方形MNKT 的面积分别为1S 、2S 、3S ,若123144S S S ++=,则2S 的值是( ) A .36 cm B .48cm C .54 cm D .64 cm二、填空题(本大题共8小题,每空2分,共18分):11. 49的算术平方根是 ,-27的立方根是 . 12. 若等腰三角形的一个角为80°,则顶角为 . 13.若等腰三角形的腰长为5,底边长为6,则其面积为 。
江苏省无锡市洛社中学2020-2021学年第一学期八年级数学第四周能力训练

江苏省无锡市洛社中学2020-2021学年第一学期八年级数学第四周能力训练一.精心选一选1. 如图,下面有4个汽车标志图案,其中不是轴对称图形的是( )A B C D2. 如图1 所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )A .△ABC 的三条中线的交点B .△ABC 三边的中垂线的交点 C .△ABC 三条角平分线的交点D .△ABC 三条高所在直线的交点3. 如图所示的正方形网格中,网格线的交点称为格点.已知A 、B 是两格点,如果C 也是图中的格点,且使得ABC 为等腰三角形.....,则点C 的个数是( ) A .6 B .7 C .8 D .94. .如图,AD 是△ABC 的角平分线,DF ⊥AB ,垂足为F ,DE=DG ,△ADG 和△AED 的面积分别为20和9,则△EDF 的面积为:( )A 、11B 、5.5C 、7D 、3.55.如图,△ABC 的周长为30cm ,把△ABC 的边AC 对折,使顶点C 和点A 重合,折痕交BC 边于点D ,交AC 边于点E ,连接AD ,若AE =4cm ,则△ABD 的周长是( ) A .22cm B .20 cm C .18cm D .15cm6. 如果一个等腰三角形的一个角为30º,则这个三角形的顶角为( ) A .120º B .30º C .120º或30º D .90º7. 已知:如图,BD 为△ABC 的的角平分线,且BD =BC ,E 为BD 延长线上的一点,BE =BA ,过E 作EF ⊥AB ,F 为垂足.下列结论:①△ABD ≌△EBC ; ②∠BCE +∠BCD =180°; ③AD =AE =EC ;④BA +BC =2BF .其中正确的是( ) A .①②③ B .①③④ C .①②④ D .①②③④第2题 第3题 第4题 第7题8.如图,直线l ∥m ∥n ,等边△ABC 的顶点B 、C 分别在直线n 和m 上,边BC 与直线n 所夹锐角为25°,则∠α的度数为 ( ) A .25° B .45° C .35° D .30°9.如图,AD 平分∠BAC ,EG ⊥AD 于H ,则下列等式中成立的是( )A .∠α=(∠β+∠γ)B .∠α=(∠β﹣∠γ)C .∠G=(∠β+∠γ)D .∠G=∠α10.如图,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图中实线所围成的图形的面积S是()A.50 B.62 C.65 D.68第8题第9题第10题二、用心填一填11. 在Rt△ABC中,CD是中线,且CD=4cm,则AB的长为.12.如图,∠C=90°,∠1=∠2,若BC=10,BD=6,则D到AB的距离为_______.13. 已知等腰三角形的两边长分别是4和6,则第三边的长是14. 已知等腰三角形的顶角为80°,则一个底角的度数是.15. 如图,已知△ABC是等边三角形,点B、C、D、E在同一直线上,且CG=CD,DF=DE,则∠E=°16.如图已知等边△ABC中,点D,E分别在边AB,BC上,把△BDE沿直线DE翻折,使点B落在点Bˊ处,DBˊ,EBˊ分别交边AC于点F,G,若∠ADF=80º,则∠EGC的度数为 ____.第12题第15题第16题17. 如图B、D、F在AN上,C、E在AM上,且AB=BC=CD,EC=ED=EF,∠A=20°,则∠FEM度数是18.已知:在∠ABC中,D是∠ABC平分线上一点,E、F分别在AB、AC上,且DE=DF.则∠BED与∠BFD的关系是_________19.如图,在Rt△ABC中,∠BAC=90°,AB=3,M为边BC上的点,连接AM.如果将△ABM沿直线AM翻折后,点B恰好落在边AC的中点处,那么点M到AC的距离是__________.20.如图,在△ABC中,AC=BC>AB,点P为△ABC所在平面内一点,且点P与△ABC的任意两个顶点构成△PAB,△PBC,△PAC均是等腰三角形,则满足上述条件的所有点P的个数为个.第17题第19题第20题三、耐心解一解21. 如图,在△ABC的一边AB上有一点P.(1)能否在另外两边AC和BC上各找一点M、N,使得△PMN的周长最短.若能,请画出点M、N的位置,若不能,请说明理由;22.如图:△AB C中,AB=AC=5,AB的垂直平分线DE交AB、AC于E、D,(2)若∠ABD=∠DBC,求∠A的度数.23.如图所示a∥b∥c,小明在这一组平行线中进行如下操作:过点A作AM⊥b于M,作∠MAN=60°,且AN=AM,过点N作CN⊥AN,交直线c于点C,在直线b上取点B使BM=CN,那么小明所作的△ABC是等边三角形吗?请说明理由?bc24.如图,在等腰△ABC 中,顶角的平分线BD 交AC 于点D ,AD=3,作△ABC 的高AE 交CB 的延长线于点E ,且AE 与BC 的长是方程组55101,10552x y m x y m +=-⎧⎨-=-⎩的解.已知()1205ABCm m S=≠,求△ABC 的周长.25.如图,直线a 、b 相交于点A ,C 、E 分别是直线b 、a 上两点且BC ⊥a ,DE ⊥b ,点M 、N 是EC 、DB 的中点.求证: MN ⊥BD26. 已知,△ABC 中,AC=BC ,∠ACB=90°,D 为AB 的中点,若E 在直线AC 上任意一点,DF ⊥DE ,交直线BC 于F 点.G 为EF 的中点,延长CG 交AB 于点H .若E 在边AC 上. (1)试说明DE=DF ; (2)试说明CG=GH ;27.一节数学课后,老师布置了一道课后练习题:如图,已知在Rt △ABC 中,AB=BC ,∠ABC =90°,O 为AC 中点.(1)如图1,若把三角板的直角顶点放置于点O ,两直角边分别与AB 、BC 交于点M 、N ,求证:BM=CN ;(2)若点P 是线段AC 上一动点,在射线BC 上找一点D ,使PD=PB ,再过点D 作BO 的平行线,交直线AC 于一点E ,试在备用图上探索线段ED 和OP 的关系,并说明理由.28.如图,已知∠AOB =120°,OM 平分∠AOB ,将等边三角形的一个顶点P 放在射线OM 上,两边分别与OA 、OB 交于点C 、D .(1)如图1,当三角形绕点P 旋转到PC ⊥OA 时,则有结论:①CP =PD ②CO +DO =OP (2)如图2,当三角形绕点P 旋转到PC 与OA 不垂直时,(1)中的两个结论还成立吗?并说明理由.图2D CGB HOAPM D C GA OHPM29.数学课上,李老师出示了如下框中的题目.A小敏与同桌小聪讨论后,进行了如下解答: (1)特殊情况,探索结论当点E为AB 的中点时,如图1,确定线段AE 与DB 的大小关系,请你直接写出结论: AE DB (填“>”,“<”或“=”).CDD(2)特例启发,解答题目解:题目中,AE 与DB 的大小关系是:AE DB (填“>”,“<”或“=”).理由如下:如图2,过点E 作//EF BC ,交AC 于点F . (请你完成以下解答过程)(3)拓展结论,设计新题在等边三角形ABC 中,点E 在直线AB 上,点D 在直线BC 上,且ED EC =.若ABC ∆的边长为1,2AE =,则CD 的长为 (请你直接写出结果).。
人教版初中数学八年级上册期中模拟试题(一)2020年秋

2020年秋绵阳外国语学校人教版初中八年级数学上册期中试题(附答案)一、选择题(每小题3分,共30分)1.(2020独家原创试题)2020年的春节,对于所有人来说真的不一般.为了打好疫情攻坚战,医护人员在岗位上同时间赛跑,与病魔较量,而我们每个人都能为打赢这场仗贡献一份力量.勤洗手,戴口罩,少聚会,积极配合防控工作,照顾好自己和家人,还有,说出一句简单的:中国加油,武汉加油.在“中国加油”这4个汉字中,不可以看作轴对称图形的个数为 ()A.1B.2C.3D.42.(2019山东济宁邹城期中)如图,将△ABC的三个顶点坐标的横坐标都乘-1,并保持纵坐标不变,则所得图形与原图形的关系是 ()A.关于x轴对称B.关于y轴对称C.将原图形沿x轴的负方向平移了1个单位D.将原图形沿y轴的负方向平移了1个单位3.已知等腰三角形的周长为17 cm,一边长为4 cm,则它的腰长为 ()A.4 cmB.6.5 cmC.6.5 cm或9 cmD.4 cm或6.5 cm4.如图,已知∠1=∠2,下列添加的条件不能使△ADC≌△CBA的是 () A.AB∥DCB.AB=CDC.AD=BCD.∠B=∠D5.如图,在△ABC中,∠C=90°,∠A=30°,AB的垂直平分线分别交AB,AC于点D,E,则下列结论正确的是 ()A.AE=3CEB.AE=2CEC.AE=BDD.BC=2CE6.如图,在△ABC中,AB=AC,D为BC边上一点,E点在AC边上,AD=AE,若∠BAD=24°,则∠EDC= () A.24° B.20° C.15° D.12°7.如图,正五边形ABCDE中,直线l过点B,且l⊥ED,下列说法:①l是线段AC的垂直平分线;②∠BAC=36°;③正五边形ABCDE有五条对称轴.其中说法正确的是 ()A.①②B.①③C.②③D.①②③8.如图,等腰△ABC中,AB=AC,∠A=36°.用尺规作图作出线段BD,则下列结论错误的是 ()A.AD=BDB.∠DBC=36°C.S△ABD=S△BCDD.△BCD的周长=AB+BC9.如图,在四边形ABCD中,BC∥AD,CD⊥AD,P是CD边上的动点,要使PA+PB的值最小,则点P应满足的条件是 ()A.PB=PAB.PC=PDC.∠APB=90°D.∠BPC=∠APD10.如图,已知△ABC和△CDE都是等边三角形,且A、C、E三点共线.AD 与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:①AD=BE;②∠AOB=60°;③AP=BQ;④△PCQ是等边三角形;⑤PQ∥AE.其中正确结论的个数是 ()A.5B.4C.3D.2二、填空题(每小题3分,共24分)11.(2019四川资阳中考)若正多边形的一个外角是60°,则这个正多边形的内角和是.12.图①是一张Rt△ABC纸片,如果用两张相同的这种纸片恰好能拼成一个正三角形,如图9②,那么在Rt△ABC中,BC=6,则AB=.13.如图,∠A=∠D,要使△ABC≌△DBC,还需要补充一个条件:(填一个即可).14.如图,在直角坐标系中,AD是Rt△OAB的角平分线,已知点D的坐标是(0,-4),AB的长是12,则△ABD的面积为.15.我们规定:等腰三角形的顶角与一个底角度数的比值叫做等腰三角形的“特征值”,记作k.若k=2,则该等腰三角形的顶角为度.16.如图,已知△ABC关于直线y=1对称,C到AB的距离为2,AB的长为6,则点A、点B的坐标分别为.17.(2019江苏南通中考)如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF,若∠BAE=25°,则∠ACF=度.18.在△ABC中,AH是BC边上的高,若CH-BH=AB,∠ABH=70°,则∠BAC=.三、解答题(共66分)19.(6分)如图,学校要在两条小路OM和ON之间的S区域修建一处“英语角”,按照设计要求,英语角C到两栋教学楼A、B的距离必须相等,到两条小路的距离也必须相等,则英语角C应修建在什么位置?请在图上标出它的位置.(尺规作图,保留痕迹)20.(6分)如图,在平面直角坐标系中,A(-3,2),B(-4,-3),C(-1,-1).(1)在图中作出△ABC关于y轴对称的△A1B1C1;(2)写出点A1,B1,C1的坐标(直接写答案):A1;B1;C1;(3)△A1B1C1的面积为;(4)在y轴上画出点P,使PB+PC最小.21.(2019四川眉山中考)(7分)如图,在四边形ABCD中,AB∥DC,点E是CD 的中点,AE=BE.求证:∠D=∠C.22.(7分)如图,在△ABC中,AB=AC,BE平分∠ABC交AC于点E,过点E作EF∥BC交AB于点F,D是BC边上的中点,连接AD.(1)若∠BAD=55°,求∠C的度数;(2)猜想FB与FE的数量关系,并证明你的猜想.23.(8分)如图,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC的中点,CE⊥AD 于E,BF∥AC交CE的延长线于F.(1)求证:△ACD≌△CBF;(2)连接DF,求证:AB垂直平分DF.24.(10分)定义:如果一个三角形的一个内角等于另一个内角的两倍,则称这样的三角形为“倍角三角形”.(1)如图①,△ABC中,AB=AC,∠A=36°,求证:△ABC是倍角三角形;(2)如图②,△ABC的外角平分线AD与CB的延长线相交于点D,延长CA 到点E,使得AE=AB,若AB+AC=BD,请你找出图中的倍角三角形,并进行证明.25.(10分)数学课上,王老师出示了下面的题目:在△ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,试确定线段AE与DB的大小关系.小明与同桌小聪讨论后,进行了如下解答.(1)特殊情况,探索结论:在等边三角形ABC中,当点E为AB的中点时,点D在CB的延长线上,且ED=EC,如图①,确定线段AE与DB的大小关系,请你直接写出结论;(2)特例启发,解答题目:王老师给出的题目中,AE与DB的大小关系是.理由如下:如图②,过点E作EF∥BC,交AC于点F.(请你完成以下解答过程)26.(12分)如图,已知△ABC中,AB=AC=12厘米,BC=9厘米,点D为AB的中点.(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,1秒钟时,△BPD与△CQP 是否全等?请说明理由;②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD≌△CPQ?(2)若点Q以②的运动速度从点C出发,点P以原来的运动速度从点B 同时出发,都逆时针沿△ABC的三边运动,求多长时间点P与点Q第一次在△ABC的哪条边上相遇参考答案1. 答案 C “中国加油”这4个汉字中,不可以看作轴对称图形的汉字有“国”“加”“油”,共三个,故选C.2. 答案 B 将△ABC 的三个顶点坐标的横坐标都乘-1,纵坐标不变,则横坐标互为相反数,纵坐标相等,所得图形与原图形关于y 轴对称,故选B.3. 答案 B 若4 cm 是腰长,则底边长为20-4-4=12(cm),∵4+4<12,不能组成三角形,∴舍去;若4 cm 是底边长,则腰长为 =6.5(cm).故它的腰长为6.5 cm.故选 B.4. 答案 B A.由AB ∥CD ,可得∠DCA =∠CAB ,又因为∠1=∠2,AC =AC ,故能判定△ADC ≌△CBA ,故选项A 不符合题意;B.由AB =CD ,∠1=∠2,AC =AC ,不能判定 △ADC ≌△CBA ,故选项B 符合题意;C.由AD =BC ,∠1=∠2,AC =AC ,能判定△ADC≌△CBA ,故选项C 不符合题意;D.由∠D =∠B ,∠1=∠2,AC =AC ,能判定△ADC 17-42≌△CBA,故选项D不符合题意.故选B.5.答案B连接BE,∵DE垂直平分AB,∴AE=BE,∴∠ABE=∠A=30°,∴∠CBE=∠ABC-∠ABE=30°.在Rt△BCE中,BE=2CE,∴AE=2CE,故选B. 6.答案D∵∠ADC是△ABD的外角,∴∠ADC=∠B+∠BAD=∠B+24°,∵∠AED是△CDE的外角,∴∠AED=∠C+∠EDC,∵AB=AC,AD=AE,∴∠B=∠C,∠ADE=∠AED,∴∠C+∠EDC=∠ADC-∠EDC=∠B+24°-∠EDC,解得∠EDC=12°.故选D7.答案D∵正五边形ABCDE中,直线l过点B,且l⊥ED,∴l是线段AC的垂直平分线,∠BAC=36°,∴①②正确;正五边形ABCDE有五条对称轴,③正确.故选D.8.答案C∵等腰△ABC中,AB=AC,∠A=36°,∴∠ABC=∠ACB=72°,由作图痕迹可知BD平分∠ABC,∴∠A=∠ABD=∠DBC=36°,∴AD=BD,故A,B结论正确;∵AD≠CD,∴S△ABD=S△BCD错误,故C结论错误;△BCD的周长=BC+CD+BD=BC+AC=BC+AB,故D结论正确.故选C.9.答案D如图所示,作点A关于CD的对称点A',连接A'B,交CD于点P,连接AP,则PA+PB的最小值为A'B的长,点P即为所求.∵点A'与点A关于CD对称,∴∠APD=∠A'PD,∵∠BPC=∠A'PD,∴∠BPC=∠APD,故D符合题意.由图可知,选项A和选项B不成立,而C只有在PC=BC时才成立,故选项C不一定成立.故选D.10.答案A①∵△ABC和△CDE为等边三角形,∴AC=BC,CD=CE,∠BCA=∠DCE=60°,∴∠ACD=∠BCE.在△ACD和△BCE中,AC=BC,∠ACD=∠BCE,CD=CE,∴△ACD≌△BCE(SAS),∴AD=BE,∠ADC=∠BEC,①正确.②∵∠ACB=∠DCE=60°,∴∠BCD=60°,∵△DCE是等边三角形,∴∠EDC=60°=∠BCD,∴BC∥DE,∴∠CBE=∠DEO,∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°,②正确.④在△CDP和△CEQ中,∠ADC=∠BEC,CD=CE,∠DCP=∠ECQ,∴△CDP≌△CEQ(ASA).∴CP=CQ,∴∠CPQ=∠CQP=60°,△PCQ是等边三角形,④正确.⑤∵∠CPQ=∠CQP=60°,∴∠QPC=∠BCA,∴PQ ∥AE ,⑤正确.③同④得△ACP ≌△BCQ (ASA),∴AP =BQ ,③正确.故选A.11. 答案 720°解析 这个正多边形的边数为360°÷60°=6,则这个正多边形的内角和为(6-2)×180°=720°.12. 答案 12解析 由题意得AB =2BC =12.13. 答案 ∠ABC =∠DBC 或∠ACB =∠DCB解析 ∵∠A =∠D ,BC =BC ,∴当∠ABC =∠DBC 或∠ACB =∠DCB 时,△ABC ≌△DBC (AAS),∴还需要补充一个条件为∠ABC =∠DBC 或∠ACB =∠DCB .14. 答案 24解析 如图,作DE ⊥AB 于E ,∵点D 的坐标是(0,-4),∴OD =4,∵AD 是Rt △OAB 的角平分线,∴DE =OD =4,∴S △ABD = ×12×4=24.15. 答案 90解析 ∵k =2,∴设该等腰三角形的顶角=2α,则底角=α,∴α+α+2α=180°,12∴α=45°,∴该等腰三角形的顶角为90°.16. 答案 (2,-2),(2,4)解析 由题意可得点A 、B 的连线与直线y =1垂直,且两点到直线y =1的距离相等,∵AB =6,∴A 、B 两点的纵坐标分别为-2和4,又∵C 到AB 的距离为2,∴A 、B 两点的横坐标都为2.∴A 、B 两点的坐标分别为(2,-2),(2,4).17. 答案 70解析 在Rt △ABE 与Rt △CBF 中, ∴Rt △ABE ≌Rt △CBF (HL).∴∠BAE =∠BCF =25°.∵AB =BC ,∠ABC =90°,∴∠ACB =45°,∴∠ACF =25°+45°=70°.18. 答案 75°或35°解析 当∠ABC 为锐角时,过点A 作AD =AB ,交BC 于点D ,如图1所示. ∵AB =AD ,∴∠ADB =∠ABH =70°,BH =DH .∵CH -BH =AB ,∴AB +BH =CH ,又∵CH =CD +DH ,∴CD =AB =AD ,∴∠C = ∠ADB =35°,,,AE CF AB BC =⎧⎨=⎩∴∠BAC =180°-∠ABH -∠C =75°.当∠ABC 为钝角时,作AH ⊥BC ,交CB 的延长线于H , 如图2所示.∵CH -BH =AB ,∴AB +BH =CH ,又∵BH +BC =CH ,∴AB =BC ,∴∠BAC =∠ACB = ∠ABH =35°.故∠BAC =75°或35°.图1图2 19. 解析 如图所示,点C 即为英语角应修建的位置. 1220. 解析 (1)△A 1B 1C 1如图所示.(2)(3,2);(4,-3);(1,-1).(3)△A 1B 1C 1的面积=3×5- ×2×3- ×1×5- ×2×3=6.5.故填6.5.(4)如图所示,P 点即为所求.21. 证明 ∵AE =BE ,∴∠EAB =∠EBA , ∵AB ∥DC ,∴∠DEA =∠EAB ,∠CEB =∠EBA ,∴∠DEA =∠CEB ,∵点E 是CD 的中点,∴DE =CE . 在△ADE 和△BCE 中, 121212∴△ADE ≌△BCE (SAS),∴∠D =∠C .22. 解析 (1)∵AB =AC ,∴∠C =∠ABC ,∵BD =CD ,AB =AC ,∴AD ⊥BC ,∴∠ADB =90°,∵∠BAD =55°,∴∠C =∠ABC =90°-55°=35°.(2)FB =FE .证明:∵BE 平分∠ABC ,∴∠ABE =∠CBE = ∠ABC ,∵EF ∥BC ,∴∠FEB =∠CBE ,∴∠FBE =∠FEB ,∴FB =FE .23. 证明 (1)∵BF ∥AC ,∴∠ACB +∠CBF =180°,又∵∠ACB =90°,∴∠CBF =90°,又∵CE ⊥AD ,∴∠CAE +∠ACF =∠ACF +∠ECD =90°,∴∠CAE =∠ECD ,即∠DAC =∠FCB .,,,DE CE DEA CEB AE BE =⎧⎪∠=∠⎨⎪=⎩12在Rt △ACD 和Rt △CBF 中, ∴△ACD ≌△CBF .(2)由(1)得CD =BF ,∵D 为BC 的中点,∴CD =BD ,∴BF =BD .∵△ABC 为等腰直角三角形,∴∠CBA =45°,∵∠CBF =90°,∴∠FBA =45°,∴∠CBA =∠FBA ,∴BA 平分∠CBF .根据等腰三角形“三线合一”的性质得AB 垂直平分DF24. 解析 (1)证明:∵AB=AC,∴∠B=∠C,∵∠A+∠B+∠C=180°,∠A=36°,∴∠B=∠C=72°,∴∠C=2∠A,即△ABC 是倍角三角形.(2)△ADC 是倍角三角形.证明:∵AD 平分∠BAE,∴∠BAD=∠EAD,∵AB=AE,AD=AD,∴△ABD ≌△AED(SAS),∴∠ADE=∠ADB,BD=DE.又∵AB +AC =BD ,90?,,,ACD CBF AC BC DAC FCB ∠=∠=⎧⎪=⎨⎪∠=∠⎩∴AE +AC =BD ,即CE =BD .∴CE =DE .∴∠C =∠BDE =2∠ADC .∴△ADC 是倍角三角形.25. 解析 (1)AE =DB .(2)AE =DB .补充的过程如下:∵△ABC 为等边三角形,∴∠AFE =∠ACB =∠ABC =60°,△AEF 为等边三角形, ∴∠EFC =∠EBD =120°,EF =AE ,∵ED =EC ,∴∠EDB =∠ECB ,∠ECB =∠FEC ,∴∠EDB =∠FEC .在△BDE 和△FEC 中, ∴△BDE ≌△FEC (AAS),∴BD =EF ,∴AE =BD26. 解析 (1)①全等.理由如下:当点P 与点Q 运动1秒时,BP=CQ=3厘米.∵AB=12厘米,D 为AB 的中点,∴BD=6厘米.又∵PC=BC -BP=9-3=6(厘米),∴PC=BD.∵AB=AC,∴∠B=∠C.在△BPD 与△CQP 中,,,,EBD EFC EDB FEC ED EC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BPD ≌△CQP (SAS).②若点Q 与点P 的运动速度不相等,要使△BPD ≌△CPQ ,只能BP =CP =4.5厘米,BD =CQ =6厘米.∴点P 的运动时间t = = =1.5(秒),此时v Q = = =4(厘米/秒).(2)因为v Q >v P ,所以只能是点Q 追上点P ,即点Q 比点P 多走AB +AC 的路程.设经过x 秒后P 与Q 第一次相遇,依题意得4x =3x +2×12,解得x =24.此时点P 运动了24×3=72(厘米).又∵△ABC 的周长为33厘米,72=33×2+6,∴点P 、Q 在BC 边上相遇,故经过了24秒,点P 与点Q 第一次在BC 边上相遇.,,,BP CQ B C BD PC =⎧⎪∠=∠⎨⎪=⎩3BP4.53CQ t 61.5。
无锡市太湖格致中学2020-2021学年八年级上学期期中数学试题
即 x2 8x 14 = x2 2x 4
x5
5
解得, 3 ,即 OF 的长为 3 .…………………………………………………(12 分)
∠BAC=∠FCD∠ABC=∠CDFAC=CF, ∴△ABC≌△CDF(AAS), ∴FD=BC=2, 故答案为 2;……………………………………………………………………………(4 分) (2)如图 2 中,过点 E 作 EH⊥CF 于 H.由 OF=x,则 OC=4-x.
①在 Rt△OCB 中, OB2 OC 2 BC 2 (4 x)2 22 x2 8x 14
∠B=∠C AB=DC ∠BAD=∠CDE
∴△ABD≌△DCE(ASA);…………………………………………………(6 分) (3)能,当∠BAD=15°或 30°时,△ADE 能成为等腰三角形. 理由:①当∠BAD=15°时, ∵∠B=∠C=50°, ∴∠BAC=80°, ∵∠ADE=50°,∠BAD=15°, ∴∠DAE=65°, ∴∠AED=180°−50°−65°=65°, ∴DA=DE, ∴△ADE 为等腰三角形; ②当∠BAD=30°时, ∵∠B=∠C=50°, ∴∠BAC=80°, ∵∠ADE=50°,∠BAD=30°,∠DAE=50°, ∴EA=ED,
16. 24
17. 11
18. 8
三、解答题 (本大题共 6 小题,共 56 分.)
8.C 15.120
19.(1)画出 ABC 关于直线 l 的对称 A1 B1C1 ……(3 分)
(2)4 个…………(6 分)
(3)画出点 Q…………(9 分)
2020.10 9.C 10.B
20.证明:(1)∵AB∥CD, ∴∠B=∠C,……………………………………(3 分) 在△ABF 和△DCE 中,
2020年人教版八年级数学上册期中检测卷(含答案)

2020年人教版八年级数学上册期中检测卷时间:90分钟满分:100分一、选择题(每题3分,共30分)1.下面四个图形分别是绿色食品、节水、节能和低碳标志,其中是轴对称图形的是()A B CD2.一个正多边形的内角和为540°,则这个正多边形的每一个外角等于()A.108°B.90°C.72°D.60°3.已知在△ABC中,∠B=∠C,与△ABC全等的三角形有一个角是100°,则△ABC中与这个100°角对应相等的角是()A.∠AB.∠BC.∠CD.∠B或∠C4.将一副直角三角尺按如图所示的位置放置,使含30°角的三角尺的一条直角边和含45°角的三角尺的一条直角边放在同一条直线上,则∠α的度数是() A.45° B.60° C.75° D.85°第4题图第6题图5.下列说法:①两条直角边对应相等的两个直角三角形全等;②斜边对应相等的两个等腰直角三角形全等;③一条直角边和斜边上的高对应相等的两个直角三角形全等;④一条边相等的两个等腰直角三角形全等.其中正确的有() A.1个 B.2个 C.3个 D.4个=10,DF=2,AC=4,则6.如图,AD平分∠BAC交BC于点D,DE⊥AB于点E,DF⊥AC于点F.若S△ABCAB的长是() A.5 B.6 C.7 D.8BC的长为半径画弧,两弧相7.如图,在△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于12交于M,N两点;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为() A.90° B.95° C.100° D.105°第7题图第8题图8.如图,AD⊥CD,AE⊥BE,垂足分别为D,E,且AB=AC,AD=AE,则下列结论:①△ABE≌△ACD;②AM=AN;③△ABN≌△ACM;④BO=EO.其中正确的有()A.1个B.2个C.3个D.4个9.如图,把△ABC沿EF对折,点B,C分别落在点B',C'处,若∠A=60°,∠1=95°,则∠2的度数为() A.24° B.25° C.30° D.35°第9题图第10题图10.如图,在△ABC中,∠ACB=90°,以AC为一边在△ABC外侧作等边三角形ACD,过点D作DF⊥AC于点F,延长DF交AB于点E,AB=15 cm,BC=9 cm,P是射线DE上一点,连接PC,PB,则△PBC的周长的最小值为()A.21 cmB.22 cmC.24 cmD.27 cm二、填空题(每题3分,共18分)11.从长度分别为2,5,6,8的四条线段中任选三条,可构成个不同的三角形.12.若点A(1+m,1-n)与点B(-3,2)关于y轴对称,则m+n的值是 .13.如图,已知AD是△ABC的中线,BE是△ABD的中线,若△ABC的面积为18,则△ABE的面积为.第13题图第14题图第16题图14.如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.若BF=AC,则∠ABC 的度数为.15.有一三角形纸片ABC,∠A=80°,点D是AC边上一点,沿BD方向剪开三角形纸片后,发现所得两纸片均为等腰三角形,则∠C的度数为.16.如图,等边三角形A1C1C2的周长为1,过点C1作C1D1⊥A1C2于点D1,在C1C2的延长线上取点C3,使D1C3=D1C1,连接D1C3,以C2C3为边作等边三角形A2C2C3;过点C2作C2D2⊥A2C3于点D2,在C2C3的延长线上取点C4,使D2C4=D2C2,连接D2C4,以C3C4为边作等边三角形A3C3C4……且点A1,A2,A3,…都在的周长和直线C1C2的同侧,如此下去,则△A1C1C2,△A2C2C3,△A3C3C4,…,△A n C n C n+1为.(n≥2,且n为整数)三、解答题(共52分)17.(6分)如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-3,2),B(-1,4),C(0,2). (1)画出△ABC关于y轴对称的△A1B1C1,并直接写出点A1,B1,C1的坐标;(2)若将△ABC三个顶点的纵坐标分别乘以-1,横坐标不变,将所得的三个点用线段顺次连接,得到的三角形与△ABC的位置关系是.18.(8分)如图,在锐角三角形ABC中,直线l为BC的垂直平分线,射线BM平分∠ABC,且与l相交于点P.若∠A=60°,∠ACP=24°,求∠ABP的度数.19.(8分)如图,AD是△ABC的外角∠EAC的平分线,AD∥BC.(1)求证:△ABC是等腰三角形;(2)当∠CAE等于多少度时,△ABC是等边三角形?证明你的结论.20.(8分)如图,AO,BO,CO,DO分别是四边形ABCD四个内角的平分线.(1)判断∠AOB与∠COD有怎样的数量关系,为什么?(2)若∠AOD=∠BOC,则AB,CD有怎样的位置关系?为什么?21.(10分)如图,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC的中点,CE⊥AD于点E,BF∥AC交CE 的延长线于点F,连接DF.(1)求证:△ACD≌△CBF;(2)求证:AB垂直平分DF.22.(12分)已知△ABC中,AC=BC,∠C=120°,D为AB边的中点,∠EDF=60°,DE,DF分别交AC,BC 于点E,F.(1)如图1,若EF∥AB,求证:DE=DF;(2)如图2,若EF与AB不平行,则(1)中的结论是否仍成立?请说明理由.参 考 答 案 与 解 析期中检测卷题号12345678910答案 A C A C C B D C B C11.2 12.1 13.4.5 14.45° 15.40°或25°或10° 16.2n -12n -1 1.A2.C 【解析】 设此正多边形为正n 边形,根据题意,得(n-2)×180°=540°,解得n=5,所以这个正多边形的每一个外角等于360°5=72°.故选C .3.A 【解析】 在△ABC 中,∠B=∠C ,∴∠B ,∠C 不可能等于100°,∴△ABC 中与这个100°角对应相等的角是∠A.故选A .4.C 【解析】 如图,∠ACD=90°,∠F=45°,∴∠CGF=45°,∴∠DGB=45°,∴∠α=∠D+∠DGB=30°+45°=75°.故选C .5.C 【解析】 ①利用“SAS ”可判定两条直角边对应相等的两个直角三角形全等;②利用“ASA ”可判定斜边对应相等的两个等腰直角三角形全等;③利用“HL ”和“ASA ”可判定一条直角边和斜边上的高对应相等的两个直角三角形全等;④一条边相等的两个等腰直角三角形不一定全等.故选C .6.B 【解析】 ∵AD 平分∠BAC ,DE ⊥AB ,DF ⊥AC ,∴DE=DF=2.∵S △ABC=S △ABD+S △ACD,∴10=12AB×DE+12AC ×DF ,即10=12AB ×2+12×4×2,∴AB=6.故选B .7.D 【解析】 ∵CD=AC ,∠A=50°,∴∠ADC=∠A=50°.根据题意,得MN 是BC 的垂直平分线,∴CD=BD ,∴∠BCD=∠B=12∠ADC=25°,∴∠ACB=180°-∠A-∠B=105°.故选D .8.C 【解析】 ∵AD ⊥CD ,AE ⊥BE ,∴∠D=∠E=90°.在Rt △ABE 和Rt △ACD 中,{AB =AC,AE =AD, ∴Rt △ABE ≌Rt △ACD (HL),故①正确.由Rt △ABE ≌Rt △ACD ,得∠B=∠C.在△ABN 和△ACM 中,{∠BAN =∠CAM,AB =AC,∠B =∠C,∴△ABN ≌△ACM (ASA),∴AM=AN ,故②③正确.由已知条件无法得出BO=EO ,故④错误.故选C .9.B 【解析】 ∵∠A=60°,∴∠AEF+∠AFE=180°-60°=120°,∴∠FEB+∠EFC=360°-120°=240°.由折叠,可得∠B'EF+∠C'FE=240°,∴∠1+∠2=240°-(∠AEF+∠AFE )=240°-120°=120°,又∠1=95°,∴∠2=120°-95°=25°.故选B .10.C 【解析】 △PBC 的周长为PC+PB+CB ,∵CB 的长为定值,∴当PC+PB 的值最小时,△PBC 的周长最小.∵△ACD 为等边三角形,PF ⊥AC ,∴点A 与点C 关于DE 对称,∴当点P 运动到点E 处时,△PBC 的周长最小,∴△PBC 的周长的最小值为AB+BC=24 cm .故选C .11.2 【解析】 由三角形的三边关系,得选取长度为2,5,6和5,6,8的三条线段可构成三角形,所以可构成2个不同的三角形.12.1 【解析】 ∵点A (1+m ,1-n )与点B (-3,2)关于y 轴对称,∴{1+m =3,1−n =2,解得{m =2,n =−1,∴m+n=2-1=1.13.4.5 【解析】 ∵AD 是△ABC 的中线,∴S △ABD=12S △ABC=9.∵BE 是△ABD 的中线,∴S △ABE=12S △ABD=4.5.14.45° 【解析】 ∵AD ⊥BC ,BE ⊥AC ,∴∠ADC=∠BDF ,∠CAD+∠C=90°,∠FBD+∠C=90°,∴∠CAD=∠FBD.在△ADC 和△BDF 中,{∠CAD =∠FBD,∠ADC =∠BDF,AC =BF,∴△ADC ≌△BDF (AAS),∴AD=BD ,∴△ABD是等腰直角三角形,∴∠ABC=45°.15.40°或25°或10° 【解析】 由题意知△ABD 与△DBC 均为等腰三角形.分情况讨论:①若AB=BD ,则∠ADB=∠A=80°,∴∠BDC=180°-∠ADB=180°-80°=100°,∴∠C=12×(180°-100°)=40°;②若AB=AD ,则∠ADB=12(180°-∠A )=12×(180°-80°)=50°,∴∠BDC=180°-∠ADB=180°-50°=130°,∴∠C=12×(180°-130°)=25°;③若AD=BD ,则∠ADB=180°-2×80°=20°,∴∠BDC=180°-∠ADB=180°-20°=160°,∴∠C=12×(180°-160°)=10°.综上,∠C 的度数为40°或25°或10°. 16.2n -12 【解析】 ∵等边三角形A 1C 1C 2的周长为1,C 1D 1⊥A 1C 2,∴A 1D 1=D 1C 2,∴易证△A 2C 2C 3的周长=12△A 1C 1C 2的周长=12,∴△A 1C 1C 2,△A 2C 2C 3,△A 3C 3C 4,…,△A n C n C n +1的周长分别为1,12,122,…,12n -1,∴△A 1C 1C 2,△A 2C 2C 3,△A 3C 3C 4,…,△A n C n C n +1的周长和为1+12+122+…+12n -1=2n -12n -1. 17.【解析】 (1)△A 1B 1C 1如图所示,A 1(3,2),B 1(1,4),C 1(0,2).(2)关于x 轴对称18.【解析】 ∵BP 平分∠ABC ,∴∠ABP=∠CBP.∵直线l 是线段BC 的垂直平分线, ∴BP=CP ,∴∠CBP=∠BCP ,∴∠ABP=∠BCP.∵∠A+∠ACB+∠ABC=180°,∠A=60°,∠ACP=24°, ∴3∠ABP+24°+60°=180°, ∴∠ABP=32°.19.【解析】 (1)∵AD 平分∠CAE ,∴∠EAD=∠CAD.∵AD ∥BC ,∴∠EAD=∠B ,∠CAD=∠C , ∴∠B=∠C ,∴AB=AC , ∴△ABC 是等腰三角形.(2)当∠CAE=120°时,△ABC 是等边三角形.证明如下: 当∠CAE=120°时,∠BAC=180°-120°=60°, 由(1)知△ABC 是等腰三角形,∴△ABC 是等边三角形.20.【解析】 (1)∠AOB+∠COD=180°.理由如下:如图,∵AO ,BO ,CO ,DO 分别是四边形ABCD 四个内角的平分线,∴∠1=12∠DAB ,∠2=12∠ABC ,∠3=∠ADC ,∠4=12∠BCD , ∴∠1+∠2+∠3+∠4=12(∠DAB+∠ABC+∠ADC+∠BCD )=180°,∴∠AOB+∠COD=180°-(∠1+∠2)+180°-(∠3+∠4)=360°-(∠1+∠2+∠3+∠4)=180°.(2)AB ∥CD.理由如下: 由(1)得∠AOB+∠COD=180°,∴∠AOD+∠BOC=180°. ∵∠AOD=∠BOC ,∴∠AOD=90°. ∴∠OAD+∠ADO=12(∠BAD+∠ADC )=90°, ∴∠BAD+∠ADC=180°, ∴AB ∥CD.21.【解析】 (1)∵∠ACB=90°,CE ⊥AD ,∴∠ACE+∠BCF=90°,∠CAD+∠ACE=90°, ∴∠CAD=∠BCF.∵BF ∥AC ,∴∠ACD+∠CBF=180°,∴∠CBF=90°. 在△ACD 和△CBF 中,{∠CAD =∠BCF,AC =CB,∠ACD =∠CBF,∴△ACD ≌△CBF.(2)由(1)得△ACD ≌△CBF ,∴CD=BF.∵D 为BC 的中点,∴CD=BD ,∴BF=BD ,∴△BFD 为等腰直角三角形.∵∠ACB=90°,CA=CB ,∴∠ABC=45°.∵∠FBD=90°,∴∠ABF=45°.∴∠ABC=∠ABF ,即BA 是∠FBD 的平分线.根据等腰三角形三线合一的性质,得AB 垂直平分DF.22.【解析】 (1)∵AC=BC ,∠C=120°,∴∠A=∠B=30°.∵EF ∥AB ,∴∠FEC=∠A=30°,∠EFC=∠B=30°,∴EC=CF.又AC=BC ,∴AE=BF.∵D 是AB 的中点,∴AD=BD.在△ADE 和△BDF 中,{AE =BF,∠A =∠B,AD =BD,∴△ADE ≌△BDF ,∴DE=DF.(2)(1)中的结论仍成立.理由如下:如图,过点D 作DM ⊥AC 于点M ,DN ⊥BC 于点N ,连接CD.∵AC=BC ,∠C=120°,∴∠A=∠B=30°,∴∠ADM=∠BDN=60°,∴∠MDN=180°-∠ADM-∠BDN=60°.∵AC=BC ,AD=BD ,∴∠ACD=∠BCD ,∴DM=DN.由∠MDN=60°,∠EDF=60°可知:①当点M 与点E 重合时,点N 一定与点F 重合,此时DM=DE ,DN=DF ,∵DM=DN ,∴DE=DF.②当点M 落在点C ,E 之间时,点N 一定落在点B ,F 之间,此时∠EDM=∠EDF-∠MDF=60°-∠MDF ,∠FDN=∠MDN-∠MDF=60°-∠MDF , ∴∠EDM=∠FDN.在△DEM 和△DFN 中,{∠DME =∠DNF,DM =DN,∠EDM =∠FDN,∴△DEM ≌△DFN ,∴DE=DF.③当点M 落在点A ,E 之间时,点N 一定落在点C ,F 之间,此时∠EDM=∠MDN-∠EDN=60°-∠EDN ,∠FDN=∠EDF-∠EDN=60°-∠EDN , ∴∠EDM=∠FDN.在△DEM 和△DFN 中,{∠DME =∠DNF,DM =DN,∠EDM =∠FDN,∴△DEM ≌△DFN ,∴DE=DF.综上,得DE=DF ,即(1)中的结论仍成立.。
