计算题讲解
三大计算逐题讲解

三大计算在生活中的应用一、微积分在生活中的应用微积分是数学中的一个分支,主要研究函数的变化和极限,在生活中有广泛的应用。
1. 物理学:微积分在物理学中有着广泛的应用,可以用来研究物体的运动、力学、热力学等。
例如,微积分可以用来求解牛顿力学中的运动方程,预测物体的运动轨迹。
2. 工程学:微积分在工程学中有着广泛的应用,可以用来设计建筑、制造机器、制作电路板等。
例如,微积分可以用来求解机械力学、电路分析等问题。
3. 计算机科学:微积分在计算机科学中也有着广泛的应用,可以用来处理数据、优化算法、设计程序等。
例如,微积分可以用来求解算法复杂度、优化计算速度等问题。
二、线性代数在生活中的应用线性代数是数学中的一个分支,主要研究向量空间和线性变换,在生活中也有着广泛的应用。
1. 计算机科学:线性代数在计算机科学中有着广泛的应用,可以用来解决数据结构和算法问题。
例如,线性代数可以用来求解哈希表的查找效率、优化动态规划算法等。
2. 物理学:线性代数在物理学中也有着广泛的应用,可以用来研究力学、电磁学、热力学等。
例如,线性代数可以用来求解牛顿力学、量子力学等问题。
3. 工程学:线性代数在工程学中也有着广泛的应用,可以用来设计机器、制造机器、优化生产过程等。
例如,线性代数可以用来求解生产线上的调度问题、优化生产流程等问题。
三、概率论与数理统计在生活中的应用概率论与数理统计是数学中的两个分支,主要研究随机事件和概率分布,在生活中也有着广泛的应用。
1. 统计学:概率论与数理统计在统计学中有着广泛的应用,可以用来研究数据的分布、推断变量的性质等。
例如,概率论可以用来求解置信区间、假设检验等问题。
2. 金融学:概率论与数理统计在金融学中也有着广泛的应用,可以用来预测股票价格、分析投资风险等。
例如,概率论可以用来求解随机变量的期望、方差等问题。
3. 生物学:概率论与数理统计在生物学中也有着广泛的应用,可以用来研究生物进化、种群数量变化等。
微观经济学计算题加答案解析讲解学习

1、假定需求函数为Q=MP -N ,其中M 表示收入,P 表示商品价格,N (N>0)为常数。
求:需求的价格点弹性和需求的收入点弹性。
解 因为Q=MP -N 所以PQ d d =-MNP -N-1,MQ d d =P -N所以N MP MNP Q Q P d d E N N P Q da===⋅-=⋅-=---N 1-N -MNP Q P )-MNP (E m= 1P N -===⋅=⋅---N N N M Q MPMP Q MP Q M Q M d d 2、 假定某消费者的需求的价格弹性E d =1.3,需求的收入弹性E m =2.2 。
求:(1)在其他条件不变的情况下,商品价格下降2%对需求数量的影响。
(2)在其他条件不变的情况下,消费者收入提高5%对需求数量的影响。
解 (1) 由题知E d =1.3所以当价格下降2%时,商需求量会上升2.6%. (2)由于 E m =2.2所以当消费者收入提高5%时,消费者对该商品的需求数量会上升11%。
3、 假定某市场上A 、B 两厂商是生产同种有差异的产品的竞争者;该市场对A 厂商的需求曲线为P A =200-Q A ,对B 厂商的需求曲线为P B =300-0.5×Q B ;两厂商目前的销售情况分别为Q A =50,Q B =100。
求:(1)A 、B 两厂商的需求的价格弹性分别为多少?i. 如果B 厂商降价后,使得B 厂商的需求量增加为Q B =160,同时使竞争对手A 厂商的需求量减少为Q A =40。
那么,A 厂商的需求的交叉价格弹性E AB 是多少? ii. 如果B 厂商追求销售收入最大化,那么,你认为B 厂商的降价是一个正确的选择吗? 解(1)当Q A =50时,P A =200-50=150 当Q B =100时,P B =300-0.5×100=250 所以350150)1(=⋅--=⋅-=A A PA QA dA Q P d d E 5100250)2(=⋅--=⋅-=B B PB QB dBQ P d d E(2) 当Q A1=40时,P A1=200-40=160 且101-=∆A Q 当时,1601=B Q P B1=300-0.5×160=220 且301-=∆B P所以355025030101111=⋅--=⋅∆∆=A B B A AB Q P P Q E (3)∵R=Q B ·P B =100·250=25000 R 1=Q B1·P B1=160·220=35200 R 〈 R 1 , 即销售收入增加∴B 厂商降价是一个正确的选择效用论1、据基数效用论的消费均衡条件若2211P MU P MU ≠,消费者应如何调整两种商品的购买量?为什么?若λ≠i iP MU ,i=1、2有应如何调整?为什么?解:1211p M p M u u ≠,可分为1211p M p M u u >或1211p M p M u u < 当1211p M p M u u >时,说明同样的一元钱购买商品1所得到的边际效用大于购买商品2所得到的边际效用,理性的消费者就应该增加对商品1的购买,而减少对商品2的购买。
负荷计算_例题讲解
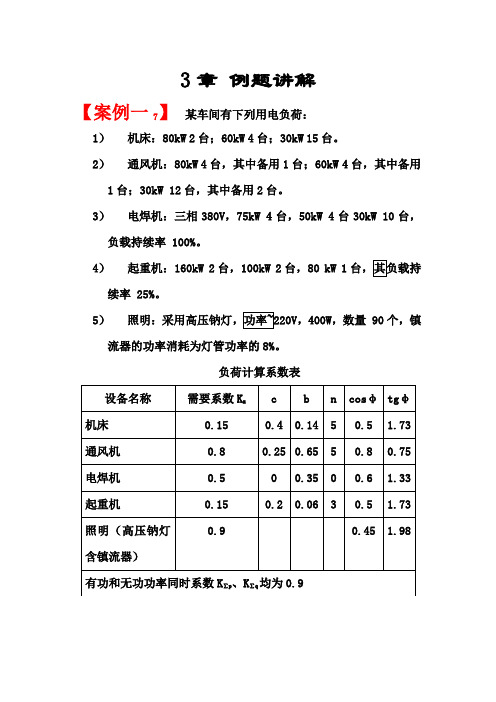
3章例题讲解【案例一7】某车间有下列用电负荷:1)机床:80kW2台;60kW4台;30kW15台。
2)通风机:80kW4台,其中备用1台;60kW 4台,其中备用1台;30kW 12台,其中备用2台。
3)电焊机:三相380V,75kW 4台,50kW 4台30kW 10台,负载持续率 100%。
4)起重机:160kW 2台,100kW 2台,80 kW 1续率 25%。
5),400W,数量 90个,镇流器的功率消耗为灯管功率的8%。
负荷计算系数表负荷。
请回答下列问题:1. 采用需要系数法确定本车间的照明计算负荷,并确定把照明负荷功率因数提高到0.9,计算需要无功功率的补偿容量是多少?(A)58.16kvar (B)52.35 kvar(C)48.47 kvar (D)16.94 kvar答案【 B 】解答过程:依据《配电手册》P2、P3、P21。
气体放电灯的设备功率应计入镇流器损耗,即 P e= 0.4×90×1.08 = 38.88 kW;照明负荷计算功率 P c = K x P e = 0.9×38.88 = 34.99 kW。
功率因数提高到0.9所需的补偿容量 Q C = P c(tgφ1- tgφ2)= 34.99(1.98-0.484)= 52.35 kvar。
2. 采用二项式法计算本车间通风机组的视在功率应为()。
(A) 697.5 kVA (B) 716.2 kVA(C) 720 kVA (D) 853.6 kVA答案【 A 】解答过程:依据《钢铁手册》。
通风机设备功率不应包括备用设备,即P e = 80×3 + 60×3 + 30×10 = 720 kW;最大5台设备功率之和P5 = 80×3 + 60×2 = 360 kW。
二项式法计算功率P c= cP5+ bP c =0.25×360 + 0.65×720 = 558 kW;Q c = P c tg φ = 558×0.75 = 418.5 kvar ; S c = =+=+22225.418558c c Q P 697.5 kVA 。
六年级利息问题练习题讲解

六年级利息问题练习题讲解利息问题是数学中常见的应用题型之一,在实际生活中也会经常遇到。
六年级的学生需要学会如何计算利息问题,下面我将为大家详细讲解一些典型的利息问题练习题。
题目一:小明借给小红1000元,月利率为2%,求1年后小红应还给小明多少钱?解析:由题可知,小明借给小红1000元,月利率为2%,1年有12个月。
我们可以通过计算每个月的利息数来得到小红应该还给小明的总金额。
首先,计算第一个月的利息数:利息 = 1000元 × 2% = 20元小红第一个月应该还给小明的金额为:1000元 + 20元 = 1020元接下来,计算第二个月的利息数:利息 = 1020元 × 2% = 20.4元(取两位小数点后一位四舍五入)小红第二个月应该还给小明的金额为:1020元 + 20.4元 = 1040.4元(取两位小数点后一位四舍五入)同样地,我们可以继续计算出每个月的利息数和还款金额。
最后,小红应还给小明的总金额为 1148.07元(取两位小数点后两位四舍五入)。
题目二:小张将1000元存入银行,年利率为3%,求10年后小张会获得多少利息?解析:将1000元存入银行,年利率为3%。
我们需要计算出10年后小张获得的利息数。
首先,计算每年的利息数:利息 = 1000元 × 3% = 30元由于是连续10年的存款,所以小张会获得10年的利息。
总利息数为:30元 × 10年 = 300元因此,小张将会获得300元的利息。
题目三:甲乙两人分别向银行存款,甲存款1000元,年利率为4%;乙存款2000元,年利率为3%。
请问,两人分别连续存款10年后,谁获得的利息更多?解析:甲存款1000元,年利率为4%;乙存款2000元,年利率为3%。
我们需要计算出甲和乙分别连续存款10年后所获得的利息数。
甲的利息数为:1000元 × 4% × 10年 = 400元乙的利息数为:2000元 × 3% × 10年 = 600元通过比较可以发现,乙获得的利息数更多,因此乙获得的利息更多。
集合的基本运算例题讲解

1集合的基本运算例题讲解题型一 并集运算一般地,由所有属于集合A 或属于集合B 的元素组成的集合,称为集合A 与集合B 的并集,记作B A ,读作“A 并B ”.即{}B x A x x B A ∈∈=或, .求并集的方法(1)求两个有限集的并集 按照并集的定义进行计算,但要特别注意集合元素的互异性.(2)求两个无限集的并集 借助于数轴进行计算.注意两个集合的并集等于这两个集合在数轴上对应的图形所覆盖的全部范围.例1. 已知集合{}31≤≤∈=x N x A ,{}5,4,3,2=B ,则=B A 【 】 (A ){}2 (B ){}3,2(C ){}5,4,3,2 (D ){}5,4,3,2,1 分析:将一个用描述法表示的集合转化为用列举法表示时,一定要弄清代表元素的含义或特征.求两个集合的并集运算时,可以按照并集的定义进行,也可以用Venn 图求解或借助于数轴求解.解:∵{}{}3,2,131=≤≤∈=x N x A∴=B A {}{}{}5,4,3,2,15,4,3,23,2,1= . 选择【 D 】.例2. 已知集合{}1≥=x x A ,{}0322<--=x x x B ,则=B A ____________. 分析:先解一元二次不等式0322<--x x ,求出集合B ,然后把集合A 、B 在数轴上画出来,它们对应图形所覆盖的全部范围即为B A . 解:∵{}{}310322<<-=<--=x x x x x B ∴=B A {}{}{}1311->=<<-≥x x x x x x .例3. 已知集合{}m A ,3,1=,{}m B ,1=,若A B A = ,则m 等于【 】 (A )0或3 (B )0或3 (C )1或3 (D )1或3分析:{}m B ,1=,由集合元素的互异性,得1≠m ,排除C 、D 选项. 因为A B A = ,根据并集的性质,所以A B ⊆,这样就将两个集合的并集运算转化为了这两个集合之间的关系,从而可以确定参数的值或取值范围. 解:∵A B A = ,∴3=m 或m m =当m m =时,解之得:0=m (1=m 不符合题意,舍去) 综上,3=m 或0=m .例 4. 已知集合{}012≤-=x x P ,{}a M =,若P M P = ,则实数a 的取值范围是__________.分析:∵P M P = ,∴P M ⊆. 解:{}{}11012≤≤-=≤-=x x x x P ∵P M P = ,∴P M ⊆,∴P a ∈ ∴实数a 的取值范围是{}11≤≤-a a .例5. 已知集合{}x A ,3,2,1=,{}2,3x B =,且{}x B A ,3,2,1= ,求x 的值. 分析:由题意可知:A B A = ,所以A B ⊆,从而A x ∈2,且32≠x . 解:分为三种情况:①当12=x 时,解之得:1-=x (1=x 不符合题意,舍去); ②当22=x 时,解之得:2±=x ; ③当x x =2时,解之得:0=x . 综上所述,x 的值为0或2±或1-.注意:在求参数的值时,参数的值要满足集合元素的互异性.例6. 已知集合{}32>-=x x A ,{}a x x x B ->-=332,求B A . 分析:对于含参集合参与的集合运算,要注意分类讨论.解:{}{}532>=>-=x x x x A ,{}{}3332-<=->-=a x x a x x x B . 当3-a ≤5,即a ≤8时,{}53>-<=x a x x B A 或 ; 当53>-a 时,即8>a 时,=B A R .a例7.(易错题)已知集合{}1,1-=A ,{}1==mx x B ,且A B A = ,求由m 的取值构成的集合.分析:因为A B A = ,所以A B ⊆.由于集合B 是一个含参集合,所以要对集合B 分∅=B 和∅≠B 两种情况进行讨论. 解:∵A B A = ,∴A B ⊆. 当0=m 时,∅=B ,满足A B ⊆;当0≠m 时,{}11-=⎭⎬⎫⎩⎨⎧==m x x B 或{}1=B :①若{}1-=B ,则11-=m,解之得:1-=m ; ②若{}1=B ,则11=m,解之得:1=m . 综上所述,m 的取值构成的集合为{}1,0,1-.例8. 设集合{}52<<-=x x M ,{}122+<<-=t x t x N ,若M N M = ,则实数t 的取值范围是__________.分析:先将并集运算的结果M N M = 转化为两个集合M , N 之间的关系M N ⊆,从而列出关于参数t 的不等式(组)求解.注意含参集合的分类讨论. 解:∵M N M = ,∴M N ⊆. 分为两种情况:①当∅=N 时,有t -2≥12+t ,解之得:t ≤31;②当∅≠N 时,则有:⎪⎩⎪⎨⎧≤+-≥-+<-51222122t t t t ,解之得:t <31≤2. 综上所述,实数t 的取值范围是{}2≤t t .警示:在解决本题时,任意忽略∅=N 的情况,另外要注意端点值能否取到.例9. 已知集合{}2,1-=A ,{}01>+=mx x B ,若B B A = ,求实数m 的取值范围. 分析:注意本题与例7的区别. 解:∵B B A = ,∴B A ⊆. 分为三种情况:①当0=m 时,01>恒成立,∴{}=>+=01mx x B R ,满足B A ⊆;②当0>m 时,{}⎭⎬⎫⎩⎨⎧->=>+=m x x mx x B 101,有11-<-m ,解之得:1<m∴10<<m ;③当0<m 时,{}⎭⎬⎫⎩⎨⎧-<=>+=m x x mx x B 101,有21>-m ,解之得:21->m∴021<<-m . 综上所述,实数m 的取值范围是⎭⎬⎫⎩⎨⎧<<-121m m .题型二 交集运算一般地,由属于集合A 且属于集合B 的所有元素组成的集合,称为集合A 与集合B 的交集,记作B A ,读作“A 交B ”.{}B x A x x B A ∈∈=且, .求交集的方法(1)求两个有限集的交集 按照交集的定义进行计算,但要特别注意一定要找出两个集合中的所有公共元素.(或可借助于Venn 图)(2)求两个无限集的交集 借助于数轴进行计算.两个集合的解集等于这两个集合在数轴上对应的图形所覆盖的公共范围.例10. 设集合{}01>+∈=x Z x A ,集合{}02≤-=x x B ,则=B A 【 】 (A ){}21<<-x x (B ){}21≤<-x x (C ){}2,1- (D ){}2,1,0分析:在进行集合的运算之前,要先弄清楚各个集合的本质.本题中集合A 的代表元素x 为整数,所以集合A 为1->x 范围内的整数集.解:∵{}{}101->∈=>+∈=x Z x x Z x A ,{}{}202≤=≤-=x x x x B ∴=B A {}{}2,1,021=≤<-∈x Z x . 选择【 D 】.例11. 设集合{}21<≤-=x x A ,{}a x x B <=,若∅≠B A ,则实数a 的取值范围是__________.分析:∅≠B A 说明集合A 、B 有公共元素,在数轴上集合A 、B 所对应的图形覆盖的区域有公共部分. 解:{}1->a a .1例12. 设集合{}52<<-=x x M ,{}122+<<-=t x t x N ,若N N M = ,求实数t 的取值范围.分析:若N N M = ,则由交集的性质知M N ⊆,在得到这两个集合之间的关系后借助于数轴就可以列出不等式(组)进行求解了. 解:∵N N M = ,∴M N ⊆. 分为两种情况:①当∅=N 时,满足M N ⊆,有t -2≥12+t ,解之得:t ≤31;②当∅≠N 时,则有:⎪⎩⎪⎨⎧≤+-≥-+<-51222122t t t t ,解之得:t <31≤2.综上所述,实数t 的取值范围是{}2≤t t .★例13.(易错题)设集合{}R x x y y A ∈+==,12,{}R x x y y B ∈+==,1,则B A 等于【 】(A ){}1≥y y (B ){}2,1 (C )()(){}2,1,1,0 (D )∅错解:解方程组⎩⎨⎧+=+=112x y x y 得:⎩⎨⎧==10y x 或⎩⎨⎧==21y x ,故选【 C 】.错因分析:这里好多学生认为是求抛物线12+=x y 和直线1+=x y 的交点坐标所构成的集合,根源在于没有搞清楚集合A , B 的本质,没有弄清楚集合的代表元素的特征.分析:本题中的两个集合都是由函数值构成的,它们的代表元素是函数值y .B A 表示函数12+=x y 和函数1+=x y 的函数值的交集. 解:∵{}{}1,12≥=∈+==y y R x x y y A ,{}=∈+==R x x y y B ,1R . ∴{} 1≥=y y B A R {}1≥=y y . 选择【 A 】.变式: 设集合(){}1,2+==x y y x A ,(){}1,+==x y y x B ,则B A 等于【 】 (A ){}1≥y y (B ){}2,1 (C )()(){}2,1,1,0 (D )∅例14. 已知集合(){}1,22=+=y x y x A ,集合(){}x y y x B ==,,则B A 中元素的个数为【 】(A )3 (B )2 (C )1 (D )0解:解方程组⎩⎨⎧==+xy y x 122得:⎪⎪⎩⎪⎪⎨⎧==2222y x 或⎪⎪⎩⎪⎪⎨⎧-=-=2222y x ∴B A ⎭⎬⎫⎩⎨⎧⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛=22,22,22,22,共有2个元素.选择【 B 】. 方法二:由后面的学习可以知道,方程122=+y x 是单位圆的方程(以原点为圆心,以1为半径的圆).集合A 是由圆122=+y x 上的所有点构成的,集合B 是由直线x y =上的所有点构成的,所以B A 就是由单位圆与直线的交点构成的,如图所示,交点有两个,故B A 中元素的个数为2.例15.(2018沈阳重点高中)设集合{}52≤≤-=x x A ,{}121-≤≤+=m x m x B . (1)若{}52≤≤-∈=x Z x A ,求A 的非空真子集的个数; (2)若B B A = ,求实数m 的取值范围. 分析:(1)子集、真子集个数的确定 若集合A 含有n 个元素,则集合A : (1)含有n 2个子集; (2)含有12-n 个非空子集; (3)含有12-n 个真子集; (4)含有22-n 个非空真子集.(2)若B B A = ,则A B ⊆,注意分类讨论. 解:(1){}{}5,4,3,2,1,0,1,2-52-=≤≤-∈=x Z x A∵集合A 中含有8个元素∴集合A 的非空真子集的个数为2542-28=; (2)∵B B A = ,∴A B ⊆. 分为两种情况:①当∅=B 时,满足A B ⊆,有121->+m m ,解之得:2<m ; ②当∅≠B 时,则有:⎪⎩⎪⎨⎧≤--≥+-≤+51221121m m m m ,解之得:2≤m ≤3. 综上所述,实数m 的取值范围是{}3≤m m .例16. 设{}042=+=x x x A ,(){}011222=-+++=a x a x x B ,其中∈x R ,如果B B A = ,求实数a 的取值范围. 解:{}{}4,0042-==+=x x x A ∵B B A = ,∴A B ⊆ 分为两种情况:①当∅=B 时,满足B B A =∴()[]()0141222<--+=∆a a ,解之得:1-<a ;②当∅≠B 时,{}0=B 或{}4-=B 或{}4,0-=B .若{}0=B 或{}4-=B ,则有()[]()0141222=--+=∆a a ,解之得:1-=a经检验,此时{}0=B ;若{}4,0-=B ,则由根与系数的关系定理可得:()⎩⎨⎧=--=+-014122a a ,解之得:1=a . 综上所述,实数a 的取值范围是{}11-≤=a a a 或.例17. 设集合{}3+≤≤=a x a x A ,{}51>-<=x x x B 或,若∅=B A ,求实数a 的取值范围.分析:对于任意实数a ,都有3+<a a ,所以本题中集合A 不会是空集. 解:∵3+<a a ,∴∅≠A . ∵∅=B A∴⎩⎨⎧≤+-≥531a a ,解之得:1-≤a ≤2. ∴实数a 的取值范围是{}21≤≤-a a .★★例18.(综合性强)已知集合()(){}011222>++++-=a a y a a y y A ,集合⎭⎬⎫⎩⎨⎧≤≤+-==30,25212x x x y y B ,若∅=B A :(1)求实数a 的取值范围;(2)当ax x ≥+12恒成立时,求a 的最小值.分析:(1)求集合A 时要解含参一元二次不等式,可借助于因式分解:()()()()()()()()()[]11111122222222+--=-+--=++-+-=++++-a y a y a y a a y y a a ay a y y a a y a a y对于集合B ,代表元素是y ,所以集合B 是函数值的集合,通过配方得:()2121252122+-=+-=x x x y ∵0≤x ≤3,∴2≤y ≤4,∴{}42≤≤=y y B ;(2)这是与二次函数有关的恒成立问题,使用数形结合方法.解:(1)()(){}()()[]{}010112222>+--=>++++-=a y a y y a a y a a y y A∵04321122>+⎪⎭⎫ ⎝⎛-=-+a a a (这里作差比较12+a 与a 的大小)∴a a >+12∴{}12+><=a y a y y A 或.{}4230,25212≤≤=⎭⎬⎫⎩⎨⎧≤≤+-==y y x x x y y B∵∅=B A∴⎩⎨⎧≥+≤4122a a ,解之得:a ≤3-或3≤a ≤2. ∴实数a 的取值范围是{}233≤≤-≤a a a 或; (2)∵ax x ≥+12恒成立,即12+-ax x ≥0恒成立. ∴()42--=∆a ≤0,解之得:2-≤a ≤2.∴a 的最小值为2-.(雅慧,通过这道题你勇敢地挑战一下自己)题型三 补集运算全集 一般地,如果一个集合含有我们所研究问题中涉及的所有元素,那么就称这个集合为全集,记作U .补集 对于一个集合A ,由全集U 中不属于A 的所有元素组成的集合称为集合A相对于全集U 的补集,简称集合A 的补集,记作C U A ,即C U A {}A x U x x ∉∈=且,.补集的性质①(C U A )U A = ; ②(C U A )∅=A ; ③ C U (C U A )A =; ④ C U U ∅=; ⑤ C U U =∅.例19. 已知全集{}60<<=x x U ,集合{}a x x A <<=1,若C U A U ≠,则实数a 的取值范围是__________.分析: C U A U ≠说明∅≠A ,且U A ⊆. 解:∵C U A U ≠,∴∅≠A ,且U A ⊆. ∴实数a 的取值范围是{}61≤<a a .例20. 已知全集{}5,4,3,2,1=U ,集合{}042=++=px x x A ,求C U A . 分析:集合A 是由方程042=++px x 的解构成的,而方程042=++px x 可能无解、有两个不相等的实数根或有两个相等的实数根,需要分类讨论. 解:由题意可知:U A ⊆.分为两种情况:①当∅=A 时,方程无实数根,∴0162<-=∆p ,解之得:44<<-p ∴C U A =C U ∅{}5,4,3,2,1==U ;②当∅≠A 时,则有162-=∆p ≥0,解之得:p ≤4-或p ≥4. 设方程042=++px x 的两个实数根分别为21,x x 由根与系数的关系定理可得:421=x x :若4,121==x x ,则5-=p ,符合题意,此时{}4,1=A ,C U A {}5,3,2=; 若221==x x ,则4-=p ,符合题意,此时{}2=A ,C U A {}5,4,3,1=. 综上所述,当44<<-p 时,C U A ={}5,4,3,2,1;当5-=p 时,C U A {}5,3,2=;当4-=p 时,C U A {}5,4,3,1=.例21. 已知{}31≤<-=x x A ,{}m x m x B 31+<≤=. (1)当1=m 时,求B A ;(2)若⊆B C R A ,求实数m 的取值范围.分析:(1)求两个连续型实数集合的并集时,借助于数轴进行求解能将抽象的问题直观化,但要特别注意端点的实心和空心以及端点值的取舍;(2)求连续型实数集合的补集也是借助于数轴进行.解:(1)当1=m 时,{}{}4131<≤=+<≤=x x m x m x B ∴{}{}{}414131<<-=<≤≤<-=x x x x x x B A ; (2)∵{}31≤<-=x x A ,∴C R A {}31>-≤=x x x 或 ∵⊆B C R A ,∴分为两种情况:①当∅=B 时,有m ≥m 31+,解之得:m ≤21-; ②当∅≠B 时,则有:⎩⎨⎧-≤++<13131m m m 或⎩⎨⎧>+<331m mm解之得:无解或3>m .综上,实数m 的取值范围是⎭⎬⎫⎩⎨⎧>-≤321m m m 或.★例22. 设全集(){}R y R x y x I ∈∈=,,,()⎭⎬⎫⎩⎨⎧=--=123,x y y x A ,(){}1,+==x y y x B ,求C I A B .解:()(){}2,1,123,≠+==⎭⎬⎫⎩⎨⎧=--=x x y y x x y y x A ∴集合A 是由直线1+=x y 上除点()3,2外的所有点构成的集合 ∴C I A =(){}3,2 ∵(){}1,+==x y y x B∴集合B 是由直线1+=x y 上所有的点构成的集合 ∴C I A =B (){}3,2. 附:函数123=--x y ,即1+=x y ()2≠x 的图象如图所示.例23. 设全集{}32,3,22-+=a a U ,{}2,12-=a A ,C U A {}5=,求实数a 的值. 分析:∵C U A U ⊆,∴U ∈5,∴5322=-+a a .还要注意U A ⊆. 解:∵{}32,3,22-+=a a U ,C U A {}5= ∴5322=-+a a整理得:0822=-+a a ,解之得:4,221-==a a .U4321B A 852917643B AU当2=a 时,{}3,2=A ,满足题意; 当4-=a 时,{}9,2=A ,不满足题意. 综上,实数a 的值为2.例24. 设全集{}*,10N x x x U ∈<=,U B U A ⊆⊆,,( C U B ){}9,1=A ,{}3=B A , ( C U A ) ( C U B ){}7,6,4=,求集合A , B . 分析:本题条件较多,考查集合的综合运算.重要结论如图所示,集合A , B 将全集U 分成了四部分,这四部分用集合表示如下: (1)①表示B A ; (2)②表示 A (C U B ); (3)③表示 B (C U A ); (4)④表示(C U A ) (C U B ).德·摩根定律(1)C U ()=B A (C U A ) (C U B ); (2)C U ()=B A (C U A ) (C U B ).解法一:{}{}9,8,7,6,5,4,3,2,1*,10=∈<=N x x x U ∵( C U A ) ( C U B ){}7,6,4=,∴C U ()=B A {}7,6,4∴{}9,8,5,3,2,1=B A ∵( C U B ){}9,1=A ∴=B {}8,5,3,2∵{}3=B A ,∴{}9,3,1=A . 解法二:由题意作出Venn 图如图所示:由图可知:{}9,3,1=A ,{}8,5,3,2=B .例25. 已知全集=U R ,集合{}0,,32≠∈-==x R x x y y A 且,集合⎭⎬⎫⎩⎨⎧-+-==x x y x B 522,集合{}a x a x C <<-=5.(1)求集合 A ( C U B );(2)若()B A C ⊆,求实数a 的取值范围.分析:先来确定集合A , B 的本质:集合A 是函数()032≠-=x x y 的函数值构成的集合,即函数()032≠-=x x y 的值域;集合B 是使函数xx y -+-=522有意义的自变量的值构成的集合.解:{}{}{}330,,32<=<=≠∈-==x x y y x R x x y y A 且.{}52522<≤=⎭⎬⎫⎩⎨⎧-+-==x x x x y x B .∴C U B {}52≥<=x x x 或 ∴ A ( C U B ){}53≥<=x x x 或; (2)由(1)可知:{}32<≤=x x B A ∵()B A C ⊆,∴分为两种情况:①当∅=C 时,满足()B A C ⊆,有a -5≥a ,解之得:a ≤25; ②当∅≠C 时,则有:⎪⎩⎪⎨⎧≤≥-<-3255a a aa ,解之得:a <25 ≤3.综上所述,实数a 的取值范围是{}3≤a a .例26. 若{}0232=+-=x x x A ,{}012=-+-=a ax x x B ,{}022=+-=mx x x C ,且C C A A B A == ,,求a 的值和m 的取值范围.分析:设置本题的目的是帮助雅慧复习由集合间的基本关系确定参数的值或取值范围.本题要先将三个集合之间的运算及其结果转化为集合之间的关系:因为C C A A B A == ,,∴A C A B ⊆⊆,.本来由A B ⊆需要对集合B 分两种情况进行讨论,但考虑到集合B 中的方程结构比较复杂,所以先判断一下方程012=-+-a ax x 的根的情况: ∵()()()22224414-=+-=---=∆a a a a a ≥0∴方程012=-+-a ax x 总有两个实数根.也因此,在处理关系A B ⊆时,一定有∅≠B ,不再对集合B 进行分类讨论. 解:{}{}2,10232==+-=x x x A{}()()[]{}011012=---==-+-=a x x x a ax x x B ∴集合B 中必含有元素1,∴∅≠B . ∵A B A = ,∴A B ⊆.①当11=-a ,即2=a 时,{}1=B ,符合题意;②当21=-a ,即3=a 时,{}2,1=B ,符合题意. 综上,a 的值为2或3.∵C C A = ,∴A C ⊆,分为两种情况:①当∅=C 时,满足A C ⊆,有()082<--=∆m ,解之得:2222<<-m ;②当∅≠C 时,则{}1=C 或{}2=C 或{}2,1=C :若{}1=C 或{}2=C ,则()082=--=∆m ,解之得:22±=m .经检验,当22±=m 时,{}2=C 或{}2-=C ,不符合题意,舍去;若{}2,1=C ,则由根与系数的关系定理可得:⎭⎬⎫⎩⎨⎧⨯=+=21221m ,解之得:3=m ,符合题意.综上所述,m 的取值范围是2222<<-m 或3=m .题型四 补集思想的应用(正难则反)对于某些问题,如果从正面求解比较困难,则可考虑先求解问题的反面,采用“正难则反”的解题策略.具体地说,就是将研究对象的全体实为全集,求出使问题反面成立的集合A ,则A 的补集即为所求.补集思想的原理或依据是:C U (C U A )A =.例27. 已知集合{}R x m mx x x A ∈=++-=,06242,{}0<=x x B ,若∅≠B A ,求实数m 的取值范围.分析:集合A 是方程06242=++-m mx x 的实数根构成的集合,∅≠B A 意味着方程有负根,则方程的根有以下三种情况:①两负根;②一负根,一零根;③一负根,一正根.分别求解相当麻烦.如果考虑∅≠B A 的反面∅=B A ,先求方程无实数根或两根均非负时m 的取值范围,然后再用补集思想求解∅≠B A 时m 的取值范围解:若∅=B A ,则分为两种情况:①当∅=A 时,()()062442<+--=∆m m ,解之得:231<<-m ; ②当∅≠A 时,方程06242=++-m mx x 的两个实数根均为非负数,则有:()()⎪⎩⎪⎨⎧≥+≥≥+--=∆06204062442m m m m ,解之得:m ≥23. 综上所述,当1->m 时,∅=B A .∴当∅≠B A 时,实数m 的取值范围是{}1-≤m m .结论:一元二次方程()002≠=++a c bx ax 有两个非负实数根的条件是:⎪⎪⎪⎩⎪⎪⎪⎨⎧≥=⋅≥-=+≥∆0002121ac x x a b x x .例28. 已知集合{}a y a y y A <+>=或12,{}42≤≤=y y B ,若∅≠B A ,求实数a 的取值范围.解:当∅=B A 时,则有:⎩⎨⎧≥+≤4122a a ,解之得:a ≤3-或3≤a ≤2. ∴当∅=B A 时,实数a 的取值范围是{}233≤≤-≤a a a 或. ∴当∅≠B A 时,实数a 的取值范围是{}332<<->a a a 或.例29. 若集合{}0232=++=x ax x A 中至多有1个元素,则实数a 的取值范围是__________.分析:题目要求“至多有1个元素”,若采取分类讨论的方法,求解比较麻烦,可考虑用补集思想解决问题.本题中集合A 至多有1个元素的反面是集合A 有两个元素,即方程0232=++x ax 有两个不相等的实数根.解:当集合A 中有两个元素时,方程0232=++x ax 有两个不相等的实数根,则有:⎩⎨⎧>-=∆≠0890a a ,解之得:89<a 且0≠a ∴集合A 中有两个元素时实数a 的取值范围是⎭⎬⎫⎩⎨⎧≠<089a a a 且.∴集合A 中至多有1个元素时实数a 的取值范围是⎭⎬⎫⎩⎨⎧=≥089a a a 或.总结:求集合运算中参数的思路(1)将集合中的运算关系转化为两个集合之间的关系;(2)将集合之间的关系转化为方程(组)或不等式(组)是否有解、或解集为怎样的范围; (3)解方程(组)或不等式(组)来确定参数的值或取值范围. 题型五 集合中元素的个数若集合A 为有限集,则用card(A )表示集合A 中元素的个数. 如果集合A 中含有m 个元素,那么有card(A )m =. (1)一般地,对于任意两个有限集合A , B ,有 card ()=B A card(A )+card(B )-card ()B A . (2)一般地,对于任意三个有限集合A , B , C ,有card ()=C B A card(A )+card(B )-card ()B A -card ()C A -card ()C B + card ()C B A .。
三年级计算题讲解教案

三年级计算题讲解教案教案标题:三年级计算题讲解教案教案目标:1. 学生能够理解和解决三年级数学计算题;2. 学生能够熟练应用不同的计算方法和策略。
教学准备:1. 教师准备白板、黑板、彩色粉笔或白板笔;2. 教师准备三年级数学教材和练习册;3. 教师准备一些示例计算题。
教学过程:步骤一:导入(5分钟)1. 教师将标题写在黑板上,并询问学生他们对计算题的理解;2. 教师简要介绍本节课的目标和重点。
步骤二:概念讲解(10分钟)1. 教师通过白板或幻灯片展示一些常见的三年级计算题,如加法、减法、乘法和除法;2. 教师解释每个计算题的含义和解题方法;3. 教师引导学生思考和讨论每个计算题的策略和技巧。
步骤三:示范演示(15分钟)1. 教师选择一道加法计算题作为示例,并在黑板上详细演示解题过程;2. 教师解释每个步骤的目的和方法;3. 教师鼓励学生积极参与,提问和回答问题。
步骤四:学生练习(15分钟)1. 教师分发练习册,并要求学生独立完成一些计算题;2. 教师巡视并提供必要的帮助和指导;3. 教师鼓励学生相互合作,互相讨论和解答问题。
步骤五:总结(5分钟)1. 教师与学生一起回顾本节课的内容和重点;2. 教师强调学生在解决计算题时应该注意的事项;3. 教师鼓励学生继续练习和巩固所学知识。
教学延伸:1. 学生可以尝试解决更复杂的计算题,如多步骤的问题或应用题;2. 学生可以通过游戏或竞赛形式进行计算题的练习,增加趣味性和竞争性。
教学评估:1. 教师观察学生在课堂上的参与度和理解程度;2. 教师收集学生完成的练习册,并对学生的答案进行评估;3. 教师可以设计一些小测验或考试来评估学生对计算题的掌握程度。
密度基础计算题分类练习讲解
密度基础计算题分类练习一、同体积问题1、一个容积为2、5升的塑料壶,用它装酒精,最多能装多少克?2、一个瓶子能盛1千克水,用这个瓶子能盛多少千克酒精?3、有一只玻璃瓶,它的质量为0.1kg,当瓶内装满水时,瓶和水的总质量为0.4kg,用此瓶装另一种液体,瓶和液体的质量为0.64kg,求这种液体的密度。
4. 把一块金属放入盛满酒精(ρ酒精=0.8g/cm3)的杯中时,从杯中溢出8g酒精。
若将该金属块放入盛满水的杯中时,从杯中溢出水的质量是多少?5.铸造车间浇铸合金工件,已知所用木模质量为500 g,木料密度为0.7×103 kg/m3.今称得每个合金工件的质量为4.9 kg,则该合金的密度是多少?6.假设钢瓶内储满9千克液化气,钢瓶容积为0。
3m 3,今用去一半,则钢瓶内剩下的液化气密度为多少7、某铜制机件的质量为0.445千克,如改用铝制品质量可减轻多少?8、如图3所示,一只容积为3×10-4m3的瓶内盛有0.2kg的水,一只口渴的乌鸦每次将一块质量为0.01kg的小石块投入瓶中,当乌鸦投入了25块相同的小石块后,水面升到瓶口。
求:(1)瓶内石块的总体积;(2)石块的密度。
9、一个容器盛满水总质量为450g,若将150g小石子投入容器中,溢出水后再称量,其总质量为550g,求:(1)小石子的体积为多大?(2)小石子的密度为多少?10、一空杯装满水的总质量为500克,把一小物块放入水中,水溢出后,杯的总质量为800克,最后把物块取出后,杯的总质量为200克,求此物块的密度是多少?11.某同学没有利用量筒也测出了一满杯牛奶的密度.他的方法是这样的:先用天平测出一满杯牛奶的总质量是120 g,然后测得空杯子的质量是50 g,最后他将该杯装满水,又用天平测得水和杯子的总质量是100 g.请你帮该同学算一算此杯牛奶的密度是多少?二、同质量问题1、体积为 1 m3的冰化成水的体积多大?(ρ冰=0.9×103kg/m3)2、体积为9 m33的水化成冰的体积多大?3、郑小胖家的一只瓶子,买0.5kg酒刚好装满.小胖用这只瓶子去买0.5kg酱油,结果没有装满,小胖以为营业员弄错了.现在请你思考一下,到底是谁弄错了?(通过计算说明)4.质量为9千克的冰块,密度为0.9×103千克/米3.(1)求冰块的体积.(2)若冰块吸热后,有3分米3的冰融化成水,求水的质量.5、学校安装电路需用铜线,现手头有一卷铜线,其质量是178千克,横截面积是 2.5平方毫米,这卷铜线的长度是多少米?(ρ铜=8.9×103千克/米3)6.在一块表面积为6米2的铁件上镀铜后,铁件的质量增加了 1.068千克,求所镀铜的厚度(ρ铜=8.9×103千克/米3)。
高中数学基础运算练习题及讲解
高中数学基础运算练习题及讲解### 高中数学基础运算练习题及讲解#### 一、实数运算练习题1:计算下列表达式的值:\[ 3x^2 - 2x + 1 \]其中 \( x = 2 \)。
解答:将 \( x = 2 \) 代入表达式中,得:\[ 3(2)^2 - 2(2) + 1 = 12 - 4 + 1 = 9 \]练习题2:简化下列表达式:\[ 5a^2 - 3ab + 2b^2 \]其中 \( a = 1 \),\( b = 2 \)。
解答:将 \( a = 1 \) 和 \( b = 2 \) 代入表达式中,得:\[ 5(1)^2 - 3(1)(2) + 2(2)^2 = 5 - 6 + 8 = 7 \]#### 二、方程求解练习题3:解方程:\[ 2x + 3 = 7 \]解答:移项得:\[ 2x = 4 \]两边同时除以2,得:\[ x = 2 \]练习题4:解方程:\[ 3y - 4 = 2y + 5 \]解答:移项得:\[ 3y - 2y = 5 + 4 \]\[ y = 9 \]#### 三、不等式求解练习题5:解不等式:\[ 5x - 2 < 3x + 8 \]解答:移项得:\[ 5x - 3x < 8 + 2 \]\[ 2x < 10 \]两边同时除以2,得:\[ x < 5 \]练习题6:解不等式:\[ 4 - 3z \geq 2z - 6 \]解答:移项得:\[ 4 + 6 \geq 2z + 3z \]两边同时除以5,得:\[ 2 \geq z \]或\[ z \leq 2 \]#### 四、函数与图像练习题7:画出函数 \( y = x^2 \) 在 \( x = -2 \) 到 \( x = 2 \) 的图像,并标出顶点。
解答:函数 \( y = x^2 \) 是一个开口向上的抛物线,顶点在原点 \( (0, 0) \)。
在 \( x = -2 \) 到 \( x = 2 \) 的区间内,图像从 \( (-2, 4) \) 经过顶点到 \( (2, 4) \)。
压强、浮力综合计算题题型讲解
3. 【2017,贵港】如图甲所示,放在水平桌面上的圆柱形容器的底面积为100cm2,装有 20cm深的水,容器的质量为0.02kg,厚度忽略不计。A、B是由密度不同的材料制成的两实 心物块,已知B物块的体积是A物块体积的 1/8 。当把A、B两物块用细线相连放入水中时, 两物块恰好悬浮,且没有水溢出,如图乙所示,现剪断细线,A物块上浮,稳定后水对容器 底的压强变化了60Pa,物块A有1/4体积露出水面。已知水的密度为1.0×103kg/m3,g取 10N/kg 。试求: (1)如图甲所示,容器对水平桌面的压强; (2)细线被剪断后水面的高度差; (3)A、B两物块的密度。
项目 规格 空重 最大负荷 乘员 参数 长8.2m,宽3.0m,高3.4m 22t(不含乘员、装备、压载铁块) 220kg(不含乘员) 准载3人,每人不超过80kg
(1)“蚊龙”号搭载3名乘员及装备 (不含压载铁块)时的总质量; (2)“蚊龙”号下潜到顶部距海面7200m 深处时顶部受到海水的压强;
1. 【2017,遵义】我国自主设计研发的“蚊龙”号载人深潜器不断刷新潜水深度纪录, 为我国探究深海海洋资源提供了大量宝贵资料.“蛟龙”号的一些主要参数如表所示, 蚊龙”号可在潜水器外搭载几块压载铁块作无动力下潜.在一次下潜中,搭载3名乘 员下潜到7200m深处作业,3名乘员总质量为180kg,自带装备总质量为220kg,海水 密度取1.0×103kg/m3,压载铁的密度为7.9×103kg/m3,g取10N/kg.求:
4
2.【2017,威海】某实验小组在研究某种物质的属性时,日常需将物体浸没在煤油中保存, 将体积为1×10﹣3m3、重6N的该物体用细线系在底面积为250cm2的圆柱形容器的底部,物 体浸没在煤油中,如图所示,(g=10N/kg,ρ煤油=0.8×103kg/m3) (1)细线受到的拉力是多大? (2)若细线与物体脱落,待物体静止后煤油对容器底的压强变化了多少?
子网规划计算练习题及讲解
一、单选或多选,请认真谨慎。
1. 192.168.1.0/24使用掩码255.255.255.240划分子网,其可用子网数为(),每个子网内可用主机地址数为()A. 14 14B. 16 14C. 254 6D. 14 622. 子网掩码为255.255.0.0,下列哪个IP地址不在同一网段中()A. 172.25.15.201B. 172.25.16.15C. 172.16.25.16D. 172.25.201.153. B类地址子网掩码为255.255.255.248,则每个子网内可用主机地址数为()A. 10B. 8C. 6D. 44. 对于C类IP地址,子网掩码为255.255.255.248,则能提供子网数为()A. 16B. 32C. 30D. 1285. 三个网段192.168.1.0/24,192.168.2.0/24,192.168.3.0/24能够汇聚成下面哪个网段()A. 192.168.1.0/22B. 192.168.2.0/22C. 192.168.3.0/22D. 192.168.0.0/226.IP地址219.25.23.56的缺省子网掩码有几位?A.8B.16C.24D.327.某公司申请到一个C类IP 地址,但要连接6个子公司,最大的一个子公司有26台计算机,每个子公司在一个网段中,则子网掩码应设为?A.255.255.255.0B.255.255.255.128C.255.255.255.192D.255.255.255.2248.一台IP地址为10.110.9.113/21主机在启动时发出的广播IP是?A.10.110.9.255B.10.110.15.255C.10.110.255.255D.10.255.255.2559.规划一个C类网,需要将网络分为9个子网,每个子网最多15台主机,下列哪个是合适的子网掩码?A.255.255.224.0B.255.255.255.224C.255.255.255.240D.没有合适的子网掩码10.与10.110.12.29 mask 255.255.255.224 属于同一网段的主机IP地址是?A.10.110.12.0B.10.110.12.30C.10.110.12.31D.10.110.12.3211.IP地址190.233.27.13/16的网络部分地址是?A.190.0.0.0B.190.233.0.0C.190.233.27.0D.190.233.27.112.没有任何子网划分的IP地址125.3.54.56的网段地址是?A.125.0.0.0B.125.3.0.0C.125.3.54.0D.125.3.54.3213.一个子网网段地址为2.0.0.0掩码为255.255.224.0网络,它一个有效子网网段地址是?A.2.1.16.0B.2.2.32.0C.2.3.48.0D.2.4.172.014.一个子网网段地址为5.32.0.0掩码为255.224.0.0网络,它允许的最大主机地址是?A.5.32.254.254B.5.32.255.254C.5.63.255.254D.5.63.255.25515.在一个子网掩码为255.255.240.0的网络中,哪些是合法的网段地址?A.150.150.0.0B.150.150.0.8C.150.150.8.0D.150.150.16.016.如果C 类子网的掩码为255.255.255.224,则包含的子网位数、子网数目、每个子网中主机数目正确的是?A.2,2,62B.3,8,30C.4,14,14D.5,30,617. 网络地址172.16.0.0,如果采用子网掩码255.255.192.0,那么以下说法正确的是()A. 划分了2个子网;B. 划分了4个子网;C. 其中一个子网的广播地址为:172.16.191.255;D. 其中一个子网的广播地址为:172.16.128.255。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 第一章:物流供需调查与分析 一、简单平均法:(P13) 公式:NtNxxxyNtttt11
1
y:
预测值 x:发生值
字母含义: t:当期发生值 t+1:下一期预测值
t-1:上一期发生值
例:已经调查得出某商场今年前8个月用户的配送车次见表,现在需要预测估
计该商场9月的配送车次。 月份t 1 2 3 4 5 6 7 8
配送车次tx 10 12 11 10 8 9 10 12
分析:根据题意,就是要求9月份的预测值,可用9月份之前N个月进行平均求得。
解:如果N=3,则3.1039101236789xxxy
如果N=4,则75.94891012456789xxxxy 如果N=5,则8.95108910125456789xxxxxy 结论:可见,组距N的取值不同,预测的结果也是不同的即误差不同。但结果都是合理
的,最后确定预测结果,要进行误差分析,因为考虑到最后几个月是上升的趋势,9月份的预测结果应当取大为好,可取,3.109y或10,或11皆可。
二、加权平均法:(P14) 权:相同发生值出现的次数;加权:有目的分配权重(加大发生值影响成分) 公式:NtwwwxwxwxwyNNtNttt2111211 字母含义: t:当期发生值(配送车次) t+1:下一月预测期发生值
t-1:上一期发生值 :表示求总和 W:加权值
例:已经调查得出某商场今年前8个月用户的配送车次见表,现在需要预测估
计该商场9月的配送车次。(采用加权平均法预测) 2
月份t 1 2 3 4 5 6 7 8 配送车次tx 10 12 11 10 8 9 10 12
分析: 解:如果N=3,权数iw{ 3,2,1 },越靠近9月份的序列值,权数越高,则:
83.10123911021233216372819wwwxwxwxwy 如果N=4,权数iw{ 4,3,2,1 },则: 4.10123481921031244321546372819wwwwxwxwxwxwy 如果N=5,权数iw{ 5,4,3,2,1 },则: 2.101234510182931041255432145546372819wwwwwxwxwxwxwxwy结论:与简单平均法相比,这里的预测值分别都有所升高,更靠近8月份的发生值12,
这是增加了权数的结果。
三·移动平均法:(P15)略 四·指数平滑法:(P18) 公式:tttyxy11
字母含义: t:当期发生值 t+1:下一月预测期值 :指数平滑系数,.10
初始化: 11xy
例:数据资料见下表1、2列,现在用指数平滑法预测9月份的预测值。] 3
时间t 配送车次tx 指数平滑预测值3.01ty
(1) (2) (3) 1月 10 y1=x1=10 初始化
2月 12 y2=ax1+(1-a)y1=0.3×10+(1-0.3) ×10=10.0
3月 11 y3=ax2+(1-a)y2=0.3×12+(1-0.3) ×10=10.6 4月 10 y4=ax3+(1-a)y3=0.3×11+(1-0.3) ×10.6=10.7 5月 8 y5=ax4+(1-a)y4=0.3×10+(1-0.3) ×10.7=10.5 6月 9 y6=ax5+(1-a)y5=0.3×8+(1-0.3) ×10.5=9.8 7月 10 y7=ax6+(1-a)y6=0.3×9+(1-0.3) ×9.8=9.6 8月 12 y8=ax7+(1-a)y7=0.3×10+(1-0.3) ×9.6=9.7 9月 y9=ax8+(1-a)y8=0.3×12+(1-0.3) ×9.7=10.4
解:(1)10.0 0.1011xy(即一月tx值等于一月1ty值),因为指数平滑预测
值3.0,所以1ty数值精确到小数点后一位即可。 (2)10.0 0.100.107.0103.03.013.0112yxy (3)10.6 6.100.107.0123.03.013.0223yxy
依此类推„„ (9)10.4 4.1039.107.97.0123.03.013.0889yxy
结论:
五·季节指数法:(P20) 公式:(1)12121iixX ;x:计算全年的平均值(全年各月发生值加总除以12) (2)%100Xxii ; ai:计算每个月的月季节指数(每月发生值分别除以x)
(3)1211200iik ; k:计算修正系数(月季节指数之和大于1200,k<1,反之亦然) 4
(4)iijjxy
字母含义:ix: 当月发生值 i
:
当月月季节指数
jy=预测月份预测值 j=预测月份季节指数
例:某物流公司调查了武汉市场去年空调器的购进物流量,数据资料如下表1、
2列所示,已经知道今年4月份已经购进空调的购进物流量是40车次,现在想预测今年6月份空调器的购进物流量是多少车次。 时间t 购进车次ix 月季节指数i(%) 月季节指数k(%)
1 2 3 4 1月 5 11 11
2月 4 9 9
3月 10 23 23
4月 25 57 57
5月 45 102 102
6月 106 241 241
7月 94 214 214
8月 90 205 205
9月 60 136 136
10月 50 114 114
11月 29 66 66
12月 10 23 23
合计 528 1021
月平均X 44
分析:表中第3列数值为计算结果,第4列数值为调整结果,计算步骤如下:
解:1. 441252812121iixX
2. (1)11%100113636.0%100445%10011Xx (2)9%100909090.0%100444%10022Xx 依此类推„„ (12)23%1002272727.0%1004410%1001212Xx 5
3. 999167.0120112001200121iik 用k乘以第3列各数得到的第4列数(调整数值)没有变化,因此不用理会。 4. 已知: 4月份的购进车次4x为40车次,其月季节指数4为57(%),6月份
的月季节指数6为241(%),求6月份的购进车次预测值6y
16940572414466xy
(车次)
结论: 第五章:运输管理 盈亏平衡分析模型:P163 X0 =CWF F:固定资本
W:运输综合费率
C:单位变动成本
x0: 保本经营业务量
已知某运输企业的单位变动成本为1.8元,运输综合费率为2.3元,固定资本为20万元,月经营业务量为100万元,请问其经营安全率为多少?
解:根据盈亏平衡分析模型 平衡盈亏经营业务量X0 =CWF=20/(2.3-1.8)=40(万元) 经营安全率 B= (X-X0)/X = (100-40)/100=0.6
第六章:仓储管理与库存控制 一、物资储存计算 6
5个重要的公式 1.仓库有效容积=仓库有效面积×堆码有效高度P173 2.仓库面积利用率=库房有效面积/库房使用 3.Ni=qi/si Ni: 某类物资单位面积储存定额(T/㎡) qi: 某类物资实际储存量
Si: 某类物资储存实际占用面积
例题:某仓库近期有8400件计算机显示器到库,单件外形尺寸为:60CM
×60CM×60CM,重50公斤,外包装标示的堆码极限标志为6,问需要为此批货物准备多大的货位?其储存定额是多大?若该批加湿器全部存放在一个使用面积为650㎡的仓库中,问该仓库的面积利用率和有效容积为多大?
解:此批货物占货位面积S为:
每层占用面积(货位面积)=入库总件数÷允许堆码层数×单件物资底面积
S=60.60.68400=504㎡ 该类物资的储存定额 = 总储存面积总重量=504508400=8公斤/㎡ 仓库的面积利用率=650504×100%≈77.54% 仓库有效容积=504×0.6×6=1814.4m³
