2018年中考总复习 与圆有关的计算训练试题及答案(Word版)
18年中考复习第28讲 圆和圆(含答案)

第28讲圆和圆◆考点链接1.圆和圆的位置关系、两圆连心线垂直平分公共弦或过切点;2.两圆内、外公切线长的计算公式.◆典例精析【例题1】(大连)如图,以⊙O上一点P为圆心作⊙P,•交⊙O于A、B两点,过点P的直线交⊙P于点G、D,交⊙O于点C,直线CA、CB分别交⊙P于点E、F,连结DF、•EG、BG.求证:DF·CE=EG·CD.说明:(1)如果你经历反复探索,没有找到解决问题的方法,请你把探索过程中的某种思路写出来(要求至少要写3步);(2)在你经历说明(1)的过程后,•可以从下列①②③中选取一个补充或更换已知条件,完成你的证明.①AE=AF;②AD=DF;③EG=BG.解题思路:本题证明方法很多,但不管什么方法,都必须先设法证明△CDF•∽△CEG.证明时充分利用点P既是⊙P的圆心,又在⊙O上以及点P在线段CG上,•因此构造辅助线时,可从点P出发考虑,如连结OA、OE、OB,还可过点P作弦心距等都是很好的方法.【例题2】(甘肃)如图,半圆O的直径AB=4,与半圆O内切的动圆O1与AB切于点M,设⊙O1的半径为y,AM=x,则y关于x的函数关系是().A.y=14x2+x B.y=-14x2+x C.y=-14x2-x D.14x2-x解题思路:本题属于在几何图形中求两个变量的函数关系的题型,如何利用几何图形的性质求出两个变量的对应关系式,进而把有关的量用函数的自变量表示,再代入对应关系式,化成函数关系式.解:连结OO1、O1M,则OO1=12AB-y=2-y,OM=12AB-AM=2-x,O1M=y,∠O1MO=90°,∵OM2+O1M2=OO12,∴(2-x)2+y2=(2-y)2整理,得y=-14x2+x,故选B.◆探究实践【问题1】(太原)如图,⊙O2与半圆O1内切于点C,与半圆的半径AB切于点D,•若AB=6,⊙O2的半径为1,则∠ABC的度数为______.解题思路:本题考查两圆位置关系及“直径所对的圆周角为直角”等知识,连结AC,BC,通过O1,O2和C点共线,则O2C=1,O1C=3,故O1O2=2,而O2D=1,且O2D⊥AB,所以∠O2O1D=30°,又由∠CO1B=2∠CAB,所以∠CAB=15°,又由∠ACB=90°,可知∠ABC=75°.【问题2】(威海)在矩形ABCD中,AB=5,BC=12,若分别以点A、C•为圆心的两圆相切,点D在⊙C内,点B在⊙C外,则⊙A的半径r的取值范围是________.解题思路:本题考查了两圆相切的有关计算,要从连心线与半径的关系方面考虑.答案:1<r<8或18<r<25◆中考演练一、填空题1.若⊙O1的半径是3,⊙O2的半径是4,O1O2=8,则这两圆的位置关系是_____.2.已知相切两圆的半径分别为3cm和2cm,则两圆的圆心距为______cm.3.⊙O的半径为2,点P是⊙O外一点,OP的长为3,那么以P为圆心,且与⊙O•相切的圆的半径一定是_______.二、选择题1.如果两圆的半径分别为3cm和5cm,圆心距为10cm,那么这两圆的公切线共有(• ). A.1条 B.2条 C.3条 D.4条2.(长春)如图,半径相等的两个圆相交于A、B两点,若∠ACB=40°,•则∠ADB的度数是().A.80° B.60° C.40° D.20°3.(四川)已知相交两圆的半径分别是5和8,那么这两圆的圆心距d的取值范围是(). A.d>3 B.d<13 C.3<d<13 D.d=3或d=13三、解答题1.(盐城)已知:AB为⊙O的直径,P为AB弧的中点.(1)若⊙O′与⊙O外切于点P(见图8-3-5甲),AP、BP的延长线分别交⊙O•′于点C、D,连接CD,则△PCD是_______.(2)若⊙O′与⊙O相交于点P、Q(见图8-3-5乙),连接AQ、BQ并延长分别交⊙O′于点E、F,请选择下列两个问题中的一个作答:问题1:判断△PEF的形状,并证明你的结论;问题2:判断线段AE与BF的关系,并证明你的结论.我选择问题_______,结论:_________.证明:2.(南通)如图8-3-6,已知:AO为⊙O的直径,⊙O与⊙O的一个交点为E,直线AO•交⊙O于B、C两点,过⊙O上一点G作⊙O的切线GF,交直线AO于点D,与AE的延长线垂直相交于点F.(1)求证:AE是⊙O的切线;(2)若AB=2,AE=6,求△ODG的周长.◆实战模拟一、填空题1.(河南)平面内两圆半径恰好为方程x2-8x+6=0的两个根,圆心距d=5,•这两个圆的位置关系是_______.2.矩形ABCD中,如图1,两个半径都为5cm的圆外切,•且每个圆分别与矩形的两边相切,CD=16cm,则AD长为________cm.(1) (2) (3)3.(天津)如图2,已知两个等圆⊙O1与⊙O2相交于A、B两点,•一条直线经过点A,分别与两圆相交于点C、D,MC切⊙O1于C,MD切⊙O2于点D,若∠BCD=30°,则∠M•等于________度.二、选择题1.(广州)如图3,⊙O1、⊙O2内切于点A,⊙O1的半径为3,⊙O2的半径为2,点P•是⊙O1上的任一点(与点A不重合),直线PA交⊙O2于点C,PB与⊙O2相切于点B,则PBPC=().A.32D.22.(陕西)如图5,⊙O1和⊙O2内切,它们的半径分别为3和1,过O1作⊙O2的切线,切点为A,则O1A的长为().A.2 B.4 C(4) (5)3.(武汉)如图6,已知⊙O1、⊙O2相交于A、B两点,直线O1O2交两圆于点C、D,•若∠O1AO2=40°,则∠CBD等于().A.110° B.120° C.130° D.140°三、解答题1.(成都)已知:如图,⊙O与⊙A相交于C、D两点,A、O•分别是两圆的圆心,△ABC内接于⊙O,弦CD交AB于点G,交⊙O的直径AE于点F,连结BD.(1)求证:△ACG∽△DBG;(2)求证:AC2=AG·AB;(3)若⊙A、⊙O直径分别为15,且CG:CD=1:4.求AB和BD的长.2.(宁波)已知AB是半圆O的直径,AB=16,P点是AB上的一动点(不与A、B重合),•PQ ⊥AB,垂足为P,交半圆O于Q;PB是半圆O1的直径,⊙O2与半圆O、半圆O1及PQ都相切,•切点分别为M、N、C.(1)当P点与O点重合时(如图甲),求⊙O2的半径r;(2)当P点在AB上移动时(如图乙),设PQ=x,⊙O2的半径为r,求r与x• 的函数关系式,并求出r的取值范围.答案:中考演练一、1.外离 2.1或5 3.1或5二、1.D 2.C 3.C三、1.(1)等腰Rt △ (2)1.△PEF 是等腰直角三角形,∵∠AQP=∠FQP=∠PEF=•45°2.AE ⊥BF ,∵AB 是⊙O 的直径,∴∠AQB=90°3.如图,(1)证AE ⊥OE .(2)由切割线定理,得AE 2=AB ·AC ,得AC=18,⊙O 的半径为8,⊙O 的半径为5. 由Rt △AOE ∽Rt △ODG , 6810,,83240,,33AE OE AO OG DG OD DG OD DG OD ∴====∴==即 ∴△ODG 的周长为OG+DG+OD=32实战模拟一、1.内含 2.18 3.60二、1.B 2.C 3.A三、1.(1)∠ACD=∠ABD ,∠AGC=∠BGD ,∴△ACG ∽△DBG ,(2)CD ⊥AB ,∴∠ACD=∠ABC ,△ACG ∽△ABC ,故AC 2=AG·AB(3)AC 2=AF·AE ,∴AF=3,CF=6,CG=GF=3,DG=9,∴AB=2,2AC BD AG ==2.(1)连CO 2、OO 2、O 1O 2,作O 2D ⊥AB 于D ,由OO 22-OD 2=O 1O 22-O 1D 2,有(8-r )2-r 2=(r+4)2-(4-r )2,得r=2(2)连O 2O ,O 2O 1,作O 2D ⊥AB 于D ,设⊙O 1半径是a ,则由PQ 2=AP·PB ,有x 2=2a (16-2a )=4(•8a-a 2),又由O 1O 22-O 1D 2=OO 22-OD 2,得(a+r )2-(a-r )2=(8-r )2-(2a-r-8)2,得8r=8a-a 2,1 32x2,∵0<x≤8,∴0<r≤2.∴x2=32r,即r=。
2018届初三数学中考复习 圆与解直角三角形的综合 专项复习练习 含答案
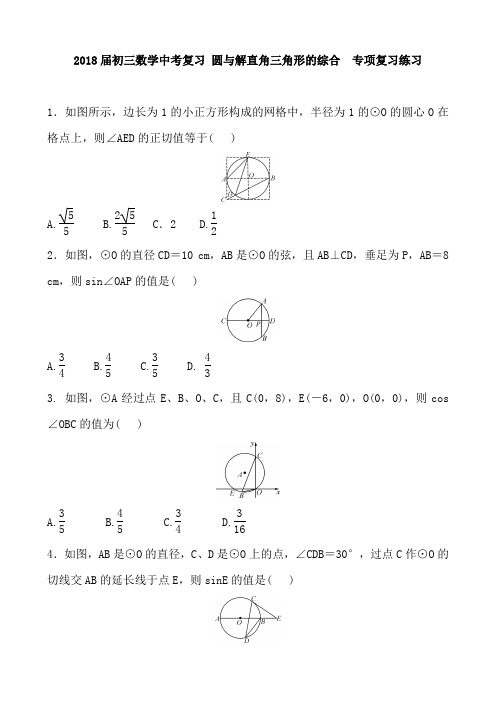
2018届初三数学中考复习 圆与解直角三角形的综合 专项复习练习1.如图所示,边长为1的小正方形构成的网格中,半径为1的⊙O 的圆心O 在格点上,则∠AED 的正切值等于( )A.55B.255 C .2 D.122.如图,⊙O 的直径CD =10 cm ,AB 是⊙O 的弦,且AB ⊥CD ,垂足为P ,AB =8 cm ,则sin ∠OAP 的值是( )A.34B.45C.35D. 433. 如图,⊙A 经过点E 、B 、O 、C ,且C(0,8),E(-6,0),O(0,0),则cos ∠OBC 的值为( )A.35B.45C.34D.3164.如图,AB 是⊙O 的直径,C 、D 是⊙O 上的点,∠CDB =30°,过点C 作⊙O 的切线交AB 的延长线于点E ,则sinE 的值是( )A.12B.13C.55D.325.如图,已知⊙O 的半径为5,锐角△ABC 内接于⊙O ,BD ⊥AC 于点D ,AB =8,则tan ∠CBD 的值等于( )A.43B.45C.35D.346.如图,在半径为6的⊙O 内有两条互相垂直的弦AB 和CD ,AB =8,CD =6,垂足为E ,则tan ∠OEA 的值是( )A.34B.63C.156D.21597.如图,△ABC 内接于⊙O ,连结OA 、OC ,⊙O 的半径为3,且sinB = 56,则弦AC 的长为( )A.11 B .5 C.56 D.538.如图,以点O 为圆心的两个圆中,大圆的弦AB 切小圆于点C ,OA 交小圆于点D ,若OD =2,tan ∠OAB =12,则AB 的长是 ____.9.在半径为1的⊙O 中,弦AB 、AC 的长分别为1和 2 ,则∠BAC 的度数为 .10.在△ABC 中,AB =AC =10,cos B =35,如果圆O 的半径为210, 且经过点B 、C ,那么线段AO 的长等于 __________.11.如图所示,以锐角△ABC 的边AB 为直径作⊙O ,交AC 、BC 于E 、 D 两点,若AC =14,CD =4,7sin C =3tan B ,则BD = _____.12. 如图所示,在⊙O 中,直径AB =6,AB 与弦CD 相交于点E ,连结AC 、BD ,若AC =2,则cos D 的值为____.13. 如图,已知AB 是圆O 的直径,弦CD ⊥AB ,垂足为H ,与AC 平行的圆O 的一条切线交CD 的延长线于点M ,交AB 的延长线于点E ,切点为F ,连结AF 交CD 于点N.(1)求证:CA =CN ;(2)连结DF ,若cos ∠DFA =45,AN =210 ,求⊙O 的直径的长度.参考答案:1---7 DCAAD DB8. 89. 15°或105°10. 6或1011. 612. 1313. 解:(1)证明:连结OF ,则∠OAF =∠OFA.∵ME 与⊙O 相切,∴OF ⊥ME.∵CD ⊥AB ,∴∠M +∠FOH =180°.∵∠BOF =∠OAF +∠OFA =2∠OAF ,∠FOH +∠BOF =180°, ∴∠M =2∠OAF.∵ME ∥AC ,∴∠M =∠ACM =2∠OAF.∵CD ⊥AB ,∴∠ANC +∠OAF =∠BAC +∠ACM =90°,∴∠ANC =90°-∠OAF ,∠BAC =90°-∠ACM =90°-2∠OAF , ∴∠CAN =∠OAF +∠BAC =90°-∠OAF =∠ANC ,∴CA =CN.(2)连结OC.∵cos ∠DFA =45,∠DFA =∠ACH , ∴CH AC =45. 设CH =4a ,则AC =5a ,AH =3a. ∵CA =CN ,∴NH =a.∴AN =AH 2+NH 2=10a =210, ∴a =2,AH =3a =6,CH =4a =8. 设圆的半径为r ,则OH =r -6.在Rt △OCH 中,∵OC 2=CH 2+OH 2,OC =r , CH =8,OH =r -6,∴r 2=82+(r -6)2,解得r =253. ∴⊙O 的直径的长度为2r =503.。
通用版2018年中考数学总复习专题突破预测与详解第六单元圆专题21与圆有关的计算试题新版新人教版2018011212
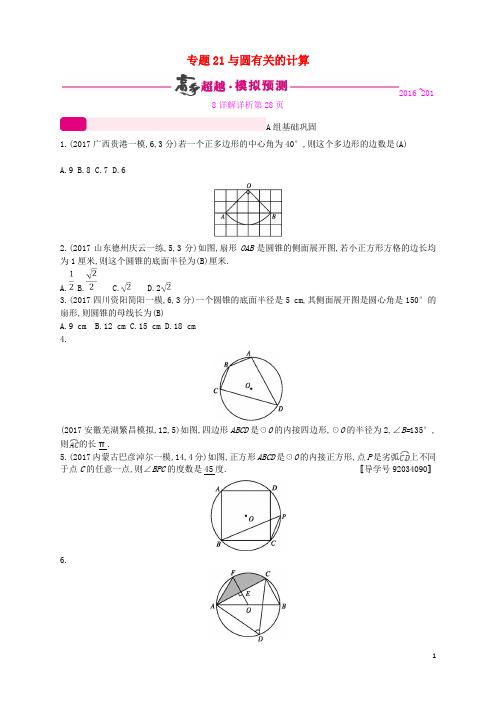
专题21与圆有关的计算2016~2018详解详析第28页A组基础巩固1.(2017广西贵港一模,6,3分)若一个正多边形的中心角为40°,则这个多边形的边数是(A)A.9B.8C.7D.62.(2017山东德州庆云一练,5,3分)如图,扇形OAB是圆锥的侧面展开图,若小正方形方格的边长均为1厘米,则这个圆锥的底面半径为(B)厘米.A. B.C.D.23.(2017四川资阳简阳一模,6,3分)一个圆锥的底面半径是5 cm,其侧面展开图是圆心角是150°的扇形,则圆锥的母线长为(B)A.9 cmB.12 cmC.15 cmD.18 cm4.(2017安徽芜湖繁昌模拟,12,5)如图,四边形ABCD是☉O的内接四边形,☉O的半径为2,∠B=135°,则的长π.5.(2017内蒙古巴彦淖尔一模,14,4分)如图,正方形ABCD是☉O的内接正方形,点P是劣弧上不同于点C的任意一点,则∠BPC的度数是45度.〚导学号92034090〛6.(2017山东滨州博兴模拟,22,10分)如图,已知AB是☉O的直径,点C,D在☉O上,∠D=60°且AB=6,过O点作OE⊥AC,垂足为E.(1)求OE的长;(2)若OE的延长线交☉O于点F,求弦AF,AC和弧CF围成的图形(阴影部分)的面积S.解(1)∵∠D=60°,∴∠B=60°(圆周角定理),∵AB是☉O的直径,∴∠ACB=90°.又AB=6,∴BC=3.∵OE⊥AC,∴OE∥BC.又点O是AB中点,∴OE是△ABC的中位线.∴OE=BC=.(2)连接OC,则易得△COE≌△AFE,故阴影部分的面积=扇形FOC的面积,S扇形FOC==π.即可得阴影部分的面积为π.B组能力提升1.(2017天津南开一模,10,3分)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是(D)A.B.C.D.2.(2017江苏苏州一模,10,24)如图,已知Rt△ABD中,∠A=90°,将斜边BD绕点B顺时针方向旋转至BC,使BC∥AD,过点C作CE⊥BD于点E.(1)求证:△ABD≌△ECB;(2)若∠ABD=30°,BE=3,求弧CD的长.(1)证明∵∠A=90°,CE⊥BD,∴∠A=∠BEC=90°.∵BC∥AD,∴∠ADB=∠EBC.∵将斜边BD绕点B顺时针方向旋转至BC,∴BD=BC.在△ABD和△ECB中,∠ADB=∠EBC,∠A=∠BEC,BD=CB,∴△ABD≌△ECB.(2)解∵△ABD≌△ECB,∴AD=BE=3.∵∠A=90°,∠ABD=30°,∴BD=2AD=6.∵BC∥AD,∴∠A+∠ABC=180°,∴∠ABC=90°.∴的长为=2π.〚导学号92034091〛C组综合创新(2017山东青岛市北区模拟,13,3分)如图,一根5米长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动),那么小羊A在草地上的最大活动区域面积是π平方米.。
天津市河西区2018年中考数学《圆》解答题强化训练(有答案)

2018年九年级中考数学专题复习圆解答题强化训练1.如图,已知⊙O内接于△ABC,BC为⊙O直径,延长AC至D,过D作⊙O切线,切点为E,且∠D=90°,连接CE.(1)求证:CE平分∠BCD;(2)若⊙O的半径为5,CD=2,求DE的长.2.如图,△ABC内接于⊙O,弦AD⊥AB交BC于点E,过点B作⊙O的切线交DA的延长线于点F,且∠ABF=∠ABC.(1)求证:AB=AC;(2)若AD=4,cos∠ABF=0.8,求DE的长.3.如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,AE是⊙O的切线,∠CAE=60°.(1)求∠D的度数;(2)当BC=4时,求劣弧AC的长.4.如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连结BD.(1)求证:∠A=∠BDC;(2)若CM平分∠ACD,且分别交AD、BD于点M、N,当DM=1时,求MN的长.5.如图,已知△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.(1)求证:AE=BE;(2)求证:FE是⊙O的切线;(3)若FE=4,FC=2,求⊙O的半径及CG的长.6.如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙O的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.⑴求证:AD平分∠BAC;⑵若AC=8,tan∠DAC=0.75,求⊙O的半径.7.如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.(1)求证:ED是⊙O的切线;(2)若⊙O半径为2.5,OE=10时,求DE的长.8.如图,在△ABC中,AB=AC.以AC为直径的⊙O交AB于点D,交BC于点E.过E点作⊙O的切线,交AB于点F.(1)求证:EF⊥AB;(2)若BD=2,BE=3,求AC的长.9.如图,在Rt△ABC中,∠C=90°,AD是∠BAC的平分线,经过A.D两点的圆的圆心O恰好落在AB上,⊙O分别与AB、AC相交于点E、F.(1)判断直线BC与⊙O的位置关系并证明;(2)若⊙O的半径为2,AC=3,求BD的长度.10.如图,⊙O是△ABC的外接圆,AC是⊙O的直径,弦BD=BA,AB=12,BC=5,BE⊥DC,交DC的延长线于点E.(1)求证:∠BCA=∠BAD;(2)求证:BE是⊙O的切线;(3)求DE的长.参考答案1.答案为:(1)证明略;(2)DE=4.2.3.解:(1)∵AE是⊙O的切线,∴AB⊥AE,∴∠BAE=90°,∵∠CAE=60°,∴∠BAC=∠BAE﹣∠CAE=90°﹣60°=30°,∵AB是⊙O的直径,∴∠ABC=90°,∴∠B=60°,∵∠D=∠B,∴∠D=60°;(2)连接OC,∵OB=OC,∠B=60°,∴△OBC是等边三角形,∵BC=4,∴OB=BC=4,∠BOC=60°,∴∠AOC=120°,∴劣弧AC的长是:=.4.解:(1)如图,连接OD,∵AB为⊙O的直径,∴∠ADB=90°,即∠A+∠ABD=90°,又∵CD与⊙O相切于点D,∴∠CDB+∠ODB=90°,∵OD=OB,∴∠ABD=∠ODB,∴∠A=∠BDC;(2)∵CM平分∠ACD,∴∠DCM=∠ACM,又∵∠A=∠BDC,∴∠A+∠ACM=∠BDC+∠DCM,即∠DMN=∠DNM,∵∠ADB=90°,DM=1,∴DN=DM=1,∴MN==.5.(1)证明:连接CE,如图1所示:∵BC是直径,∴∠BEC=90°,∴CE⊥AB;又∵AC=BC,∴AE=BE.(2)证明:连接OE,如图2所示:∵BE=AE,OB=OC,∴OE是△ABC的中位线,∴OE∥AC,AC=2OE=6.又∵EG⊥AC,∴FE⊥OE,∴FE是⊙O的切线.(3)解:∵EF是⊙O的切线,∴FE2=FC•FB.设FC=x,则有2FB=16,∴FB=8,∴BC=FB﹣FC=8﹣2=6,∴OB=OC=3,即⊙O的半径为3;∴OE=3,∵OE∥AC,∴△FCG∽△FOE,∴,即,解得:CG=.6.解:(1)连接OD,∵BC是⊙O的切线,∴OD⊥BC ∴∠ODB=90°又∵∠C=90°∴AC∥OD ∴∠CAD=∠ADO又∵OA=OD ∴∠OAD=∠ADO ∴∠CAD= AD平分∠BAC(2)在Rt△ACD中 AD=10连接DE,∵AE为⊙O的直径∴∠ADE=90°∴∠ADE=∠C∵∠CAD=∠OAD∴△ACD∽△ADE∴AE=12.5. ∴⊙O的半径是6.25.7.8.解:(1)证明:如图1所示:连结OE.∵AB=AC,∴∠B=∠ACB.又∵OE=OC,∴∠OEC=∠ACB,∴∠OEC=∠ABC.∴OE∥AB.∵EF与⊙O 相切,∴OE⊥EF.∴∠OEF=90°.∵OE∥AB,∴∠AFE=90°.∴OE⊥AB.(2)如图2所示:连结DE、AE.∵四边形ACED为⊙O的内接四边形,∴∠DEC+∠BAC=180°.又∵∠DEB+∠DEC=180°,∴∠BED=∠BAC.又∵∠B=∠B,∴△BED∽△BAC.∴BE:AB=BD:BC.∵AC为⊙O的直径,∴∠AEC=90°.∵在△ABC中,AB=AC,∴BE=CE=3,∴BC=6.∴3:AB=2:6,∴AB=9.即AC=AB=9.9.解:(1)BC与⊙O相切.证明:连接OD.∵AD是∠BAC的平分线,∴∠BAD=∠CAD.又∵OD=OA,∴∠OAD=∠ODA.∴∠CAD=∠ODA.∴OD∥AC.∴∠ODB=∠C=90°,即OD⊥BC.又∵BC过半径OD的外端点D,∴BC与⊙O相切.(2)由(1)知OD∥AC.∴△BDO∽△BCA.∴OB:AB=OD:AC.∵⊙O的半径为2,∴DO=OE=2,AE=4.∴(BE+2):(BE+4)=2:3.∴BE=2.∴BO=4,∴在Rt△BDO中,BD=2.10.(1)证明:∵BD=BA,∴∠BDA=∠BAD.∵∠BCA=∠BDA,∴∠BCA=∠BAD.(2)证明:连结OB,如图,∵∠BCA=∠BDA,又∵∠BCE=∠BAD,∴∠BCA=∠BCE,∵OB=OC,∴∠BCO=∠CBO,∴∠BCE=∠CBO,∴OB∥ED.∵BE⊥ED,∴EB⊥BO.∴BE是⊙O的切线.(3)解:∵AC是⊙O的直径,∴∠ABC=90°,∴AC===13.∵∠BDE=∠CAB,∠BED=∠CBA=90°,∴△BED∽△CBA,∴,即,∴DE=.。
(通用版)2018年中考数学总复习 专题检测19 圆的有关性质试题

专题检测19 圆的有关性质(时间90分钟满分100分)一、选择题(每小题3分,共36分)1.下列说法:①直径是弦;②弦是直径;③过圆上任意一点有无数条弦,且这些弦都相等;④直径是圆中最长的弦.其中正确的是(B)A.1个B.2个C.3个D.4个2.数学课上,老师让学生尺规作图画Rt△ABC,使斜边AB=c,BC=a,小明的作法如图所示,你认为这种作法中判断∠ACB是直角的依据是(B)A.勾股定理B.直径所对的圆周角是直角C.勾股定理的逆定理D.90°的圆周角所对的弦是直径3.如图,经过原点O的☉P与x轴,y轴分别交于A,B两点,点C是劣弧OB上一点,则∠ACB=(B)A.80°B.90°C.100°D.无法确定(第3题图)(第4题图)4.如图,AB是☉O的直径,弦CD⊥AB于点E,若AB=8,AE=1,则弦CD的长是(B)A. B.2 C.6 D.85.如图所示,四边形ABCD内接于☉O,点F是劣弧CD上一点,且=,连接CF并延长交AD的延长线于点E,连接AC,若∠ABC=105°,∠BAC=25°,则∠E的度数为(B)A.45°B.50°C.55°D.60°(第5题图)(第6题图)6.如图,在5×5正方形网格中,如果一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是(B)A.点PB.点QC.点RD.点M7.如图,四边形ABCD为☉O的内接四边形,已知∠BOD=100°,则∠BCD的度数为(D)A.50°B.80°C.100°D.130°(第7题图)(第8题图)8.如图,已知☉O过点B,C,圆心O在等腰直角三角形ABC内部,∠BAC=90°,OA=1,BC=6,则☉O的半径为(C)A.B.2C.D.39.如图,DC是以AB为直径的半圆上的弦,DM⊥CD交AB于点M,CN⊥CD交AB于点N.若AB=10,CD=6.则四边形DMNC的面积(A)A.等于24B.最小为24C.等于48D.最大为4810.如图,已知在☉O内有折线OABC,点B,C在圆上,点A在☉O内,其中OA=4 cm,BC=10 cm,∠A=∠B=60°,则AB的长为(B)A.5 cmB.6 cmC.7 cmD.8 cm11.如图,已知直线l与☉O相交于点E,F,AB是☉O的直径,AD⊥l于点D,若∠DAE=22°,则∠BAF为(C)A.12°B.18°C.22°D.30°〚导学号92034200〛(第11题图)(第12题图)12.如图,已知点P是☉O外一点,点Q是☉O上的动点,线段PQ的中点为点M,连接OP,OM,若☉O的半径为2,OP=4,则线段OM的最小值是(B)A.0B.1C.2D.3二、填空题(每小题4分,共24分)13.如图,若一块含45°角的直角三角板的一个锐角顶点A在☉O上,边AB,AC分别与☉O交于点D,E,则∠DOE为90°.14.在半径为5 cm的圆内有两条平行弦,若一条弦长为8 cm,另一条弦长为6 cm,则两弦之间的距离为1 cm或7 cm.15.如图,☉C过原点并与坐标轴分别交于A,D两点.已知∠OBA=30°,点D的坐标为(0,2),则点C 的坐标为(-1,).(第15题图)(第16题图)16.如图,有一圆形展厅,在其圆形边缘上的点A处安装了一台监视器,它的监控角度是65°.为了监控整个展厅,最少需在圆形边缘上共安装这样的监视器3台.17.如下图,已知四边形ABCD内接于半径为4的☉O中,且∠C=2∠A,则BD=4.(第17题图)(第18题图)18.如图,在平面直角坐标系xOy中,点A,B,P的坐标分别为(1,0),(2,5),(4,2),若点C在第一象限内,且横坐标、纵坐标均为整数,P是△ABC的外心,则点C的坐标为(7,4)或(6,5).三、解答题(共40分)19.(20分)如图,AB是半圆O的直径,C,D是半圆O上的两点,且OD∥BC,OD与AC交于点E.(1)若∠B=70°,求∠CAD的度数;(2)若AB=4,AC=3,求DE的长.是半圆O的直径,∴∠ACB=90°.∴∠CAB=90°-∠B=90°-70°=20°.又∵OD∥BC,∴∠AEO=90°.∵OA=OD,∴∠DAO=∠ADO===55°.∴∠CAD=∠DAO-∠CAB=55°-20°=35°.(2)在Rt△ABC中,BC===.∵OE⊥AC,∴AE=EC.又∵OA=OB,∴OE=BC=.又∵OD=AB=2,∴DE=OD-OE=2-.20.(20分)如图,A,B为☉O上的两个定点,P是☉O上的动点(P不与A,B重合),我们称∠APB为☉O 上关于点A,B的滑动角.已知∠APB是☉O上关于点A,B的滑动角.备用图(1)若AB 为☉O 的直径,则∠APB= ; (2)若☉O 半径为1,AB=,求∠APB 的度数;若☉O 半径为1,AB=,AC=,求∠BAC 的度数.为☉O 的直径,∴∠APB=90°.故答案为90°. (2)如图1,连接OA,OB,AB,∵☉O 半径为1,AB=,∴OA=OB=1,AB=.∴OA 2+OB 2=AB 2.∴∠AOB=90°.∴当点P 在优弧AB 上时,∠APB=∠AOB=45°, 当点P 在劣弧AB 上时,∠APB=180°-45°=135°, ∴∠APB 的度数为45°或135°.(3)如图2,分别作OD⊥AB,OE⊥AC,垂足分别是D,E. ∵OE⊥AC,OD⊥AB,∴AE=AC=,AD=AB=.∴sin∠AOE==,sin∠AOD==.∴∠AOE=60°,∠AOD=45°.∴∠BAO=45°,∠CAO=90°-60°=30°.∴∠BAC=45°+30°=75°,或∠BAC'=45°-30°=15°. ∴∠BAC=15°或75°.〚导学号92034201〛。
2018年中考一轮基础复习试卷专题二十:圆的有关性质(有答案)

备考2018年中考数学一轮基础复习:专题二十圆的有关性质一、单选题(共15题;共30分)1.(2017•新疆)如图,⊙O的半径OD垂直于弦AB,垂足为点C,连接AO并延长交⊙O于点E,连接BE,CE.若AB=8,CD=2,则△BCE的面积为()A. 12B. 15C. 16D. 182.(2017•云南)如图,B,C是⊙A上的两点,AB的垂直平分线与⊙A交于E,F两点,与线段AC交于D点.若∠BFC=20°,则∠DBC=()A. 30°B. 29°C. 28°D. 20°3.(2017•乐山)如图是“明清影视城”的一扇圆弧形门,小红到影视城游玩,他了解到这扇门的相关数据:这扇圆弧形门所在的圆与水平地面是相切的,AB=CD=0.25米,BD=1.5米,且AB,CD与水平地面都是垂直的.根据以上数据,请你帮小红计算出这扇圆弧形门的最高点离地面的距离是()A. 2米B. 2.5米C. 2.4米D. 2.1米4.(2017•阿坝州)如图将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为()A. 2cmB. cmC. 2 cmD. 2 cm5.(2017•锦州)如图,四边形ABCD是⊙O的内接四边形,AD与BC的延长线交于点E,BA与CD的延长线交于点F,∠DCE=80°,∠F=25°,则∠E的度数为()A. 55°B. 50°C. 45°D. 40°6.(2017•南通)已知∠AOB,作图.步骤1:在OB上任取一点M,以点M为圆心,MO长为半径画半圆,分别交OA、OB于点P、Q;步骤2:过点M作PQ的垂线交于点C;步骤3:画射线OC.则下列判断:① = ;②MC∥OA;③OP=PQ;④OC平分∠AOB,其中正确的个数为()A. 1B. 2C. 3D. 47.(2017•永州)小红不小心把家里的一块圆形玻璃打碎了,需要配制一块同样大小的玻璃镜,工人师傅在一块如图所示的玻璃镜残片的边缘描出了点A,B,C,给出三角形ABC,则这块玻璃镜的圆心是()A. AB,AC边上的中线的交点B. AB,AC边上的垂直平分线的交点C. AB,AC边上的高所在直线的交点D. ∠BAC与∠ABC的角平分线的交点8.(2017•贺州)如图,在⊙O中,AB是⊙O的直径,AB=10,= = ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED= ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是()A. 1B. 2C. 3D. 49.把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则的度数是()A. 120°B. 135°C. 150°D. 165°10.(2017•青岛)如图,AB是⊙O的直径,点C,D,E在⊙O上,若∠AED=20°,则∠BCD的度数为()A. 100°B. 110°C. 115°D. 120°11.(2017•烟台)如图,▱ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则的长为()A. πB. πC. πD. π12.(2017•贵港)如图,A,B,C,D是⊙O上的四个点,B是的中点,M是半径OD上任意一点.若∠BDC=40°,则∠AMB的度数不可能是()A. 45°B. 60°C. 75°D. 85°13.如图,AB是⊙O的直径,= = ,∠COD=34°,则∠AEO的度数是()A. 51°B. 56°C. 68°D. 78°14.(2017•泸州)如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=8,AE=1,则弦CD的长是()A. B. 2 C. 6 D. 815.(2017•西宁)如图,AB是⊙O的直径,弦CD交AB于点P,AP=2,BP=6,∠APC=30°,则CD的长为()A. B. 2 C. 2 D. 8二、填空题(共6题;共6分)16.(2017•大庆)如图,点M,N在半圆的直径AB上,点P,Q在上,四边形MNPQ为正方形.若半圆的半径为,则正方形的边长为________.17.(2017•十堰)如图,△ABC内接于⊙O,∠ACB=90°,∠ACB的角平分线交⊙O于D.若AC=6,BD=5 ,则BC的长为________.18.(2017•海南)如图,AB是⊙O的弦,AB=5,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是AB、AC的中点,则MN长的最大值是________.19.(2017•南京)如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=78°,则∠EAC=________°.20.(2017•广元)已知⊙O的半径为10,弦AB∥CD,AB=12,CD=16,则AB和CD的距离为________.21.(2017•襄阳)在半径为1的⊙O中,弦AB、AC的长分别为1和,则∠BAC的度数为________.三、综合题(共4题;共40分)22.(2017•乐山)如图,以AB边为直径的⊙O经过点P,C是⊙O上一点,连结PC交AB于点E,且∠ACP=60°,PA=PD.(1)试判断PD与⊙O的位置关系,并说明理由;(2)若点C是弧AB的中点,已知AB=4,求CE•CP的值.23.(2017•株洲)如图示AB为⊙O的一条弦,点C为劣弧AB的中点,E为优弧AB上一点,点F在AE的延长线上,且BE=EF,线段CE交弦AB于点D.①求证:CE∥BF;②若BD=2,且EA:EB:EC=3:1:,求△BCD的面积(注:根据圆的对称性可知OC⊥AB).24.(2017•广东)如图,AB是⊙O的直径,AB=4 ,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.(1)求证:CB是∠ECP的平分线;(2)求证:CF=CE;(3)当= 时,求劣弧的长度(结果保留π)25.(2017•绵阳)如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.(1)求证:CA=CN;(2)连接DF,若cos∠DFA= ,AN=2 ,求圆O的直径的长度.答案解析部分一、单选题1.【答案】A2.【答案】A3.【答案】B4.【答案】D5.【答案】C6.【答案】C7.【答案】B8.【答案】C9.【答案】C10.【答案】B11.【答案】B12.【答案】D13.【答案】A14.【答案】B15.【答案】C二、填空题16.【答案】217.【答案】818.【答案】19.【答案】2720.【答案】14或221.【答案】15°或105°三、综合题22.【答案】(1)解:如图,PD是⊙O的切线.证明如下:连结OP,∵∠ACP=60°,∴∠AOP=120°,∵OA=OP,∴∠OAP=∠OPA=30°,∵PA=PD,∴∠PAO=∠D=30°,∴∠OPD=90°,∴PD是⊙O的切线.(2)解:连结BC,∵AB是⊙O的直径,∴∠ACB=90°,又∵C为弧AB的中点,∴∠CAB=∠ABC=∠APC=45°∵AB=4,°.∵∠C=∠C,∠CAB=∠APC,∴△CAE∽△CPA,∴,∴CP•CE=CA2=(2 )2=8.23.【答案】①证明:连接AC,BE,作直线OC,如图所示:∵BE=EF,∴∠F=∠EBF;∵∠AEB=∠EBF+∠F,∴∠F= ∠AEB,∵C是的中点,∴,∴∠AEC=∠BEC,∵∠AEB=∠AEC+∠BEC,∴∠AEC= ∠AEB,∴∠AEC=∠F,∴CE∥BF;②解:∵∠DAE=∠DCB,∠AED=∠CEB,∴△ADE∽△CBE,∴,即,∵∠CBD=∠CEB,∠BCD=∠ECB,∴△CBE∽△CDB,∴,即,∴CB=2 ,∴AD=6,∴AB=8,∵点C为劣弧AB的中点,∴OC⊥AB,AG=BG= AB=4,∴CG= =2,∴△BCD的面积= BD•CG= ×2×2=2.24.【答案】(1)证明:∵OC=OB,∴∠OCB=∠OBC,∵PF是⊙O的切线,CE⊥AB,∴∠OCP=∠CEB=90°,∴∠PCB+∠OCB=90°,∠BCE+∠OBC=90°,∴∠BCE=∠BCP,∴BC平分∠PCE(2)证明:连接AC.∵AB是直径,∴∠ACB=90°,∴∠BCP+∠ACF=90°,∠ACE+∠BCE=90°,∵∠BCP=∠BCE,∴∠ACF=∠ACE,∵∠F=∠AEC=90°,AC=AC,∴△ACF≌△ACE,∴CF=CE.(3)解:作BM⊥PF于M.则CE=CM=CF,设CE=CM=CF=4a,PC=4a,PM=a,∵△BMC∽△PMB,∴= ,∴BM2=CM•PM=3a2,∴BM= a,∴tan∠BCM= = ,∴∠BCM=30°,∴∠OCB=∠OBC=∠BOC=60°,∴的长= = π25.【答案】(1)证明:连接OF,则∠OAF=∠OFA,如图所示.∵ME与⊙O相切,∴OF⊥ME.∵CD⊥AB,∴∠M+∠FOH=180°.∵∠BOF=∠OAF+∠OFA=2∠OAF,∠FOH+∠BOF=180°,∴∠M=2∠OAF.∵ME∥AC,∴∠M=∠C=2∠OAF.∵CD⊥AB,∴∠ANC+∠OAF=∠BAC+∠C=90°,∴∠ANC=90°﹣∠OAF,∠BAC=90°﹣∠C=90°﹣2∠OAF,∴∠CAN=∠OAF+∠BAC=90°﹣∠OAF=∠ANC,∴CA=CN.(2)连接OC,如图2所示.∵cos∠DFA= ,∠DFA=∠ACH,∴= .设CH=4a,则AC=5a,AH=3a,∵CA=CN,∴NH=a,∴AN= = = a=2 ,∴a=2,AH=3a=6,CH=4a=8.设圆的半径为r,则OH=r﹣6,在Rt△OCH中,OC=r,CH=8,OH=r﹣6,∴OC2=CH2+OH2,r2=82+(r﹣6)2,解得:r= ,∴圆O的直径的长度为2r= .。
【中考强化】2018年九年级数学 中考复习 圆 解答题 强化练习(含答案)
2018年九年级数学中考复习圆解答题强化练习1.如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.(1)判断DE与⊙O的位置关系并说明理由;(2)若tanC=,DE=2,求AD的长.2.已知:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q在⊙O上,连接PQ.(1)如图①,线段PQ所在的直线与⊙O相切,求线段PQ的长;(2)如图②,线段PQ与⊙O还有一个公共点C,且PC=CQ,连接OQ,AC交于点D.①判断OQ与AC的位置关系,并说明理由;②求线段PQ的长.3.如图,已知Rt△ABC,C=900,O在AB上,以O为圆心,OA为半径作⊙O,交AB于D点,与BC 相切于E点,连接AE.(1)求证:AE平分∠CAB;(2)若CE=2,BE=6,求sinB及⊙O的半径.4.如图,△ABC内接于⊙O,过点B作⊙O的切线DE,F为射线BD上一点,连接CF.(1)求证:CBE=A;(2)若⊙O 的直径为5,BF=2,tanA=2.求CF的长.5.如图,已知直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.(1)求证:DE是⊙O的切线;(2)若DE=6cm,AE=3cm,求⊙O的半径.6.如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O,与斜边AB交于点D、E为BC边的中点,连接DE.(1)求证:DE是⊙O的切线;(2)填空:①若∠B=30°,AC=2,则DE= ;②当∠B= °时,以O,D,E,C为顶点的四边形是正方形.7.如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F.过点D作⊙O的切线交AB的延长线于点E,过点A作⊙O的切线交ED的延长线于点G.(1)求证:△EFD为等腰三角形;(2)若OF:OB=1:3,⊙O的半径为3,求AG的长.8.如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连结BD.(1)求证:∠A=∠BDC;(2)若CM平分∠ACD,且分别交AD、BD于点M、N,当DM=1时,求MN的长.9.如图,已知⊙O的直径为AB,AC⊥AB于点A,BC与⊙O相交于点D,在AC上取一点E,使得ED=EA.(1)求证:ED是⊙O的切线;(2)若⊙O半径为2.5,OE=10时,求DE的长.10.如图,在等腰梯形ABCD中,AD∥BC.O是CD边的中点,以O为圆心,OC长为半径作圆,交BC边于点E.过E作EH⊥AB,垂足为H.已知⊙O与AB边相切,切点为F.(1)求证:OE∥AB; (2)求证:EH=AB; (3)若BH=1,EC=,求⊙O的半径.11.如图,四边形ABCD是⊙O的内接四边形,AC为直径,弧BD=弧AD,DE⊥BC,垂足为E.(1)求证:CD平分∠ACE;(2)判断直线ED与⊙O的位置关系,并说明理由;(3)若CE=1,AC=4,求阴影部分的面积.12.如图,△ABC中,E是AC上一点,且AE=AB,∠BAC=2∠EBC,以AB为直径的⊙O交AC于点D,交EB于点F.(1)求证:BC与⊙O相切;(2)若AB=8,sin∠EBC=0.25,求AC的长.13.如图,已知矩形ABCD,⊙O经过A、B两点,与CD切于E点.(1)如图1,若四边形ABCD为正方形,AB=4,求⊙O的半径;(2)如图2,BC与⊙O交于F点,若四边形OBFE为平行四边形,求AB:AD的值.14.在平面直角坐标中,△ABC三个顶点坐标为A(﹣,0)、B(,0)、C(0,3).(1)求△ABC内切圆⊙D的半径.(2)过点E(0,﹣1)的直线与⊙D相切于点F(点F在第一象限),求直线EF的解析式.(3)以(2)为条件,P为直线EF上一点,以P为圆心,以2为半径作⊙P.若⊙P上存在一点到△ABC三个顶点的距离相等,求此时圆心P的坐标.15.以坐标原点为圆心,1为半径的圆分别交x,y轴的正半轴于点A,B.(1)如图一,动点P从点A处出发,沿x轴向右匀速运动,与此同时,动点Q从点B处出发,沿圆周按顺时针方向匀速运动.若点Q的运动速度比点P的运动速度慢,经过1秒后点P运动到点(2,0),此时PQ恰好是⊙O的切线,连接OQ. 求∠QOP的大小;(2)若点Q按照(1)中的方向和速度继续运动,点P停留在点(2,0)处不动,求点Q再经过5秒后直线PQ被⊙O截得的弦长.参考答案1.解:2.解:(1)如图①,连接OQ.∵线段PQ所在的直线与⊙O相切,点Q在⊙O上,∴OQ⊥OP.又∵BP=OB=OQ=2,∴PQ=2,即PQ=2;(2)OQ⊥AC.理由如下:如图②,连接BC.∵BP=OB,∴点B是OP的中点,又∵PC=CQ,∴点C是PQ的中点,∴BC是△PQO的中位线,∴BC∥OQ.又∵AB是直径,∴∠ACB=90°,即BC⊥AC,∴OQ⊥AC.(3)如图②,PC•PQ=PB•PA,即0.5PQ2=2×6,解得PQ=2.3.答案:(1)连OE,证明略;(2)sinB=1/3,圆O的半径为.4.5.(1)略;(2)7.5;.6.7.(1)证明:连接OD,∵OC=OD,∴∠C=∠ODC,∵OC⊥AB,∴∠COF=90°,∴∠OCD+∠CFO=90°,∵GE为⊙O的切线,∴∠ODC+∠EDF=90°,∵∠EFD=∠CFO,∴∠EFD=∠EDF,∴EF=ED.(2)解:∵OF:OB=1:3,⊙O的半径为3,∴OF=1,∵∠EFD=∠EDF,∴EF=ED,在Rt△ODE中,OD=3,DE=x,则EF=x,OE=1+x,21·世纪*教育网∵OD2+DE2=OE2,∴32+x2=(x+1)2,解得x=4,∴DE=4,OE=5,∵AG为⊙O的切线,∴AG⊥AE,∴∠GAE=90°,而∠OED=∠GEA,∴Rt△EOD∽Rt△EGA,∴OD:AG=DE:AE,即3:AG=4:8,∴AG=6.8.解:(1)如图,连接OD,∵AB为⊙O的直径,∴∠ADB=90°,即∠A+∠ABD=90°,又∵CD与⊙O相切于点D,∴∠CDB+∠ODB=90°,∵OD=OB,∴∠ABD=∠ODB,∴∠A=∠BDC;(2)∵CM平分∠ACD,∴∠DCM=∠ACM,又∵∠A=∠BDC,∴∠A+∠ACM=∠BDC+∠DCM,即∠DMN=∠DNM,∵∠ADB=90°,DM=1,∴DN=DM=1,∴MN==.9.10.(1)连接OM,过点O作ON⊥CD,垂足为N.∵⊙O与BC相切于M,∴OM⊥BC.∵正方形ABCD中,AC平分∠BCD,∴OM=ON.∴CD与⊙O相切(2)设正方形ABCD的边长为a.可证得△COM∽△CAB∴,∴解得 a =∴正方形ABCD的边长为.11.解:(1)∵,∴∠BAD=∠ACD,∵∠DCE=∠BAD,∴∠ACD=∠DCE,即CD平分∠ACE;(2)直线ED与⊙O相切.理由如下:连结OD,如图,∵OC=OD,∴∠OCD=∠ODC,而∠OCD=∠DCE,∴∠DCE=∠ODC,∴OD∥BC,∵DE⊥BC,∴OD⊥DE,∴DE为⊙O的切线;(3)作OH⊥BC于H,则四边形ODEH为矩形,∴OD=EH,∵CE=1,AC=4,∴OC=OD=2,∴CH=HE﹣CE=2﹣1=1,在Rt△OHC中,∠HOC=30°,∴∠COD=60°,∴阴影部分的面积=S扇形OCD﹣S==.△OCD12. (1)证明:连接AF.∵AB为直径,∴∠AFB=90°.∵AE=AB,∴△ABE为等腰三角形.∴∠BAC=2∠BAF.∵BAC=2EBC,∴∠BAF∠EBC∴∠FAB+∠FBA=∠EBC+∠FBA=90°.∴∠ABC=90° .∴BC与⊙0相切.(2) 解:过E作EG⊥BC于点G∵∠BAF=∠EBC,∴sin∠BAF=sin∠EBC=0.25..在△AFB中,∠AFB=90°,∵AB=8,∴BF=2∴BE=2BF=4.在△EGB中,∠EGB=90°,∴EG=1∵EG⊥BC,AB⊥BC,∴EG∥AB∴△CEG∽△CAB∴CE:CA=EG:AB.∴CE=8/7.∴AC=AE+CE=64/7.13.解:(1)r=2.5;(2)AB:AD=.14.解:(1)连接BD ,∵B (,0),C (0,3),∴OB=,OC=3,∴tan ∠CBO==,∴∠CBO=60°∵点D 是△ABC 的内心,∴BD 平分∠CBO ,∴∠DBO=30°,∴tan ∠DBO=,∴OD=1,∴△ABC 内切圆⊙D 的半径为1;(2)连接DF ,过点F 作FG ⊥y 轴于点G ,∵E (0,﹣1)∴OE=1,DE=2,∵直线EF 与⊙D 相切,∴∠DFE=90°,DF=1,∴sin ∠DEF=,∴∠DEF=30°,∴∠GDF=60°,∴在Rt △DGF 中,∠DFG=30°,∴DG=,由勾股定理可求得:GF=,∴F (,),设直线EF 的解析式为:y=kx+b ,∴,∴直线EF 的解析式为:y=x ﹣1;(3)∵⊙P 上存在一点到△ABC 三个顶点的距离相等,∴该点必为△ABC 外接圆的圆心,由(1)可知:△ABC 是等边三角形,∴△ABC 外接圆的圆心为点D ∴DP=2,设直线EF 与x 轴交于点H ,∴令y=0代入y=x ﹣1,∴x=,∴H (,0),∴FH=,当P 在x 轴上方时,过点P 1作P 1M ⊥x 轴于M ,由勾股定理可求得:P 1F=3,∴P 1H=P 1F+FH=,∵∠DEF=∠HP 1M=30°,∴HM=P 1H=,P 1M=5,∴OM=2,∴P 1(2,5),当P 在x 轴下方时,过点P 2作P 2N ⊥x 轴于点N ,由勾股定理可求得:P 2F=3,∴P 2H=P 2F ﹣FH=,∴∠DEF=30°∴∠OHE=60°∴sin ∠OHE=,∴P 2N=4,令y=﹣4代入y=x ﹣1,∴x=﹣,∴P 2(﹣,﹣4),综上所述,若⊙P 上存在一点到△ABC 三个顶点的距离相等,此时圆心P 的坐标为(2,5)或(﹣,﹣4).15.(1)连AQ,△OAQ为等边三角形,∴∠QOP=60°由(1)可知点Q运动1秒时经过的弧长所对的圆心角为30°,若Q按照(1)中的方向和速度继续运动,那么再过5秒,则Q点落在⊙O与y轴负半轴的交点处(如图二).设直线PQ与⊙O 的另外一个交点为D,过O作OC⊥QD于点C,则C为QD的中点.∵∠QOP=90°,OQ=1,OP=2,∴QP=∵0.5OQ•OP=0.5QP•OC,∴OC=∵OC⊥QD,∴QC=∴QD=。
2018年江西省中考数学《第六单元圆》总复习检测卷含解析
__________ .
图7 11.将直角△ ABC 绕顶点 B 旋转至如图 8 位置,其中∠ C= 90°,AB= 4,BC= 2,点 C,
B,A′在同一直线上,则阴影部分的面积是 __________ .
图8 12.如图 9,直线 AB,CD 相交于点 O,∠ AOC= 30°,⊙ P 的半径为 1 cm,且 OP =4 cm, 如果⊙ P 以 1 cm/s 的速度沿由 A 向 B 的方向移动, 那么 __________ 秒后⊙ P 与直线 CD 相切.
图9
三、 (本大题共 5 小题,每小题 6 分,共 30 分 )
13.赵州桥是我国建筑史上的一大创举,它距今约
1 400 年,历经无数次洪水冲击和 8
次地震却安然无恙.如图 10,若桥跨度 AB 约为 40 米,主拱高 CD 约 10 米,求桥弧 AB 所
在圆的半径.
图 10
14.如图 11,四边形 ABCD 内接于⊙ O,AC 平分∠ BAD,延长 DC 交 AB 的延长线于点 E.若 AC= EC,求证: AD = BE.
CE,∠ EAC+∠ BAE= 180 °, AB = CD .
图 13 (1) 判断 BE 与 CE 之间的数量关系,并说明理由; (2) 求证:△ ABE≌△ DCE .
17. (2017 贵阳 )如图 14, C,D 是半圆 O 上的三等分点,直径 AB=4,连接 AD,AC, DE ⊥ AB,垂足为 E,DE 交 AC 于点 F .
图2
A . 25°
B. 40°
C. 50°
D. 65°
5.如图 3,AB 是⊙ O 的直径, CD 是⊙ O 的弦,∠ ACD =30°,则∠ BAD 的度数为 ( )
【中考数学】2018最新版本中考数学圆综合练习题含答案(历年真题-可打印)
1 数学中考圆综合题附参考答案
1.如图,△ABC 中,以BC 为直径的圆交
AB 于点D ,∠ACD =∠ABC .(1)求证:CA 是圆的切线;
(2)若点E 是BC 上一点,已知BE =6,tan ∠ABC =32
,tan ∠AEC =35
,求圆的直径.
2. 如图右,已知直线
PA 交⊙0于A 、B 两点,AE 是⊙0的直径.点C 为⊙0上一点,且AC 平分∠PAE ,过C 作CD
⊥PA ,垂足为D 。
(1)求证:CD 为⊙0的切线;
(2)若DC+DA=6,⊙0的直径为l0,求AB 的长度.
1. (1)证明:连接OC,
∵点C 在⊙0上,0A=OC,∴∠OCA=∠OAC ,∵CD ⊥PA ,∴∠CDA=90°,有∠CAD+∠DCA=90°,∵AC 平分∠PAE ,∴∠DAC=∠CAO 。
∴∠DC0=∠DCA+∠ACO=∠DCA+∠CAO=∠DCA+∠DAC=90°。
又∵点C 在⊙O 上,OC 为⊙0的半径,∴CD 为⊙0的切线.
(2)解:过0作0F ⊥AB ,垂足为F ,∴∠OCA=∠CDA=∠OFD=90°,∴四边形OCDF 为矩形,∴0C=FD ,OF=CD.
∵DC+DA=6,设AD=x ,则OF=CD=6-x
,∵⊙O 的直径为10,∴DF=OC=5,∴AF=5-x ,在Rt △AOF 中,由勾股定理得
222AF +OF =OA .即22(5)(6)25x x ,化简得:211180x x 解得2x 或9x 。
由AD<DF ,知05x ,故2x 。
通用版2018年中考数学总复习专题突破预测与详解第六单元圆专题21与圆有关的计算试题新版新人教版2018011212
专题21与圆有关的计算2016~2018详解详析第28页A组基础巩固1.(2017广西贵港一模,6,3分)若一个正多边形的中心角为40°,则这个多边形的边数是(A)A.9B.8C.7D.62.(2017山东德州庆云一练,5,3分)如图,扇形OAB是圆锥的侧面展开图,若小正方形方格的边长均为1厘米,则这个圆锥的底面半径为(B)厘米.A. B.C.D.23.(2017四川资阳简阳一模,6,3分)一个圆锥的底面半径是5 cm,其侧面展开图是圆心角是150°的扇形,则圆锥的母线长为(B)A.9 cmB.12 cmC.15 cmD.18 cm4.(2017安徽芜湖繁昌模拟,12,5)如图,四边形ABCD是☉O的内接四边形,☉O的半径为2,∠B=135°,则的长π.5.(2017内蒙古巴彦淖尔一模,14,4分)如图,正方形ABCD是☉O的内接正方形,点P是劣弧上不同于点C的任意一点,则∠BPC的度数是45度.〚导学号92034090〛6.(2017山东滨州博兴模拟,22,10分)如图,已知AB是☉O的直径,点C,D在☉O上,∠D=60°且AB=6,过O点作OE⊥AC,垂足为E.(1)求OE的长;(2)若OE的延长线交☉O于点F,求弦AF,AC和弧CF围成的图形(阴影部分)的面积S.解(1)∵∠D=60°,∴∠B=60°(圆周角定理),∵AB是☉O的直径,∴∠ACB=90°.又AB=6,∴BC=3.∵OE⊥AC,∴OE∥BC.又点O是AB中点,∴OE是△ABC的中位线.∴OE=BC=.(2)连接OC,则易得△COE≌△AFE,故阴影部分的面积=扇形FOC的面积,S扇形FOC==π.即可得阴影部分的面积为π.B组能力提升1.(2017天津南开一模,10,3分)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是(D)A.B.C.D.2.(2017江苏苏州一模,10,24)如图,已知Rt△ABD中,∠A=90°,将斜边BD绕点B顺时针方向旋转至BC,使BC∥AD,过点C作CE⊥BD于点E.(1)求证:△ABD≌△ECB;(2)若∠ABD=30°,BE=3,求弧CD的长.(1)证明∵∠A=90°,CE⊥BD,∴∠A=∠BEC=90°.∵BC∥AD,∴∠ADB=∠EBC.∵将斜边BD绕点B顺时针方向旋转至BC,∴BD=BC.在△ABD和△ECB中,∠ADB=∠EBC,∠A=∠BEC,BD=CB,∴△ABD≌△ECB.(2)解∵△ABD≌△ECB,∴AD=BE=3.∵∠A=90°,∠ABD=30°,∴BD=2AD=6.∵BC∥AD,∴∠A+∠ABC=180°,∴∠ABC=90°.∴的长为=2π.〚导学号92034091〛C组综合创新(2017山东青岛市北区模拟,13,3分)如图,一根5米长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A(羊只能在草地上活动),那么小羊A在草地上的最大活动区域面积是π平方米.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六单元 圆 与圆有关的计算 基础达标训练 1. (2017株洲)下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( ) A. 正三角形 B. 正方形 C. 正五边形 D. 正六边形 2. (2017南宁)如图,⊙O是△ABC的外接圆,BC=2,∠BAC=30°,则劣弧BC︵
的长等于( )
A. 2π3 B. π3 C. 23π3 D. 3π3
第2题图 第3题图 3. (2017宁夏)圆锥的底面半径r=3,高h=4,则圆锥的侧面积是( ) A. 12π B. 15π C. 24π D. 30π 4. (2017麓山国际实验学校一模)如图,某数学兴趣小组将边长为6的正方形铁丝框ABCD变形为以A为圆心,AB为半径的扇形(忽略铁丝的粗细),则所得扇形DAB的面积为( )
第4题图 A. 12 B. 14 C. 16 D. 36 5. (2017沈阳)正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( ) A. 3 B. 2 C. 22 D. 23
第5题图 第6题图 6. (2017烟台)如图,▱ABCD中,∠B=70°,BC=6,以AD为直径的⊙O交CD于点E,则DE︵的长为( ) A. 13π B. 23π C. 76π D. 43π
7. (2017宁波)如图,在Rt△ABC中,∠A=90°,BC=22,以BC的中点O为圆心的圆分别与AB,AC相切于D,E两点,则DE︵的长为( )
A. π4 B. π2 C. π D. 2π
第7题图 第8题图 8. (2017淄博)如图,半圆的直径BC恰与等腰直角三角形ABC的一条直角边完全重合,若BC=4,则图中阴影部分的面积是( ) A. 2+π B. 2+2π C. 4+π D. 2+4π 9. (2017兰州)如图,正方形ABCD内接于半径为2的⊙O,则图中阴影部分的面积为( ) A. π+1 B. π+2 C. π-1 D. π-2 第9题图 第11题图 10. (2017哈尔滨)已知扇形的弧长为4π,半径为8,则此扇形的圆心角为__________度. 11. (2017台州)如图,扇形纸扇完全打开后,外侧两竹条AB,AC的夹角为120°,AB长为30厘米,则BC︵的长为________厘米(结果保留π). 12. 关注传统文化(2017长沙中考模拟卷二)打陀螺是一项古老的中国民间娱乐活动,在云南的少数民族地区开展广泛,特别是在思茅地区有着悠久的历史传统,在思茅地区又以景谷县陀螺运动开展得最好,有着“陀螺之乡”的称号.已知木质陀螺的外观为圆锥形,测得该圆锥的母线长为6 cm,底面圆的半径为3 cm,则该圆锥的全面积为________cm2. 13. (2017安徽)如图,已知等边△ABC的边长为6,以AB为直径的⊙O与边AC,BC分别交于D,E两点,则劣弧DE︵的长为________.
第13题图 第14题图 14. (2017湖南师大附中第一次联考)如图,△ABC是⊙O的内接正三角形,⊙O的半径为3,则图中阴影部分的面积是________.
15. 关注数学文化(2017岳阳)我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率π的近似值.设半径为r的圆内接正n边形的周长为L,圆的直径为d,如图所示,当n=6时,π≈Ld=6r2r=3,那么当n=12时,π≈Ld=________.(结果精确到0.01,参考数据:sin15°=cos75°≈0.259)
第15题图 能力提升训练 1. 如图,半径为1 cm的⊙O中,AB为⊙O内接正九边形的一边,点C、D分
别在优弧与劣弧上.则下列结论:①S扇形AOB=19πcm2;②lAB︵=29πcm;③∠ACB
=20°;④∠ADB=140°.其中错误的有( ) A. 0个 B. 1个 C. 2个 D. 3个
第1题图 第2题图 2. (2017重庆A卷)如图,矩形ABCD的边AB=1,BE平分∠ABC,交AD于点E.若点E是AD的中点,以点B为圆心,BE长为半径画弧,交BC于点F,则图中阴影部分的面积是( )
A. 2-π4 B. 32-π4 C. 2-π8 D. 32-π8
3. (2017十堰)如图,已知圆柱的底面直径BC=6π cm,高AB=3 cm,小虫在圆柱表面爬行,从点C爬到点A,然后再沿另一面爬回到点C,则小虫爬行的最短路程为( ) A. 32 cm B. 35 cm C. 65 cm D. 62 cm
第3题图 第4题图 4. (2017山西)如图是某商品的标志图案.AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD. 若AC=10 cm,∠BAC=36°,则图中阴影部分的面积为( ) A. 5π cm2 B. 10π cm2 C. 15π cm2 D. 20π cm2 5. (2017上海)我们规定:一个正n边形(n为整数,n≥4)的最短对角线与最长对角线长度的比值叫做这个正n边形的“特征值”,记为λn,那么λ6=________. 6. (2017云南)如图,边长为4的正方形ABCD外切于⊙O,切点分别为E、F、G、H,则图中阴影部分的面积为________.
第6题图 7. (9分)(2017河北)如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧CD︵于点P,Q,且点P,Q在AB异侧,连接OP. (1)求证:AP=BQ;
(2)当BQ=43时,求QD︵的长(结果保留π); (3)若△APO的外心在扇形COD的内部,求OC的取值范围. 第7题图 圆的相关证明与计算巩固集训 类型一 圆的基本性质 1. (8分)(2017南雅中学一模)如图,已知四边形ABCD内接于⊙O,连接BD,∠BAD=105°,∠DBC=75°. (1)求证:BD=CD; (2)若⊙O的半径为6,求BC︵的长.
第1题图
2. (9分)(2017苏州)如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F. (1)求证:△DOE∽△ABC; (2)求证:∠ODF=∠BDE;
(3)连接OC,设△DOE的面积为S1,四边形BCOD的面积为S2,若S1S2=27,求sinA的值. 第2题图 类型二 切线的相关证明与计算 3. (8分)(2017陕西)如图,已知⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C、交PB于点D,连接BC.当∠P=30°时, (1)求弦AC的长; (2)求证:BC∥PA.
第3题图 4. (8分)(2017山西)如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D. (1)若AC=4,BC=2,求OE的长; (2)试判断∠A与∠CDE的数量关系,并说明理由.
第4题图 5. (8分)(2017湖南师大附中三模)如图,⊙O为△ABD的外接圆,AB为⊙O的直径,BC为⊙O的切线. (1)求证:∠BAD=∠DBC; (2)若⊙O的半径为3,BD⊥OC,交OC于点E,且BD=BC,求AD的长.
第5题图 6. (8分)(2017枣庄)如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F. (1)试判断直线BC与⊙O的位置关系,并说明理由; (2)若BD=23,BF=2,求阴影部分的面积(结果保留π).
第6题图 7. (9分)(2017达州)如图,△ABC内接于⊙O,CD平分∠ACB交⊙O于D,过点D作PQ∥AB分别交CA、CB延长线于P、Q,连接BD. (1)求证:PQ是⊙O的切线; (2)求证:BD2=AC·BQ;
(3)若AC、BQ的长是关于x的方程x+4x=m的两实根,且tan∠PCD=13,求⊙O的半径. 第7题图 8. (9分)(2017雅礼实验中学期中考试)在平面直角坐标系xOy中,已知点A(8,0),点B(0,8),动点C在以半径为4的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列),连接AB. (1)当OC∥AB时,求∠BOC的度数; (2)连接AD,当OC∥AD时,求出点C的坐标; (3)在(2)的条件下,连接BC,直线BC是否为⊙O的切线?请作出判断,并说明理由.
第8题图 答案 1. A 【解析】内接正多边形的边数越少,则边就越长,所对的圆心角就越大. 2. A 【解析】如解图,连接OB,OC,∵∠BAC=30°,∴∠BOC=2∠BAC=60°,∴△BOC为等边三角形,又∵BC=2,∴OB=OC=BC=2,∴lBC︵=60×π×2180=2π3.
