九年级数学下册244第3课时切线长定理小册子课件沪科版
合集下载
九年级数学《切线长定理》课件

PB,切点分别是A、B.
求证: AP=BP, ∠OPA=∠OPB
证明:连接OA,OB
A
∵PA,PB与⊙O相切,
点A,B是切点
∴OA⊥PA,OB⊥PB
即 ∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
B
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB ∠OPA=∠OPB
切线长定理
从圆外一点可以引圆的两条切线,它们的切线长 相等,这一点和圆心的连线平分两条切线的夹角
AD、BE、CF C
A D
O
C B
PF
A
E
O B
D
24.4.3 切线长定理
平面内任取一点P,作圆O的切线, 你能作几条?怎么作?
O
概念辨析
切线长:切线上一点与切点之间的线段 长叫做这点到圆的切线长
思考:切线和切线长有何区别和联系?
(1)切线是一条与圆相切的直线,不能度量.
(2)切线长是一条线段的长,它是一个数量,
可以度量.
A
B
已知:从⊙O外的一点P引两条切线PA,
(2)若∠APB=60°,则∠AOB= ,PA= ;
连接AB,则AB=
;
在A、B之间弧上任取
A
一点C,则∠ACB= .
4 30°
2
B
3、如左图,PA、PB、DE是圆O的三条切线,
∆PCD的周长为8,则PA=
.
4、如图,∆ABC的内切圆O与AB、BC、AC相
切于点D、E、F,且AB=5,BC=9,AC=6,求
符号语言:
A
∵PA、PB分别切⊙O于点A、B
∴PA = PB;∠OPA=∠OPB
九年级数学下册第24章圆24、4直线与圆的位置关系第3课时切线长定理教学课件新版沪科版
O P
B
课程讲授
1 切线长定理
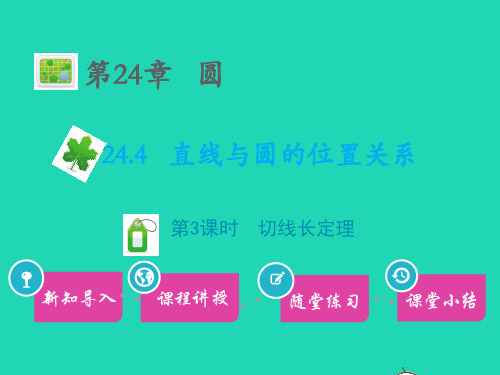
问题1:如图,PA、PB是的两条切线,切点分别为A、
B.在半透明的纸上画出这个图形,沿着直线PO将图形
对折,图中的PA与PB,∠APO与∠BPO有什么关系?
A
我们发现:
PA__=__PB,
O
∠APO__=__∠BPO
P
BA
课程讲授
1 切线长定理
A
O
B
如图,连接OA ,OB. ∵PA,PB是⊙O的两条切线
两点,PA=4 cm,∠APB=40°,C是AB上任意一点,过
C作⊙O的切线分别交PA,PB于点D,E.求:
(1)△PDE的周长; (2)∠DOE的度数.
随堂练习
解 (1)∵PA,PB分别切⊙O于点A,B,
∴PB=PA=4 cm.
同理可得DA=DC,EC=EB.
∵△PDE的周长=PD+PE+DE, DE=DC+CE, ∴△PDE的周长 =(PD+DA)+(PE+EB) =PA+PB =8 cm.
∴∠DOE=
1 2
∠AOB=70°.
∵四边形内角和为360°,
课堂小结
切线长定理
过圆外一点作圆的两条 切线,两条切线长相等, 圆心与这一点的连线平分 两条切线的夹角.
∴OA ⊥ AP,OB ⊥ BP.
P 又OA =OB ,OP =OP.
∴Rt△AOP≌Rt△ BOP. ∴AP=BP.
∠APO=∠BPO
课程讲授
1 切线长定理
切线长定理: 过圆外一点作圆的两条切线,它们的切线长_相__等__.这 一点与圆心的连线_平__分___两条切线的夹角.
B
课程讲授
1 切线长定理
问题1:如图,PA、PB是的两条切线,切点分别为A、
B.在半透明的纸上画出这个图形,沿着直线PO将图形
对折,图中的PA与PB,∠APO与∠BPO有什么关系?
A
我们发现:
PA__=__PB,
O
∠APO__=__∠BPO
P
BA
课程讲授
1 切线长定理
A
O
B
如图,连接OA ,OB. ∵PA,PB是⊙O的两条切线
两点,PA=4 cm,∠APB=40°,C是AB上任意一点,过
C作⊙O的切线分别交PA,PB于点D,E.求:
(1)△PDE的周长; (2)∠DOE的度数.
随堂练习
解 (1)∵PA,PB分别切⊙O于点A,B,
∴PB=PA=4 cm.
同理可得DA=DC,EC=EB.
∵△PDE的周长=PD+PE+DE, DE=DC+CE, ∴△PDE的周长 =(PD+DA)+(PE+EB) =PA+PB =8 cm.
∴∠DOE=
1 2
∠AOB=70°.
∵四边形内角和为360°,
课堂小结
切线长定理
过圆外一点作圆的两条 切线,两条切线长相等, 圆心与这一点的连线平分 两条切线的夹角.
∴OA ⊥ AP,OB ⊥ BP.
P 又OA =OB ,OP =OP.
∴Rt△AOP≌Rt△ BOP. ∴AP=BP.
∠APO=∠BPO
课程讲授
1 切线长定理
切线长定理: 过圆外一点作圆的两条切线,它们的切线长_相__等__.这 一点与圆心的连线_平__分___两条切线的夹角.
2017年春季新版沪科版九年级数学下学期24.4.3、切线长定理课件5

图24-4-50
第3课时
切线长定理
[归纳] 从圆外一点能够作圆的 ________ 条切线,切线上这 两 一点到切点之间的线段长叫做这点到圆的________ 切线长 .
第3课时
切线长定理
学习目标2
认识切线长定理
2.如图24-4-9,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O 于点C,下列结论中,错误的是( D )
AM 1 ∴AM=0.5,MB=4.5,∴ = . BM 9
第3课时
切线长定理
[听课笔记] _______________________________________________________
______________
第3课时
切线长定理
课 堂 小 结
相等 平分
第3课时
切线长定理
[反思] 在解决有关圆的切线长问题时,往往需要构建哪些 基本图形?
∴AM=AR,BM=BN,CN=CP,DP=DQ,EQ=ER,
∴BN=y. ∵AB=5,∴x+y=5. ∵BC=7,∴CN=CP=7-y. ∵CD=8,∴DQ=DP=y+1.
∵DE=9,∴EQ=ER=8-y.
∵EA=4,∴AR=AM=y-4. ∴y-4=x.
第3课时
切线长定理
x+y=5, ∴ y-4=x, x=0.5, 解得 y=4.5.
24.4 直线与圆的位置关系
第3课时 切线长定理
第3课时
切线长定理
自 主 学 习 学习目标1 会过圆外一点作圆的切线,知道切线长的概念
1.如图24-4-8,以OP为直径画圆,使它和⊙O交于A,B两 点,连接PA,PB.则PA,PB与⊙O有什么关系?
图24-4-8
2018年春沪科版九年级数学下24.4第3课时切线长定理ppt公开课优质教学课件

3. 如图,AB、AC、BD是☉O的切线,P、C、D为切点, 如果AB= 5,AC=3,则BD = 2 . A
P B
◑切线长与切线的区别 ①切线是直线,不能度量. ②切线长是线段的长,这条线段的两个端点分别 是圆外一点和切点,可以度量.
O,A,B,P四 点共圆哦!
问题2 沿直线PO将图形折叠,你有什么发现? 试着 自己证明. PA = PB, ∠APO =∠BPO. 证明:连接OA,OB, ∵ PA切☉O于点A, ∴ OA⊥PA. 同理可得 OB⊥PB. ∵ OA = OB,OP = OP, A
C O
·
F B
E
例2 如图,PA、PB 分别与 ⊙O 相切于点 A、B,⊙O 的 切线 EF 分别交 PA、PB 于点 E、F,切点 C 在弧 AB上. 若PA长为2,则△PEF的周长是________ . 4
解析:因为PA、PB分别与⊙O 相切于点 A、B,所以PA=PB. 因为 ⊙O 的切线EF分别交PA、 PB于点E、F,切点为C,所以 EA = EC,CF = BF,所以 △PEF 的周长是PE+EF+PF =PE+EC+CF+PF=PA+PB =2+2=4.
例3 如图,PA、PB 是 ⊙O 的切线,切点分别为 A、B, 点 C 在⊙O上,如果 ∠ACB=70°,那么 ∠OPA 的度 数是________ 20 度. 解析:如图所示,连接OA、OB. ∠AOB=2∠ACB= 140°. ∵PA、PB是⊙O的切线,切点分别为A、B, ∴O,A,B,P四点共圆,OP平分∠APB,∴∠APB= 180°-∠AOB=180°-140° =40°=2∠OPA. ∴∠OPA=20°. 故答案为 20.
P
2. 若PO交⊙O于点C,连接CA、CB,你又能得出什么 新的结论? 请给出证明. CA=CB 证明:∵ PA,PB是⊙O的切线,点 A,B是切点, ∴PA = PB ,∠OPA=∠OPB. 又∵ PC=PC. A ∴ △PCA ≌ △PCB, C ∴CA=CB. O. P B
初三下数学课件(沪科版)-切线长定理
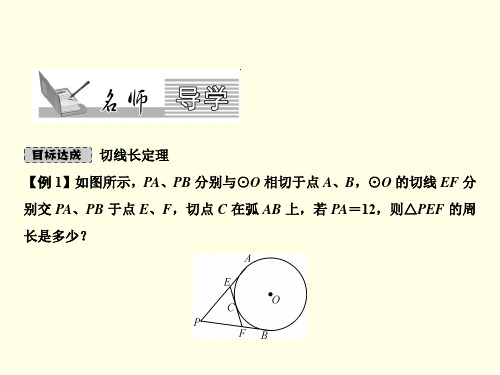
解:(1)∵PA、PB 是⊙O 的切线,∴∠BAP=90°-∠1=70°,∵PA=PB,
∴∠BAP=∠ABP=70°.∴∠APB=180°-70°×2=40°; (2)当∠1=30°时,OP=OD.理由:∵∠1=30°,由(1)知∠BAP=∠ABP=
60°.∴∠APB=180°-60°×2=60°.∵PA、PB 是⊙O 的切线,∴∠OPB=12
7.如图,AD、AE 和 BC 分别与⊙O 相切,切点为 D、E、F,若 AD=20, 则△ABC 的周长是 40 .
8.如图,AB 为⊙O 的直径,弦 CD⊥AB 于点 E,过点 C 作⊙O 的切线交
︵︵
AB 的延长线于点 M,下列结论:①CE=DE;②BC=BD;③MD 为⊙O 的切线;④MC=MD.其中正确结论的个数是( D )
∴DA=2PO,又 AD=AC,∴AC=2OP=PC,∴AC=PC.
×18=9(cm),∵PA、PB 是⊙O 的切线,∴∠APO=12∠APB=30°,在 Rt△AOP 中,PO=2AO,∴OA2+92=(2AO)2,解得 AO=3 3.即⊙O 的半
径为 3 3cm.
13.如图,PA、PB 是⊙O 的切线,A、B 为切点,AC 是⊙O 的直径,AC、 PB 的延长线相交于点 D. (1)若∠1=20°,求∠APB 的度数; (2)当∠1 为多少度时,OP=OD,并说明理由.
⊙O 与 AC、BC 分别相切于点 D、E,点 F 是⊙O 与 AB 的一个交点,连接 DF 并延长交 CB 的延长线于点 G.则 CG= 3+3 2 .
11.如图,在直角坐标系中,⊙A 的圆心 A 的坐标为(-1,0),半径为 1,点
P 为直线 y=-34x+3 上的动点,过点 P 作⊙A 的切线,切点为 Q,则切线 长 PQ 的最小值是 2 2 .
初三九年级数学沪科版 第24章 圆 训练习题课件24.4.3 切线长定理

能力提升练
11.如图,已知 AB 为⊙O 的直径,AB=2,AD 和 BE 是⊙O 的 两条切线,A,B 为切点,过圆上一点 C 作⊙O 的切线 CF, 分别交 AD,BE 于点 M,N,连接 AC,CB.若∠ABC=30°, 3 则 AM=____3____.
能力提升练
12.已知在⊙O 中,AC 为直径,MA,MB 分别切⊙O 于点 A,B. (1)如图①,若∠BAC=25°,求∠AMB 的大小; 解:∵MA 切⊙O 于点 A, ∴∠MAC=90°. ∴∠MAB=∠MAC-∠BAC=65°. ∵MA,MB 分别切⊙O 于点 A,B, ∴MA=MB.∴∠MAB=∠MBA. ∴∠AMB=180°-(∠MAB+∠MBA)=50°.
【答案】D
基础巩固练
4.如图,AD,AE,CB 均为⊙O 的切线,D,E,F 分别是切点,
AD=8,则△ABC 的周长为( C )
A.8
B.12
C.16
D.不能确定
基础巩固练
5.如图,已知⊙O 分别与△ABC 的 BC 边、AB 的延长线、AC
的延长线相切,则∠BOC 等于( C )
A.∠A
B.90°+∠A
能力提升练
∴四边形 MADB 是菱形.∴AD=BD. 又∵AC 为直径,BD⊥AC,
︵︵ ∴AB=AD. ∴AB=AD. ∴△ABD 是等边三角形,∴∠D=60°. ∴在菱形 MADB 中,∠AMB=∠D=60°.
能力提升练
13.如图①,直线 y=-34x+3 与 x 轴相交于点 A,与 y 轴相交 于点 B,点 C(m,n)是第二象限内一点,以点 C 为圆心的圆 与 x 轴相切于点 E,与直线 AB 相切于点 F.
基础巩固练
8.如图,AC⊥BC 于点 C,BC=4,AC=3,⊙O 与直线 AB, BC,CA 都相切,则⊙O 的半径为___2_____.
沪科版数学九年级下册沪科版九年级数学下册24.4.4《切线长定理修正版》ppt课件
三、自学提纲 看书本上第37-38页内容,解决以下问题: 1.过圆外一点如何作圆的切线? 2.切线长定义和切线长定理的内容是什么? 3.阅读例5,总结圆外切四边形具有什么性质? 4.完成课后练习1,2,3
灿若寒星
四、合作探究
1.从圆外一点作圆的切线,可以作几条?
已知:点P为⊙O外一点,过点P作直线与⊙O相切.
3,圆外切等腰梯形上、下底分别是9cm和25cm,则其内 切圆面积为_________.
4,已知圆外切等腰梯形的中位线长为3cm,则腰长为__
A 4
P
8
O
灿若寒星
B
5、四边形ABCD外切于⊙O
(1)若AB:BC:CD:DA=2:3:n:4
BA
则n=____ (2)若AB:BC:CD=5:4:7,周长为48 C
补例:如图:从⊙O外的定点P作
⊙O
D
的 在弧两A条B上切任线取,一分点别C,切⊙O于点A
和 过点B,C作⊙O的切线,分别交PA、
C
O
PB于点D、E。
E
试证:⑴ △PDE的周长(PA+PB) 是定值
⑵ ∠DOE的大小是定值(∠AOB/2)
若∠P=40°,你能说出∠DOE的 度数吗?
灿若寒星
补例:如图,AB是⊙O的弦,BD切⊙O于点 B,OD⊥OA, 与AB相交于点C, 求证:BD=CD. 解:连接OB,则OB⊥BD
灿若寒星
祝同学们学习进步,天天快乐
灿若寒星
五,理解应用
1,⊙O的半径为4,点P到圆心的距离为8,过P作⊙O的两 条切线,则这两条切线的夹角为__________.
2,在梯形 ABCD中,AD∥BC,∠ABC=90°,以 AB为直 径的半圆切 CD于点 M,若这个梯形的面积是10 cm2,周 长是14 cm,则半圆O的半径为_________
灿若寒星
四、合作探究
1.从圆外一点作圆的切线,可以作几条?
已知:点P为⊙O外一点,过点P作直线与⊙O相切.
3,圆外切等腰梯形上、下底分别是9cm和25cm,则其内 切圆面积为_________.
4,已知圆外切等腰梯形的中位线长为3cm,则腰长为__
A 4
P
8
O
灿若寒星
B
5、四边形ABCD外切于⊙O
(1)若AB:BC:CD:DA=2:3:n:4
BA
则n=____ (2)若AB:BC:CD=5:4:7,周长为48 C
补例:如图:从⊙O外的定点P作
⊙O
D
的 在弧两A条B上切任线取,一分点别C,切⊙O于点A
和 过点B,C作⊙O的切线,分别交PA、
C
O
PB于点D、E。
E
试证:⑴ △PDE的周长(PA+PB) 是定值
⑵ ∠DOE的大小是定值(∠AOB/2)
若∠P=40°,你能说出∠DOE的 度数吗?
灿若寒星
补例:如图,AB是⊙O的弦,BD切⊙O于点 B,OD⊥OA, 与AB相交于点C, 求证:BD=CD. 解:连接OB,则OB⊥BD
灿若寒星
祝同学们学习进步,天天快乐
灿若寒星
五,理解应用
1,⊙O的半径为4,点P到圆心的距离为8,过P作⊙O的两 条切线,则这两条切线的夹角为__________.
2,在梯形 ABCD中,AD∥BC,∠ABC=90°,以 AB为直 径的半圆切 CD于点 M,若这个梯形的面积是10 cm2,周 长是14 cm,则半圆O的半径为_________
合作市第七中学九年级数学下册第24章圆24.4直线与圆的位置关系第3课时切线长定理课件新版沪科版
即AB+CD=DA+BC.
探究 : PA、PB是⊙O的两条切线 ,
A
A、B为切点 , 直线OP交于⊙O于
点D、E , 交AB于C.
E O CD
P
〔1〕写出图中所有的垂直关系 ;
OA⊥PA , OB ⊥PB , AB ⊥OP
B
〔2〕写出图中与∠OAC相等的角和图中相等的线段 ;
∠OAC=∠OBC=∠APC=∠BPC ,
• 解 : 由切线长定理可知PA=PB. • ∵PA是⊙O的切线. • ∴∠OAP=90°. • ∵∠BAC=25°,∴∠BAP=65°. • 又∵PA=PB,∴∠BAP=∠ABP=65°.
• 2.如下图 , 一个油桶靠在墙边 , 量得 WY=1.65m , 并且XY⊥WY , 这个油桶底面 半径是多少?
∴ PA = PB , ∠OPA=∠OPB.
切线长定理
过圆外一点作圆的两条切线 , 两条切线长相等 , 圆心与这一点的 连线平分两条切线的夹角.
A P. B
. O
几何语言: PA、PB分别切⊙O于A、B
PA = PB ∠OPA=∠OPB
切线长定理为证明线段 相等、角相等提供新的方法.
例5 已知 : 如下图四边形ABCD的边AB , BC ,
如下图,是一条圆弧形弯道 , 已知 OA =20 m ,
OC = 12 m , C D 的长度为 9π m , 求圆弧形弯道的面积. 【教材P80页]
解设∠AOB = n° ,
∵ OC = 12 m ,C D 的长度为 9π m ,
∴
9
n12,
180
解得 n = 135 , 即圆心角∠COD = 135 ° .
求 : 〔1〕拱形的弧长 ;
2020春沪科版九年级数学下册习题课件-第24章 圆-24.4.3 切线长定理
∴∠ADO+∠EDO+∠OCB+∠OCE=180°, 又∠ADO=∠EDO, ∴2∠EDO+2∠OCE=180°,即∠EDO+∠OCE=90°. 在 Rt△DOC 中,∵F 是 DC 的中点,∴OF=12CD.
10.如图,PA,PB,CD 分别切⊙O 于 A,B,E,CD 交 PA, PB 于 C,D 两点,若∠P=60°,则∠PAE+∠PBE 的度数 为( C ) A.90° B.75° C.60° D.45°
【点拨】设光盘圆心为 O,三角板与光盘的切点为 C,连接 OA, OB,如图.由切线长定理知 AB=AC=3,AO 平分∠BAC, ∴∠OAB=60°.在 Rt△ABO 中,OB=ABtan∠OAB=3 3, ∴光盘的直径为 6 3.
【答案】D
4.如图,AD,AE,CB 均为⊙O 的切线,D,E,F 分别是切点,
证明:连接 OE,如图. ∵AM,DE 是⊙O 的切线,OA,OE 是⊙O 的半径, ∴∠ADO=∠EDO,∠DAO=∠DEO=90°,
∴∠AOD=∠EOD=12∠AOE. ∵∠ABE=12∠AOE. ∴∠AOD=∠ABE,∴OD∥BE.
(2)猜想:OF 与 CD 有何数量关系?并说明理由. 解:OF=12CD. 理由:连接 OC,如图. ∵BC,CE 是⊙O 的切线, ∴∠OCB=∠OCE. ∵AB 是⊙O 的直径,AM 和 BN 是它的两条切线, ∴AM∥BN,
1.过圆外一点能够作圆的两条切线,切__线__上__一__点__到__切__点____之 间的线段长叫做这点到圆的切线长.
2.切线长定理:过圆外一点作圆的___两_____条切线,两条切线 长__相__等____,圆心与这一点的连线__平__分____两条切线的夹角.
1.如图,从⊙O 外一点 P 引两条切线 PA,PB,切点分别为 A, B.如果∠APB=60°,PA=8,那么弦 AB 的长是( B ) A.4 B.8 C.4 3 D.8 3
