中考数学复习指导抛物线内接三角形面积计算通法.doc
抛物线上的三角形的面积
抛物线上的三角形的面积
抛物线是一种二次函数的图像，其形式为$y=ax^2+bx+c$（其中$a$ 不等于0）。
如果在抛物线上存在一个三角形，则它的底边一定是抛物线的某一条直线切线，并且顶点在抛物线的极值处。
如果要计算抛物线上三角形的面积，可以使用以下步骤：
找出抛物线的极值点。
极值点的坐标为$(h,k)$，其中$h$ 是抛物线的横坐标，$k$ 是抛物线的纵坐标。
极值点的横坐标可以通过求解方程$ax^2+bx+c=0$ 来获得，其中$a$、$b$ 和$c$ 分别是抛物线的系数。
求出抛物线的切线方程。
切线的斜率为抛物线的导数$2ax+b$，可以使用斜截式$y=mx+b$ 来表示切线的方程，其中$m$ 是斜率，$b$ 是切线的截距。
求出抛物线的底边长。
底边的两个端点的坐标分别为抛物线的两个交点，可以使用切线的方程求解。
计算三角形的面积。
可以使用海伦公式求解三角形的面积，公式为$\sqrt{s(s-a)(s-b)(s-c)}$，其中$s$ 为三角形的半周长，即$s=\frac{a+b+c}{2}$，$a$、$b$ 和$c$ 分别是三角形的三条边长。
因此，计算抛物线上三角形的面积的步骤如下：
求出抛物线的极值点$(h,k)$。
求出抛物线的切线方程$y=mx+b$。
求出抛物线的底边长$a$。
计算三角形的半周长$s$。
使用海伦公式计算三角形的面积。
举个例子，假设抛物线的方程为$y=x^2-2x+1$，底边长为$a=2$，那么抛物线上三角形的面积就是$\sqrt{s(s-2)(s-2)(s-2)}=\sqrt{s(s-2)^3}$。
第五讲+抛物线中三角形的面积问题
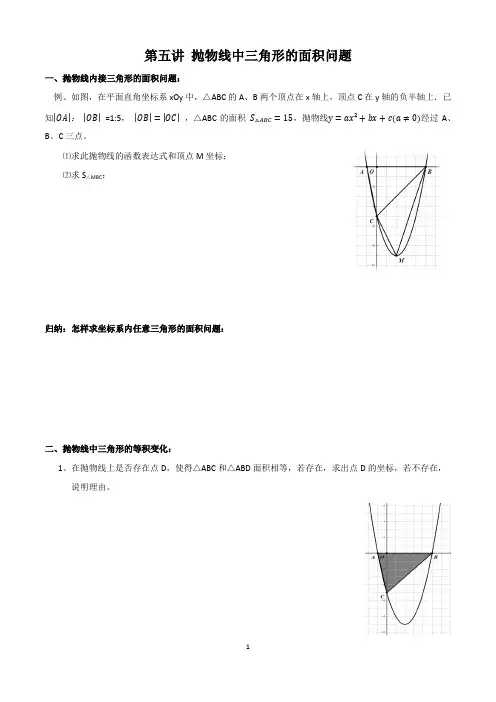
第五讲抛物线中三角形的面积问题一、抛物线内接三角形的面积问题：例、如图，在平面直角坐标系xOy中，△ABC的A、B两个顶点在x轴上，顶点C在y轴的负半轴上．已知|OA|：|OB|=1:5，|OB|=|OC|，△ABC的面积S△ABC=15，抛物线y=ax²+bx+c(a≠0)经过A、B、C三点。
⑴求此抛物线的函数表达式和顶点M坐标；⑵求S△MBC；归纳：怎样求坐标系内任意三角形的面积问题：二、抛物线中三角形的等积变化：1、在抛物线上是否存在点D，使得△ABC和△ABD面积相等，若存在，求出点D的坐标，若不存在，说明理由。
2、在抛物线上是否存在点E，使得△ABC和△BCE面积相等，若存在，求出点E的坐标，若不存在，说明理由。
S△ABC。
若存在，求出点M的坐标；若不存在，请说明理由3、在抛物线上是否存在点M，使S△MBC= 134、（2011成都）在抛物线上是否存在异于B、C的点M，使△MBC中BC边上的高为7√？若存在，求出点M的坐标；若不存在，说明理由.5、点P（2，-3）是抛物线对称轴上的一点，在线段OC上有一动点M，以每秒2个单位的速度从O向C 运动，（不与点O，C重合），过点M作MH∥BC，交X轴于点H，设点M的运动时间为t秒，试把△PMH 的面积S表示成t的函数，当t为何值时，S有最大值，并求出最大值；6、在抛物线的对称轴上有一点P的纵坐标为5，在直线上BC求一点M使得S△PBM∶S△ABC=1:5.7、在直线BC下方抛物线上是否存在一个点F，使得△BCF的面积最大，若存在，求出点F的坐标，并求出最大面积，若不存在，说明理由。
练习：1、如图，抛物线与x轴交于A（x1，0）、B（x2，0）两点，且x1＜x2，与y轴交于点C（0，-4），其中x1，x2是方程x2-4x-12=0的两个根．（1）求A、B两点坐标；（2）求抛物线的解析式；（3）点M是线段AB上的一个动点（不与A、B两点重合），过点M作MN∥BC，交AC于点N，连接CM，在M点运动时，△CMN的面积是否存在最大值？若存在，求出△CMN面积最大时点M的坐标；若不存在，请说明理由．2、（2010玉溪）如图，在平面直角坐标系中，点A的坐标为（1，△AOB（1）求点B的坐标；（2）求过点A、O、B的抛物线的解析式；（4）在（2）中x轴下方的抛物线上是否存在一点P，过点P作x轴的垂线，交直线AB于点D，线段OD 把△AOB分成两个三角形．使其中一个三角形面积与四边形BPOD面积比为2：3 ？若存在，求出点P的坐标；若不存在，请说明理由．yAB。
抛物线与三角形的面积
抛物线与三角形的面积抛物线与三角形面积相结合的问题涉及代数、几何的许多定理、公式，有一定的难度，近年来的中考试题中，经常出现抛物线与三角形面积结合的综合题，以考查学生的综合运用所学知识解决问题的能力。
这节课我们共同来探索一下顶点都在抛物线2y ax bx c =++上的三角形面积的求法。
1、已知抛物线: 224233y x x =--+(1)求抛物线与坐标轴交点坐标及顶点坐标; (2)画出抛物线的草图;(3)设抛物线与x 轴交于A 、B 两点（点A 在点B 的左边），与y 轴交于C 点，顶点为D 。
求：①△DAB 和△CAB 的面积； ②四边形ABCD 的面积； ③△ACD 的面积(4)求直线AC 的解析式；（5）抛物线上有一动点P 在直线AC 上方，问：是否存在一点P ，使△PAC 的面积最大，若存在，求出△PAC 的最大面积及P 点坐标； 若不存在，请说明理由。
2、如图，抛物线c bx x y ++-=2与x 轴交与A(1,0),B(- 3，0)两点， （1）求该抛物线的解析式；（2）设（1）中的抛物线交y 轴与C 点，在该抛物线的对称轴上是否存在点Q ，使得△QAC 的周长最小？若存在，求出Q 点的坐标；若不存在，请说明理由.（3）在（1）中的抛物线上的第二象限上是否存在一点P ，使△PBC 的面积最大？，若存在，求出点P 的坐标及△PBC 的面积最大值.若没有，请说明理由.练习：1、在△ABC 中，∠A ＝90°，AB ＝4，AC ＝3，M 是AB 上的动点（不与A ，B 重合），过M 点作MN ∥BC 交AC 于点N ．以MN 为直径作⊙O ，并在⊙O 内作内接矩形AMPN ．令AM ＝x ． （1）用含x 的代数式表示△ＭNP 的面积S ； （2）当x 为何值时，⊙O 与直线BC 相切？（3）在动点M 的运动过程中，记△ＭNP 与梯形BCNM重合的面积ABC为y ，试求y 关于x 的函数表达式，并求x 为何值时，y 的值最大，最大值是多少？2、如图1，抛物线经过点A (4，0)、B （1，0)、C （0，－2）三点． （1）求此抛物线的解析式；（2）P 是抛物线上的一个动点，过P 作PM ⊥x 轴，垂足为M ，是否存在点P ，使得以A 、P 、M 为顶点的三角形与△OAC 相似？若存在，请求出符合条件的 点P 的坐标；若不存在，请说明理由；（3）在直线AC 上方的抛物线是有一点D ，使得△DCA 的面积最大，求出点D 的坐标．ABMND 图 2OABMN 图 3O图13、(2011漳州中考题)如图1，抛物线y=mx2-1lmx+24m(m<0)与x轴交于B、C两点(点B在点C的左侧)，抛物线上另有一点A在第一象限内，且∠BAC=900．(1)填空：OB=________，）OC=________；(2)连结OA，将△OAC沿x轴翻折后得到△ODC，当四边形OACD是菱形时，求此时抛物线的解析式；(3)如图2，设垂直于x轴的直线l：x=n与(2)中所求的抛物线交于点M，与CD交于点N，若直线l沿x轴方向左右平移，且交点M始终位于抛物线上A、C两点之间时，试探究：当n为何值时，四边形AMCN的面积取得最大值，并求出这个最大值。
高中抛物线三角形面积公式
高中抛物线三角形面积公式高中数学中，抛物线是一个常见的曲线类型。
而抛物线的一个重要性质是，它可以被用来构造出一个三角形，其面积可以通过一个简单的公式来计算。
我们需要了解抛物线的基本概念。
抛物线是一个平面曲线，其形状类似于一个开口向上或向下的碗。
它可以由一个二次方程来描述，即y=ax^2+bx+c，其中a、b、c是常数，x和y是抛物线上的点的坐标。
接下来，我们来看看如何构造一个抛物线三角形。
首先，在抛物线上任选三个点，将它们连接起来，就可以得到一个三角形。
这个三角形的一个顶点是抛物线的顶点，而另外两个顶点则是我们任选的两个点。
接着，我们来看看如何计算这个三角形的面积。
首先，我们需要求出三角形的底边长和高。
底边长可以通过两个顶点的横坐标之差来计算，而高则是从三角形的顶点到底边的垂直距离。
具体来说，我们可以先求出三角形的底边长b，即b=x2-x1，其中x1和x2分别是任选的两个点的横坐标。
接着，我们需要求出三角形的高h。
由于三角形的顶点在抛物线上，因此我们可以通过求出抛物线在顶点处的切线来得到高的长度。
在这里，我们就需要用到一些微积分的知识。
我们可以先求出抛物线在顶点处的导数，即y'=2ax+b。
由于导数表示的是曲线在某一点处的斜率，因此我们可以用这个导数来求出抛物线在顶点处的切线的斜率。
接着，我们可以得到这条切线的方程，即y=2ax0+b，其中x0是抛物线的顶点的横坐标。
我们可以求出这条切线与底边的交点的纵坐标，即三角形的高h。
具体来说，我们可以将这条切线的方程代入三角形底边的方程中，得到一个二次方程。
通过求解这个二次方程，我们可以得到这条切线与底边的交点的纵坐标y0。
因此，三角形的面积可以通过公式S=1/2bh来计算，其中b是底边长，h是三角形的高。
需要注意的是，由于抛物线的形状类似于一个碗，因此在选取三个点构成三角形时，我们需要保证这个三角形是有意义的。
具体来说，三个点应该按照从左到右或从右到左的顺序排列，这样才能够构成一个有意义的三角形。
抛物线中的内接三角形面积问题
抛物线中的内接三角形面积问题抛物线与三角形是初中数学的两个支柱型图形，而它们有机的结合，则可以构建综合题和探究型的试题．特别是有关抛物线中的内接三角形面积问题更是成为各地中考的热点题型，求解时若能灵活运用二次函数、方程、三角形等知识，充分利用数形结合、分类讨论和待定系数法等方法，就能找到求解的最佳切入点．例（重庆市）已知：是方程的两个实数根，且，抛物线的图像经过点．（1）求这个抛物线的解析式；（2）设（1）中抛物线与轴的另一交点为，抛物线的顶点为，试求出点C、D的坐标和的面积．[注：抛物线的顶点坐标为]．（3）是线段OC上的一点，过点P作PH⊥x轴，与抛物线交于H点，若直线BC把△PCH 分成面积之比为2∶3的两部分，请求出P点的坐标．解：（1）解方程，得，由，有，所以点A、B的坐标分别为A（1，0），B（0，5）．将A（1，0），B（0，5）的坐标分别代入，得解这个方程组，得所以，抛物线的解析式为．（2）由，令，得．解这个方程，得，所以C点的坐标为（－5，0）．由顶点坐标公式计算得点D（－2，9）．过D作x轴的垂线交x轴于M．则，，，所以．（3）设P点的坐标为（a，0），因为线段BC过B，C两点，所以BC所在的直线方程为．那么，PH与直线BC的交点坐标为．PH与抛物线的交点坐标为．由题意，得①，即．解这个方程，得或（舍去）．②，即．解这个方程，得或（舍去）．即P点的坐标为或．说明：处理抛物线的内接三角形的面积问题还要能运用相关的知识来构造出与所求点的坐标相关的方程．要注意在设抛物线上的点的坐标时，应注意与函数表达式的联用，如本题中和，这样就可以简捷求解．抛物线内三角形问题题型的覆盖面广，涉及知识点多，求解时既要求我们掌握有关抛物线的基础知识，又要求我们能够熟练地运用直角三角形、相似三角形等图形的性质，综合运用点坐标与线段长的关系，利用方程、数形结合、转化归纳、分类等数学思想方法，才能顺利解决问题．。
中考专题—抛物线与三角形面积专题
抛物线与三角形面积抛物线与三角形面积问题涉及代数、几何知识，有一定难度。
本文通过举例来谈这类题的解法。
一、顶点在抛物线y=ax2+bx+c的三角形面积的一般情况有：（1）、以抛物线与x轴的两交点和抛物线的顶点为顶点的三角形，其底边的长是抛物线与x轴两交点间的距离，高的长是抛物线顶点的纵坐标的绝对值。
其面积为：SΔ=|x1-x2|·||=··||（2）、以抛物线与x轴、y轴的三个交点为顶点的三角形。
其底边的长是抛物线与x轴两交点间的距离，高的长是抛物线与y轴上的截距(原点与y轴交点构成的线段长)的绝对值。
其面积为：SΔ=·|x1-x2|·|c|＝··|c|（3）、三角形三个顶点在抛物线其他位置时，应根据图形的具体特征，灵活运用几何和代数的有关知识。
二、1．求内接于抛物线的三角形面积。
例1．已知抛物线的顶点C（2，），它与x轴两交点A、B的横坐标是方程x2-4x+3=0的两根，求ΔABC的面积。
解：由方程x2-4x+3=0，得x1=1, x2=3,∴AB=|x2-x1|=|3-1|=2.=×2×=.∴SΔABC例2．已知二次函数y=x2+3x+2的图像与x轴交于A、B两点，与y轴交于D点，顶点为C，求四边形ACBD的面积。
解：如图1，S=SΔABC+SΔABD四边形ACBD=××||+××|2|=.例3．如图：已知抛物线y=x2-2x+3与直线y=2x相交于A、B，抛物线与y轴相交于C点，求ΔABC的面积。
解：由得点A的坐标为（1，2），点B的坐标为（3，6）；抛物线与y轴交点C的坐标为（0，3）如图2，由A、B、C三点的坐标可知，AB=＝2，BC=＝3，AC=＝。
∵AC2+BC2=AB2，∴ΔABC为直角三角形，并且∠BCA=900，AC·BC=××3=3。
抛物线焦点三角形面积公式
抛物线焦点三角形面积公式
抛物线焦点三角形面积公式：
1、抛物线焦点三角形的基本概念：抛物线焦点三角形是一种由抛物线的两个焦点所围成的三角形。
它是一种特殊的三角形，因为它的全部边都是由两个抛物线的焦点和一条直线组成的。
2、抛物线两个焦点间距离公式：在抛物线中，首先需要计算两个焦点之间的距离，计算公式如下：
距离=抛物线焦点距离=2*抛物线离心率。
3、抛物线焦点三角形面积公式：抛物线焦点三角形的面积可通过下式计算：
S=½*[(2*焦点距离)+(外边长)^2-4*(外边长*内边长)].
4、该公式应用场景：抛物线焦点三角形面积计算可以在有关椭圆和抛物线的数学问题中得到应用，如抛物线的焦点定理以及大约椭圆和抛物线的物理应用等。
因此，抛物线焦点三角形面积公式是在计算椭圆和抛物线方面极其重要的公式。
抛物线三角形面积最大值公式
抛物线三角形面积最大值公式在数学中，我们经常需要研究最大化或最小化某个量的问题。
本文将探讨一个有趣的数学问题：如何求解抛物线上的三角形面积的最大值，并给出相应的公式。
问题引入考虑一个抛物线y=ax2+bx+c，我们希望找到一条直线y=mx+n和抛物线所围成的三角形的最大面积。
解决方法为了求解这个问题，我们首先需要确定直线和抛物线的交点。
令二者相交时的x值为x0，则有：ax02+bx0+c=mx0+n化简可得：mx0=ax02+bx0+c−n整理后可得：ax02+(b−m)x0+(c−n)=0这是一个一元二次方程，我们可以根据二次函数的性质求解出x0。
接下来，我们需要计算三角形的面积。
设两条线与x轴围成的三角形面积为S，则有：$$ S = \\frac{1}{2}(\\text{底边} \\times \\text{高}) = \\frac{1}{2}|x_1-x_2|\\times|y_1-y_2| $$求解最大值我们的目标是求解三角形面积的最大值。
根据前面的讨论，我们将三角形的面积公式代入：$$ S = \\frac{1}{2}|x_0-x_1|\\times|y_0-y_1| $$其中，x0为抛物线和直线的交点x坐标，(x1,y1)为抛物线上的点。
将直线方程y=mx+n代入上式，求解最大值问题可以转化为对S的求导问题，即求 $\\frac{dS}{dx_0}=0$。
通过对 $\\frac{dS}{dx_0}$ 求导，并令导数为零，可以得到抛物线三角形面积的最大值。
这个最大面积对应的x坐标即为我们要找的交点x0。
结论通过以上推导和计算，我们得到了抛物线上与给定直线围成的三角形面积的最大值公式。
这个公式可以帮助我们在解决相关数学问题时快速找到最优解。
希望本文的内容能对读者有所启发，也希望读者能在实际问题中灵活运用这些数学知识。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2019-2020 年中考数学复习指导抛物线内接三角形面积的计算通法
一、问题的提出
(2016年酒泉中考题) 如图 1(1) ，已知抛物线经过A(3,0) ， B(0,3) 两点.
(1)求此抛物线的解析式和直线AB 的解析式;
(2)如图 1(1) ，动点E，从O点出发，沿着OA的方向以 1 个单位 / 秒的速度向终点 A 匀速运动，同时，动点 F 从点 A出发，沿着 AB 方向以 2 个单位/秒的速度向终点B 匀速运
动，当 EF 中任意一点到达终点时另一点也随之停止运动. 连结EF，设运动时间为t 秒，当
t 为何值时，V AEF为直角三角形?
(3)如图 1(2) ，取一根橡皮筋，两端点分别固定在 A ， B 处，用铅笔拉着这根橡皮筋使
笔尖 P 在直线 AB 上方的抛物线上移动，动点P 与 A ， B 两点构成无数个三角形，在这些
三角形中是否存在一个面积最大的三角形?如果存在，求出最大面积，并指出此时点P 的坐
标; 如果不存在，请简要说明理由.
本题第 (3) 问是求抛物线内接不规则三角形的最大面积问题，解这类问题有没有一种通用的方法呢 ?值得我们探究 .
二、几种特殊情况
1.抛物线内接三角形有一边在 x 轴上:(这里约定A点的横坐标记为 x A，A点的纵坐标记
为为 y A)
如图 2(1) ，有
S ABC 1 AB OC 1x A x B y C.
2 2
如图 2(2) ，有
S ABC
1
AB DC 1
x A x B y C .
2 2
如图 2(3) ，有
S
ABC
1 AB DC 1
x A x B y C .
2
2 x 轴平行 : 如图 3(1) ，有
2. 抛物线内接三角形有一边与
S ABC
1
AB DC 1
x A x B y C y D , 2 1 AB OC 2 1 x B 或 S ABC
x A y D y C ; 如图 3(2) 2 2 ，有
S
ABC
1
AB DC 1
x A x B y C y D ,
2 1 2 1
S
ABC
x A y D y C . 或 2 AB OC 2 x B
在以上特殊情况下，只要求出
A 、
B 、
C 、
D 的坐标，代入即可以求出抛物线内接三
角形的面积 .
三、建立模型
当抛物线内接三角形的三边均不与坐标轴平行时
( 如图 4) ，三角形的面积又该怎么计算
呢?
解题的基本思路是将任意三角形转化为上述特殊的三角形，然后类比解决 .
如图 4，过点 C 作“轴的垂线交 AB 于点 D , 则 ABC 被分成了两个以 CD 为一公共边
的三角形 .
过点 A 作 AE
CD 于点 E ，过 B 作 BF CD 于点 F ，则
S ABC
S
CDA
S ABC 1 1 CD BF CD ( AE BF ) ，
CD AE
2 2
CD y C y D ，
AE BF x C x A x B x C. Q x A x C x B,
AE BF x A x B ,
S
ABC 1
x A x B y C y D.
2
ABC 的面积公式:
综合上述，已知三角形三个顶点坐标，可得抛物线内接
设 a x A x B , h y C y D.
a 为两点的横坐标之差，可看成是两点之间的水平距离，可以称为水平宽 ; h表示的是两点的纵坐标之差，可称为铅直高. 在坐标系中，不规则三角形的面积公式可表示为:
S
ABC 1
ah .
2
.
此公式适用于坐标系中的任意三角形，它和一般三角形的面积公式形成了完美的一致
当三角形的三个顶点都在抛物线上时，点的横坐标不可能州样，不妨设x A x C x B.
则 a x A x B ，即是水平宽.
过点 C 作x轴的垂线，与直线AB 的交点记为 D ，则 h y C y D，即是铅直高，于是有
S
ABC 1
ah
1
x A x B y C y D.
2 2
四、问题解决
上述问题中，过点P 作 PN // x轴，垂足为 N ，交 AB 于点 M ( 如图 1(2)) ，抛物线解析式为
y x2 2x 3 ,
直线 AB 的解析式为
y x 3 .
设 N ( x, x 3) ，则 M ( x, x2 2x 3) .
于是有
S
ABC 1 x A x B y P x M
2
1 (3 0) ( x
2 2x 3) ( x 3)
2
3 9
x2 x
2 2
3 (x 3 )2 27 ,
2 2 8
即当x 3 时， V ABP 面积最大，最大面积是27
，此时 P 点的坐标为( 3 , 27 )
.
2 8 2 8
五、模型应用 ( 动点B在定点A与C之内 )
例 1 如图 5，二次函数与x 轴交于点C,与y轴交于点A，B为直线AC下方抛物线上一点，求V ABC 面积的最大值.
解易得点 A(0, 4) ，点 C (6,0) ，则水平宽 a x A x C 6 .
直线 AC 的解析式为 y 2 x 4 .
设点 B 的坐标为 (x, 1
x2
3
3 x 4) , 3 4
则点 D 的坐标为 ( x, 2
x 4) .
3
铅垂高 h y B y D 2 x 4 ( 1 2 4 x 4) 1 x2 2x ,
3 2 3 3
故 S ABC 1 6 ( 1 x2 2x) x2 6x ( x 3)2 9 .
2 3
Q 0 x 6 ,
当 x 3 时，即当点B(3, 5) 时，ABC 面积最大，最大面积是9.
评注题中的ABC 满足公式中的A, C 为定点，B为一动点，但在运动过程中，B的横坐标介于 A, C 的横坐标之间，所以直接套用公式即得. 由此题可看出，在这种动点问题中，水平宽是两个定点间的水平跨度，铅直高即是由动点向x 轴作垂线，垂线与两定点的连线交于一点，动点和这个交点在竖直方向的跨度.
六、模型拓展 ( 动点P在定点A与C之外 )
例 2 如图 6(1) ，二次函数与x 轴交于点C，与y轴交于点A，直线AB与 x 轴平行，且点 B 在抛物线上，点 P 是直线 AC 上方抛物线上的动点，是否存在点 P ，使S P A C 2S A B,C若存在，求出点P 的坐标，若不存在，说明理由.
解析由题意不难得出S ABC 8 ,
要使 S PAC 2S ABC，即求 S PAC 16 .
因为PAC 为动点三角形，由通用公式S PAC ah ，其中 a 为水平宽， a x C x A 6 , h 为铅直高，应该过动点P 向x轴作垂线;交直线 AC 于点 D ，则h y P y D.
问题是此时动点 P 不在两定点A,C之间，而是运动到了两定点A, C 之外，那么通用公式还成立吗 ?
由图 6(2) 可知，当动点P 在两定点A, C之外时，
S
PAC S
PDC
S
PDA
1 1
PD AF
2
PD CE
1
PD (CE
1
PD
2 1
ah .
AF ) ( x C x A )
2 2 2
由此可见，当动点运动到两定点之外时，通用公式依然成立. 区别是 : 动点在两定点之间时，动点图形的面积是两个规则图形的面积之和，用的是加法运算; 动点在两定点之外时，动点图形的面积是两个规则图形的面积之差，用的是减法运算.。