02-第2讲基本初等函数与图形
基本初等函数图像及性质
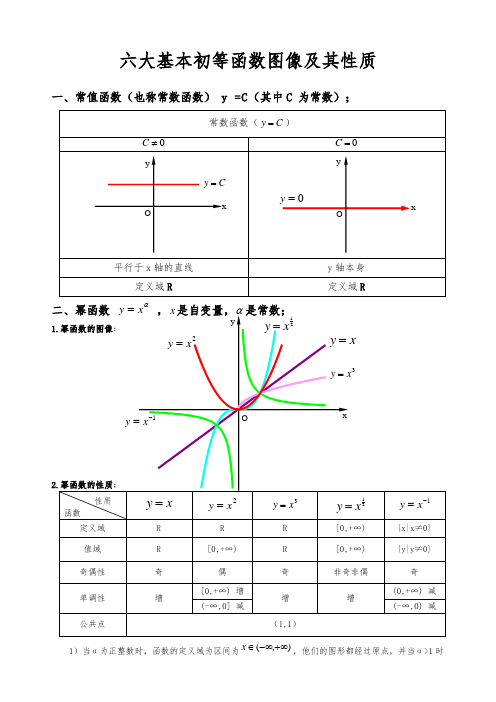
六大基本初等函数图像及其性质一、常值函数(也称常数函数) y =C (其中C 为常数);α1)当α为正整数时,函数的定义域为区间为),(+∞-∞∈x ,他们的图形都经过原点,并当α>1时在原点处与x 轴相切。
且α为奇数时,图形关于原点对称;α为偶数时图形关于y 轴对称;2)当α为负整数时。
函数的定义域为除去x=0的所有实数; 3)当α为正有理数nm时,n 为偶数时函数的定义域为(0, +∞),n 为奇数时函数的定义域为(-∞,+∞),函数的图形均经过原点和(1 ,1);4)如果m>n 图形于x 轴相切,如果m<n,图形于y 轴相切,且m 为偶数时,还跟y 轴对称;m ,n 均为奇数时,跟原点对称;5)当α为负有理数时,n 为偶数时,函数的定义域为大于零的一切实数;n 为奇数时,定义域为去除x=0以外的一切实数。
三、指数函数xa y =(x 是自变量,a 是常数且0>a ,1≠a ),定义域是R ;[无界函数]1.指数函数的图象:2.1)当1>a时函数为单调增,当10<<a 时函数为单调减; 2)不论x 为何值,y 总是正的,图形在x 轴上方; 3)当0=x 时,1=y ,所以它的图形通过(0,1)点。
3.(选,补充)指数函数值的大小比较*N ∈a ;a.底数互为倒数的两个指数函数1(yf (xx a x f =)(,xa x f ⎪⎭⎫ ⎝⎛=1)(的函数图像关于y 轴对称。
b.1.当1>a 时,a 值越大,xa y =的图像越靠近y 轴;b.2.当10<<a 时,a 值越大,x a y =的图像越远离y 轴。
4.指数的运算法则(公式);a.整数指数幂的运算性质),,0(Q n m a ∈≥;(1) n m n m a a a +=⋅(2)nm n m aa a -=÷(3)()()mn nmnm aaa ==(4) ()n n n b a ab=b.根式的性质;(1)()a a nn= ; (2)当n 为奇数时,a a nn =当n 为偶数时,⎩⎨⎧<-≥==)0(0)(a a a a a a nnc.分数指数幂; (1))1,,,0(*>∈>=n Z n m a a a n m nm(2))1,,,0(11*>∈>==-n Z n m a a aanmnm nm 四、对数函数x y a log =(a 是常数且1,0≠>a a ),定义域),0(+∞∈x [无界]1.对数的概念:如果a(a >0,a ≠1)的b 次幂等于N ,就是 N a b=,那么数b 叫做以a 为底N 的对数,f xxxx g ⎪⎫⎛=1)(记作b N a =log ,其中a 叫做对数的底数,N 叫做真数,式子N a log 叫做对数式。
第2讲 函数概念与基本初等函数

第2讲函数概念与基本初等函数一.【考纲导读】(一)函数1.了解构成函数的要素,了解映射的概念,会求一些简单函数的定义域和值域.2.理解函数的三种表示法:解析法、图象法和列表法,能根据不同的要求选择恰当的方法表示简单的函数.3.了解分段函数,能用分段函数来解决一些简单的数学问题.4.理解函数的单调性,会讨论和证明一些简单的函数的单调性;理解函数奇偶性的含义,会判断简单的函数奇偶性.5.理解函数的最大(小)值及其几何意义,并能求出一些简单的函数的最大(小)值6.会运用函数图像理解和研究函数的性质.(二)指数函数1.了解指数函数模型的实际背景.2.理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算.3.理解指数函数的概念,会求与指数函数性质有关的问题.4.知道指数函数是一类重要的函数模型.(三)对数函数1.理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用.2.理解对数函数的概念;会求与对数函数性质有关的问题.3.知道对数函数是一类重要的函数模型.4.了解指数函数与对数函数互为反函数.(四)幂函数1.了解幂函数的概念.2.结合函数的图像,了解它们的变化情况.(五)函数与方程1.了解函数零点的概念,结合二次函数的图像,了解函数的零点与方程根的联系.2.理解并掌握连续函数在某个区间上存在零点的判定方法。
能利用函数的图象和性质判别函数零点的个数.(六)函数模型及其应用1.了解指数函数、对数函数以及幂函数的增长特征。
知道直线上升、指数增长、对数增长等不同函数类型增长的含义.2.了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用.3.能利用给定的函数模型解决简单的实际问题.二.【命题走向】分析近几年的高考试题,可以发现函数是高考数学的重点内容之一,函数的观点和思想方法贯穿整个高中数学的全过程,包括解决几何问题.在近几年的高考试卷中,选择题、填空题、解答题三种题型中每年都有函数试题,而且常考常新.以基本函数为模型的应用题和综合题是高考命题的新趋势.2015年高考热点主要有:①考查函数的表示法、定义域、值域、单调性、奇偶性、反函数和函数的图象.②函数与方程、不等式、数列是相互关联的概念,通过对实际问题的抽象分析,建立相应的函数模型并用来解决问题,是考试的热点.③考查运用函数的思想来观察问题、分析问题和解决问题,渗透数形结合和分类讨论的基本数学思想.三.【要点精讲】 1、知识网络定义定义域区间对应法则值域一元二次函数一元二次不等式映射函数性质奇偶性单调性周期性指数函数根式分数指数指数函数的图像和性质指数方程对数方程反函数互为反函数的函数图像关系对数函数对数对数的性质积、商、幂与根的对数对数恒等式和不等式常用对数自然对数对数函数的图像和性质1.2.1 对函数的进一步认识一、映射1.映射:设A 、B 是两个集合,如果按照某种对应关系f ,对于集合A 中的 元素,在集合B 中都有 元素和它对应,这样的对应叫做 到 的映射,记作 .2.象与原象:如果f :A →B 是一个A 到B 的映射,那么和A 中的元素a 对应的 叫做象, 叫做原象。
五大基本初等函数性质及其图像

五、基本初等函数及其性质和图形1.幂函数函数称为幂函数。
如,,,都是幂函数。
没有统一的定义域,定义域由值确定。
如,。
但在内总是有定义的,且都经过(1,1)点。
当时,函数在上是单调增加的,当时,函数在内是单调减少的。
下面给出几个常用的幂函数:的图形,如图1-1-2、图1-1-3。
图1-1-2图1-1-32.指数函数函数称为指数函数,定义域,值域;当时函数为单调增加的;当时为单调减少的,曲线过点。
高等数学中常用的指数函数是时,即。
以与为例绘出图形,如图1-1-4。
图1-1-43.对数函数函数称为对数函数,其定义域,值域。
当时单调增加,当时单调减少,曲线过(1,0)点,都在右半平面内。
与互为反函数。
当时的对数函数称为自然对数,当时,称为常用对数。
以为例绘出图形,如图1-1-5。
图1-1-54.三角函数有,它们都是周期函数。
对三角函数作简要的叙述:(1)正弦函数与余弦函数:与定义域都是,值域都是。
它们都是有界函数,周期都是,为奇函数,为偶函数。
图形为图1-1-6、图1-1-7。
图1-1-6 正弦函数图形图1-1-7 余弦函数图形(2)正切函数,定义域,值域为。
周期,在其定义域内单调增加的奇函数,图形为图1-1-8图1-1-8(3)余切函数,定义域,值域为,周期。
在定义域内是单调减少的奇函数,图形如图1-1-9。
图1-1-9(4)正割函数,定义域,值域为,为无界函数,周期的偶函数,图形如图1-1-10。
图1-1-10(5)余割函数,定义域,值域为,为无界函数,周期在定义域为奇函数,图形如图1-1-11。
图1-1-115.反三角函数反正弦函数,定义域,值域,为有界函数,在其定义域内是单调增加的奇函数,图形如图1-1-12;图1-1-12,为有界函数,在其定义域内为单调减少的非奇非偶函数,图形如图1-1-13;图1-1-13反正切函数,定义域,值域为,为有界函数,在定义域内是单调增加的奇函数,图形如图1-1-14;图1-1-14为有界函数,在其定义域内单调减少的非奇非偶函数。
常用函数图像
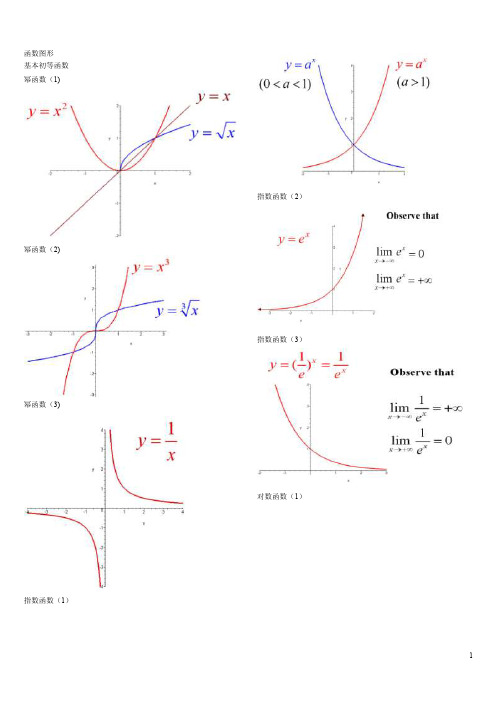
函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1) 极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性) 极限的性质(3) (不等式性质) 极限的性质(4) (局部有界性) 极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e的值(1)等价无穷小(x->0)sinx等价于xarcsinx等价于x tanx等价于x arctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2)数列的夹逼性(1) 数列的夹逼性(2) pi 是派的意思(如果你没有切换到公式版本)^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了文案编辑词条B 添加义项?文案,原指放书的桌子,后来指在桌子上写字的人。
第2讲基本初等函数及其应用(原卷版)

第2讲 基本初等函数及其应用目录第一部分:知识强化第二部分:重难点题型突破突破一:指数与对数运算突破二:基本初等函数的图象与性质突破三:函数的零点及其应用角度1:确定函数零点的个数或范围角度2:根据函数零点求参数的取值范围突破四:函数模型应用第三部分:冲刺重难点特训第一部分:知识强化1、函数的零点与方程的根之间的联系(1)函数()y f x =的零点就是方程()0f x =的实数根,也就是函数()y f x =的图象与x 轴的交点的横坐标,即方程()0f x =有实数根⇔函数()y f x =的图象与x 轴有交点⇔函数()y f x =有零点.(2)函数()()()F x f x g x =-的零点就是方程()()f x g x =的根,即函数()y f x =的图象与函数()y g x =的图象交点的横坐标.2、确定函数零点的常用方法:①直接解方程法;②利用零点存在性定理;③数形结合,利用两个函数图象的交点求解.A.B.C.D.()⊆f x[],m n D60C.一杯茶泡好后置于室80C、65C,给出三个茶温(单位:C)关于茶泡好后(0T at b a;③=+<.根据生活常识,从这三个函数模型中选择一个,模拟茶温T(单位:C)关(单位:分钟)的关系,并依此计算该杯茶泡好后到饮用至少需要等待的时间为x f x,则(f1)()000x x >,若关于的解,且 0x ∈cos m x 在区间A .B .C .D .2,00x x -⎧>,则满f .(湖北省鄂西北六校(宜城、枣阳、曾都、襄州、南漳、河口)1%,一年后是.可以计算得到,一年后的“进步”A .9B .10C .11D .12。
高等数学初等函数ppt课件

•当 为奇数时, 幂函数为奇函数;当 为偶数时,
幂函数为偶函数.
•当 0 时, 函数为常数函数 y 1
5
指数函数
定义:函数 y a x 叫做指数函数, a 其中 是一个大于0,且不等于1的常量,函
数的定义域是R.
y a x (a 0,a 1) x R
2
ymin= 1
f(x)= 0 x k (k Z )
R [1,1]
x 2k (k Z ) 时 ymax=1 x 2k (k Z ) 时 ymin= 1
x k (k Z ) 11
2
f(x)=sinx
f(x)= cosx
图象
x
x
周期性 奇偶性
在 (0,) 上是减函数 在 (0,) 上是增函数 9
三角函数
三角函数常用公式
10
f(x)=sinx
f(x)= cosx
y
y
图1
1
象
0
-1 -
2
3
2 x 0
2
-1
2
3
2 x
2
定义域 值域
最值
R
[1,1]
x 2k (k Z ) 时
2
ymax=1 x 2k (k Z ) 时
商 f: g
( f )(x) f (x) , x D \{x | g(x) 0, x D}Biblioteka gg(x)29
三. 初等函数
由常数及基本初等函数 经过有限次四则运算和复合步
骤所构成 , 并可用一个式子表示的函数 , 称为初等函数 .
02初等函数及数列极限的概念

通常所说的反双曲余弦函数即指此主支。
类似于上面的作法, 可以得到 arth x , arcth x , arsech x , arcsch x 的表达式.
第二章 极限
本章学习要求:
了解数列极限的概念, 会用《 N》语言描述数列的 极限。正确理解 和 N 的含义。
双曲余弦函数的 定义域为 (, )
双曲余弦函数 在(, 0)内单调减少 在[0, )内单调增加
双曲余弦函数是偶函数
y
y = cth x
1
O y = th x
x
1
双曲正切、双曲余切的图形
双曲正切函数 定义域为 (, )
双曲正切函数 是单调增加的且有界
| th x | 1
4
x1 x
1 2
1 2n
,
有界 (可取 M 1 ). 2
(2) { (1)n1}: 1, 1, 1, 1,, (1)n1,
x2n
–1
0
x 2 n 1
x
1
{(1)n1}不单调, 但有界 (可取 M 1 ).
(3)
1
(1)n n
:
x3
••
•
(••x•2n•-•1••(•••
*
•••)•
x2n
••• •••)•
•
x4
•
1 103
1 102n
1
0
1
1
102n
y y f (x) M
yM
I (
O
) x
M y M
数列的有界性的定义
若 M 0, 使得 | xn | M , n N 成立, 则称数列{xn} 有界. 否则称{xn} 是无界的.
第2讲函数基本初等函数的图像与性质课件课件

第二页,编辑于星期二:二十点 分。
第三页,编辑于星期二:二十点 分。
第四页,编辑于星期二:二十点 分。
第五页,编辑于星期二:二十点 分。
第六页,编辑于星期二:二十点 分。
第七页,编辑于星期二:二十点 分。
第八页,编辑于星期二:二十点 分。
第九页,编辑于星期二:二十点 分。
第十八页,编辑于星期二:二十点 分。
第十九页,编辑于星期二:二十点 分。
第二十页,编辑于星期二:二十点 分。
第二十一页,编辑于星期二:二十点 分。
第二十二页,编辑于星期二:二十点 分。
第二十三页,编辑于星期二:二十点 分。
第二十四页,编辑于星期二:二十点 分。
第二十五页,编辑于星期二:二十点 分。
第二十六页,编辑于星期二:二十点 分。
第二十七页,编辑于星期二:二十点 分。
第二十八页,编辑于星期二:二十点 分。
第二十九页,编辑于星期二:二十点 分。
第三十页,编辑于星期二:二十点 分。
第三十一页,编辑于星期二:二十点 分。
第三十二页,编于星期二:二十点 分。
第十一页,编辑于星期二:二十点 分。
第十二页,编辑于星期二:二十点 分。
第十三页,编辑于星期二:二十点 分。
第十四页,编辑于星期二:二十点 分。
第十五页,编辑于星期二:二十点 分。
第十六页,编辑于星期二:二十点 分。
第十七页,编辑于星期二:二十点 分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4. 对数函数 y = loga x ( a > 0, a 1 ) 5. 三角函数 y = sin x y = cos x y = tan x y = cot x y = sec x y = csc x 6. 反三角函数 y = arcsin x y = arccos y = arctan x y = arccot x y = arcsec x y = arccsc x 具体图形见书第5页
2
4
6
-6
-4
-2 -10 -20
2
4
6
像
-0.5
-0.5
-20
-30
-1
-1
-30
定义域 值 域 奇偶性 周期性
(-∞,+∞) [-1,1] 奇函数 T=
(-∞,+∞) [-1,1] 偶函数 T=
( k
2
, k
2
)
(k , (k 1) )
(-∞,+∞) 奇函数 T=
(-∞,+∞) 奇函数 T=
幂函数 f(x)=xα
y
y=x3 y=x
yx x
y 1 x
1 2
y=x2
O
x
指数函数与对数函数
函 数 a>1 y=ax (a>0,a≠1) 0<a<1 y=logax (a>0,a≠1) a>1 0<a<1
图
4
10
4
0.5
8 6
0.5 1 1.5 2
3
3
-0.5
4 2
2
2
-1
1
1
像
-1 -0.5 0.5 1 1.5
2
2
单调增 单调减 单调减 单调增
单调减 单调减 单调增 单调增
单调增 单调增 单调增 单调增
单调减 单调减 单调减 单调减
反三角函数
函数 y=arcsinx y=arccosx y=arctanx y=arccotx
图
1.5 1 0.5
3
1.5
1
2.5 2 1.5
1
0.5
0.5
像
-1
-0.5 -0.5 -1 -1.5
f(-x)=-f(x)
f ( x) f ( x)
平移与翻折 例如:函数y=x2+4是把y=x2的图像向上移动4,而 y=(x-2)2是把y=x2的图像向右移动2 .如图所示
上加下减,左加右减
y y
y=x2+4
y=x2
上移4
4
0
0
x
y=(x-2)2
x
右移2
y
0
2
x
y=-f(x)是将y=f(x)关于x轴翻折
两个特殊三角形的三边比例
1 斜边 csc x 对边 sin x
4 1 2
2 4
2 1
2 4
30
1 4 2
3 2 3
三角函数
函数 y=sinx y=cosx y=tanx y=cotx
1
图
-6 -4 -2
1
30 20
30 20 10
0.5
0.5
10
2
4
6
-6
-4
-2
2
4
6
-6
-4
-2 -10
0
对边 sin x 斜边 邻边 cos x 斜边 对边 tan x 邻边 邻边 cot x 对边
3
3 sin 60 2 1 0 cos 60 2
0
tan600 3
3 cot 60 3
0
cot 30 3
0
secx
cscx 的定义及角度值
1 斜边 sec x 邻边 cos x
-1.5 -2
0.5 -2
1
1.5
2
-1.5
-1
-0.5
0.5
1
定义域
(-∞,+∞)
(-∞,+∞)
பைடு நூலகம்
(0,+∞)
(0,+∞)
值 域
(0,+∞)
(0,+∞)
(-∞,+∞)
(-∞,+∞)
单调性
单调增
单调减
单调增
单调减
三角函数的定义
60
2
30
1
1 sin 30 2 3 0 cos30 2 3 0 tan30 3
高等院校高等数学课程
大 学 数 学(一)
—— 一元微积分学
第2讲 基本初等函数与图形
主讲:庆阳职业技术学院 郭海龙
第二节 基本初等函数及其图形
一.幂函数
二.指数函数 三.对数函数 四.三角函数 五.反三角函数
以下六种简单函数 称为基本初等函数
1. 常值函数 y = C ( C 为常数 ) 2. 幂函数 y = x ( R 为常数 ) 3. 指数函数 y = a x ( a > 0, a 1 )
0.5
1
1
-4
-2 -0.5
2
4
-4
-2 -0.5 -1 -1.5
2
4
0.5
-1
-1 -0.5 0.5 1
定义域
[-1,1]
[-1,1]
(-∞,+∞)
(-∞,+∞)
值 域
[
2
,] 2
[0, ]
单调减
(
2
,) 2
(0,)
单调减
单调性
单调增
单调增
f(-x)
f(-x)=-f(x)
f ( x) f ( x)
