必修1第二章2.3幂函数导学案
人教版数学高二必修1导学案 2.3幂函数学生版

2.3 幂函数学习目标 1.理解幂函数的概念.2.掌握y =x α(α=-1,12,1,2,3)的图象与性质.3.理解和掌握幂函数在第一象限的分类特征,能运用数形结合的方法处理幂函数的有关问题.学习过程 一、自主学习 1.幂函数的概念阅读教材P 77至倒数第二自然段,完成下列问题.幂函数:一般地,函数 叫做幂函数,其中 是自变量,α是 . 2.幂函数的图象与性质阅读教材P 77倒数第二自然段至P 78“例1”以上部分,完成下列问题. 幂函数的图象与性质:R R R 问题1 y =1x ,y =x ,y =x 2三个函数有什么共同特征?问题2 类比y =x 3的图象和性质,研究y =x 5的图象与性质.探究点1:幂函数的概念 例1 已知y =(m 2+2m -2)22m x -+2n -3是幂函数,求m ,n 的值.探究点2:幂函数的图象及应用例2 若点(2,2)在幂函数f (x )的图象上,点(-2,14)在幂函数g (x )的图象上,问当x为何值时,(1)f (x )>g (x );(2)f (x )=g (x );(3)f (x )<g (x ).变式探究若对于例2中的f (x ),g (x ),定义h (x )=⎩⎪⎨⎪⎧f x ,f x ≤g x ,g x ,f x >g x ,试画出h (x )的图象.探究点3:幂函数性质的综合应用 命题角度1:比较大小例3 设a =2323⎛⎫ ⎪⎝⎭,b =1323⎛⎫ ⎪⎝⎭,c =2325⎛⎫⎪⎝⎭,则a ,b ,c 的大小关系是( ) A.a >b >c B.b >a >c C.b >c >a D.c >b >a命题角度2:幂函数性质的综合应用例4 已知幂函数y =x 3m -9 (m ∈N *)的图象关于y 轴对称且在(0,+∞)上单调递减,求满足()31m a -+<()332m a --的a 的取值范围.三、当堂检测1.已知幂函数f (x )=k ·x α的图象过点⎝⎛⎭⎫12,22,则k +α等于( )A.12B.1C.32 D.2 2.已知幂函数f (x )的图象经过点(2,22),则f (4)的值等于( ) A.16 B.116 C.2D.123.设α∈{-1,1,12,3},则使函数y =x α的定义域为R 的所有α的值为( )A.1,3B.-1,1C.-1,3D.-1,1,34.下列是y =23x 的图象的是( )5.以下结论正确的是()A.当α=0时,函数y=xα的图象是一条直线B.幂函数的图象都经过(0,0),(1,1)两点C.若幂函数y=xα的图象关于原点对称,则y=xα在定义域内y随x的增大而增大D.幂函数的图象不可能在第四象限,但可能在第二象限四、课堂小结本节课我们学习过哪些知识内容?五、学后反思1、我的疑问:2、我的收获:。
必修1第二章基本初等函数数学:2.3《幂函数》教案(新人教A必修1)

2.3幂函数教学目的:使学生掌握幂函数的概念,会画幂函数的图象,能判定一个幂函数是增函 数还是减函数,能判断一个幂函数的奇偶性。
教学重点:幂函数的图象、幂函数的增减性的证明。
教学难点:幂函数增减性的证明。
教学过程一、新课引入课本P90,p=w, S=a 2, V=a 3 ,a=S 21,v=t -1,上述问题中的函数具有什么共同特征?二、新课上述问题中涉及的函数,都是形如y =x a 的函数。
一般地,函数y =x a 叫做幂函数(power function)。
其中x 是自变量,a 是常数。
当a =1,2,3,21,-1时,得到下列的幂函数,画出它们的图象,并观察图象, 将你发现的结论写在下表中:y =x y =x 2 y =x 3 y =x 21y =x -1 定义域 R R R [0,+∞) (-∞,0)∪(0,+∞) 值域 R [0,+∞) R [0,+∞) (-∞,0)∪(0,+∞)奇偶性 奇 偶 奇 非奇非偶 奇单调性 增 [0,+∞)增 增 增 (-∞,0)减(-∞,0)减 [0,+∞)减定点 (1,1) (1,1) (1,1) (1,1) (1,1)例1、证明幂函数f(x)=x 在[0,+∞)上是增函数。
证明:任取1x 、2x ∈[0,+∞),且1x <2x ,则f(1x )-f(2x )=21x x -=212121))((x x x x x x ++-=2121x x x x +-因为1x -2x <0,21x x +>0,所以,f(1x )<f(2x )即幂函数f(x)=x 在[0,+∞)上是增函数。
注意:证明函数的单调性时既可以用作差的方法,也可以用作比的方法,应用用比的 方法时应注意分母不为零,及去母时考虑符号问题。
作业:P92 1、2、3。
2.3幂函数教案-人教版数学高一上必修1第二章

第二章基本初等函数(1)2.3 幂函数1 教学目标1.1 知识与技能:[1] 理解并掌握幂函数的概念。
[2] 了解幂函数的图像和性质,并掌握了解幂函数的图像和性质,并掌握11,232,,,,y x y x y x y x y x -=====这五个常见幂函数的图像和性质。
1.2过程与方法:[1] 通过实例观察得出幂函数的概念和一般形式; [2] 通过画图掌握五个常见幂函数的图像和性质。
1.3 情感态度与价值观:[1] 通过细致作图,培养学生的动手能力和识图能力。
[2] 通过学习幂函数以及相关练习,培养学生逻辑思维。
2 教学重点/难点/易考点2.1 教学重点 [1] 幂函数的概念2.2 教学难点[1]五个常见幂函数的图像和性质。
3 专家建议此节为高中数学基本初等函数1中的一个函数幂函数,一定要让学生充分理解幂函数的概念,并能区分它和指数函数的区别。
可对比指数函数和对数函数教学,巩固其的定义域,值域,图像和单调性等问题。
4 教学方法实例探究——归纳总结——补充讲解——练习提高5 教学用具多媒体,教学用直尺、三角板。
6 教学过程6.1 引入新课[1]幂函数的概念【师】这节课是这一章的最后一节,之前我们学习了指数函数和对数函数,这节课我们来学习幂函数。
【板书】第二章基本初等函数(1) 2.3 幂函数 大家先看下面这几个具体问题。
【板演/PPT 】1.如果回收旧报纸每公斤1元,某班每年卖旧报纸x公斤,所得价钱y是关于x的函数;2.如果正方形的边长为x,面积为y,这里y是关于x的函数;3.如果正方体的棱长为x, 正方体的体积为y,这里y是关于x的函数;4.如果一个正方形场地的面积为x, 这个正方形的边长为y,这里y是关于x的函数;5.如果某人x秒内骑车行驶了1km,他骑车的平均速度是y,这里y是关于x的函数. 【师】我们已经明确了上述问题所涉及的函数关系, 你能找出它们有什么共同的特征吗? 【生】(1)都是以自变量x 为底数; (2)指数为常数;(3)幂的系数为1;x 的系数为1 (4)只有一项;(5)都是形如ay x 的函数。
人教A版数学必修一第二章《幂函数》导学案

海南省海口市第十四中学高中数学必修一 导学案 第二章 幂函数导学案一、【学习过程】知识链接:1.如何画函数图象?2.如何研究一个函数?研究函数性质从那几方面入手?二、预习:1.幂函数的定义: 2.在同一坐标系中画出下列函数图象:y=x 、y =x 2、y =x 3、y =x 21、y =x 1-三、新课探究(一)、情景设置:阅读材料并填空:(1) 如果张红购买了每千克1元的蔬菜w 千克,那么她需要支付p = 元(2) 如果正方形的边长为a ,那么正方形的面积 S=(3) 如果立方体的边长为a ,那么立方体的体积V=(4)如果一个正方形场地的面积为S ,那么这个正方形的边长a=(5)如果人t 秒内骑车行进了1 km ,那么他骑车的平均速度v=若将它们的自变量全部用x 来表示,函数值用y 来表示,则它们的函数关系式将是:(二)、新课探究1.幂函数: 强调结构:2.图像与性质公共○.所有的幂函数在 都有定义,并且函数图象都通过点 ; ○2.如果a>0,则幂函数的图象过点 并在(0,+∞)上为 (增、减)函数;○3.如果a<0,则幂函数的图象过点 ,并在(0,+∞)上为 (增、减)函数; 例1.已知幂函数y =f(x)的图像过点(3,1/9)求函数解析式3、奇偶函数的概念一般地,图像关于原点对称的函数叫奇函数,即有 如f(x)=x 3图像关于轴对称的函数叫偶函数,即有 如f(x)=x 2例、判断函数f(x)=-2x 5和f(x)=-x 4+2的奇偶性 练习:1.P80动手实践 完成书中图2-302.求下列幂函数的定义域:(1)y =x 52 (2)y =x 31 (3)y =x 43(4)y =x 2-(四)、随堂练习1.如图所示,曲线是幂函数 y = x k在第一象限内的图象,已知 k 分别取 212,1,1-,四个值,则相应图象依次为:________2.比较下列各组中两个值的大小①0.7521,0.7621;②(-0.95)31,(-0.96)31;③0.313.2,0.314.23.通过图像求下列函数的定义域和值域4.(1)y =x 23 (2)y =x 72 (3)y =x 53。
高中数学导学案 2.3 幂函数 新人教A版必修1

《2.3 幂函数》导学案主编:段小文 班次 姓名【学习目标】其中2、3是重点和难点1.通过具体实例了解幂函数的图象和性质,体会幂函数的变化规律及蕴含其中的对称性。
2.画五个幂函数的图象并由图象概括其性质。
3.从五个具体幂函数中认识幂函数的一些性质,能利用性质解决数学问题。
【课前导学】预习教材第77-78页,找出疑惑之处,完成新知学习。
1.幂函数的概念:形如 的函数称为幂函数,其中 是自变量, 是常数。
2.幂函数的性质:(1)幂函数的图象都过点 ; (2)当0α>时,幂函数在[0,)+∞上 ;当0α<时,幂函数在(0,)+∞上 ; (3)当2,2α=-时,幂函数是 ;当11,1,3,3α=-时,幂函数是 。
【预习自测】首先完成教材上P79第1、2题,然后做自测题。
1、幂函数()f x的图象过点,则()f x 的解析式是 __ 。
2、下列所给出的函数中,是幂函数的是( )A .3x y -=B .3-=x yC .32x y =D .13-=x y3、如图所示,幂函数αx y =在第一象限的图象, 比较1,,,,,04321αααα的大小( ) A .102431<<<<<αααα B .104321<<<<<αααα C .134210αααα<<<<< D .142310αααα<<<<<4、函数2-=x y 在区间]2,21[上的最大值是 ( )A .41 B .1- C .4 D .4-【课中导学】首先独立思考探究,然后合作交流展示。
探究一:看教材P77页5个具体的问题,这些函数的解析式结构有何共同特点?其一般形式如何?定义:幂函数的概念。
注意:幂函数与指数函数的区别。
探究二:在同一平面直角坐标系内作出函数12312,,,,y x y x y x y x y x -=====的图象,它们的定义域、值域、奇偶性、单调性、公共点分别如何? 归纳:幂函数的性质。
高中数学 第二章 2.3 幂函数导学案(无答案)新人教A版必修1

训练 1 已知 y (m2 2m 2)xm21 2n 3 是定义域为 R 的幂函数,求 m,n 的值.
求幂函数的定义域时,通常要对幂的指数做变形,把负指数变成正指数,把分数指数 变
成根式的形式,这样易于看出自变量的受限程度. 【幂函数的图象和性质】
1
如下图在同一坐标系内作出函 数 y x ; y x2 ; y x3 ; y x 2 ; y x1 的 图
①当 α =0 时,函数 y=xα 的图象是一条直线;
②幂函数的图象都经过(0,0),(1,1)两点; ③若幂函数 y=xα 的图象关于原点对称,则 y=xα 在定义域内 y 随 x 的增大而增大; ④幂函数的图象不可能在第四象限,但可能在第二象限. 则正确结论的个数为______.
2.已知幂函数 f(x)=xα 的图象经过点(2, 2 ),则 f(4)=________. 2
1
(1)y=x2,y=x3, y x 2 ,y=x-1;
(2)y=2x,y=3x,y=(12)x,y=0 .3x.
共同点:均是幂的形式.
不同点:第一组:
是自变量,第二组:
是自变量.
例 1 写出下列函数的定义域,并分别指出它们的奇偶性:
1
(1) y x3 ;(2) y x 2 ;(3 y x2 .
3.如图所示,曲线是幂函数 y=xα 在第一象限内的图象,已知 α 分别取-1,1,12,2 四 个值,则相应图象依次为______________.
3.写出下列函数的定义域,并指出它们的奇偶性:
(1)f(x)=x2+x-2;
1
1
(2)f(x) = x 2 x 2
1
1
(3)f(x)= x 2 3(x) 4
高中-数学-人教A版-高中数学必修一第二章2.3《幂函数》 导学案(无答案)
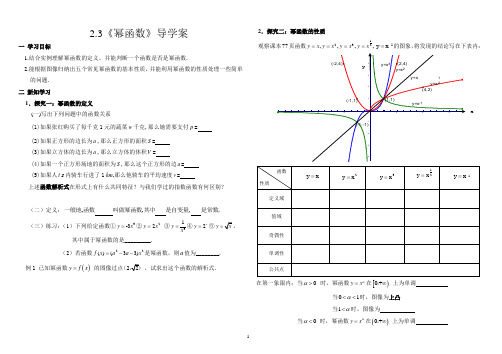
2.3《幂函数》导学案一 学习目标1.结合实例理解幂函数的定义,并能判断一个函数是否是幂函数.2.能根据图像归纳出五个常见幂函数的基本性质,并能利用幂函数的性质处理一些简单的问题.二 新知学习1.探究一:幂函数的定义 (一)写出下列问题中的函数关系(1)如果张红购买了每千克1元的蔬菜w 千克,那么她需要支付p = (2)如果正方形的边长为a ,那么正方形的面积S =(3)如果立方体的边长为a ,那么立方体的体积V =(4)如果一个正方形场地的面积为S ,那么这个正方形的边a = (5)如果人t s 内骑车行进了1 km ,那么他骑车的平均速度v =上述函数解析式在形式上有什么共同特征?与我们学过的指数函数有何区别?(二)定义:,,,一般地函数叫做幂函数其中是自变量是常数.(三)练习:(1)下列给定函数①3-3y x =②22y x = ③31y x=④2x y =⑤y = 其中属于幂函数的是_________.(2)若函数22)33()(x a a x f --=是幂函数,则a 值为________.例1 已知幂函数()y f x =的图像过点(2 ,试求出这个函数的解析式.2.探究二:幂函数的性质观察课本77页函数,,,,2132x y x y x y x y ====x y =-1的图象,将发现的结论写在下表内:.在第一象限内:当0α> 时,幂函数y x α=在[)0+∞, 上为单调 当01α<<时,图像为上凸 当1α<时,图像为当0α< 时,幂函数y x α=在()0+∞, 上为单调3.幂函数性质的简单应用例2 证明幂函数()f x x = 在[)0+∞, 上是增函数.三 练习反馈1.下列函数中不是幂函数的是 ( )A. 3y x =B.y x =C.2y x =D.1y x -=2.如图所示,曲线是幂函数y x α=在第一象限内的图象,已知α分别取1-1,122,,四个值,则相应图象依次为:_______________.3.若幂函数()y f x =的图像经过点()93,,则()25f =______________. 4.比较下列各组数的大小:(1)11220.750.76 (2)()22-3.14π5. 幂函数()21m y m m x =--在区间()0+∞,上是减函数,则m 的值为_____. 四 小结1.幂函数的定义; 2.幂函数的基本性质. 五 作业A 组课本82页第10题;B 组资料课时作业142页12题和13题.。
人教版高中数学必修1第二章基本初等函数(I)-《2.3幂函数》教案(8)

在第一象限内,当 向原点靠近时,图象在 轴的右方无限逼近 轴正半轴,当 慢慢地变大时,图象在 轴上方并无限逼近 轴的正半轴.
例题:
1.证明幂函数 上是增函数
思考:
我们知道,若 得 ,你能否用这种作比的方法来证明 上是增函数,利用这种方法需要注意些什么?
(1) (2) (3)
(4) (5)
思考:如何画出以上五个函数图像
通过观察图像,填P91探究中的表格
定义域
奇偶性
在第Ⅰ象限单调增减性
定点
3.幂函数性质
(1)
(2)
特别地,当 >1, >1时, ∈(0,1), 的图象都在 图象的下方,形状向下凸越大,下凸的程度越大(你能找出原因吗?)
当∠α<1时, ∈(0,1), 的图象都在 的图象上方,形状向上凸,α越小,上凸的程度越大(你能说出原因吗?)
作业:P79习题2.3第2、3题
2.2.3幂函数学案
1.学习目标:
(1)理解幂函数的概念;
(2)通过具体实例了解幂函数的图象和质,并能进行初步的应用.
2.重点、难点
重点:从五个具体的幂函数中认识的概念和性质
难点:从幂函数的图象中概括其性质
3.自学内容:通读教材。
4.思考并回答以下问题:
阅读教材P77的具体实例(1)~(5),思考下列问题.
(1)它们的对应法则分别是什么?
(2)以上问题中的函数有什么共同特征?
答:
上述的问题涉及到的函数,都是形如: ,其中 是自变量, 是常数.
探究新知
1.幂函数的定义
一般地,的函数称为幂孙函数,其中 是自变量, 是常数.
如等都是幂函数,幂函数与指数函数,对数函数一样,都是基本初等函数.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 基本初等函数(I ) 人教A 版数学•必修1
2.3 幂函数
导:
【复习目标
】
1
.理解幂函数的概念,熟悉幂函数的解析式,会画简单幂函数的图象; 2.熟练掌握幂函数y =x a (a 为有理数)的性质和图象之间的关系; 3.理解当a>0与a<0时幂函数在第一象限的图象和增减性,并运用它 进一步分析解决有关幂函数的问题;
4.培养学生观察和归纳能力,培养学生数形结合的意识和思想. 【教学重点】
掌握常见的幂函数的图象和性质,解决有关问题. 【教学难点】
幂函数的图象和性质的总结,熟练运用幂函数的性质解决相关问题, 特别是含参数讨论的一类问题.
学:
幂函数的概念
基本概念
概念 定义
幂函数
一般地,函数 叫做幂函数, 其中
是自变量, 常数
【练习】 下列函数是幂函数的是
① y=2x 2 ② y=2x ③ y=x 3 ④ y=x -1
幂函数的图象和性质
阅读教材P 77——P 78的内容,完成下列问题. 幂函数y=x ,y=x 2,y=x 3,2
1x y ,y=x -1
y=x
y=x 2
y=x 3
y=
2
1x
y=x -1
图象
续 表
y=x
y=x 2
y=x 3
y=2
1x
y=x -1
定义域
值域
奇偶性
单调性
公共点
【思考】 指数函数、对数函数在其定义域上都是单调函数,幂函数呢?
预习完成后,请把你认为难以解决的问题记录在下面,并在小组内交流.
问题1
问题2 问题3 问题4
议:
[探究背景] [背景1] 对于等式
b a N =
(1)如果a 一定,N 随b 的变化而变化,我们建立了指数函数:x a y =(2)如果
a 一定,
b 随N 的变化而变化,我们建立了对数函数:
x y a log =
(3)如果b 一定,N 随a 的变化而变化,我们建立了幂函数:αx y =
[背景2]
幂函数 y=x ,y=x 2
,y=x 3
,2
1x y =,y=x -1
[探究问题]
1.幂函数与指数函数的定义有何异同点? 表达式 相同点 不同点
指数函数
)
0,0(≠>=a a a y x
且
右边都是 幂的形式
指数是自变量x ,底数是常数
幂函数 )(R x y ∈=αα
底数是自变量x ,指数是常数
2.幂函数的图象能过第四象限吗?
3.幂函数α
x y =在(0,∞+)上的单调性与哪个量有关?
[探究成果]
1.幂函数解析式的结构特征
(1)指数为常数。
(2)底数是自变量,自变量的系数为1.
(3)幂α
x 的系数为1.(4)只有1项。
2.幂函数的图象
(1)在第一象限的图象大致形状与位置: ①当0<α
时,其图象为双曲线型,过点(1,1),其形状如曲线①所示;
②当10<<α
时,其图象为抛物线型,过(0,0),(1,1)两点,形状如曲线②所示;
③当1=α时,其图象为直线,如直线③所示; ④当1>α时,其图象为抛物线型,过(0,
0),(1,1)两点,形状如曲线④所示。
(2)结合函数的奇偶性可得一般幂函数的图象。
x
y
④
③
②
①
o
幂函数的概念
关键词:
α
x
y=的特征
例1:已知函数
3
2
)2
2
(2
2-
+
-
+
=+n
x
m
m
y m是幂函数,求m,n的值。
解答此类问题的关键是紧扣幂函数的定义,建立等量关系,求解相应方程便可。
[变式训练]
1.已知函数m
x
m
m
x
f m
m,
)
2
(
)
(1
22-
+
+
=为何值时f(x)是:
(1)正比例函数?(2)反比例函数?(3)二次函数?(4)幂函数?
幂函数的图象和性质
关键词:定义证明对称性作图
例2:证明幂函数[)∞
+
=,
在0
)
(x
x
f上是增函数。
例:3:已知幂函数的图象过点
)4,
2
1
(P.讨论y=f(x)的定义域、值域。
奇偶性、单
调性,并画出草图.
1.定义法证明或判断函数单调性的五个步骤
(1)取值设2
1
,x
x是区间上的任意两个值且
2
1
x
x<
(2)作差作
)
(
)
(
2
1
x
f
x
f-
(3)变形方法、技巧:因式分解,配方或分子(分母)有理化等
(4)定号确定
)
(
)
(
2
1
x
f
x
f-的符号
(5)判断根据定义得出结论
2.求幂函数
α
x
y=(其中α是分数形式)定义域的基本步骤
(1)还原为根式
(2)根据根式和分式有意义的条件求幂函数的定义域
[变式训练]
2.已知函数3
2
x
y=.
(1)求定义域;
(2)判断奇偶性;
(3)已知该函数在第一象限的图象如图所示,试补全图象,并由图象确定单调区间。
y
o
x
练:
1.下列函数中是幂函数的是( ) A.
x x y 2= B. x
y 2= C. 2
x
y = D.
23+=x y
2.下列结论中,正确的是( )
A.幂函数的图象都通过点(0,0)(1,1)
B.幂函数的图象可以出现在第四象限
C.当幂指数α取2
1
,3,1时,幂函数αx y =是增函数 D.当幂指数1-=α时,幂函数αx y =在定义域上是减函数
结:
1.判断一个函数是否是幂函数,其关键是看该函数是否有)(R x y ∈=αα的形式;
2.已知幂函数的图象和性质求解析式,常用待定系数法;
3.(1)在第一象限的图象大致形状与位置: ①当0<α
时,其图象为双曲线型,过点(1,1),但不过(0,0)点;
②当10<<α
时,其图象为抛物线型,过(0,0),(1,1)两点;
③当1=α时,其图象为直线;
④当1>α时,其图象为抛物线型,过(0,0),(1,1)两点。
(2)结合函数的奇偶性可得一般幂函数的图象。
请完成《学业达标限时自测(十九)》。
