沈阳二中下学期第五次模拟考试.docx
辽宁省沈阳市第二中学2022届高三下学期第五次模拟考试数学试题 (2)

一、单选题1. 如图所示,是棱长为的正方体,、分别是棱、上的动点,且.当、、、共面时,平面与平面所成锐二面角的余弦值为()A.B.C.D.2.如图,在矩形中,分别为边上的点,且,,设分别为线段的中点,将四边形沿着直线进行翻折,使得点不在平面上,在这一过程中,下列关系成立的是()A .直线直线B .直线直线C .直线直线D .直线平面不能3. 已知集合,则集合的子集个数是( )A.B.C.D.4. 若,则在复平面内对应的点位于( )A .第一象限B .第二象限C .第三象限D .第四象限5. 德国数学家高斯是近代数学奠基者之一,有“数学王子”之称,在历史上有很大的影响.他幼年时就表现出超人的数学天赋,10岁时,他在进行的求和运算时,就提出了倒序相加法的原理,该原理基于所给数据前后对应项的和呈现一定的规律生成,因此,此方法也称之为高斯算法.已知某数列通项,则( )A .98B .99C .100D .1016. 蹴鞠(如图所示),2006年5月20日,已作为非物质文化遗产经国务院批准列入第一批国家非物质文化遗产名录.蹴有用脚蹴、踢、蹋的含义,鞠最早系外包皮革、内实米糠的球,因而蹴鞠就是指古人以脚蹴、蹋、踢皮球的活动,类似今日的足球.已知某鞠(球)的表面上有四个点、、、,且球心在上,,,,则该鞠(球)的表面积为().A.B.C.D.辽宁省沈阳市第二中学2022届高三下学期第五次模拟考试数学试题 (2)辽宁省沈阳市第二中学2022届高三下学期第五次模拟考试数学试题 (2)二、多选题三、填空题7. 已知点是抛物线的对称轴与准线的交点,点为抛物线的焦点,点在抛物线上且满足,若取最大值时,点恰好在以为焦点的双曲线上,则双曲线的离心率为A.B.C.D.8. 在中,,,,则的形状是( )A .锐角三角形B .直角三角形C .钝角三角形D .无法判断9. 已知函数,的定义域均为,导函数分别为,,若,,且,则( )A .4为函数的一个周期B .函数的图象关于点对称C.D.10. 数学美的表现形式不同于自然美或艺术美那样直观,它蕴藏于特有的抽象概念、公式符号、推理论证、思维方法等之中,揭示了规律性,是一种科学的真实美.在平面直角坐标系中,曲线就是一条形状优美的曲线,则( )A .曲线围成的图形的周长是B.曲线上的任意两点间的距离不超过4C .曲线围成的图形的面积是D .若是曲线上任意一点,则的最小值是11. 函数,则在区间内可能( )A .单调递增B .单调递减C .有最小值,无最大值D .有最大值,无最小值12.由倍角公式,可知可以表示为的二次多项式.一般地,存在一个()次多项式(),使得,这些多项式称为切比雪夫(P .L .Tschebyscheff )多项式.运用探究切比雪夫多项式的方法可得( )A.B.C.D.13. 已知抛物线的焦点为,准线为,是上一点,是直线与的一个交点,若,则_____________.14. 参加数学兴趣小组的小何同学在打篮球时,发现当篮球放在地面上时,篮球的斜上方灯泡照过来的光线使得篮球在地面上留下的影子有点像数学课堂上学过的椭圆,但他自己还是不太确定这个想法,于是回到家里翻阅了很多参考资料,终于明白自己的猜想是没有问题的,而且通过学习,他还确定地面和篮球的接触点(切点)就是影子椭圆的焦点.他在家里做了个探究实验:如图所示,桌面上有一个篮球,若篮球的半径为个单位长度,在球的右上方有一个灯泡(当成质点),灯泡与桌面的距离为个单位长度,灯泡垂直照射在平面的点为,影子椭圆的右顶点到点的距离为个单位长度,则这个影子椭圆的离心率______.四、解答题15.的展开式中的系数为______.(用数字作答)16. 已知抛物线:,直线,且点在抛物线上.(1)若点在直线上,且四点构成菱形,求直线的方程;(2)若点为抛物线和直线的交点(位于轴下方),点在直线上,且四点构成矩形,求直线的斜率.17. 已知函数,.(1)若函数在处取得极值,求函数的单调区间;(2)设,对于时,恒成立,求参数a 的取值范围.18. 为了验证甲、乙两种药物对治疗某种病毒的感染是否有差异,某医学科研单位用两种药物对感染病毒的小白鼠进行药物注射实验.取200只感染病毒的小白鼠,其中100只注射甲药物,另外100只注射乙药物,治疗效果的统计数据如下:康复未康复合计甲药物6040100乙药物7525100合计13565200(1)分别估计小白鼠注射甲、乙两种药物康复的概率;(2)能否有97.5%的把握认为甲、乙两种药物对治疗该种病毒的感染有差异?参考公式:.临界值表:19.已知有限数列,从数列中选取第项、第项、、第项(),顺次排列构成数列,其中,,则称新数列为的长度为m的子列.规定:数列的任意一项都是的长度为1的子列,若数列的每一子列的所有项的和都不相同,则称数列为完全数列.设数列满足,.(1)判断下面数列的两个子列是否为完全数列,并说明由;数列①:3,5,7,9,11;数列②:2,4,8,16.(2)数列的子列长度为m ,且为完全数列,证明:m 的最大值为6;(3)数列的子列长度,且为完全数列,求的最大值.20. 已知函数在区间单调,其中ω为正整数,|φ|<,且.(1)求图像的一个对称中心;(2)若,求.21. 有三个车队分别有2辆、3辆、4辆车,现分别从其中两个车队各抽调两辆车执行任务,则不同的抽调方案共有 种.。
辽宁省沈阳市第二中学2020届高三下学期第五次模拟考试 生物试题 Word版含答案

沈阳二中2019—2020学年度下学期高三第五次模拟考试理科综合能力测试命题人:高三理科综合审校人:高三理科综合说明:1、测试时间:150分钟总分:300分2、客观题答在答题纸上,主观题答在答题纸相应位置上第Ⅰ卷(选择题,共126分)一、选择题:本大题共13小题,每小题6分。
在每小题给出的4个选项中,只有一项符合题目要求。
1.下列关于各种物质的描述,正确的是()A.脂质存在于所有的细胞中B.动物细胞通过自由扩散排出Na+C.细胞癌变后,细胞膜上的糖蛋白增多D.生命系统的结构层次包括从原子、分子到生物圈的各个层次2.将同一部位的紫色洋葱外表皮细胞分别浸在甲、乙、丙3种溶液中,测得原生质层的外界面与细胞壁间距离变化如图所示,下列相关分析错误的是()A.实验开始时,洋葱表皮细胞细胞液浓度均小于甲、乙溶液的浓度B.与t0时相比,t2时乙溶液中洋葱表皮细胞的细胞液浓度未曾发生变化C.实验过程中,丙溶液中有水分子进出洋葱表皮细胞D.实验结束时,乙溶液的浓度可能有所下降3.启动子是RNA聚合酶识别结合的位点,RNA聚合酶与启动子结合以后启动基因的转录。
许多基因的启动子内富含CG重复序列,若其中的部分胞嘧啶(C)被甲基化成为5-甲基胞嘧啶,就会抑制基因的转录。
下列与之相关的叙述中,正确的是()A.在一条单链上相邻的C和G之间通过氢键连接B.胞嘧啶甲基化导致已表达的蛋白质结构改变C.基因的表达水平与基因的甲基化程度无关D.胞嘧啶甲基化会阻碍RNA聚合酶与启动子结合4.下列有关教材实验中使用的试剂和实验原理的叙述,正确的是()A.低温诱导染色体数目加倍实验中,将大蒜根尖制成装片后再进行低温处理B.盐酸在观察细胞有丝分裂和观察DNA和RNA在细胞中的分布实验中的作用相同C.向某溶液中加入双缩脲试剂,出现紫色反应,说明该溶液中一定含有蛋白质D.在提取纯净的动物细胞膜和植物细胞的质壁分离与复原实验中水的作用原理相近5.在某草原上存在甲、乙和丙三种主要牧草,牛羊对牧草喜食程度甲>乙>丙,放牧强度越大,牧草地上生物量越小。
辽宁省沈阳市第二中学高三第五次模拟考试英语

沈阳二中2022-2023学年度下学期第五次模拟考试高三(23届)英语试题考试时间:120分钟满分:150分注意事项:1.答题前,考生务必将自己的姓名和准考证号填写在答题卡上,并将条形码贴在相应位置。
2.答选择题时,选出每小题答案后,用铅笔把答题卡对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第一部分听力(共两节,满分30分)第一节(共5小题,每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.What time will the flight take off?A.At2p.m..B.At3p.m..C.At5p.m..2.Which restaurant do the speakers probably decide to go?A.The Burger King.B.A French restaurant.C.An Italian restaurant.3.Where do the speakers plan to meet?A.In the office.B.At the cafeteria.C.In the lab.4.When did the man plan to go to the beach originally?A.Tonight.B.Next week.C.This Tuesday.5.What are the speakers talking about?A.Getting a ticket.B.Recommending a song.ing an app.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
辽宁省沈阳市第二中学2022届高三下学期第五次模拟考试数学试题(1)
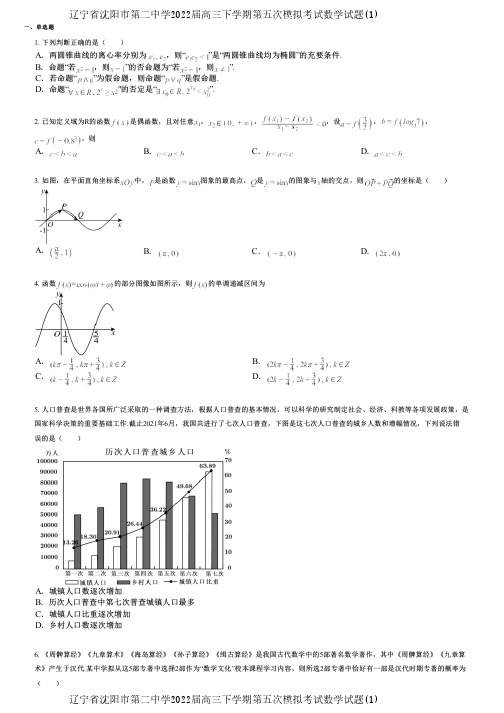
一、单选题1. 下列判断正确的是( )A .两圆锥曲线的离心率分别为 ,则“”是“两圆锥曲线均为椭圆”的充要条件.B .命题“若,则”的否命题为“若,则”.C .若命题“”为假命题,则命题“”是假命题.D .命题“"的否定是“”.2. 已知定义域为R 的函数是偶函数,且对任意,,,设,,,则A.B.C.D.3.如图,在平面直角坐标系中,是函数图象的最高点,是的图象与轴的交点,则的坐标是()A.B.C.D.4. 函数=的部分图像如图所示,则的单调递减区间为A.B.C.D.5. 人口普查是世界各国所广泛采取的一种调查方法,根据人口普查的基本情况,可以科学的研究制定社会、经济、科教等各项发展政策,是国家科学决策的重要基础工作.截止2021年6月,我国共进行了七次人口普查,下图是这七次人口普查的城乡人数和增幅情况,下列说法的是()A .城镇人口数逐次增加B .历次人口普查中第七次普查城镇人口最多C .城镇人口比重逐次增加D .乡村人口数逐次增加错误6. 《周髀算经》《九章算术》《海岛算经》《孙子算经》《缉古算经》是我国古代数学中的5部著名数学著作,其中《周髀算经》《九章算术》产生于汉代.某中学拟从这5部专著中选择2部作为“数学文化”校本课程学习内容,则所选2部专著中恰好有一部是汉代时期专著的概率为( )辽宁省沈阳市第二中学2022届高三下学期第五次模拟考试数学试题(1)辽宁省沈阳市第二中学2022届高三下学期第五次模拟考试数学试题(1)二、多选题A.B.C.D.7.函数的最小正周期是( )A.B.C.D.8. 教室通风的目的是通过空气的流动,排出室内的污浊空气和致病微生物,降低室内二氧化碳和致病微生物的浓度,送进室外的新鲜空气.按照国家标准,教室内空气中二氧化碳日平均最高容许浓度应小于等于.经测定,刚下课时,空气中含有的二氧化碳,若开窗通风后教室内二氧化碳的浓度为,且随时间(单位:分钟)的变化规律可以用函数描述,则该教室内的二氧化碳浓度达到国家标准至少需要的时间为(参考数据:)( )A .10分钟B .14分钟C .15分钟D .20分钟9. 设函数,则( )A.的图象关于直线对称B .在上单调递减C .若且时,D .关于的方程恒有个不同的实根10. 如图,透明塑料制成的长方体容器内灌进一些水,固定容器一边于地面上,再将容器倾斜,随着倾斜度的不同,有下面几个结论,其中正确的命题有( )A .没有水的部分始终呈棱柱形B.水面所在四边形的面积为定值C.随着容器倾斜度的不同,始终与水面所在平面平行D .当容器倾斜如图(3)所示时,为定值11. 已知圆上两点A 、B 满足,点满足,则不正确的是( )A .当时,B .当时,过M 点的圆C的最短弦长是C .线段AB的中点纵坐标最小值是D .过M 点作圆C 的切线且切线为A ,B ,则的取值范围是12.已知函数满足,函数在上单调,对于,(等号可以取到),则下列结论中正确的有( )A.函数的解析式为B.函数的单调递增区间为C .不等式的解集为三、填空题四、解答题D .将函数的图象保持纵坐标不变,横坐标伸长为原来的2倍,然后将其向左平移个单位长度,得到函数的图象13.已知函数的部分图象如图所示,函数的图象过点,且的图象的两条对称轴之间的最短距离为,则______;将的图象向右平移个单位长度,得到函数的图象,则图象的对称轴方程为______.14. 已知在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且2cos A sin B =sin A +2sin C .则B =______;15.记为等比数列的前项和.设,,则公比______,______.16.已知抛物线的焦点为,准线为.直线与抛物线相切于点且与轴交于点,点是点关于点的对称点,直线与抛物线交于另一点,与准线交于点.(1)证明:直线直线;(2)设的面积分别为,若,求点的横坐标的取值范围.17.数列的前项和为,,且.(1)求数列的通项公式;(2)若,求数列的前项和.18. 已知函数,,其中e 为自然对数的底数.(1)求曲线在点处的切线方程;(2)当时,有,求证:对,有;(3)若,且,求实数a 的取值范围.19. 已知函数.(1)若,求函数的单调递增区间;(2)(ⅰ)若是函数的极大值点,记函数的极小值为,求证:;(ⅱ)若在区间上有两个极值点.求证:.(提示:).20. 设 .(1)证明:在上单调递减;(2)若,证明:.21. 设函数,其中.(1)当时,在时取得极值,求;(2)当时,若在上单调递增,求的取值范围;(3)证明对任意的正整数,不等式都成立.。
辽宁省沈阳市第二中学2020届高三数学(文)下学期第五次模拟试卷(Word版带答案)

沈阳二中2019——2020学年度下学期高三(20届)模拟考试数学(文科)试题命题人:高三数学组审校人:高三数学组说明:1.测试时间:120分钟总分:150分2.客观题涂在答题纸上,主观题答在答题纸的相应位置上第Ⅰ卷(60分)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.双曲线的左焦点的坐标为A. B. C. D.2.设角的终边过点,则A. B. C. D.3.已知命题“ ,使”是假命题,则实数的取值范围是A. B. C. D.4.已知平面向量,则下列关系正确的是A. B. C. D.5.在中,,则的面积为A. B. C. D.6.函数的一个零点所在的区间是A. B. C. D.7.已知 , 满足条件,则的最大值是 ( )A. B. C. 3 D. 48. 在等比数列中,“ ”是“ 为递增数列”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要9.已知函数的定义域为,满足,当时,,则函数的大致图象是()A B C D10.已知球O的直径,A,B,C是球O球面上的三点,是等边三角形,且 ,则三棱锥P—ABC的体积为A. B. C. D.11.已知函数,则关于x的方程的实根个数不可能为A.2B.3C.4D.512.已知函数有两个零点,则下列说法错误的是A. B.C. D.有极小值点,且第Ⅱ卷(90分)本卷包括必考题和选考题两部分,第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答.二、填空题: 本大题共4小题,每小题5分,共20分.13.复数满足方程,则 =____.14.设为等差数列的前项和,,则其通项公式 ______ .15.中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的,依次输入的为2,2,5,则输出的 = .16. 在四棱锥中,平面平面,底面为梯形, , .(1)平面;(2)平面;(3)是棱的中点,棱上存在一点,使 .正确命题的序号为.三、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)为迎接年冬奥会,北京市组织中学生开展冰雪运动的培训活动,并在培训结束后对学生进行了考核. 记表示学生的考核成绩,并规定为考核优秀.为了了解本次培训活动的效果,在参加培训的学生中随机抽取了名学生的考核成绩,并作成如下茎叶图:5 0 1 1 66 0 1 4 3 3 5 87 2 3 7 6 8 7 1 78 1 1 4 5 2 99 0 2 1 3 0(Ⅰ) 从参加培训的学生中随机选取1人,请根据图中数据,估计这名学生考核成绩为优秀的概率;(Ⅱ)从图中考核成绩满足的学生中任取人,求至少有一人考核优秀的概率;(Ⅲ)记表示学生的考核成绩在区间内的概率,根据以往培训数据,规定当时培训有效. 请你根据图中数据,判断此次中学生冰雪培训活动是否有效,并说明理由. 18.(本小题满分12分)已知的面积为,且内角A,B,C依次成等差数列。
2023届辽宁省沈阳市第二中学高三下学期第五次模拟英语试卷(3)

2023届辽宁省沈阳市第二中学高三下学期第五次模拟英语试卷(3)一、听力选择题1. What makes the man feel good about the new job?A.The salary.B.The working time.C.The traveling.2. Why does the man want to leave the umbrella behind?A.His mother has told him to do so.B.He didn’t watch the weather report.C.He’s going away from the rain.3.A.He’s willing to help run the experiment.B.He’s busy working on his own experiment.C.He can act as a subject in the experiment.D.He thinks the experiment is hard to understand.4. Who taught Bill Chinese poems?A.His mother.B.His father.C.His sister.5. When will the speakers meet?A.At 10:30.B.At 11:00.C.At 12:00.二、听力选择题6. 听下面一段较长对话,回答以下小题。
1. How long have the speakers been waiting?A.One hour.B.Two hours.C.Three hours.2. What does the woman want to be?A.An engineer.B.A news reporter.C.An astronaut.7. 听下面一段较长对话,回答以下小题。
2023届辽宁省沈阳市第二中学高三第五次模拟考试 物理

沈阳二中2022-2023学年度下学期第五次模拟考试高三(23届)物理试题命题人:陈阳王国军审校人:李红梅沈小冬说明:1.测试时间:75分钟总分:100分2.客观题涂在答题纸上,主观题答在答题纸的相应位置第I卷(46分)一、选择题:本题共10小题,共46分。
在每小题给出的四个选项中,第1~7题只有一项符合题目要求,每小题4分;第8~10题有多项符合题目要求,每小题6分,全部选对的得6分,选对但不全的得3分,有选错的得0分。
A.B.C.D.的复色光从空气射向两束单色光,单色光a偏折到C 上,分别固定三个电荷量相等处的点电荷带负电,O 为三角形中心,已知A .2a B .kQ a 2 C .6kQ a 2D .3kQ a 27.某次冰壶运动训练中,甲壶与静止的乙壶发生正碰。
已知冰面粗糙程度处处相同,不计空气阻力,两壶完全相同且均可视为质点,碰撞时间极短可不计,碰撞前、后两壶运动轨迹始终在同一水平直线上。
从开始碰撞到两壶都静止过程中,测得乙壶位移是甲壶位移的k 倍,则( )A .k <1B .k 值越大,两壶碰撞过程中损失机械能越大C .k 值越大,两壶碰撞过程中损失机械能越小D .碰撞后瞬时,乙壶速度为零8.如图所示,阻值为R 的金属棒从图示位置ab 分别以v 1、v 2的速度沿光滑水平导轨(电阻不计)匀速滑到a ′b ′位置,若v 1∶v 2=1∶2,则在这两次过程中( )A .回路电流I 1∶I 2=1∶2B .产生的热量Q 1∶Q 2=1∶4C .通过任一截面的电荷量q 1∶q 2=1∶1D .外力的功率P 1∶P 2=1∶210. 两列简谐横波分别沿x轴正方向和负方向传播,波速均为0.2m/sv=,两个波源分别位于 1.2m x = 和0.2m x =- 处,波源的振幅均为2cm 。
如图所示为0=t 时刻两列波的图像,此刻平衡位置在0.2m x = 和0.8m x = 的P Q 、两质点刚开始振动。
辽宁省沈阳市第二中学2023届高三第五次模拟考试数学试题(1)

一、单选题二、多选题1. 过平行六面体任意两条棱的中点作直线,其中与平面平行的直线共有( )A .4条B .6条C .8条D .12条2. 已知等差数列()的前n 项和为,公差,,则使得的最大整数n 为( )A .9B .10C .17D .183.已知等差数列的前项和为,且,,则( )A .52B .54C .56D .584. 已知函数()有四个不同的零点,则实数的取值范围是A.B.C.D.5. 设x 是实数,则“x >0”是“|x |>0”的 ( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件6. 已知函数,其导函数为,有以下两个命题:①若为偶函数,则为奇函数;②若为周期函数,则也为周期函数.那么( ).A .①是真命题,②是假命题B .①是假命题,②是真命题C .①、②都是真命题D .①、②都是假命题7. 已知集合,则( )A.B.C.D.8. 在中,已知,,,则的面积为( )A.B.C.D.9. 下列大小关系正确的是( )A.B.C.D.10. 已知函数,则下列说法正确的是( )A.函数有两个极值点B .若关于x的方程恰有1个解,则C.函数的图象与直线有且仅有一个交点D .若,且,则无最值11. 已知点P 在棱长为2的正方体的表面上运动,点Q 是的中点,点P满足,下列结论正确的是( )A .点P的轨迹的周长为B .点P的轨迹的周长为C.三棱锥的体积的最大值为D.三棱锥的体积的最大值为辽宁省沈阳市第二中学2023届高三第五次模拟考试数学试题(1)辽宁省沈阳市第二中学2023届高三第五次模拟考试数学试题(1)三、填空题四、解答题12. 对于函数和,设,若存在,使得,则称与互为“零点相邻函数”.若函数与互为“零点相邻函数”,则实数的值可以是( )A.B.C.D.13. 已知椭圆C :,点M 与C 的焦点不重合,若M 关于C 的焦点的对称点分别为A ,B ,线段MN 的中点在C上,则_________.14. 已知有L ,M ,S 三种尺寸的检测样品盒,其中每个L 盒至多放置10支完全相同的样品,且L 盒至少比M 盒多2支样品,M 盒至少比S 盒多2只样品,则不同的放置方法共有________种.(注:L ,M ,S 不可为空盒)15. 若复数满足(是虚数单位),则复数的实部是______.16. 如图,在中,,D 为AC 边上一点且.(1)若,求的面积;(2)求的取值范围.17. 某地下车库在排气扇发生故障的情况下,测得空气中一氧化碳的含量达到了危险状态,经抢修后恢复正常.排气4分钟后测得车库内一氧化碳浓度为64 ppm (ppm 为浓度单位,1 ppm 表示百万分之一),再过4分钟又测得浓度为32 ppm .经检验知,该地下车库一氧化碳浓度y (ppm )与排气时间t (分钟)之间存在函数关系y =(c ,m 为常数).(1)求c ,m 的值;(2)若空气中一氧化碳浓度不高于0.5 ppm 为正常,问至少排气多少分钟才能使这个地下车库中一氧化碳含量达到正常状态?18. 在平面直角坐标系xOy 中,点A 在轴上滑动,点B 在轴上滑动,A 、B 两点间距离为.点P 满足,且点P 的轨迹为C .(1)求C 的方程;(2)设M ,N 是C 上的不同两点,直线MN 斜率存在且与曲线相切,若点F 为,那么的周长是否有最大值.若有,求出这个最大值,若没有,请说明理由.19. 为了有针对性地提高学生体育锻炼的积极性,某校需要了解学生是否经常锻炼与性别因素有关,为此随机对该校100名学生进行问卷调查,得到如下列联表.经常锻炼不经常锻炼总计男35女25总计100已知从这100名学生中任选1人,女生被选中的概率为.(1)完成上面的列联表,并根据列联表中的数据,判断能否有的把握认为该校学生是否经常锻炼与性别因素有关.(2)若按分层抽样法从女生中抽取8人,再从8人中随机抽取2人进行访谈,求抽取的2人都不经常锻炼的概率.附:,其中,.0.10.050.010.0012.7063.841 6.63510.82820. 为迎接2022年北京冬奥会,推广滑雪运动,某滑雪场开展滑雪促销活动.该滑雪场的收费标准是:滑雪时间不超过1小时免费,超过1小时的部分每小时收费标准为40元(不足1小时的部分按1小时计算).有甲、乙两人相互独立地来该滑雪场运动,设甲、乙不超过1小时离开的概率分别为;1小时以上且不超过2小时离开的概率分别为;两人滑雪时间都不会超过3小时.(1)求甲、乙两人所付滑雪费用相同的概率;(2)设甲、乙两人所付的滑雪费用之和为随机变量ξ,求ξ的分布列与均值E(ξ),方差D(ξ).21. 已知函数,.(1)求函数的单调增区间;(2)在锐角中,角A、B、C的对边分别为a、b、c,当,,且三角形ABC的面积为时,求a.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
沈阳二中2015—2016学年度下学期第五次模拟考试高三(16届)数学(文科)试题说明:1.测试时间:120分钟 总分:150分2.客观题涂在答题纸上,主观题答在答题纸的相应位置上第Ⅰ卷 (选择题, 共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合A ={}2,1,0,1,2--,B =[2,1)-,则A B I =( ) A .{}2,1,0--B .{}2,1,0,1--C .(2,1)- D .[2,1]-2. 已知复数312a ii+-是纯虚数,则实数a = ( ) A .-2 B .4 C .6 D .-63. 设,x y 满足约束条件1010330x y x y x y +-≥⎧⎪--≤⎨⎪-+≥⎩,则2z x y =+的最小值为( )A. 8B. 7C. 2D. 14. 已知πα<<0,21cos sin =+αα ,则α2cos 的值为( )A .47B .47-C .47±D .43-. 5、已知2,4a b ==r r ,且()a b a +⊥r r r,则a r 与b r 的夹角是( )A 、3π B 、23π C 、6π D 、56π6. 如图(1)是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到第14次的考试成绩依次记为A1,A2,…,A14.图(2)是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是( ) A .7 B .8 C .9 D .107. 已知点P 是抛物线241y x =上的一个动点,则点P 到点A (0, 2)的距离与点P 到y 轴的距 离之和的最小值为( )A .2B .5C .15-D .15+8. .若m R ∈,“函数21xy m =+-有零点”是“函数log m y x =在0+∞(,)上为减函数” 的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 9. 已知函数)20(sin 2sin cos 2cos )(πϕϕϕ<<-=x x x f 的图象的一个对称中心为(6π,0),则下列说法错误的是 ( ) A .直线π125=x 是函数)(x f 的图象的一条对称轴B .函数)(x f 在]6,0[π上单调递减C .函数)(x f 的图象向右平移6π个单位可得到x y 2cos =的图象 D . 函数)(x f 在]2,0[π上的最小值为-110. “牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几 何体.它由完全相同的四个曲面构成,相对的两个曲面在同一个圆柱的侧面上,好似两个 扣合(牟合)在一起的方形伞(方盖).其直观图如图所示,图中四边形是为体现其直观 性所作的辅助线.当其正视图和侧视图完全相同时,它的俯视图可能是( )A B C D 直观图11. 已知点P 是双曲线C :22221(0,0)x y a b a b-=>>左支上一点,1F ,2F 是双曲线的左、右两个焦点,且12PF PF ⊥,2PF 与两条渐近线相交于M ,N 两点(如图),点N 恰好平分线段2PF ,则双曲线的离心率是( )A.5B.2C.3D.2 12. 如图,已知直线y kx m =+与曲线()y f x =相 切于两点,则()()F x f x kx =-有( ) A.2个零点B.3个极值点C.2个极大值点D.3个极大值点第12题图Oyxy kx m=+()y f x =ABFPEDC第Ⅱ卷 (非选择题, 共90分)二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中横线上. 13. 点P 为ABC ∆边AB 上任一点,则使ABC PBC S S ∆∆≤31的概率是 . 14. ABC ∆中,,,a b c 分别是,,A B C ∠∠∠的对边且222ac c b a +=-,若ABC ∆最大边长 是7且sin 2sin C A =,则ABC ∆最小边的边长为 .15.在正方体1111ABCD A B C D -中,M 是线段11A C 的中点,若四面体M ABD -的外接球 体积为36π,则正方体棱长为 .16. 已知函数2log ()0()20x x f x x x -<⎧=⎨-≥⎩若函数()()g x a f x =-有四个零点1234,,,x x x x 且1234x x x x <<<,则3412x x ax x a++的取值范围是 . 三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.) 17. (本小题满分12分)若数列{}n a 的前n 项和n S 满足2n n S a n =+. (Ⅰ)求证:数列{}1n a -是等比数列; (Ⅱ)记()()2211log 1log 1n n n b a a +=--,求数列{}n b 的前n 项和为n T .18. (本小题满分12分)如图,在四棱锥ABCD P -中,底面ABCD 为菱形,ο60=∠DAB ,ABCD PD 平面⊥,2PD AD ==,点F E ,分别为PD AB 和的中点.(Ⅰ)求证:直线AF ∥平面PEC ;(Ⅱ)求点F 到平面PEC 的距离. 19. (本小题满分12分)随着国民生活水平的提高,利用长假旅游的人越来越多.某公司统计了2012到2016年五年间本公司职员每年春节期间外出旅游的家庭数,具体统计数据如下表所示:年份(x ) 2012 2013 2014 2015 2016 家庭数(y )610162226(Ⅰ)从这5年中随机抽取两年,求外出旅游的家庭数至少有1年多于20个的概率;(Ⅱ)利用所给数据,求出春节期间外出旅游的家庭数与年份之间的回归直线方程ˆˆˆybx a =+,判断它们之间是正相关还是负相关;并根据所求出的直线方程估计该公司2019年春节期间外出旅游的家庭数.参考公式:121()()ˆˆˆ,()nii i nii xx y y bay bx xx ==--==--∑∑ 20. (本小题满分12分)已知椭圆C :()222210x y a b a b+=>>的离心率为154,12,F F 是椭圆的两个焦点,P 是椭圆上任意一点,且21F PF ∆的周长是8215+.(Ⅰ)求椭圆C 的方程;(Ⅱ)设圆T :94)2(22=+-y x ,过椭圆的上顶点M 作圆T 的两条切线交椭圆于E 、F 两点,求直线EF 的斜率.21. (本小题满分12分)已知函数21()ln 2f x a x bx x =++,(,a b ∈R )(Ⅰ)若函数()f x 在121,2x x ==处取得极值,求,a b 的值,并求出极值 (Ⅱ)若函数()f x 在(1,(1)f )处的切线的斜率为1,存在[1,]x e ∈,使得 21())2f x x a x x -+≤(+2)(-成立,求实数a 的取值范围;※考生注意:请考生在第(22)、(23)、(24)三题中任选一题作答,如果多做,则按所做的第一题计分.做答时,用2B 铅笔在答题卡上把所选题目对应的题号涂黑.22.(本小题满分10分)选修4-1:几何证明选讲如图,ABC ∆内接于圆O ,AB 为其直径,CH AB ⊥于H ,延长后交圆O 于D ,连接DB 并延长交过C 点的直线于P ,且CB 平分DCP ∠. (Ⅰ)求证:PC 是圆O 的切线; (Ⅱ)若4,3AC BC ==,求PCPB的值. 23. (本小题满分10分)选修4-4:坐标系与参数方程 已知曲线E 的极坐标方程为4tan cos θρθ=,倾斜角为α的直线l 过点(2,2)P .(Ⅰ)求E 的直角坐标方程和直线l 的参数方程;MExOyF(Ⅱ)设12,l l 是过点P 且关于直线2x =对称的两条直线,1l 与E 交于,A B 两点,2l 与E 交 于,C D 两点,求证:||:||||:||PA PD PC PB =. 24. (本小题满分10分)选修4-5:不等式选讲 已知函数()|3|f x x =-.(Ⅰ)若不等式(1)()f x f x a -+<的解集为空集,求实数a 的取值范围; (Ⅱ)若||1||3a b <<,,且0a ≠,求证:()||()bf ab a f a>.沈阳二中2015—2016学年度下学期第五次模拟考试高三(16届)数学(文科)试题答案一. 选择题:1 2 3 4 5 6 7 8 9 10 11 12 ACDBBDCBCBAD二. 填空题:13.3114. 1 15.4 16. [4,+∞) 三. 解答题:17.解:(1) 当1n =时,11121a S a ==+,解得11a =- …………… 1分 当1n >时,由题意,()1121n n S a n --=+-所以,()111(2)21221n n n n n n S S a n a n a a ----=+---=-+⎡⎤⎣⎦,即121n n a a -=- 所以 ()1121n n a a --=- 即1121n n a a --=-所以,数列{}1n a -是首项为2-,公比为2等比数列 ……………6分 (2)由上,11222n n n a --=-⋅=- 所以12n n a =- …………… 8分 ()()()111221221111log 1log 1log 2log 21n n n n n n n b a a n n ⋅+++====---⋅+ …10分 所以,11111111223111n nT n n n n =-+-++-=-=+++L ………12分 18. 解:(1)设PC 的中点为Q ,连接,EQ FQ ,由题意,FQ ∥DC 且12FQ CD =,AE ∥CD 且12AE CD =故AE ∥FQ 且AE FQ =,所以,四边形AEQF 为平行四边形 所以,AF ∥EQ ,且EQ PEC AF AEC ⊂⊄平面,平面 所以,AF ∥平面PEC ……… 6分(2)由上,点F 到平面PEC 的距离等于点A 到平面PEC 的距离,设为d . 由条件易求7,7,22,5EC PE PC EQ ====,故1225102PEC S ∆=⨯⨯=131322AEC S ∆=⨯⨯=, 所以由A PEC P AEC V V --=得113102332d ⋅=⋅⋅解得3010d =………12分 19. 解:(Ⅰ)从这5年中任意抽取两年,所有的事件有:(2012,2013),(2012,2014),(2012, 2015),(2012,2016),(2013,2014),(2013,2015),(2013,2016),(2014,2015), (2014,2016),(2015,2016)共10种, ……2分至少有1年多于20人的事件有: (2012,2015),(2012,2016),(2013,2015),(2013,2016), (2014,2015),(2014,2016),(2015,2016)共7种, ……4分 则至少有1年多于20人的概率为710P =. ……………5分 (Ⅱ)由已知数据得16,2014==y x ,……………6分1()()2(10)(1)(6)1621052nii i xx y y =--=-⨯-+-⨯-+⨯+⨯=∑ ……………7分222221()(1)(2)1210nii xx =-=-+-++=∑ ……………8分所以121()()52ˆ 5.210()nii i nii xx y y bxx ==--===-∑∑,ˆ16 5.2201410456.8a=-⨯=- ……10分 所以是正相关,回归直线的方程为ˆ 5.210456.8yx =- ……………11分 则第2019年的估计值为ˆ 5.2201910456.842y=⨯-= ……………12分 20.解:(I )由题415==a c e ,222c b a +=,可知b a 4=, b c 15=,Θ 21F PF ∆的周长是8215+,∴ 228215a c +=+,∴4=a ,1=b ,所求椭圆方程为22116x y += …………………4分(Ⅱ)椭圆的上顶点为M(0,1),由题知过点M 与圆T 相切的直线有斜率, 则设其方程为l :1y kx =+,由直线1y kx =+与圆T 相切可知321|12|2=++k k , 即0536322=++k k ,∴8921-=+k k ,32521=k k ,…………6分由1221116y k x x y =+⎧⎪⎨+=⎪⎩得()2211116320k x k x ++=, 12132116E k x k ∴=-+ 同理 22232116Fk x k =-+ ………9分 ()()121211E F E F E F EF E F E F E Fk x k x y y k x k x k x x x x x x +-+--===--- 43325161891612121=⨯--=-+=k k k k 故直线EF 的斜率为43. …………12分21. 解:(Ⅰ)因为()1a f x bx x '=++,(1)10f a b '=++=①,1(2)2102f a b '=++=②。
