2011年江苏省南通市中考数学试题(解析版)
2005-2011年江苏省南通市中考数学试卷及答案(7套)

2005年苏州市初中毕业暨升学考试试卷数 学第I 卷(选择题,共24分)一.选择题:本大题共8小题,每小题3分,共24分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列运算错误的是A .()326aa --= B .()325a a = C .231a a a -÷= D .532a a a =⋅2.右图可以看作是一个等腰直角三角形旋转若干次而生成的则每次旋转的度数可以是A .900B .60C .450D .3003.苏州红十字会统计,2004年苏州是无偿鲜血者总量为12.4万人次,已连续6年保持全省第一。
12.4万这个数用科学记数法来表示是A .1.24×104B .1.24×105C .1.24×106D .12.4×1044.将直线y=2x 向上平移两个单位,所得的直线是A .y=2x+2B .y=2x-2C .y=2(x-2)D .y=2(x+2) 5.如图,在平行四边形ABCD 中,下列各式不一定正确的是A .012180∠+∠= B .023180∠+∠= C .034180∠+∠= D .024180∠+∠=6.初二(1)班有48位学生,春游前,班长把全班学生对春游地点的意向绘制成了扇形统计图,其中“想去苏州乐园的学生数”的扇形圆心角600,则下列说法正确的是 A .想去苏州乐园的学生占全班学生的60% B .想去苏州乐园的学生有12人 C .想去苏州乐园的学生肯定最多D .想去苏州乐园的学生占全班学生的1/67.如图,已知等腰提醒梯形ABCD 的中位线EF 的长为6,腰AD 的长为5,则该等腰梯形的周长为A .11B .16C .17D .228.如图的转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等,四位同学各自发表了下述见解:甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形了乙:只要指针连续转六次,一定会有一次停在6号扇形丙:指针停在奇数号扇形的概率和停在偶数号扇形的概率相等丁:运气好的时候,只要在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大。
南通数学中考卷.docx

南通市2011年初中毕业、升学考试试卷数学—— --------------- 注重事项考生在答HttWU*阅读*注重事项:】.本试卷共6萸.椅分为150分,考■试时间为,2。
分的.与试结电后,请捋奉试卷和答瞠卡一, 并交回.2.答题前,请务必将自己的姓名,考试证号用°-5*米黑色字卷的签字笔填写在试卷及答题 卡上指定的位置・ 〔3.答案必须按妾京填涂•书写在答矍卡上,在试卷、草暗我上芬题-律无数.一、选择题(本大题共10小题.每小鹿3分.共30分.在每小睑治出的四个逸项中,检有一项是符合噎目要求的.谓将正嘛小的字2代号坟涂在巷鼠飞学区您里上)1. 如果60 m 表示"向北走60 m".W 么"向南走40 m”可以&小为4. 下列长度的三条线段,不能组成三角形的是• ・ 3.计算国的结果.足A, 120,C. 100,A. ±3^3B. 3V35. 巳知:如图,AB 〃CD.,DCE-80",JH/BEF 的度救为B. 110*A. — 20 mB. — 40 tn C, 20 m2. 下面的图形中.既是轴对称图形又是中心对林图形的矩A. 3,8,4B. 4・9,6C. 15.20.86.下列水平放置的几何体中.俯视(8压蛆彪的是D. 68.如ffi.OO 的弦AB-8.M 是AB 的中点,且OM-3.R3O 的半径等于A. 8B. 4D. 59.甲、乙购人沿相同的路线由A 地到B 地勾速前进.A.J3两地间的路程为20千米.他们耕史 的路程为式单位:千米).甲出发后的时间为可单位:小时),甲、乙前进的路程与时闻的词数 图象如图所示.根据国象信息,F 列说法正确的是A.C. 甲的速度第4千米/小时 乙的速度是10千米/小时乙比甲晚出发1小时 甲比乙晚到B 地3小时10.设 m>n>0.E : + ”:=4,e.SM 竺二^的ff!等于 ranB. V3 Q 76二、填空通(本大题共8小48.每小慝3分,共24分.不需写出解答过程.请把答案直接填写在 旨革专单度但星上)11. 巳知匕『・20•.则/<,的余角等于 ▲ 度.12. 计算:而一搪=▲.*+213.函数岩中,自变量N 的取值范圈是 A.14.七位女生的体直(单位:kg )分别是36.42,38.42.35.45.40,则这七位女生体直的中位二▲ kg.7-巳如3是关于工的方fBx l -5x+c-0的一个机.财这个方fg 的另一个根是A. —2B. 215. 如图,矩形旋片ABCD 中,AB-2 cm,点E 在BC 上.且 AAE-EC.若将蛾片沿AE 折建.点B 恰好与AC 上的威8'重合.则 AC- A erm16. 分解珥式;3m(2x —y)T —3mn : =-▲ 17.如图.测量河竟AB (假设河的两岸平行),在C^MWZACB = 3O\D AMftZADB-60..又CD-60 m.J«河宛AB 为 ▲ m 《结果保留根号).18.巳知;如图,三个半06依次相外切•它们的08心都在X 袖的正半轴上.并与直蟆y-yx 相 切.设牛08 G 、半跚C :,半IM C,的半径分别是r.r.r ,购当r = 1时,,=.▲ •rt /三、解答题(本大题共10小题.共96分.靖在内作答.解答时应写出必要的文字说明、证明过程或演算步骤)19. (本小厩滴分10分)(1)计算 2,+(-1)4 +('/?-2)0-|-3| I(2〉先化简.再求值:。
2011年南通数学中考卷

专业课原理概述部分一、选择题(每题1分,共5分)1. 若a是实数,且(a1)²=0,则a的值为()A. 0B. 1C. 1D. 22. 下列函数中,既是奇函数又是偶函数的是()A. y=x³B. y=x²C. y=|x|D. y=cos(x)3. 已知等差数列{an}的公差为3,且a3=7,则a1的值为()A. 1B. 4C. 7D. 104. 在直角坐标系中,点P(2, 2)关于原点的对称点是()A. (2, 2)B. (2, 2)C. (2, 2)D. (2, 2)5. 下列命题中,正确的是()A. 任何两个实数的和都是一个实数B. 任何两个实数的乘积都是一个实数C. 任何两个实数的商都是一个实数D. 任何两个实数的差都是一个实数二、判断题(每题1分,共5分)1. 若函数f(x)在区间(a,b)上单调递增,则f'(x)>0。
()2. 两个平行线的斜率相等。
()3. 等差数列的通项公式为an=a1+(n1)d。
()4. 向量a与向量b垂直的充分必要条件是a·b=0。
()5. 任何两个复数都可以进行四则运算。
()三、填空题(每题1分,共5分)1. 已知函数f(x)=x²2x+1,则f(x)的零点为______。
2. 若向量a=(3,4),则向量a的模长是______。
3. 已知等差数列{an}的公差为2,a1=1,则a5的值为______。
4. 设复数z=2+3i,则z的共轭复数为______。
5. 若函数f(x)=|x1|,则f(x)在x=1处的导数为______。
四、简答题(每题2分,共10分)1. 简述实数与虚数的关系。
2. 解释等差数列与等比数列的区别。
3. 如何判断一个函数的单调性?4. 什么是向量的数量积(点积)?5. 简述复数乘法的运算规律。
五、应用题(每题2分,共10分)1. 已知函数f(x)=x²4x+3,求f(x)在区间[0, 3]上的最大值和最小值。
【2011年】年江苏省南通市中考数学试题(解析)

2011年江苏省南通市中考数学试题一、选择题(本大题共10小题,每小题3分,满分30分)1.如果60m 表示“向北走60m”,那么“向南走40m”可以表示为【 】A .-20mB .-40mC .20mD .40m【答案】B .【考点】相反数。
【分析】向北与向南是相反方向两个概念,向北为+,向南则为负。
故根据相反数的定义,可直接得出结果2.下面的图形中,既是轴对称图形又是中心对称图形的是【 】【答案】C .【考点】轴对称图形,中心对称图形。
【分析】根据轴对称图形和中心对称图形的定义,可知A 是中心对称图形而不是轴对称图形;B 也是中心对称图形而不是轴对称图形;C 既是轴对称图形又是中心对称图形,它有四条对称轴,分别是连接三个小圆线段所在的水平和竖直直线,这水平和竖直直线之间的两条角平分线;D 既不是轴对称图形也不是中心对称图形。
3.计算的结果是【 】A .±3 3B .3 3C .±3D .3【答案】D .【考点】立方根。
【分析】根据立方根的定义,因为33=27,所以。
4.下列长度的三条线段,不能组成三角形的是【 】A .3,8,4B .4,9,6C .15,20,8D .9,15,8【答案】A .【考点】三角形的构成条件。
【分析】根据三角形任两边之和大于第三边的构成条件,A 中3+4<8,故A 的三条线段不能组成三角形。
5.如图,AB ∥CD ,∥DCE =80°,则∥BEF =【 】A .120°B .110°C .100°D .80°【答案】C .【考点】平行线的性质。
【分析】根据同旁内角互补的平行线性质,由于AB ∥CD ,∥DCE 和∥BEF 是同旁内角,从而∥BEF =。
6.下列水平放置的几何体中,俯视图是矩形的为【 】【答案】B . 【考点】几何体的三视图。
3273273=00018080100-=A . B . C . D . D AE B CF A . B . C . D .圆柱 长方体 三棱柱 圆锥【分析】根据几何体的俯视图视图规则,A 和D 的俯视图是圆,B 的俯视图是矩形,C 的俯视图是三角形。
2011年江苏省南通市中考数学试题(解析版)3

27.(12分)已知A (1,0)、B (0,-1)、C (-1,2)、D (2,-1)、E (4,2)五个点,抛物线y =a (x -1)2+k (a >0)经过其中的三个点.(1)求证:C 、E 两点不可能同时在抛物线y =a (x -1)2+k (a >0)上;(2)点A 在抛物线y =a (x -1)2+k (a >0)上吗?为什么?(3)求a 和k 的值.【答案】解:(1)1,2)和E (4,2)都在抛物线y =a (x -1)2+k(a >0)上,联立方程, 解之得a =0,k =2。
这与要求的a >0不符。
∴C 、E 两点不可能同时在抛物线y =a (x -1)2+k (a >0)上。
(2)点A 不在抛物线y =a (x -1)2+k (a >0)上。
这是因为如果点A 在抛物线上,则k =0。
B (0,-1)在抛物线上,得到a =-1,D (2,-1)在抛物线上,得到a =-1,这与已知a >0不符;而由(1)知,C 、E 两点不可能同时在抛物线上。
因此点A 不在抛物线y =a (x -1)2+k (a >0)上。
(3)综合(1)(2),分两种情况讨论:①抛物线y =a (x -1)2+k (a >0)经过B (0,-1)、C (-1,2)、D (2,-1)三个点, a (0-1)2+k =-1联立方程 a (-1-1)2+k =2,a (2-1)2+k =-1解之得a =1,k =-2。
②抛物线y =a (x -1)2+k (a >0)经过B (0,-1)、D (2,-1)、E (4,2)三个点,a (0-1)2+k =-1联立方程 a (2-1)2+k =-1,a (4-1)2+k =2解之得a =38,k =118-。
因此,抛物线经过B 、C 、D 三个点时,a =1,k =-2。
抛物线经过B 、D 、E 三个点时, a =38,k =118-。
【考点】二次函数,二元一次方程组。
江苏南通中考数学模拟试卷及答案-解析版

江苏省南通市2011年中考数学试题一、选择题(本大题共10小题,每小题3分,满分30分)1.如果60m 表示“向北走60m”,那么“向南走40m”可以表示为【 】A .-20mB .-40mC .20mD .40m【答案】B .【考点】相反数。
【分析】向北与向南是相反方向两个概念,向北为+,向南则为负。
故根据相反数的定义,可直接得出结果2】【答案】C .【考点】轴对称图形,中心对称图形。
【分析】根据轴对称图形和中心对称图形的定义,可知A 是中心对称图形而不是轴对称图形;B 也是中心对称图形而不是轴对称图形;C 既是轴对称图形又是中心对称图形,它有四条对称轴,分别是连接三个小圆线段所在的水平和竖直直线,这水平和竖直直线之间的两条角平分线;D 既不是轴对称图形也不是中心对称图形。
3.计算327的结果是【 】A .±3 3B .3 3C .±3D .3【答案】D .【考点】立方根。
【分析】根据立方根的定义,因为33=273。
4.下列长度的三条线段,不能组成三角形的是【 】A .3,8,4B .4,9,6C .15,20,8D .9,15,8【答案】A .【考点】三角形的构成条件。
【分析】根据三角形任两边之和大于第三边的构成条件,A 中3+,故A 的三条线段不能组成三角形。
5.如图,AB ∥CD ,∠DCE =80°,则∠BEF =【 】 A .120° B .110° C .100° D .80° 【答案】C .【考点】平行线的性质。
【分析】根据同旁内角互补的平行线性质,由于AB ∥CD ,∠DCE 和∠BEF 是同旁内角,从而∠BEF =00018080100-=。
6.下列水平放置的几何体中,俯视图是矩形的为【 】【答案】B .【考点】几何体的三视图。
【分析】根据几何体的俯视图视图规则,A 和D 的俯视图是圆,B 的俯视图是矩形,C 的A .B .C . A . B . C .D . 圆柱 长方体 三棱柱 圆锥D AE BC F俯视图是三角形。
2011年南通中考数学试卷
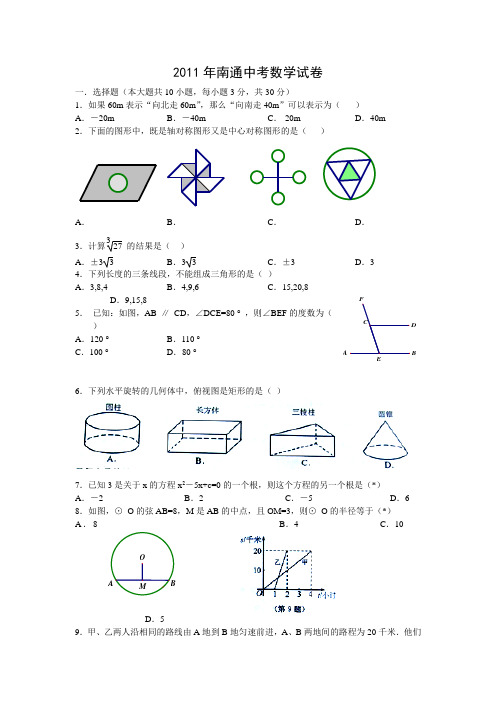
ABCDEF OABM2011年南通中考数学试卷一.选择题(本大题共10小题,每小题3分,共30分) 1.如果60m 表示“向北走60m ”,那么“向南走40m ”可以表示为( )A .-20mB .-40mC . 20mD .40m2.下面的图形中,既是轴对称图形又是中心对称图形的是( )A .B .C .D .3.计算327 的结果是( )A .±3 3B .3 3C .±3D .34.下列长度的三条线段,不能组成三角形的是( ) A .3,8,4 B .4,9,6 C .15,20,8 D .9,15,85. 已知:如图,AB ∥ CD ,∠DCE=80 ° ,则∠BEF 的度数为( ) A .120 ° B .110 ° C .100 ° D .80 °6.下列水平旋转的几何体中,俯视图是矩形的是( )7.已知3是关于x 的方程x 2-5x+c=0的一个根,则这个方程的另一个根是(*) A .-2 B .2 C .-5 D .6 8.如图,⊙ O 的弦AB=8,M 是AB 的中点,且OM=3,则⊙ O 的半径等于(*) A .8 B .4 C .10D .59.甲、乙两人沿相同的路线由A 地到B 地匀速前进,A 、B 两地间的路程为20千米.他们ABC DEB'前进的路程为s (单位:千米),甲出发后的时间为t (单位:小时),甲、乙前进的路程与时间的函数图像如图所示,根据图像信息,下列说法正确的是(*) A .甲的速度 4千米/小时 B .乙的速度 10千米/小时 C .乙比甲晚出发1小时 D .甲比乙晚到B 地3小时10.设m > n > 0, m 2+n 2=4mn,则m 2-n 2mn的值等于(*)A .2 3B . 3C . 6D .3二.填空题(本大题共8小题,每小题3分,共24分) 11.已知∠α ° ,则∠α的余角等于 度. 12.计算:8 - 2 = .13.函数y=x+2x -1中,自变量x 的取值范围是 .14.七位女生的体重(单位:Kg )分别是36、42、38、42、35、45、40,则这七位女生的体重的中位数为 Kg .15.如图,矩形纸片A BCD ,AB=2cm ,点E 在BC 上,且AE=EC ,若将纸片折叠,点B 恰好与AC 上的点B ′重合,则AC= cm . 16.分解因式:3m(2x -y)2-3mn 2= . 17.如图,测量河宽AB (假设河的两岸平行),在C 点测得∠ ACB=30 ° ,点D 测得∠ ADB=60 ° ,又CD=60m ,则河宽AB 为 m (结果保留根号).18.已知:如图,三个半圆依次相外切,它们的圆心都在x 轴的正半轴上,并与直线y=33x 相切,设半圆C 1、半圆C 2、半圆C 3的半径分别是r 1、r 2、r 3,则当r 1=1时,r 3=三.解答题(本大题共10小题,共96分) 19.(本小题满分10分) (1)计算:22+(-1)4+( 5 -2)0-︱-3︱(2)先化简,再求值: (4ab 3-8a 2b 2)÷ 4ab+(2a+b)(2a -b),其中a=2,b=1.20.(本小题满分8分) ABD C求不等式组⎩⎨⎧3x -6≥x -42x+1>3(x -1)的解集,并写出它的整数解.21.(本小题满分9分)某中学学生会为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类)并将调查的结果绘制成如下的两幅不完整的统计图.请根据图中提供的信息,解答下面的问题: (1)参加调查的学生共有 人;在扇形图中,表示“其他球类”的扇形的圆心角为 度 (2)将条形图补充完整;(3)若该校有2000名学生,则估计喜欢“篮球”的学生共有 人. 22.(本小题满分8分)如图,AM 为⊙ O 的切线,A 为切点,BD ⊥ AM 于点D ,BD 交⊙ O 于点C ,OC 平分∠ AOB .求∠ B 的度数.23.(本小题满分8分)列方程解应用题:在社区全民健身活动中,父子俩参加跳绳比赛,相同时间内父亲跳180个,儿子跳210个.已知儿子每分钟比父亲多跳20个,父亲、儿子每分钟各跳多少个? 24.(本小题满分8分)比较正五边形与正六边形,可以发现它们的相同点与不同点. 例如 它们的一个相同点:正五边形的各边相等,正六边形的各边也相等. 它们的一个不同点:正五边形不是中心对称图形,正六边形是中心对称图形. 请你再写出它们的两个相同点和两个不同点. 3060120其他球类足球乒乓球篮球12090600项目人数30CO A M B DAD 其他球类篮球中球乒乓球篮球 乒乓球 足球相同点:(1) (2) 不同点:(1) (2) 25.(本小题满分9分)光明中学十分重视中学生的用眼卫生,并定期进行视力检测,某次检测设有A 、B 两处检测点,甲、乙、丙三名学生各自随机选择其中的一处检测视力. (1) 求甲、乙、丙三名学生在同一处检测视力的概率;(2) 求甲、乙、丙三名学生中至少有两人在B 处检测视力的概率. 26.(本小题满分10分)已知:如图1,O 为正方形ABCD 的中心,分别延长OA 到点F ,OD 到点E ,使OF=2OA ,OE=2OD ,连接EF ,将△ FOE 绕点O 逆时针旋转α角得到△ F ′OE ′(如图2). (1) 探究AE ′与BF ′的数量关系,并给予证明;(2) 当α=30 ° 时,求证:△AOE ′为直角三角形.27.(本小题满分12分)已知A (1,0),B (0,-1),C (-1,2),D (2,-1),E (4,2)五个点,抛物线y=a(x -1)2+k(a > 0),经过其中三个点.(1) 求证:C 、E 两点不可能同时在抛物线y=a(x -1)2+k(a > 0)上. (2) 点A 抛物线y=a(x -1)2+k(a > 0)上吗?为什么? (3) 求a 与k 的值. 28.(本小题满分14分) 如图,直线l 经过点A (1,0),且与曲线y=m x (x > 0)交于点B (2,1),过点P (p ,p -1)(p > 1)作x 轴的平行线分别交曲线y=m x (x > 0)和y=-mx (x < 0)于M 、N 两点.(1) 求m 的值及直线l 的解析式;(2) 若点P 在直线y=2上,求证:△PMB ∽ △PNA ;(3) 是否存在实数p ,使得S △AMN =4S △APM ?若存在,请求出所有满足条件的p 的值;若不存在,请说明理由.a E'F'O C D E F OC D ABB A xylOBA2011年南通中考数学试题参考答案1-10:B.C.D.A.C.B.B.D.C.A.11.7012. 213.x≠114. 4015.416.3m(2x-y+n)(2x-y-n)17.30 318.9.19.(1)3 (2)4a²-2ab, 12.20.1≤x<4, 整数解为:1、2、321.(1)300 36 (2)略(3)80022.60度23.父亲每分钟跳120个,儿子每分钟跳140个24.正五边形的各内角相等,正六边形各内角相等;正五边形是轴对称图形,正六边形也是轴对称图形.正五边形不能密铺,正六边形可以密铺;正五边形的各边不平行,正六边形的对边平行.25.1/4, 1/226.(1)用边角边证明△AOE’和△BOF’全等,即可证得AE’=BF’(2)取OE ’的中点G,得到等边△AOG ,等到∠AGO=60°,又由AG=E ’G 得到∠AE ’O =30°,从而得到∠OAE ’是90°,即为直角三角形。
江苏省2011年中考数学试题(13份含有解析)-7

盐城市二○一一年高中阶段教育招生统一考试数 学 试 题注意事项:1.本试卷考试时间为120分钟,试卷满分150分,考试形式闭卷. 2.本试卷中所有试题必须作答在答题卡上规定的位置,否则不给分.3.答题前,务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上.一、选择题(本大题共有8小题,每小题3分,共24分.在每小题所给出的四个选项中,只有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上) 1.-2的绝对值是 A .-2 B .- 12C .2D .12【答案】C 。
【考点】绝对值。
【分析】根据绝对值的定义,直接得出结果。
2.下列运算正确的是A .x 2+ x 3= x 5B .x 4·x 2= x 6 C .x 6÷x 2 = x 3D .( x 2)3 = x 8【答案】B 。
【考点】同底幂的乘法。
【分析】42426x x x x +⋅==3.下面四个几何体中,俯视图为四边形的是【答案】D 。
【考点】几何体的三视图。
【分析】根据几何体的三视图,直接得出结果。
4.已知a -b =1,则代数式2a -2b -3的值是A .-1B .1C .-5D .5【答案】A 。
【考点】代数式代换。
【分析】()22323231a b a b --=--=-=-5.若⊙O 1、⊙O 2的半径分别为4和6,圆心距O 1O 2=8,则⊙O 1与⊙O 2的位置关系是 A .内切 B .相交 C .外切 D .外离A B CD【答案】B 。
【考点】圆心距。
【分析】126464<O O <-+∴ 两圆相交。
6.对于反比例函数y = 1x,下列说法正确的是A .图象经过点(1,-1)B .图象位于第二、四象限C .图象是中心对称图形D .当x <0时,y 随x 的增大而增大 【答案】C 。
【考点】反比例函数。
【分析】根据反比例函数性质,直接得出结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年江苏省南通市中考数学试题一、选择题(本大题共10小题,每小题3分,满分30分)1.如果60m 表示“向北走60m”,那么“向南走40m”可以表示为【 】A .-20mB .-40mC .20mD .40m【答案】B .【考点】相反数。
【分析】向北与向南是相反方向两个概念,向北为+,向南则为负。
故根据相反数的定义,可直接得出结果2】【答案】C .【考点】轴对称图形,中心对称图形。
【分析】根据轴对称图形和中心对称图形的定义,可知A 是中心对称图形而不是轴对称图形;B 也是中心对称图形而不是轴对称图形;C 既是轴对称图形又是中心对称图形,它有四条对称轴,分别是连接三个小圆线段所在的水平和竖直直线,这水平和竖直直线之间的两条角平分线;D 既不是轴对称图形也不是中心对称图形。
3.计算327的结果是【 】A .±3 3B .3 3C .±3 D.3【答案】D .【考点】立方根。
【分析】根据立方根的定义,因为33=273=。
4.下列长度的三条线段,不能组成三角形的是【 】A .3,8,4B .4,9,6C .15,20,8D .9,15,8【答案】A .【考点】三角形的构成条件。
【分析】根据三角形任两边之和大于第三边的构成条件,A 中3+4<8,故A 的三条线段不能组成三角形。
5.如图,AB ∥CD ,∠DCE =80°,则∠BEF =【 】A .120° B.110° C.100° D.80° 【答案】C . 【考点】平行线的性质。
【分析】根据同旁内角互补的平行线性质,由于AB ∥CD ,∠DCE 和∠BEF 是同旁内角,从而∠BEF =00018080100-=。
6.下列水平放置的几何体中,俯视图是矩形的为【 】 A . B . C . DA EBC F【答案】B .【考点】几何体的三视图。
【分析】根据几何体的俯视图视图规则,A 和D 的俯视图是圆,B 的俯视图是矩形,C 的 俯视图是三角形。
7.若3是关于方程x 2-5x +c =的一个根,则这个方程的另一个根是【 】A .-2B .2C .-5D .5【答案】B .【考点】一元二次方程根与系数的关系。
【分析】根据一元二次方程根与系数的关系:两根之和等于一次项系数与二次项系数商的相反数,所以有22352x x +=⇒=。
8.如图,⊙O 的弦AB =8,M 是AB 的中点,且OM =3,则⊙O 的半径等于【 】A .8B .4C .10D .5【答案】5.【考点】圆的直径垂直平分弦,勾股定理。
【分析】根据圆的直径垂直平分弦的定理,∆OAM 是直角三角形,在Rt ∆OAM中运用勾股定理有,2222223455OA OM AM OA =+=+=⇒=。
9.甲、乙两人沿相同的路线由A 地到B 地匀速前进,A 、B 两地间的路程为20km .他们前进的路程为s (km),甲出发后的时间为t (h),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法正确的是【 】A .甲的速度是4km/hB .乙的速度是10km/hC .乙比甲晚出发1hD .甲比乙晚到B 地3h【答案】A .【考点】一次函数。
【分析】根据所给的一次函数图象有:A.甲的速度是205/4km h =;B. 乙的速度是2020/1km h =;C .乙比甲晚出发101h -=; D .甲比乙晚到B 地422h -=。
10.设m >n >0,m 2+n 2=4mn ,则 m 2-n 2mn=【 】 A .2 3 B . 3 C . 6 D .3【答案】A .【考点】代数式变换,完全平方公式,平方差公式,根式计算。
【分析】由m 2+n 2=4mn 有()()2262m n mn m n mn +=-= ,,因为m >n >0,所以m n m n +=-=,则()()22m n m n m n mn mn +--=== 二、填空题(本大题共8小题,每小题3分,满分24分)A B O M A . B . C . D .圆柱 长方体 三棱柱 圆锥CD B11.已知α∠=20°,则α∠的余角等于 .【答案】700.【考点】余角。
【分析】根据余角的定义,直接得出结果:900-200=700。
12.计算:8-2= .【答案】2。
【考点】根式计算。
【分析】=13.函数y =x +2 x -1中,自变量x 的取值范围是 .【答案】1x ≠。
【考点】分式定义。
【分析】根据分式定义,分母不能为0,从而得出结论。
14.七位女生的体重(单位:kg)分别为36、42、38、42、35、45、40,则这七位女生的体 重的中位数为 kg .【答案】40。
【考点】中位数。
【分析】根据的中位数定义,中位数是指将数据按大小顺序排列起来,形成一个数列,居 于数列中间位置的那个数据。
故应先将七位女生的体重重新排列:35,36,38,40,42,42, 45,从而得到中位数为40。
15.如图,在矩形纸片ABCD 中,AB =2cm ,点E 在BC 上,且AE =CE .若将纸片沿AE 折叠,点B 恰好与AC 上的点B 1重合,则AC= cm . 【答案】4。
【考点】矩形性质,折叠,等腰三角形性质,直角三角形性质,300角直角三角形的性质。
【分析】由矩形性质知,∠B=900,又由折叠知∠BAC=∠EAC。
根据等腰三角形等边对等角的性质,由AE =CE 得∠EAC=∠ECA。
而根据直角三角形两锐角互余的性质,可以得到∠ECA=300。
因此根据300角直角三角形中,300角所对直角边是斜边一半的性质有,Rt ∆ABC 中AC=2AB=4。
16.分解因式:3m (2x ―y )2―3mn 2= .【答案】()()322m x y n x y n -+--。
【考点】提取公因式法和应用公式法因式分解。
【分析】()()()()222232332322m x y mn m x y n m x y n x y n ⎡⎤--=--=-+--⎣⎦。
17.如图,为了测量河宽AB (假设河的两岸平行),测得∠ACB =30°,∠ADB =60°,CD =60m ,则河宽AB 为 m(结果保留根号).【答案】A .【考点】解直角三角形,特殊角三角函数,根式计算。
【分析】在Rt ∆ABD 和Rt ∆ABC 中 tan tan AB AB ADB ACB DB CB == , A B B 1 C D00tan60 tan3060606032AB AB AB ABABDB DB DB DBAB AB AB AB⇒==⇒==⇒=+++⎝⇒=⇒==,18.如图,三个半圆依次相外切,它们的圆心都在x轴上,并与直线y=33x相切.设三个半圆的半径依次为r1、r2、r3,则当r1=1时,r3=.【答案】9。
【考点】一次函数,直角三角形的性质,相似三角形。
【分析】设直线y=33x与三个半圆分别切于A,B,C,作AE⊥X轴于E,则在Rt∆AEO1中,易得∠AOE=∠EAO1=300,由r1=1得EO=12,OE=32,OO1=2。
则。
1112222221233r OOR AOO R BOO rr OO r r∆∆⇒=⇒=⇒=+∽t t同理,1113333331299r OOR AOO R COO rr OO r r∆∆⇒=⇒=⇒=+∽t t。
三、解答题(本大题共10小题,满分96分)19.(10分)(1)计算:22+(-1)4+(5-2)0-|-3|;(2)先化简,再求值:(4ab3-8a2b2)÷4ab+(2a+b)(2a-b),其中a=2,b=1.【答案】解:(1)原式=4+1+1-3=1。
(2)原式=4ab(b2-2ab)÷4ab+4a2-b2=b2-2ab+4a2-b2=4a2-2ab当a=2,b=1时,原式=4³22-2³2³1=16-4=12。
【考点】负数的偶次幂,0次幂,绝对值,代数式化简,平方差公式。
【分析】(1)利用负数的偶次幂,0次幂和绝对值的定义,直接得出结果。
(2)利用提取公因式先把分式化简,应用平方差公式把多项式乘多项式化简,然后合并同类项,再代入。
20.(8分)求不等式组⎩⎨⎧3x-6≥x-42x+1>3(x-1)的解集,并写出它的整数解.【答案】解:由①,得x≥1,由②,得x<4。
所以不等式组的解集为14x≤<。
它的整数解1,2,3。
【考点】-元一次不等式组。
【分析】利用-元一次不等式组求解方法,直接得出结果,然后写出它的整数解。
21.(9分)某中学学生为了解该校学生喜欢球类活动的情况,随机抽取了若干名学生进行问卷调查(要求每位学生只能填写一种自己喜欢的球类),并将调查的结果绘制成如下的两幅不完整的统计图.①请根据图中提供的信息,解答下面的问题:(1)参加调查的学生共有 人,在扇形图中,表示“其他球类”的扇形的圆心角为 度; (2)将条形图补充完整;(3)若该校有2000名学生,则估计喜欢“篮球”的学生共有 人.【答案】解:(1)300,36。
(2)喜欢足球的有300-120-60-30=90人,所以据此将条形图补充完整(如右图)。
(3)在参加调查的学生中,喜欢篮球的有120人,占120÷300=40%,所以该校2000名学生中,估计喜欢“篮球”的学生共有2000³40%=800(人)。
【考点】扇形统计图,条形统计图,频率,频数。
【分析】(1)从图中知,喜欢乒乓球的有60人,占20%,所以参加调查的学生共有60÷20%=300(人)喜欢其他球类的有30人,占30÷300=10%,所以表示“其他球类”的扇形的圆心角为3600³10%=360。
(2)由(1)参加调查学生的总数减去另外各项就可得喜欢足球的人数,将条形图补充完整。
(3)先求出在参加调查的学生中,喜欢篮球的人,占参加调查的学生的百分比就能估计出全校喜欢“篮球”的学生人数。
22.(8分)如图,AM 切⊙O 于点A ,BD ⊥AM 于点D ,BD 交⊙O 于点C ,OC 平分∠AOB .求∠B 的度数. 【答案】解:∵OC 平分∠AOB ,∴∠AOC =∠COB , ∵AM 切⊙O 于点A ,即OA ⊥AM ,又BD ⊥AM , ∴OA ∥BD ,∴∠AOC =∠OCB又∵OC =OB ,∴∠OCB =∠B ,∴∠B =∠OCB =∠COB =600。
【考点】圆的切线,角平分线,直线平行,三角形的内角和。
【分析】要求∠B ,由于OC =OB ,根据等边对等角可知∠OCB =∠B 。
由于OA ,BD 都垂直于同一条直线AM ,从而OA ∥BD ,根据两直线平行内错角相等,有∠AOC =∠OCB 。
