运筹学最短路
运筹学05_图与网络分析2-最短路

v4
v7
-1
42
终 点
lij
P(t)1j
起 v1 v2 v3 v4 v5 v6 v7 v8 t=1 t=2 t=3 t=4 点
v1 0 -1 -2 3 0 0 0 0
v2 6 0 2 -1 -5 -5 -5
v3 -3 0 -5 1 -2 -2 -2 -2
v4 8 0 2 3 -7 -7 -7
60
v1 v2 v3 v4 v5 v6 0 0 12 1 04 5 2 2 0 5 5 1 4 0 6 v5 2 3 0 v6 2 2 0
61
v1 v2 v3 v4 v5 v6 0 0 12 1 04 5 2 2 05 5 1 4 0 6 3 23 0 v6 2 2 0
54
v1 v2 v3 v4 v5 v6 0 0 12 1 04 5 v3 2 0 5 1 1 4 0 4 v5 2 3 0 v6 2 2 0
55
v1 v2 v3 v4 v5 v6 0 0 12 1 04 5 v3 2 0 5 1 1 4 0 4+2 v5 2 3 0 v6 2 2 0
0
2
7
1
5 3 5 55 7
1
3
3
1
4
6
7
5
12
③从已标号的点出发,找与这
(1,2)
2
些相邻点最小权数(距离)者, 找到之后:标号;边变红。
2
0
2
7
1
5 3 5 55 7
1
3
3
1
34 5 6
7
13
④重复上述步骤,直至全部的
(1,2)
点都标完。
2
2
0
2
运筹学课件 最短路、最大流、邮路

最短路径问题的应用
例 设备更新问题
把求总费用最小问题化为最短路径问题。用点 i (i=1,2,3,4,5)表示第 i 年买进一台新 设备。增设一点 6 表示第五年末。从i点到i+1,……, 6 各画一条弧,弧(i , j)表示在 第 i 年买进的设备一直使用到第 j 年年初(第 j -1年年末)。求1点到6点的最短路径。 路径的权数为购买和维修费用。 弧(i , j)的权数为第i年的购置费ai+从第i年使用至第j-1年末的维修费之和。 从第i年使用至第j-1年末的维修费:b1+…+bj-i
1 1 2 3 4 5 2 16 3 22 16
(使用寿命为j-i年) 具体权数计算结果如下:
5 41 30 23 17 6 59 41 31 23 18
如:(2-4)权数为:a2+b1+b2=11+5+6=22
4 30 22 17
通过一个网络的最短路径
例 设备更新问题 :
2 16 30 22 41 4 23
最大流问题
两个重要结论: 1、任何一个可行流的流量都不会超过任一截集的容量。 2、若对于一个可行流f *,网络中有一个截集( V1*,V1*), 使v( f *)=C(V1*,V1 *),则f *必是最大流,而( V1*, V1 *)必是所有截集中容量最小的一个,即最小截集。
定理:可行流f *是最大流,当且仅当不存在关于f *的增广链。 于是有如下结论:最大流量最小截量定理:任一个网络中,从vs 到vt的最大流量等于分离vs,vt的最小截集的容量。
运筹学课件12

价格 11 12 13 12 (万元)
解 用点vi表示“第i年年初购进一台新设备”这种状态i=1,2,…,5, 用v6表示第5年底的状态。 对每个i=1,2,…,5,从vi到vi+1 ,…, v6各画一条弧, 弧(vi,vj)表示在第 i 年初购进一台设备一直使用到 第 j 年初(即第 j -1年底)。 弧(vi,vj)的权为在第 i 年初购进一台新设备 一直使用到第 j -1年年底所发生的总费用。 例如(v1,v4)表示第1年年初购进一台新设备,一直使用到第3年底。 第1年年初购进一台新设备,需支付11万元, 一直使用到第3年底,需维修费5+6+8=19万元, 故该弧的权为30。
实例1:求下图所示网络中从顶点 v 1 到 v 3 的最短路。
5
v4
2 7 1 2 10 3 4 4
v3
v5
4
1
v2
1
v1
3.求给定两点间最短路的Dijkstra算法 (1)基本思想 对网络中每个顶点赋以一个标号,用来记录从顶点v1到该顶点 的最短路的长度(此时称为永久标号)或最短路长度的上界 (此时称为暂时标号)。 算法开始时,只有顶点v1被赋予永久标号 u1=0, 其它顶点vj 被赋予暂时标号uj =w1j 。 算法在被暂时标号的顶点中寻找一个顶点, 其暂时标号最小,然后将其赋予永久标号, 且对其余暂时标号的顶点按下述方式修正其标号: uj =min{uj ,uk +wkj } 算法在所求顶点被赋予永久标号后终止。
u j,置 第二步(永久标号)在R中找一顶点vk,使 u k = min v ∈R
j
S = S U {v k }, R = R \ {v k },若 R = φ,停止;否则转第三步。
S = {v1 , v 2 , v5 , v 4 , v3 }
运筹学图与网络分析-最短路

(P0
)
min P
(P)
路P0的权称为从vs到vt的距离,记为d(vs,vt)。
求网络上的一点到其它点 的最短路
Dinkstra标号法
这是解决网络中某一点到其它点的最 短路问题时目前认为的最好方法。
适用于有向图权值非负的情况
有向图权值非负---- Dijkstra算法
Dijkstra算法的基本步骤(权值非负) 1、给顶点v1标号(0),v1称为已标号点,记标号点集为
(1,2)
2
2
0
1
2
5
7
(2,4)
3 5 55
7
3
1 (4,4) 3 1
4
6
7
(1,3)
5
④重复上述步骤,直至全部的
点都标完。
(1,2)
2
2
0
1
2
5
7
(2,4)
3 5 55
7
1
3
3
1
4
6
7
(1,3)
5
7
(1,2)
2
2
0
2
7
1
5
(2,4)
35
55
7
1
3
3
1
4
6
7
(1,3)
5
(3,7)
(1,2)
2
2
0
2
7
1
5 3 5 55 7
3
1
3 1
34 5 6
7
④重复上述步骤,直至全部的
(1,2)
点都标完。
2
2
0
2
7
1
5 3 5 55 7
运筹学:第2章 图与网络分析 第3节 最短路
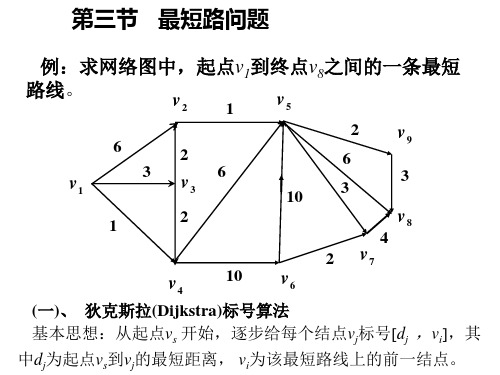
年份 购置费 使用年数 维修费
1
2
3
4
5
18 20 21 23 24
0~1 1~2 2~3 3~4 4~5
5
7 12 18 25
方法:将此问题用一个赋权有向图来描述,然后求这个赋权有向图 的最短路。
求解步骤:
1)画赋权有向图:
设 vi 表示第i年初, (vi ,vj )表示第i 年初购买新设备用到第j年初(j-1年底), 而wi j 表示相应费用, 则5年的一个更新计划相当于从v1 到v6的一条路。 2)求解 (标号法)
v5 29
45
v6
62
算法步骤:
1.给始点v1标号[0,v1] 。
2. :把顶点集V分成VA :已标号点集 VB :未标号点集
3.考虑所有这样的边[vi ,vj] :其中vi VA ,v j VB ,挑选
其与起点v1距离最短(mindi cij )的vj,对vj进行标号
4.重复步骤2、3,直至终点vn标上号[dn ,vj],则dn 即为vs到
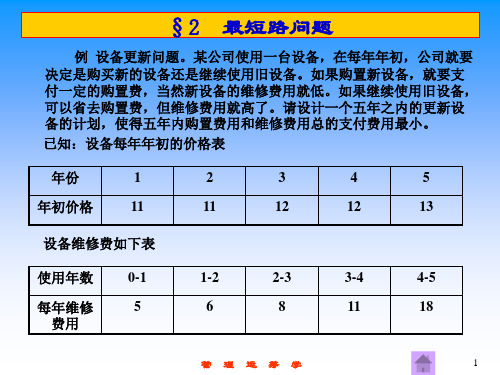
第三节 最短路问题
例:求网络图中,起点v1到终点v8之间的一条最短
路线。
v2
1
v5
6
2
3
6
v1
v3
2
v9
6 3
10 3
1
2
v8
4
2 v7
v4
10
v6
(一)、 狄克斯拉(Dijkstra)标号算法
Байду номын сангаас
基本思想:从起点vs 开始,逐步给每个结点vj标号[dj ,vi],其
中dj为起点vs到vj的最短距离, vi为该最短路线上的前一结点。
vj的最短距离,反向追踪可求出最短路。
管理运筹学 第7章 最短路实例
8
§4 最大流问题
• 最大流问题:给一个带收发点的网络,其每条弧的赋权称之为容量, 在不超过每条弧的容量的前提下,求出从发点到收点的最大流量。 一、最大流的数学模型 例6 某石油公司拥有一个管道网络,使用这个网络可以把石油从采地 运送到一些销售点,这个网络的一部分如下图所示。由于管道的直径 的变化,它的各段管道(vi,vj)的流量cij(容量)也是不一样的。cij的 单位为万加仑/小时。如果使用这个网络系统从采地 v1向销地 v7运送石 油,问每小时能运送多少加仑石油?
2 0 0
2 0 2 1
3 v6 4
3 01
2
v7
3 5
3 1 v4
第五次迭代:选择路为v1 v2 v3 v5 v7 。弧( v2 , v3 )的顺流容 量为2,决定了pf=2,改进的网络流量图如下图:
1 v2 0 5 2 3 0 0 2 3 v5 2 0 0 0
管 理 运 筹 学
15
20
v1 1
3
(a)
图11-12
管 理 运
(b)
筹 学
(c)
5
§3 最小生成树问题
一、求解最小生成树的破圈算法 算法的步骤:
1、在给定的赋权的连通图上任找一个圈。
2、在所找的圈中去掉一个权数最大的边(如果有两条或两条 以上的边都是权数最大的边,则任意去掉其中一条)。
3、如果所余下的图已不包含圈,则计算结束,所余下的图即 为最小生成树,否则返回第1步。
§2 最短路问题
例 设备更新问题。某公司使用一台设备,在每年年初,公司就要 决定是购买新的设备还是继续使用旧设备。如果购置新设备,就要支 付一定的购置费,当然新设备的维修费用就低。如果继续使用旧设备, 可以省去购置费,但维修费用就高了。请设计一个五年之内的更新设 备的计划,使得五年内购置费用和维修费用总的支付费用最小。 已知:设备每年年初的价格表
运筹学课件(第十讲)—最短路问题

Dijkstra法的适用条件
求出一点到图中任意点最短路
求解思路
从vs出发,逐步地向外探索最短路。执行过程中,与每个点记下一个数, 它或者表示从vs到该点的最短路的权(称为P(perpetual)标号),或者是 从vs到该点的最短路的权的上界(称为T(temporary)标号),方法的每一 步是去修改T标号,并且把某一个T标号点改为P标号点,从而使D中P标 号顶点多一个,这样最多经过p-1步就可以求出从vs到各点的最短路。
(2)起点发出的流的总和(称为流量),必须等于终点接收的流的总 和;
(3)各中间点流入的流量之和必须等于从该点流出的流量之和,即 流入的流量之和与流出的流量 之和的差为0,也就是说各中间点只 起转运作用,它既不产出新的物资,也不得截留过境的物资.
Operation Research
网络最大流的基本概念(3)
第八讲
Operation Research
网络最大流的基本概念(6)
增广链的基本概念
第八讲
Operation Research
第八讲
Operation Research
第八讲
Operation Research
实例:寻找图中增广链
第八讲
Operation Research
第八讲
网络最大流的基本概念(7)
运筹学课程
Operation Research
最短路问题
定义
第八讲
求最短路有两种算法,一是求从某一点至其他各点之间最短距离的Dijkstra(狄 克斯屈拉)算法;另一种是求网络图上任意两点之间最短距离的矩阵算法.
运筹学05_图与网络分析2-最短路

根 据 Dijkstra 算 法 , 可 以 得 出 从 v1 到 v2 最 短路权是2,但是这显然不对,因为从v1到 v2的最短路是(v1, v3, v2),权是-1。
2
v1
v2
2
-3
vh 3
38
有向图某些权值为负
逐次逼近算法
1、先对图中各个点按照Dijkstra算法标号,称之为第 一次标号,令m=1,转入第二步;
2.5
3
1
2
v3
4 3
4
v7 2
v4
v9
4 v8
h
27
v5
3
5
3
3 0 v1
v2
3
2
v6
2.5
3
1
2
v3
4 3
4
v7 2
v4
v9
4 v8
h
28
v5
3
5
3
3 0 v1
v2
3
v6
2.5
2
53
1
2
v3
4 3
4
v7 2
v4
v9
4 v8
h
29
v5
3
5
3
3 0 v1
v2
3
v6
2.5
2
53
1
2
v3
4 3
4
v7 2
h
60
v1 v2 v3 v4 v5 v6 0 0 12 1 04 5 2 2 0 5 5 1 4 0 6 v5 2 3 0 v6 2 2 0
h
61
v1 v2 v3 v4 v5 v6 0 0 12 1 04 5 2 2 05 5 1 4 0 6 3 23 0 v6 2 2 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
附件2《运筹学》最短路、最小费用最大流经典作品关于钢管订购和运输的优化模型队员:陈显健陈瑜斌陈振松2007年6月5日摘 要: 本文首先运用图论知识中的最短路算法求出i S 到j A 的最优路径。
然后将模型转化为最小费用最大流的网络优化问题,从而求出近似最优解。
在分析出求解该网络优化模型的解法后,运用Lingo 软件包求出了该问题的近似最优解。
对问题一而言,求出了较优的订购和运输计划(见表三),其最小费用为1291630万元。
对于第二个问题而言,可得出钢厂6S 的钢管销价的变化对购运计划和总费用的影响最大;钢管厂1S 的钢管产量的上限的变化对总费用的影响最大,钢管厂3S 的产量上限的变化对购运计划的影响最大。
对问题三,给出了一般解,求出了较优的订购和运输计划(见表四),其最小费用为1396099万元,最后对模型进行了综合评价并提出了改进方向。
关键词:网络流 最小费用最大流一、 问题重述要铺设一条1521A A A →→→ 的输送天然气的主管道,如图一所示,经筛选后可以生产这种主管道的钢厂有721,,,S S S 。
图中粗线表示铁路,单细线表示公路,双细线表示要铺设的管道(假设沿管道或者原来有公路,或者建有施工公路),圆圈表示火车站,每段铁路、公路和管道旁的阿拉伯数字表示里程(单位km )。
为了方便,1km 主管道称为1单位钢管。
一个钢厂如果承担制造这种钢管,至少需要生产500个单位。
钢厂i S 在指定期限内能生产该钢管的最大生产数量为i s 个单位,钢厂出厂销价为i p 万元,如下表:表一1单位钢管的铁路运价如下表:(表二)1000km 以上每增加1至100km 运价增加5万元。
公路运输费用为1单位管道每公里0.1万元(不足整公里的按整公里计算)。
管道可由铁路、公路运往铺设地点(不只是运到点1521A A A →→→ ,而是管道全线)。
要求:(1) 请制定一个主管道钢管的订购和运输计划,使总费用最小,并给出总费用。
(2) 请就(1)的模型进行分析:哪个钢厂钢管的销价的变化对购运计划和总费用影响最大,哪个钢厂钢管的产量的上限的变化对购运计划和总费用的影响最大,并给出相应的数字结果。
(3) 如果要铺设的管道不是一条线,而是一个树形图。
铁路、公路和管道购成网络,请就这种更一般的情形给出一种解决办法,并对图二按(1)的要求给出数学模型和结果。
二、 基本假设1. 沿管道铺设路线上有公路,在计算运费时,与其它普通公路相同; 2. 订购的钢管数量刚好等于需要铺设的钢管数量;3. 公路运输费用为1单位钢管每公里0.1万元(不足整公里的按整公里计算); 4. 1km 主管道钢管称为1单位钢管;5. 一个钢厂如果承担制造这种钢管,至少需要生产500个单位;6. 1单位钢管的铁路运价如(表二)所示,1000km 以上每增加1至100km 运价增加5万元; 7. 管道可由铁路、公路运往铺设地点(不只是运到点1521,,,A A A ,而是管道全线); 8. 本问题只考虑在铁路和公路上运输的问题,而不考虑在其它路径上的情况; 9. 每个钢管厂生产的钢管均满足铺设要求;10. 模型只考虑钢管销价费用和钢管从钢管厂运送到铺设点的钢管运费,而不考虑其它费用, 如转运费用等;11. 在公路上卸货,按铺路的要求卸车;12. 销售价和运输价不受市场价格变化的影响。
三、符号说明i S第i 钢管厂i s表示i S 的最大生产能力j A 表示需要铺设管道路径上的车站 j i x ,从所有i S 运往j A 的钢管用于铺设j A 点前后侧的钢管数 j i F , 单位产品从i S 到j A 地的运费j i f , 表示单位钢管从i S 地运往j A 地的最小费用 1 ,+j j A 表示1+j j A A 和两车站之间需要铺设的管道长度 i p从i S 订购钢管的单位价格 z用于订购和运输的总费用四、 模型的建立与求解问题一1、 模型的建立对本问题而言,实际上是一个要求制定订购和运输计划,使总费用最小的优化问题。
本模型的总费用包括钢管的销价和运输总的费用。
首先,向某厂订购钢管,然后将在每个厂订购的钢管运往需要铺设的全路段。
由本题的要求可以知道在铺设管道时必须经过1521,,A A A 点。
欲解决本问题可以按以下方案进行思考:首先,需要确定将货物从i 地运往j 地的最优路线;然后,求出向每个钢管厂的订购计划,并确定出运输计划;最后计算将运往j 地的钢管铺到各个管道上的运输费用,我们不妨假设运往以j 为终点的钢管只铺到与j 点相邻的两段管道上。
因此,本问题可以按以下步骤求解。
第一步:确定从i 地到j 地的最优路径,从而确定出单位钢管从i 地运往j 地的最小运费。
设)7,2,1( =i S i 表示钢管厂,)7,2,1( =i s i 表示i S 的最大生产能力,)15,,2,1( =j A j 表示需要铺设钢管路径上的车站。
假设从i S 运往j A 的钢管用于铺设jA 点前后侧的钢管数为j i x ,单位,单位产品从i S 到j A 地的运费为j i F ,万元,用j i f ,表示单位钢管从i S 地运往j A 地的最小费用,则:j , ,min i j i F f = (1)第二步:建立从i S 厂运送j ,i x 单位钢管到j A 点的运费的模型:用1z 表示订购的所有钢管全部运到j A 点的总运费,则:0 1 500 .. ,1,171,151,151,15171 , ,1≥=+=+⎩⎨⎧=≥≤∙=+-++=-+====∑∑∑∑∑j i j j j j i ji jji i i ij j i ii j j i j i ji j i x A y y x y y S S x s x t s f x z 不生产时当生产时当λλλ (2)其中:+j y 和-j y 分别表示运到j A 地钢管用于铺j A 点前边和后边的钢管长度;1 ,+j j A 表示1+j j A A 和之间需要铺设的管道长度第三步:将运到j A 处的钢管铺到相邻两段路上的运输费用根据假设,在铺设钢管时,dx 单位钢管从第1+k k 点运到点的运费为:⎰+10.1 k kdx =0.1 (3)由(3)式可得如下模型(1)当-++1j j y y 和均为整单位数时,设其运费用21z 表示,则:∑=-+-+++∙++∙+⨯=15111212)1()1(1.0j j j j j y y y y z(2)当-++1j j y y 和均为非整单位数时,设其运费用22z 表示,则:])}[2()1(])[2(])[1{(05.0 2])[1(])[(2][)1(1.0 2])[1(])[(2][])[1(1.0111111122-+-+-++++-+-++-+-++++++-∙++-∙+⨯=+∙-+∙+⨯++∙-+∙+⨯=∑j j j j jj j j j j j j j j j j y y y y y y y y y y y y y y y y z其中:][+j y 表示+j y 的整数部分;][1-+j y 表示-+1j y 的整数部分;综合上述两式可得:∑=-+-+-++++-∙++-∙+⨯=1511112])}[2()1(])[2(])[1{(05.0j j j j j j j y y y y y y z (4)1][][ 0 1 500 .. ,1 ,11 ,171,151,151,≥-=+=+=+⎩⎨⎧=≥≤+-+++-++=-+==∑∑∑j i j j j j j j j j i ji jji i i ij j i ii j j i x A y y A y y x y y S S x s x t s 不生产时当生产时当λλλ其中:2z 表示运到j A 处的钢管铺到相邻两段路上的运输费用第四步:建立订购费用的模型设3z 表示订购管道的总费用,则可建立如下模型:j i i i x p z ,71151j 3∙=∑∑==(5)用z 表示订购和运输的总费用,由(2)、(4)、(5)可得本问题的优化模型如下:321min z z z z ++=即:ji i i j i j i j i j j j j j j j x p f x y y y y y y z ,71151j 15171, ,151111 ])}[2()1(])[2(])[1{(05.0min ∙+∙+-∙++-∙+⨯=∑∑∑∑∑=====-+-+-++++1][][ 0 1 500 .. ,1 ,11 ,171,151,151,≥-=+=+=+⎩⎨⎧=≥≤+-+++-++=-+==∑∑∑j i j j j j j j j j i ji jji i i ij j i ii j j i x A y y A y y x y y S S x S x t s 不生产时当生产时当λλλ2、 模型的求解 (1)首先求解j i f ,此问题相当于求解最小费用流问题,即求出从i S 点运送单位钢管到j A 点的最小费用。
按常规,本问题可以按求最短路的常规方法求解。
但由于本问题中沿铁路的单位运费由它前边经过的铁路长度而变化。
根据问题的需要,我们不妨假设如果从i S 点到j A 点的钢管经过铁路后,一旦走公路,那么,该钢管将不会再通过铁路运输。
则假设沿铁路行走,直到走到与公路相连为止。
那么,我们可以将已知图中铁路的费用直接表示出。
因此从i S 点到j A 点的通路如图三所示。
(图三)A现在需要求出每个钢管厂i S 到每条公路上的节点j A 的最优路径,即:如果需要从i S 点运钢管到j A 点,则需要找出从该点到目的点间的最优路线。
现在从每个钢厂出发,求出每个钢厂到需要铺设管道的路径上的每个节点的单位钢管量的最小费用。
那么,我们以i S ,j A 以及铁路的端点等为点,以钢管的可能运输路线为边,以单位钢管的运输费用为权建立形如(图三)所示的加权图。
(其中,边上的权的确定的具体方案参见文献[2],本题中,以i S 为起点,以需铺设管道的路上的节点为终点,那么从i S 到j A 的路程中根据铁路和公路的运费特点不难得出形如图三所示的赋权图),根据Dijkstra 标号法[2]可以求出每个钢管厂i S 到各个节点j A 的最小单位运输费用。
现在我们以2S 点为起点,以每个铺设管道的节点为终点,通过观察与简单运算得出图三的加权图,则以图三为基础,运用Lingo 软件包中的求最短路问题的程序DYNAMB.LG4(见附录一)可求得单位钢管的最小运输费用如下:其中:F(j)(j=1,…,15)表示从2S 到j A 的最小单位钢管运费。
同理可得1S ,3S ,4S ,5S ,6S ,7S 各点到目的点的最优单位运费如下1S 点到需要铺设管道的路上的各节点的单位运输费F( 1) 170.7000 F( 2) 160.3000 F( 3) 140.2000 F( 4) 98.60000 F( 5) 38.00000 F( 6) 20.50000 F( 7) 3.100000 F( 8) 21.20000 F( 9) 64.20000 F( 10) 92.00000 F( 11) 96.00000 F( 12) 106.0000 F( 13) 121.2000F( 14) 128.0000F( 15) 142.0000S点到需要铺设管道的路上的各节点的单位运输费3F( 1) 230.7000 F( 2) 220.3000 F( 3) 200.2000 F( 4) 181.6000 F( 5) 121.0000 F( 6) 105.5000 F( 7) 96.00000 F( 8) 86.20000 F( 9) 48.20000 F( 10) 82.00000 F( 11) 86.00000 F( 12) 96.00000 F( 13) 111.2000 F( 14) 118.0000 F( 15) 132.0000S点到需要铺设管道的路上的各节点的单位运输费4F( 1) 260.7000 F( 2) 250.3000 F( 3) 235.2000 F( 4) 216.6000 F( 5) 156.0000 F( 6) 140.5000 F( 7) 131.0000 F( 8) 116.2000 F( 9) 84.20000 F( 10) 62.00000 F( 11) 51.00000 F( 12) 61.00000 F( 13) 76.20000 F( 14) 83.00000 F( 15) 97.00000S点到需要铺设管道的路上的各节点的单位运输费5F( 1) 255.7000 F( 2) 245.3000 F( 3) 225.2000 F( 4) 206.6000 F( 5) 146.0000 F( 6) 130.5000 F( 7) 121.0000 F( 8) 111.2000 F( 9) 79.20000 F( 10) 57.00000 F( 11) 33.00000 F( 12) 51.00000 F( 13) 71.20000 F( 14) 73.00000 F( 15) 87.00000S点到需要铺设管道的路上的各节点的单位运输费6F( 1) 265.7000 F( 2) 255.3000 F( 3) 235.2000 F( 4) 216.6000 F( 5) 156.0000 F( 6) 140.5000 F( 7) 131.0000 F( 8) 121.2000 F( 9) 84.20000 F( 10) 62.00000 F( 11) 51.00000 F( 12) 45.00000 F( 13) 53.00000 F( 14) 11.00000 F( 15) 28.000007S 点到需要铺设管道的路上的各节点的单位运输费F( 1) 280.7000 F( 2) 270.3000 F( 3) 250.2000 F( 4) 231.6000 F( 5) 171.0000 F( 6) 155.5000 F( 7) 146.0000 F( 8) 136.2000 F( 9) 104.2000 F( 10) 77.00000 F( 11) 66.00000 F( 12) 56.00000 F( 13) 38.20000F( 14) 26.00000F( 15) 2.000000(2)根据以上结果, 继续求解最小总费用的模型原问题属于非线性规划问题的最优解,但针对我们现在的情况来说,不能找到较好的方法求解,我们可以根据线性(非线性)规划问题与网络流分析之间的密切联系,将原问题转化为下面的网络流问题进行求解。
