CH6图—学生
小学生识字表(2500字)

d阿d啊ai哀ai唉ai挨di矮di爱di碍an安dn岸dn按in案an暗dng昂00袄do傲ao奥小学生识字表〔2500字〕ba八ba巴ba扒ba吧bd疤bd拔b6把bd坝bd爸bd罢bd霸bdi白bdi百bdi柏bdi摆bdi败bdi拜ban班ban般ban斑ban搬ban板bdn版ban办bdn半bdn伴ban扮bdn拌bdn滤bang 帮bdng 绑bdng 榜bdng 膀bdng 傍bdng 棒bao包bao胞bdo直bdo宝bdo饱bdo保bdo堡bdo报bdo抱bdo暴bdo爆bei杯bei悲bei碑bM北b6i贝bM备bM背b6i倍b6i被b6i辈ben奔b$n本b6n笨bdng 蹦bl逼bi鼻bl比bl彼bi笔bl鄙bl币bl必bl毕bi闭bi毙bi弊bl碧bl蔽bl壁bl避bl臂bian 边bian 编bian 鞭bidn 扁bian 便bidn 变bian 遍bidn 辨bidn 辩bian 辫biao 标bido 表biC别bin宾bln滨bi ng 冰b lng 兵blng 丙blng 柄blng 饼blng 并blng 病b6拨b6波bo玻bao剥b6脖b6菠bo播b6伯b6驳b6泊b6博b6搏b6膊bdo薄bo卜bO补bO捕bu不bu布bu步bu怖bu部ca擦cai猜cdi才cdi材cdi财cdi裁cdi采cdi彩cdi睬cdi踩cdi菜can参can餐cdn残cdn蚕cdn惭cdn惨can灿cang 仓cang 苍cang 舱cang 藏cao操cdo槽cdo草c6册zk侧2厕c6测c6策c6ng 层cha叉cha插chd查chd茶chd察chd岔cha差chai 拆chdi 柴chdn 馋chdn 缠chdn chdn 铲chdn 颤chang昌chdng长chang肠chang尝chdng偿chang,害, 吊chang rchang场chang敞chdng畅chdng倡chdng唱chao 抄chao 钞chao 超chdo 朝chao 潮chdo 吵chdo 炒ch.车ch.扯ch6彻che撤ch6n 尘ch6n 臣ch6n 沉ch^n 辰ch6n 陈ch6n 晨chua 闯ch6n 衬cheng称chen 趁cheng撑ch6ng成ch6ng 呈ch^ng承ch^ng诚ch6ng城ch^ng乘chdng惩chdng程cheng秤chi吃chi驰chi 迟chi持chi匙chi尺chi齿chi耻chi斥chi赤chi翅chdng充chdng 冲chdng 虫chdng崇chdu 抽chdu 仇chdu 绸ch6u 愁chdu 稠chdu 筹chdu 酬chdu 丑chdu 臭chu出chu初chu除chu厨chu锄ch£i 础chO储chO楚chO处chu触chuan川chuan穿chuan传chudn船chuan喘chuan串chuang疮chuang窗chuang 床chuang创chui 吹chui 炊chui 垂chui 锤chun 春chun 纯chun 唇chun 蠢ci词cl慈cl辞cl磁cl此ci次cl刺c6ng 从cong 匆cong 葱cong 聪c6ng 丛cdu凑cu粗cu促cu醋cuan 窜cul催cul摧cul脆cul翠cun村cun存cun寸cud错chu畜c6ng 曾da搭dd达d6答dd打dd大ddi呆dai代ddi带ddi待ddi怠ddi贷ddi袋dai逮ddi戴dan丹dan单dan担dan耽ddn胆dan旦ddn但ddn诞dan弹ddn淡ddn蛋dang 当ddng 挡ddng 党dang 荡dang 档dao刀ddo叨ddo导ddo岛ddo倒ddo蹈dao到ddo悼ddo盗dao道ddo稻加得d6德de的deng 灯deng 登d$ng 等ddng 凳di低dl堤di滴di敌di笛di底di抵di地dl弟di帝dl递di第dian 颠dian 典didn 点didn 电didn 店didn 垫dian 殿diao 叼diao 雕did吊dido 钓diao 调diao 掉die爹die跌di6叠diC蝶ding T ding □J ding 盯ding 钉ding 顶ding 订ding 定diU丢ddng 东ddng 冬ddng 董ddng 懂ddng 动ddng 冻ddng 栋ddng 洞d6u都dbu斗ddu抖dou陡ddu豆ddu逗du督du毒加读du独dO堵da赌du杜du肚du度如渡duan 端duan 短duan 段dudn 断duan 缎dudn 锻dul堆dul队dul对dim吨dun蹲dun盾dun顿dud多du6夺dud朵dud躲dud惰6鹅6蛾6额e恶6饿◎n恩鬻儿6r而迎耳er 二比发f6乏f6伐fd罚f6阀窕法fan帆fan番fan翻fdn凡fdn烦f如繁fdn反fan返fdn犯fdn泛fdn饭fdn范fdn贩fang 方fang 坊fang 芳fang 防fdng 妨fdng 房fdng 仿fdng 访fdng 纺fdng 放他飞fei非f6i肥f$i匪■废f6i沸侬肺卷i费fen分fen吩fen纷fen芬f6n坟f€n粉fdn份f^n奋f6n愤fdn粪f6ng 丰feng 风feng 封feng 疯feng 峰feng 锋feng 蜂f6ng 逢f 6ng 缝f$ng 讽f 6ng 凤f eng 奉 f6佛fdu否fu夫fu肤加伏田扶fu服由俘fU浮fu符fU幅fO福fu抚田府fo斧比俯元辅fO腐fCi父ft!付妇fu负m附f(i咐fu复比赴fu副fu傅f£i富fu腹田覆gai该gdi改gdi盖gdi溉gai概gan干gan甘gdn杆gan肝gan竿gan秆gdn赶gan敢gdn感gang 冈gang 刚gang 岗gang 纲gang 缸gang 钢gdng 港gang 杠gao高gao膏gao糕gao搞gao稿gao告g6哥ge胳g.鸽ge 害g◎搁g◎歌g6阁g6革g6格gS葛g6隔g6个g6各gUi给gen根gen跟g6ng 更geng 耕gong 工gong 弓gong 公gong 功gong 攻gdng 供gong 宫gong 恭gong 躬gdng 巩gdng 共g6ng 贡gou勾gou沟gou钩gdu狗g6u构gdu购gdu够gu估gu姑gu孤gu辜gU古gU谷gU股go骨gO鼓gu固gu故gu顾gua瓜gua刮gua挂guai 乖guai 拐guai 怪guan 美guan 观guan 官guan 冠guan 馆gu限管gudn 贯gudn 惯guan 灌guan 罐guang 光gudng 广gul归gul龟gul规gul轨gul鬼gul柜gul贵gul桂gul跪gOn滚gun棍guo锅gu6国gud果gud裹gud过ha哈hdi孩hdi海hdi害hdn含hdn寒hdn喊hdn汉han汗hdn旱hdng 航hao亳hdo豪hdo好hao号hdo浩hdo耗h白喝h6禾h6合h6何h6和h6河h6核h6荷h6盒*贺hei黑h6n痕h6n很h6n狠h6n恨h6ng 恒h6ng 横h6ng 衡hong 轰hdng 哄hong 烘h6ng红h6ng 宏h6ng 洪h6ng 虹h6u喉h6u猴hdu吼hdu后hdu 厚- hdu候hu乎hu呼hu忽hU狐hu胡hu壶hU湖h.糊h蝴ha虎hCi互hu户Mi护hua花hud华hud哗hud滑hud猾hud化hua划hua画hua话hudi 怀hudi 槐hudi 坏huan 欢hdi还hudn 环hudn 缓hudn 幻liuan唤hudn换hudn 患huang 荒h uang 慌hudng 皇hudng 黄h uang 煌hudng 晃huang 谎hul灰hul恢hul挥hul辉hul回hul悔hul汇hul会hul绘hul贿hul惠hul毁hul 慧 hun 昏 hun 婚 hun 浑 hUn 魂hun 混 hu6活 hud 火 hud 伙 hub 或hud 货 hud 获 hud 祸 hud 惑jl 击 ji 饥 jl 圾 ji 机 jl 肌 ji 鸡 ji 迹 jl 积 ji 基 ji 绩 jl 激 jl 及 n 吉 jl 级 ji 即 jl 极 jl 急、 ji 疾 n 集 ji 籍 jl 几 jl 己 ji 挤 ji 脊 ji 计 jl 记 ji 纪jl 忌ji 技ji 际jl 剂jl 季ji 既ji 济jl 继ji 寄jia 加 jia 夹 jia 佳 Jia 豕••一Jia 暴 jid 甲 jid 价 jid 驾 jid 架 jid 假 jia 嫁 jid 稼 jidn 奸 jian 尖jian 坚 jian 歹干 jian 间 ••一 • jian 肩 jian 艰 ••一 ・If; Jian 兼 jian 监 jian 煎 jidn 拣 jidn 俭jidn 茧 jidn 捡 jidn 减 jidn 剪 jidn 检 jidn 简 jidn 见 jidn 件 jidn 建 jidn 剑 jidn 荐 jian 贱 jian 健 jidn 舰 jidn 渐 jian 践 jidn 鉴 jidn 键 jian 箭jiang江Jiang 姜jiang 将jiang 浆jiang 僵jiang 疆jidng 讲jidng 奖jidng 桨jidng 匠jidng降jidng酱jiao 交 jiao 交Bjiao 娇 jiao 浇 jiao 骄 jiao 胶 jiao 椒 jiao 焦 jiao 熊jido 角 jido 狡 jido 绞 jido 饺 jido 脚 jiao 搅 jido 缴 jidoni|jido 轿 jido 较jido 教 ji ◎阶 jie 皆 jie 接 jie 揭 jie 街 ji6节 jiG 劫 ji6杰 jiC 洁 ji6结 ji .捷 jiC 截 ji6竭 j 迪姐 j 通解 ji©介 ji .戒ji6届 ji .界ji6借 jin 巾 jin 今 jin 斤 jin 金 jin 津 jin 筋 jin 仅 jin 紧 jin 谨 jin 锦 jin 尽 jin 劲 jin 近 jin 进 jin 晋 jin 浸 jin 禁 Jlng 京 jing 经 Jing 茎 jlng 惊 jlng 晶 jing 睛 jlng 精 jing 井 jing 颈 jing 景 jlng 警 jlng 净 Jing 径 Jing 竞 jing 竟 jlng 敬 jing 境 jing 静 jing 镜 jiu 纠 jiU 究 jiu 揪 jiO 九 jiO 久 ji 口酒 jiu 旧 jiu 救 jiCi 就 JIU 男 ju 居ju 拘 ju 鞠ju局jO菊ju橘世举汕矩2句ju巨用拒ju具ju俱ju剧■惧ju据jd距ju锯前聚juan in juan 卷judn 倦juan 绢ju6决ju6绝ju6觉ju6掘ji6.嚼jun军jun君jun均jun菌jun俊kd卡kai开kdi凯kdi慨kan刊kan堪kan砍kan看kang 康kang 糠kdng 扛kdng抗kdng 炕kdo考kdo烤kao靠ke科ke棵k◎颗k6壳k6咳可依渴蜡克kd刻蛇客kd课k^n肯k4n垦k6n恳keng 坑kdng 空kdng 孔kbng 恐kdng 控kdu 口kdu扣kbu寇ku枯ku哭kU苦kCi库kCi裤kCi酷kua夸kud垮kud挎kua跨kudi块kudi 快kuan 宽kuan 款kuang 筐kuang狂kuang 况kuang旷kudng矿kudng 框kul亏kul葵kui愧kun昆kOnffl kun困kud扩kud括kud阔la垃la拉la啦16喇Id腊14蜡K辣16i来Idi赖Idn兰Idn拦Idn栏Idn蓝Ian篮Idn览13懒Idn烂Idn滥Idng 郎lang 狼Idng 廊Idng 朗lang 浪1G捞16.劳Ido牢Ido老140姥14.涝Id乐16勒1包雷l§i垒16i泪1M类16i累16ng 冷11厘11梨11狸11离11犁11鹏11璃11黎11礼11李11里11理n力11历11厉11立11丽11利11励11例11隶11栗11粒liang lidn 连lidn 帘lidn 怜lidn 莲lidn 联lidn 廉lidn 镰lidn 脸lidn 练俩lidn 炼lidn 恋lidn 链lidng良liang凉lidng梁lidng粮lidng粱liang两liang凫lidng 际liang俩lidng量lido 辽liGo 疗lid.僚leT lido 料lid列li©劣li6烈lid猎Ii6裂lln邻Un林Un临Hn淋Ung伶ling 灵ling 岭Ung铃Ung陵Ung零11 ng 龄l ing 领ling 令ling 另liu溜liU刘liU流liO留liU榴M0柳liU六16ng 龙16ng 笼16ng 聋16ng 隆16ng 垄Idng 拢16u楼16u搂Ibu漏10露1U芦ia炉10虏10鲁10陆lu录ICi鹿1(1滤lu碌1匕路1U驴1.旅屡律1(1虑1(1率1(1绿luin 卵ludn 乱1迎掠1U6略lUn轮10n论lu6罗lud萝lu6锣lu6梦lu6骡lu6螺lub络lud骆lud落ma妈ma麻md马nd码md蚂md骂ma吗mdi埋mdi买mdi迈卜di麦mdi卖mai脉uidn 蛮mdn馒mdn瞒man满man慢mdn漫mdng 忙Ldng 芒mang 盲mdng 茫mao猫mao毛mao矛mdo茅mdo茂mdo冒mdo贸mdo帽mdo貌me么皿£没m6i眉梅m6i煤m6i霉磅i每m$i美磅i妹m6n门mdn闷m6n们m6ng 萌1116ng盟m^ng 猛m6ng 蒙 m^ng 孟mdng 梦ml迷ml谜mi米cnl眯ml秘mi密mi蜜raidn眠midn 绵midn 棉mian 免mian 勉mian 面mido 苗mido 描mido 秒miao 妙miao 庙mid灭mid蔑mln民mln敏ml ng 名m i ng 明m l ng 鸣ml ng命mo摸m6模m6膜m6摩m6磨m6魔md抹aid末md沫md莫md漠md墨md默m6u谋mdu某mO母mu亩mu木mu目mu牧mu墓mu幕mu慕mu暮。
中学化学仪器装置图大全,画图不再难!(、可编辑)

中学化学仪器装置图大全,画图不再难!(、可编辑)
一天一个教育方法|助你成为卓越的家长
果老师说语文
每个家长应该告诉自己的孩子:“学校不是你混日子的地方,吃不学校的苦,就等着吃社会的
苦。
”共勉!#正能量 #学校 #学习 #努力 #父母
视频号
今天给大家整理分享中学化学仪器图,以后可以直接用啦!
点击查看大图
* 延伸推荐
(点击下方蓝字标题可前往观看)
· 100集纪录片《中国通史》
◎009:武王克商
◎ 010:周公摄政
◎ 011:周王室的衰落
◎ 012:春秋争霸
◎ 013:孔子
◎ 014:列国变法
◎ 015:战国七雄
◎ 016:诸子百家
◎017:秦国崛起
◎ 018:秦始皇统一中国
◎ 019:楚汉战争
◎ 020:郡国并行
* 学习工具
(海量学习资料都在关注后获得)。
小学生100个成语积累

100个成语积累1、黯然神伤(anfnshOnshang):形容由于心情沮丧而面带感伤的神色。
2、跋山涉水(bashansheshui):形容旅途上艰辛劳苦。
3、白璧无瑕(baibiwdxia):比喻人或事物十分完美,没有丝毫缺点。
4、变本加厉(bi^nb总njiali):指变的比原来更严重。
5、波澜壮阔(bolanzhuangkuo):形容江河湖海等水势辽阔。
比喻气势宏伟、浩大。
6、不寒而栗(bDhanOrli):天气不寒冷而身体发抖。
形容非常惊恐、害怕。
7、不屈不挠(buqubunao):指在压迫或困难面前不低头、不屈服。
8、步履维艰(bU临wOijian):指行走十分困难。
9、瞠目结舌(chengmujieshe):形容惊讶或受窘的样子。
10重蹈覆辙(ch6ngd$ofUzhe):比喻不吸取失败的教训,重犯以往的错误。
11、垂涎欲滴(chuixianyUdi):形容非常贪馋或羡慕。
12、大气磅礴(daqipangb6):形容气势盛大。
13、大相径庭(daxiangjingting):指彼此相差很远或截然不同。
14、独具匠心(dujujiangxin):具有独到的想法或创造性。
15、独辟蹊径(dUpix車ng):比喻独创一种新的方法或风格。
16、耳濡目染住rrUmUr^n):因经常听到看到而不知不觉受到影响。
17、粉饰太平(传nshit^iping):掩盖社会黑暗现象、装饰成平和安定的景象。
18、高瞻远瞩(gaozhanyuanzhu):形容目光远大。
19、光阴荏苒(guangyin论nran):时光不知不觉地流逝。
20、废寝忘食(fOiqYnwangshi):形容对某事专心致志。
21、釜底抽薪(fudichouxin):比喻从根本上解决问题。
22、感激涕零(ganjitiling):感激得流下泪来。
23、根深蒂固(genshendigu):比喻基础稳固。
24、孤苦伶仃(gUkUHngding):形容孤单困苦,无依无靠。
CH图

回路(环):第一个顶点和最后一个顶点相同的路径。
简单路径:序列中顶点不重复出现的路径。
简单回路(简单环):除了第一个顶点和最后一个顶点 外,其余顶点不重复出现的回路。
6.1 图的逻辑结构
如何判断一个子图是极大连通子图?
A
B
C 首先是子图;然后子图是连通的V1,并且连通V子2
图含有极大顶点数;最后依附于这些顶点的边
都加上。 D
V3
E
F
V4
V5
6.1 图的逻辑结构
例:
A C
B
连通分量1
A
B
D
E
F
无向图
E
F
C
连通分量2
D
6.1 图的逻辑结构
在有向图中,对图中任意一对顶点vi和vj (i≠j),若 从顶点vi到顶点vj和从顶点vj到顶点vi均有路径,则 称该有向图是强连通图。非强连通图的极大强连通 子图称为强连通分量。
在具有n个顶点、e条边的无向图G中,各顶点
的度之和等于?
n
TD (vi ) 2e
例: V1
V2
i 1
握手定理
V3
求该无向图各顶点的度数之和。
V4
V5
6.1 图的逻辑结构
在有向图中,顶点v的入度是指以该顶点为 弧头的弧的数目,记为ID (v);顶点v出度是指以 该顶点为弧尾的弧的数目,记为OD (v)。
V1 V3V4ຫໍສະໝຸດ V1V3V2 若顶点vi和vj之间的边没有方向,则 称这条边为无向边。 如果图的任意两个顶点之间的边都 是无向边,则称该图为无向图。
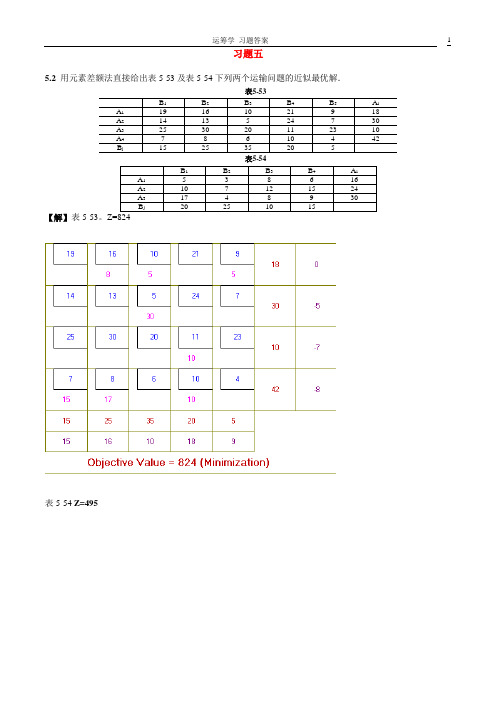
运筹学课后习题答案 熊伟(第二版)
v5
v6
v1
0
8.8
8.6
5.6
8
6
v2
0
8
5
13
4
v3
0
3
4.8
12
v4
0
7.8
9
v5
0
9
v6
0
v1、v2、…、v6到各点的最优路线图分别为:
6.9设图6-43是某汽车公司的6个零配件加工厂,边上的数字为两点间的距离(km)。现要在6个工厂中选一个建装配车间。
(1)应选那个工厂使零配件的运输最方便。
距离表C
1
2
3
4
5
6
1
∞
8.8
9
5.6
8
6
2
8.8
∞
10
5
∞
4
3
9
10
∞
3
4.8
14
4
5.6
5
3
∞
12
∞
5
8
∞
4.8
12
∞
9
6
6
4
14
∞
9
∞
在C中行列分别减除对应行列中的最小数,得到距离表C1。
距离表C1
1
2
3
4
5
6
1
∞
3.2
3.4
0
0.6
0.4
2
2.8
∞
6
1
∞
0
3
4
7
∞
0
0
11
4
0.6
2
0
∞
7.2
A到H的最短路PAH={A,B,F,H},{A,C,F,H}最短路长22;A到I的最短路PAI={A,B,F,I},{A,C,F,I}最短路长21。
浙江省桐庐分水高级中学高中美术课件:苹果中的五角星(2)(共43张PPT)

一式多变
请挑选1个模特跟着画一画
第二步:画上密集线条,深入分析体态
• 第二种:曲线密集线条。
范例
女 错叠式
性 礼 服 裙 的 各 种 款 式 欣 赏
层叠式
公主型
高 度
鱼尾型
• 圆弧鱼尾
缀式鱼•尾直线小鱼尾
本校学生设计的礼小服礼裙服式鱼尾
第四步:发现设计师作品的特点
1、从整朵花开始的创意
2、再加上头、脖子及四肢
试3、从短裙到长裙的款式 4、点缀细节
方法2:这朵“花”放在哪里很重要
方法3:点缀礼服裙的小细节
• 荷叶边、 思蝴考:蝶结、 多如层果次从这的 样蛋的角糕度式出发样, 你知还以抽能识有根经哪及褶据验些折等已,植有说物裁皱的说的剪、
形组态合和礼元服素裙,细 节这之些间的细联节系处吗?
——植物形态与女性礼服裙设计
开启我们的灵感之旅吧!
• 窈窕的植物们!大自然赋予我们的眼
睛去感受丰富的色彩,多姿的形状,一年四季曼妙不同。
当春天 来临的时候 你会看到 教室的窗外 蓝色的鸢尾 摇曳生姿……
看一看:这些植物 和模特有什么样的 关联呢?
两株似模特的花
1 2 组合花朵 的想象 3
比 如 这 样 一 棵 树
2、这朵花放在哪里很重要
3、点缀礼服裙的小细节
下图是设计师的灵感来源,请说说你的发现。
1 2
方法1:从整朵花开始的创意开端
请跟老师画:
1、画出右边图案的花瓣 2、再加上头、脖子及四肢 3、从短裙到长裙的款式 4、点缀细节
方法1:从整朵花开始的创意开端
请跟老师画: 请1、你画出自右边己图案试的花一瓣
3ቤተ መጻሕፍቲ ባይዱ点缀礼服裙的小细节
实验六 图及其应用

实验六图及其应用数据结构实验六图及其应用1、实验目的? 熟练掌握图的两种存储结构(邻接矩阵和邻接表)的表示方法 ? 掌握图的基本运算及应用? 加深对图的理解,逐步培养解决实际问题的编程能力2、实验内容:采用邻接表或邻接矩阵方式存储图,实现图的深度遍历和广度遍历;用广度优先搜索方法找出从一顶点到另一顶点边数最少的路径。
1.问题描述:利用邻接表存储结构,设计一种图(有向或无向),并能够对其进行如下操作:1) 创建一个可以随机确定结点数和弧(有向或无向)数的图; 2) 根据图结点的序号,得到该结点的值;3) 根据图结点的位置的第一个邻接顶点的序号,以及下一个邻接顶点的序号;4) 实现从第v 个顶点出发对图进行深度优先递归遍历; 5) 实现对图作深度优先遍历;6) 实现对图进行广度优先非递归遍历; 编写主程序,实现对各不同的算法调用。
2.实现要求:(以邻接表存储形式为例)编写图的基本操作函数::对图的各项操作一定要编写成为C(C++)语言函数,组合成模块化的形式,每个算法的实现要从时间复杂度和空间复杂度上进行评价。
1)“建立图的邻接表算法”:CreateGraph(ALGraph *G) 操作结果:采用邻接表存储结构,构造没有相关信息的图G2)“邻接表表示的图的递归深度优先遍历算法”:DFSTraverse(ALGraphG,void(*Visit)(char*)) 初始条件:图G 已经存在;操作结果:返回图的按深度遍历的结果。
3)“邻接表表示的图的广度优先遍历算法”: BFSTraverse(ALGraphG,void(*Visit)(char*)) 初始条件:图G 已经存在;操作结果:返回图的按广度遍历的结果。
4)“邻接表从某个结点开始的广度优先遍历算法”:BFS(ALGraph G, int v)初始条件:图G 已经存在;操作结果:返回图从某个结点开始的按广度遍历的结果。
分析: 修改输入数据,预期输出并验证输出的结果,加深对有关算法的理解。
原《数据挖掘》习题

ch11.讨论下列每项活动是否是数据挖掘任务:(fgh是)(a) 根据性别划分公司的顾客。
(b) 根据可赢利性划分公司的顾客。
(c) 计算公司的总销售额。
(d) 按学生的标识号对学生数据库排序。
(e) 预测掷一对骰子的结果。
(f) 使用历史记录预测某公司未来的股票价格。
(g) 监视病人心率的异常变化。
(h) 监视地震活动的地震波。
(i) 提取声波的频率。
2. (ch1)数据挖掘可以在很多数据源上进行,如关系数据库,空间数据库,多媒体数据库,文本数据库等。
3. (ch1)数据挖掘一定可以得到有趣的强关联规则。
4. (ch1)为了提高挖掘质量,通常要进行数据预处理,包括数据清理、集成、选择、变换等。
5. (ch5){发烧,上呼吸道感染}是(2)项集6.企业要建立预测模型,需准备建模数据集,以下四条描述建模数据集正确的是( B )。
A 数据越多越好B 尽可能多的适合的数据C数据越少越好D 以上三条都正确7. 数据挖掘算法以( D )形式来组织数据。
A 行 B列 C 记录 D 表格Ch28. (ch2)假定用于分析的数据包含属性age。
数据元组中age的值如下(按递增序):13,15,16,16,19,20,20,21,22,22,25,25,25,25,30,33,33,35,35,35,35,36,40,45,46,52,70,求:1)使用按箱平均值平滑对以上数据进行平滑,箱的深度是3。
解释你的步骤。
2)使用按箱边界值平滑对以上数据进行平滑,箱的深度是3。
解释你的步骤。
7、P98 3.4(ch3)假定大学的数据仓库包含4个维{student学生、course课程、semester学期、instructor教师},2个度量count和avg_grade。
在最低的概念层(例如对于给定的学生、课程、学期和教师组合),度量avg_grade存放学生的实际成绩。
为数据仓库画出雪花模式图8、P98 3.5(ch3)假定数据仓库包含4个维date,spectator,location和game,2个度量count和charge。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本章小结图论的起源——哥尼斯堡七桥问题ABCD§6.1 图的定义和术语图(Graph)——由两个集合V(G)和VR(G)组成,记为G=(V,VR)其中:V(G)是顶点的非空有限集VR(G)是边的有限集合,边是顶点的有序对或无序对 有向图(Digraph)——由两个集合V(G)和VR(G)组成其中:V(G)是顶点的非空有限集VR(G)是有向边(即弧)的有限集合,弧是顶点的有序对,记<v,w>,v为弧尾(Tail),w为弧头(Head) 无向图(Undigraph)——由两个集合V(G)和VR(G)组成其中:V(G)是顶点的非空有限集VR(G)是边的有限集合,边是顶点的无序对,记(v,w)或(w,v),并且(v,w)=(w,v)2 1 5 34 35 连通图 66强连通图1 32 4非连通图 有两个连通分量抽象数据类型图的定义ADT Graph { 数据对象: V是具有相同特性的数据元素的集合称为顶点集 R={VR},两个顶点关系的集合 数据关系: VR={<v,w>| v,w∈V, <v,w>表示从v到w的弧} 基本操作: CreatGraph(&G, V, VR); DestroyGraph(&G): LocateVex(G, u); GetVex(G, v); PutVex(&G, v, value); FirstAdjVex(G, v); NextAdjVex(G, v, w); 按V和VR的定义构造图G 销毁图G 返回图G中顶点u的"位置" 返回图G中顶点v 的值 将图G中顶点v 赋值为value 返回 v 的第一个邻接点 返回 v 的(相对于w)下一个邻接点基本操作(续): InsertVex(&G, v); DeleteVex(&G, v); 在图G中增添新顶点v 删除图G中顶点v及其相关的弧InsertArc(&G, v, w); 在G中增添弧<v,w>,若G是无向的, 则还增添对称弧<w,v> DeleteArc(&G, v, w); 在G中删除弧<v,w>,若G是无向的, 则还删除对称弧<w,v> DFSTraverse(G, v, Visit()); 从顶点v起深度优先遍历图G BFSTraverse(G, v, Visit()); 从顶点v起广度优先遍历图G } ADT Graph§6.2 图的存储结构 邻接矩阵(数组表示法)设G=(V,E)是有n≥1个顶点的图,邻接矩阵存储 结构用两个数组分别存储图中顶点的信息(一维 数组)和顶点间相关联的关系(边或弧,n阶方阵)弧及邻接矩阵结构 AdjMatrix[i][j]= 弧及邻接矩阵结构 1 (vi,vj) 或<vi,vj> ∈VR 0 否则# define Max_Vertex_Num 20 //图中最大顶点个数 typedef struct ArcCell { VRType adj; // VRType——顶点关系类型,对无权图, 用1或0表示相邻否;对带权图,则为权值 InfoType *info; //该弧相关信息指针(可无) } ArcCell, AdjMatrix[Max_Vertex_Num] [Max_Vertex_Num]; //ArcCell表示弧,AdjMatrix表示邻接矩阵§6.2 图的存储结构 邻接矩阵(数组表示法)设G=(V,E)是有n≥1个顶点的图,邻接矩阵存储 结构用两个数组分别存储图中顶点的信息(一维 数组)和顶点间相关联的关系(边或弧,n阶方阵)图的定义 图的定义 typedef struct { VertexType vexs[Max_Vertex_Num]; // 顶点向量 AdjMatrix arcs; // 邻接矩阵 int vexnum, arcnum; // 图中顶点及弧的数目 } MGraph;§6.2 图的存储结构 邻接矩阵(数组表示法)设G=(V,E)是有n≥1个顶点的图,邻接矩阵存储 结构用两个数组分别存储图中顶点的信息(一维 数组)和顶点间相关联的关系(边或弧,n阶方阵)1 3 G1 20 0 0 1G1.arcs=41 1 0 0 0 0 0 01 00 0 MGraph G1; G1.vexnum=4; //顶点数 G1.arcnum=4; //弧数 for(k=0;k<G1.vexnum;k++) //顶点向量 G1.vexs[k]=k+1;§6.2 图的存储结构 邻接矩阵(数组表示法)设G=(V,E)是有n≥1个顶点的图,邻接矩阵存储 结构用两个数组分别存储图中顶点的信息(一维 数组)和顶点间相关联的关系(边或弧,n阶方阵)1 3 4 G2 5 20 1 0 1 0G2.arcs=1 0 1 0 10 1 0 1 11 0 1 00 1 1 0MGraph G2; G2.vexnum=5; //顶点数 G2.arcnum=6; //边数 for(k=0;k<G2.vexnum;k++) //顶点向量 G2.vexs[k]=k+1;0 0特点: 无向图的邻接矩阵对称,可压缩存储; 有向图邻接矩阵不一定对称; 无向图中顶点Vi的度是 邻接矩阵中第i行元素之和 有向图中, 顶点Vi的出度是 邻接矩阵中第i行元素之和 顶点Vi的入度是 邻接矩阵中第i列元素之和 判断两顶点是否为邻接点:只需判邻接矩阵对应分量是否为1 在图中增加,删除边:只需对邻接矩阵对应分量赋值1或清01 3 4 G2 5 20 1 0 1 0 1 0 1 0 1 0 1 0 1 1 1 0 1 0 0 0 1 1 0 0 1 3 G12 40 0 0 1 1 0 0 01 0 0 00 0 1 0 G2.arcsG1.arcs带权图(网)的邻接矩阵:ω ij (vi,vj) 或<vi,vj> ∈VR AdjMatrix[i][j]= 0或∞ 否则1 3 7 3 1 5 6 2 V2 8 V1 4 V5 7 9 6 V4 2 V6 2 1 3 2 2 V3 8 4 4 5 20 5 7 0 3 5 0 0 4 81 2 3 4 5 67 0 0 2 110 4 2 06 0 2 3 4 5 63 8 1 6 ∞ 8 ∞ 7 48 ∞ 2 1 ∞∞ 2 ∞ 3 27 1 3 ∞ ∞ 24 ∞ ∞ ∞ ∞9 ∞ 2 2 69 ∞ 26 ∞邻接表实现:为图中每个顶点建立一个单链表,第i个单链表中 的结点表示依附于顶点Vi的边(有向图中指以Vi为尾的弧) 顶 顶 点 点 结 结 点 点 弧 弧 结 结 点 点 图 图 的 的 定 定 义 义typedef struct Vnode data firstarc { VertexType data; //顶点信息 ArcNode *firstarc; //指向第一条依附该顶点的弧 } VNode, AdjList[Max_Vertex_Num];adjvex nextarc info typedef struct Arcnode { int adjvex; //该弧所指向顶点(在表头数组中)的位置 struct Arcnode *nextarc; //指向依附该顶点下一条边或弧 InfoType *info; //该弧相关信息指针(可无) } ArcNode;typedef struct { AdjList vertices; // 表头数组 int vexnum, arcnum; // 图中顶点及弧的数目 } ALGraph;data firstarc a c d G1 e b 1 2 3 4 5 a b c d e G1. vertices data firstarc a c G2 b d 1 2 3 4 a b c d G2. vertices ^ 4 1 3 2 1 2 1 2adjvex nextarc 4 ^ 3 4 3 3 ^ ^ 5 5 ^ ^adjvex nextarc 2 ^^ ^特点 无向图中顶点Vi的度为 第i个单链表中的结点数data firstarc a c d G1 e b 1 2 3 4 5 a b c d e 2 1 2 1 2adjvex nextarc 4 ^ 3 4 3 3 ^ ^ 5 5 ^ ^特点 无向图中顶点Vi的度为 第i个单链表中的结点数 有向图中 顶点Vi的出度为 第i个单链表中的结点数 顶点Vi的入度为 整个单链表中邻接点域值是i 的结点个数data firstarc a c G2 b d 1 2 3 4 a b c d ^ 4 1 ^ ^ 3adjvex nextarc 2 ^逆邻接表:有向图中对每个结点建立以Vi为头的弧 的单链表a c G1b ddata firstarcadjvex nextarc 1 4 a ^ 2 3 4 b c d 1 1 3 ^ ^ ^网的邻接表表示表头顶点的 边的相关 指向下一个 邻接点编号 信息(权) 邻接点的指针 弧结点结构V2 8 V1 4 V5 7 9 6 V4 2 V6 2 1 3 2 2 V31 2 3 4 5 6V1 V2 V3 V4 V5 V62 1 2 1 1 18 8 2 7 4 94 3 4 2 3 3邻接表7 2 3 1 2 25 4 5 3 6 44 1 2 3 6 26 ∧ 6 6 ∧ 59 2 2 6∧ ∧ ∧ ∧§6.3 图的遍历深度优先遍历(DFS)——类似于树的先根遍历方法:从图的某一顶点V0出发,访问此顶点;然后依 次从V0的未被访问的邻接点出发,深度优先遍历图, 直至图中所有和V0相通的顶点都被访问到; 若此时图中尚有顶点未被访问,则另选图中一个 未被访问的顶点作起点,重复上述过程,直至图中所 有顶点都被访问为止 V1 例V2 V4 V5 V8 V6 V3 V7深度遍历:V1 V2 V4 V8 V5 V3 V6 V7深度优先遍历(DFS)V1 V2 V4 V5 V8 V6 V3 V7深度遍历:V1 V2 V4 V8 V5 V6 V3 V7 深度遍历:V1 V2 V5 V8 V7 V3 V6 V4V1 V2 V4 V5 V8 V6 V3 V7深度遍历:V1 V2 V4 V8 V3 V6 V7 V5深度优先遍历算法实现V12 V2visited[M]V3 1 0 1 V7 深度遍历:V1 1 0 2 1 0 3 1 0 4 1 0 5 1 0 6 1 0 7 1 0 8V4V58 V8V6V3 V7 V6 V2 V5 V8 V4data firstarc 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 3 5 7 8 8 7 6 5adjvexnextarc 2 ^ 4 6 2 2 3 3 4 ^ ^ ^ ^ ^ 1 1 ^ ^结束深度优先遍历算法实现1 V1visited[M]V3 0 1 1 V7 7 深度遍历:V1 0 1 2 0 1 3 0 1 4 0 1 5 0 1 6 0 1 7 1 0 8V2 V2 V4 4 V5 V8 V8 V6V3 V7 V6 V2 V4 V8 V5vexdata firstarc 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 ^ ^ 3 4 7 8 8 7 ^ ^ ^adjvex next 2 ^6^结束2^深度优先遍历算法(图用邻接表存储)开始 标志数组初始化 i=1 Vi访问过 Y i=i+1 N i==M Y 结束 N DFS//深度优先遍历图G int visited[Max_Vertex_Num]; void DFSTraver (ALGraph G) { 标志数组 初始化 int i; for(i=1;i<=G.vexnum;i++) visited[i]=0; for(i=1;i<=G.vexnum;i++) if(visited[i]==0) 对未访问 的顶点调 DFS(G,i); 用DFS }深度优先遍历算法(图用邻接表存储)开始 访问V,置标志 求V邻接点 有邻接点w N 结束 Y 求下一邻接点//从第v个顶点出发深度遍历图G void DFS(ALGraph G, int v) { ArcNode *w; int i; printf("%d\t",v); visited[v]=1; w=G.vertices[v].firstarc;//顶点v的第一个邻接点递归Y W访问过 N wVwhile(w!=NULL) //是否存在 { i=w->adjvex; //邻接点下标 if(visited[i]==0) DFS(G,i); w=w->nextarc; //v的下一个邻接点 2 ^ 3 } 1 a }2 3 4 b c d 4 ^ 1 ^DFS(G,v)广度优先遍历(BFS)——类似于树的层次遍历方法:从图的某一顶点V0出发,访问此顶点后,依次 访问V0的所有未曾访问过的邻接点; 然后分别从这些邻接点出发,广度优先遍历图, 直至图中所有已被访问的顶点的邻接点都被访问到; 若此时图中尚有顶点未被访问,则另选图中一个 未被访问的顶点作起点,重复上述过程,直至图中所 有顶点都被访问为止 例V2 V4 V5 V8 V6 V1 V3 V7利用队列实现图 的广度优先遍历广度遍历:V1 V2 V3 V4 V5 V6 V7 V8广度优先遍历(BFS)V1 V2 V4 V5 V8 V6 V3 V7广度遍历:V1 V2 V3 V4 V6 V7 V8 V5V1 V2 V4 V5 V8 V6 V3 V7广度遍历:V1 V2 V3 V4 V5 V6 V7 V8 广度遍历:V8 V4 V5 V6 V7 V2 V3 V1广度优先遍历的实现vexdata firstarc 1 2 3 5 4 1 2 3 4 5 1 2 3 4 5 4 5 5 5 4 adjvex nextarc 2 3 1 1 1 3 ^ ^ ^ 2 ^ ^fff ff f14 32 50 1 2 3 4 5 r r r r r结束 visited[M]1 0 1 1 0 2 1 0 3 1 0 4 1 0 5遍历序列:1 4 3 2 5广度优先遍历算法(图用邻接表存储)开始 标志数组初始化 i=1 Vi访问过 Y i=i+1 N i==M Y 结束 N BFS//广度优先遍历图G int visited[Max_Vertex_Num]; void BFStraver(ALGraph G) { int i; for(i=1;i<=G.vexnum;i++) visited[i]=0; for(i=1;i<=G.vexnum;i++) if(visited[i]==0) BFS(G , i ); }开始 BFS 访问V0,置标志 初始化队列 V0入队 Y 结束 队列空吗 N 队头V出队 求V邻接点w N w存在吗 Y w访问过 N a Y a 访问w,置标志 w入队 V下一邻接点w开始 BFS 访问V0,置标志 初始化队列 V0入队 Y 结束 队列空吗 N 队头V出队 求V邻接点w N w存在吗 Y w访问过 N a Y//从顶点v出发广度优先遍历图G void BFS( ALGraph G, int v) { int qu[Max_Vertex_Num],f=0,r=0; ArcNode *p; printf("%d\t",v); visited[v]=1; qu[0]=v; //v入队 while(f<=r) { v=qu[f++];//出队 a p=G.vertices[v].firstarc; while(p!=NULL) //是否存在 访问w,置标志 { v=p->adjvex; //邻接点下标 if(visited[v]==0) w入队 { visited[v]=1; printf("%d\t",v); V下一邻接点w qu[++r]=v; } p=p->nextarc; //下一个邻接点} } }§6.4 生成树——解决最小代价问题生成树定义:所有顶点均由边连接在一起,但不存在回路的图; 说明 一个图可以有许多棵不同的生成树 所有生成树具有以下共同特点: 生成树的顶点个数与图的顶点个数相同 生成树是图的极小连通子图 一个有n个顶点的连通图的生成树有n-1条边 G 生成树中任意两个顶点间的路径是唯一的 K I 在生成树中再加一条边必然形成回路 含n个顶点n-1条边的图不一定是生成树 H生成树V0 V2 V3 V4 V3 V1 V0 V2 V4 V1连通图G1 B A F E C D连通图G1的一棵生成树 B A F E C D生成树V2 V2 V1 V3 V5 V6 V5 V1 V4 V6 V5 V3 V2 V4 V6 V3V1V4生成树不唯一(0)用顶点数组和边数组存放顶点和边信息(1)初始时,令每个顶点的SubNet 互不相同;每个边的flag 为0(2)选出权值最小且flag 为0的边(3)若该边依附的两个顶点的SubNet 值不同,即非连通,则令该边的flag=1, 选中该边;再令该边依附的两顶点的SubNet 以及两集合中所有顶点的SubNet 相同若该边依附的两个顶点的SubNet 值相同,即连通,则令该边的flag=2, 即舍去该边(4)重复上述步骤,直到选出n-1条边为止//顶点结点typedef struct{ int data; //顶点信息int jihe; }VEX ;VEX v[N];//边结点typedef struct{ int vexh, vext; //边依附的两顶点int weight; //边的权值int flag; //标志域}EDGE ;EDGE e[M];算法实现:。
