南京理工大学工程流体力学基础 第2章_流体静力学
合集下载
南京理工大学工程流体力学1

2.
4.
由于静止流体的压力沿表面的内法线方向作用,故
∫τFρdτ + ∫ pdS = 0
S
∫τFρdτ − ∫ pndS = 0
S
应用奥氏公式,有
∫τ(Fρ −∇p)dτ = 0
§1-1 静止流体的平衡方程
静止流体的平衡方程
由于体积τ是任取的,故被积函数为零
F=
1
ρ
∇p
欧拉平衡方程
1 ∂p X= ρ ∂x 1 ∂p Y= ρ ∂y 1 ∂p Z= ρ ∂z
dSz1 = dSz2 = dSz
∫
结论:浮力等于与物体同体积的液体的重量。
§1-2 重力场中不可压缩流体的静力平衡
Sz
dP = ρg∫ (h1 − h2 )dSz 阿基米德定理 = −ρgV z
Sz
第二章 流体静力学
§1-3 标准大气
§1-3 标准大气
地球大气层的结构
地球大气层厚度约为2000~3000km。分为几层: 对流层:平均11km,空气质量 约占3/4,温度随高度而降低, 各种气象变化。 平流层:对流层之上到32km, 空气质量约占1/4,空气水平流 动,20km以下为同温层。 中间层:平流层之上到80km, 空气质量约占1/3000,温度随高 度先升后降。
§1-2 重力场中不可压缩流体的静力平衡
重力场中静止液体对柱面的作用力
P = p0Sz + ρgV z
结论: p0Sz为压力p0在Sz上的作用力, 作用线通过Sz的形心; ρgV为体积V中液体的重力,作 用线通过其重心。
P = P i + Pk x z
§1-2 重力场中不可压缩流体的静力平衡
浮力问题
第二章 流体静力学
工程流体力学课件第二章 流体静力学1

fx
1
p x
0
乘以dx
1 p
f y y 0
乘以dy
1 p
fz z 0
乘以dz
1 p
f xdx
dx x
0
1 p
f ydy y dy 0
1 p
fzdz z dz 0
❖三式相加,整理
( f xdx
f ydy
fzdz)
p dx x
p dy y
p dz z
39
(
f xdx
❖ 适用范围: 静止状态
0
0
实际流体、理想流体都是适用的。
2021/3/12
2
3
在什么情况下有惯性力? 惯性坐标系:将坐标系建立在静止或匀速直线运动的
物体上 非惯性坐标系:将坐标系建立在有加速度运动的物体上 结论:
在惯性坐标系内运动的物体不考虑惯性力 在非惯性坐标系内加速运动的物体考虑惯性力
1 6
dxdydzf x
0
15
静压强两个特征(证明续)
❖ 化简得
px
pn
1 3
f xdx
0
❖ 由于等式左侧第三项为无穷小,可以略去,故得
❖ 同理可得
px pn py pn pz pn
❖ 所以
px py pz pn
❖ 结论 n的方向可以任意选择,从而证明了在静止流体 中任一点上来自各个方向的流体静压强都相等。
❖ 将质量力和表面力代入上式,则
p
1 2
p dx dydz
x
p
1 2
p dx dydz x
f x dxdydz
0
❖ 整理上式,并把各项都除以ρdxdydz,则得
工程流体力学第2章流体静力学

① 沿任意方向 ② 沿外法线方向
有切向分力 流体受拉力
都将破坏流体平衡。
这与静止前提不符,故假设不成立,则原命题成立。
①
②
4
第2章 流体静力学
特性二、静止流体中任何一点上各个方向的静压力大小相等,与作用面方位无关。
证明:采用微元体分析法 ① 取微单元体
在静止流体中,在O点附近取出各边长分别 为dx、dy、dz的微小四面体OABC。相应坐标 轴为x、y、z。
第2章 流体静力学
流体静力学:研究流体在静止状态下的平衡规律及其应用。 静止:流体质点相对于参考系没有运动,质点之间也没有相对运动。 静止状态包括两种情况: 1、绝对静止:流体整体对地球没有相对运动。
2、相对静止:流体整体对地球有运动,但流体各质点之间没有相对运动。
举例:
绝对静止
等加速水平直线运动 等角速定轴转动
2
第2章 流体静力学
§2.1 流体静压力及其特性
1、静压力的概念
(1)静压力:静止流体作用在单位面积上的压力,称为静压力,或静压强。记作“p”
一点的静压力表示方法:
设静止流体中某一点m,围绕该点取一微小作用面积A,其上压力为P,则: 平均静压力: p P
A
m点的静压力:p lim P
单位:
A0 A
m
国际单位:Pa
物理单位:dyn/cm2
工程单位:kgf/m2
混合单位:1大气压(工程大气压) = 1kgf/cm2
(2)总压力:作用在某一面积上的总静压力,称为总压力。记作“P”
单位:N
3
第2章 流体静力学
2、静压力的两个重要特性
特性一、静压力方向永远沿着作用面内法线方向。
化工原理(南京理工大学)01流体流动(1)_流体静力学

讨论:
a. 当将U形管一端与被测点连接、另一端与大 气相通时,可测得流体的表压或真空度;
p1
p1
pa
pa
表压
真空度
南京理工大学化工学院化学工程系
b. 指示液的选取: 指示液与被测流体不互溶,不发生化 学反应;
其密度要大于被测流体密度。
应根据被测流体的种类及压差的大小选
择指示液。
南京理工大学化工学院化学工程系
南京理工大学化工学院化学工程系
1.1.1 密度
一、定义 单位体积流体的质量,称为流体的密度。
m V
kg/m3
(1)
二、单组分流体密度
f ( p, T )
南京理工大学化工学院化学工程系
液体 密度仅随温度变化(极高压力除外),其 变化关系可从手册中查得。 气体 当压力不太高、温度不太低时,可按理想 气体状态方程计算:
质量守恒:
混合前后流体的总质量相等。
南京理工大学化工学院化学工程系
已知各组分体积分率
m 1 xV1 2 xV 2 n xVn (3)
xV1 , xV 2 , n xVn
——各组分的体积分率。
南京理工大学化工学院化学工程系
已知各组分质量分率
1 xw1 xw 2 x wn
p11
2p
2
m
b
R a a’
南京理工大学化工学院化学工程系
所以 整理得
p1 B g(m R) p2 B gm A gR
p1 p2 ( A B ) gR
若被测流体是气体, B A,则有
p1 p2 Rg A
南京理工大学化工学院化学工程系
工程流体力学第二章 流体静力学

只有重力作用下的等压面应满足的条件:
1.静止; 2.连通; 3.连通的介质为同一均质流体; 4.质量力仅有重力; 5.同一水平面。
提问:如图所示,哪个断面为等压面? 您的答案是: C-C 断面 B-B 断面
第三节 重力作用下的流体平衡
在自然界和实际工程中,经常 遇到并要研究的流体是不可压缩的 重力液体,也就是作用在液体上的 质量力只有重力的液体。
f ds f x dx f y dy f z dz 0
f
图2-4 两个矢量的数量积
两个矢量的数量积等于零,必 须f和ds互相垂直,其夹角φ等于900。 也就是说,通过静止流体中的任一点 的等压面都垂直于该点处的质量力。 例如,当质量力只有重力时,等压面 处处与重力方向正交,是一个与地球 同心的近似球面。但是,通常我们所 研究的仅是这个球面上非常小的一部 分,所以可以看成是水平面 。
一、重力作用下的静力学基本方程 在一盛有静止液体的容器上取 直角坐标系(只画出OYZ平面,Z轴 垂直向上),如图2-5所示。
P0 P2 P1 Z1 Z2
图2-5 推导静力学基本方程式用图
这时,作用在液体上的质量力 只有重力 G=mg ,其单位质量力在各 坐 标 轴 上 的 分 力 为 fx=0 , fy=0 , fz=-g, 代入式(2-4),得 dp gdz dp 写成 dz g 0 (2-8)
或
1 p x p n f x dx 0 3
由于等式左侧第三项为无穷小, 可以略去,故得:
(2-1)
因为n的方向完全可以任意选择, 从而证明了在静止流体中任一点上来 自各个方向的流体静压强都相等。但 是,静止流体中深度不同的点处流体 的静压强是不一样的,而流体又是连 续介质,所以流体静压强仅是空间点 坐标的连续函数,即
流体力学第2章资料
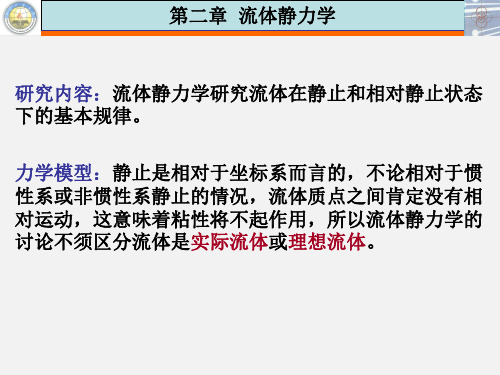
解 按题意,活塞底面上的压力可按静力平衡条件 来确定
pB
pa
油h1
水h2
4F
d 2
105 7840 0.5 9800 0.3 5788 4
0.42
1.53105
(N / m2)
第五节 压力的单位和压力的测量方法
一、 压力的单位
1. 应力单位-- Pa(=N/m2), MPa, kgf/cm2
作用在流体上的力 流体的静压力及其特性 流体的平衡微分方程式 重力场中流体静力学基本方程 压力的单位和压力的测量方法 流体的相对平衡 静止流体作用力
第一节 作用在流体上的力
作用于流体上的力按作用方式可分为表面力和质量 力两类。 一、 表面力
表面力指作用在所研究的流体表面的力。它是由所研 究流体的表面与相接触的物体的相互作用而产生的。 单位是N/m2(Pa) 。
Xdx Ydy Zdz p dx p dy p dz
x y z
dp=ρ(Xdx+Ydy+Zdz)
流体静平衡方程 式,也称压力差 公式
二、等压面
在平衡流体中,压力相等的各点所组成的面称为等 压面。
在等压面上dp=0。因流体密度ρ≠0,可得等压面微分 方程:
Xdx+Ydy+Zdz=0
(2-4)
第四节 重力场中流体静力学基本方程
在重力场中:X=0, Y=0, Z=-g
dp=ρ(Xdx+Ydy+Zdz)
dp gdz dz
dz dp 0
对于不可压缩流体,γ=常数。
z p c
z1
p1
z2
p2
c
流体静力学基 本方程式
z
p
c=z0
p0
pB
pa
油h1
水h2
4F
d 2
105 7840 0.5 9800 0.3 5788 4
0.42
1.53105
(N / m2)
第五节 压力的单位和压力的测量方法
一、 压力的单位
1. 应力单位-- Pa(=N/m2), MPa, kgf/cm2
作用在流体上的力 流体的静压力及其特性 流体的平衡微分方程式 重力场中流体静力学基本方程 压力的单位和压力的测量方法 流体的相对平衡 静止流体作用力
第一节 作用在流体上的力
作用于流体上的力按作用方式可分为表面力和质量 力两类。 一、 表面力
表面力指作用在所研究的流体表面的力。它是由所研 究流体的表面与相接触的物体的相互作用而产生的。 单位是N/m2(Pa) 。
Xdx Ydy Zdz p dx p dy p dz
x y z
dp=ρ(Xdx+Ydy+Zdz)
流体静平衡方程 式,也称压力差 公式
二、等压面
在平衡流体中,压力相等的各点所组成的面称为等 压面。
在等压面上dp=0。因流体密度ρ≠0,可得等压面微分 方程:
Xdx+Ydy+Zdz=0
(2-4)
第四节 重力场中流体静力学基本方程
在重力场中:X=0, Y=0, Z=-g
dp=ρ(Xdx+Ydy+Zdz)
dp gdz dz
dz dp 0
对于不可压缩流体,γ=常数。
z p c
z1
p1
z2
p2
c
流体静力学基 本方程式
z
p
c=z0
p0
工程流体力学第二章

pxdydz pnds • sin dz 0
p y dxdz
pnds
•
cos
dz
1 2
dxdydz
g
0
所以:
px pn 0
故
py
pn
1 2
dyg
0
y b
pxdy
o
px pn py pn
pnds
G x a
p y dx
得证
微元体分析法的步骤: 1 取合适的微元体 2 受力分析 3 建立方程
F pcg A ghc A
y D
y C
J cx yA
c
常见几何形状的惯性矩(表2-2)
矩形 圆型
c
l
J cx
1 12
bl 3
b
cR
J cx
1 R4
4
¼圆
xc c yc
xc
yc
4R
3
J cx
(1 4
16
9 2
R4
) 4
例2-5 设矩形闸门的宽为6米,长10米,铰链到低水面的 距离为4米。按图示方式打开该闸门,求所需要的力 R。
z
p0
o
B
z
p0
o
B
R
(a)
pg
2
2r2
R
(b)
pg
2
2(r2
R2)
例2-4 设内装水银的U型管绕过D点的铅垂线等角速度旋 转,求旋转角速度和D点的压强。设水银密度为
13600kg/m3 且不计液面变化带来的影响。
ω
关键:
10cm 5cm
1 写出所有的体积力
20c m
z
12cm 2 根据压力差公式写出压强
工程流体力学 第二章 流体静力学201012

Y = ω 2 r sin α = ω 2 y Z = −g
z ω
1.等压面方程 1.等压面方程
dp = ω 2 xdx + ω 2 ydy − gdz = 0
⇓ 积分
ω 2 x2
2 +
p0
o
m
h z
zs y
ω 2 y2
2
− gz = C
ω 2r 2
2
− gz = C
等压面是一簇绕z轴的旋转抛物面。 等压面是一簇绕z轴的旋转抛物面。 自由液面: 自由液面: x=0 z=0 C=0
z g p0
2
⇒
dp = ρ(Xdx +Ydy + Zdz)
dp = −ρgdz
p2
p1
1
⇒
dp dz + =0 ρg
z1
z2
积分得: 积分得:
p z+ =C ρg
o
p p z1 + 1 = z2 + 2 ρg ρg
基准面
x
2.物理意义 2.物理意义
z+ p =C ρg
总 势 能
3.几何意义 3.几何意义
o y
αr
y x ω2y ω2r
⇓
zs =
ω 2r 2
2g
x
ω2x
二、等角速旋转容器中液体的相对平衡
2. 静压强分布规律
dp = ρ (ω 2 xdx + ω 2 ydy − gdz )
z ω
⇓ 积分
p = ρ(
ω 2x2
2
+
ω 2 y2
2
− gz ) + C
p = ρg (
ω 2r 2
z ω
1.等压面方程 1.等压面方程
dp = ω 2 xdx + ω 2 ydy − gdz = 0
⇓ 积分
ω 2 x2
2 +
p0
o
m
h z
zs y
ω 2 y2
2
− gz = C
ω 2r 2
2
− gz = C
等压面是一簇绕z轴的旋转抛物面。 等压面是一簇绕z轴的旋转抛物面。 自由液面: 自由液面: x=0 z=0 C=0
z g p0
2
⇒
dp = ρ(Xdx +Ydy + Zdz)
dp = −ρgdz
p2
p1
1
⇒
dp dz + =0 ρg
z1
z2
积分得: 积分得:
p z+ =C ρg
o
p p z1 + 1 = z2 + 2 ρg ρg
基准面
x
2.物理意义 2.物理意义
z+ p =C ρg
总 势 能
3.几何意义 3.几何意义
o y
αr
y x ω2y ω2r
⇓
zs =
ω 2r 2
2g
x
ω2x
二、等角速旋转容器中液体的相对平衡
2. 静压强分布规律
dp = ρ (ω 2 xdx + ω 2 ydy − gdz )
z ω
⇓ 积分
p = ρ(
ω 2x2
2
+
ω 2 y2
2
− gz ) + C
p = ρg (
ω 2r 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
p1 pA 1 gh1 p4 p3 3 gh4 p2 p1 3 gh2 pB p4 1 g h5 h4 p3 p2 2 gh3
逐一代入,得
pB pA 1 gh1 3 gh2 2 gh3
dp f x dx f y dy f z dz dp dz 0 dp gdz g 流体静力学 p 设不可压缩,积分 基本方程 z C g
fx f y 0 f z g
对图中1、2点
p1 p2 z1 z2 g g
适用条件:同一容器、同种不可 压缩重力流体。 §2-3
p 0
欧拉平衡 微分方程
§2-2 欧拉平衡微分方程
等压面
取一微元矢量
dl dx, dy, dz
与欧拉平衡微分方程点乘
dp
p p p f x dx f y dy f z dz dx dy dz x y z
dp f x dx f y dy f z dz
绝对压强 以完全真空为基准计量的压强。 p pa gh 计示压强 以大气压为基准计量的压强,也称为 相对压强或表压强。 pe p pa gh 真空 绝对压强低于大气压时,负的计示压强。
pv pe pa p
§2-3 重力场中流体的平衡
压强的单位
单位面积上的力:
重力场中流体的平衡
流体静力学基本方程
物理意义
p z C g
单位重量流体 的压强势能 单位重量流体 的总势能
单位重量流体 的重力势能
不可压缩的重力流体处于平衡状态时,其中任 意点上的单位重量流体的总势能为常数。
§2-3 重力场中流体的平衡
流体静力学基本方程
几何意义
位置水头
p z C g
标准大气
T0 288.15K p0 101325Pa
0.0065K/m
§2-3 重力场中流体的平衡
可压缩流体中压强的变化
对于可压缩流体,密度随压强和温度变化。 p 完全气体的状态方程为
考虑大气层中对流层和同温层的情况。 T T1 标准大气同温层(11-20km): 代入压强差公式 dp gdz
等压强 压强差 压强差
pA 1 gh pB 1 gh2 2 gh 1
p pA pB 2 1 gh
§2-3 重力场中流体的平衡
压强的测量
测压计分类 液柱测压计(直接测量,测量量程较小):
倾斜式微压计:较大的容器和带刻度的倾斜玻璃 管,内有工作液体(蒸馏水或酒精)。测量精度 较高,常用来测量微小压强或压强差。
表明不可压缩的重力流体处于平衡状态时: z p 静压强随深度线性分布; H h 静压强包括自由表面压强 a 和液重产生的压强; g z 自由表面的压强以相同大 o 帕斯卡原理 小传到液体内部任意点。
0
p
§2-3 重力场中流体的平衡
可压缩流体中压强的变化
对于可压缩流体,密度随压强和温度变化。 p 完全气体的状态方程为
1 p fx 0 x 1 p fy 0 y 1 p fz 0 z f 1
p 0
欧拉平衡 微分方程
§2-2 欧拉平衡微分方程
等压面
取一微元矢量
dl dx, dy, dz
与欧拉平衡微分方程点乘
p p p f x dx f y dy f z dz dx dy dz x y z 1 p fx 0 x 1 p fy 0 y 1 p fz 0 z f 1
计示压强 等压强
p 1 gh 2 gh2 pa 1
p pa 绝对压强
真空
p pa 2 gh2 1 gh1
pv 2 gh2 1 gh 1
§2-3 重力场中流体的平衡
压强的测量
测压计分类 液柱测压计(直接测量,测量量程较小):
U形管测压计:还可测量压强差。
1 p fy 0 y 1 p fz 0 z
欧拉平衡微分方程
流体平衡的条件
结论: 质量力有势是不可压缩流体静止的必要条件; 对于不可压缩流体,等压面与等势面重合。
§2-2 欧拉平衡微分方程
第二章 流体静力学
第三节 重力场中流体的平衡
流体静力学基本方程
质量力仅为重力 由压强差公式
fx x fy y fz z
fx
x
0
由压强差公式 dp f x dx f y dy f z dz
x dx y dy z dz d §2-2
C
f px pn B n
h→0: px py pz pn 0 分别投影到x、y、z轴上
pn p x p y pz
静压强只是空间坐标的函数
p px, y, z
第二章 流体静力学
第二节 欧拉平衡微分方程
流体平衡微分方程
在静止流体中取一微元六面体,各面平行于坐 标平面。 微元体边长:dx dy dz 中心点坐标:a(x, y, z) 中心点压强:p 单位质量力:fx fy fz 中心点压强按泰勒级数展开 可得各面中心压强。
§2-1 流体静压强
证明:静压强大小与作用面方向无关
任取微元四面体MABC,作用有表面力和质量 力f。 斜面ABC外法线n的方向余弦为
cosn, x cosn, y cosn, z
z
py M A o y x §2-1 流体静压强 pz
C
f px pn B n
§2-3 重力场中流体的平衡
压强的测量
测压计分类 液柱测压计(直接测量,测量量程较小):
测压管:玻璃管,直接连接到测量压强的容器上。
绝对压强
p pa
p pa gh
pe gh
计示压强 绝对压强
真空
p pa
p pa gh
pv gh
§2-3 重力场中流体的平衡
压强的测量
压强水头 总水头
静水头线 计示静水头线
不可压缩的重力流体 处于平衡状态时,静 水头线或计示静水头 线为平行于基准面的 水平线。
§2-3 重力场中流体的平衡
重力场中静止液体内的静压强
对淹深为h的a点和压强为p0的自由液面列静力 学基本方程
p0 p z z h g g
p p0 gh
国际单位制:N/m2(Pa) bar
工程单位制:kgf/cm2
液柱高:mH2O mmHg 大气压:工程大气压 标准大气压
§2-3 重力场中流体的平衡
压强的测量
测压计分类 金属测压计(间接测量,可测量较高压强):
波登管测压计:利用椭圆截面的金属弯管受压变 形原理制作。 膜片式测压计:利用膜片受压变形原理制作。
x
p
p dx x 2
z
p
fx
a dx
o
p dx x 2
y
§2-2 欧拉平衡微分方程
流体平衡微分方程
微元体在静压强和质量力的作用下平衡。 微元体上的力在x方向的平衡方程:
p dx p dx p dydz p dydz f x dxdydz 0 x 2 x 2 p dx
第二章 流体静力学
第一节 流体静压强
流体静压强
流体平衡,则作用在流体上的应力只有法向应 力,而没有切向应力。流体作用面上负的法向 应力就是静压强。
dF pn pnn dA
§2-1 流体静压强
流体静压强的特性
特性一 流体静压强的作用方向沿作用面的内 法线方向。
特性二 流体静压强的大小与作用面在空间的 方位无关,只是坐标的函数。
设ABC面积为dS,则
ABC面 MBC面 MCA面 MAB面 dS αdS βdS γdS
证明:静压强大小与作用面方向无关
流体微元静力平衡 fd pxdS py dS pzdS pn dS 0
1 d hdS 3
z
py M A o y x §2-1 流体静压强 pz
1 p fx 0 x 同理: f y 1 p 0 y 1 p fz 0 z
p
化简:
f
1
x 2
p 0
z
p
fx
a dx
欧拉平衡 微分方程 x
o
p dx x 2
y
§2-2 欧拉平衡微分方程
流体平衡微分方程
物理意义:静止流体内质量力与静压强相平衡。 适用范围:理想流体 黏性流体 可压缩流体 不可压缩流体 静止 相对静止
压强差公式
重要性质:静止流体中,质量力垂直于等压面。
f 1
p 0
§2-2 欧拉平衡微分方程
流体平衡的条件
由欧拉平衡微分方程,对坐标交错求导,可得
f x f y y x f y f z z y f z f x x z
(不可压缩)
根据场论,此式表明质量力场是有势场,存在 势函数π(x, y, z),且 1 p
p2 p1
h1 l sin
h2 l A1 A2
h h1 h2 l sin A1 A2
p p2 p1 gh g sin A1 A2 l kl
§2-3 重力场中流体的平衡
例2-3
活塞直径d=35mm,重15N,油密度ρ1=920kg/m3 ,水 银密度ρ2=13600kg/m3,h=0.7m,求Δh。 解:活塞重量造成的其底面压强为
p g z - z1 ln p1 RT1 dp gdz p RT1
标准大气
z1 11000m T1 216.7K p1 22638Pa
逐一代入,得
pB pA 1 gh1 3 gh2 2 gh3
dp f x dx f y dy f z dz dp dz 0 dp gdz g 流体静力学 p 设不可压缩,积分 基本方程 z C g
fx f y 0 f z g
对图中1、2点
p1 p2 z1 z2 g g
适用条件:同一容器、同种不可 压缩重力流体。 §2-3
p 0
欧拉平衡 微分方程
§2-2 欧拉平衡微分方程
等压面
取一微元矢量
dl dx, dy, dz
与欧拉平衡微分方程点乘
dp
p p p f x dx f y dy f z dz dx dy dz x y z
dp f x dx f y dy f z dz
绝对压强 以完全真空为基准计量的压强。 p pa gh 计示压强 以大气压为基准计量的压强,也称为 相对压强或表压强。 pe p pa gh 真空 绝对压强低于大气压时,负的计示压强。
pv pe pa p
§2-3 重力场中流体的平衡
压强的单位
单位面积上的力:
重力场中流体的平衡
流体静力学基本方程
物理意义
p z C g
单位重量流体 的压强势能 单位重量流体 的总势能
单位重量流体 的重力势能
不可压缩的重力流体处于平衡状态时,其中任 意点上的单位重量流体的总势能为常数。
§2-3 重力场中流体的平衡
流体静力学基本方程
几何意义
位置水头
p z C g
标准大气
T0 288.15K p0 101325Pa
0.0065K/m
§2-3 重力场中流体的平衡
可压缩流体中压强的变化
对于可压缩流体,密度随压强和温度变化。 p 完全气体的状态方程为
考虑大气层中对流层和同温层的情况。 T T1 标准大气同温层(11-20km): 代入压强差公式 dp gdz
等压强 压强差 压强差
pA 1 gh pB 1 gh2 2 gh 1
p pA pB 2 1 gh
§2-3 重力场中流体的平衡
压强的测量
测压计分类 液柱测压计(直接测量,测量量程较小):
倾斜式微压计:较大的容器和带刻度的倾斜玻璃 管,内有工作液体(蒸馏水或酒精)。测量精度 较高,常用来测量微小压强或压强差。
表明不可压缩的重力流体处于平衡状态时: z p 静压强随深度线性分布; H h 静压强包括自由表面压强 a 和液重产生的压强; g z 自由表面的压强以相同大 o 帕斯卡原理 小传到液体内部任意点。
0
p
§2-3 重力场中流体的平衡
可压缩流体中压强的变化
对于可压缩流体,密度随压强和温度变化。 p 完全气体的状态方程为
1 p fx 0 x 1 p fy 0 y 1 p fz 0 z f 1
p 0
欧拉平衡 微分方程
§2-2 欧拉平衡微分方程
等压面
取一微元矢量
dl dx, dy, dz
与欧拉平衡微分方程点乘
p p p f x dx f y dy f z dz dx dy dz x y z 1 p fx 0 x 1 p fy 0 y 1 p fz 0 z f 1
计示压强 等压强
p 1 gh 2 gh2 pa 1
p pa 绝对压强
真空
p pa 2 gh2 1 gh1
pv 2 gh2 1 gh 1
§2-3 重力场中流体的平衡
压强的测量
测压计分类 液柱测压计(直接测量,测量量程较小):
U形管测压计:还可测量压强差。
1 p fy 0 y 1 p fz 0 z
欧拉平衡微分方程
流体平衡的条件
结论: 质量力有势是不可压缩流体静止的必要条件; 对于不可压缩流体,等压面与等势面重合。
§2-2 欧拉平衡微分方程
第二章 流体静力学
第三节 重力场中流体的平衡
流体静力学基本方程
质量力仅为重力 由压强差公式
fx x fy y fz z
fx
x
0
由压强差公式 dp f x dx f y dy f z dz
x dx y dy z dz d §2-2
C
f px pn B n
h→0: px py pz pn 0 分别投影到x、y、z轴上
pn p x p y pz
静压强只是空间坐标的函数
p px, y, z
第二章 流体静力学
第二节 欧拉平衡微分方程
流体平衡微分方程
在静止流体中取一微元六面体,各面平行于坐 标平面。 微元体边长:dx dy dz 中心点坐标:a(x, y, z) 中心点压强:p 单位质量力:fx fy fz 中心点压强按泰勒级数展开 可得各面中心压强。
§2-1 流体静压强
证明:静压强大小与作用面方向无关
任取微元四面体MABC,作用有表面力和质量 力f。 斜面ABC外法线n的方向余弦为
cosn, x cosn, y cosn, z
z
py M A o y x §2-1 流体静压强 pz
C
f px pn B n
§2-3 重力场中流体的平衡
压强的测量
测压计分类 液柱测压计(直接测量,测量量程较小):
测压管:玻璃管,直接连接到测量压强的容器上。
绝对压强
p pa
p pa gh
pe gh
计示压强 绝对压强
真空
p pa
p pa gh
pv gh
§2-3 重力场中流体的平衡
压强的测量
压强水头 总水头
静水头线 计示静水头线
不可压缩的重力流体 处于平衡状态时,静 水头线或计示静水头 线为平行于基准面的 水平线。
§2-3 重力场中流体的平衡
重力场中静止液体内的静压强
对淹深为h的a点和压强为p0的自由液面列静力 学基本方程
p0 p z z h g g
p p0 gh
国际单位制:N/m2(Pa) bar
工程单位制:kgf/cm2
液柱高:mH2O mmHg 大气压:工程大气压 标准大气压
§2-3 重力场中流体的平衡
压强的测量
测压计分类 金属测压计(间接测量,可测量较高压强):
波登管测压计:利用椭圆截面的金属弯管受压变 形原理制作。 膜片式测压计:利用膜片受压变形原理制作。
x
p
p dx x 2
z
p
fx
a dx
o
p dx x 2
y
§2-2 欧拉平衡微分方程
流体平衡微分方程
微元体在静压强和质量力的作用下平衡。 微元体上的力在x方向的平衡方程:
p dx p dx p dydz p dydz f x dxdydz 0 x 2 x 2 p dx
第二章 流体静力学
第一节 流体静压强
流体静压强
流体平衡,则作用在流体上的应力只有法向应 力,而没有切向应力。流体作用面上负的法向 应力就是静压强。
dF pn pnn dA
§2-1 流体静压强
流体静压强的特性
特性一 流体静压强的作用方向沿作用面的内 法线方向。
特性二 流体静压强的大小与作用面在空间的 方位无关,只是坐标的函数。
设ABC面积为dS,则
ABC面 MBC面 MCA面 MAB面 dS αdS βdS γdS
证明:静压强大小与作用面方向无关
流体微元静力平衡 fd pxdS py dS pzdS pn dS 0
1 d hdS 3
z
py M A o y x §2-1 流体静压强 pz
1 p fx 0 x 同理: f y 1 p 0 y 1 p fz 0 z
p
化简:
f
1
x 2
p 0
z
p
fx
a dx
欧拉平衡 微分方程 x
o
p dx x 2
y
§2-2 欧拉平衡微分方程
流体平衡微分方程
物理意义:静止流体内质量力与静压强相平衡。 适用范围:理想流体 黏性流体 可压缩流体 不可压缩流体 静止 相对静止
压强差公式
重要性质:静止流体中,质量力垂直于等压面。
f 1
p 0
§2-2 欧拉平衡微分方程
流体平衡的条件
由欧拉平衡微分方程,对坐标交错求导,可得
f x f y y x f y f z z y f z f x x z
(不可压缩)
根据场论,此式表明质量力场是有势场,存在 势函数π(x, y, z),且 1 p
p2 p1
h1 l sin
h2 l A1 A2
h h1 h2 l sin A1 A2
p p2 p1 gh g sin A1 A2 l kl
§2-3 重力场中流体的平衡
例2-3
活塞直径d=35mm,重15N,油密度ρ1=920kg/m3 ,水 银密度ρ2=13600kg/m3,h=0.7m,求Δh。 解:活塞重量造成的其底面压强为
p g z - z1 ln p1 RT1 dp gdz p RT1
标准大气
z1 11000m T1 216.7K p1 22638Pa
