母函数法求解数列
母函数(生成函数)

母函数(⽣成函数)介绍母函数是组合数学中相当重要的⼀个知识点,可以⽤来解决⼀些排列组合问题,还有所有的常系数线性齐次递推问题。
如果系数不是常数,需要根据具体情况进⾏处理。
具体的内容可以看组合数学相关书籍或者,由于⼤佬总是想当然地把别⼈当成⼤佬,⼀些内容对(像我这种)蒟蒻来说不是很友好,在这⾥讲⼀下母函数的基础。
(研究母函数时,钦定|x|<1),这样,由等⽐数列求和公式有:11−x=∑∞i=0x i=1+x+ (x)11−kx=∑∞i=0k i x i=1+kx+...+k∞x∞1.普通型母函数。
假设有⼀个数列a,那么它的母函数其实就是⼀个关于x的多项式,x n的系数为a n,对于已知通项的数列,其母函数可以直接写出来。
⽽对于未知的数列,主要分为两类:递推型和组合型。
递推型就是利⽤错位相消,举个栗⼦:a n=3a n−1+10a n−2,a0=1,a1=2移项,得a n−3a n−1−10a n−2=0,设a n的母函数为G(x)G(x)=a0+a1x+a2x2+a3x3...−3xG(x)=−3a0x+(−3)a1x2+(−3)a2x3...−10x2G(x)=−10a0x2+(−10)a1x3三⾏相加,可以发现等式右侧除了第⼀⾏的第1,2项和第⼆⾏的第1项外全消掉了。
所以我们可以得到(1−3x−10x2)G(x)=a0+a1x−3a0x=1−x,即G(x)=1−x1−3x−10x2,⽣成函数就求出来了,那如果我们还要求an的通项呢?对于这种东西,我们可以把他化成k1x−A+k2x−B这种形式,其中A和B由分母的因式分解唯⼀确定,然后k1,k2可由待定系数法解得。
然后对于kx−A,总可以化成k′∗11−Nx,就是k′∑∞i=0N i x i,找出x k的系数就是a n,如果母函数拆开成多个该类分式的话各部分相加就好。
具体计算就不算了。
PS:⼀部分⾮齐次线性递推其实也可以这样解,⽐如a n−3a n−1−10a n−2=f(n),按照上述⽅法错项后会剩下⼀个等⽐数列和前⼏项余项。
母函数与指数型母函数

比较等式两端的常数项,可以得到恒等式:
C(m n, m) C (n, 0)C (m, 0) C (n,1)C (m,1) C(n, m)C(m, m).
又如在等式 (1 x)n C(n,0) C(n,1)x C(n, n)xn
注意到,出现1,5有两种选法,出现2,4也有两 种选法,而出现3,3只有一种选法,按加法法则, 共有2+2+1=5种不同选法。
或者,第一个骰子除了6以外都可选,有5种选法, 一旦第一个选定,第二个骰子就只有一种可能的选 法,按乘法法则有5×1=5种。
但碰到用三个或四个骰子掷出n点,上述两方法就 不胜其烦了。
a1 a3 a5 a7 0, a0 1, a2 C(8, 2) 28,
a4 C(8, 4) 70, a6 C(8, 6) 28, a8 1. 因此序列a1,a2,…,a8对应的母函数为:
A( x) 1 28x2 70x4 28x6 x8 .
类似可得女同志的允许组合数对应的母函数为
1: b0 a0 x: b1 a0 a1 x2: b2 a0 a1 a2
__+_)___x_k:_b_k _a_0 __a1__a_2 ____ak________
B( x) a0 /(1 x) a1 x /(1 x) a2 x2 /(1 x)
[a0 a1 x a2 x2 ] /(1 x) A( x) /(1 x).
中令x=1 可得 C(n, 0) C(n,1) C(n, 2) C(n, n) 2n.
两端对x求导可得:
n(1 x)n1 C(n,1) 2C(n,2)x nC(n,n)xn1,
组合数学第2章答案

组合数学第2章答案2.1 求序列{0,1,8,27,…3n …}的母函数。
解:()()++++++=++++++=nn n x n x x x x G x a x a x a x a a x G 3323322102780()46414321313=+-+--==-----n n n n n n n a a a a a n a n a左右同乘再连加:464:0464:0464:0464:4321543211123455012344=+-+-=+-+-=+-+-=+-+-----------n n n n n n n n n n n n a a a a a x a a a a a x a a a a a x a a a a a x母函数:()()42162036-+-=x x x x G2.2 已知序列()()3433{,,……()33,,n +……},求母函数。
解:1(1)nx -的第k 项为:11()k n n +-- ,对于本题,n=4, ∴母函数为:41(1)x -2.3 已知母函数G (X )=25431783x x x--+,求序列{ n a }解:G (X )=)61)(91(783x x x +-+=)61()91(x Bx A ++-从而有: ⎩⎨⎧-==⇒⎩⎨⎧=-=+4778963B A B A B A G (X )=)61(4)91(7x x +-+-G (X )=7)999x (13322 ++++x x -4))6((-6)(-6)x (13322 +-+++x xn a =7*n )6(*49n -- 2.4.已知母函数239156xx x ---,求对应的序列{}n a 。
解:母函数为239()156x G x x x -=--39(17)(18)xx x -=+- A BG(x)17x 18xA(18x)B(17x)39x=++--++=-令 A B 38A +7B =9+=⎧⎨--⎩解得:A=2 B=1所以 ii i 0i 021G(x)2*(7x)(8x)17x 18x ∞∞===+=-++-∑∑n n n a 2*(7)8=-+2.5 设n n F G 2=,其中F n 是第n 个Fibonacci 数。
《组合数学》教案 2章(母函数)《组合数学》教案 2章(母函数)
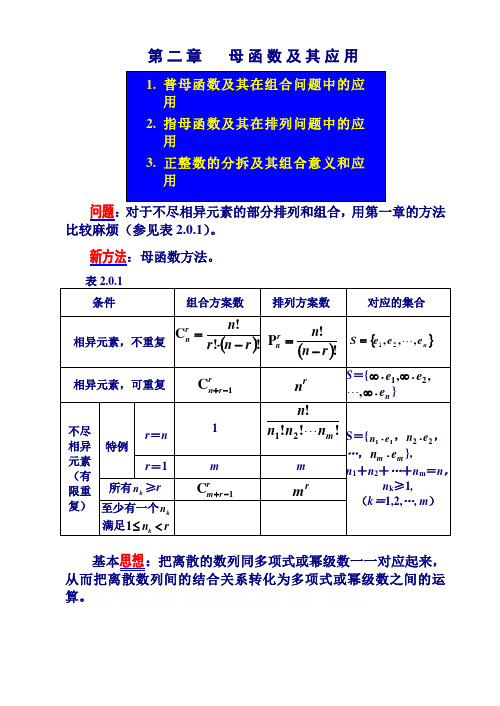
第二章母函数及其应用问题:对于不尽相异元素的部分排列和组合,用第一章的方法比较麻烦(参见表2.0.1)。
新方法:母函数方法。
基本思想:把离散的数列同多项式或幂级数一一对应起来,从而把离散数列间的结合关系转化为多项式或幂级数之间的运算。
2.1 母函数(一) 母函数 (1)定义【定义2.1.1】对于数列{}n a ,称无穷级数()∑∞=≡n n n x a x G 为该数列的(普通型)母函数,简称普母函数或母函数。
(2)例【例2.1.1】有限数列rn C (r =0, 1, 2, …, n )的普母函数是:()x G =nn n n n n x C x C x C C ++++ 2210=()nx +1【例2.1.2】无限数列{1, 1. …, 1, …}的普母函数是()x G = +++++n x x x 21=x-11(3)说明● n a 可以为有限个或无限个。
● 数列{}n a 与母函数一一对应。
{0, 1, 1, …, 1, …}↔ +++++nx x x 20=xx-1● 将母函数视为形式函数,目的是利用其有关运算性质完成计数问题,故不考虑“收敛问题”,而且始终认为它是可“逐项微分”和“逐项积分”的。
(4)常用母函数(二) 组合问题 (1)组合的母函数【定理2.1.1】组合的母函数:设{}m m e n e n e n S ⋅⋅⋅=,,,2211 ,且n 1+n 2+…+n m =n ,则S 的r 可重组合的母函数为()x G =∏∑==⎪⎪⎭⎫ ⎝⎛mi n j j i x 10=∑=n r rr x a 0其中,r 可重组合数为rx 之系数r a ,r =0, 1, 2, …, n 。
理论依据:多项式的任何一项与组合结果一一对应。
优点:● 将无重组合与重复组合统一起来处理; ● 使处理可重组合的枚举问题变得非常简单。
(2)特例【推论1】{}n e e e S ,,,21 =,则r 无重组合的母函数为G (x )= (1+x )n组合数为r x 之系数rn C 。
5.5母函数法

于是有
x1 5 x2 5 F x x1 1 x1 x 1 x2 x x
n 0
5
x x x
n n 0 1
2
5
x x
n 0 2
n
n 1 1
5x
n 1 2
5
n
xn
n 1 因此 Fn x1n 1 x2
F
n2 n2
n F x n 1 n2
F0 F1 x x Fn 1 x
n 1
x Fn 2 x n 2
2 n2
2 n F0 F1 x x Fn x F0 x Fn x n n 0 n 0 1 xF x x 2 F x
n2 n
n 1
2x
2
2
n2 n 1 x n2
ห้องสมุดไป่ตู้
2 x x an x 2 x
n 1
n 1 x
n 0
n
2 x xf x
2x2
2 (由式(1.22)) 1 x
解 f x 得
由式(1.22)知
而
2 x f x 2an x
2 n 0
n2
2an 2 x n
n2
将以上三个式子的两边分别相加并由式(5.28)有
x x f x 1 x 2 x f x n 1 a n 2 a
2
又由式(1.21)知
在上式中令 z 4 x 有
母函数详解——精选推荐

母函数详解在数学中,某个序列的母函数(Generating function,⼜称⽣成函数)是⼀种形式幂级数,其每⼀项的系数可以提供关于这个序列的信息。
使⽤母函数解决问题的⽅法称为母函数⽅法。
母函数———把组合问题的加法法则和幂级数的的乘幂的相加对应起来我们从经典的砝码的例⼦讲起题⽬:有1g 2g 3g 4g的砝码各⼀枚,能称出多少种重量?每种重量的可能组合砝码是什么穷举的话,很容易得出结果,单数时间复杂的度为n的四次⽅,较⼤,不能采取所以,我么可以采⽤⼀个类似离散数学的逻辑式⼦表⽰前两种砝码组合产⽣的情况这⾥ ||代表或 &&代表与(使⽤1g||不使⽤1g)&&(使⽤2g||不适⽤2g)=使⽤1g&&使⽤2g||不使⽤1g&&使⽤2g||使⽤1g&&不使⽤2g||不使⽤1g&&不使⽤2g思考:⼤家可以发现这个表达式和⼀种表达式很像,没错,如果把“||”看成加法,“&&”看成乘法,和多项式的乘法⼀模⼀样。
那么我们直觉的想到,有没有可能⽤多项式乘法来表⽰组合的情况呢?我们再来看题⽬,题⽬需要的是⼏种砝码组合后的重量,是⼀个加法关系,但是在上式中“&&”是⼀种类似于乘法的运算关系,这怎么办呢?有没有什么这样⼀种运算关系,以乘法的形式运算,但是结果表现出类似于加法的关系呢?正好有⼀个,那就是幂运算。
Xm 乘上Xn结果是Xm+n,他完美的符合了我们的要求。
那么以次数表⽰砝码的质量,就可以以多项式的形式表⽰砝码组合的所有⽅案。
还是以前俩个砝码为例说明。
表⽰1g砝码的两种多项式就是(x^0+x^1),表⽰2g砝码的两种多项式就是(x^0+x^2),x的0次⽅表⽰没有使⽤该砝码,当然x的0次⽅等于1,所以写成1也是对的。
注意,砝码的重量是⽤次数表⽰的,⽽不是⽤下标表⽰的 (x^0+x^1)*(x^0+x^2) =x^0*x^0+x^1*x^1+x^0*x^1+x^1*x^2 =x^0+x^1+x^2+x^3 结果很显然,有四个⽅案;0g 1g 2g 3g 再试试四个砝码加⼀起的结果 ⼀个1g 2g 3g 4g (x^0+x^1)* (x^0+x^2) * (x^0+x^3)* (x^0+x^4) =x^0 + x^1 + x^2 + 2x^3 + 2x^4 + 2x^5 + 2x^6 + 2x^7 + x^8+ x^9 + x^10 结果就是0g 1g 2g 2个3g 2个4g 2个5g 2个6g 2个7g ⼀个8g ⼀个9g ⼀个10g ⾄此也就得出了答案。
算法合集之《母函数的性质及应用》

x 取 f ( x ) e , x 0 0 ,得 e x 1 x
x 2 x3 x 4 G ( x) , 2! 3! 4!
也就是说序列 1,1,1,1, 的指数型母函数的闭形式为 e x 。 同样运用 Taylor 公式,我们可以得到: 序列 1,1,1,1,1,1, 的指数型母函数为 e x 。 序列 0,1,0,1,0,1, 的指数型母函数为
m1 学归纳法同样可以得到结果 g n Cm n1 。
1 1 1 ,之后运用数 m 1 x (1 x) m1 (1 x)
那么闭形式
1 m1 m1 m1 对应的序列为 1, Cm , Cm 1 , Cm 2 , 。 (1 x) m
1 1 , 我们可以把 x 看成一个整体后来展开, 参考 的 1 x 1 x
关键字
母函数 递推 排列组合
§1.母函数的性质
§1.1. 定义
母函数是用于对应一个无穷序列的幂级数,一般来说母函数有形式:
G ( x) g 0 g1 x g 2 x 2 g n x n
n0
我们称 G( x) 是序列 g 0 , g1 , g 2 , 的母函数,下文表示为:
(1 x) m
§1.4. 指数型母函数
有时候序列 g n 所具有的母函数的性质十分复杂, 而序列
gn 所具有的母函数的 n!
性质十分简单,那我们宁愿选择
gn 来研究,然后再乘以 n! 。 n!
我们称:
G ( x) g n
n0
xn 为序列 g 0 , g1 , g 2 , 的指数型母函数。 n!
G( x) g 0 , g1 , g 2 ,
组合数学(第二版)母函数及其应用

考虑座位号),其中,甲、乙两 班最少1张,甲班最多5张,乙班最
多6张;丙班最少2张,最多7张;丁班最少4张,最 多10张.可有多
少种不同的分配方案?
母函数及其应用
母函数及其应用
【例 2.1.5】 从n 双互相不同的鞋中取出r 只(r≤n),要求
其中没有任何两只是成对 的,共有多少种不同的取法?
母函数及其应用
(1+x)n .
【例 2.1.2】 无限数列{1,1,…,1,…}的普母函数是
母函数及其应用
说明
(1)an 的非零值可以为有限个或无限个;
(2)数列{an}与母函数一一对应,即给定数列便得知它的
母函数;反之,求得母函数则数列也随之而定;
(3)这里将母函数只看作一个形式函数,目的是利用其有
关运算性质完成计数问题, 故不考虑“收敛问题”,即始终认
红红、黄黄、蓝蓝、红黄、黄红、红蓝、蓝红、黄蓝、 蓝
黄.其它情形依此类推.
母函数及其应用
这里需要说明的是:
(1)在例2.1.3中,利用普母函数可以将组合的每一种情况
都枚举出来,但是对排列问 题,指母函数却做不到,只能对排列
进行分类枚举.正如例2.3.1这样,项ryb 的系数6说 明红、蓝、
黄球各取一个时,有6种排列方案,但每一种方案具体是什么,
(每个数字可重复出现), 要求其中3,7出现的次数为偶数,1,5,9
出现的次数不加限制.
母函数及其应用
【例 2.3.4】 把上例的条件改为要求1、3、7出现的次数
一样多,5和9出现的次数不 加限制.求这样的n 位数的个数.
解 设满足条件的数有bn 个,与例2.1.6的分配问题类似,即
将n 个不同的球放入标号 为1、3、5、7、9的5个盒子,其中
