(通用版)2018学高考数学二轮复习练酷专题高考第21题函数与导数课件文
合集下载
全国2018学高考数学第2轮复习 练酷专题 高考第21题 函数与导数 文

[思路提示] 第(2)问把函数g(x)转化为方程来判断方程解的个数,即 为函数g(x)的零点个数;若不能直接判断出零点个数的,可 构造函数F(x),通过讨论函数F(x)的单调性并结合函数零点 存在性定理确定函数g(x)的零点个数.
[障碍提醒] 3.对于函 数零点个 数的判 断,不会 转化构造 函数而无 从下手.
[障碍提醒] 3.由f(x1)=0, f(x2)=0不会转化 x1与x2的关系而导 致滞做. 4.对要证明的不 等式无思路,不 会构造变形导致 无从下手.
所以 ln x2-ln x1=a(x1-x2),………6 分 所以(x1-x2)f′(x1+x2) =(x1-x2)x1+1 x2+a=xx11-+xx22+a(x1-x2) =xx11-+xx22+lnxx21=11-+xxxx2211+lnxx21.…………8 分
[障碍提醒] 4.求最小值 时不会讨论 或求错最小 值.
若a=0,❷则 f(x)=e2x,
所以 f(x)≥0.
7分
若a>0,❷则由(1)得,
[解题关键点]
当 x=ln a 时,f(x)取得最小值,②处利用1中单
最小值为 f(ln a)=-a2ln a.
调性求解 fx≥0
从而当且仅当-a2ln a≥0, 成立得分类点 2.
高考第 21 题 函数与导数
题型一 函数单调性、极值问题——分类讨论思想 利用导数研究含参数的函数单调性、极值问题时,常用 到分类讨论思想,其分类讨论点一般步骤
[典例] (2017·全国卷Ⅰ)(本题满分 12 分)已知函数 f(x)=
ex(ex-a)-a2x. (1)讨论 f(x)的单调性; [思路提示]
所以φ(t)在[e2,+∞)上单调递增,
φt≥φe2=1+e2+2 1>1+32+2 1=65. 11分
[障碍提醒] 3.对于函 数零点个 数的判 断,不会 转化构造 函数而无 从下手.
[障碍提醒] 3.由f(x1)=0, f(x2)=0不会转化 x1与x2的关系而导 致滞做. 4.对要证明的不 等式无思路,不 会构造变形导致 无从下手.
所以 ln x2-ln x1=a(x1-x2),………6 分 所以(x1-x2)f′(x1+x2) =(x1-x2)x1+1 x2+a=xx11-+xx22+a(x1-x2) =xx11-+xx22+lnxx21=11-+xxxx2211+lnxx21.…………8 分
[障碍提醒] 4.求最小值 时不会讨论 或求错最小 值.
若a=0,❷则 f(x)=e2x,
所以 f(x)≥0.
7分
若a>0,❷则由(1)得,
[解题关键点]
当 x=ln a 时,f(x)取得最小值,②处利用1中单
最小值为 f(ln a)=-a2ln a.
调性求解 fx≥0
从而当且仅当-a2ln a≥0, 成立得分类点 2.
高考第 21 题 函数与导数
题型一 函数单调性、极值问题——分类讨论思想 利用导数研究含参数的函数单调性、极值问题时,常用 到分类讨论思想,其分类讨论点一般步骤
[典例] (2017·全国卷Ⅰ)(本题满分 12 分)已知函数 f(x)=
ex(ex-a)-a2x. (1)讨论 f(x)的单调性; [思路提示]
所以φ(t)在[e2,+∞)上单调递增,
φt≥φe2=1+e2+2 1>1+32+2 1=65. 11分
2018届高考数学二轮复习 导数与不等式及参数范围 ppt课件(全国通用)

-7-
解 (1)由题设易知 f(x)=ln x,g(x)=ln x+ ,∴g'(x)=
������
1
������-1 ������ 2
,
令g'(x)=0得x=1, 当x∈(0,1)时,g'(x)<0, 故(0,1)是g(x)的单调减区间, 当x∈(1,+∞)时,g'(x)>0, 故(1,+∞)是g(x)的单调增区间, 因此,x=1是g(x)的唯一极值点,且为极小值点,从而是最小值点, 所以最小值为g(1)=1.
-8-
(2)g
1 ������
=-ln x+x,设 h(x)=g(x)-g
1 ������
1 ������
=2ln x-x+ ,则 h'(x)=������
1
(������ -1)2 ������ 2
,
当 x=1 时,h(1)=0,即 g(x)=g
,
当x∈(0,1)∪(1,+∞)时,h'(x)<0,h'(1)=0, 因此,h(x)在(0,+∞)内单调递减,当0<x<1时,h(x)>h(1)=0,
2.4.2
导数与不等式及参数范围
-2-
求参数的取值范围(多维探究) 解题策略一 构造函数法 角度一 从条件关系式中构造函数 例1设函数f(x)=x2+ax+b,g(x)=ex(cx+d).若曲线y=f(x)和曲线y=g(x) 都过点P(0,2),且在点P处有相同的切线y=4x+2. (1)求a,b,c,d的值; (2)若x≥-2时,f(x)≤kg(x),求k的取值范围. 难点突破一(作差构造) f(x)≤kg(x)⇔kg(x)-f(x)≥0,设F(x)=kg(x)f(x)=2kex(x+1)-x2-4x-2⇒F'(x)=2kex(x+2)-2x-4=2(x+2)(kex-1)⇒令 F'(x)=0得x1=-ln k,x2=-2. 此时,类比二次函数根的分布进行分类讨论F(x)的最小值大于或等 于0时的k的范围.
函数与导数全国卷第21题ppt课件

(5 分)
采用PP管及配件:根据给水设计图配置好PP管及配件,用管件在 管材垂 直角切 断管材 ,边剪 边旋转 ,以保 证切口 面的圆 度,保 持熔接 部位干 净无污 物
若a<-2e, 则 ln(-2a)>1, 故当 x∈(-∞,1)∪(ln(-2a),+∞)时,f′(x)>0; 当 x∈(1,ln(-2a))时,f′(x)<0, 所以 f(x)在(-∞,1),(ln(-2a),+∞)上单调递增, 在(1,ln(-2a))上单调递减.
k切=f′(x0). y0=f(x0). (x0,y0)满足切线.
联立方程组求解(有时分开求解亦可)
采用PP管及配件:根据给水设计图配置好PP管及配件,用管件在 管材垂 直角切 断管材 ,边剪 边旋转 ,以保 证切口 面的圆 度,保 持熔接 部位干 净无污 物
(2)求参数的范围问题 法一:分离参数法 在确定了函数的定义域或给定的某区间的条件下,若能将参 数分离开来,即变形为 a>g(x)(或 a≥g(x),a≤g(x),a<g(x)) 等,且 g(x)在给定的区间上易于判断单调性,易求出其值域, 从而得出参数 a 的范围;若不能判断其单调性或值域,分离 即失败.
采用PP管及配件:根据给水设计图配置好PP管及配件,用管件在 管材垂 直角切 断管材 ,边剪 边旋转 ,以保 证切口 面的圆 度,保 持熔接 部位干 净无污 物
例如,本例中,第(2)问,直接证明,当 x∈(1,+∞)时,求
证 1<xln-x1<x,如下:
证明:因为
x∈(1,+∞),所以不等式
x-1 1< ln x <x
令 g(x)=x-1-xln x(x>1),
g′(x)=1-(ln x+1)=-ln x<0.
采用PP管及配件:根据给水设计图配置好PP管及配件,用管件在 管材垂 直角切 断管材 ,边剪 边旋转 ,以保 证切口 面的圆 度,保 持熔接 部位干 净无污 物
若a<-2e, 则 ln(-2a)>1, 故当 x∈(-∞,1)∪(ln(-2a),+∞)时,f′(x)>0; 当 x∈(1,ln(-2a))时,f′(x)<0, 所以 f(x)在(-∞,1),(ln(-2a),+∞)上单调递增, 在(1,ln(-2a))上单调递减.
k切=f′(x0). y0=f(x0). (x0,y0)满足切线.
联立方程组求解(有时分开求解亦可)
采用PP管及配件:根据给水设计图配置好PP管及配件,用管件在 管材垂 直角切 断管材 ,边剪 边旋转 ,以保 证切口 面的圆 度,保 持熔接 部位干 净无污 物
(2)求参数的范围问题 法一:分离参数法 在确定了函数的定义域或给定的某区间的条件下,若能将参 数分离开来,即变形为 a>g(x)(或 a≥g(x),a≤g(x),a<g(x)) 等,且 g(x)在给定的区间上易于判断单调性,易求出其值域, 从而得出参数 a 的范围;若不能判断其单调性或值域,分离 即失败.
采用PP管及配件:根据给水设计图配置好PP管及配件,用管件在 管材垂 直角切 断管材 ,边剪 边旋转 ,以保 证切口 面的圆 度,保 持熔接 部位干 净无污 物
例如,本例中,第(2)问,直接证明,当 x∈(1,+∞)时,求
证 1<xln-x1<x,如下:
证明:因为
x∈(1,+∞),所以不等式
x-1 1< ln x <x
令 g(x)=x-1-xln x(x>1),
g′(x)=1-(ln x+1)=-ln x<0.
2018届高考数学二轮复习 第一部分 层级三 30分的拉分题 压轴专题(三)第21题解答题“函数、导数与不等式”
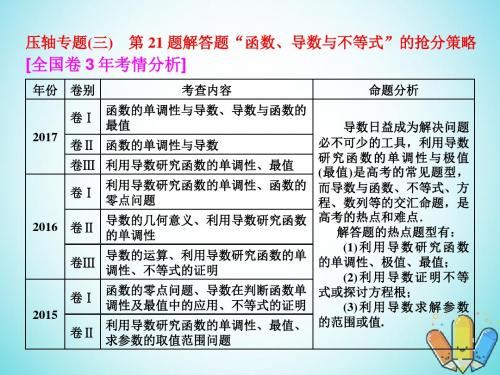
x (0, a)
a
( a,+∞)
f′(x)
-
0
+
a1-ln a
f(x)
2
所以函数 f(x)的单调递减区间是(0, a),Байду номын сангаас调递增区间是( a, +∞).
函数 f(x)在 x= a处取得极小值 f( a)=a1-2ln a,无极大值. 综上可知,当 a≤0 时,函数 f(x)的单调递增区间为(0,+∞), 函数 f(x)既无极大值也无极小值; 当 a>0 时,函数 f(x)的单调递减区间是(0, a),单调递增区间 为( a,+∞),函数 f(x)有极小值a1-2ln a,无极大值.
解答题的热点题型有: (1) 利 用 导 数 研 究 函 数
的单调性、极值、最值; (2) 利 用 导 数 证 明 不 等
式或探讨方程根; (3) 利 用 导 数 求 解 参 数
的范围或值.
[常考题点逐一突破]
利用分类讨论思想探究函数性质 [典例] (2017·张掖诊断)设函数f(x)=x22-aln x. (1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程; (2)求函数f(x)的单调区间和极值. [解] (1)当a=1时,f(x)=x22-ln x, 则f′(x)=x-1x,所以f′(1)=0,又f(1)=12, 所以曲线y=f(x)在点(1,f(1))处的切线方程为y=12.
所以 f a+b b>f(1),即1-aa++bbb+lna+b b>0,化简得a+1 b<ln a+b b, a· b
lna+b b<ab等价于 lna+b b-ab=ln1+ab-ab<0,
令 g(x)=ln(1+x)-x(x∈(0,+∞)),
2018届高考数学文二轮复习全国通用课件:专题一 函数与导数、不等式 第3讲 精品

第3讲 导数与函数的单调性、 极值、最值问题
高考定位 常以指数、对数式为载体,考查函数单调性的求 法或讨论,以及考查函数极值、最值的求法,综合考查与范 围有关的问题.
真题感悟
(2016·山东卷)设f(x)=xln x-ax2+(2a-1)x,a∈R. (1)令g(x)=f ′(x),求g(x)的单调区间; (2)已知f(x)在x=1处取得极大值.求实数a的取值范围.
[微题型2] 已知函数的单调区间求参数范围
【例 1-2】 (2016·广东湛江二模)已知函数 f(x)=x2+2aln x. (1)若函数 f(x)的图象在(2,f(2))处的切线斜率为 1,求实数 a 的值; (2)若函数 g(x)=2x+f(x)在[1,2]上是减函数,求实数 a 的取 值范围.
热点三 利用导数研究函数的最值 【例3】 (2016·武汉二模)设函数f(x)=ቤተ መጻሕፍቲ ባይዱ+(1+a)x-x2-x3,其
探究提高 已知函数的单调性,求参数的取值范围,应用条件 f ′(x)≥0(或f ′(x)≤0),x∈(a,b)恒成立,解出参数的取值范围 (一般可用不等式恒成立的理论求解),应注意参数的取值是f ′(x) 不恒等于0的参数的范围.
【训练 1】 已知函数 f(x)=(ax2-x)lnx-12ax2+x(a∈R). (1)当 a=0 时,求曲线 y=f(x)在点(e,f(e))处的切线方程(e= 2.718…); (2)求函数 f(x)的单调区间. 解 (1)当 a=0 时,f(x)=x-xln x,f′(x)=-ln x,所以 f(e)=0, f′(e)=-1.所以曲线 y=f(x)在点(e,f(e))处的切线方程为 y= -x+e,即 x+y-e=0. (2)函数 f(x)的定义域为(0,+∞), f ′(x)=(ax2-x)1x+(2ax-1)ln x-ax+1=(2ax-1)ln x.
高考定位 常以指数、对数式为载体,考查函数单调性的求 法或讨论,以及考查函数极值、最值的求法,综合考查与范 围有关的问题.
真题感悟
(2016·山东卷)设f(x)=xln x-ax2+(2a-1)x,a∈R. (1)令g(x)=f ′(x),求g(x)的单调区间; (2)已知f(x)在x=1处取得极大值.求实数a的取值范围.
[微题型2] 已知函数的单调区间求参数范围
【例 1-2】 (2016·广东湛江二模)已知函数 f(x)=x2+2aln x. (1)若函数 f(x)的图象在(2,f(2))处的切线斜率为 1,求实数 a 的值; (2)若函数 g(x)=2x+f(x)在[1,2]上是减函数,求实数 a 的取 值范围.
热点三 利用导数研究函数的最值 【例3】 (2016·武汉二模)设函数f(x)=ቤተ መጻሕፍቲ ባይዱ+(1+a)x-x2-x3,其
探究提高 已知函数的单调性,求参数的取值范围,应用条件 f ′(x)≥0(或f ′(x)≤0),x∈(a,b)恒成立,解出参数的取值范围 (一般可用不等式恒成立的理论求解),应注意参数的取值是f ′(x) 不恒等于0的参数的范围.
【训练 1】 已知函数 f(x)=(ax2-x)lnx-12ax2+x(a∈R). (1)当 a=0 时,求曲线 y=f(x)在点(e,f(e))处的切线方程(e= 2.718…); (2)求函数 f(x)的单调区间. 解 (1)当 a=0 时,f(x)=x-xln x,f′(x)=-ln x,所以 f(e)=0, f′(e)=-1.所以曲线 y=f(x)在点(e,f(e))处的切线方程为 y= -x+e,即 x+y-e=0. (2)函数 f(x)的定义域为(0,+∞), f ′(x)=(ax2-x)1x+(2ax-1)ln x-ax+1=(2ax-1)ln x.
2018届高考数学文二轮复习课件:2.2.3 导数的简单应用 精品

解析:已知函数 f(x)=ax在 x=1 处的导数为-2,则可得-xa2=-a =-2,故有 a=2,则实数 a 的值是 2,故答案为 2.
答案:2
2.(热点一)已知 f(x)为偶函数,当 x≤0 时,f(x)=e-x-1-x,则曲 线 y=f(x)在点(1,2)处的切线方程是__________.
解:(1)由 f(x)=-x+lnx,得 f′(x)=-1+1x,令 f′(x)=1,得 x =12
∴所求距离的最小值即为 P(12,f(12))到直线 x-y+3=0 的距离 d=|12--12-2ln2+3|=12(4+ln2) 2
(2)假设存在正数 a,令 F(x)=f(x)-g(x)(x>0),则 F(x)max≤0 由 F′(x)=a+1x-2a2x=0 得 x=1a ∵x>1a时,F′(x)<0,∴F(x)为减函数; 当 0<x<1a时,F′(x)>0, ∴F(x)为增函数 ∴F(x)max=F(1a) ∴ln1a≤0 即 a≥1 所以 a 的取值范围是[1,+∞)
的取值范围为21,1. ②当 x≥1 时,k≤x+1x1+lnx恒成立,令 g(x)=x+1x1+lnx,
则 g′(x)=1+lnx+1+1xxx-2 x+11+lnx=x-x2lnx. 令 h(x)=x-lnx,则 h′(x)=1-1x≥0,所以 h(x)≥h(1)=1,所以 g′(x)>0,所以 g(x)为[1,+∞)上的增函数,所以 g(x)≥g(1)=2,故 k≤2.
(2)已知函数 f(x)=3x3+2x2-1 在区间(m,0)上总有 f ′(x)≤0 成立, 则 m 的取值范围为__-__49_,__0___.
[自主解答] (1)因为函数 f(x)的导函数为 f′(x)=sinx+xcosx- sinx=xcosx,所以 k=g(t)=tcost.则函数 g(t)为奇函数,图象关于原点 对称,所以排除 A、C.又当 0<t<2π时,g(t)>0,所以排除 D,选 B.
答案:2
2.(热点一)已知 f(x)为偶函数,当 x≤0 时,f(x)=e-x-1-x,则曲 线 y=f(x)在点(1,2)处的切线方程是__________.
解:(1)由 f(x)=-x+lnx,得 f′(x)=-1+1x,令 f′(x)=1,得 x =12
∴所求距离的最小值即为 P(12,f(12))到直线 x-y+3=0 的距离 d=|12--12-2ln2+3|=12(4+ln2) 2
(2)假设存在正数 a,令 F(x)=f(x)-g(x)(x>0),则 F(x)max≤0 由 F′(x)=a+1x-2a2x=0 得 x=1a ∵x>1a时,F′(x)<0,∴F(x)为减函数; 当 0<x<1a时,F′(x)>0, ∴F(x)为增函数 ∴F(x)max=F(1a) ∴ln1a≤0 即 a≥1 所以 a 的取值范围是[1,+∞)
的取值范围为21,1. ②当 x≥1 时,k≤x+1x1+lnx恒成立,令 g(x)=x+1x1+lnx,
则 g′(x)=1+lnx+1+1xxx-2 x+11+lnx=x-x2lnx. 令 h(x)=x-lnx,则 h′(x)=1-1x≥0,所以 h(x)≥h(1)=1,所以 g′(x)>0,所以 g(x)为[1,+∞)上的增函数,所以 g(x)≥g(1)=2,故 k≤2.
(2)已知函数 f(x)=3x3+2x2-1 在区间(m,0)上总有 f ′(x)≤0 成立, 则 m 的取值范围为__-__49_,__0___.
[自主解答] (1)因为函数 f(x)的导函数为 f′(x)=sinx+xcosx- sinx=xcosx,所以 k=g(t)=tcost.则函数 g(t)为奇函数,图象关于原点 对称,所以排除 A、C.又当 0<t<2π时,g(t)>0,所以排除 D,选 B.
2018届高考数学二轮复习 函数与导数的应用专项练 ppt课件(全国通用)

在点(-1,-1)处的切线方程为( A ) B.y=2x-1 D.y=-2x-2
解析: ∵y'=
������ +2-������
(������ ++2)2
,
2
∴在点(-1,-1)处的切线方程的斜率为(-1+2)2=2.
∴切线方程为y+1=2(x+1),
即y=2x+1.
-7一、选择题 二、填空题
2.3
函数与导数的应用专项练
-2-
1.导数的几何意义 函数y=f(x)在点x0处的导数的几何意义:函数y=f(x)在点x0处的导 数是曲线y=f(x)在P(x0,f(x0))处的切线的斜率f'(x0),相应的切线方程 是y-y0=f'(x0)(x-x0). 注意:在某点处的切线只有一条,但过某点的切线不一定只有一 条. 2.常用的求导方法 (1)(xm)'=mxm-1,(sin x)'=cos x,(cos x)'=-sin x,(ex)'=ex,
2 2
C
)
解析: f'(x)=excos x-exsin x,∴k=f'(0)=e0(cos 0-sin 0)=1.
-4一、选择题 二、填空题
2.(2017全国Ⅱ,理11)若x=-2是函数f(x)=(x2+ax-1)ex-1的极值点,则f(x) 的极小值为( A ) A.-1 B.-2e-3 C.5e-3 D.1
4.函数 f(x)= 的图象大致为(
������
e ������
B )
解析: 函数 f(x)= 的定义域为 x≠0,x∈R,当 x>0 时,函数 f'(x)=
2018届高考数学理二轮复习全国通用课件 专题一 函数与导数、不等式 第5讲 精品

由零点存在定理,知存在 x0∈(2,3),使得 h(x0)=0,
即 1+ln(x0+1)=x0,
又函数 h(x)在(0,+∞)上单调递增,
所以当 x∈(0,x0)时,h(x)<h(x0)=0;
当 x∈(x0,+∞)时,h(x)>h(x0)=0. 从而当 x∈(0,x0)时,g′(x)=h(xx2)<0; 当 x∈(x0,+∞)时,g′(x)=h(xx2)>0, 所以 g(x)在(0,+∞)上的最小值为 g(x0)=(x0+1)[1+x0ln(x0+1)]=x0+1. 因此 f(x)>x+kx1-x2 在(0,+∞)上恒成立等价于 k<g(x)min=x0 +1.由 x0∈(2,3),知 x0+1∈(3,4),所以 k 的最大值为 3.
【训练1】 (2016·武汉模拟)设函数f(x)=1-x2+ln(x+1).
(1)求函数 f(x)的单调区间; (2)若不等式 f(x)>x+kx1-x2(k∈N*)在(0,+∞)上恒成立, 求 k 的最大值.
解 (1)函数 f(x)的定义域为(-1,+∞), f′(x)=x+1 1-2x,由 f′(x)>0,得-1<x< 32-1; 由 f′(x)<0,得 x> 32-1.所以函数 f(x)的单调递增区间为 -1, 32-1,单调递减区间为 32-1,+∞.
设 g(x)=ln x-mx-1x, 即∀x∈[1,+∞),g(x)≤0 恒成立, 等价于函数 g(x)在[1,+∞)上的最大值 g(x)max≤0. g′(x)=1x-m1+x12=-mx2x+2 x-m. ①若 m≤0,g′(x)>0,g(x)在[1,+∞)上单调递增, 即 g(x)≥g(1)=0,这与要求的 g(x)≤0 矛盾. ②若 m>0,方程-mx2+x-m=0 的判别式 Δ=1-4m2.
即 1+ln(x0+1)=x0,
又函数 h(x)在(0,+∞)上单调递增,
所以当 x∈(0,x0)时,h(x)<h(x0)=0;
当 x∈(x0,+∞)时,h(x)>h(x0)=0. 从而当 x∈(0,x0)时,g′(x)=h(xx2)<0; 当 x∈(x0,+∞)时,g′(x)=h(xx2)>0, 所以 g(x)在(0,+∞)上的最小值为 g(x0)=(x0+1)[1+x0ln(x0+1)]=x0+1. 因此 f(x)>x+kx1-x2 在(0,+∞)上恒成立等价于 k<g(x)min=x0 +1.由 x0∈(2,3),知 x0+1∈(3,4),所以 k 的最大值为 3.
【训练1】 (2016·武汉模拟)设函数f(x)=1-x2+ln(x+1).
(1)求函数 f(x)的单调区间; (2)若不等式 f(x)>x+kx1-x2(k∈N*)在(0,+∞)上恒成立, 求 k 的最大值.
解 (1)函数 f(x)的定义域为(-1,+∞), f′(x)=x+1 1-2x,由 f′(x)>0,得-1<x< 32-1; 由 f′(x)<0,得 x> 32-1.所以函数 f(x)的单调递增区间为 -1, 32-1,单调递减区间为 32-1,+∞.
设 g(x)=ln x-mx-1x, 即∀x∈[1,+∞),g(x)≤0 恒成立, 等价于函数 g(x)在[1,+∞)上的最大值 g(x)max≤0. g′(x)=1x-m1+x12=-mx2x+2 x-m. ①若 m≤0,g′(x)>0,g(x)在[1,+∞)上单调递增, 即 g(x)≥g(1)=0,这与要求的 g(x)≤0 矛盾. ②若 m>0,方程-mx2+x-m=0 的判别式 Δ=1-4m2.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[障碍提醒] 3.对于函 数零点个 数的判 断,不会 转化构造 函数而无 从下手.
9分
当
[障碍提醒] 4. 求最小值 时不会讨论 或求错最小 值.
a x=ln-2时,f(x)取得最小值, 3 a a 2 fln-2=a 4-ln-2.
23
最小值为
从而当且仅当 a
3 4
a - - ln ≥0, 4 2
a a 解:(1)由 f(x)=x-1+ex,得 f′(x)=1-ex. 又曲线 y=f(x)在点(1,f(1))处的切线平行于 x 轴, a 得 f′(1)=0,即 1- e=0,解得 a=e.
(2)求函数 f(x)的极值. a 解:f′(x)=1-ex,
①当 a≤0 时,f′(x)>0,f(x)为(-∞,+∞)上的增函数,所以 函数 f(x)无极值. ②当 a>0 时,令 f′(x)=0,得 ex=a,即 x=ln a.x∈(-∞, ln a)时, f′(x)<0; x∈(ln a, +∞)时, f′(x)>0, 所以 f(x)在(- ∞,ln a)上单调递减,在(ln a,+∞)上单调递增,故 f(x)在 x= ln a 处取得极小值,且极小值为 f(ln a)=ln a,无极大值. 综上,当 a≤0 时,函数 f(x)无极值; 当 a>0 时,f(x)在 x=ln a 处取得极小值 ln a,无极大值.
❶
4分
a x=ln-2.
[解题关键点] ①处分解变形后观察得分类点 1.
当
a x∈-∞,ln-2时,f′(x)<0; a x∈ln-2,+∞时,f′(x)>0. a f(x)在-∞,ln-2上单调递减,
即-2e ≤a<0 时,f(x)≥0.
11 分
3 4
综上,a 的取值范围是 -2e ,1 . 12 分
题型对点练见课堂练习第1题
[课堂练习第 1 题]
a 已知函数 f(x)=x-1+ x(a∈R,e 为自然对数的底数). e (1)若曲线 y=f(x)在点(1,f(1))处的切线平行于 x 轴,求 a 的值; (2)求函数 f(x)的极值.
[障碍提醒] 3. 不理解 f(x)≥0 是恒成立问题, 可转化为最值问 题求解.
当 故
a 在ln-2,+∞上单调递增.6
分
(2)若要 f(x)≥0,只需 f(x)min≥0 即可.
若a=0,❷则 f(x)=e2x,
[障碍提醒] 4. 求最小值 时不会讨论 或求错最小 值.
是自然对数的底数,a∈R. (1)求函数f(x)的单调区间;
[思路提示] 第(1)问求函数f(x)的导数并讨论函数的单调性;
[障碍提醒] 1.对函数 f(x)求导计算错而 导致解题错误.
[解] (1)因为f(x)=(x+a)ex,x∈R, 所以f′(x)=(x+a+1)ex.…………1分 令f′(x)=0,得x=-a-1. ……2分
当x变化时,f′(x)和f(x)的变化情况如下: x f′(x) f(x) (-∞,-a-1) - -a-1 0 极小值 (-a-1,+∞) +
故f(x)的单调递减区间为(-∞,-a-1), 单调递增区间为(-a-1,+∞). ………………4分
[障碍提醒] 2.不会利用导数求解函数的单调区间.
(2)当a<1时,试确定函数g(x)=f(x-a)-x2的零点个 数,并说明理由.
所以 f(x)≥0. 若a>0,❷则由(1)得,
7分
[解题关键点]
②处利用 1 中单 当 x=ln a 时,f(x)取得最小值, 调性求解 fx≥0 2 最小值为 f(ln a)=-a ln a. 成立得分类点 2. 2 从而当且仅当-a ln a≥0,
即 0<a≤1 时,f(x)≥0. 若a<0,❷则由(1)得,
若a=0,❶则 f(x)=e2x 在(-∞,+∞)上单调递增.2 分
[障碍提醒] 2.对含参数 的函数单调 性问题无分 类讨论意识 而导致解题 错误.
若a>0,❶则由 f′(x)=0,得 x=ln a. 当 x∈(-∞,ln a)时,f′(x)<0; 当 x∈(ln a,+∞)时,f′(x)>0. 故 f(x)在(-∞,ln a)上单调递减, 在(ln a,+∞)上单调递增. 若a<0, 则由 f′(x)=0,得
[思路提示] 第(2)问把函数g(x)转化为方程来判断方程解的个数,即 为函数g(x)的零点个数;若不能直接判断出零点个数的,可 构造函数F(x),通过讨论函数F(x)的单调性并结合函数零点 存在性定理确定函数g(x)的零点个数.
(2)结论:当a<1时,函数g(x)有且仅有 一个零点.…………………………5分
题型二
讨论函数零点的个数或已知方程根求参数问题 ——数形结合思想
研究方程根的情况,可以通过导数研究函数的单调 性、最值、变化趋势等,根据题目要求,画出函数图象的 走势规律,标明函数极最值的位置,通过数形结合的思 想去分析问题,可以使问题的求解有一个清晰、直观的整 体展现.
[典例]
(本题满分12分)已知函数f(x)=(x+a)ex,其中e
第(1)问先求 f(x)的导数 f′(x),再对 a 分区间讨论 f′(x)的符 号,从而得到 f(x)的单调性;
[障碍提醒] 1. 求错 f(x)或求出 f′(x) 后不会分解 因式而滞做.
[解] (1)函数 f(x)的定义域为(-∞,+∞),
f′(x)=2e2x-aex-a2=(2ex+a)(ex-a).1 分
高考第 21 题
题型一
函数与导数
函数单调性、极值问题——分类讨论思想
利用导数研究含参数的函数单调性、极值问题时,常用 到分类讨论思想,其分类讨论点一般步骤
[典例]
(2017· 全国卷Ⅰ)(本题满分 12 分)已知函数 f(x)= (1)讨论 f(x)的单调性;
[思路提示]
ex(ex-a)-aቤተ መጻሕፍቲ ባይዱx.
9分
当
[障碍提醒] 4. 求最小值 时不会讨论 或求错最小 值.
a x=ln-2时,f(x)取得最小值, 3 a a 2 fln-2=a 4-ln-2.
23
最小值为
从而当且仅当 a
3 4
a - - ln ≥0, 4 2
a a 解:(1)由 f(x)=x-1+ex,得 f′(x)=1-ex. 又曲线 y=f(x)在点(1,f(1))处的切线平行于 x 轴, a 得 f′(1)=0,即 1- e=0,解得 a=e.
(2)求函数 f(x)的极值. a 解:f′(x)=1-ex,
①当 a≤0 时,f′(x)>0,f(x)为(-∞,+∞)上的增函数,所以 函数 f(x)无极值. ②当 a>0 时,令 f′(x)=0,得 ex=a,即 x=ln a.x∈(-∞, ln a)时, f′(x)<0; x∈(ln a, +∞)时, f′(x)>0, 所以 f(x)在(- ∞,ln a)上单调递减,在(ln a,+∞)上单调递增,故 f(x)在 x= ln a 处取得极小值,且极小值为 f(ln a)=ln a,无极大值. 综上,当 a≤0 时,函数 f(x)无极值; 当 a>0 时,f(x)在 x=ln a 处取得极小值 ln a,无极大值.
❶
4分
a x=ln-2.
[解题关键点] ①处分解变形后观察得分类点 1.
当
a x∈-∞,ln-2时,f′(x)<0; a x∈ln-2,+∞时,f′(x)>0. a f(x)在-∞,ln-2上单调递减,
即-2e ≤a<0 时,f(x)≥0.
11 分
3 4
综上,a 的取值范围是 -2e ,1 . 12 分
题型对点练见课堂练习第1题
[课堂练习第 1 题]
a 已知函数 f(x)=x-1+ x(a∈R,e 为自然对数的底数). e (1)若曲线 y=f(x)在点(1,f(1))处的切线平行于 x 轴,求 a 的值; (2)求函数 f(x)的极值.
[障碍提醒] 3. 不理解 f(x)≥0 是恒成立问题, 可转化为最值问 题求解.
当 故
a 在ln-2,+∞上单调递增.6
分
(2)若要 f(x)≥0,只需 f(x)min≥0 即可.
若a=0,❷则 f(x)=e2x,
[障碍提醒] 4. 求最小值 时不会讨论 或求错最小 值.
是自然对数的底数,a∈R. (1)求函数f(x)的单调区间;
[思路提示] 第(1)问求函数f(x)的导数并讨论函数的单调性;
[障碍提醒] 1.对函数 f(x)求导计算错而 导致解题错误.
[解] (1)因为f(x)=(x+a)ex,x∈R, 所以f′(x)=(x+a+1)ex.…………1分 令f′(x)=0,得x=-a-1. ……2分
当x变化时,f′(x)和f(x)的变化情况如下: x f′(x) f(x) (-∞,-a-1) - -a-1 0 极小值 (-a-1,+∞) +
故f(x)的单调递减区间为(-∞,-a-1), 单调递增区间为(-a-1,+∞). ………………4分
[障碍提醒] 2.不会利用导数求解函数的单调区间.
(2)当a<1时,试确定函数g(x)=f(x-a)-x2的零点个 数,并说明理由.
所以 f(x)≥0. 若a>0,❷则由(1)得,
7分
[解题关键点]
②处利用 1 中单 当 x=ln a 时,f(x)取得最小值, 调性求解 fx≥0 2 最小值为 f(ln a)=-a ln a. 成立得分类点 2. 2 从而当且仅当-a ln a≥0,
即 0<a≤1 时,f(x)≥0. 若a<0,❷则由(1)得,
若a=0,❶则 f(x)=e2x 在(-∞,+∞)上单调递增.2 分
[障碍提醒] 2.对含参数 的函数单调 性问题无分 类讨论意识 而导致解题 错误.
若a>0,❶则由 f′(x)=0,得 x=ln a. 当 x∈(-∞,ln a)时,f′(x)<0; 当 x∈(ln a,+∞)时,f′(x)>0. 故 f(x)在(-∞,ln a)上单调递减, 在(ln a,+∞)上单调递增. 若a<0, 则由 f′(x)=0,得
[思路提示] 第(2)问把函数g(x)转化为方程来判断方程解的个数,即 为函数g(x)的零点个数;若不能直接判断出零点个数的,可 构造函数F(x),通过讨论函数F(x)的单调性并结合函数零点 存在性定理确定函数g(x)的零点个数.
(2)结论:当a<1时,函数g(x)有且仅有 一个零点.…………………………5分
题型二
讨论函数零点的个数或已知方程根求参数问题 ——数形结合思想
研究方程根的情况,可以通过导数研究函数的单调 性、最值、变化趋势等,根据题目要求,画出函数图象的 走势规律,标明函数极最值的位置,通过数形结合的思 想去分析问题,可以使问题的求解有一个清晰、直观的整 体展现.
[典例]
(本题满分12分)已知函数f(x)=(x+a)ex,其中e
第(1)问先求 f(x)的导数 f′(x),再对 a 分区间讨论 f′(x)的符 号,从而得到 f(x)的单调性;
[障碍提醒] 1. 求错 f(x)或求出 f′(x) 后不会分解 因式而滞做.
[解] (1)函数 f(x)的定义域为(-∞,+∞),
f′(x)=2e2x-aex-a2=(2ex+a)(ex-a).1 分
高考第 21 题
题型一
函数与导数
函数单调性、极值问题——分类讨论思想
利用导数研究含参数的函数单调性、极值问题时,常用 到分类讨论思想,其分类讨论点一般步骤
[典例]
(2017· 全国卷Ⅰ)(本题满分 12 分)已知函数 f(x)= (1)讨论 f(x)的单调性;
[思路提示]
ex(ex-a)-aቤተ መጻሕፍቲ ባይዱx.
