第五章 相交线和平行线复习课件
合集下载
第五章 相交线与平行线复习 课件(共19张ppt)

平行线的性质
1、两直线平行,同位角相等 2、两直线平行,内错角相等 3、两直线平行,同旁内角互补
基础演练2: 看图填空
(1)∵_____∥ _____(已知)
A
∴∠1= ∠4(
)
(2)∵_____∥ _____(已知)
1
∴∠C= ∠ADE(
)
(3)∵_____∥ _____(已知)
2 B
∴∠A+∠ABC=1800(
并用所学的知识推理它的正确性。
E
F
A
B
C
D
(1)如图,已知① AB∥CD,②BC ∥DE,则③∠B+∠D=1800
E
F
A
B
C
D
(2)如图,已知① AB∥CD,③∠B+∠D=1800 ,则②BC ∥DE
ELeabharlann FABC
D
(3)如图,已知,②BC ∥DE ,③∠B+∠D=1800 ,则①AB∥CD
课堂检测:
已知:如图,AC∥DE,AE平分∠CAB,
DF平分∠EDB,那么AE∥DF吗?请说明理由。
AE∥DF
C
理由:∵ AC∥DE(已知)
E
F ∴ ∠CAB= ∠EDB
1
3
( 两直线平行,同位角相等 )
2
4
B
A
D
∵ AE平分∠CAB, DF平∠EDB(已知)
∴ ∠2=1/2( ∠CAB),∠4=1/2( ∠EDB) ( 角平分线定义 )
致我亲爱的同学们
天空的幸福是穿一身蓝 森林的幸福是披一身绿 阳光的幸福是如钻石般耀眼 老师的幸福是因为认识了你们
愿你们努力进取,永不言败
七年级数学下册第五章相交线与平行线复习(共14张PPT)

第1页,共14页。
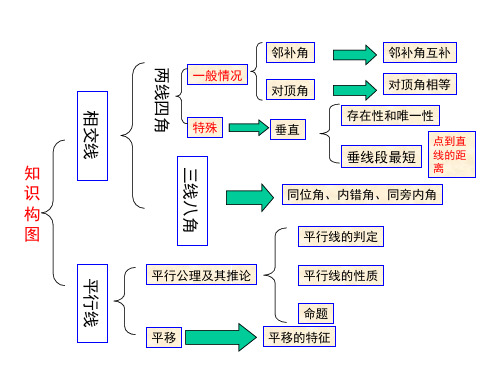
知识系统
对顶角相等
一般情况
3 12
4
两
条 直
邻补角互补
对顶角和邻补角的存在前 提是两条直线相交
线
相
交
过一点有且只有一条直线与已知直线垂直
垂
特殊情况
直
垂线段最短 点到直线的距离
第2页,共14页。
E
三线八角 A
34
21
B
65
D
C
78
F
同位角是: ∠1和∠8; ∠2和∠7;
∠3和∠6; ∠4和∠5.
第4页,共14页。
一、知识回顾
平行线的性质:
1、两直线平行,同位角相等。
2、两直线平行,内错角相等。
3、两直线平行,同旁内角互补。
第5页,共14页。
中考题我能行!
(1).
年东莞〕能由△AOB平移而得的图
形是哪个?
A
F
A
B
B
E
O
E
C
D
C
D
(2)( 年四川省广安市〕如图,AB ∥CD,
假设∠ABE=120o ∠DCE=35o,那么 ∠ BEC =___
第12页,共14页。
10.如图,已知DE、BF分别平分∠ADC 和∠ABC, ∠1 =∠2, ∠ADC= ∠ABC 说明AB∥CD的理由。
第13页,共14页。
11. 如图,直线EF过点A, D是BA延长线上的点 , 具备什么条件时,可以判定EF BC ? 为什么 ?
D
E
ቤተ መጻሕፍቲ ባይዱ
A
F
B
C
第14页,共14页。
内错角是: ∠1和∠6; ∠2和∠5.
知识系统
对顶角相等
一般情况
3 12
4
两
条 直
邻补角互补
对顶角和邻补角的存在前 提是两条直线相交
线
相
交
过一点有且只有一条直线与已知直线垂直
垂
特殊情况
直
垂线段最短 点到直线的距离
第2页,共14页。
E
三线八角 A
34
21
B
65
D
C
78
F
同位角是: ∠1和∠8; ∠2和∠7;
∠3和∠6; ∠4和∠5.
第4页,共14页。
一、知识回顾
平行线的性质:
1、两直线平行,同位角相等。
2、两直线平行,内错角相等。
3、两直线平行,同旁内角互补。
第5页,共14页。
中考题我能行!
(1).
年东莞〕能由△AOB平移而得的图
形是哪个?
A
F
A
B
B
E
O
E
C
D
C
D
(2)( 年四川省广安市〕如图,AB ∥CD,
假设∠ABE=120o ∠DCE=35o,那么 ∠ BEC =___
第12页,共14页。
10.如图,已知DE、BF分别平分∠ADC 和∠ABC, ∠1 =∠2, ∠ADC= ∠ABC 说明AB∥CD的理由。
第13页,共14页。
11. 如图,直线EF过点A, D是BA延长线上的点 , 具备什么条件时,可以判定EF BC ? 为什么 ?
D
E
ቤተ መጻሕፍቲ ባይዱ
A
F
B
C
第14页,共14页。
内错角是: ∠1和∠6; ∠2和∠5.
第五章相交线与平行线复习课件

此题需要正确地 应用、对顶角、 邻补角、垂直的 概念和性质。
例2:如图,要把水渠中的水引到水池C中,在渠岸的 什么地方开沟,水沟的长度才能最短?请画出图来, 并说明理由。
理由:垂线段最短
C
例3:你能量出C到AB的距离,B到AC的距离,A到BC 的距离吗?
F
E
C
A
D
B
平 行
1. 平行线的概念:在同一平面内,不相交的两条直线叫做平行线。 2. 两直线的位置关系: 在同一平面内,两直线的位置关系只 有两种:(1)相交; (2)平行。 3. 平行线的基本性质: (1) 平行公理(平行线的存在性和唯一性) 经过直线外一点,有且只有一条直线与已知直线平行。 (2) 推论(平行线的传递性) 如果两条直线都和第三条直线 平行,那么这两条直线也互相平行。 4.同位角、内错角、同旁内角的概念
对应点所连的线段平行且相等。
例2. 如图所示,△ABC平移到△A′B′C′的位置,则点A的 A′ 点B的对应点是____ B′ C′。 对应点是____, ,点C的对应点是____
A'B ' 线段AB的对应线段是___________ ,线段BC的对应线段是
B ' C ' ,线段AC的对应线段是_______ A ' C ' 。∠BAC的对应 ______
又因为∠BOC与∠AOD是对顶角
所以∠BOC=∠AOD=126°
垂 线
1.垂线的定义: 两条直线相交,所构成的四个角中,有一 个角是90°时,就说这两条直线互相垂直。其中一条直线 叫做另一条直线的垂线。它们的交点叫垂足。
2. 垂线的性质: (1)在同一平面内,过一点有且只有一条 直线与已知直线垂直。(2): 直线外一点与直线上各点连结 的所有线段中,垂线段最短。简称:垂线段最短。 3.点到直线的距离: 从直线外一点到这条直线的垂线段的 长度,叫做点到直线的距离。 4.垂线是直线,垂线段特指一条线段是图形,点到直线距 离是指垂线段的长度,是指一个数量,是有单位的。
人教版七年级数学下册 第五章相交线与平行线单元复习 (共44张ppt)

四、平行线的判定与性质
平行线的性质: 1.两直线平行,同位角相等 . 2.两直线平行,内错角相等. 3.两直线平行,同旁内角互补.
平
条件
行
线
的 性 两直线平 行
质
性质
线的关系
平 行
同位角相等
线
的
内错角相等
判 定 同旁内角互补
判定
角的关系
结论 同位角相 等
内错角相等
同旁内角互补
角的关系
两直线平行
线的关系
C
H
D
F
F 形模式
同位角
Z 形模式
内错角
U 形模式
同旁内角
四、平行线的判定与性质
判定两条直线是否平行的方法有:
1.同位角相等, 两直线平行. 2.内错角相等, 两直线平行. 3.同旁内角互补, 两直线平行. 4.平行于同一直线的两直线平行. 5.同一平面内, 垂直于同一直线的两直线平行. 6.平行线的定义.
C
A
1
O
B
2D E
解: ∵∠1=35°,∠2=55°(已知)
∴ ∠AOE=180°-∠1-∠2 = 180°-35°-55° =90°
∴OE⊥AB (垂直的定义)
5.如图,直线AD、BE、CF相交于O,OG⊥AD, 且∠BOC = 35°,∠FOG = 30°,求DOE的度数。
∵OG⊥AD, ∴∠GOD=90°, ∵∠BOC=35°, ∴∠FOE=∠BOC=35°, 又∵∠GOD=∠GOF+∠FOE+∠DOE=90°, ∵∠FOG=30°, ∴∠DOE=∠GOD-∠FOE-∠GOF=90°-35°-30°=25°.
2. 垂线的性质 (1)在同一平面内,过一点有且只有一条直
相交线与平行线复习ppt课件

• 解答:当两条直线被第三条直线所截,会形成各种角。其中, 位于两条直线同一侧且在被截直线的同一方的两个角叫做同位 角;位于两条直线内侧且在被截直线两侧的两个角叫做内错角 ;位于两条直线内侧且在被截直线同一方的两个角叫做同旁内 角。
2024/1/28
24
常见疑难问题解答
问题3
相交线与平行线有哪些性质?
两平行直线永不相交,且距离保 持不变。
一条直线平行移动时,其斜率不 变。
两平行直线可以确定一个平面。
2024/1/28
17
判定定理和性质定
05
理应用举例
2024/1/28
18
判定定理介绍及证明过程回顾
判定定理1
同位角相等,两直线平 行。
2024/1/28
判定定理2
内错角相等,两直线平 行。
判定定理3
2024/1/28
11
平行线性质探讨
性质1
两条平行线被第三条直线所截,同位 角相等。
性质3
两条平行线被第三条直线所截,同旁 内角互补。
性质2
两条平行线被第三条直线所截,内错 角相等。
2024/1/28
12
典型例题解析
例题1
已知直线a∥b,直线c和直线a、 b分别交于点C、D,若∠1=40°
,则∠2的度数为____。
策略3
规范书写和作图
建议
在考试中,规范书写和作图是非常重要的。要保持卷面 整洁,字迹清晰,作图准确。对于需要作辅助线的题目 ,要标明辅助线的名称和作用。
27
THANKS.
2024/1/28
28
确性。
20
综合应用举例
举例1
利用判定定理证明两直线平行 ,并应用性质定理求解角度问
2024/1/28
24
常见疑难问题解答
问题3
相交线与平行线有哪些性质?
两平行直线永不相交,且距离保 持不变。
一条直线平行移动时,其斜率不 变。
两平行直线可以确定一个平面。
2024/1/28
17
判定定理和性质定
05
理应用举例
2024/1/28
18
判定定理介绍及证明过程回顾
判定定理1
同位角相等,两直线平 行。
2024/1/28
判定定理2
内错角相等,两直线平 行。
判定定理3
2024/1/28
11
平行线性质探讨
性质1
两条平行线被第三条直线所截,同位 角相等。
性质3
两条平行线被第三条直线所截,同旁 内角互补。
性质2
两条平行线被第三条直线所截,内错 角相等。
2024/1/28
12
典型例题解析
例题1
已知直线a∥b,直线c和直线a、 b分别交于点C、D,若∠1=40°
,则∠2的度数为____。
策略3
规范书写和作图
建议
在考试中,规范书写和作图是非常重要的。要保持卷面 整洁,字迹清晰,作图准确。对于需要作辅助线的题目 ,要标明辅助线的名称和作用。
27
THANKS.
2024/1/28
28
确性。
20
综合应用举例
举例1
利用判定定理证明两直线平行 ,并应用性质定理求解角度问
人教版数学七年级下册第五章相交线与平行线 复习课件(共21张PPT)

③ ②
A
①
C
B
④
D
学习了本节课你 有哪些收获?
教学反思:
1、本节课要注重板书重要知识点,不能因为 课件上有就不写。 2、比武擂台环节要控制好时间。 3、挑战一下环节注意知识点要讲透。
人教版七年级下册第五章
相交线与平行线 (复习课)
教学目标:
经历对本章的知识回顾与思考的过程,将 本章内容条理化,系统化,梳理本章的知 识结构。 通过对知识的梳理,进一步加深对所学概 念的理解,进一步熟悉和掌握几何语言, 能用语言说明几何图形。
知识框架图:
相交线 相交线与 平行线 对顶角邻补角 直线平行的判定 区别
∠1的邻补角是 ∠2 与∠4, 对顶角是∠3
F
若∠1与∠2的关系为内错角,∠1=40°, 则∠2等于( D ) A. 40° c B. 140° C. 40°或140° a D. 不确定 1
2
b
平行的大楼顶部各有一个射灯, 当光柱相交时,如图, 360 ∠1+∠2+∠3=___° .
C
1
A
4 2
5 3
B
D
用吸管吸易拉罐中的饮料时, 如图,∠1=110°, 则∠2= 70 ° (易拉罐的上下底面互相平行)
1
2
如图,将一副三角板的直角顶点 重合,摆放在桌面上,• 若 ∠AOD=145°,则 35 度. ∠BOC=_______
1
3
2
有一条直的等宽纸带,按如图所示折叠 时,∠1=30°则∠3=______. 75 °
E F
1
C
2 3
B
4
A
如图,如果AD∥BC, 则有①∠A+∠B=180°; ②∠B+∠C=180°; ③∠C+∠D=180°,上述结论中正 确的是( D ) (A)只有①; (B)只有②; (C)只有③; (D)只有①和③
A
①
C
B
④
D
学习了本节课你 有哪些收获?
教学反思:
1、本节课要注重板书重要知识点,不能因为 课件上有就不写。 2、比武擂台环节要控制好时间。 3、挑战一下环节注意知识点要讲透。
人教版七年级下册第五章
相交线与平行线 (复习课)
教学目标:
经历对本章的知识回顾与思考的过程,将 本章内容条理化,系统化,梳理本章的知 识结构。 通过对知识的梳理,进一步加深对所学概 念的理解,进一步熟悉和掌握几何语言, 能用语言说明几何图形。
知识框架图:
相交线 相交线与 平行线 对顶角邻补角 直线平行的判定 区别
∠1的邻补角是 ∠2 与∠4, 对顶角是∠3
F
若∠1与∠2的关系为内错角,∠1=40°, 则∠2等于( D ) A. 40° c B. 140° C. 40°或140° a D. 不确定 1
2
b
平行的大楼顶部各有一个射灯, 当光柱相交时,如图, 360 ∠1+∠2+∠3=___° .
C
1
A
4 2
5 3
B
D
用吸管吸易拉罐中的饮料时, 如图,∠1=110°, 则∠2= 70 ° (易拉罐的上下底面互相平行)
1
2
如图,将一副三角板的直角顶点 重合,摆放在桌面上,• 若 ∠AOD=145°,则 35 度. ∠BOC=_______
1
3
2
有一条直的等宽纸带,按如图所示折叠 时,∠1=30°则∠3=______. 75 °
E F
1
C
2 3
B
4
A
如图,如果AD∥BC, 则有①∠A+∠B=180°; ②∠B+∠C=180°; ③∠C+∠D=180°,上述结论中正 确的是( D ) (A)只有①; (B)只有②; (C)只有③; (D)只有①和③
第五章相交线与平行线复习课课件

C
A
D
B
易错点
1、直线m外有点P,它到直线 m上点A、B、C的距离
分别是6厘米、3厘米、5厘米,则点P到直线m的距离
(
D
)
A等于6厘米.
C.等于5厘米
B.等于3厘米
D.不大于3厘米
(1)如图直线AB和CD交于点O,则图中共有 几个角,几组特殊的角?
邻补角和对顶角分别有什么性质呢?
C A 1 2 B O 4 3 D
A、75°
B、45°
C、30°
D、15°
相 交 线 知 识 结 构 图 平 行 线
两条 直线 相交
一般情况
特殊
邻补角 对顶角 垂直
邻补角互补 对顶角相等
垂线存在性和唯一性 垂线段最短
点到直线的距离
两条直线被 第三条所截 平行线的判定 平行线的性质
同位角、内错角、同旁内角
平行公理
会做+会说=真正的成功
A
B
C
D
m
垂线段最短
1、垂线段的长度表示点到直线的距离. 2、经过一点有且只有一条直线与已知直线垂直.
如图,AC⊥BC,CD ⊥AB,垂足分别是C点、 D点。
(1)点B到CD的距离是线段______ BD 的长度; CD 的长度; (2)点C到AB的距离是线段______ AC 的长度。 (3)点A到CB的距离是线段______
2、若直线AB⊥CD ,则∠AOD= 90 °
这个推理过程可以写成: ∵AB⊥CD(已知), ∵∠AOD=90° (垂直的定义) .
重点知识回顾
在河边的A处,有一个牧童在放牛,牛吃饱后要到河边饮 水,问牧童怎样把牛牵到河边,才能走最少的路?能说明 理由吗?
A
D
B
易错点
1、直线m外有点P,它到直线 m上点A、B、C的距离
分别是6厘米、3厘米、5厘米,则点P到直线m的距离
(
D
)
A等于6厘米.
C.等于5厘米
B.等于3厘米
D.不大于3厘米
(1)如图直线AB和CD交于点O,则图中共有 几个角,几组特殊的角?
邻补角和对顶角分别有什么性质呢?
C A 1 2 B O 4 3 D
A、75°
B、45°
C、30°
D、15°
相 交 线 知 识 结 构 图 平 行 线
两条 直线 相交
一般情况
特殊
邻补角 对顶角 垂直
邻补角互补 对顶角相等
垂线存在性和唯一性 垂线段最短
点到直线的距离
两条直线被 第三条所截 平行线的判定 平行线的性质
同位角、内错角、同旁内角
平行公理
会做+会说=真正的成功
A
B
C
D
m
垂线段最短
1、垂线段的长度表示点到直线的距离. 2、经过一点有且只有一条直线与已知直线垂直.
如图,AC⊥BC,CD ⊥AB,垂足分别是C点、 D点。
(1)点B到CD的距离是线段______ BD 的长度; CD 的长度; (2)点C到AB的距离是线段______ AC 的长度。 (3)点A到CB的距离是线段______
2、若直线AB⊥CD ,则∠AOD= 90 °
这个推理过程可以写成: ∵AB⊥CD(已知), ∵∠AOD=90° (垂直的定义) .
重点知识回顾
在河边的A处,有一个牧童在放牛,牛吃饱后要到河边饮 水,问牧童怎样把牛牵到河边,才能走最少的路?能说明 理由吗?
人教版七年级数学下册第五章相交线与平行线单元复习共44张课件
例2.如图AB∥CD,BE平分 A
B
∠ ABC,CE平分∠ BCD,
则∠ 1与∠ 2的关系是什么?
说明理由。
D
解:∠ 1与∠ 2互余
1
E2
C
∵AB ∥ CD(已知)
∴∠ABC+ ∠BCD=180O(两直线平行,同旁内角互补)
∵ BE平分∠ ABC,CE平分∠ BCD(已知)
∴ ∠1= 1 ∠ABC, ∠2= 1 ∠BCD(角平分线定义)
∵AB∥CD, ∴∠BMN=∠MNC, ∵MG、NH分别 平分∠BMN、∠CNM, ∴∠MNH=∠MNC, ∠NMG=∠BMN, ∴∠MNH=∠NMG, ∴NH∥MG。
延伸训练
如图所示,已知∠OEB=130°,∠FOD=25°,OF平分∠EOD.试说 明AB∥CD.
证明:∵OF平分∠EOD, ∴∠FOD= ∠EOD; ∵∠FOD=25°, ∴∠EOD=50°; ∵∠OEB=130°, ∴∠OEB+∠EOD=180°, ∴AB∥CD(同旁内角互补,两直线平行).
∴ ∠1= 12∠ABC, ∠2= 12∠BCD(角平分线定义) ∴ ∠=1+∠12(∠2=AB12∠C+A∠BBCC+D)12=∠90B°CD(等式的性质 )
∵∠ 1+ ∠ 2+ ∠ E=180° (三角形的内角和等于 180°)
∴ ∠ E=90°(等式的性质)
• 1、通过复习你有何收获? • 要判定两条直线平行,可以运用哪些方法? • 要判定两个角相等或互补,可以运用方法?
两线四角
一般情况
邻补角 对顶角
邻补角互补 对顶角相等
相交线
特殊
垂直
存在性和唯一性
点到直
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
1 B
例 直线AB与CD相交于O,AOC : AOD 2 : 3 1. 求BOD的度数。
D
A
O B C
解: ∵直线AB与直线CD相交于O
AOC BOD(对顶角相等) AOC AOD=180 (邻补角互补)
AOC : AOD 2 : 3 2 AOC 180 72 5
平移
1. 平移变换的定义: 把一个图形整体沿某一方向移动,会得到 一个新图形,这样的图形运动,叫做平移变换,简称平移。 2. 平移的特征: (1)平移不改变图形的形状和大小。 (2)新图形中的每一点,都是由原图形中的某一点移动后得到
的,这两个点是对应点,对应点连结而成的线段平行且相等。
3. 决定平移的因素是平移的方向和距离。 4. 经过平移,图形上的每一点都沿同一方向移动相同的距离。 5. 经过平移,对应角相等;对应线段平行且相等;对应点所连的线 段平行且相等。
AB ED ∴ ——∥——( 平行于同直线的两条直线互相平行。 )
例. 如图 已知:∠1+∠2=180°,求证: AB∥CD。 证明:∵∠1+∠2=180°(已知) 又∵∠1=∠3(对顶角相等) ∠2=∠4(对顶角相等) ∴∠3+∠4=180°(等量代换)
A E 1 3 4 B
C
2
D
F
(同旁内角互补,两直线平行) ∴AB//CD
C
同位角、内错角、同旁内角
同位角、内错角、同旁内角,指的是一条直线分别与两条 直线相交构成的八个角中,不共顶点的角之间的特殊位置 关系。它们与对顶角、邻补角一样,总是成对存在着的。 1、同位角的位置特征是: (1)在截线的同旁, (2)在被截两直线的同方向。 2、内错角的位置特征是: 截线 (1)在截线的两旁, C 3 E (2)在被截两直线之间。 1 7 5 3、同旁内角的位置特征是: D 4 (1)在截线的同旁, 2 B (2)在被截两直线之间。 A
(3)∠4和 ∠6是由直线 CD 、 EF 被直线 AB 所截成的 同旁内 角 ; (4)由直线AB、CD被直线EF 所截成的同位角有 ;
∠1 和∠9、 ∠4和 ∠12、∠2和 ∠10、 ∠3 和∠11 (5)∠7和 ∠12是 同旁内 角 ;
在判断两个角时一 定要先知道由哪两 条直线被哪条直线 所截呦!
解. (1)、(3)不是命题; (2)、(4)、(5)是命题; (2)、(4)都是 真命,(5)是假命题。
例.如图给出下列论断: (1)AB//CD;(2)AD//BC; (3)∠A=∠C以其中两个作为题设,另一个作为结论,用“如 果……,那么……”的形式,写出一个你认为正确的命题。
A
D
B
C
分析: 不妨选择(1)与(2)作条件,由 平行性质 “两直线平行,同旁内角 互补”可得∠A=∠C,故满足要求。
A
G
F
C
1. 命题的概念: 判断一件事情的句子,叫做命题。 命题必须是一个完整的句子; 这个句子必须对某件事情做出肯 定或者否定的判断。两者缺一不可。 2. 命题的组成: 每个命是由题设、结论两部分组成。
题设是已知事项;结论是由已知事项推出的事项。命题常写成
“如果……,那么……”的形式。或 “若……,则……”等形式。 3. 真命题和假命题: 命题是一个判断,这个判断可能是正确的, 也可以是错误的。由此可以把命题分成真命题和假命题。 真命题: 如果题设成立,那么结论一定成立的命题。
A
1 4
B 6 C
5
2
E
D
∴
∵ ∴
AF BE ——∥—— ( 同位角相等,两直线平行。 )
∠5= ∠6 (已知)
BC EF ——∥—— ( ) 内错角相等,两直线平行。
∵ ∠5+ ∠AFE=180 (已知)
AF BE ∴ ——∥—— (同旁内角互补,两直线平行。)
∵ AB ∥FC,
ED ∥FC (已知)
随堂练习
1、观察右图并填空: ∠4 (1) ∠1 与 是同位角; ∠3 (2) ∠5 与 是同旁内角; (3) ∠1 与 是内错角; ∠2 2、 指出图中的同位角、内错 角、同旁内角 同位角:∠4与∠1 内错角:∠4与∠2 同旁内角:∠3与∠1 m
2
1 4
n
3 5
a b a
n
m
l
4
2 3
b
1
平 行
例. 在以下生活现象中,不是平移现象的是: A.站在运动着的电梯上的人 B.左右推动的推拉窗扇
C.小李荡秋千运动
D.躺在火车上睡觉的旅客 分析: A、B、D属平移,在一个位置取两点连 成一条线,在另一个位置再观察这条线段,发 现是平行的,而C同样取两点连成一条线段,运 动到另一位置时,可能已不平行
A′
A
B′ C
C′
B
探究创新:
8
三线八角
F
6
被截线
如图:直线a、b被直线 l 截的8个角中
l
1
a
2
同位角: ∠1与∠5 , ∠2与∠6 , ∠3与∠7 , ∠4与∠8.
4
5 b 6 7
3
内错角: ∠3与∠5 , ∠4与∠6.
同旁内角: ∠4与∠5 , ∠3与∠6.
8
例:如图中的∠1和∠2是同位角吗? 为什么?
2 1 1
∠1和∠2不是同位角, ∠1和∠2是同位角,
A ' B ' C ' B ' A ' C ' 角是________,∠ABC的对应角是_________,∠ACB的
沿着射线AA′ A ' C ' B ' 对应角是_________。△ABC的平移方向是_____________ (或BB′,或CC′)的方向 线段AA′的长 ___________________________,平移距离是_____________ (或线段BB′的长或线段CC′的长 ________________________________。
BOD AOC 72
例2.已知直线AB、CD、EF相交于点O,DOE 900,AOE 360
求BOE、BOC的度数。
解. AOB是直线
E O A C F B D
AOE与BOE是互为邻补角 AOE BOE 1800 又 AOE 360 BOE 1800 360 1440 又 DOE 900 AOD AOE DOE 1260 又 BOC与AOD是对顶角 BOC AOD 1260
2
∵∠1和∠2无一边共线。 ∵∠1和∠2有一边共线、同向 且不共顶点。
练一练
(1)∠1和 ∠9是由直线 AB (2)∠6和 ∠12是由直线 AB 、 CD 被直线 EF 所截成的 同位 角 ; 、 EF 被直线 CD 所截成的 内错 角 ;
E
2A 1 3 4 10 9 D 12 11 F
C 5 6 8 7 B论 两直线平行
平 行 线 的 性 质
同位角相等
两直线平行
内错角相等 同旁内角互补
平行线的判定应用练习:
如图: 填空,并注明理由。 F (1)、∵ ∠1= ∠2 (已知) ∴ ——∥—— ( 内错角相等。两 ) AB ED 直线平行, ∵ ∠3= ∠4 (已知) 3
(在这六种方法中,定义一般不常用。)
b
C a
A
C F
2
E
1
3 4
B D
4. 平行线的基本性质:
(1) 平行公理(平行线的存在性和唯一性) 经过直线外一点,有且只有一 条直线与已知直线平行。 (2) 推论(平行线的传递性) 如果两条直线都和第三条直线平行,那么这 两条直线也互相平行。 平 行 线 的 判 定
1. 平行线的概念:在同一平面内,不相交的两条直线叫做平行线。 2. 两直线的位置关系: 在同一平面内,两直线的位置关系只有 两种:(1)相交; (2)平行。 3.判定两直线平行的方法有六种: (1)定义法;在同一平面内不相交的两条直线是平行线。 (2)传递法;两条直线都和第三条直线平行,这两条直线也平行。 (3)因为a⊥c, a⊥b;所以b//c (4)三种角判定(3种方法): 同位角相等,两直线平行; 内错角相等,两直线平行; 同旁内角互补,两直线平行。
例.已知∠DAC= ∠ACB, ∠D+∠DFE=1800, 求:EF//BC D F 证明: ∵ ∠DAC= ∠ACB (已知)
∴ AD// BC (内错角相等,两直线平行) ∵ ∠D+∠DFE=180°(已知)
C
B E
A ∴ AD// EF (同旁内角互补,两直线平行) ∴ EF// BC (平行于同一条直线的两条直线互相平行)
例. 如图,已知:AC∥DE,∠1=∠2,试证明 AB∥CD。 A 1 证明: ∵ AC∥DE (已知) 2 ∴ ∠ACD= ∠2 ∵ ∠1=∠2(已知) ∴ ∠1=∠ACD (等量代换) ∴AB ∥ CD(内错角相等,两直线平行)
B
D
(两直线平行,内错角相等)
C
E
例3.已知 EF⊥AB,CD⊥AB,∠EFB=∠GDC ,求证:∠AGD=∠ACB。
假命题: 如果题设成立时,不能保证结论总是成立的命题。
例. 判断下列语句,是不是命题,如果是命题,是 真命题,还是假命题?
(1)画线段AB=2cm。 (2)直角都相等。 (3)两条直线相交,有几个交点? (4)如果两个角不相等,那么这两个角不是对顶角。 (5)相等的角都是直角。 分析: 因为(1)、(3)不是对某一件事作出判断的句子,所以 (1)、(3)不是命题。
解: 选C
例. 如图所示,△ABC平移到△A′B′C′的位置,则点A的 A′ B′ C′ 对应点是____,点B的对应点是____,点C的对应点是____。
