四川大学2009-2020真题汇总
四川大学931高等代数2009年(回忆版)考研专业课真题试卷

X ′M
+ MX
= 0},∀X
∈ M 2r+1(F ), eX
=
∞ k =0
Xk k!
,
(1)求B的维数和一组基
(2)证明det(eX ) = 1
i
(3)设(,
)是F上的一个双线性型,ε = i
(0,...,1,...0),
i
=
1,
2,
..,
2r
+ 1.
M 是这个双线性型在上述基下的一个度量矩阵,证明对任意的α,β
精都教育——全国 100000 考生的选择
我们的梦想,为成就更多人的梦想
四 川 大 学 研 究 生 入 学 考 试 试 题
原版考研真题试卷
更多考研真题、笔记、模拟、题库、讲义资料就上精都考研网 /
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
证明Ax=β 在F中有解当且仅当它在K中有解
2 2 −2
3.
A
=
2 −2
−1 4
−41 大概数字是这样吧,具体忘了
(1)A在F上是否相似与对角矩阵,说明理由 (2)求A的最小多项式 (3)f (X)=X′AX,求f (X)的一个标准形
4.好像是前几年的一个类似题吧,说明 A 与 B 在任何数域上都不相似,另一问忘记了,这 些忘记的题一般都不难,掌握方法都很简单的。呵呵
有(eXα, eXβ ) = (α , β )
五、证明数域 F 上的任意一个 n 元多项式都可以表示成一次齐次多项式幂的线性组合。
f (x)使得f (A) = 0
4.设 f (x) = 3x2 + 2x +1,α1,α2,α3是f (x)的三个根,求值
四川大学数电2009级A卷试题(制造)

2、用两片集成二进制计数器74LS161和附加门电路设计一个24进制计数器,画出连线图。(74LS161为同步16进制加计数器,CO为进位输出端,其逻辑图和功能表如下)
CTPCTTCP D3D2D1D0
Q3Q2Q1Q0
0 × × × × ××××
5、图示触发器电路,初始状态为0,正确的输出波形是(B)。
6、图示各逻辑电路中,为一位二进制计数器的是(A)。
A B C D
7、由n个触发器构成的计数器,最多计数个数为(D)。
A、nB、2nC、2n-1D、2n
8、随机存储器RAM的I/O端口为输入端口时,应使片选信号 和读写信号 为(A)。
A、 B、
(F)7.要改变触发器的状态必须有CP脉冲的配合。
(F)8、即使电源关闭,移位寄存器中的内容也可以保持下去。
(F)9、ROM和RAM是结构相同但性能不同的存储器。
(F)10、555定时器是仅用于定时操作的时序逻辑功能器件。
三、电路分析(本大题4小题,共计40分)
1.(6分)写出逻辑函数 的最简与或表达式。
A、( 1101111 )2B、( 52 )8C、( 4A )16D、( 01110110 )8421BCD
2、和函数 不相等的表达式为(D)。
3、下列关于异或运算的式子中,不正确的是(B)。
A、 B、 C、 D、
4、如图所示OC门组成的电路,可等效为(C)。
A、与非门B、或非门
C、与或非门D、异或门
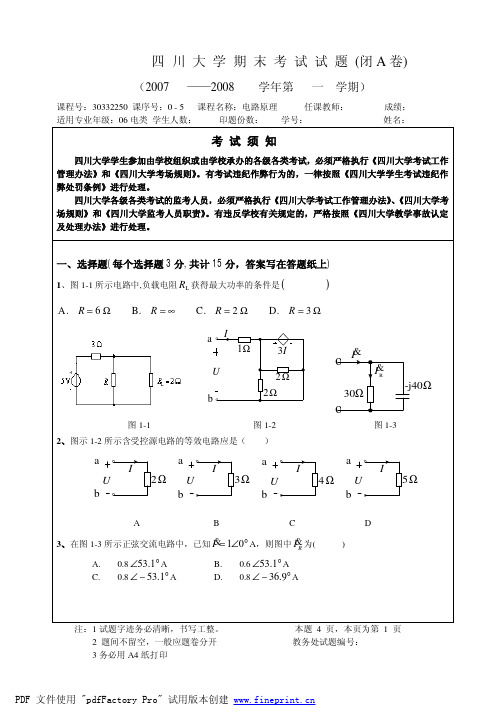
四川大学期末考试试题(A卷)(闭卷)
(2010—2011学年第一学期)
课程号:907025030课序号:课程名称:数字电子技术任课老师:成绩:
四川大学电路期末试题及答案1
+ 30°)
4 分 得:
uR 2
(t)
=
−
100 3
cos(2ω
1t
+
30°)
V
2分
uR
(t)
=
200
−
100 3
cos(2ω
1t
+
30°)
V
2分
UR =
2002
+
1 2
×
1030
2
= 201.38 V
2分
4、(15 分)
I (s)
5
+2
6
(A 卷)
学号:
5、含理想变压器电路如图 2-5 所示,欲使负载电阻 RL 获得最大功率,则 n=
PLmax 值为
。
姓名 和所获得的
2Ω 4sinωtV
1:n ••
RL = 8Ω
图 2-5
图 2-7
6、某 RC 串联电路的零输入响应 i(t) = 20 e −5000t mA ,已知 t = 0 时电容电压为 2 V,则该电路的电阻
R 为_ __,电容 C 为_ ___。
7、图 2-7 所示对称三相四线制电路中,已知星形联接负载的 R = 8Ω,ωL = 2Ω, 当相电压 uA = 2sinωtV
时,中线电流有效值等于_
___;当 uA = 50 2 sin 3ωtV 时,中线电流有效值等于_
___。
三、计算题(共 4 小题,共计 55 分)
图 2-1
2、电路如图 2-2 所示,当 R = 0 时, I =
。
图 2-2
3、图示电路 2-3 中, N 0 内不含独立电源。当U S =1V, IS =0 时,U ab =3V;当U S =0, IS =2A 时,
(完整)09川大高等代数及答案

四川大学2009年攻读硕士学位研究生入学考试题一、解答下列各题.1.(5分)设)(x f 是数域F 上次数为2008的多项式,证明:20092不可能是)(x f 的根.F 为有理数域该命题成立如题:设)(x f 是有理数域Q 上一个m 次多项式(0≥m ),n 是大于m 的正整数,证明:n2不可能是)(x f 的根.证明:反证法:假设n2是)(x f 的根,有)2()2(--n nx x 对于2-nx ,存在素数2=p110,,,-n a a a p Λ、p 不能整除n a 、2p 不能整除0a由艾森斯坦判别法,有2-nx 在有理数域不可约,则有)()2(x f x n -则n x f ≥∂))((与题设矛盾,故假设不成立,即n 2不可能是)(x f 的根.2.(10分)用代数基本定理证明,实数域R 上的任意不可约多项式只能是一次多项式或满足042<-ac b 的二次多项式:c bx ax ++2.证明:由代数基本定理,任意多项式在复数域都可以分解为一次多项式的乘积 则令多项式为)())(()(21n a x a x a x k x f ---=Λ (C a i ∈,R k ∈且0≠k ) 当R a i ∈时,则i a x -是实数域R 上的一次不可约多项式当R a i ∉时,有i a 也是)(x f 的根,有i i i i i i a a x a a x a x a x ++-=--)())((2i i i i a a x a a x ++-)(2满足042<-ac b由)(i i a a +-,R a a i i ∈,则i i i i a a x a a x ++-)(2是实数域R 上的二次不可约多项式故实数域R 上的任意不可约多项式只能是一次多项式或满足042<-ac b 的二次多项式:c bx ax ++2.3.(5分)设A 是数域F 上的n 阶方阵.要求不用Hamilton-Caylay 定理,证明:存在F 上的多项式)(x f 使得O A f =)(. 证明:取A 的特征多项式A E g -=λλ)(设)(λB 为A E -λ的伴随矩阵,有E g E A E A E B )())((λλλλ=-=- 由)(λB 的元素是A E -λ各个代数余子式,则1))((-≤∂n B λ 有11201)(---+++=n n n B B B B Λλλλ令n n n a a g +++=-Λ11)(λλλ,得E a E a E E g n n n +++=-Λ11)(λλλ ①A B A B B A B B A B B B A E B n n n n n n 1211220110)()()())((-------++-+-+=-λλλλλλΛ ②比较①、②,有⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=-=-=-=-=----E a A B Ea A B B E a A B B E a A B B EB n n n n n 11212121010ΛΛΛ,得⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=-=-=-=-=---------Ea A B A a A B A B A a A B A B A a A B A B A A B n n n n n n n n n nn n n 11221221122110110ΛΛΛ左边和右边全部相加,有O E g =)(λ,即0)(=λg 任取)()()(x g x q x f =,则有O A f =)(4.(10分)设1α、2α、3α是多项式123)(3++=x x x f 的全部根.求下式的值 ))()((212331223221ααααααααα+++解:由根与系数的关系得0321=++ααα、32323121=++αααααα、31321-=ααα)31)(31)(31())()((323222121212331223221ααααααααααααααα---=+++]1)()([91)1)(1)(1(271333231333233313231333231333231321-+++++--=---=αααααααααααααααααα)(91)(9124328333231333233313231ααααααααα++-++-=① )(91)111(243124328333231333231αααααα++-++-=)(91243124328333231333231333233313231αααααααααααα++-++-= ② 由①、②得,0333233313231=++αααααα,则原式)(9124328333231ααα++-=由13))((3)(3213231213213321333231-=+++++-++=++αααααααααααααααααα得原式24355=二、解答下列各题.1(10分)叙述并证明线性方程组的克莱默(Cramer )法则.2(5分)设F ,K 都是数域且K F ⊆,设β=AX 是数域F 上的线性方程组. 证明:β=AX 在F 上有解当且仅当β=AX 在K 上有解. 证明:令A 为n m ⨯矩阵 必要性:令X 为β=AX 在F 上的解,有n F X ∈,由K F ⊆,得nK X ∈X 也为β=AX 在K 上的解充分性:β=AX 在K 上有解, 有)()(A r A r =由A ,)(F M A n m ⨯∈,则在F 上,也有)()(A r A r =,故β=AX 在F 上有解3.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=142412222A (1)(5分)在任意数域F 上,A 能否相似于一个对角阵?说明理由. (2)(5分)求A 的极小多项式.(3)(5分)设AX X X f ')(=,其中)',,(321x x x X =是列向量.求)(X f 的一个标准型.解:(1))6()3(1424122222+-=+---+--=-λλλλλλA EA 的特征值为3,3,6-当3=λ时,000002214424422213-=----=-A E基础解系由2)3(=--A E r n 个线性无关的向量构成)'1,1,4(-、)'1,1,0(当6-=λ时,0009904525424522286--→-------=--A E 基础解系由1)6(=---A E r n 个向量构成)'2,2,1(- 故A 对应3个线性无关的特征向量,A 可对角化取⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=211211104P ,则有)6,3,3(1-=-diag AP P 由)(,3Q M C A ∈、又Q ∈-6,3,则A 在有理数域可以对角化由任何数域都包含有理数域,故在任意数域F 上,A 都能相似于一个对角阵(2)A 的特征多项式为O E A E A A f =+-=)6()3()(2由O E A E A =+-)6)(3(,有A 的极小多项式为)6)(3()(+-=λλλm(3)把P 的列向量单位化,得⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--=32212313221231310234C ,C 为正交矩阵 令CY X =,有232221633''')(y y y ACY C Y AX X X f -+===4.(10分)证明:在任意数域F 上矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=111001012A 与⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=110011001B 都不相似. 证明:3)1(11101012-=----=-λλλλλA E 有A 的特征值为1,1,1 1=λ时,00000001101101111-=---=-A E基础解系有2)(=--A E r n 个线性无关的向量构成 ①3)1(11011001-=-----=-λλλλλB E 有B 的特征值为1,1,1 1=λ时,01000100--=-B E 基础解系有1)(=--B E r n 个向量构成 ②由①、②,得在任意数域F 上矩阵A 与B 都不相似5.(5分)设A 是n 阶实对称矩阵.证明:A 是正定矩阵的充分必要条件是,对任意整数k ,k A 也是正定的.证明:必要性:令A 的特征值为i λ(n i ,,2,1Λ=),则k A 的特征值为k i λ A 是正定矩阵,0>i λ,则0>ki λ,有k A 为正定矩阵充分性:k A 的特征值为k i λ,有0>ki λ,由k 的任意性,有0>i λ,故A 是正定矩阵三、(15分)设)(F M n 是数域F 上的全体n 阶方阵组成的集合.对任意可逆矩阵)(F M A n ∈,定义集合})({1X XA A F M X n A =∈=T -. 设A A F M A n V T =≠∈0):(I,即V 是所有可能的A T 的交集(A 可逆).求V dim 和V 的一个基.解: 取)(F M n 的一个基nn E E E Λ,,1211,令n n ij a A ⨯=)(、n n ij x X ⨯=)( 有nn nn E a E a E a A +++=Λ12121111由X XA A =-1,有AX XA =,则X E XE ij ij =有行第列第i 111j 21⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡==⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=j j j ijnii i ij x x x X E x x x XE ΛM 得0=ij x (j i ≠)且nn x x x ===Λ2211,故kE X =为数量矩阵 有)(E L A =T ,则V 由数量矩阵和全体对角元素为零的矩阵构成令V B ∈,有∑=+=nj i ij ij E k kE B 1,(j i ≠),有1dim 2+-=n n VE 与全体ij E (j i ≠)构成V 的一个基.四、设)(12F M r +是数域F 上的全体12+r 阶方阵组成的集合.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=O E O E O O O OM r r 2是分块矩阵,其中r E 是r 阶单位阵.设}')({12O MX M X F M X B r =+∈=+,其中'X 表示X 的转置矩阵.进一步B X ∈,设∑∞==0!1k kXX k e .已知:)(12F M e r X+∈.1.(15分)求B dim 和B 的一个基.2.(15分)证明:对任意B X ∈都有行列式1)det(=Xe3.(10分)设列向量空间12+r F上的一个双线性函数),(--在它的基)'0,,0,1(1Λ=ε,)'0,,1,0(2Λ=ε,……,)'1,,0,0(12Λ=+r ε下的度量矩阵为上述M .证明:对任意B X ∈和列向量12,+∈r Fβα都有),(),(βαβα=XX e e .1.解:令⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333231232221131211X X X X X X X X x X (12X 、13X 为r 维行向量,21X 、31X 为r 维列向量,22X 、23X 、32X 、33X 为r 阶方阵)有⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=232221333231131211222X X X X X X X X x MX ,有⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡='''2'''2''2)'(233313223212213111X X X X X X X X x MX 由O MX M X =+',又M 为对称矩阵,有O MX MX =+)'(则O X X X X X X X X X X XX X X X X x =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++++++++2323223321133322323231121321123111'''2'''22'2'4,有011=x 自由变量有12X 、13X 、22X 、23X 、32X 且23X 、32X 为反对称矩阵有r r r r r r r r r B +=-+-+++=2222222dim2.证明:根据矩阵指数的性质,有)()det(X tr X e e =)'()()'()()()()(3322332233223322X X tr X tr X tr X tr X tr X X tr X tr e e e e e ++++====由O X X =+3322',有10)'(3322==+e e X X tr ,则1)det(=X e注:关于)()det(X tr X e e =的证明由存在可逆矩阵P ,使得⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=-n XP P λλλ******211O有121******-⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=P P X k n kk k λλλO11020100******!1***!1***!1!121--∞=∞=∞=∞=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=∑∑∑∑P e e e P P k k k P X k n k nk kk k k k kλλλλλλOO有)(2121)det(X tr Xe e e e e e n n ===+++λλλλλλΛΛ3.证明:五、(20分)证明:在数域F 上的任意n 元多项式都是线性多项式(即:一次齐次多项式)的幂的线性组合.证明:由任何一个m 次n 元多项式f 都可以唯一的表示成∑==mi i f f 0,其中i f 是n 元i 次齐次多项式由i f 是i 次齐次多项式,那么n x x x ,,,21Λ有ii n C k 1-+=种组合方式令⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=+++=--k i n i i i n k i i i b b b x x x x x b x x b x b f M ΛΛ212111211211),,,(取k 个一次齐次多项式k g g g ,,,21Λ,它们的i 次方为ik i i g g g ,,,21Λ令ij g 的k 个系数为kj j j a a a ,,,21Λ(k j ,,2,1Λ=)⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=+++=--kj j j i n i i i n kj i j i j i j a a a x x x x x a x x a x a g M ΛΛ212111211211),,,( 得到系数方程⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡k k kk k k k k b b b y y y a a a a a aa a a M MΛM MM ΛΛ2121212222111211 只要k g g g ,,,21Λ选取得当,则此方程有解则有∑==+++=kl i ll i kki ii g y g y g y g y f 12211Λ,故∑∑===m i kl il l g y f 01,即证.。
四川大学2009年数学分析考研真题与解答

四川大学2009数学分析考研真题与解析1·求下列极限。
(a )∑=∞→nk k nn Cn2.ln 1lim解: 原极限=()221111121ln ln limln 1limnn C C Cn n k nk kn k n n k nnk n ++-=∑∑∑+==+∞→=∞→=∑=∞→-++nk n k n nn 11ln 121lim =∑=∞→∞→--⋅+n k n n nk n n n 1111ln 1lim 12lim =⎰=--1021)1ln(21dx x(b)().sin lim 22n n n +∞→π解: 原极限=nn n nn n n n n ++=-+∞→∞→22sinlim )sin(lim πππ=12sin 111limsin ==⎪⎪⎭⎫ ⎝⎛++∞→ππn n (c )().sin sin lim2302dtt t t tdtx x x ⎰⎰-→解: 原极限=()().1262limsin sin 2lim 53302230=⎥⎦⎤⎢⎣⎡+--=-⋅→→x x x x x x x x x x x x ο (d )xx xe x x cos 11lim 0----+→ 解: 原极限=()()()⎥⎦⎤⎢⎣⎡++--⎥⎦⎤⎢⎣⎡+--++→222222024218212lim x x x x x x x x x οοο =.32418121-=--2·计算下列积分。
(a ),222dxdy y x yx D⎰⎰--+其中{()}1;R ,222≤+∈=y x y x D 解: 原积分=rdr r r r d ⎰⎰-+12202sin cos θθθπ=dr r r d 220104sin ⎰⎰-⎪⎭⎫⎝⎛+ππθθ=()()θθθπθθd dr r r dr r r ⎰⎰⎰⎥⎦⎤⎢⎣⎡-+-201sin 23sin 032sin sin=θθθπd ⎰⎪⎪⎭⎫ ⎝⎛+-204413sin 6sin =85π(b) ⎰l yzds ,其中l 是球面⎪⎪⎭⎫ ⎝⎛>=++332222a a z y x 与平面1=++z y x 的交线.解: 原积分=()ds z z ds zx yz l l ⎰⎰-=+121)(21 =()()ds z y x ds z y x l l ⎰⎰++-++2226161 =⎰-l ds a 612 =().3131312612222--=-⋅-a a a a ππ(c )设()x f 在()+∞∞-,内有连续导函数,求积分()()[]dy xy f y y x dx y xy f y L11222-++⎰,其中L 是从点⎪⎭⎫⎝⎛32,3A 到()2,1B 的直线段。
2009川大数学分析及答案

四川大学2009年攻读硕士学位研究生入学考试题一、(每题7分,共28分)求下列极限1. ∑=∞→nk k nn Cn2ln 1lim解:定理(∞∞型Stolz 公式,数列极限)设}{n x 严格递增(即N n ∈∀,有1+<n n x x ),且+∞=∞→n n x lim . 若1)a x x y y n n n n n =----∞→11lim(有限数),则a x y nnn =∞→lim . 2)a 为∞+或∞-,结论任然成立. 因2n ↗∞+,用Stolz 公式1211ln lim 12ln lim )1(ln ln lim ln 1lim 00122010102+-++=+=-+-=∑∑∑∑∑=∞→=+∞→=+=+∞→=∞→n k n n n C C n n C C C n nk n nk kn k n n nk kn n k k n n n k k n n 12ln )1ln()1(lim12)1ln()1ln(lim 11+-++=+-+-+=∑∑∑+=∞→==∞→n kn n n k n n n k n nk n k n (再次用Stolz 公式)212)11ln(lim )12()12()ln ln (]ln )1ln()1[(lim111=+=--+---++=∞→=+=∞→∑∑nn n k n k n n n n k n n k n n2. )(sin lim 22n n n +∞→π 解:)111(sin )(sin )(sin 22222++=-+=+nn n n n n ππππ 初等函数在有定义的地方皆连续12s i n l i m )111(s i n l i m )(s i n l i m 2222==++=+∞→∞→∞→πππn n n nn n3. dtt t t dtt x x x ⎰⎰-+→0230)sin (sin lim 2解:x x x x x x x x x x x x x dt t t t dtt x x x x x x sin 2lim )sin ()(2)(sin lim )sin ()(sin 2lim )sin (sin lim 30232223202320002302-=-⋅=-=-++++→→→→⎰⎰1226lim cos 16lim 22020==-=++→→x x x x x x4. xx xe x x cos 11lim 0----→ 解:泰勒公式∑∞==++++++=032!!!3!21n nn xn x n x x x x e ,(+∞<<∞-x ) +----++--+-++=+!)]1([)2)(1(!3)2)(1(!2)1(1)1(2n n x x x ααααααααααα,(11<<-x )∑∞=-=+-+-+-+-=022642)!2()1()!2()1(!6!4!21cos n n n n n n x n x x x x x ,(+∞<<∞-x ) )](!4)(!2)(1[)(!2)121(21)(2111)(21lim cos 11lim 24222220x o x x x o x x xx o x x x x xe x x x ++--+-+-+--+++=----→→3)(24181)(2lim 222220-=+--+=→x o x x x o x x二、(每题10分,共40分)计算下列积分 (1)dxdy y x yx D⎰⎰--+222,其中}1:),{(222≤+∈=y x R y x D 解:2222)221()221(412----=--+y x y x y x 当),(y x 在41)221()221(22=-+-y x 内和上时0222≥--+y x yx ,记作1D ; 当),(y x 在41)221()221(22=-+-y x 外,且在122≤+y x 内时0222<--+y x y x ,记作2D 则dxdy y x yx dxdy y x y x I D D ⎰⎰⎰⎰--+---+=21)2()2(2222 2122222)2()2(2211I I d x d y y x y x d x d y y x y x I DD D D -=--+---+=⎰⎰⎰⎰=+ d x d y y x y x I D ⎰⎰--+=1)2(221 令θcos 221r x =-、θsin 221r y =- πθπ321)81(213201=-=⎰⎰dr r r d I d x d y y x yx I D⎰⎰--+=)2(222 令θcos r x =、θsin r y = πθθθπ21)2c o s s i n (1032202-=-+=⎰⎰dr r r d Iπ169221=-=I I I(2)ds yz l⎰,其中l 是球面2222a z y x =++与平面1=++z y x 的交线。
四川大学期末考试试题(闭卷

四川大学期末考试试题(闭卷、开卷、半开卷)(2007-2008学年第1学期)课程号:30403030 课程名称:计算机图形学(A卷)任课教师:陈蓉,代术成适用专业年级:计算机科学技术学号:姓名:一、单项选择题(本大题共10小题,每小题3分,共30分)提示:在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分1)灰度等级为256级,分辨率为1024*1024的显示模式,至少需要的帧缓存容量为___B____bit。
A、7MB、8MC、10MD、16M2) ___C___是在高于显示分辨率的较高分辨率下用点取样方法计算,然后对几个像素的属性进行平均得到较低分辨率下的像素属性。
实际上是把显示器看成是比实际更细的网格来增加取样率。
A、提高显示分辨率B、图像分割C、过取样(supersampling)D、区域取样(areasampling)3)用一个n位的整数表示一个位串,用它控制线型时,可以n个像素为周期进行重复显示。
若Patten=11100101,而i表示画线程序中的第i个像素,则画线程序中的SETPIXEL(X,Y,COLOR)可改写为___C__A、if(pattern[i%4])setixel(x,y,color);B、if(pattern[i%6])setixel(x,y,color);C、if(pattern[i%8])setixel(x,y,color);D、if(pattern[i%12])setixel(x,y,color);4、点P 的齐次坐标为(8,6,2),其对应的空间坐标为__D ____。
A 、(8,6,2) B 、(8,6) C 、(4,3,1) D 、(4,3)5)在多边形的逐边裁剪法中,对于某条多边形的边(方向为从端点S 到端点P)与某条裁剪线(窗口的某一边)的比较结果共有以下四种情况,分别需输出一些顶点.请问哪种情况下输出的顶点是错误的____A ____。
四川大学考研真题2009年环境科学

四川大学
2009年攻读硕士学位研究生入学考试试题考试科目:环境学导论
考试代码:838#
适用专业:环境科学环境资源
一名词解释(每题4分,共40分)
热岛效应食物网环境污染危险废弃物适度人口
VOCS Leq BaP PM2.5 CFCS
二简答题(每题10分,共50分)
1,简述生态系统的组成?
2,目前世界上土地资源退化和减少的主要原因有哪些?
3,森林生态系统在生物圈中有哪些主要作用?
4,请分析矿业开发对环境的影响有哪些?
5,农药污染物的主要特点及其产生的主要环境问题有哪些?
三问答题(第1 2 题每题25分,第三题10分,共60分)
1,试从外部性理论的观点出发,举例并分析说明环境恶化的经济原因?
2,什么是生态城市?生态城市应该满足什么要求?我国目前正在开展全国的生态市建设规划活动,这是科学发展观在城市规划与建设中的体现。
请你从环境科学专业角度分析生态城市建设中如何处理好经济发展,社会进步与生态环境保护的关系。
3,喜鹊曾是各地最常见的鸟类之一,广布与各市,县,乡镇的山林,田园,城镇,是人们熟悉的一种留鸟。
喜鹊是杂食性的鸟类,又常在耕地,菜园,果园中觅食,喜欢将巢筑在高大的乔木上。
但从上个世纪70年代末在现在,短短二十多年,喜鹊就在四川盆地中消失了。
进入90年代四川盆地已成为喜鹊的罕见地,盆周山地,川西南山地为部分布区,川西高原为广布区。
喜鹊消失地域占四川总面积的三分之一。
从生态学的角度讲,鸟类是生态环境变化最敏感的指示者,鸟类数量的变化,对生态环境监测与保护和可持续利用,意义重大。
请你总结生态环境的可能变化分析喜鹊种数数量变化的可能原因。
