代数式
代数式的概念及分类

代数式的概念及分类代数式的概念及分类________________________________________代数式是数学中的一种表达方式,它是由数字、字母和符号组成的,表示数学关系的算术表达式。
代数式用于简化复杂的数学问题,帮助我们更容易理解。
代数式可以分为三类,即一元代数式、二元代数式和多元代数式。
一、一元代数式一元代数式是一个变量的函数表达式,即只有一个未知量的代数式。
它包括一元一次方程式、一元二次方程式、一元三次方程式、一元四次方程式等。
例如:2x+3=5,这是一个一元一次方程式,其中x是未知量,可以用来求解x的值。
二、二元代数式二元代数式是两个变量的函数表达式,即有两个未知量的代数式。
它包括二元一次方程式、二元二次方程式、二元三次方程式、二元四次方程式等。
例如:2x+3y=5,这是一个二元一次方程式,其中x和y是未知量,可以用来求解x和y的值。
三、多元代数式多元代数式是三个或以上变量的函数表达式,即有三个或以上未知量的代数式。
它包括多元一次方程式、多元二次方程式、多元三次方程式、多元四次方程式等。
例如:2x+3y+z=5,这是一个多元一次方程式,其中x、y和z是未知量,可以用来求解x、y和z的值。
四、复合代数式复合代数式是包含多个未知量的复杂代数式,它由一个或多个子项组成,可以由多个未知量联合而成。
例如:2x+3y+z-5xy=7,这是一个复合代数式,它包含有x、y和z三个未知量,可以用来求解x、y和z的值。
总之,代数式是由数字、字母和符号组成的表达式,可以分为一元代数式、二元代数式、多元代数式和复合代数式四类。
它们都可以用来帮助我们解决复杂的数学问题。
代数式知识点

第二章:代数式基础知识点:一、代数式1、代数式:用运算符号把数或表示数得字母连结而成得式子,叫代数式。
单独一个数或者一个字母也就是代数式。
2、代数式得值:用数值代替代数里得字母,计算后得到得结果叫做代数式得值。
3、代数式得分类:二、整式得有关概念及运算1、概念(1)单项式:像x、7、,这种数与字母得积叫做单项式。
单独一个数或字母也就是单项式。
单项式得次数:一个单项式中,所有字母得指数叫做这个单项式得次数.单项式得系数:单项式中得数字因数叫单项式得系数。
(2)多项式:几个单项式得与叫做多项式.多项式得项:多项式中每一个单项式都叫多项式得项。
一个多项式含有几项,就叫几项式.多项式得次数:多项式里,次数最高得项得次数,就就是这个多项式得次数。
不含字母得项叫常数项。
升(降)幂排列:把一个多项式按某一个字母得指数从小(大)到大(小)得顺序排列起来,叫做把多项式按这个字母升(降)幂排列.(3)同类项:所含字母相同,并且相同字母得指数也分别相同得项叫做同类项。
2、运算(1)整式得加减:合并同类项:把同类项得系数相加,所得结果作为系数,字母及字母得指数不变。
去括号法则:括号前面就是“+”号,把括号与它前面得“+”号去掉,括号里各项都不变;括号前面就是“–”号,把括号与它前面得“–"号去掉,括号里得各项都变号。
添括号法则:括号前面就是“+”号,括到括号里得各项都不变;括号前面就是“–”号,括到括号里得各项都变号。
整式得加减实际上就就是合并同类项,在运算时,如果遇到括号,先去括号,再合并同类项。
(2)整式得乘除:幂得运算法则:其中m、n都就是正整数同底数幂相乘:;同底数幂相除:;幂得乘方:积得乘方:。
单项式乘以单项式:用它们系数得积作为积得系数,对于相同得字母,用它们得指数得与作为这个字母得指数;对于只在一个单项式里含有得字母,则连同它得指数作为积得一个因式。
单项式乘以多项式:就就是用单项式去乘多项式得每一项,再把所得得积相加。
代数式_精品文档

代数式代数式是数学中一个重要的概念,它是由符号、数字和运算符组成的表达式。
在数学中,代数式被广泛用于解决各种数学问题,特别是代数问题。
在本文中,我们将探讨代数式的基本概念、性质和应用。
首先,让我们来了解代数式的基本结构。
代数式是由各种运算符(如加、减、乘、除)连接数字、字母和符号组成的数学表达式。
代数式可以包含常数、未知量和运算符。
常数是已知的数字,而未知量是用字母表示的数。
例如,以下是一些代数式的例子:1. 2x + 32. 4y - 73. 5a + 2b - c4. x^2 + 3x + 4代数式可以有不同的形式和类型。
例如,一次代数式是只包含一次幂的代数式,如2x + 3y。
二次代数式是包含二次幂的代数式,如x^2 + 3x + 4。
代数式还可以是线性的或非线性的,取决于未知量的幂次。
线性代数式只包含一次幂,非线性代数式包含高于一次幂的幂。
接下来,让我们讨论代数式的性质。
代数式有许多重要的性质,其中一些包括:1. 代数式可以通过合并类似项来简化。
例如,在代数式2x + 3x中,x是一个类似项,我们可以将其合并为5x。
2. 代数式可以通过展开来扩展。
例如,在代数式(x + 2)(x + 3)中,我们可以将其展开为x^2 + 5x + 6。
3. 代数式可以通过因式分解来分解成较简单的形式。
例如,在代数式x^2 + 5x + 6中,我们可以将其因式分解为(x + 2)(x + 3)。
4. 代数式可以通过代入特定的值来求解未知量。
例如,在代数式2x + 3中,若给定x的值为2,则可计算出代数式的值为7。
代数式在数学中具有广泛的应用。
它们可以用于解决线性方程组、研究函数的性质、推导数学公式等。
通过使用代数式,我们能够表达和处理复杂的数学问题。
解方程是代数式应用的一个重要领域。
代数式可用于求解线性方程、二次方程和高阶方程。
通过使用代数式,我们可以在未知量的值域中找到方程的解集。
例如,考虑下面的方程:2x + 3 = 9我们可以通过移项和合并项的方法来求解x的值。
什么叫代数式

什么叫代数式
代数式:由数和表示数的字母经有限次加、减、乘、除、乘方和开方等代数运算所得的式子,或含有字母的数学表达式称为代数式。
例如:ax+2b,-2/3,b^2/26,√a+√2等。
注意:
1、不包括等于号(=、≡)、不等号(≠、≤、≥、<、>、≮、≯)、约等号≈。
2、可以有绝对值。
例如:|x|,|-2.25|等。
用运算符导(指加、减、乘、除、乘方、开方)把数或表示数的字母连接而成的式子叫做代数式。
数的一切运算规律也适用于代数式。
单独的一个数或者一个字母也是代数式。
带有“<(≤)”“>(≥)”“=”“≠”等符号的不是代数式。
代数式是一种常见的解析式,对变数字母仅限于有限次代数运算(加、减、乘、除、乘方、开方)的解析式称为代数式。
代数式
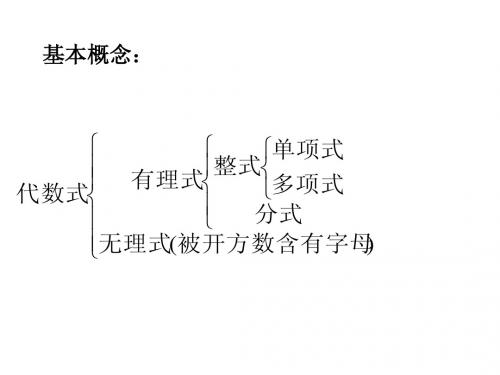
整式的概念
都是数与字母的积的代数式叫做单项式,单独的一 都是数与字母的积的代数式叫做单项式 单独的一 个数或字母也是单项式. 个数或字母也是单项式 单项式中数字因数叫做单项式的系数. 单项式中数字因数叫做单项式的系数 一个单项式中,所有字母的指数和叫做这个单项式 一个单项式中 所有字母的指数和叫做这个单项式 的次数,单独一个非 数的次数是0. 单独一个非0数的次数是 的次数 单独一个非 数的次数是 几个单项式的和叫做多项式. 几个单项式的和叫做多项式 一个多项式中,次数最高的项的次数 叫做这个多 一个多项式中 次数最高的项的次数,叫做这个多 次数最高的项的次数 项式的次数. 项式的次数 单项式和多项式统称整式. 单项式和多项式统称整式
例4
• 已知a b c 是三角形三边,且满足 (a + b + c) 2 = 3ab + 3bc + 3ac, • 试判断三角形的形状 • 解:a + b + c) = a + b + c + 2ab + 2bc + 2ac (
2 2 2 2
2a 2 + 2b 2 + 2c 2 − 2ab − 2bc − 2ac = 0
单项式与多项式相乘
•m(a+b+c m a+b+c a+b+c)
提公因式法
ma+mb+mc
(2)运用公式法: (2)运用公式法: 运用公式法 • ①平方差公式:a2-b2=(a+b)(a-b). 平方差公式: (a+b)(a-b). 代数式: 叫做完全平方式: 代数式 a2+2ab+b2及a2-2ab+b2叫做完全平方式:
b d bd (1 ). × = ; a c ac
初中数学知识点总结:代数式的相关概念

初中数学知识点总结:代数式的相关概念知识点总结一、代数式的定义:用运算符号把数或表示数的字母连结而成的式子,叫做代数式。
单独的一个数或字母也是代数式。
注意:(1)单个数字与字母也是代数式;(2)代数式与公式、等式的区别是代数式中不含等号,而公式和等式中都含有等号;(3)代数式可按运算关系和运算结果两种情形明白得。
三、整式:单项式与多项式统称为整式。
1.单项式:数与字母的积所表示的代数式叫做单项式,单项式中的数字因数叫做单项式的系数;单项式中所有字母的指数的和叫做单项式的次数。
专门地,单独一个数或者一个字母也是单项式。
2.多项式:几个单项式的和叫做多项式,在多项式中,每个单项式叫做多项式的项,其中不含字母的项叫做常数项;在多项式里,次数最高项的次数确实是那个多项式的次数。
四、升(降)幂排列:把一个多项式按某一个字母的指数从小到大(或从大到小)的顺序排列起来,叫做把多项式按那个字母升(降)幂排列。
五、代数式书写要求:1.代数式中显现的乘号通常用“·”表示或者省略不写;数与字母相乘时,数应写在字母前面;数与数相乘时,仍用“×”号;2.数字与字母相乘、单项式与多项式相乘时,一样按照先写数字,再写单项式,最后写多项式的书写顺序.如式子(a+b)·2·a应写成2a(a+b);3.带分数与字母相乘时,应先把带分数化成假分数后再与字母相乘;4.在代数式中显现除法运算时,按分数的写法来写;5.在一些实际问题中,有时表示数量的代数式有单位名称,假如代数式是积或商的形式,则单位直截了当写在式子后面;假如代数式是和或差的形式,则必须先把代数式用括号括起来,再将单位名称写在式子的后面,如2a米,(2a-b)kg。
六、系数与次数单项式的系数和次数,多项式的项数和次数。
1.单项式的系数:单项式中的数字因数叫做单项式的系数。
注意:(1)单项式的系数包括它前面的符号;(2)若单项式的系数是"1”或-1“时,"1"通常省略不写,但“-”号不能省略。
代数式的计算

如不等式 2x - 3 > 5,通过移 项可以得到 2x > 8,再除以2
可以得到 x > 4。
03
函数与图像
一次函数与图像
01
02
03
定义与性质
一次函数形如y=kx+b( k≠0),其中k和b为常数 ,k表示斜率,b表示y轴 截距。一次函数图像是一 条直线。
斜率与方向
当k>0时,直线从左向右 上升;当k<0时,直线从 左向右下降。
交换律
结合律
在加法与乘法运算中,任意交换两个数的 位置,结果不变。
在加法与乘法运算中,任意改变运算顺序 ,结果不变。
分配律
零律与单位元
乘法对加法满足分配律,即a * (b + c) = a * b + a * c。
在加法中,零是加法零元,任何数与零相 加结果仍为该数;在乘法中,1是乘法单位 元,任何数与1相乘结果仍为该数。
代数式化简技巧
合并同类项
在代数式中,将相同字母且相同字母 的指数也分别相同的项合并成一个项 ,使式子更为简洁。
提取公因式
当多个项具有相同因式时,可以将公 因式提取出来,简化代数式的表达。
利用分配律展开与合并
运用分配律可以将复杂表达式展开, 或者将多个项合并为更简单的形式。
分解因式
对于某些多项式,可以通过分解因式 的方法将其化为若干个简单多项式的 乘积,达到化简的目的。
分式的乘法与除法
两个分式相乘时,分子乘分子,分母乘分母;两个分式相除时,分 子的分母乘除数的分子,分母的分母乘除数的分母。
根与指数的计算与应用
01
02
03
04
平方根的计算
通过逆运算求解一个数的平方 根,即找到一个数使其平方等
代数式的定义和运算法则

代数式减法的注意事项:在进行加减运算时,要注意运算符号和运算次序,避免出现计算错误。
代数式的乘法
分配律:a(b+c) = ab+ac
05
代数式在数学中的应用
在方程中的应用
代数式在方程中表示 未知数的关系
通过代入法、消元法 等解方程的方法,利 用代数式求解未知数
代数式在解方程中起 到关键作用
代数式在方程中的应 用广泛,是数学中重
要的基础概念之一
在不等式中的应用
代数式可以用于表示不等式
代数式可以用于解不等式
代数式可以用于证明不等式
单独的一个数或一个字母也称为代数式。
代数式的值是代数式里字母取给定的值后得到的数。
代数式的表示方法
代数式是由数和表示数的字母 经有限次加、减、乘、除、乘 方和开方等代数运算所得的式 子,或含有字母的数学表达式
称为代数式。
代数式的值是代数式中字母取 给定值时代数式的值。
单独的一个数或一个字母也称 为代数式。
应用:结合律是代数式运算的基本性质之一,是代数式运算中非常重要的性质,对于代数式的化简和计算非常重 要。
分配律
定义:代数式中, 加法和乘法满足 分配律,即 a(b+c)=ab+ac。
证明:根据代数 式的运算法则, 我们可以证明分 配律的正确性。
应用:分配律在 代数式中有着广 泛的应用,可以 帮助我们简化复
运算顺序的规则:先进行乘除 法运算,再进行加减法运算
运算顺序的依据:乘除法是基 本的四则运算之一,加减法是 乘除法的简化形式
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
代数式在生活中的应用题
安徽省蒙城县板桥中学 张飞轮 邮政编码 233529
小朋友们,我们前面学习了列代数式的有关知识,我相信你们都掌握的很好了。
下面有
几道实际生活中的题目,你能用代数式帮助解决吗?如果能把所学的代数式的知识用到解决
实际问题中,那你就能真正地体会学习代数式的价值了。
1.传说上帝的女儿看中了尼罗河岸边的土地,于是她向上帝请求赐给她大片的土地,上帝
就给她一根绳子,要求她用这根绳子围出尽可能大的面积。
现有两种设计方案:一种是围成
正方形的场地,另一种是围成圆形的场地,请你帮助她选用哪一种方法,并说明理由.
解:设1S ,2S 分别表示围成的正方形场地和圆形场地的面积,则2
21416
a a S ⎛⎫== ⎪⎝⎭,222π2π4πa a S ⎛⎫== ⎪⎝⎭
,因为π4<,所以11π4>,22164πa a <. 所以21S S >,故应选用围成圆形场地的方案,它的面积较大. 2.为鼓励节约用电,某地对居民用户用电收费标准作如下规定:每户每月用电如
果不超过100度,那么每度电价按a 元收费;如果超过100度,那么超过部分....
每度电价按b 元收费.某户居民在一个月内用电160度,他这个月应缴纳电费是 ______元(用含a 、b 的代数式表示)
分析: 因为160度超过了100度,所以电费应分两部分计算,不超过100度的收费为
100a 元,超过部分的电费为(160-100)b=60b 元,所以他这个月应缴纳电费是
(100a+60b)元.
解:填(100a+60b ).
注意:当代数式是和的形式,且后面有单位,要把代数式用括号括起来.
3.某书店出售图书的同时,推出一项租书业务。
每租看1本书,租期不超过3天,每天租金a
元;租期超过3天,从第4天开始每天另加收b 元。
如果租看1本书7天归还,那么租金
为 。
解析:由题意知,该租金由两部分组成:3天以内的租金3a 元和3天以外的租金4(a+b)元,
从而租金共为3a+4(a+b)=7a+4b 元。
解:填(7a+4b )元
4.在五环图案内,分别填写五个数a b c d e ,,,,,如图, ,其中a b c ,,是
三个连续偶数()a b d e <,,是两个连续奇数()d e <,且满足a b
+
如 请你在0到20 .
解析:a b c ,,是三个连续偶数,可以设b=a+2,c=a+4;d,e 是连续的奇数,可以设e=d+2.
因为a b c d e ++=+,所以a+(a+2)+(a+4)=d+(d+2),整理得:3a+4=2d,从而得到:d=342
a +,a 是偶数,
b 是奇数,并且在0到20之间,因此a=2或10。
因此符合题意的另一组数是啊
a=10,b=12,c=14,d=17,e=19.
解:填10,12,14,17,19
5.本商店积压了100件某种商品,为使这批货物尽快出售,该商店采取了如下销售方案,先将价格提高到原来的2.5倍,再作三次降价处理;第一次降价30%标出了“亏本价”,第二次降价30%,标出“破产价”,第三次又降价30%,标出“跳楼价”,三次降价处理销售情况如下表。
问:(1)跳楼价占原价的百分比是多少?
(2)该商品按新销售方案销售,相比原价全部售完,哪一种方案更盈利,请通过计算加以说明.
解析:设原价为1
(1)亏本价=1×2.5(1-30%)=1.75
破产价=1.75(1-30%)=1.225
跳楼价=1.225(1-30%)=0.8575
跳楼价占原价的百分比为85.75%
(2)原价销售额:100×1=100
实际销售额:10×1.75+40×1.225+50×0.8575=109.375
∴按新销售方案销售更盈利。
练习
1.某商贩去菜摊买黄瓜,他上午买了30斤,价格为每斤x 元;下午,他又买了20斤,价格为每斤y 元.后来他以每斤2
x y +元的价格卖完后,结果发现自己赔了钱,其原因是( ) A .x <y B. x >y C. x ≤y D. x ≥y
2.小明在中考前到文具店买了2支2B 铅笔和一副三角板,2B 铅笔每支x 元,三角板每副2元,小明共花了 元。
3.某商店进了一批商品,每件商品的进价为a 元,若要获利20%,则每件商品的零售价应定为:( ).
(A)20%a (元) (B)(1-20%)a (元) (C)120%
a +(元) (D)(1+20%)a (元) 4.如果a 个人
b 天做
c 个零件,那么b 个人用相同的速度做c 个零件所需要的天数是( )
(A )2a c (B )2c a
(C )2c a (D )2a c 5.一条山路长skm ,一个游人上山的速度是每小时akm ,下山的速度是每小时bkm ,则它的平均速度是( )
(A )2a b +(B )2s a b +(C )s s s a b +(D )2s s s a b
+ 答案:1。
B 2。
(2x+2) 3。
D 4。
A 5。
D。
