流体力学第4章习题
李玉柱流体力学课后题标准答案第四章
第四章 流体动力学基础4-1 设固定平行平板间液体的断面流速分布为1/7max /2/2u B y u B -⎛⎫= ⎪⎝⎭，0y ≥总流的动能修正系数为何值?解：172max max 0127282B A A B y v ud u dy u B A B ⎛⎫- ⎪=== ⎪⎝⎭⎰⎰因为31.0A A u d A v α∆⎛⎫≈+⎪⎝⎭⎰ u u v ∆=-所以 172233821.0 1.01 1.0572B B A A B y u v d dy B A v B α-⎛⎫⎛⎫-- ⎪⎛⎫⎪≈+=+⋅-= ⎪⎪ ⎪⎝⎭ ⎪⎝⎭⎝⎭⎰⎰4-2 如图示一股水流自狭长的缝中水平射出，其厚度00.03m δ=，平均流速V 0＝8m/s ，假设此射流受重力作用而向下弯曲，但其水平分速保持不变。
试求(1)在倾斜角45θ=o 处的平均流速V ；(2)该处的水股厚度δ。
解：（1）由题意可知：在45度水流处，其水平分速度仍为8m/s,由勾股定理可得：V=︒45sin 8=11.31m/s （2）水股厚度由流量守恒可得：VD D V δδ=000，由于缝狭长，所以两处厚度近似相等，所以000.0380.02111.31V V δδ⨯===m 。
4-3 如图所示管路，出口接一收缩管嘴，水流射人大气的速度V 2=20m/s ，管径d 1＝0.1m ，管嘴出口直径d 2＝0.05m ，压力表断面至出口断面高差H ＝5m ，两断面间的水头损失为210.5(/2)V g 。
试求此时压力表的读数。
解：取压力表处截面为截面1-1，收缩管嘴处截面为截面2-2，选择两截面包围的空间为控制体，由实际流体的恒定总流能量方程得：2211221222wV p V p z z h g g g g ρρ'++=+++， 由连续性方程2211V A V A =可得1-1断面流速s m 51=V ，由上述两个方程可得压力表的读数（相对压强）：222112212wV V p p z z h g g ρ⎛⎫-'-=+-+ ⎪⎝⎭， 上式计算结果为：2.48at 。
工程流体水力学第四章习题答案
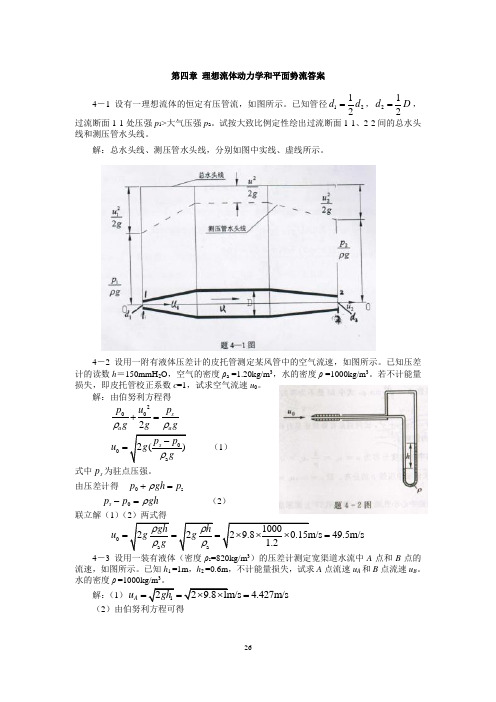
第四章 理想流体动力学和平面势流答案4－1 设有一理想流体的恒定有压管流，如图所示。
已知管径1212d d =，212d D =，过流断面1-1处压强p 1>大气压强p a 。
试按大致比例定性绘出过流断面1-1、2-2间的总水头线和测压管水头线。
解：总水头线、测压管水头线，分别如图中实线、虚线所示。
4－2 设用一附有液体压差计的皮托管测定某风管中的空气流速，如图所示。
已知压差计的读数h ＝150mmH 2O ，空气的密度ρa =1.20kg/m 3，水的密度ρ =1000kg/m 3。
若不计能量损失，即皮托管校正系数c =1，试求空气流速u 0。
解：由伯努利方程得2002s a a p u p g g gρρ+= 00a 2()s p p u g gρ-=（1） 式中s p 为驻点压强。
由压差计得 0s p gh p ρ+=0s p p gh ρ-= （2）联立解（1）（2）两式得0a a 10002229.80.15m/s 49.5m/s 1.2gh h u gg g ρρρρ===⨯⨯⨯= 4－3 设用一装有液体（密度ρs =820kg/m 3）的压差计测定宽渠道水流中A 点和B 点的流速，如图所示。
已知h 1 =1m ，h 2 =0.6m ，不计能量损失，试求A 点流速u A 和B 点流速u B 。
水的密度ρ =1000kg/m 3。
解：（1）1229.81m/s 4.427m/s A u gh ==⨯⨯= （2）由伯努利方程可得22A AA u p h g gρ+= （1）22B BB u p h g gρ+= （2）式中A h 、A p 和B h 、B p 分别为A 点和B 点处的水深和驻点压强。
由（1）、（2）式可得2222A B A BA B p p u u h h g g gρ-=+-- （3） 由压差计得，22ρρρρ--++=A A s B B p gh gh gh gh p ，所以220.82A BA B p p h h h h gρ-=+-- (4) 由（3）式、（4）式得2222 4.427(10.82)0.6(10.82)0.8922229.8B A u u h g g =--=--=⨯ 29.80.892m/s 4.18m/s B u =⨯⨯=。
李玉柱流体力学课后题答案-第四章
第四章 流体动力学基础4-1 设固定平行平板间液体的断面流速分布为1/7max /2/2u B y u B -⎛⎫= ⎪⎝⎭，0y ≥总流的动能修正系数为何值?解：172max max 0127282B A A B y v ud u dy u B A B ⎛⎫- ⎪=== ⎪⎝⎭⎰⎰因为31.0A A u d A v α∆⎛⎫≈+⎪⎝⎭⎰ u u v ∆=-所以 172233821.0 1.01 1.0572B B A A B y u v d dy B A v B α-⎛⎫⎛⎫-- ⎪⎛⎫⎪≈+=+⋅-= ⎪⎪ ⎪⎝⎭ ⎪⎝⎭⎝⎭⎰⎰4-2 如图示一股水流自狭长的缝中水平射出，其厚度00.03m δ=，平均流速V 0＝8m/s ，假设此射流受重力作用而向下弯曲，但其水平分速保持不变。
试求(1)在倾斜角45θ=o 处的平均流速V ；(2)该处的水股厚度δ。
解：（1）由题意可知：在45度水流处，其水平分速度仍为8m/s,由勾股定理可得：V=︒45sin 8=11.31m/s （2）水股厚度由流量守恒可得：VD D V δδ=000，由于缝狭长，所以两处厚度近似相等，所以000.0380.02111.31V V δδ⨯===m 。
4-3 如图所示管路，出口接一收缩管嘴，水流射人大气的速度V 2=20m/s ，管径d 1＝0.1m ，管嘴出口直径d 2＝0.05m ，压力表断面至出口断面高差H ＝5m ，两断面间的水头损失为210.5(/2)V g 。
试求此时压力表的读数。
解：取压力表处截面为截面1-1，收缩管嘴处截面为截面2-2，选择两截面包围的空间为控制体，由实际流体的恒定总流能量方程得：2211221222wV p V p z z h g g g g ρρ'++=+++， 由连续性方程2211V A V A =可得1-1断面流速s m 51=V ，由上述两个方程可得压力表的读数（相对压强）：222112212w V V p p z z h g g ρ⎛⎫-'-=+-+ ⎪⎝⎭，上式计算结果为：2.48at 。
流体力学第四章习题答案
第四章习题答案选择题(单选题)4、1等直径水管,A-A 为过流断面,B-B 为水平面,1、2、3、4为面上各点,各点的流动参数有以下关系:(c)(a)1p =2p ;(b)3p =4p ;(c)1z +1p g ρ=2z +2p g ρ;(d)3z +3p g ρ=4z +4pgρ。
4、2伯努利方程中z +p g ρ+22v gα表示:(a)(a)单位重量流体具有的机械能;(b)单位质量流体具有的机械能;(c)单位体积流体具有的机械能;(d)通过过流断面流体的总机械能。
4、3水平放置的渐扩管,如忽略水头损失,断面形心点的压强,有以下关系:(c)p p 2(a)1p >2p ;(b)1p =2p ;(c)1p <2p ;(d)不定。
4、4黏性流体总水头线沿程的变化就是:(a)(a)沿程下降;(b)沿程上升;(c)保持水平;(d)前三种情况都有可能。
4、5黏性流体测压管水头线的沿程变化就是:(d)(a)沿程下降;(b)沿程上升;(c)保持水平;(d)前三种情况都有可能。
4、6平面流动具有流函数的条件就是:(d)无黏性流体;(b)无旋流动;(c)具有速度势;(d)满足连续性。
4、7一变直径的管段AB ,直径A d =0、2m,B d =0、4m,高差h ∆=1、5m,今测得A p =302/m kN ,B p =402/m kN , B 处断面平均流速B v =1、5s m /、。
试判断水在管中的流动方向。
解: 以过A 的水平面为基准面,则A 、B 点单位重量断面平均总机械能为:42323010 1.0 1.50.40 4.89210009.80729.8070.2A A A A A p v H z g g αρ⨯⨯⎛⎫=++=++⨯= ⎪⨯⨯⎝⎭(m)2324010 1.0 1.51.5 5.69210009.80729.807B B B B B p v H z g g αρ⨯⨯=++=++=⨯⨯(m)∴水流从B 点向A 点流动。
[工程流体力学(水力学)]4-5章习题解答
![[工程流体力学(水力学)]4-5章习题解答](https://img.taocdn.com/s3/m/56af9a41a8956bec0975e35f.png)
即
2
d
对于 3 ，
M 0 L0T 0 L3 T 3 L3 M 3 L3 3 ML3
L : 0 3 3 3 3 3 T : 0 3
即
M : 0 3 1
3 0 3 0 1 3
3
p
p
故(
gd
2
,
d
,
) =0
化简整理，解出
11
2
gd
(
p
, Re )
p
又 与 p 成正比，将
提出，则
2
gd
p
2 ( Re )
p
gd
3 ( Re ) gd (
1 1)3 ( Re )
4-8 设螺旋浆推进器的牵引力 F 取决于它的直径 D、前进速度 、流体密度 、粘度 和 螺旋浆转速度 n 。证明牵引力可用下式表示：
所以在管壁处：
RJ 9800 0.05 0.008 3.92 N / m2
r 0.05 1.96 N / m2 r 0.9 3.92
r 0.05 m 处：
水头损失： h f Jl 0.008 100 0.8 m
5-5 输油管管径 d 150mm, 输送油量 Q 15.5t / h ，求油管管轴上的流速 umax 和 1 km 长 的沿程水头损失。已知 油 8.43kN / m3 ， 油 0.2cm2 / s 。 解： （1）判别流态 将油量 Q 换成体积流量 Q
L : 0 3 3 3 3 T : 0 3 1
中北大学流体力学第四章习题
第四章 流体运动学基础一 选择题1. 用欧拉法表示流体质点加速度a等于 。
(A) t u (B) u u )( (C) u u t u)( (D) u u tu)(2. 恒定流就是流场中 的流动。
(A) 各断面流速分布相同 (B) 流线就是相互平行的直线 (C) 运动要素不随时间而变化 (D) 流动随时间按一定规律变化 3. 一元流动就是 。
(A) 运动参数就是一个空间坐标与时间变量的函数 (B) 速度分布按直线变化 (C) 均匀直线流 (D) 流动参数随时间而变化 4. 均匀流的 加速度为零。
(A) 当地 (B) 迁移 (C) 向心 (D) 质点 5. 在 流动中,流线与迹线重合。
(A) 恒定 (B) 非恒定 (C) 不可压缩流体 (D) 一元 6. 连续性方程表示流体运动遵循 守恒定律。
(A) 能量 (B) 动量 (C) 质量 (D) 流量7. 水在一条管道中流动,如果两断面的管径比为d 1/d 2 =2,则速度比v 1/v 2= 。
(A) 2 (B) 1/2 (C) 4 (D) 1/4 8. 流体微团 。
(A) 具有规则的几何形状 (B) 质量大小不受限制 (C) 就是由大量流体质点组成的微小质团 (D) 就是质量、体积均可忽略的微元 9. 在 流动中,伯努利方程不成立。
D(A) 恒定 (B) 理想流体 (C) 不可压缩 (D) 可压缩 10. 在总流伯努利方程中,速度 v 就是 速度。
B(A) 某点 (B) 断面平均 (C) 断面形心处 (D) 断面上最大 11. 文透里管用于测量 。
D(A) 点流速 (B) 压强 (C) 密度 (D) 流量 12. 毕托管用于测量 。
A(A) 点流速 (B) 压强 (C) 密度 (D) 流量13. 密度 = 800kg/m 3 的油在管中流动,若压强水头为2m 油柱,则压强为 N/m 2。
C(A) 1、96×104 (B) 2×103 (C) 1、57×104 (D) 1、6×103 14. 应用总流能量方程时,两断面之间 。
工程流体力学课后习题答案4-7章
第四章 流体动力学【4-1】直径d =100mm 的虹吸管，位置如图所示。
求流量和2、3点的压力（不计水头损失）。
【解】列1、4点所在断面的伯努利方程，以过4点的水平面为基准面。
24500 0029.8v ++=++⨯得 4 =9.9 m/s v 2234 3.140.19.90.078 m /s 44π==⨯⨯=Q d v列1、2点所在断面的伯努利方程，以过1点的水平面为基准面222000 02p v g gρ++=++ （v 2=v 4）得 2242210009.9 4.910Pa 22ρ⨯=-=-=-⨯v p列1、3点所在断面的伯努利方程，以过1点的水平面为基准面233000 22p v g gρ++=++ （v 3=v 4）得 2439.9298001000 6.8610Pa 2=-⨯-⨯=-⨯p【4-2】一个倒置的U 形测压管，上部为相对密度0.8的油，用来测定水管中点的速度。
若读数△h =200mm ，求管中流速u =?【解】选取如图所示1-1、2-2断面列伯努利方程，以水管轴线为基准线212 0 002w w p p u g g gρρ++=++其中：p 1和p 2分别为1-1、2-2断面轴线上的压力。
设U 形测压管中油的最低液面到轴线的距离为x ，选取U 形测压管中油的最高液面为等压面，则12()w o w p gx g h p g x h ρρρ--∆=-+∆题 4-1图21()w o p p g h ρρ-=-∆则0.885m/s u ==【4-3】图示为一文丘里管和压力计，试推导体积流量和压力计读数之间的关系式。
当z 1=z 2时，ρ=1000kg/m 3，ρH =13.6×103kg/m 3，d 1=500mm ，d 2=50mm ，H =0.4m ，流量系数α=0.9时，求Q =？ 【解】列1-1、2-2断面的伯努利方程、以过1-1断面中心点的水平线为基准线。
工程流体力学第四章自测题答案
所以
a1＝－1， b1 ＝－1， c1 ＝－1
1
π1 =
μ ρVD
对于 Π2 项：
[ M 0 L0T 0 ] = [ L][ ML−3 ] a2 [ LT −1 ]b2 [ L]c2
对于
M：0＝a2 L： 0＝1－3a2+b2+c2 T： 0＝－b2
所以
a2＝0， b2 ＝0， c2 ＝－1
Δ D 对于 Π3 项：
V1 + V3 2
② h j2 所以，
V + V3 ⎞ ⎛ ⎛ V1 + V3 ⎞ − V3 ⎟ ⎜V1 − 1 ⎟ ⎜ (V1 − V3 )2 2 ⎠ 2 ⎝ ⎝ ⎠ + = = 2g 2g 4g
2
2
h j2 h j1
=
1 2
即分两次扩大最多可减少一半损失。
4-5．
如图所示，水在压强作用下从密封的下水箱沿竖直管道流入上水箱中，已知 h＝
解：① 求 V2 一次扩大的： h j1 =
(V1 − V3 )2
2g
两次扩大的： h j 2 =
(V1 − V2 )2 (V2 − V3 )2
2g + 2g
当 V1、V3 确定时，产生的最小阻力的值 V2 由下式求出：
3
dh j 2 dV2 ∴ V2 =
=
1 [− 2(V1 − V2 ) + 2(V2 − V3 )] = 0 2g
第 4 章 流动阻力和水头损失
4-1． 在圆管层流中， 沿壁面的切应力 τ0 与管径 d、 流速 V 及粘性系数 µ 有关，
用量纲分析法导出此关系的一般表达式。 解：n＝4，应用雷利法，假设变量之间可能的关系为一简单的指数方程：
李玉柱流体力学课后题解答第四章
李玉柱流体力学课后题解答-第四章————————————————————————————————作者：————————————————————————————————日期:第四章 流体动力学基础4-１ 设固定平行平板间液体的断面流速分布为1/7max /2/2u B y u B -⎛⎫= ⎪⎝⎭,0y ≥总流的动能修正系数为何值?解:172max max 0127282B A A B y v ud u dy u B A B ⎛⎫- ⎪=== ⎪⎝⎭⎰⎰因为31.0A A u d A v α∆⎛⎫≈+⎪⎝⎭⎰ u u v ∆=-所以 172233821.0 1.01 1.0572B B A AB y u v d dy B A v B α-⎛⎫⎛⎫-- ⎪⎛⎫⎪≈+=+⋅-= ⎪ ⎪ ⎪⎝⎭ ⎪⎝⎭⎝⎭⎰⎰4－2 如图示一股水流自狭长的缝中水平射出，其厚度00.03m δ=,平均流速V 0=8ｍ/s ，假设此射流受重力作用而向下弯曲，但其水平分速保持不变。
试求（1)在倾斜角45θ=处的平均流速V ;(２）该处的水股厚度δ。
解：（1)由题意可知:在45度水流处,其水平分速度仍为８m/s,由勾股定理可得:Ｖ=︒45sin 8=１1．３1m/s (2)水股厚度由流量守恒可得：VD D V δδ=000,由于缝狭长，所以两处厚度近似相等，所以000.0380.02111.31V V δδ⨯===m 。
4－3 如图所示管路,出口接一收缩管嘴,水流射人大气的速度V 2=2０m/s ，管径ｄ1＝０.1ｍ，管嘴出口直径d 2＝０．05ｍ,压力表断面至出口断面高差Ｈ=５m ，两断面间的水头损失为210.5(/2)V g 。
试求此时压力表的读数。
解:取压力表处截面为截面１-１，收缩管嘴处截面为截面2-2,选择两截面包围的空间为控制体，由实际流体的恒定总流能量方程得:2211221222wV p V p z z h g g g g ρρ'++=+++, 由连续性方程2211V A V A =可得1-1断面流速s m 51=V ,由上述两个方程可得压力表的读数(相对压强）:222112212w V V p p z z h g g ρ⎛⎫-'-=+-+⎪⎝⎭, 上式计算结果为：2．48at 。
第4章-静力学及理想流体力学
⎧ Fr = ω 2 r ⎪ 其中：⎨ ⎪ Fz = − g ⎩
其中 c 为常数。
⎛ ω 2r 2 ⎞ ⇒ p = ρg ⎜ − z⎟+C ⎝ 2g ⎠
代入边界条件：z = 0, r = r0 , p = ρ gh
习题五
⎛ ω 2 r02 ⎞ C = ρg ⎜h − ⎟ 2g ⎠ ⎝
所以，容器顶盖上（z= 0）压力分布为：
（3）、 比较两个速度场所得的结果 从计算结果可以看出，场①的等势线族为圆心为原点的一系列圆， 等流线族为通过原点的一系列射线，它的复位势对应着点源（汇）的复 位势。场②的等势线族为通过原点的一系列射线，等流线族为圆心为原 点的一系列圆，它的复位势对应着点涡的复位势。
习题五 3、证明不可压流体的理想、定常、二维流动，在忽略质量力 时，流函数ψ 和涡旋 Ω 满足 ∂ (Ω,ψ ) ∂Ω ∂ψ ∂Ω ∂ψ = − =0 ∂ ( x, y ) ∂x ∂y ∂y ∂x p 1 2 若Ω是常数，则压力方程为 + V + Ωψ = const ρ 2
习题五
（1）、速度分布②的速度势、流函数及复位势 ∂ϕ 2 −cy ⎫ ⎛ y⎞ = 2 ⇒ ϕ 2 = carctg ⎜ ⎟ + C ( y ) ⎪ ∂x x + y2 ⎪ ⎝x⎠ ⎛ y⎞ ⎬ ⇒ ϕ 2 = carctg ⎜ ⎟ + C ∂ϕ 2 cx ⎪ ⎝x⎠ = 2 x + y2 ⎪ ∂y ⎭ 等势线族为： arctg ( y x ) = θ c
习题五
⎡ ⎛V 2 p ⎞ ⎤ ⎛V 2 p ⎞ ∇⎜ + ⎟ + Ω × V = 0 ⇒ ∇ × ⎢∇ ⎜ + ⎟ + Ω ×V ⎥ = 0 ⎝ 2 ρ⎠ ⎣ ⎝ 2 ρ⎠ ⎦
工程流体力学第4、第6章 习题解答
第四章 习题解答4-1 用直径为100mm 的管道输送流量为10kg/s 的水，如水温为5℃，试确定管内水的流态。
如用这管道输送同样质量流量的石油，已知石油密度为3/850m kg =ρ运动粘滞系数为s cm /14.12，试确定石油的流态。
解：水温为5℃时，其密度为3/1000m kg =ρ，运动粘滞系数为s m /10519.126−×=γ因此，水在管道中流动的体积流量为： s m mkg skg Q /01.0/1000/1033== 流速为：s m mm sm A Q /27.11000100(14.341/01.023=××==υ雷诺数为：83863/10519.11000100/27.1Re 26=××=−sm mms m 为紊流 当输送石油时： s m mkg s kg Q /012.0/850/1033== 流速为：s m mm sm A Q /5.1)1000100(14.341/012.023=××==υ雷诺数为：1316/1014.11000100/5.1Re 24=××=−sm mms m 为层流 4-2 一圆形风道，管径为300mm ，输送的空气温度为20℃，求气流保持层流时的最大流量。
若输送的空气量为200kg/h ，气流是层流还是紊流？解：空气温度为20℃时，运动粘滞系数s m /107.1526-×=γ，根据题意有：6107.1510003002000−××=mm υ 解方程得：s m /105.0=υ气体流量为： s m s m mm Q /0074.0/105.01000300(14.34132=×××=质量流量为：h kg s kg m kg s m Q /29/0081.0/093.1/0074.033==×= 若输送的空气量为200kg/h ，因此，空气在管道中流动的体积流量为：s m m kg hkg Q /051.03600/093.1/20033=×= 流速为：s m mm sm A Q /72.0)1000300(14.341/051.023=××==υ雷诺数为：13758/107.151000300/72.0Re 26=××=−sm mms m 为紊流 4-3 断面为矩形的排水沟，沟底宽为20cm ，水深为15cm ，流速为0.15m/s ，水温为15℃。
流体力学第四章 习题
第四章 流体阻力与水头损失计算习题一、填空题1．雷诺数Re 是反映流体流动状态的准数，它反映了流体流动时 粘性力 与 惯性力 的对比关系，雷诺数Re 越大，说明液流的惯性力越大；雷诺数Re 越小，说明液流的粘滞力越大；2. 流体在管道中流动时，流动阻力包括 沿程阻力 和 局部阻力 ；3．流体流动阻力产生的根本原因是流体本身的 惯性 与 粘性 ，其中 粘性 是流动阻力的根本原因。
4．由紊流转变为层流的临界流速k v 小于 由层流转变为紊流的临界流速kv '， 其中kv '称为 上临界速度 ，k v 称为 下临界速度 ； 5.达西公式的表达式为 22f L v h d g λ= ，计算局部水头损失的通用公式是22j v h gξ= ; 7、对圆管来说，临界雷诺数值=k Re 2000 。
8、雷诺数的表达公式为 vd vd Re ρμν==，当Re ≤2000,则液体的流动状态为层流，当Re ＞2000,则液体的流动状态为紊流；9、通过雷诺实验，可知，流体的流动状态分为层流与紊流；其中，质点以平行于管轴方向呈直线运动而无横向运动的流动状态，称为层流状态。
液体质点的互相撞击和掺混，有横向位移，称为紊流状态。
层流到紊流的过渡，称为临界状态。
10、紊流由紊流核心、层流边层和过渡层三部分组成。
11、我们把在管壁附近作层流运动的液层称为层流边界层，其厚度用“δ”，表示。
12、壁面的粗糙度有两种表示方法：绝对粗糙度和相对粗糙度。
13、绝对粗糙度△是壁面粗糙突出的平均高度。
14、紊流的三种类型有水力光滑管、水力粗糙管、混合摩擦管 。
二、选择题1、雷诺数的物理意义表示：（c ）A 、粘滞力与重力之比；B 、重力与惯性力之比；C 、惯性力与粘滞力之比；D 、压力与粘滞力之比。
2、圆管紊流粗糙区的沿程摩阻系数λ D ；A 、与雷诺数Re 有关B 、与和管长l 有关C 、与Re 和d∆有关 D 、与管壁相对粗糙度d D 有关 3、在圆管流动中，层流的断面速度分布符合 C ； A 、均匀规律 B 、直线变化规律 C 、抛物线变化规律 D 、对数曲线规律4、流体在管内作层流流动时，其沿程损失h f 值与断面平均流速v 的 A 次方成正比。
流体力学第四章
第四章习题简答4-2 管径cm d 5=，管长m L 6=的水平管中有比重为0.9油液流动，水银差压计读数为cm h 2.14=，三分钟内流出的油液重量为N 5000。
管中作层流流动，求油液的运动粘度ν。
解: 管内平均流速为s m d Q v /604.1)4/05.0/(180/)9.09800/(5000)4//(22=⨯⨯==ππ 园管沿程损失h f 为γ(h 水银γ/油)1-=0.142(13.6/0.9-1)=2.004m园管沿程损失h f 可以用达西公式表示： gvd l h f 22λ=,对层流, Re /64=λ, 有fgdhlv 264Re 2=, 但νvd=Re , 从而lvh gd f 6422=ν, 代入已知量, 可得到s m /10597.124-⨯=ν题 4-2 图4-4 为了确定圆管内径，在管内通过s cm /013.02=ν的水，实测流量为s cm /353，长m 15管段上的水头损失为cm 2水柱。
试求此圆管的内径。
解：422222212842642642642Re 64gdlQ d d g lQ gdlv gvd l vdgvd l h f πνπννν=⎪⎭⎫ ⎝⎛====m gdlQ d 0194.002.08.9210013.0351********4=⨯⨯⨯⨯⨯⨯==∴-ππν4-6 比重85.0, s m /10125.024-⨯=ν的油在粗糙度mm 04.0=∆的无缝钢管中流动，管径cm d 30=，流量s m Q /1.03=, 求沿程阻力系数λ。
解: 当78)(98.26∆d >Re>4000时，使用光滑管紊流区公式：237.0Re221.00032.0+=λ。
园管平均速度s m d q v /4147.1)4//(2==π, 流动的33953Re ==νvd, ：723908)(98.2678=∆d , 从而02185.0Re/221.00032.0237.=+=o λ4-8 输油管的直径mm d 150=,流量h m Q /3.163=，油的运动黏度s cm /2.02=ν,试求每公里长的沿程水头损失。
(完整word版)流体力学习题及答案-第四章
第四章流体动力学基本定理及其应用4-1欧拉运动微分方程和伯努利方程的前提条件是什么，其中每一项代表什么意义？答：（1）欧拉运动微分方程是牛顿第二定律在理想流体中的具体应用，其矢量表达式为:.:t其物理意义为：从左至右，方程每一项分别表示单位质量理想流体的局部惯性力、迁移惯性力、质量力和压力表面力。
（2）伯努利方程的应用前提条件是：理想流体的定常运动，质量力有势，正压流体，沿流2线积分。
单位质量理想流体的伯努利方程的表达式为：- p g^ C，从左至右方程2 P每项分别表示单位质量理想流体的动能、压力能和位能，方程右端常数称流线常数，因此方程表示沿流线流体质点的机械能守恒。
4-2设进入汽化器的空气体积流量为Q = 0.15m3 / S,进气管最狭窄断面直径D=40mm，喷油嘴直径d=10mm。
试确定汽化器的真空度。
又若喷油嘴内径d=6mm，汽油液面距喷油嘴高度为50cm，试计算喷油量。
汽油的重度=7355N/m3。
答：（1）求A点处空气的速度：设进气管最狭窄处的空气速度为V i，压力为p i，则根据流管的连续方程可以得到:丄二D2_d2V i =Q，44Q因此：v14Q 厂。
江（D2-d2）（2 ）求真空度p v选一条流线，流线上一点在无穷远处F，—点为A点；并且:在F点：P F二P o ，V F = 0 ；在A点：P A二P1 二？，V A二W。
将以上述条件代入到伯努利方程中，可以得到:2也.0. v_02g-—；v f ， v A = v 2 = ?， z A = h = 50cm = 0.5m ；2在 B 点：P B = p 0， V B = 0，Z B = 0 ； 代入到伯努利方程中，可以得到:Ip 0才v 22rh 』0 0；整理得到:v ；二」V 12 -2gh ；2因此汽油喷出速度为:1V 2 -2gh ；其中空气重度1 = Sg =1.226 9.81 =12N/m 3 ； V 1缪 龙，并注意到喷油嘴的 兀(D -d )直径是6mm ，而不是原来的10mm ，则计算得到:因此汽油流量为:12 _43 3因此真空度为:P v 二 P o - P i4Q冷心2] D2—d 28 322 JI(D 2 —d 2 2若取空气的密度为3::=1.226kg/m ，那么计算得到:8 1.226 0.152pv3.1421 32 =9.95 103Pa 。
流体动力学习题
p1 w gx o g h p2 w g ( x h) p2 p1 ( w o ) g h
解上述方程可得
u
2
p2 p1
w
o 2(1 ) g h w
5
2 0.2 9.8 0.2 0.885m/s
工程流体力学 Engineering Fluid Mechanics
第4章 流体动力学基本原理习题
（2）列自由液面和管子出口断面的伯努利方程，则
2 2 v2 v12 v2 H 4 3 2g 2g 2g A1v1 A2 v2
v1 4.427m/s
2 p1 v12 v2 00 0 g 2g 2g
列A点所在断面和管子出口断面的伯努利方程
则
2 v2 v12 8.8542 4.427 2 p1 1000 29.398kPa 2 2
20
工程流体力学 Engineering Fluid Mechanics
第4章 流体动力学基本原理习题
【解】当管路阀门关闭时，由压力表度数可确定管路轴线到自由液面的高度H
p 49.8 103 H 5.082m 3 g 1 10 9.8
当管路打开时，列1-1和2-2断面的伯努利方程，则
2 2 p2 v2 v2 00 H 02 g 2g 2g
第4章 流体动力学基本原理习题
【解】列1-1、2-2断面的伯努利方程。
其中：p1和p2分别为1-1、2-2断面轴线上的压力。
设过1-1断面中心点的水平线到压力计中水银与水分界面的低液面的距离 为x，则可列出U形测压管中水银与水分界面的低液面的等压面条件
p1 p2 H 1 H z1 z2 g 2 由上述方程可得 v2 v12 H 1 H 2g 2 2 d1 d2 代入 v1 Q , v2 Q 4 4 1 1 解得 Q 2 g H 1 H 4 4 0.0195m3 /s 4 d2 d1
流体力学（刘鹤年）第4章答案
4.1一变直径管段AB ，直径d A =0.2m ，d B =0.4m ，高差△h=1.5m，测得p A =30kPa ，p B =40kPa ，B 点处断面平均流速v B =1.5m/s ．水在管中的流动方向。
解：s m d d v v ABB A 62.04.05.1442222=⨯=⋅=ππ以过A 点的水平面为等压面，则OmH g v g p h H OmH g v g p H B B B A A A 2222226964.58.925.18.9405.128980.48.9268.9302=⨯++=++==⨯+=+=ρρ可以看出：，水将从B 点流向A 点。
A B H H >或：wB B B A A A h gvg p z g v g p z +++=++2222ρρ解得水头损失为：，水将从B 点流向A 点。
O mH h w 27984.0-=4.2利用毕托管原理，测量水管中的流速u 。
水银差压计读书⊿h =60mm ，求该点流速。
解：m/s8530606128922....h g u =⋅⋅⋅=∆=汞ρ4.3水管直径50mm ，末端阀门关闭时，压力表读值为21kPa ，阀门打开后读值降为5.5kPa ，求不计水头损失时通过的流量Q.解：所以 m/s 57555212221.g .g g p p g V =-=⎪⎪⎭⎫ ⎝⎛-=ρρQ=VA=5.57×π(0.05)2/4=10.9 l/s4.4水在变直径竖管中流动，已知粗管直径d 1=300mm ，流速v 1=6m/s ，为使两断面的压力表读值相同，试求细管直径（水头损失不计）。
gV g p g p 20221++=ρρ解： gvg P g v g P 223222211+⋅=+⋅+ρρ21P P =流量相等222121v d v d =mmd 2352=4.5 为了测量石油管道的流量，安装文丘里流量计，管道直径d 1 =200mm ，流量计喉管直径d 2 =100mm ，石油密度ρ=850kg/m ，流量计流量系数μ=0.95。
流体力学第四章习题答案-精选.
第四章习题答案选择题（单选题）4.1等直径水管，A-A 为过流断面，B-B 为水平面，1、2、3、4为面上各点，各点的流动参数有以下关系：（c ）（a ）1p =2p ；（b ）3p =4p ；（c ）1z +1p g ρ=2z +2p g ρ；（d ）3z +3p g ρ=4z +4pgρ。
4.2伯努利方程中z +p g ρ+22v gα表示：（a ）（a ）单位重量流体具有的机械能；（b ）单位质量流体具有的机械能；（c ）单位体积流体具有的机械能；（d ）通过过流断面流体的总机械能。
4.3水平放置的渐扩管，如忽略水头损失，断面形心点的压强，有以下关系：（c ）p p 2（a ）1p >2p ；（b ）1p =2p ；（c ）1p <2p ；（d ）不定。
4.4黏性流体总水头线沿程的变化是：（a ） （a ）沿程下降；（b ）沿程上升；（c ）保持水平；（d ）前三种情况都有可能。
4.5黏性流体测压管水头线的沿程变化是：（d ） （a ）沿程下降；（b ）沿程上升；（c ）保持水平；（d ）前三种情况都有可能。
4.6平面流动具有流函数的条件是：（d ）无黏性流体；（b ）无旋流动；（c ）具有速度势；（d ）满足连续性。
4.7一变直径的管段AB ，直径A d =0.2m ，B d =0.4m ，高差h ∆=1.5m ，今测得A p =302/m kN ，B p =402/m kN ， B 处断面平均流速B v =1.5s m /.。
试判断水在管中的流动方向。
解： 以过A 的水平面为基准面，则A 、B 点单位重量断面平均总机械能为：42323010 1.0 1.50.40 4.89210009.80729.8070.2A A A A A p v H z g g αρ⨯⨯⎛⎫=++=++⨯= ⎪⨯⨯⎝⎭（m ）2324010 1.0 1.51.5 5.69210009.80729.807B B B B B p v H z g g αρ⨯⨯=++=++=⨯⨯（m ）∴水流从B 点向A 点流动。
流体力学第4章课后习题答案
第一章习题答案选择题（单选题）1.1 按连续介质的概念，流体质点是指：（d ）（a ）流体的分子；（b ）流体内的固体颗粒；（c ）几何的点；（d ）几何尺寸同流动空间相比是极小量，又含有大量分子的微元体。
1.2 作用于流体的质量力包括：（c ）（a ）压力；（b ）摩擦阻力；（c ）重力；（d ）表面张力。
1.3 单位质量力的国际单位是：（d ）（a ）N ；（b ）Pa ；（c ）kg N /；（d ）2/s m 。
1.4 与牛顿内摩擦定律直接有关的因素是：（b ）（a ）剪应力和压强；（b ）剪应力和剪应变率；（c ）剪应力和剪应变；（d ）剪应力和流速。
1.5 水的动力黏度μ随温度的升高：（b ）（a ）增大；（b ）减小；（c ）不变；（d ）不定。
1.6 流体运动黏度ν的国际单位是：（a ）（a ）2/s m ；（b ）2/m N ；（c ）m kg /；（d ）2/m s N ⋅。
1.7 无黏性流体的特征是：（c ）（a ）黏度是常数；（b ）不可压缩；（c ）无黏性；（d ）符合RT p=ρ。
1.8 当水的压强增加1个大气压时，水的密度增大约为：（a ）（a ）1/20000；（b ）1/10000；（c ）1/4000；（d ）1/2000。
1.9 水的密度为10003kg/m ，2L 水的质量和重量是多少？ 解： 10000.0022m V ρ==⨯=（kg ）29.80719.614G mg ==⨯=（N ）答：2L 水的质量是2 kg ，重量是19.614N 。
1.10 体积为0.53m 的油料，重量为4410N ，试求该油料的密度是多少？ 解： 44109.807899.3580.5m G g V V ρ====（kg/m 3） 答：该油料的密度是899.358 kg/m 3。
1.11 某液体的动力黏度为0.005Pa s ⋅，其密度为8503/kg m ，试求其运动黏度。
流体力学第1、2、3、4章课后习题答案
GAGGAGAGGAFFFFAFAF第一章習題答案選擇題（單選題）1.1按連續介質的概念，流體質點是指：（d ）（a ）流體的分子；（b ）流體內的固體顆粒；（c ）幾何的點；（d ）幾何尺寸同流動空間相比是極小量，又含有大量分子的微元體。
1.2作用于流體的質量力包括：（c ）（a ）壓力；（b ）摩擦阻力；（c ）重力；（d ）表面張力。
1.3單位質量力的國際單位是：（d ）（a ）N ；（b ）Pa ；（c ）kg N /；（d ）2/s m 。
1.4與牛頓內摩擦定律直接有關的因素是：（b ）（a ）剪應力和壓強；（b ）剪應力和剪應變率；（c ）剪應力和剪應變；（d ）剪應力和流速。
1.5水的動力黏度μ隨溫度的升高：（b ）（a ）增大；（b ）減小；（c ）不變；（d ）不定。
1.6流體運動黏度ν的國際單位是：（a ）（a ）2/s m ；（b ）2/m N ；（c ）m kg /；（d ）2/m s N ⋅。
1.7無黏性流體的特征是：（c ）（a ）黏度是常數；（b ）不可壓縮；（c ）無黏性；（d ）符合RT p =ρ。
GAGGAGAGGAFFFFAFAF1.8當水的壓強增加1個大氣壓時，水的密度增大約為：（a ） （a ）1/20000；（b ）1/10000；（c ）1/4000；（d ）1/2000。
1.9 水的密度為10003kg/m ，2L 水的質量和重量是多少？解： 10000.0022m V ρ==⨯=（kg ）29.80719.614G mg ==⨯=（N ）答：2L 水的質量是2 kg ，重量是19.614N 。
1.10 體積為0.53m 的油料，重量為4410N ，試求該油料的密度是多少？ 解： 44109.807899.3580.5m Gg VVρ====（kg/m 3）答：該油料的密度是899.358 kg/m 3。
1.11某液體的動力黏度為0.005Pa s ⋅，其密度為8503/kg m ，試求其運動黏度。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
d
v
α
38
（2）对于喷嘴固定叶片以速度u向后退的情况 可用相对于叶片的流量和流速计算：
F (d / 4)(v u) (1 cos )
2 2
v
d
u
α
39
第四章 基本内容
系统与控制体
研究问题的两个研究对象
基本 概念
基本 原理
雷诺输运公式
联系系统与控制体的纽带 质量守恒原理 动量守恒原理 动量矩守恒原理 能量守恒原理——伯努利方程
1
物料恒算 系 统 与 控 制 体
质量守恒原理
雷诺输 运公式 能量守恒原理 伯努利方程
动 量 守 恒 原 理
动 量 矩 守 恒 原 理
2 2
1 B
C 4m
2m 2
2
3m A
D
思考题：为什么B点与自由液面同一高度，但压力
却不是大气压？
36
11. 固定喷嘴以速度v将水流喷射到对称弯 曲的叶片上，已知喷嘴出口直径为d，叶片 出口角为α，水的密度为ρ。设阻力损失和 重力影响可忽略，求射流对弯曲对称叶片 的冲击力。
v
d
α
37
（1）对于喷嘴和叶片都是固定的情况
流 体 机 械
2
1.已知有密度为850kg/m3的液体，在 内径为0.2m的输油管道截面上的流 速为2m/s，求在另一内径为0.05m的 截面上的流速以及管道内的质量流 量。
32m/s；53.4kg/s
3
解：根据不可压缩流体 的质量守恒方程，有 v1 A1 v2 A2 则 v2 v1 (d1 / d 2 ) 2 (0.2 / 0.05) 32m / s
射流的压强等于周围气体的压强，根据能量方程 式，如不计水头损失的话，各断面的流速数值应保持 不变。设射流断面为A，流速为v，体积流量为Q，叶片 转角为α，则根据动量方程式，叶片的反力为：
R (d / 4)v(v cos v)
2
故射流的推力为
F R (d / 4)v (1 cos )
29
o
10.已知虹吸管的直径d=15mm，布置情况如 图，喷嘴出口直径d2=5mm，不计水头损失， 求虹吸管的输水量及管中A、B、C、D各点 的压强值。
1 B C 4m 2 3m A
33
2m
D
解： ( 1 )取喷嘴出口处为计算位 能的基准， 列1 1和2 - 2截面的伯努力方程式
2 2 p1 v1 p2 v2 z1 z2 g 2 g g 2g
2 1 2
5.6m / s 由于介质连续流动，则 有 v1 A1 v2 A2 于是有 d 2 d1 v1 1.4 0.1 0.05m 5cm v2 5.6
15
6.由喷嘴射出速度为v=7m/s的自由射流，欲 达到H=2m，试问喷嘴轴线的倾角是多少？
63.5°
y x 1 v 2 H
19
解：列y方向的伯努利方程 p1 p2 H g 2 g g 2 g 对于自由射流， 1 p2，v1 y v sin , v2 y 0 p 则最高射程为 v 2 sin 2 H 2g 2g v12y 2 gH sin 2 v 6330 2 9.81 2 0.8949 49
20
v12y
2 v2 y
8.边长为b=30cm的正方形铁板闸门，上边铰 接于O点，其重量为G=117.7N，水射流直径 d=2cm的中心线通过闸板中心C，射流速度 v=15m/s，求：
(1)为使闸门保持垂
o C G P
直位置在其下边应加 多大的力P。 (2)撤销P力后，闸门 倾角是多少？忽略 铰链摩擦。
d
35.3N；17.45°
26
y x F d
o C G P
27
解：取控制体如图所示 。受力分析如图。
(1)根据动量定理，可得 控制体所受作用力为
y x F d
2 2
o C G P
F q v v 1000
4
d 2v 2
4 70.65 N
0.02 15
则射流对闸门的作用力大小为：R=70.65 N， 方向与F相反。
Fx=38416N
45° y x
Q
Fy=1806.88N
5
解：该流动为稳态流动。设水流对弯管的作 用力为R，其分量为Rx,Ry，则弯管对水流的 作用力F必与R相等、反向。
取弯管为控制体，则控制体受力为：
45° y x p Fx Ry Fy Rx R
6
Q
根据动量守恒方程，在 方向有 x
F
x
Q( v2 x v1 x )
2 2
质量流量为 G
4
d v 850
2 1 1
4
0.2 2 53.4 kg / s
2
4
2.水平平面上的45°弯管，入口直径d1=600mm， 出口直径d2=300mm，入口压强p1=0.14MPa，出 口与大气相通。流量Q=0.425m3/s，忽略摩擦和 重力作用，试求水对弯管的作用力。
4Q 4Q 即： Fx p1 d Q( 2 cos 45 2 ) 4 d 2 d1
2 1
Fx 38416N
45° y x p Fx Ry Fy Rx R
7
Q
在y方向有
F
可得
y
Q( v2 y v1 y )
45° y x p Fx Ry Fy
Q
4Q Fy Q( 2 sin 45 0 ) d 2 解得： Fy 1806.88N
28
若要保证闸门处于垂直 位置，则 力R和P对o点取矩之和应为零。 b R 70.65 R Pb P 35.3N 2 2 2 (2)闸门在倾斜位置平衡时 有 b b R R G sin arcsin 17.45 2 2 G
y x F d C G P
2 2 p1 v1 pA vA z1 zA g 2 g g 2g 2 pA vA 4 3 g 2g
1
C B
4m
2m
2
3m A
D
p A 68.2 kN / m 2
35
同理可得 pB 0.48 kN / m pC 20.1 kN / m pD 3.95 kN / m
1 B
C 4m
2m 2
v 即 4 v2 8.86 m / s 2g qv
2 2
4
d v
2 2 2
3m ADFra bibliotek4 0.000174 3 / s m
0.005 8.86
2
34
( 2 )根据质量守恒方程有 d2 2 5 2 v A vB vC vD v2 ( ) 8.86 ( ) d1 15 0.984m / s 列1 1和A A截面的伯努里方程式
5.6m/s
d1
5cm
v1 v2 d2
H
13
解：对管口和油柱下端 列伯努利方程 p1 v p2 v H g 2 g g 2 g 由于管出口与大气接触 ，有p1 p2 , 则上式变为 v v H 2g 2g
v2
2 1 2 2 2 1 2 2
d1
v1
H
14
d2
于是有 v2 v 2 gH 1.4 2 9.811.5
Rx R
8
所以水流对弯管作用力 大小为 R R R Fx Fy 38460 N
2 x 2 y 2 2
其方向与x轴成角， 1806 88 . arctan arctan 2.42 Rx 38416 Ry
9
4.油从铅直管向下流出，管直径d1=10cm， 管口处的速度为v1=1.4m/s，试求管口下方 H=1.5m处的速度和油柱直径。