关于载流长直螺线管磁场的讨论
用对称性和安培环路定理求解长直载流螺线管磁场分布

用对称性和安培环路定理求解长直载流螺线管磁场分布作者:孙松阳来源:《课程教育研究》2017年第52期【摘要】一般教材应用安培环路定理求解无限长直载流螺线管的磁场分布时,将磁场线平行于轴线、管内外磁场均匀、管外磁场为零作为已知结论,然后应用安培环路定理,并未提及这些已知结论的证明过程。
针对此点,本文结合磁场的对称性特征,给出这些已知结论的证明过程,然后应用安培环路定理给出螺线管磁场分布。
【关键词】安培环路定理长直载流螺线管对称性【中图分类号】G642.3 【文献标识码】A 【文章编号】2095-3089(2017)52-0185-01一、引言设一无限长直载流螺线管,单位长度上密绕匝线圈,通过每匝的电流强度为,求螺线管内外的磁场分布。
这一问题是应用安培环路定理的典型例题[1],对于这一问题,一般教材通常指出磁场线平行于轴线、管内外磁场均匀以及管外磁场为零,然后直接使用安培环路定理,缺乏对磁场线平行于轴线、管内外磁场均匀以及管外磁场为零的具体证明。
本文旨在补充对磁场线平行于轴线、管内外磁场均匀以及管外磁场为零的证明过程,从而给出求解长直载流螺线管磁场分布的完整过程。
二、分析和计算我们接下来先给出一对镜像对称的电流元所产生磁场的特征,然后利用长直螺线管电流分布的对称性,证明磁场线平行于轴线、管内外磁场均匀以及管外磁场为零,最后应用安培环路定理给出管内的磁场。
1.引理:一对镜像对称的电流元在对称面上产生的合磁场B与此对称面垂直[2]。
一对电流元和相对于平面P镜像对称分布,电流大小相等,长度相等。
相对于P平面镜像对称的电流元和根据毕奥-萨伐尔定律,两个电流元在对称面上任一点产生的磁感应强度为根据镜像对称性所以由于垂直于对称面P,与平行,故上式括号内为0,而平行于对称面,故上式括号内垂直于对称面,上述引理成立。
2.磁场线平行于轴线Z轴设长直螺线管轴线为Z轴,在轴上任一位置,作与轴垂直的平面P。
螺线管的匝密度均匀,螺线管沿Z轴方向具有平移对称性,故螺线管的电流相对平面P镜像对称。
长直载流螺线管的磁场的研讨

长直载流螺线管的磁场的研讨本文主要讨论了长直载流螺线管的磁场。
一、螺线管概述1.1螺线管简介螺线管是由一组精密发条逐渐交错烘焙而成,其最大特征是根据普朗克定律而构成的圆弧形发条结合而成。
其取名于“螺旋线”,因为它们可以形成一个三维的螺旋状结构。
它们在日常生活中有很多用途,比如用于水泵,减速机和升降机中的推动机构,甚至可以用于摩托车和轿车的分动器中。
1.2螺线管的结构形式螺线管的结构有多种多样,其中最常用的是“长直型螺线管”。
这种结构形式是由一根长轴(即供料极),上面安装有发条,形成螺旋型发条形状,以此来推动物体。
二、长直载流螺线管的磁场2.1磁性材料的特性长直的载流螺旋线管,一般采用的是磁性材料,磁性材料具有极化和抗磁性的特性。
磁化作用可以使磁性材料上的某个部分的磁场强度增强,而抗磁性使得它能够有效地抵制外部磁场的影响,从而实现对物体运动的控制。
2.2长直载流螺线管的形成当长直载流螺线管成形后,它形成一个环形磁块,通过外部电路来驱动发条,形成一个多轴转向受电的直轴磁场。
轴上的磁场强烈,沿着半径的磁场则有较大的弱化,中心有一点点的磁力线,且轴上的磁场非常均匀。
2.3磁场的传递原理长直载流螺线管施加了坐标系外的直线电流,这样就形成了环形磁力线,但当物体通过环形磁力线 s 周围时,所产生的磁场将随着它们之间的距离而由强转弱,即所谓的磁距效应,进而可以控制物体的移动。
三、结论以上,本文就长直载流螺线管的磁场的研究展开了介绍,从螺线管的概述、结构形式、磁性材料的特性及磁场的特性,以及磁场的传递原理这几个方面来介绍。
本文的研究主要强调了载流螺线管驱动直线电流形成环形磁力线,在磁场的作用下,可以控制物体的移动轨迹,因而在推动和传输机械结构上有着广泛的应用。
当前,螺线管的磁场在技术领域被越来越多地应用,特别是在精确测量和控制方面有很多不可替代的优势,因此,开发其磁场的应用越来越受到全世界的重视。
载流直螺线管轴线上磁场的讨论

载流直螺线管轴线上磁场的讨论
直螺线管轴线上磁场是指将直螺管安装在轴线上,并使用电流生成定向悬浮磁场,实现对物体的吊挂、悬浮和定向运动。
随着技术的发展,直螺线管轴线上磁场已被广泛地用于工业生产线,尤其是车间生产线上的调度原理。
直螺线管轴线上磁场的形成原理是:通过电动机为直螺线管轴线带电,实现在
轴线上的电动力的交互作用,形成定向的悬浮力,使得装有物体在轴线之外悬浮,形成悬浮磁场。
由于定向悬浮磁力,使得悬浮物体能够在轴线中移动,从而达到控制物体移动的目的。
在工业生产线中,使用直螺线管轴线上磁场可以有效提高生产效率,并减少不
必要的损失。
由于直螺线管轴线上磁场的悬浮物体不受地面干扰,处理货物的速度更快,从而减少货物在车间中的移动时间,进一步提高了生产率。
此外,由于直螺线管轴线上磁场的定向悬浮力使得悬浮物体不会受到外部干扰,使得物体定向运动时不用担心因其他物体撞击而发生碰撞,大大减少货物损坏。
综上所述,直螺线管轴线上磁场具有很强的优势,特别适用于工业生产线。
通
过技术发展,直螺线管轴线上磁场可以改善工业生产过程中管理和控制方面的问题,因此,正在得到越来越多的使用和推崇。
长直载流导线空间磁场分布的分析
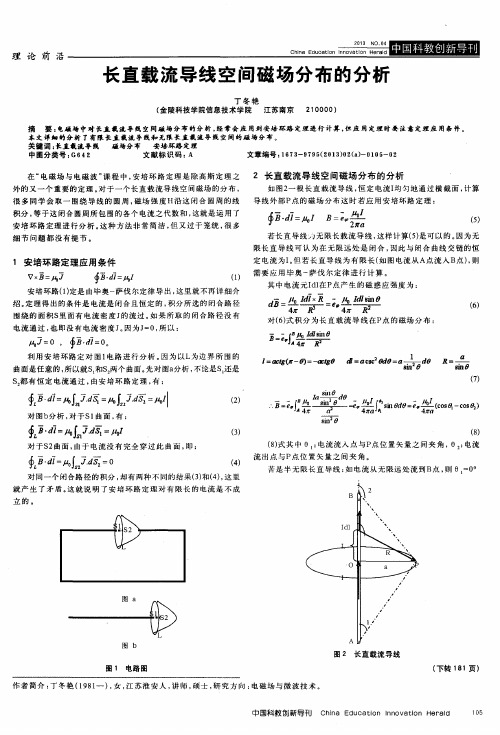
积分 , 和 , 这就 是 运 用 了 安培环路定理进行分析 。 这种方法非常简洁 , 但又过于笼统 , 很 多 细节 问题都没有提节 。
=
曰-_
( 5 )
若长 直 导 线 , 0 无 限长 载 流 导 线 , 这 样 计 算( 5 ) 是可以的。 因为 无 限长 直 导 线 可 认 为 在 无限 远 处 是 闭 合 , 因此 与闭 合 曲线 交 链 的 恒
1  ̄ l d l x R
:
安 培 环路 ( 1 ) 定是 由毕 奥 一 萨 伐 尔定 律 导 出 , 这 里 就 不再 详 细介
绍。 定 理 得 出 的条 件 是 电 流是 闭合 且恒 定 的 , 积 分 所 选的 闭合 路 径 围绕 的 面积 S 里面 有 电流 密 度J 的流过。 如 果 所 取 的 闭 合路 径 没 有 电流 通 过 , 也 即没 有 电流 密 度 J 。 因为 J =O , 所以:
4
r j
:
; 1  ̄ I d l s i n 0
’ 4 R
( 6 )
…
对( 6 ) 式 积 分 为长 直 载 流 导 线 在 P 点的磁场分布 : , & 否 = ; f
^
I a l s i no
2
- 厂 = 0,中 B・ d l = 0 。
利用安培环路定对 图1 电路 进 行 分 析 。 因为以L 为边 界 所 围 的 曲面 是任 意 的 , 所 以就 S , , n s , 两 个 曲面 。 先 对 图a 分析 , 不 论是 S 。 还是 S , 都 有 恒 定 电流 通 过 , 由 安 培 环 路 定理 , 有:
1 安培环路定 理应用条件
V x B= B・ d l = 硒, ( 1 )
长直载流螺线管的磁场的研讨

fol (< , ln ̄ r ) t
∞oi egcun Si= v, kim e mn i n 1 。 n n us a廿di isI ‘ d 1 en o tB > y ’ …
Ke r s s ln i ; u f c u r n ; g e i i d ci n i tn i ; au lto s b u d r o d t n y wo d : o e o d s ra ec r e t ma n t u t e st v l er ai n ; o n a y c n i o s cn o n y e i
r
.
+ 嚷
玎 具有 1 数量级, > ( 0 >
+( Xz一 /) 1 n
厂— ■ ——— — — ■
), 这正是采用将载流螺线管“ 近似地看成一系列圆线 圈并排起来组成 .
的【” 1 ‘ 电流【’ 圆形 J ’ 3 这一物理模型的物理 内涵. J , 故可取
圈 /匝,载 电流为 当 L> , / >R时 , 可视 为无 限长 载流 螺线 管.
取螺线管轴线为 z轴, z轴正方向与导线绕向成右手螺旋关系, 建柱面坐标系. 载流螺线管的电流分 布, 可视为 r =R之圆柱面上 的螺旋形面电流, 其面电流密度为 = I 采用螺旋形面电流这一物理模型 n,
> . )
场分布, 得到其磁感应强度为 =f』 感应强度 ; 磁 边值 关系;边界务件 中图分类号: 4 1 0 4 文献标识码 : A 文章编号: 6 25 9 (0 00 —0 20 17 .2 82 1)10 7.2
Re e r h o h a n tcFil f s a c n t eM g ei ed o n t a g t Lo g S r i h Cu r n - a r i gS ln i r e tc r y n o e o d ・
无限长密绕载流螺线管内外磁场的深入分析

宋宏权: 无限长密绕载流螺线管内外磁场的深入分析
第2 O期
无 限长密绕载 流螺线 管 内外磁 场 的深入 分析
宋宏 权
周 口师范 学 院物理 与 电子 工程 系 河南 周 口 4 60 60 0 籀 薹 针 对 普通 物理 学 中理想 螺线 管外 磁场 为 零 的 问题 ,提 出建立 与实 际更 接近 的螺 线 管模
量 。 因在6 边 和幽 边 的 管 内 部分 处 的磁 场 ( 内磁 场 ) c 管 否与 垂 直 ,故 对积 分无 贡 献 ;而 在6 边 和 出 边 的 管 外 c
壳 层表 面平 行 于轴 向的 电流 螺 线管 内不产 生磁 场 ,对 在
I
1 : ———— ——一 — ——— — 0
生的硝 直的计 汤 算
1)先 计 算 氡 的 径 向 分 量 巨 。作 如
图 3所 示 的 同 轴 圆 柱 面 。 根 据 磁 场 GauSS 定 理 ,通 过 上 述 闭 合 圆 柱 面 的 磁 通 量 为 零 , 即
・
图1
其 中 为 螺 线 管 半 径 , 轴 向 与 环 向 分 量 为 :
i i
相 等 ,并 与侧 面 垂 直 ,则 上式 积 分可 得 : , =0,
一oo
轴 向 总 电流 为 :
: ; 向= 向2w =,。 通 过 单 位 长 度 线 R
的大 小为 :
亭 f + =f 一 君
・ ・ 0 + = 。
2 兀Rsn仪 i
由 于 左 右 底 面 、
墨与蜃 垂直,故积分 ,
为 零 。 则 由上 式 可 得 :
的 面%
图3
l瓦・ l 一
由 轴对称可知, 侧面各点径向 磁场强度蜃 大小都 ,
螺线管自感系数的讨论

1.圆线圈载流轴线上磁感应强度的大小
线圈半径为R,通以 电流I,则其轴线上 点Z处
Bz
0 IR2
3
2 R2 Z 2 2
2.没有铁芯时有限长密绕螺线管轴线上磁 感应强度的大小.
没有铁芯时有限长密绕螺线管轴线上磁感应强度
Bp
0 nI
2
cos 2
cos1
3.沿轴向均匀磁化的有限长磁棒轴线上磁 感应强度的大小.
引言
考虑如图的螺线管, 其自感系数
L 0n 2V
若从P点剪断,再接 合。即视为AP,PB 两螺线管的串联,则
A
P
B
LAP 0n2s Ap LBp 0n2sBp
L` LAP LBP 2M
0n2s Ap 0n2sBp 2M
L 2M
M K LAp LBp
2
l12 R 2 R
l 2 R 2
l
2 2
R2
l12 R 2 R ]
l1 l2
l1 n20 Is l12 R2 R
是l1在自身处产生的磁通,则l1自感L1为
L1
1 I
n 2 0 s
l12 R2 R
l2
n 2 0 Is
2
l 2 R2 l22 R2 l12 R2 R
为l2在l1处产生的磁通量,则互感M为:
M 21
n20s
2
l2 R2
l
2 2
R2
l12 R 2 R
若为无限长螺线管,l>>R,l1>>R,l2>>R
载流长直导线的磁场

B 0nI / 2
实 际 上 , L>>R 时,螺线管内部的
0nI
0nI
B
磁场近似均匀,大
2
小为 0nI
A1
O
A2
载流圆线圈轴线上的磁场
例 一个半径R为的塑料薄圆盘,电量+q均匀分布其上,圆
盘以角速度绕通过盘心并与盘面垂直的轴匀速转动。求
圆盘中心处的磁感应强度。
解:带电圆盘转动形成圆电流,取距盘心r处宽度
1 r
2
p
dB
R A2
又 R2 l 2 R2 csc2
B
L
0R2nI d l
2(R2 l 2 )3/
2
l dl
0 nI 2 sin d
2
1
0
2
nI (cos
2
cos
1 )
载流圆线圈轴线上的磁场
讨论:
B
0nI
2
(cos
2
cos 1)
(1)螺线管无限长 1 , 2 0 B 0nI
两线圈在轴线上各点的场强方向均沿轴线向右在圆心处磁感应强度相等大小都是载流圆线圈轴线上的磁场载流圆线圈轴线上的磁场两线圈间轴线上中点p处磁感应强度大小为载流圆线圈轴线上的磁场载流圆线圈轴线上的磁场两点处磁感应强度都等于载流圆线圈轴线上的磁场载流圆线圈轴线上的磁场在线圈轴线上其他各点磁感应强度的量值都介之间
电子的轨道角动量是满足量子化条件的,在玻尔
理论中,其量值等于(h/2π)d的整数倍。所以
氢原子在基态时,其轨道磁矩为
载流圆线圈轴线上的磁场
B
e 2me
h
2
eh
4me
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
{ ( { ( R { (
“ R2 " - X A X r - Y A Y e
』 : : 引 』 ) i n 础)
) d O ( 1 2 )
( 4 )
在以上推导过程中, 没有对P 点的位置做任何约束 , 瞧
可以是长直螺旋管内部任意一点( 对应 、 ) <R, 也 可以是其外部的任意一点( 对应 、 ) >R o( 1 2 ) 式 对P 点磁感强度的求解最终转化为一个积分问题 ( 有关推 导请见附录) 。 ( a ) 当 删 : 2 订, ;
=
4
8 ) 订 J 』 0 — 嘞 + i 一 = A + , + ( z — 锄 P 一 ' P ) (
图3 长 直螺 旋 管剖 面 图
上述三种情况 中,第一种情况对应了长直螺旋管内部 任意一点的磁场 ,第二种情况对应长直螺旋管外部任意一 点的磁场 ,而第三种情况计算的是螺线管的管面电流层 中 心位置的磁场。通常情况下所谓的载流长直螺线管是指该 螺线管可视为“ 无 限长” 亦即螺线管的长度远大于其直径且 单层均匀密绕载流螺线管厚度可以忽略不计的这样一个物 理模型。而实际上不存在“ 无限长” 且厚度可忽略的理想情 况, 但在研究物理问题 的时候 , 可作近似处理 , 把它抽象为 理想载流长直螺线管模型。 因此, 一般情况下( 1 5 ) 式对考 察载流长直螺线管 的磁场没有物理意义 , 可舍弃。但是 , 从 物理意义上来讲 ,当载流长直螺线管 的电流层厚度必须考 虑时 ,电流层 中的磁场将从螺旋管 内部的 , 逐渐降低到 外部的零 。从以上理论计算可见 ,从毕奥一 萨伐尔定律出 发 ,先计算 出单匝载流园线圈在其周围任一点所产生的磁 感强度 , 再根据这一结论 , 利用等效电流叠加求出载流长直 螺线管 内任一点的磁感强度为 t , ,载流长螺线管外部磁 感强度是零 。与一般大学物理教材 中利用磁场中的安培环
( 6 )式即为单匝载流圆线圈在其周围任一点所产生 的 总磁场。
( c ) 当r p = R 时: 7 j _ 二 = ! 譬 生' d 0 - = 订 ,
| u \xr 。 c A r’\ ’} r,^) ‘
, 2
( 1 5 )
二、 载流长直螺线管的磁场 下面根据此式并利用等效电流叠加求出载流长直螺线 管内外任一点的磁场。 对于载流长直螺线管 , 其剖面图如图3 所示 , 在螺线管 上沿轴 向任取一小段d , 那么这一小段上 的线圈相当于电 流为I n d Z A 的一载流 圆线圈 ,其中, 为通电电流 、 n 为单位长 度的匝数。根据 ( 6 ) 式可知, 这一等效载流圆线圈在任一点 P 所产生的磁感强度为
标, 在载流圆线圈A 点处 , 取一电流元/ d l , 考察它在其周围
根据2 ( a ) , P  ̄ I I C 点都在o x y 平面内, 存在几何关系
、 /
—
s i n o / =— h
任一点P 所产生的磁感强度。图2 ( b ) 为其侧视图 , e l 为电流 元单位矢量。 取A 点位置为( , , g A ) , P 点位置为( , 0 ) 。 则任意电流元:
Z = 膪d O e t = I Rd O ( 一 s i n O i + c o  ̄ O j) ( 1 )
z A ’ . h c o t a
( 1 O )
对( 1 0 ) 式中最后一个等式 的两边微分 :
如 ̄ h c l f c 妇 ( 1 1 )
将上式代入( 9 ) 式可得
一
因此整个载流长直螺线管在任一点P 所产生的总磁感
-
1 0 7 -
2 0 1 4年 4 月 第 1 8期
教 育 教 学 论 坛
E D UC ATI ON TE ACH I N G F ORU M
= ・
其中:
x . = Rc o s O x t , = r p c o s e p
y A = Rs i n O y r = r e s i n  ̄
( 2 )
: ・
;
(
) j + ( y y - z . k -
( 3 )
=
・
根据毕奥一 萨伐尔定律, 电流Y  ̄ I d l ' 在P 点产生的磁场[ 3 1 :
( 1 3 )
:
生
塑
坐
41 r
:
d O - x A z a i - y a z A j ) + ( R 2 - x . x t , - - ny e ) k
,
ቤተ መጻሕፍቲ ባይዱ
41 r
( 5 )
则载流圆线圈在P 点产生的总磁场为 :
÷ +
茜 = = 筹
其 中,
— A Z 一 : ^ + ( R2 -
2 014 年 4 月 第 1 8期
一
教 育 教 学论 坛
ED UC A TI O N TE ACH I NG F OR UM
A p r . 2 01 4
N O . 1 8
、
载流圆线圈的磁场
y
1
强度可 以通过对出 在无穷长区间积分得到:
( b )
E
( 6 )
( b ) 当 r e > R 时: I 7 二 k = !
( 7 )
,2 订 n ,
x rx a J ‘ +\ ,P A ) ‘
L d , O = O , = 0 ( 1 4 )
r = AP = % / ( X  ̄X . ) 2 + ( y r - y A ) 2 + Z 2
A 1
=
图2 单 匝载流 圆线 圈与 坐标 关 系
{ (
= =
』 二 争)
( 9 )
首先考察单匝载流圆线圈在其周围空间任一点激发的
磁场 。 设有单匝载流圆线圈, 其半径为R, 通有电流I , 计算在 其周 围任一点所产生的磁感强度。如 图2 ( a ) 所示 , 选取坐
