物理化学第六章 (3)
大学物理化学核心教程课后参考答案第6章
第六章相平衡一．基本要求1．掌握相平衡的一些基本概念,会熟练运用相律来判断系统的组分数、相数和自由度数;2．能看懂单组分系统的相图,理解相图中的点、线和面的含义及自由度,知道相图中两相平衡线的斜率是如何用Clapeyron方程和Clausius-Clapeyron方程确定的,了解三相点与凝固点的区别;3．能看懂二组分液态混合物的相图,会在两相区使用杠杆规则,了解蒸馏与精馏的原理,知道最低和最高恒沸混合物产生的原因;4．了解部分互溶双液系和完全不互溶双液系相图的特点,掌握水蒸汽蒸馏的原理;5．掌握如何用热分析法绘制相图,会分析低共熔相图上的相区、平衡线和特殊点所包含的相数、相的状态和自由度,会从相图上的任意点绘制冷却时的步冷曲线;了解二组分低共熔相图和水盐相图在湿法冶金、分离和提纯等方面的应用;6．了解生成稳定化合物、不稳定化合物和形成固溶体相图的特点,知道如何利用相图来提纯物质;二．把握学习要点的建议相律是本章的重要内容之一,不一定要详细了解相律的推导,而必须理解相律中各个物理量的意义以及如何求算组分数,并能熟练地运用相律;水的相图是最简单也是最基本的相图,要把图中的点、线、面的含义搞清楚,知道确定两相平衡线的斜率,学会进行自由度的分析,了解三相点与凝固点的区别,为以后看懂相图和分析相图打好基础;超临界流体目前是分离和反应领域中的一个研究热点,了解一些二氧化碳超临界流体在萃取方面的应用例子,可以扩展自己的知识面,提高学习兴趣;二组分理想液态混合物的相图是二组分系统中最基本的相图,要根据纵坐标是压力还是温度来确定气相区和液相区的位置,理解气相和液相组成为什么会随着压力或温度的改变而改变,了解各区的条件自由度在二组分相图上都是条件自由度,为以后看懂复杂的二组分相图打下基础;最高或最低恒沸混合物不是化合物,是混合物,这混合物与化合物的最根本的区别在于,恒沸混合物含有两种化合物的分子,恒沸点的温度会随着外压的改变而改变,而且两种分子在气相和液相中的比例也会随之而改变,即恒沸混合物的组成也会随着外压的改变而改变,这与化合物有本质的区别;杠杆规则可以在任何两相区使用,但也只能在两相区使用,在三相区和在三相平衡线上是不能使用杠杆规则的;从具有最高会溶温度的相图,要认清帽形区的特点,是两液相的平衡共存区,这对今后理解两个固溶体也会形成帽形区很有帮助;在学习用热分析法绘制二组分低共熔相图时,首先要理解在步冷曲线上为什么会出现转折点和水平线段,这一方面要从散热与释放出的凝固热进行补偿的角度理解,另一方面要从自由度的变化来理解;理解了步冷曲线上自由度的变化情况,对相图中的自由度就容易理解;要花较多的精力掌握简单的二组分低共熔相图,要进行相区、两相平衡线、三相平衡线和特殊点的自由度分析,这样今后就容易看懂和理解复杂相图,因为复杂相图一般是简单相图的组合;低共熔混合物到底有几个相这个问题初学时容易混淆,答案当然是两相,不过这是两种固体以微小的结晶均匀混合的物系,纵然在金相显微镜中看起来也很均匀,但小晶体都保留着原有固体的物理和化学性质,所以仍是两相;低共熔点的温度和组成都会随着外压的改变而改变,所以低共熔混合物也不是化合物;对于形成稳定化合物和不稳定化合物的相图,要抓住相图的特点,了解稳定化合物的熔点与不稳定化合物的转熔温度之间的差别,比较一般的三相线与不稳定化合物转熔时的三相线有何不同要注意表示液相组成点的位置有什么不同,这样在分析复杂相图时,很容易将稳定化合物和不稳定化合物区别开来;固溶体是固体溶液的简称,固溶体中的“溶”是溶液的“溶”,所以不要把“溶”字误写为“熔”字;既然固溶体是溶液的一种,实际是混合物的一种即固体混合物,所以固溶体是单相,它的组成线与液态溶液的组成线一样,组成会随着温度的改变而改变;在相图上,固溶体总是处在由两根曲线封闭的两相区的下面;在分析复杂相图,首先要能正确认出固溶体或帽形区的位置,则其他相区的分析就变得简单了;三．思考题参考答案1．硫氢化铵NH HS(s)的分解反应：①在真空容器中分解；②在充有一定4NH(g)的容器中分解,两种情况的独立组分数是否一样3答：两种独立组分数不一样;在①中,C =1;因为物种数S 为3,但有一个独立的化学平衡和一个浓度限制条件,所以组分数等于1;在②中,物种数S 仍为3,有一个独立的化学平衡,但是浓度限制条件被破坏了,两个生成物之间没有量的限制条件,所以独立组分数C =2;2．纯的碳酸钙固体在真空容器中分解,这时独立组分数为多少答： 碳酸钙固体的分解反应为 32CaCO (s)CaO(s)CO (g)+物种数为3,有一个平衡限制条件,但没有浓度限制条件;因为氧化钙与二氧化碳不处在同一个相,没有摩尔分数的加和等于1的限制条件,所以独立组分数为2;3．制水煤气时有三个平衡反应,求独立组分数C1 H 2Og+ Cs= H 2g+ COg2 CO 2g+ H 2g= H 2Og+ COg3 CO 2g+ Cs= 2COg答： 三个反应中共有5个物种,5S =;方程1可以用方程3减去2得到,因而只有2个独立的化学平衡,2R =;没有明确的浓度限制条件,所以独立组分数3C =;4．在抽空容器中,氯化铵的分解平衡,43NH Cl(s)NH (g)HCl(g)+;指出该系统的独立组分数、相数和自由度数答：反应中有三个物种,一个平衡限制条件,一个浓度限制条件,所以独立组分数为1,相数为2;根据相律,自由度为1;即分解温度和分解压力两者之中只有一个可以发生变化;5．在含有氨的容器中氯化铵固体分解达平衡,43NH Cl(s)NH (g)HCl(g)+;指出该系统的独立组分数、相数和自由度答： 反应中有三个物种,一个平衡限制条件,没有浓度限制条件;所以独立组分数为2,相数为2,自由度为2;6．碳和氧在一定条件下达成两种平衡,指出该系统的独立组分数、相数和自由度数;答：物种数为4,碳,氧,一氧化碳和二氧化碳,有两个化学平衡,无浓度限制条件,所以独立组分数为2,相数为2,自由度为2;7．水的三相点与冰点是否相同答：不相同;纯水的三相点是气-液-固三相共存,其温度和压力由水本身性质决定,这时的压力为 Pa,温度为 K ;热力学温标1 K就是取水的三相点温度的1/ K ;水的冰点是指在大气压力下,冰与水共存时的温度;由于冰点受外界压力影响,在 kPa压力下,冰点下降 K,由于水中溶解了空气,冰点又下降 K,所以在大气压力为 kPa 时,水的冰点为 K ;虽然两者之间只相差 K,但三相点与冰点的物理意义完全不同;8．沸点和恒沸点有何不同答：沸点是对纯液体而言的;在大气压力下,纯物质的液-气两相达到平衡,当液体的饱和蒸气压等于大气压力时,液体沸腾,这时的温度称为沸点;恒沸点是对二组分液相混合系统而言的,是指两个液相能完全互溶,但对Raoult定律发生偏差,当偏差很大,在p x-图上出现极大值或极小值时,则在T x-图上出现极小值或极大值,这时气相的组成与液相组成相同,这个温度称为最低或最高恒沸点,用简单蒸馏的方法不可能把二组分完全分开;这时,所对应的双液系统称为最低或最高恒沸混合物;在恒沸点时自由度为1,改变外压,恒沸点的数值也改变,恒沸混合物的组成也随之改变;当压力固定时,条件自由度为零,恒沸点的温度有定值;9．恒沸混合物是不是化合物答：不是;它是完全互溶的两个组分的混合物,是由两种不同的分子组成;在外压固定时,它有一定的沸点,这时气相的组成和液相组成完全相同;但是,当外部压力改变时,恒沸混合物的沸点和组成都会随之而改变;化合物的沸点虽然也会随着外压的改变而改变,但它的组成是不会改变的;10．在汞面上加了一层水能减少汞的蒸气压吗答：不能;因为水和汞是完全不互溶的两种液体,两者共存时,各组分的蒸气压与单独存在时的蒸气压一样,液面上的总压力等于纯水和纯汞的饱和蒸气压之和;如果要蒸馏汞的话,加了水可以使混合系统的沸点降低,这就是蒸气蒸馏的原理;所以,仅仅在汞面上加一层水,是不可能减少汞的蒸气压的,但是可以降低汞的蒸发速度;11．单组分系统的三相点与低共熔点有何异同点答：共同点：两者都是气-液-固三相共存;不同点：单组分系统的三相点是该组分纯的气、液、固三种相态平衡共存,这时的自由度等于零,它的压力、温度由系统自身的性质决定,不受外界因素的影响;而二组分系统在低共熔点如T-x图上的E点温度时,是纯的A固体、B固体和组成为E的熔液三相平衡共存,这时的自由度为1,在等压下的条件自由度等于零;E点的组成由A和B的性质决定,但E点的温度受压力影响,当外压改变时,E点的温度和组成也会随之而改变;12．低共熔混合物能不能看作是化合物答：不能;低共熔混合物不是化合物,它没有确定的熔点,当压力改变时,低共熔物的熔化温度和组成都会改变;虽然低共熔混合物在金相显微镜下看起来非常均匀,但它仍是两个固相微晶的混合物,由两个相组成;13．在实验中,常用冰与盐的混合物作为致冷剂;试解释,当把食盐放入0℃的冰-水平衡系统中时,为什么会自动降温降温的程度有否限制,为什么这种致冷系统最多有几相解： 当把食盐放入0℃的冰-水平衡系统中时,由于食盐与冰有一个低共熔点,使水的冰点降低,因此破坏了冰-水平衡,冰就要融化;融化过程中要吸热,系统的温度下降;降温有一定的限度,因为它是属于二组分系统的低共熔混合物,当温度降到低共熔点时,冰、食盐与溶液达到了平衡,系统的温度就不再下降;根据相律：2f C P =+-,组分数为2H O(l)和NaCl(s),2C =;当0f =时,最多相数4P =,即气相,溶液,冰和NaCls 四相共存;如果指定压力,则条件自由度等于零时,最多相数3P =,溶液,冰和NaCls 三相平衡共存;四．概念题参考答案1．4NH HS(s)与任意量的3NH (g)及2H S(g)达平衡时,有A C = 2,P = 2,f = 2BC = 1,P = 2,f = 1C C = 2,P = 3,f = 2D C = 3,P = 2,f = 3答：A;系统中有三个物种,一个平衡条件,由于已存在3NH (g)及2H S(g),就不存在浓度限制条件,所以组分数2C =;平衡共存时有固相和气相两个相,根据相律,自由度2f =;2．在大气压力下,3FeCl (s)与2H O(l)可以生成32FeCl 2H O(s),32FeCl 5H O(s),32FeCl 6H O(s)和32FeCl 7H O(s)四种固体水合物,则该平衡系统的组分数C 和能够平衡共存的最大相数P 为A 3, 3C P ==B 3, 4C P == C 2, 3C P ==D 3, 5C P == 答：C;这是二组分系统生成稳定化合物或稳定水合物的一个例子,3FeCl (s)与2H O(l)可以生成多种水合物,但它还是二组分系统,所以组分数必定等于2;不能把生成的稳定水合物也看作是组分;如果要写出生成水合物的多个平衡方程式,则多一个水合物物种,也多一个化学平衡方程,所以组分数是不会改变的;根据组分数等于2这一点,就可以决定选C;根据相律,当自由度等于零时,能得到平衡共存的最大相数;则20f C P =+-=,理论上最大相数似乎应等于4,但是题目已标明是在大气压力下,用*13f C P P =+-=-,所以能见到的平衡共存的最大相数只有3个;如果题目不标明是在大气压力下,由于凝聚相系统受压力影响极小,也应该看作是在等压条件下进行的,能见到的平衡共存的最大相数只能是3个;3．在 100 kPa 的压力下,2I (s)在2H O(l)和4CCl (l)两个完全不互溶的液相系统中达分配平衡;设平衡时2I (s)已不存在,则该系统的组分数和自由度数分别为A *2, 1C f ==B *2, 2C f == C *3, 2C f ==D *3, 3C f == 答：C;该系统中显然有2I (s),2H O(l)和4CCl (l)三个物种,3S =,但无化学平衡,0R =,也无浓度限制条件,'0R =不要把2I 在两相中的分配平衡看作是浓度关系式,因为在推导分配常数时已用到了2I 在两相中化学势相等的条件,所以组分数3C =;由于是两相平衡,又指定了压力,所以条件自由度*13122f C P =+-=+-=;4．4CuSO 与水可生成42CuSO H O ⋅,42CuSO 3H O ⋅和42CuSO 5H O ⋅三种水合物,则在一定温度下与水蒸气达平衡的含水盐最多为A 3种B 2种C 1种D 不可能有共存的含水盐答：B;系统的组分数为2,已指定温度,根据相律,条件自由度等于零时,可得最多可以共存的相数,*1210f C P P =+-=+-=,最多可以三相共存;现在已指定有水蒸气存在,所以,可以共存的含水盐只可能有2种;5．某一物质X,在三相点时的温度是20℃,压力是200 kPa;下列哪一种说法是不正确的A 在20℃以上,X 能以液体存在B 在20℃以下,X 能以固体存在C 在25℃和100 kPa 下,液体X 是稳定的D 在20℃时,液体X 和固体X 具有相同的蒸气压答：C;可以画一张单组分系统相图的草图,C 所描述的条件只能落在气相区,所以这种说法是不正确的;6．2N 的临界温度是124 K,如果想要液化2N (g),就必须A 在恒温下增加压力B 在恒温下降低压力C 在恒压下升高温度D 在恒压下降低温度答：D;临界温度是指在这个温度之上,不能用加压的方法使气体液化,所以只有在恒压下用降低温度的方法使之液化;7．当Clausius-Clapeyron 方程应用于凝聚相转变为蒸气时,则A p 必随T 之升高而降低B p 必不随T 而变C p必随T之升高而变大D p随T之升高可变大也可减少答：C; 因为凝聚相转变为蒸气时总是吸热的,根据Clausius-Clapeyron方程,等式右方为正值,等式左方也必定为正值,所以p随T之升高而变大;8．对于恒沸混合物的描述,下列各种叙述中不正确的是A 与化合物一样,具有确定的组成B 不具有确定的组成C 平衡时,气相和液相的组成相同D 恒沸点随外压的改变而改变答：A;恒沸混合物不是化合物,不具有确定的组成,其恒沸点和组成都会随着外压的改变而改变;9．对于二组分气—液平衡系统,哪一个可以用蒸馏或精馏的方法将两个组分分离成纯组分A接近于理想的液体混合物B对Raoult定律产生最大正偏差的双液系C对Raoult定律产生最大负偏差的双液系 D部分互溶的双液系答：A;完全互溶的理想双液系,或对Raoult定律发生较小正负偏差的都可以用蒸馏或精馏的方法将其分开,两者的沸点差别越大,分离越容易;而对Raoult定律产生最大正负偏差的双液系,气－液两相区分成两个分支,形成了最低或最高恒沸混合物,用蒸馏方法只能得到一个纯组分和一个恒沸混合物;部分互溶的双液系首先要将两个液层分离,然后视具体情况而决定分离两个互溶部分的液相,或采用萃取的方法,单用蒸馏方法是不行的;10．某一固体,在25℃和大气压力下升华,这意味着A 固体比液体密度大些B 三相点的压力大于大气压力C 固体比液体密度小些D 三相点的压力小于大气压力答：B;画一单组分系统相图的草图,当三相点的压力大于大气压力时,在25℃和大气压力下处于气相区,所以固体会升华;2CO 的相图就属于这一类型;11．在相图上,当系统处于下列哪一点时,只存在一个相A 恒沸点B 熔点C 临界点D 低共熔点答：C;在临界点时,气-液界面消失,只有一个相;其余三个点是两相或三相共存;12．在水的三相点附近,其摩尔气化焓和摩尔熔化焓分别为144.82 kJ mol -⋅和15.99 kJ mol -⋅;则在三相点附近,冰的摩尔升华焓为 A 138.83 kJ mol -⋅ B 150.81 kJ mol -⋅C 138.83 kJ mol --⋅D 150.81 kJ mol --⋅答：B;摩尔升华焓等于摩尔气化焓与摩尔熔化焓之和;13．某反应系统中共有的物种为Ni(s),NiO(s),2H O(l),2H (g),CO(g)和2CO (g),它们之间可以达成如下三个化学平衡1 ,12NiO(s)CO(g)Ni(s)CO (g)p K ++ 2 ,2222H O(l)CO(g)H (g)CO (g)p K ++ 3 ,322NiO(s)H (g)Ni(s)H O(l)p K ++该反应的组分数C 和平衡常数之间的关系为A ,1,2,33, p p p C K K K ==B ,3,1,24, /p p pC K K K == C ,3,1,23, /p p p C K K K ==D ,3,2,14, /p p p C K K K ==答：B;这个系统有6个物种,在三个化学平衡中只有2个是独立的,没有其他限制条件,所以组分数4C =;因为(1)(2)(3)-=,方程式的加减关系,反应的Gibbs 自由能也是加减关系,而平衡常数之间则是乘除关系,所以,3,1,2/p p p K K K =;14．将纯的2H O(l)放入抽空、密闭的石英容器中,不断加热容器,可以观察到哪种现象A 沸腾现象B 三相共存现象C 升华现象D 临界现象 答：D;在单组分系统的相图上,是该系统自身的压力和温度,就象该实验所示;实验不是在外压下进行的,系统中也没有空气,所以不可能有沸腾现象出现;在加热过程中,水的气、液两种相态一直处于平衡状态,即22H O(l)H O(g);随着温度的升高,2H O(l)的密度不断降低,而水的蒸气压不断升高,致使2H O(g)的密度变大,当2H O(l)和2H O(g)的两种相态的密度相等时,气-液界面消失,这就是临界状态;15．Na 2CO 3和水可形成三种水合盐：Na 2CO 3·H 2O 、Na 2CO 3·7H 2O 和NaCO 3·10H 2O;在常压下,将Na 2CO 3投入冰－水混合物中达三相平衡时,若一相是冰,一相是Na 2CO 3水溶液,则另一相是A Na 2CO 3B Na 2CO 3·H 2OC Na 2CO 3·7H 2OD Na 2CO 3·10H 2O答：D;画一张草图,NaCO 3·10H 2O 的含水量最多,一定最靠近表示纯水的坐标一边;五．习题解析1．将2N (g),2H (g)和3NH (g)三种气体,输入773 K,73.210 kPa ⨯的放有催化剂的合成塔中;指出下列三种情况系统的独立组分数设催化剂不属于组分数1 2N (g),2H (g)和3NH (g)三种气体在输入合成塔之前;2 三种气体在塔内反应达平衡时;3 开始只输入3NH (g),合成塔中无其它气体,待其反应达平衡后;解： 1 进入合成塔之前,三种气体没有发生反应,故组分数3C =;2在塔内反应达平衡时,系统的物种数3S =,但有一个化学平衡条件,故2C =; 3开始只输入3NH (g),3NH (g)分解达平衡,系统的物种数3S =,但有一个化学平衡条件和一个浓度限制条件,故1C =;2．指出下列平衡系统中的物种数,组分数,相数和自由度数;1 CaSO 4的饱和水溶液;2 将5ｇ3NH (g)通入1 dm 3水中,在常温下与蒸气平衡共存;解：1物种数2S =,4CaSO (s)和2H O(l);组分数2C =,相数2P =;根据相律,22f C P =+-=;这两个自由度是指温度和压力,即在一定的温度和压力的范围内,能保持固、液两相平衡不发生变化;2 因为3NH (g)与水会发生相互作用,生成32NH H O ⋅,所以物种数3S =,3NH (g),2H O(l)和32NH H O ⋅;有一个形成一水合氨的平衡,故1R =,所以2C =;有气、液两相,2P =;根据相律,22f C P =+-=;这两个自由度是指温度和压力,即在一定的温度和压力的范围内,能维持固、气两相平衡的状态不发生变化;3．3CaCO (s)在高温下分解为CaO(s)和2CO (g),根据相律解释下述实验事实; 1 在一定压力的2CO (g)中,将3CaCO (s)加热,实验证明在加热过程中,在一定的温度范围内3CaCO (s)不会分解;2 在3CaCO (s)的分解过程中,若保持2CO (g)的压力恒定,实验证明达分解平衡时,温度有定值;解：1 该系统中有两个物种,2CO (g)和3CaCO (s),所以物种数2S =;在没有发生反应时,组分数2C =;现在是一个固相和一个气相两相共存,2P =;当2CO (g)的压力有定值时,根据相律,条件自由度*12121f C P =+-=+-=;这个自由度就是温度,即在一定的温度范围内,可维持两相平衡共存不变,所以3CaCO (s)不会分解; 2该系统有三个物种,2CO (g),3CaCO (s)和CaO(s),所以物种数3S =;有一个化学平衡,1R =;没有浓度限制条件,因为产物不在同一个相,故2C =;现在有三相共存两个固相和一个气相,3P =;若保持2CO (g)的压力恒定,条件自由度*12130f C P =+-=+-=;也就是说,在保持2CO (g)的压力恒定时,温度不能发生变化,即3CaCO (s)的分解温度有定值;4．已知固体苯的蒸气压在273 K 时为 k Pa,293 K 时为 k Pa ；液体苯的蒸气压在293 K 时为 k Pa,液体苯的摩尔气化焓为1vap m 34.17 kJ mol H -∆=⋅;试计算1 在303 K 时液体苯的蒸气压,设摩尔气化焓在这个温度区间内是常数;2 苯的摩尔升华焓;3 苯的摩尔熔化焓;解：1 用Clausius-Clapeyron 方程,求出液态苯在303 K 时的蒸气压 解得液体苯在303 K 时的蒸气压2用Clausius-Clapeyron 方程,求出固体苯的摩尔升华焓解得固体苯的摩尔升华焓3苯的摩尔熔化焓等于摩尔升华焓减去摩尔气化焓5．结霜后的早晨冷而干燥,在-5℃,当大气中的水蒸气分压降至 Pa 时,霜会升华变为水蒸气吗 若要使霜不升华,空气中水蒸气的分压要有多大已知水的三相点的温度和压力分别为 K 和611 Pa,水的摩尔气化焓1vap m 45.05 kJ mol H -∆=⋅,冰的摩尔融化焓1fus m 6.01 kJ mol H -∆=⋅;设相变时的摩尔焓变在这个温度区间内是常数;解：冰的摩尔升华焓等于摩尔熔化焓与摩尔气化焓的加和,用Clausius-Clapeyron 方程,计算 K-5℃时冰的饱和蒸气压解得 (268.15K)401.4 Pa p =而 K-5℃时,水蒸气的分压为 Pa,低于霜的水蒸气分压,所以这时霜要升华;当水蒸气分压等于或大于401.4 Pa 时,霜可以存在;6．在平均海拔为4 500 m 的高原上,大气压力只有 kPa;已知压力与温度的关系式为 5 216 K ln(/Pa)25.567p T=-;试计算在这高原上水的沸点; 解：沸点是指水的蒸气压等于外界压力时的温度;现根据压力与温度的关系式,代入压力的数据,计算蒸气压等于 kPa 时的温度,解得： 357 K T =即在海拔为4 500 m 的高原上,水的沸点只有357 K,即84 ℃,这时煮水做饭都要用压力锅才行;7．将3NH (g)加压,然后在冷凝器中用水冷却,即可得液氨,即3NH (l);已知某地区一年中最低水温为2℃,最高水温为37℃,问若要保证该地区的氮肥厂终年都能生产液氨,则所选氨气压缩机的最低压力是多少已知：氨的正常沸点为-33℃,蒸发焓为11 368 J g -⋅,设蒸发焓是与温度无关的常数;解： 氨在正常沸点-33℃240 K 时,它的蒸气压等于大气压力,为 kPa;水温为2℃275 K 时,氨的蒸气压较低,得到液氨没有问题;主要是计算在37℃310K 时氨的蒸气压,这就是压缩机所需的最低压力;已知氨的摩尔蒸发焓为：根据Clausius-Clapeyron 方程,计算310 K 时 氨的蒸气压,;解得： (310K) 1 408.3 kPa p =即在37℃时,压缩机的最低压力必须大于1 408.3 kPa ,才能终年都能生产液氨;8．CO 2的固态和液态的蒸气压与温度的关系式,分别由以下两个方程给出：试计算： 1 二氧化碳三相点的温度和压力;2 二氧化碳在三相点时的熔化焓和熔化熵;解： 1 在三相点时,固态和液态的蒸气压相等,s l p p =,即解得三相点的温度 215.3 K T =代入任意一个蒸气压与温度的方程式,计算三相点时的压力两个结果稍有不同 解得 ()466.7 kPa p =三相点2 根据Clausius-Clapeyron 方程的一般积分式式中'C 是积分常数;对照题中所给的方程,从固体的蒸气压与温度的关系式,可计算得到二氧化碳的摩尔升华焓,从液体的蒸气压与温度的关系式,可计算得到二氧化碳的摩尔蒸发焓,摩尔熔化焓等于摩尔升华焓减去摩尔蒸发焓,9．根据2CO 的相图,回答如下问题;1说出OA ,OB 和OC 三条曲线以及特殊点O 点与A 点的含义;2在常温、常压下,将2CO 高压钢瓶的阀门慢慢打开一点,喷出的2CO 呈什么相态为什么3在常温、常压下,将2CO 高压钢瓶的阀门迅速开大,喷出的2CO 呈什么相态为什么4为什么将2CO (s)称为“干冰”2CO (l)在怎样的温度和压力范围内能存在 解：1OA 线是2CO (l)的饱和蒸气压曲线;OB 线是2CO (s)的饱和蒸气压曲线,也就是升华曲线;OC 线是2CO (s)与2CO (l)的两相平衡曲线;O 点是2CO 的三相平衡共存的点,简称三相点,这时的自由度等于零,温度和压力由系统自定;A 点是2CO 的临界点,这时气-液界面消失,只有一个相;在A 点温度以上,不能用加压的方法将。
物理化学第六章资料
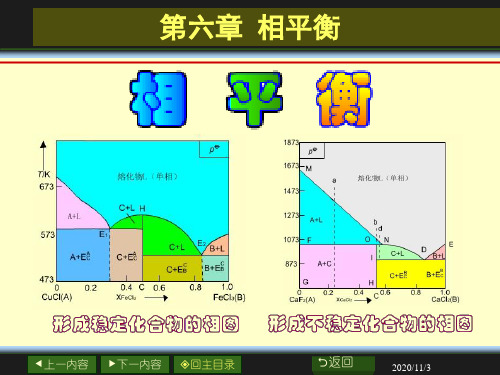
表达相平衡系统的状态如何随其组成、温度、压力等而变化。
上一内容 下一内容 回主目录
返回
2020/11/3
第六章 相平衡
相平衡的研究方法：
数学公式——如克拉佩龙方程、拉乌尔定律等。 相图——直观。 相图 多相系统的状态随温度T，压力P和组成变量
的改变而变化可用图形表示出来。 这种图称相图（又称状态图）。
上一内容 下一内容 回主目录
返回
2020/11/3
§6.1 相律
相律： 自由度数 = 总变量数－关联变量的方程式个数
F PS 2 P S P 1 R R SRR P2
令 C S R R , C为组分数，则 F C P2 —— 相律表达式
上一内容 下一内容 回主目录
返回
2020/11/3
§6.1 相律
上一内容 下一内容 回主目录
返回
2020/11/3
§6.2 单组分系统相图
单组分系统不涉及组成，要描述其状态只需T、p两个变 量，单组分系统的相图p –T 图。
1. 相律分析
P 1 F 2
(双变量系统)
F
C 3
P P
2
P
2
F
1
(单变量系统)
P3F 0
(无变量系统)
P、T均独立，在P～T图上是一个平面。
对系统相平衡的影响时，相律的形式应为
F=C-P+n
（4）对于大气压力下凝聚系统，压力影响很小，相律
的形式为F=C-P+1
上一内容 下一内容 回主目录
返回
2020/11/3
§6.1 相律
例6.1.1 在一个密闭抽空的容器中有过量的NH4I(s)，
物理化学第六章课后答案完整版
第六章 相平衡指出下列平衡系统中的组分数C ，相数P 及自由度F 。
（1） I 2(s)与其蒸气成平衡；（2） CaCO 3(s)与其分解产物CaO(s)和CO 2(g)成平衡；（3） NH 4HS(s)放入一抽空的容器中，并与其分解产物NH 3(g)和H 2S(g)成平衡； （4） 取任意量的NH 3(g)和H 2S(g)与NH 4HS(s)成平衡。
（5） I 2作为溶质在两不互溶液体H 2O 和CCl 4中达到分配平衡（凝聚系统）。
解： （1）C = 1, P = 2, F = C – P + 2 = 1–2 + 2 = 1. （2）C = 3–1 = 2, P = 3, F = C –P + 2 = 2–3 + 2 = 1. （3）C = 3–1–1 = 1, P = 2, F = C –P + 2 = 1–2 + 2 = 1. （4）C = 3–1 = 2, P = 2, F = C –P + 2 = 2–2 + 2 = 2. （5）C = 3, P = 2, F = C –P + 1 = 3–2 + 1 = 2.已知液体甲苯（A ）和液体苯（B ）在90℃时的饱和蒸气压分别为=和。
两者可形成理想液态混合物。
今有系统组成为的甲苯-苯混合物5mol ，在90 ℃下成气-液两相平衡，若气相组成为求：（1） 平衡时液相组成及系统的压力p 。
（2） 平衡时气、液两相的物质的量解：（1）对于理想液态混合物，每个组分服从拉乌尔定律，因此（2）系统代表点，根据杠杆原理mol.n mol .n n )..(n )..(.n n n )x x (n )x y (l g l g g l l l ,B o ,B g o ,B g ,B 7843216125030304556050==-=-=+-=-单组分系统的相图示意如右图。
试用相律分析图中各点、线、面的相平衡关系及自由度。
已知甲苯、苯在90℃下纯液体的饱和蒸气压分别为kPa和kPa。
物理化学第六章习题答案讲解
第六章化学动力学(三)计算题1. 293K时，敌敌畏在酸性介质中水解反应的速率常数为0.01127d-1。
若敌敌畏水解为一级反应，试求其水解反应的半衰期。
=ln2/ k =0.6931/0.01127d-1=61.5d解：t1/22．某人工放射性元素放出a粒子的半衰期为15h。
求该试样分解速率常数和分解80％所需的时间。
解：= 0.6931/15h=0.04621h-1放射性元素分解为一级反应，k=ln2/t1/2t=-ln(1-x)/k=-ln(1-0.8)/0.04621h-1=34.83h二级反应规律3. 某溶液含有NaOH 和CH3CO2C2H5，浓度均为0.0100mol ·dm-3。
在308.2K时，反应经600s 后有55.0% 的分解。
已知该皂化反应为二级反应。
在该温下，计算：(1) 反应速率常数?(2) 1200s能分解多少?(3) 分解50.0%的时间?(c A解：(1) 反应为 NaOH ＋CH 3CO 2C 2H 5 → CH 3CO 2Na + C 2H 5OH 该反应为二级且初浓度相同，故有 -d c A /d t =kc A 2 , c A =c A0(1-x ), 积分后得k = (1/t )(1/c A -1/c A0) = x /tc A0(1-x )=0.550/[600s ×0.0100mol ·dm -3×(1-0.550)]=0.204 dm 3·mol -1·s -1(2) x =1/(1+1/ktc A0) = 1/[1+1/( 0.204 dm 3·mol -1·s -1×1200s ×0.0100mol ·dm -3)]= 0.710 =71.0%(3) t 1/2= 1/kc A0 = 1/( 0.204 dm 3·mol -1·s -1×0.0100mol ·dm -3) = 490s4. 溶液反应 A + 2B → 2C + 2D 的速率方程为 -d c B /d t =kc A c B 。
物理化学试卷题库物化1000题第六章(3)
B 由动力学方程可知反应是一级的 因此反应半衰期与初浓度无关 k 的单位是 时间–1
44 气相反应 A g →2B(g)的速率常数 kp=0.1min–1 则速率常数 kc 为 A 0.1min–1 B 0.1RTmin–1 C 0.1Pamin–1 D 0.1RTPa⋅min–1
A 由 k 的单位 min–1 可知反应级数 n=1 kp 与 kc 关系为 kc=kp(RT)n–1=kp=0.1min–1
C 其速率常数为 L⋅mol–1⋅s–1 A 0.5 B 0.125 C5 D8
B
1 ∼t 为直线关系 是二级反应 截距 1 =3
C
C0
1 − 1 = kt 得 k=1/8L⋅mol–1⋅s–1 C C0
C0=1/3mol⋅L–1
当 t=8
C=3/4C0 时
代入
2A→G
A 消耗 2/3 的时间是其消耗 1/3 时间的几倍
B
双分子反应为二级反应
消耗 1/3
1 2 3 C0
−1 C0
= kt1
消耗 2/3
1 2 3 C0
−1 C0
= kt 2
两式相除 t 2 = 4 t1
59 某反应的速率常数 k=2.31×10–2S–1⋅L⋅mol–1 为
若初始浓度为 1.0mol⋅L–1
复旦大学药学院物化教研室编写
41 某一级反应 A→D A 浓度消耗 1/5 时 需要 4 秒 其半衰期为 A 12.42s B 6.21s C 4.14s D 3.11s
物化练习 1000 题
动力学
A
一级反应动力学方程为 lnC0/C=kt ln C0 =k×4 k=0.0558s–1
4 5 C0 ∴半衰期=ln2/k=12.42s
物理化学第六章习题答案
习 题1． 在293K 时，把半径为1mm 的水滴分散成半径为1μm 的小水滴，问比表面增加了多少倍？表面吉布斯自由能增加了多少？完成该变化时，环境至少需做功若干？已知293K 时水的表面张力为0.0727N·m －1。
解：半径为1.0×10-3m 水滴的表面积为A ，体积为V 1，半径为R 1；半径为1×10-6m 的水滴的表面积为A 2，体积为V 2，半径为R 2，因为1V =NV 2，所以32313434R N R ππ⋅=，式中N 为小水滴的个数。
936332110100.1100.1=⎪⎪⎭⎫ ⎝⎛⨯⨯=⎪⎭⎫⎝⎛=--R R N 1000100.1100.110442369212212=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯=⋅=--R R N A A ππ ΔG A =γΔA=()21224R NR -πγ={0.0727×4×3.14×[109×（1.0×10-6）2-（1.0×10-3）2]}J =9.13×10-4J W f = -ΔG A =-9.13×10-4J2．293K 时，根据下列表面张力的数据：试计算下列情况的铺展系数及判断能否铺展：（1）苯在水面上（未互溶前）；（2）水在汞面上；（3）苯在汞面上。
解：（1）γ（水-气）-[γ（苯-气）+γ（苯-水）] =[（72.7-28.9-35）×10-3] N·m -1=8.8×10-3 N·m -1＞0所以在苯与水未互溶前，苯可在水面上铺展。
当苯部分溶于水中后，水的表面张力下降，则当苯与水互溶到一定程度后，苯在水面上的铺展将会停止。
（2）γ（汞-气）-[γ（水-气）+γ（汞-水）] =[（486-72.7-375）×10-3]N·m -1 =38.3×10-3N·m -1＞0水在汞面上能铺展。
物理化学第六章
它们之间有如下的关系：
rA rB rE rF
ab
e
f
上页 下页 2020年7月1日星期三
回主目录
返回 11
反应速率（rate of reaction）
通常的反应速率都是指定容反应速率，它的定义为：
r 1 d
已知 d dnB
V dt
1 dnB /V 1 dcB
B
B dt B dt
对任何反应：eE fF gG hH
上页 下页 2020年7月1日星期三
回主目录
返回 10
反应速率表示方法
对于恒容反应：
aA bB eE fF
式中a，b，e，f为各反应组分计量数的绝对值，反应速率可写作：
rA
dcA dt
rB
dcB dt
rE
dcE dt
rF
dcF dt
对反应物而言，dc为负值，为使反应速率恒为正值以
上各式右边取负号；对产物而言，dc为正值，则取正号。
上页 下页 2020年7月1日星期三
回主目录
返回 3
引言
化学热力学的研究对象和局限性 化学动力学的研究对象 化学动力学发展简史
上页 下页 2020年7月1日星期三
回主目录 返回 4
化学热力学的研究对象和局限性
研究化学变化的方向、能达到的最大限度以及外界条
件对平衡的影响。化学热力学只能预测反应的可能性，
正比。幂指数就是基元反应方程中各反应物的系数。
这就是质量作用定律，它只适用于基元反应。
例如： 基元反应
反应速率r
(1) Cl2 M 2Cl M
k1[Cl2 ][M]
(2) Cl H2 HCl H k2[Cl][H2 ]
物理化学第六章知识总结分析
物理化学第六章（相平衡）知识总结在环境污染中，化学污染与物理污染是非常普遍的而且涵盖量很大的两类污染，物理化学学科是在物理与化学两大基础学科上发展起来的，所以对环境专业的学习有很大帮助，在环境专业中占有重要地位。
我国环境污染越来越严重，许多环境问题急需解决，而物理化学提供了许多基本原理，我们可以运用这些原理来解决环境问题，所以学好物理化学也是每个环境专业的学生的重中之重，下面我会对本学期物理化学学科在其中第六章（相平衡）中的知识点作一个总结与思考。
物理化学的研究内容大致可以概括为三个方面：化学体系的宏观平衡性质，以热力学的三个基本定律为理论基础，研究宏观化学体系在气态、液态、固态、溶解态以及高分散状态的平衡物理化学性质及其规律性。
而第六章讲解的内容属于宏观的平衡性质，是物理化学中较基础的部分。
在化学研究和化学生产过程中的分离操作步骤经常会遇到各种想变化的过程，比如蒸发、冷凝、溶解、萃取和结晶等，在这些过程中涉及到不同的相之间的物质的传递过程。
相平衡研究就是这些单元操作的理论基础，有着至关重要的作用。
相平衡的研究任务就是要揭示多想平衡体系中的各种强度量与相变化过程的关系，而相律是用来表示相平衡系统的独立变量数和相数、独立组分数之间关系的规律。
第一节、相律一、相、组分和自由度1、相和相数（P）相：所有的性质（物理性质、化学性质）完全均匀的部分相数：体系中相的总数，用P表示2、组分和组分数（C）在不发生化学变化时的系统中，组分数等于系统中存在的物质数目（物种数S）：发生化学变化时等于系统中存在的独立物质的数目（独立的种数）C=S-R-R’组分数=物种数-化学变化反应数-独立的浓度关系式数3、自由度和自由度数（F）自由度：能够维持系统原有的相数而可以独立改变的变量成为自由度自由度数：自由度的数目，用F表示。
二、简单相平衡系统分析1、单组份系统C=1gP=1 l F=2(T,P)sl-gP=> P=2 l-s F=1(T或P)s-gP=3 g-l-s （0.0098℃，610.5Pa）F=02、双组份系统（C=2）组分数增多，自由度数增多F随C增大，随P减小，F=C-P+2三、吉布斯相律相律的形式F=C-P+NN:包含所有处界影响因素（含温度、压力）的数目，则相律的形式应为F=C-P+N（电场、磁场、重力场等）N=2时，表示系统整体的温度，压力皆相同，即有F=C-P+2。
物理化学课后答案 第六章 相平衡
第六章相平衡6.1指出下列平衡系统中的组分数C，相数P及自由度F。
（1）I2(s)与其蒸气成平衡；（2）CaCO3(s)与其分解产物CaO(s)和CO2(g)成平衡；（3）NH4HS(s)放入一抽空的容器中，并与其分解产物NH3(g)和H2S(g)成平衡；（4）取任意量的NH3(g)和H2S(g)与NH4HS(s)成平衡。
（5）I2作为溶质在两不互溶液体H2O和CCl4中达到分配平衡（凝聚系统）。
解：（1）C = 1, P = 2, F = C–P + 2 = 1 – 2 + 2 = 1.（2）C = 3 – 1 = 2, P = 3, F = C–P + 2 = 2 – 3 + 2 = 1.（3）C = 3 – 1 – 1 = 1, P = 2, F = C–P + 2 = 1 – 2 + 2 = 1.（4）C = 3 – 1 = 2, P = 2, F = C–P + 2 = 2 – 2 + 2 = 2.（5）C = 3, P = 2, F = C–P + 1 = 3 – 2 + 1 = 2.6.2已知液体甲苯（A）和液体苯（B）在90 C时的饱和蒸气压分别为=和。
两者可形成理想液态混合物。
今有系统组成为的甲苯-苯混合物5 mol，在90 C下成气-液两相平衡，若气相组成为求：（1）平衡时液相组成及系统的压力p。
（2）平衡时气、液两相的物质的量解：（1）对于理想液态混合物，每个组分服从Raoult定律，因此（2）系统代表点，根据杠杆原理6.3单组分系统的相图示意如右图。
试用相律分析途中各点、线、面的相平衡关系及自由度。
解：单相区已标于图上。
二相线（F = 1）：三相点（F = 0）：图中虚线表示介稳态。
6.4已知甲苯、苯在90 ︒C下纯液体的饱和蒸气压分别为54.22 kPa和136.12 kPa。
两者可形成理想液态混合物。
取200.0 g甲苯和200.0 g苯置于带活塞的导热容器中，始态为一定压力下90 ︒C的液态混合物。
物理化学第六章课后答案完整版
第六章相平衡6.1(1)(2)(3)(4)(5)解：指出下列平衡系统中的组分数G相数P及自由度尸。
島(S)与其蒸气成平衡；CaC03 (s)与其分解产物CaO (s)和C02 (g)成平衡；NHJIS (s)放入一抽空的容器中，并与其分解产物NH$ (g)和H2S (g)成平衡；取任意量的NH, (g)和泾(g)与NH<HS (s)成平衡。
L作为溶质在两不互溶液体氏0和CCh中达到分配平衡(凝聚系统)。
(1) C=1,P = 2,F = C - P+2=l-2 + 2= 1・(2) C = 3- l = 2,P = 3,F = C- P + 2 = 2 ・3 + 2= 1・(3) C = 3- l- l = l,P=2,F = C- P + 2= l- 2 + 2=l.(4) C = 3- l = 2,P = 2,F = C- P + 2 = 2- 2 + 2 = 2.(5) C = 3,P = 2,F = C- P+ l= 3- 2+ l = 2・6.2已知液体甲苯（A）和液体苯（B）在90°C时的饱和蒸气压分别为卩；二54-22kPa和讥二l36.12kPa。
两者可形成理想液态混合物。
今有系统组成为So二的甲苯 -苯混合物5 mol,在90 °C下成气-液两相平衡，若气相组成为沟二°4%6求：(1)平衡时液相组成忑及系统的压力a(2)平衡时气、液两相的物质的量从8丄皿）解：（1）对于理想液态混合物，每个组分服从拉乌尔定律，因此"兀2；+恶卩;卫;十&; ■ pix0.4556X54.22珑■◎訂加為136J2- (136.12- 54.22>0.4556P = “; + 裨;=0.75X54.22+ 0.25X136.12= 74.70 kPa(2)系统代表点花。
二°6根据杠杆原理(y B.g一U H = (m一m )叫n l +— = 0.5（0.4556 —0.3”. = （0.3-0.25 Xii K = 1.216/?/<?/ n t =3.784加o/6.3 单组分系统的相图示意如右图。
《物理化学》第六章(化学动力学)知识点汇总
p 2 r
p 静 (液 气 )h g液 h g
rcosR
2cos
R
液hg
h 2 cos R液 g
r
R
h
当小液滴为球体时有： p 2 r
ln
p
* r
p*
2 M rRT
对于小液滴：r 0 ，半径愈小，蒸气压愈大； 对于小气泡：r 0 ，半径愈小，蒸气压愈大。
兰格缪尔吸附的特点：
a. 单分子层吸附； b. 固体表面是均匀的； c. 被吸附在固体表面上的分子相互之间无作用力； d. 吸附平衡是动态平衡。
k k
1 2
的增加倍数大于 k 2 的增加倍数。
若
Ea,1
Ea,2，当温度升高时，
k k
1 2
的增加倍数小于 k 2 的增加倍数。
的比值增加，k 1 随温度 的比值减少，k 1 随温度
由此可见，高温有利于活化能较大的反应，低温有利于活 化能较低的反应。
复杂反应
对峙反应
A r正 k1cA
G k1
rH
dcH dt
二、基元反应与总包反应
1. 由反应物微粒（分子、原子、离子或自由基）经碰撞后 一步直接生成产物的反应称为基元反应。
2. 由多个I 2 基M ( 高 能 元) 反2 I 应M ( 低 组能 ) 成( 2 ) 的反应称为总包反应。
H 2 I 2 2 H I
( 1 ) 总包反应
H 2 2 I 2 H I
胶体有哪些电动现象？ 会写胶团结构式！
胶 核 m n 定 位 离 子 n x 内 层 反 离 子 x 外 层 反 离 子
谢谢观看！！！
结束语
谢谢大家聆听！！！
22
0 kAdt
物理化学课后习题第六章答案教学总结
第六章相平衡6.1指出下列平衡系统中的组分数C，相数P及自由度F。
（1）I2(s)与其蒸气成平衡；（2）CaCO3(s)与其分解产物CaO(s)和CO2(g)成平衡；（3）NH4HS(s)放入一抽空的容器中，并与其分解产物NH3(g)和H2S(g)成平衡；（4）取任意量的NH3(g)和H2S(g)与NH4HS(s)成平衡。
（5）I2作为溶质在两不互溶液体H2O和CCl4中达到分配平衡（凝聚系统）。
解：（1）C = 1, P = 2, F = C–P + 2 = 1 – 2 + 2 = 1.（2）C = 3 – 1 = 2, P = 3, F = C–P + 2 = 2 – 3 + 2 = 1.（3）C = 3 – 1 – 1 = 1, P = 2, F = C–P + 2 = 1 – 2 + 2 = 1.（4）C = 3 – 1 = 2, P = 2, F = C–P + 2 = 2 – 2 + 2 = 2.（5）C = 3, P = 2, F = C–P + 1 = 3 – 2 + 1 = 2.6.2 常见的Na2CO3(s)水合物有Na2CO3∙H2O(s)，Na2CO3∙7H2O(s)和Na2CO3∙10H2O(s).（1）101.325kPa下，与Na2CO3水溶液及冰平衡共存的水合物最多能有几种？（2）20℃时，与水蒸气平衡的水合物最多可能有几种？解:（1）C = S – R - R' = 2 – 0 – 0 =2F = C–P + 1 =2 –P + 1= 3 – P ≥0，即P-2≤1，那么能与Na2CO3水溶液及冰平衡共存的水合物最多只有一种。
（2）C = S – R - R' = 2 – 0 – 0 =2F = C–P + 1 =2 –P + 1= 3 – P ≥0，即P-1≤2，那么与水蒸气平衡的水合物最多可能有两种。
6.4 单组分系统碳的想吐（示意图）如附图所示。
物理化学第六章 多媒体版 (葛华才 袁高清 彭程 着) 高等教育出版社
3. 反应速率的实验测定方法
以时间为横坐标、浓度为纵坐标，画出浓度 随时间的变化曲线，称为动力学曲线
测定反应物或生成物在不同时刻浓度的方法
化学法 在不同时刻取出少量反应混合物的样品 立即用骤冷、冲稀、加阻化剂、除去催化剂等方法 使反应停止，并确定在分析过程中反应不再进行 然后进行化学分析。这种方法的速度较慢
β υA = kAcα AcB β υB = kBcα AcB
速率方程
反应级数 1.5级 负一级
υ= k [A]
零级 一级 二级 二级
υ= k [A] υ= k [A][B] υ = k[A]
7
6.1 动力学的基本概念
6.1.1 化学反应速率
1. 反应转化速率(rate of conversion) 化学计量方程 0 = ΣvB B 根据IUPAC建议，反应转化速率定义：
ξ=
反应进度定义：
.
dξ dnB = dt vB dt
即: 单位时间(t) 内反应进度ξ 的改变量 dξ=dnΒ / vΒ
(rate equation of chemical reaction or kinetics quation of chemical reaction) α、 β : 反应组分A，B的分级数 α + β + ... = n
25
反应总级数(overall order of reaction) 简称反应级数(order of reaction)
H2+I2=2HI 反应机理 (1) I2+M 2I· +M (M为容器)
H2+Cl2 = 2HCl 反应机理 (1) Cl2+M→ 2Cl. +M (2) Cl. +H2 → HCl+H. (3) H. +Cl2 → HCl+Cl. (4) Cl. +Cl. +M → Cl2+M
物理化学课程讲义第六章
在一定温度下，1mol物质与氧气完全燃烧生成稳定氧化物时的反 应热效应。
生成焓与燃烧焓的关系
对于同一物质，其生成焓与燃烧焓之和等于该物质的标准摩尔焓。
反应焓变与温度的关系
1 2
基尔霍夫定律
在恒压条件下，化学反应的焓变随温度的变化率 等于反应热容差。
反应热容差
反应物和生成物热容之差，决定了反应焓变随温 度的变化率。
通过热力学基本方程和麦克斯韦关系式， 可以推导出各种热力学函数之间的关系， 为解决实际问题提供了方便。
学习方法建议
掌握基本概念
在学习物理化学课程时，首先要掌握 热力学的基本概念，如温度、热量、 功、内能等。
理解物理意义
在学习热力学定律和原理时，要注重 理解其物理意义，明确其适用条件和 范围。
多做练习题
04
热化学
化学反应的热效应
热效应定义
化学反应在恒压条件下所 吸收或放出的热量。
热效应测定方法
量热计是测量热效应的主 要工具，通过测量反应前 后体系温度的变化来计算 热效应。
热化学方程式
表示化学反应中物质变化 和热效应的化学方程式， 其中热效应以ΔH表示。
生成焓与燃烧焓
生成焓定义
在一定温度下，由最稳定的单质生成1mol化合物的反应热效应。
ΔU = Q + W，其中ΔU表示系统热力学能的变化，Q表示系统与环境交换的热 量，W表示环境对系统所做的功。
开放系统热力学第一定律表达式
ΔU = Q + W + ∑mi(hi + 1/2vi^2 + gzi)，其中mi、hi、vi和zi分别表示进入 或离开系统的各组分的质量、焓、速度和高度。
体积功的计算
物理化学(傅献彩著)06章_化学平衡.
K p Qp
rGm 0 反应向右自发进行
K p Qp K p Qp
rGm 0 rGm 0
反应向左自发进行 反应达平衡
上一内容 下一内容 回主目录
返回
2020/6/20
例题1
已知 N2O4的分解反应 N2O4(g) = 2NO2 (g)，在 25℃
时，ΔrG $m= 4.78 kJ mol-1。此温度时，在 p(N2O4) = 3p ，p(NO2) = 2p 的条件下，反应向 ___________ 方向进行。
VBdp
B* (T ,
p
)
B(T, p, xB) x,B(T) RT ln ax,B
上一内容 下一内容 回主目录
返回
2020/6/20
溶液中反应的平衡常数
如果溶质浓度用质量摩尔浓度表示，得：
B
(T
,
p,
mB
)
B□(T
,
p)
RT
ln
mB m
B(T, p, mB) B□(T, p ) RT ln am,B
反应自发向右进行， 趋向平衡
G
G
T , p
0
反应自发向左进 行，趋向平衡
G
T , p
0
G
T , p
0
e
反应达到平衡
0
1
系统的Gibbs自由能和ξ的关系
上一内容 下一内容 回主目录
返回
2020/6/20
为什么化学反应通常不能进行到底？
严格讲，反应物与产物处于同一系统的反应都 是可逆的，不能进行到底。
值上等于平衡时的“逸度商”，是量纲一的量。因为
它与标准化学势有关，所以又称为标准平衡常数。
物理化学第六章题 答案
选择填空题：1、在通常情况下（不考虑重力场，电磁场等特殊因素的影响），对于二组分物系能平衡共存的最多相为：(D )(A) 1 (B) 2 (C) 3 (D) 42、A与B两组分固相部分互溶凝聚系统的相图，图中有几个单相区：（C）A 1个B 2个C 3个D 4个3、由CaCO3(s),CaO(s)及CO2(g)构成的一个平衡系统，其独立组分数和自由度分别为（B）(A). 3、2 (B).2、1 (C).1、1 (D). 2、24、气态的N2，O2溶于水中达到相平衡，此多相系统的独立组分数为：3, 自由度为：3.5、I2（s）与其蒸气平衡体系，独立组分数为：1, 自由度为：16、NH4HS与任意量的NH3（g）和H2S（g）达平衡时，系统的自由度数是：21. 指出下列平衡系统中的组分数C，相数P及自由度F。
(1)CaCO3(s),CaO(s)及CO2(g)构成的一个平衡系统(2)Fe(s),FeO(s),Fe3O4(s)和O2(g),CO2(g)构成的一个平衡系统(3)NH2CO2NH4放入一抽空的容器中，并与其分解产物NH3(g)和CO2(g)成平衡解：(1)C=S-R-R'=3-1-0=2, F=C-P+2=2-3+2=1(2)C=S-R-R'=5-2-0=3, F=C-P+2=3-4+2=1(3)C=S-R-R'=3-1-1=1, F=C-P+2=1-2+2=12. 已知液体甲苯（A）和液体苯（B）在90 °C时的饱和蒸气压分别为=和。
两者可形成理想液态混合物。
今有系统组成为的甲苯-苯混合物5 mol，在90 °C下成气-液两相平衡，若气相组成为求：（1）平衡时液相组成及系统的压力p。
（2）平衡时气、液两相的物质的量解：（1）对于理想液态混合物，每个组分服从Raoult定律，因此（2）系统代表点，根据杠杆原理3. 已知甲苯、苯在90 °C下纯液体的饱和蒸气压分别为54.22 kPa和136.12 kPa。
物理化学课后习题第六章答案
第六章相平衡6、1指出下列平衡系统中得组分数C,相数P及自由度F。
(1)I2(s)与其蒸气成平衡;(2)CaCO3(s)与其分解产物CaO(s)与CO2(g)成平衡;(3)NH4HS(s)放入一抽空得容器中,并与其分解产物NH3(g)与H2S(g)成平衡;(4)取任意量得NH3(g)与H2S(g)与NH4HS(s)成平衡。
(5)I2作为溶质在两不互溶液体H2O与CCl4中达到分配平衡(凝聚系统)。
解:(1)C = 1, P = 2, F = C–P + 2 = 1 – 2 + 2 = 1、(2)C = 3 – 1 = 2, P = 3, F = C–P + 2 = 2 – 3 + 2 = 1、(3)C = 3 – 1 – 1 = 1, P = 2, F = C–P + 2 = 1 –2 + 2 = 1、(4)C = 3 – 1 = 2, P = 2, F = C–P + 2 = 2 – 2 + 2 = 2、(5)C = 3, P = 2, F = C–P + 1 = 3 – 2 + 1 = 2、6、2 常见得Na2CO3(s)水合物有Na2CO3∙H2O(s),Na2CO3∙7H2O(s)与Na2CO3∙10H2O(s)、(1)101、325kPa下,与Na2CO3水溶液及冰平衡共存得水合物最多能有几种？(2)20℃时,与水蒸气平衡得水合物最多可能有几种？解:(1)C = S – R R' = 2 – 0 – 0 =2F = C–P + 1 =2 –P + 1= 3 – P ≥0, 即P2≤1,那么能与Na2CO3水溶液及冰平衡共存得水合物最多只有一种。
(2)C = S – R R' = 2 – 0 – 0 =2F = C–P + 1 =2 –P + 1= 3 – P ≥0,即P1≤2,那么与水蒸气平衡得水合物最多可能有两种。
6、4 单组分系统碳得想吐(示意图)如附图所示。
(1)分析图中各点、线、面得相平衡关系及自由度数;(2)25℃,101、325kPa下,碳以什么状态稳定存在？(3)增加压力可以使石墨转换为金刚石。
物理化学第六章
（2）自由度和自由度数 F 能够维持系统原有相数而可以独立改 变的变量叫做自由度，这种变量的数目， 体系的自由度数。 体系的自由度是体系的独立可变的因 素数的数目，这些因素的数值在一定的范 围内，可以任意的改变，而不会引起相的 数目的改变。
4
2 相律
相律的主要目的是确定系统的自由度数，即独 立变量数。 基本思路：自由度数＝总变量数－非独立变量数
9
如将NH4Cl(s)放入真空容器中分解 NH4Cl(s) = HCl(g) + NH3 (g)
由于分解产物均为气相，存在xHCl(g)= xNH3(g) 的关系，所以该体系的组分数为 C = S - R - R =3 - 1- 1 =1 如反应体系中原有NH4Cl(s)和HCl(g)或 NH3 (g) 因 xHCl(g) xNH3(g)
11
(4) 相律是根据热力学平衡条件推导而来， 所以相律只适用于平衡条件时F、C、P的计 算。对非平衡态不适用。
(5) 相律中数字“2”是由于假定外界条件只有 温度和压力可以影响体系的平衡状态而来的 (通常情况下确是如此)。如体系恒定T或P(即 T或P一确定值)，则相律可写作: F* = C – P + 1 如体系T和P都确定，则相律为 F** = C – P F*、 F**统称为“条件自由度”。
T
19
l (水） A C
p
s(冰） O
C´
B
g (水蒸气）
T
OC 线称为水的饱和蒸汽压 曲线或蒸发曲线，这条线表示水 和水蒸气的平衡。双相单变量系 统． 若在恒温下对此两相平衡系统 加压，或在恒压下令其降温都可 使水蒸气凝结为水,反之，恒温下 减压或恒压下升温，则可使水蒸 发为水蒸气。故 OC 线以上的区 域为水的相区，线 OC 以下的区 域为水蒸气的相区。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
稳态近似
d [ HBr ] k2 [ H 2 ][ Br] k3[ H ][ Br2 ] k4 [ H ][ HBr ] dt
活泼质点 对于连串反应，一旦反应发生，活泼质点快速达到它们 的浓度最大值，并在反应过程中它们的浓度基本不变。
dc 0 dt
6.6.1
稳态近似
d [ Br] k1[ Br2 ] k 2 [ Br][ H 2 ] k3[ H ][ Br2 ] dt 2 k 4 [ H ][ HBr ] k5 [ Br] = 0
6.5 练习题
动力学实验数据的处理
某反应的计量方程为2A→B。当t=∞时，A的浓度
为零，B的浓度随时间的变化数据如下：
t/s 0 600 1200 1800 2400 ∞
[B]/(mol dm-3) 0
0.089 0.153 0.199 0.231 0.312
问如何确定反应级数？
6.6 复杂反应机理
尝试法
因此，反应速率方程为：
= k [A] [B]
1) 尝试法依赖实验数据；
2) 对于没有简单级数的反应，尝试法则无法确定反 应级数了。有时候实验的误差会导致有争议的结 果。
6.5.1 2) 图解法 根据线性关系： 级数 0 1
积分法
线性关系 C~t lnC ~ t
2
3
1/C ~ t
1/C2 ~ t
§6.5
目的是什么？
动力学实验数据的处理
建立速率方程(不同温度下反应速率与浓度的关系） 获得若干特征参数： 分级数和反应级数 速率常数或速率系数
Arrhenius活化能
指前因子
6.5
动力学实验数据的处理
如何获得实验数据？ 通常间接地测定某些物理性质随时间的变化 例如 A + B P A的浓度变化与物理性质Y的改变量成正比
k ' B
0.6 0.30 , , 2 5.38 0.90
1.81 0.15 k ' ' ' C ; ; 0 1.81 0.45
k A1 B 2 C 0 k AB 2
[C]/c0 100υ0/(c0/s)
0.15 0.6
0.15 1.81
0.15 5.38
0.45 1.81
6.5.3
解：
孤立变数法
k A B C ; k ' ' A ;
0.6 0.20 ; 1 1.81 0.60
t/s
6.5.1.2
图解法
1/c与时间关系图
160
120
1/ C(/ mol dm -3)
80
40
0 0 1000 2000 3000 4000 5000
t/s
6.5.1.2
图解法
1/c2 与时间关系图
100
1 / C2
80 60 40 20 0 0 1000 2000 3000 4000 5000
Decomposition 25 30 35 40 45 percentage v / Pa min-1 625.2 574.5 500.0 414.6 356.0
ln{} 与ln{c}关系图
lnr / Pa min-1
7.0
ln = -1.593 + 1.865 ln c
6.5
6.0
斜率＝n
2) 平衡态近似（Equilibrium approximation）
6.6
7.6.1 稳态近似
例如反应:
复杂反应机理
H2 + Br2 2 HBr
d [ HBr ] k[ H 2 ][ Br2 ] [ HBr ] dt 1 m Br2
1/ 2
1919年，J. A. Christiansen、 K. F. Herzfeld 和 M. Polanyi 三人各自提出了以下包含五 个基元反应的机理：
NaI + C2H5O C2H5 + S(CH3)2
＝k[C2H5ONa][C2H5(CH3)2SI]
反应简写成 A+B P = k [A][B]
6.5.1.1
尝试法
C2H5ONa + C2H5(CH3)2SI 反应在 337.10 K的实验数据
t/s 0 720 1200 102[A]/ mol dm-3 9.625 8.578 8.046 102[B] / mol dm-3 4.920 3.878 3.342
半衰期法
例如
NH4OCN CO(NH2)2
c0/mol dm-3 t1/2/h
0.05 37.03
0.10 19.15
0.20 9.45
t1/ 2 ln t '1/ 2 n 1 c0 ln c0 '
n1 = 2.051, n2 = 2.019
∴ n =2
6.5 6.5.2 微分法
动力学实验数据的处理
V(OH-) 0.00 3 /cm
9.87 11.68 12.69 13.69 16.00
以微分法求算该反应的级数。
6.5.2
作图：(a-x)～t，即c ～t
微分法
dc c1 0.041mol dm ,1 ( ) c c1 dt dc 3 c2 0.014 mol dm , 2 ( ) c c2 dt ln 1 ln 2 - 5.79 8.10 n 2 ln c1 ln c2 - 3.19 4.27
3
6.5.2
解除求导过程。
微分法
微分反应器：浓度不随空间和时间变化。
c A0 c A A V VR
6.5.3
孤立法
孤立法类似于准级数法，可以使问题简化。有时
再与其他方法结合来确定反应级数。
例如
k A B
1.使[A]>>[B] 2.使[B]>>[A]
k '[B]
6.5.1.2
图解法 = k[A]
例如
反应 A P
反应的动力学数据如下： t/s 0 500 1000 1500 2000 2500 C / mol dm-3 1.000 0.606 0.368 0.223 0.135 0.082 t/s 3000 3500 4000 4500 5000 C / mol dm-3 0.050 0.030 0.018 0.011 0.007
5.5 3.8 4.0 4.2 4.4 4.6 4.8
lnC / mol dm-3
6.5.2
微分法
由一次实验结果确定反应级数
一次法
6.5.2
v v v
微分法
由平行实验确定反应级数：初速率法
ln t 0 ln k n ln c0
初速率法的优点：不受产物干扰。
例：乙酸乙酯在碱性溶液中的反应如下： CH3COOC2H5+OH-→ CH3COO-+C2H5OH 在25℃条件下进行反应，两种反应物初始浓度a均为: 0.064mol.dm-3.在不同时刻取样25.00cm3,立即向样品 中加入25.00cm3 0.064mol.dm-3的盐酸，以使反应停 止进行。多余的酸用0.1000mol.dm-3的NaOH溶液滴 定，所用碱液列于下表： t/min 0.00 5.00 15.00 25.00 35.00 55.00 5.76 ∝
先确定β值 再确定α值
k ' '[A ]
6.5.3
孤立变数法
例如： 用孤立法求下面反应的级数:
反应A+B+C→产物，300 K时在各组初始 浓度下，其初始速率υ0为（c0=1 mol/dm3）
[A]/c0 [B]/c0 0.20 0.30 0.60 0.30 0.20 0.90 0.60 0.30
6.6.1
Br2 2 Br
k1
稳态近似
链反应机理
链产生 链传递 链中止
Br H 2 HBr H
k2
H Br2 k3 HBr Br H HBr H 2 Br
k4
2 Br Br2
k5
? 是正确的吗
6.6.1t ຫໍສະໝຸດ 0c A0tcA
Yt
0 Y
c A0 0 Y Y0 c A 0 Y Yt
Y0
6.5
动力学实验数据的处理
如何对实验数据进行处理？ 1) 积分法 2) 微分法
3) 孤立法
6.5 6.5.1 积分法
动力学实验数据的处理
积分法利用速率方程的积分式来确定反应级数。 包括:
1) 尝试法
=2 =0 ×103 1.764 1.604 1.550 1.333 1.093 1.042
=0 =2 ×103 7.579 7.357 10.02 10.93 11.11 13.32
=1 =1 ×103 3.642 3.678 3.760 3.773 3.731 3.729
6.5.1.1
t/s
6.5.1
积分法
3) 半衰期法
半衰期与反应物的初始浓度的1-n次方呈正比.
t1/ 2 k ' c
1 n 0
2 1 其中 k ' (n 1)k
（除n=1）
n 1
ln t1/ 2 ln k '(1 n) ln c0
半衰期随初始浓度的变化
10
1/2
ln t
9
斜率＝1-n
利用微分式确定速率方程。
1 dcB n kcB B dt