备战中考数学专题训练---二次函数的综合题分类含答案
中考数学复习《二次函数》专题训练-附带有参考答案

中考数学复习《二次函数》专题训练-附带有参考答案一、选择题1.下列函数中,是二次函数的是()A.y=x2+1x B.y=12x(x-1) C.y=-2x-1 D.y=x(x2+1).2.抛物线y=(x−2)2−3的顶点坐标是()A.(2,−3)B.(−2,3)C.(2,3)D.(−2,−3)3.把抛物线y=5x2向左平移2个单位,再向上平移3个单位,得到的抛物线是()A.y=5(x−2)2+3B.y=5(x+2)2−3C.y=5(x+2)2+3D.y=5(x−2)2−34.函数y=ax2与y=﹣ax+b的图象可能是()A. B. C. D.5.函数y=kx2-6x+3的图象与x轴有交点,则k的取值范围是()A.k<3 B.k<3且k≠0 C.k≤3且k≠0 D.k≤36.若A(−5,y1),B(1,y2),C(2,y3)为二次函数y=x2+2x+m的图象上的三点,则y1,y2,y3的大小关系是()A.y1<y2<y3B.y2<y3<y1C.y2<y1<y3D.y3<y1<y27.二次函数y=ax2+bx+c的图象如图所示,对称轴是直线x=1.下列结论:①b>0;②当x>0,y随着x 的增大而增大;③(a+c)2﹣b2<0;④a+b≥m(am+b)(m为实数).其中结论正确的个数为()A.4个B.3个C.2个D.1个8.某服装店购进单价为15元的童装若干件,销售一段时间后发现:当销售价为25元时,平均每天能售出8件,而当销售价每降低2元时,平均每天能多售出4件,为使该服装店平均每天的销售利润最大,则每件的定价为()A.21元B.22元C.23元D.24元二、填空题9.将二次函数y=x2-2x化为y=(x-h)2+k的形式,结果为10.若抛物线y=ax2+bx+c与x轴的两个交点坐标是(-1,0),(3,0),则此抛物线的对称轴是直线.11.将二次函数y=x2﹣4x+a的图象向左平移1个单位,再向上平移1个单位,若得到的函数图象与直线y=2有两个交点,则a的取值范围是.12.飞机着陆后滑行的距离y (单位:m)关于滑行时间t (单位:s)的函数解析式是y=60t-65t2,从飞机着陆至停下来共滑行米.13.已知如图:抛物线y=ax2+bx+c与直线y=kx+n相交于点A(−52,74)、B(0,3)两点,则关于x的不等式ax2+bx+c<kx+n的解集是三、解答题14.如图,在平面直角坐标系中,一次函数y1=kx−7的图象与二次函数y2=2x2+bx+c的图象交于A(1,−5)、B(3,t)两点.(1)求y1与y2的函数关系式;(2)直接写出当y1<y2时,x的取值范围;(3)点C为一次函数y1图象上一点,点C的横坐标为n,若将点C向右平移2个单位,再向上平移4个单位后刚好落在二次函数y2的图象上,求n的值.15.某品牌服装公司新设计了一款服装,其成本价为60(元/件).在大规模上市前,为了摸清款式受欢迎状况以及日销售量y(件)与销售价格x(元/件)之间的关系,进行了市场调查,部分信息如表:销售价格x(元/件)80 90 100 110日销售量y(件)240 220 200 180(1)若y与x之间满足一次函数关系,请直接写出函数的解析式(不用写自变量x的取值范围);(2)若该公司想每天获利8000元,并尽可能让利给顾客,则应如何定价?(3)为了帮助贫困山区的小朋友,公司决定每卖出一件服装向希望小学捐款10元,该公司应该如何定价,才能使每天获利最大?(利润用w表示)16.如图,抛物线y=−x2+bx+c与x轴交于A,B两点(A在B的左侧),与y轴交于点N,过A点的直线:l:y=−x−1与y轴交于点C,与抛物线y=−x2+bx+c的另一个交点为D(5,−6),已知P点为抛物线y=−x2+bx+c上一动.点(不与A、D重合).(1)求抛物线的解析式;(2)当点P在直线l上方的抛物线上时,过P点作PE∥x轴交直线l于点E,作PF∥y轴交直线l于点F,求PE+PF的最大值;(3)设M为直线l上的动点,以NC为一边且顶点为N,C,M,P的四边形是平行四边形,直接写出所有符合条件的M点坐标.17.如图是北京冬奥会举办前张家口某小型跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点作水平线的垂线为y轴,建立平面直角坐标系,图中的抛物线C1:y=−18x2+32x+32近似表示滑雪场地上的一座小山坡,某滑雪爱好者小张从点O正上方A点滑出,滑出后沿一段抛物线C2:y=−14x2+bx+c 运动.(1)当小张滑到离A处的水平距离为8米时,其滑行高度为10米,求出b,c的值;(2)在(1)的条件下,当小张滑出后离的水平距离为多少米时,他滑行高度与小山坡的竖直距离为是5米?2(3)若小张滑行到坡顶正上方,且与坡顶距离不低于4米,求b的取值范围.18.如图,在平面直角坐标系中,抛物线y=ax2+bx−4与x轴交于A(4,0)、B(−3,0)两点,与y轴交于点C.(1)求这条抛物线所对应的函数表达式.(2)如图①,点D是x轴下方抛物线上的动点,且不与点C重合.设点D的横坐标为m,以O、A、C、D 为顶点的四边形面积为S,求S与m之间的函数关系式.(3)如图②,连结BC,点M为线段AB上一点,点N为线段BC上一点,且BM=CN=n,直接写出当n为何值时△BMN为等腰三角形.参考答案 1.B 2.A 3.C 4.B 5.D 6.B 7.B 8.B9.y =(x −1)2−1 10.x =1 11.a <5 12.75013.x <−52或x >014.(1)解:把点A(1,−5)代入y 1=kx −7得−5=k −7 ∴y 1=2x −7;把点B(3,t)代入y 1=2x −7中,得t =−1 ∴A(1,−5)把点A 、B 分别代入y 2=2x 2+bx +c 中,得{−2=2+b +c−1=18+3b +c 解得{b =−6c =−1∴y 2=2x 2−6x −1; (2)x <1或x >3(3)解:∵点C 为一次函数y 1图象上一点,∴C(n ,2n −7)将点C 向右平移2个单位,再向上平移4个单位后得到点C ′(n +2,2n −3) 把C ′代入y 2=2x 2−6x −1,得2n −3=2(n +2)2−6(n +2)−1 解得n =±1 所以n 的值为1或-1 15.(1)y=-2x+400(2)解:由题意,得:(x −60)(−2x +400)=8000解得x 1=100,x 2=160 ∵公司尽可能多让利给顾客 ∴应定价100元(3)解:由题意,得w =(x −60−10)(−2x +400)=−2x 2+540x −28000 =−2(x −135)2+8450∵−2<0∴当x =135时,w 有最大值,最大值为8450. 答:当一件衣服定为135元时,才能使每天获利最大. 16.(1)解:∵直线l :y =−x −1过点A∴A(−1,0)又∵D(5,−6)将点A ,D 的坐标代入抛物线表达式可得:{−1−b +c =0−25+5b +c =−6 解得{b =3c =4.∴抛物线的解析式为:y =−x 2+3x +4. (2)解:如图设点P(x ,−x 2+3x +4) ∵PE ∥x 轴,PF ∥y 轴则E(x 2−3x −5,−x 2+3x +4),F(x ,−x −1) ∵点P 在直线l 上方的抛物线上∴−1<x <5∴PE =|x −(x 2−3x −5)|=−x 2+4x +5,PF =|−x 2+3x +4−(−x −1)|=−x 2+4x +5 ∴PE +PF =2(−x 2+4x +5)=−2(x −2)2+18. ∴当x =2时,PE +PF 取得最大值,最大值为18.(3)符合条件的M 点有三个:M 1(4,−5),M 2(2+√14,−3−√14), M 3(2−√14,−3+√14). 17.(1)解:由题意可知抛物线C 2:y=−14x 2+bx+c 过点(0, 4)和(8, 10) 将其代入得:{4=c10=−14×82+8b +c解得 ∴b=114,c=4(2)解:由(1)可得抛物线Cq 解析式为: y=−14x 2+114x+4设运动员运动的水平距离为m 米时,运动员与小山坡的竖直距离为52米,依题意得: −14m 2+114m +4−(−18m 2+32m +32)=52解得: m 1=10,m 2=0(舍)故运动员运动的水平距离为10米时,运动员与小山坡的竖直距离为为52米. (3)解:∵抛物线C 2经过点(0, 4) ∴c=4抛物线C 1: y=−18x 2+32x +32=−18(x −6)2+6 当x=6时,运动员到达坡项 即−14×62+6b+4≥4+6. ∴b ≥15618.(1)解:把A(4,0)、B(−3,0)代入y =ax 2+bx −4中 得{16a +4b −4=09a −3b −4=0解得{a =13b =−13∴这条抛物线所对应的函数表达式为y =13x 2−13x −4. (2)解:当x =0时y =−4∴C(0,−4)当−3<m <0时S =S △ODC +S △OAC =12×4×(−m)+12×4×4=−2m +8当0<m <4时S =S △ODC +S △OAD =12×4×m +12×4×(−13m 2+13m +4)=−23m 2+83m +8. (3)解:n =52,n =2511,n =3011.。
备战中考数学复习《二次函数》专项综合练习附答案解析

一、二次函数 真题与模拟题分类汇编(难题易错题)1.如图:在平面直角坐标系中,直线l :y=13x ﹣43与x 轴交于点A ,经过点A 的抛物线y=ax 2﹣3x+c 的对称轴是x=32. (1)求抛物线的解析式;(2)平移直线l 经过原点O ,得到直线m ,点P 是直线m 上任意一点,PB ⊥x 轴于点B ,PC ⊥y 轴于点C ,若点E 在线段OB 上,点F 在线段OC 的延长线上,连接PE ,PF ,且PE=3PF .求证:PE ⊥PF ;(3)若(2)中的点P 坐标为(6,2),点E 是x 轴上的点,点F 是y 轴上的点,当PE ⊥PF 时,抛物线上是否存在点Q ,使四边形PEQF 是矩形?如果存在,请求出点Q 的坐标,如果不存在,请说明理由.【答案】(1)抛物线的解析式为y=x 2﹣3x ﹣4;(2)证明见解析;(3)点Q 的坐标为(﹣2,6)或(2,﹣6).【解析】【分析】(1)先求得点A 的坐标,然后依据抛物线过点A ,对称轴是x=32列出关于a 、c 的方程组求解即可;(2)设P (3a ,a ),则PC=3a ,PB=a ,然后再证明∠FPC=∠EPB ,最后通过等量代换进行证明即可;(3)设E (a ,0),然后用含a 的式子表示BE 的长,从而可得到CF 的长,于是可得到点F 的坐标,然后依据中点坐标公式可得到22x x x x Q P F E ++=,22y y y y Q P F E ++=,从而可求得点Q 的坐标(用含a 的式子表示),最后,将点Q 的坐标代入抛物线的解析式求得a 的值即可.【详解】(1)当y=0时,140 33x-=,解得x=4,即A(4,0),抛物线过点A,对称轴是x=32,得161203322a ca-+=⎧⎪-⎨-=⎪⎩,解得14ac=⎧⎨=-⎩,抛物线的解析式为y=x2﹣3x﹣4;(2)∵平移直线l经过原点O,得到直线m,∴直线m的解析式为y=13x.∵点P是直线1上任意一点,∴设P(3a,a),则PC=3a,PB=a.又∵PE=3PF,∴PC PBPF PE=.∴∠FPC=∠EPB.∵∠CPE+∠EPB=90°,∴∠FPC+∠CPE=90°,∴FP⊥PE.(3)如图所示,点E在点B的左侧时,设E(a,0),则BE=6﹣a.∵CF=3BE=18﹣3a,∴OF=20﹣3a.∴F(0,20﹣3a).∵PEQF为矩形,∴22x x x xQ P F E++=,22y y y yQ P F E++=,∴Q x+6=0+a,Q y+2=20﹣3a+0,∴Q x=a﹣6,Q y=18﹣3a.将点Q的坐标代入抛物线的解析式得:18﹣3a=(a﹣6)2﹣3(a﹣6)﹣4,解得:a=4或a=8(舍去).∴Q(﹣2,6).如下图所示:当点E 在点B 的右侧时,设E (a ,0),则BE=a ﹣6.∵CF=3BE=3a ﹣18,∴OF=3a ﹣20.∴F (0,20﹣3a ).∵PEQF 为矩形, ∴22x x x x Q P F E ++=,22y y y y Q P F E ++=, ∴Q x +6=0+a ,Q y +2=20﹣3a+0,∴Q x =a ﹣6,Q y =18﹣3a . 将点Q 的坐标代入抛物线的解析式得:18﹣3a=(a ﹣6)2﹣3(a ﹣6)﹣4,解得:a=8或a=4(舍去).∴Q (2,﹣6).综上所述,点Q 的坐标为(﹣2,6)或(2,﹣6).【点睛】本题主要考查的是二次函数的综合应用,解答本题主要应用了矩形的性质、待定系数法求二次函数的解析式、中点坐标公式,用含a 的式子表示点Q 的坐标是解题的关键.2.如图1,抛物线y=ax 2+bx+c (a≠0)与x 轴交于点A (﹣1,0)、B (4,0)两点,与y 轴交于点C ,且OC=3OA .点P 是抛物线上的一个动点,过点P 作PE ⊥x 轴于点E ,交直线BC 于点D ,连接PC .(1)求抛物线的解析式;(2)如图2,当动点P 只在第一象限的抛物线上运动时,求过点P 作PF ⊥BC 于点F ,试问△PDF 的周长是否有最大值?如果有,请求出其最大值,如果没有,请说明理由. (3)当点P 在抛物线上运动时,将△CPD 沿直线CP 翻折,点D 的对应点为点Q ,试问,四边形CDPQ 是否成为菱形?如果能,请求出此时点P 的坐标,如果不能,请说明理由.【答案】(1) y=﹣234x +94x+3;(2) 有最大值,365;(3) 存在这样的Q 点,使得四边形CDPQ 是菱形,此时点P 的坐标为(73,256)或(173,﹣253). 【解析】试题分析: (1)利用待定系数法求二次函数的解析式;(2)设P (m ,﹣34m 2+94m+3),△PFD 的周长为L ,再利用待定系数法求直线BC 的解析式为:y=﹣34x+3,表示PD=﹣2334m m +,证明△PFD ∽△BOC ,根据周长比等于对应边的比得:=PED PD BOC BC 的周长的周长,代入得:L=﹣95(m ﹣2)2+365,求L 的最大值即可; (3)如图3,当点Q 落在y 轴上时,四边形CDPQ 是菱形,根据翻折的性质知:CD=CQ ,PQ=PD ,∠PCQ=∠PCD ,又知Q 落在y 轴上时,则CQ ∥PD ,由四边相等:CD=DP=PQ=QC ,得四边形CDPQ 是菱形,表示P (n ,﹣23n 4 +94n+3),则D (n ,﹣34n+3),G (0,﹣34n+3),利用勾股定理表示PD 和CD 的长并列式可得结论. 试题解析:(1)由OC=3OA ,有C (0,3),将A (﹣1,0),B (4,0),C (0,3)代入y=ax 2+bx+c 中,得:016403a b c a b c c -+=⎧⎪++=⎨⎪=⎩,解得:34943a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩, 故抛物线的解析式为:y=﹣234x +94x+3; (2)如图2,设P (m ,﹣34m 2+94m+3),△PFD 的周长为L , ∵直线BC 经过B (4,0),C (0,3),设直线BC 的解析式为:y=kx+b ,则403k b b +=⎧⎨=⎩解得:343k b ⎧=-⎪⎨⎪=⎩ ∴直线BC 的解析式为:y=﹣34x+3, 则D (m ,﹣334m +),PD=﹣2334m m +, ∵PE ⊥x 轴,PE ∥OC ,∴∠BDE=∠BCO ,∵∠BDE=∠PDF ,∴∠PDF=∠BCO ,∵∠PFD=∠BOC=90°,∴△PFD ∽△BOC , ∴=PED PD BOC BC的周长的周长, 由(1)得:OC=3,OB=4,BC=5,故△BOC 的周长=12,∴2334125m m L -+=, 即L=﹣95(m ﹣2)2+365, ∴当m=2时,L 最大=365; (3)存在这样的Q 点,使得四边形CDPQ 是菱形,如图3,当点Q 落在y 轴上时,四边形CDPQ 是菱形,理由是:由轴对称的性质知:CD=CQ ,PQ=PD ,∠PCQ=∠PCD ,当点Q 落在y 轴上时,CQ ∥PD ,∴∠PCQ=∠CPD ,∴∠PCD=∠CPD ,∴CD=PD ,∴CD=DP=PQ=QC ,∴四边形CDPQ 是菱形,过D 作DG ⊥y 轴于点G ,设P (n ,﹣234n +94n+3),则D (n ,﹣34n+3),G (0,﹣334n +), 在Rt △CGD 中,CD 2=CG 2+GD 2=[(﹣34n+3)﹣3]2+n 2=22516n ,而|PD|=|(﹣239344n n ++ 3n ++)﹣(﹣34n+3)|=|﹣234n +3n|, ∵PD=CD ,∴﹣235344n n n +=①, ﹣235344n n n +=-②, 解方程①得:n=73或0(不符合条件,舍去), 解方程②得:n=173或0(不符合条件,舍去), 当n=73时,P (73,256),如图3,当n=173时,P (173,﹣253),如图4,综上所述,存在这样的Q 点,使得四边形CDPQ 是菱形,此时点P 的坐标为(73,256)或(173,﹣253). 点睛: 本题是二次函数的综合题,考查了利用待定系数法求函数的解析式、菱形的性质和判定、三角形相似的性质和判定,将周长的最值问题转化为二次函数的最值问题,此类问题要熟练掌握利用解析式表示线段的长,并利用相似比或勾股定理列方程解决问题.3.已知如图,抛物线y =x 2+bx +c 过点A (3,0),B (1,0),交y 轴于点C ,点P 是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与点A重合),过点P作PD∥y 轴交直线AC于点D.(1)求抛物线的解析式;(2)求点P在运动的过程中线段PD长度的最大值;(3)△APD能否构成直角三角形?若能请直接写出点P坐标,若不能请说明理由;(4)在抛物线对称轴上是否存在点M使|MA﹣MC|最大?若存在请求出点M的坐标,若不存在请说明理由.【答案】(1)y=x2﹣4x+3;(2)94;(3)点P(1,0)或(2,﹣1);(4)M(2,﹣3).【解析】试题分析:(1)把点A、B的坐标代入抛物线解析式,解方程组得到b、c的值,即可得解;(2)求出点C的坐标,再利用待定系数法求出直线AC的解析式,再根据抛物线解析式设出点P的坐标,然后表示出PD的长度,再根据二次函数的最值问题解答;(3)①∠APD是直角时,点P与点B重合,②求出抛物线顶点坐标,然后判断出点P为在抛物线顶点时,∠PAD是直角,分别写出点P的坐标即可;(4)根据抛物线的对称性可知MA=MB,再根据三角形的任意两边之差小于第三边可知点M为直线CB与对称轴交点时,|MA﹣MC|最大,然后利用待定系数法求出直线BC的解析式,再求解即可.试题解析:解:(1)∵抛物线y=x2+bx+c过点A(3,0),B(1,0),∴93010b cb c++=⎧⎨++=⎩,解得43bc=-⎧⎨=⎩,∴抛物线解析式为y=x2﹣4x+3;(2)令x=0,则y=3,∴点C(0,3),则直线AC的解析式为y=﹣x+3,设点P(x,x2﹣4x+3).∵PD∥y轴,∴点D(x,﹣x+3),∴PD=(﹣x+3)﹣(x2﹣4x+3)=﹣x2+3x=﹣(x﹣32)2+94.∵a=﹣1<0,∴当x=32时,线段PD的长度有最大值94;(3)①∠APD是直角时,点P与点B重合,此时,点P(1,0),②∵y=x2﹣4x+3=(x ﹣2)2﹣1,∴抛物线的顶点坐标为(2,﹣1).∵A(3,0),∴点P为在抛物线顶点时,∠PAD=45°+45°=90°,此时,点P(2,﹣1).综上所述:点P(1,0)或(2,﹣1)时,△APD能构成直角三角形;(4)由抛物线的对称性,对称轴垂直平分AB ,∴MA =MB ,由三角形的三边关系,|MA ﹣MC |<BC ,∴当M 、B 、C 三点共线时,|MA ﹣MC |最大,为BC 的长度,设直线BC 的解析式为y =kx +b (k ≠0),则03k b b +=⎧⎨=⎩,解得:33k b =-⎧⎨=⎩,∴直线BC 的解析式为y =﹣3x +3.∵抛物线y =x 2﹣4x +3的对称轴为直线x =2,∴当x =2时,y =﹣3×2+3=﹣3,∴点M (2,﹣3),即,抛物线对称轴上存在点M (2,﹣3),使|MA ﹣MC |最大.点睛:本题是二次函数综合题,主要利用了待定系数法求二次函数解析式,二次函数的最值问题,二次函数的对称性以及顶点坐标的求解,(2)整理出PD 的表达式是解题的关键,(3)关键在于利用点的坐标特征作出判断,(4)根据抛物线的对称性和三角形的三边关系判断出点M 的位置是解题的关键.4.如图所示,抛物线2y ax bx c =++的顶点为()2,4M --,与x 轴交于A 、B 两点,且()6,0A -,与y 轴交于点C .()1求抛物线的函数解析式;()2求ABC 的面积;()3能否在抛物线第三象限的图象上找到一点P ,使APC 的面积最大?若能,请求出点P 的坐标;若不能,请说明理由.【答案】()1 2134y x x =+-;()212;()27334APC x S =-当时,有最大值,点P 的坐标是153,4P ⎛⎫--⎪⎝⎭. 【解析】【分析】(1)设顶点式并代入已知点()6,0A -即可;(2)令y=0,求出A 、B 和C 点坐标,运用三角形面积公式计算即可;(3)假设存在这样的点,过点P 作PE x ⊥轴于点E ,交AC 于点F ,线段PF 的长度即为两函数值之差,将APC 的面积计算拆分为APF CPF SS +即可.【详解】 ()1设此函数的解析式为2()y a x h k =++,∵函数图象顶点为()2,4M --,∴2(2)4y a x =+-,又∵函数图象经过点()6,0A -,∴20(62)4a =-+- 解得14a =, ∴此函数的解析式为21(2)44y x =+-,即2134y x x =+-; ()2∵点C 是函数2134y x x =+-的图象与y 轴的交点, ∴点C 的坐标是()0,3-,又当0y =时,有21304y x x =+-=, 解得16x =-,22x =,∴点B 的坐标是()2,0,则11831222ABC S AB OC =⋅=⨯⨯=; ()3假设存在这样的点,过点P 作PE x ⊥轴于点E ,交AC 于点F .设(),0E x ,则21,34P x x x ⎛⎫+- ⎪⎝⎭,设直线AC 的解析式为y kx b =+,∵直线AC 过点()6,0A -,()0,3C -,∴603k b b -+=⎧⎨-=⎩, 解得123k b ⎧=-⎪⎨⎪=-⎩,∴直线AC 的解析式为132y x =--, ∴点F 的坐标为1,32F x x ⎛⎫-- ⎪⎝⎭, 则221113332442PF x x x x x ⎛⎫=---+-=-- ⎪⎝⎭, ∴1122APC APF CPF S S S PF AE PF OE =+=⋅+⋅ 2221113393276(3)22424244PF OA x x x x x ⎛⎫=⋅=--⨯=--=-++ ⎪⎝⎭, ∴当3x =-时,APC S 有最大值274, 此时点P 的坐标是153,4P ⎛⎫--⎪⎝⎭. 【点睛】 本题第3问中将所求三角形拆分为两个小三角形进行求解,从而将面积最大的问题转化为PF 最大进行理解.5.对于二次函数 y=ax 2+(b+1)x+(b ﹣1),若存在实数 x 0,使得当 x=x 0,函数 y=x 0,则称x 0 为该函数的“不变值”.(1)当 a=1,b=﹣2 时,求该函数的“不变值”;(2)对任意实数 b ,函数 y 恒有两个相异的“不变值”,求 a 的取值范围;(3)在(2)的条件下,若该图象上 A 、B 两点的横坐标是该函数的“不变值”,且 A 、B 两点关于直线 y=kx-2a+3 对称,求 b 的最小值.【答案】(1)-1,3;(2)0<a<1;(3)-98【解析】【分析】(1)先确定二次函数解析式为y=x 2-x-3,根据x o 是函数y 的一个不动点的定义,把(x o ,x o )代入得x 02-x 0-3=x o ,然后解此一元二次方程即可;(2)根据x o 是函数y 的一个不动点的定义得到ax o 2+(b+1)x o +(b-1)=x o ,整理得ax 02+bx o +(b-1)=0,则根据判别式的意义得到△=b 2-4a (b-1)>0,即b 2-4ab+4a>0,把b 2-4ab+4a 看作b 的二次函数,由于对任意实数b ,b 2-4ab+4a>0成立,则(4a )2-4.4a<0,然后解此不等式即可.(3)(利用两点关于直线对称的两个结论,一是中点在已知直线上,二是两点连线和已知直线垂直.找到a ,b 之间的关系式,整理后在利用基本不等式求解可得.【详解】解:(1)当a=1,b=-2时,二次函数解析式为y=x 2-x-3,把(x o ,x o )代入得x 02-x 0-3=x o ,解得x o =-1或x o =3,所以函数y 的不动点为-1和3;(2)因为y=x o ,所以ax o 2+(b+1)x o +(b-1)=x o ,即ax 02+bx o +(b-1)=0,因为函数y 恒有两个相异的不动点,所以此方程有两个不相等的实数解,所以△=b 2-4a (b-1)>0,即b 2-4ab+4a>0,而对任意实数b ,b 2-4ab+4a>0成立,所以(4a )2-4.4a<0,解得0<a<1.(3)设A (x 1,x 1),B (x 2,x 2),则x 1+x 2b a =-A ,B 的中点的坐标为(1212,22x x x x ++ ),即M (,22b b a a-- ) A 、B 两点关于直线y=kx-2a+3对称,又∵A ,B 在直线y=x 上,∴k=-1,A ,B 的中点M 在直线y=kx-2a+3上. ∴b a -=b a-2a+3 得:b=2a 2-3a 所以当且仅当a=34 时,b 有最小值-98【点睛】 本题是在新定义下对函数知识的综合考查,是一道好题.关于两点关于直线对称的问题,有两个结论同时存在,一是中点在已知直线上,二是两点连线和已知直线垂直.6.已知抛物线2(5)6y x m x m =-+-+-.(1)求证:该抛物线与x 轴总有交点;(2)若该抛物线与x 轴有一个交点的横坐标大于3且小于5,求m 的取值范围;(3)设抛物线2(5)6y x m x m =-+-+-与y 轴交于点M ,若抛物线与x 轴的一个交点关于直线y x =-的对称点恰好是点M ,求m 的值.【答案】(1)证明见解析;(2)1?<?m?3<;(3)56m m ==或【解析】【分析】(1)本题需先根据判别式解出无论m 为任何实数都不小于零,再判断出物线与x 轴总有交点.(2)根据公式法解方程,利用已有的条件,就能确定出m 的取值范围,即可得到结果. (3)根据抛物线y=-x 2+(5-m )x+6-m ,求出与y 轴的交点M 的坐标,再确定抛物线与x 轴的两个交点关于直线y=-x 的对称点的坐标,列方程可得结论.【详解】(1)证明:∵()()()222454670b ac m m m ∆=-=-+-=-≥∴抛物线与x 轴总有交点.(2)解:由(1)()27m ∆=-,根据求根公式可知, 方程的两根为:2572m m x ()-±-=- 即1216x x m =-=-+, 由题意,有 3<-m 6<5+1<?m 3∴<(3)解:令 x = 0, y =6m -+∴ M (0,6m -+)由(2)可知抛物线与x 轴的交点为(-1,0)和(6m -+,0),它们关于直线y x =-的对称点分别为(0 , 1)和(0, 6m -),由题意,可得:6166m m m 或-+=-+=-56m m ∴==或【点睛】本题考查对抛物线与x 轴的交点,解一元一次方程,解一元一次不等式,根的判别式,对称等,解题关键是熟练理解和掌握以上性质,并能综合运用这些性质进行计算.7.如图①,已知抛物线y=ax 2+bx+c 的图像经过点A (0,3)、B (1,0),其对称轴为直线l :x=2,过点A 作AC ∥x 轴交抛物线于点C ,∠AOB 的平分线交线段AC 于点E ,点P 是抛物线上的一个动点,设其横坐标为m.(1)求抛物线的解析式;(2)若动点P 在直线OE 下方的抛物线上,连结PE 、PO ,当m 为何值时,四边形AOPE 面积最大,并求出其最大值;(3)如图②,F 是抛物线的对称轴l 上的一点,在抛物线上是否存在点P 使△POF 成为以点P 为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.【答案】(1)y=x2-4x+3.(2)当m=52时,四边形AOPE面积最大,最大值为758.(3)P点的坐标为:P1(3+5,152-),P2(352,1+52),P3(5+52,1+52),P4(55-,152-).【解析】分析:(1)利用对称性可得点D的坐标,利用交点式可得抛物线的解析式;(2)设P(m,m2-4m+3),根据OE的解析式表示点G的坐标,表示PG的长,根据面积和可得四边形AOPE的面积,利用配方法可得其最大值;(3)存在四种情况:如图3,作辅助线,构建全等三角形,证明△OMP≌△PNF,根据OM=PN列方程可得点P 的坐标;同理可得其他图形中点P的坐标.详解:(1)如图1,设抛物线与x轴的另一个交点为D,由对称性得:D(3,0),设抛物线的解析式为:y=a(x-1)(x-3),把A(0,3)代入得:3=3a,a=1,∴抛物线的解析式;y=x2-4x+3;(2)如图2,设P(m,m2-4m+3),∵OE平分∠AOB,∠AOB=90°,∴∠AOE=45°,∴△AOE是等腰直角三角形,∴AE=OA=3,∴E (3,3),易得OE 的解析式为:y=x ,过P 作PG ∥y 轴,交OE 于点G ,∴G (m ,m ),∴PG=m-(m 2-4m+3)=-m 2+5m-3,∴S 四边形AOPE =S △AOE +S △POE , =12×3×3+12PG•AE , =92+12×3×(-m 2+5m-3), =-32m 2+152m , =32(m-52)2+758, ∵-32<0, ∴当m=52时,S 有最大值是758; (3)如图3,过P 作MN ⊥y 轴,交y 轴于M ,交l 于N ,∵△OPF 是等腰直角三角形,且OP=PF ,易得△OMP ≌△PNF ,∴OM=PN ,∵P (m ,m 2-4m+3),则-m 2+4m-3=2-m ,解得:5+555- ∴P 5+51+555-152); 如图4,过P 作MN ⊥x 轴于N ,过F 作FM ⊥MN 于M ,同理得△ONP≌△PMF,∴PN=FM,则-m2+4m-3=m-2,解得:3+535;P3+5152-35,1+5综上所述,点P的坐标是:(52,1+52)或(552-,1523+515-35,1+5).点睛:本题属于二次函数综合题,主要考查了二次函数的综合应用,相似三角形的判定与性质以及解一元二次方程的方法,解第(2)问时需要运用配方法,解第(3)问时需要运用分类讨论思想和方程的思想解决问题.8.已知二次函数的图象以A(﹣1,4)为顶点,且过点B(2,﹣5)(1)求该函数的关系式;(2)求该函数图象与坐标轴的交点坐标;(3)将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,求△O A′B′的面积.【答案】(1)y=﹣x2﹣2x+3;(2)抛物线与x轴的交点为:(﹣3,0),(1,0)(3)15.【解析】【分析】(1)已知了抛物线的顶点坐标,可用顶点式设该二次函数的解析式,然后将B 点坐标代入,即可求出二次函数的解析式;(2)根据函数解析式,令x=0,可求得抛物线与y轴的交点坐标;令y=0,可求得抛物线与x轴交点坐标;(3)由(2)可知:抛物线与x轴的交点分别在原点两侧,由此可求出当抛物线与x轴负半轴的交点平移到原点时,抛物线平移的单位,由此可求出A′、B′的坐标.由于△OA′B′不规则,可用面积割补法求出△OA′B′的面积.【详解】(1)设抛物线顶点式y=a(x+1)2+4,将B(2,﹣5)代入得:a=﹣1,∴该函数的解析式为:y=﹣(x+1)2+4=﹣x2﹣2x+3;(2)令x=0,得y=3,因此抛物线与y轴的交点为:(0,3),令y=0,﹣x2﹣2x+3=0,解得:x1=﹣3,x2=1,即抛物线与x轴的交点为:(﹣3,0),(1,0);(3)设抛物线与x轴的交点为M、N(M在N的左侧),由(2)知:M(﹣3,0),N(1,0),当函数图象向右平移经过原点时,M与O重合,因此抛物线向右平移了3个单位,故A'(2,4),B'(5,﹣5),∴S△OA′B′=12×(2+5)×9﹣12×2×4﹣12×5×5=15.【点睛】本题考查了用待定系数法求抛物线解析式、函数图象与坐标轴交点、图形面积的求法等知识.熟练掌握待定系数法、函数图象与坐标轴的交点的求解方法、不规则图形的面积的求解方法等是解题的关键.9.如图1,抛物线y=ax2+2x+c与x轴交于A(﹣4,0),B(1,0)两点,过点B的直线y=kx+23分别与y轴及抛物线交于点C,D.(1)求直线和抛物线的表达式;(2)动点P从点O出发,在x轴的负半轴上以每秒1个单位长度的速度向左匀速运动,设运动时间为t秒,当t为何值时,△PDC为直角三角形?请直接写出所有满足条件的t的值;(3)如图2,将直线BD沿y轴向下平移4个单位后,与x轴,y轴分别交于E,F两点,在抛物线的对称轴上是否存在点M,在直线EF上是否存在点N,使DM+MN的值最小?若存在,求出其最小值及点M,N的坐标;若不存在,请说明理由.【答案】(1)抛物线解析式为:y=228233x x +-,BD 解析式为y=﹣2233x +;(2)t 的值为4915129±、233.(3)N 点坐标为(﹣2,﹣2),M 点坐标为(﹣32,﹣54),213 【解析】分析:(1)利用待定系数法求解可得;(2)先求得点D 的坐标,过点D 分别作DE ⊥x 轴、DF ⊥y 轴,分P 1D ⊥P 1C 、P 2D ⊥DC 、P 3C ⊥DC 三种情况,利用相似三角形的性质逐一求解可得;(3)通过作对称点,将折线转化成两点间距离,应用两点之间线段最短.详解:(1)把A (﹣4,0),B (1,0)代入y=ax 2+2x+c ,得168020a c a c -+=⎧⎨++=⎩, 解得:2383a c ⎧=⎪⎪⎨⎪=-⎪⎩, ∴抛物线解析式为:y=228233x x +-, ∵过点B 的直线y=kx+23, ∴代入(1,0),得:k=﹣23, ∴BD 解析式为y=﹣2233x +; (2)由2282332233y x x y x ﹣⎧=+-⎪⎪⎨⎪=+⎪⎩得交点坐标为D (﹣5,4), 如图1,过D 作DE ⊥x 轴于点E ,作DF ⊥y 轴于点F ,当P1D⊥P1C时,△P1DC为直角三角形,则△DEP1∽△P1OC,∴DEPO =PEOC,即4t=523t-,解得15129±,当P2D⊥DC于点D时,△P2DC为直角三角形由△P2DB∽△DEB得DBEB=2P BDB,52=526,解得:t=233;当P3C⊥DC时,△DFC∽△COP3,∴DFOC =3CFP O,即523=103t,解得:t=49,∴t的值为4915129±、233.(3)由已知直线EF解析式为:y=﹣23x﹣103,在抛物线上取点D的对称点D′,过点D′作D′N⊥EF于点N,交抛物线对称轴于点M过点N 作NH ⊥DD′于点H ,此时,DM+MN=D′N 最小.则△EOF ∽△NHD′设点N 坐标为(a ,﹣21033a -), ∴OE NH =OF HD ',即52104()33a ---=1032a -, 解得:a=﹣2,则N 点坐标为(﹣2,﹣2),求得直线ND′的解析式为y=32x+1, 当x=﹣32时,y=﹣54, ∴M 点坐标为(﹣32,﹣54), 此时,DM+MN 的值最小为22D H NH '+=2246+=213.点睛:本题是二次函数和几何问题综合题,应用了二次函数性质以及转化的数学思想、分类讨论思想.解题时注意数形结合.10.如图,已知抛物线2y ax bx c =++(a≠0)经过A (﹣1,0)、B (3,0)、C (0,﹣3)三点,直线l 是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P 是直线l 上的一个动点,当点P 到点A 、点B 的距离之和最短时,求点P 的坐标;(3)点M 也是直线l 上的动点,且△MAC 为等腰三角形,请直接写出所有符合条件的点M 的坐标.【答案】(1)223y x x =--;(2)P (1,0);(3).【解析】试题分析:(1)直接将A 、B 、C 三点坐标代入抛物线的解析式中求出待定系数即可; (2)由图知:A .B 点关于抛物线的对称轴对称,那么根据抛物线的对称性以及两点之间线段最短可知,直线l 与x 轴的交点,即为符合条件的P 点;(3)由于△MAC 的腰和底没有明确,因此要分三种情况来讨论:①MA=AC 、②MA=MC 、③AC=MC ;可先设出M 点的坐标,然后用M 点纵坐标表示△MAC 的三边长,再按上面的三种情况列式求解.试题解析:(1)将A (﹣1,0)、B (3,0)、C (0,﹣3)代入抛物线2y ax bx c=++中,得:0{9303a b c a b c c -+=++==-,解得:1{23a b c ==-=-,故抛物线的解析式:223y x x =--.(2)当P 点在x 轴上,P ,A ,B 三点在一条直线上时,点P 到点A 、点B 的距离之和最短,此时x=2b a -=1,故P (1,0); (3)如图所示:抛物线的对称轴为:x=2b a -=1,设M (1,m ),已知A (﹣1,0)、C (0,﹣3),则:2MA =24m +,2MC =2(3)1m ++=2610m m ++,2AC =10;①若MA=MC ,则22MA MC =,得:24m +=2610m m ++,解得:m=﹣1; ②若MA=AC ,则22MA AC =,得:24m +=10,得:m=6±;③若MC=AC ,则22MC AC =,得:2610m m ++=10,得:10m =,26m =-; 当m=﹣6时,M 、A 、C 三点共线,构不成三角形,不合题意,故舍去;综上可知,符合条件的M 点,且坐标为 M (1,6)(1,6-)(1,﹣1)(1,0).考点:二次函数综合题;分类讨论;综合题;动点型.。
中考数学复习---二次函数之二次函数综合知识点总结与练习题(含答案解析)

中考数学复习---二次函数之二次函数综合知识点总结与练习题(含答案解析) 知识点总结1. 二次函数与一元二次方程:①若二次函数()02≠++=a c bx ax y 与x 轴有两个交点⇔一元二次方程02=++c bx ax 有两个不相等的实数根⇔042>ac b −=∆。
②若二次函数()02≠++=a c bx ax y 与x 轴只有一个交点⇔一元二次方程02=++c bx ax 有两个相等的实数根⇔042=−=∆ac b 。
③若二次函数()02≠++=a c bx ax y 与x 轴没有交点⇔一元二次方程02=++c bx ax 没有实数根⇔042<ac b −=∆。
④若二次函数()02≠++=a c bx ax y 与直线m y =相交,则一元二次方程为m c bx ax =++2。
交点情况与方程的解的情况同与x 轴相交时一样。
2. 二次函数与不等式(组)若二次函数()02≠++=a c bx ax y 与一次函数()0≠+=k b kx y 存在交点,则不等式:b kx c bx ax +++>2的解集取二次函数图像在上方的部分所对应的自变量取值范围;b kx c bx ax +++<2的解集取二次函数图像在下方的部分所对应的自变量取值范围。
3. 二次函数的一些特殊的自变量的函数值:①当1=x 时所对应的函数值为c b a y ++=。
②当1−=x 时所对应的函数值为c b a y +−=。
③当2=x 时所对应的函数值为c b a y ++=24。
④当2−=x 时所对应的函数值为c b a y +−=24。
4. 对称轴的特殊值:①若对称轴为直线1=x 时,则02=+b a 。
②若对称轴为直线1−=x 时,则02=−b a 。
③判断b a +2与0的大小关系时,看对称轴与1=x 的位置关系。
④判断b a −2与0的大小关系时,看对称轴与1−=x 的位置关系。
练习题1、(2022•巴中)函数y =|ax 2+bx +c |(a >0,b 2﹣4ac >0)的图像是由函数y =ax 2+bx +c (a >0,b 2﹣4ac >0)的图像x 轴上方部分不变,下方部分沿x 轴向上翻折而成,如图所示,则下列结论正确的是( )①2a +b =0;②c =3;③abc >0;④将图像向上平移1个单位后与直线y =5有3个交点.A .①②B .①③C .②③④D .①③④【分析】根据函数图像与x 轴交点的横坐标求出对称轴为,进而可得2a +b =0,由图像可得抛物线y =ax 2+bx +c 与y 轴交点在x 轴下方,由抛物线y =ax 2+bx +c 的开口方向,对称轴位置和抛物线与y 轴交点位置可得abc 的符号,求出二次函数y =ax 2+bx +c 的顶点式,可得图像向上平移1个单位后与直线y =5有3个交点【解答】解:∵图像经过(﹣1,0),(3,0),∴抛物线y =ax 2+bx +c 的对称轴为直线x =1,∴﹣=1,∴b =﹣2a ,即2a +b =0,①正确.由图像可得抛物线y =ax 2+bx +c 与y 轴交点在x 轴下方,∴c<0,②错误.由抛物线y=ax2+bx+c的开口向上可得a>0,∴b=﹣2a<0,∴abc>0,③正确.设抛物线y=ax2+bx+c的解析式为y=a(x+1)(x﹣3),代入(0,3)得:3=﹣3a,解得:a=﹣1,∴y=﹣(x+1)(x﹣3)=﹣x2+2x+3=﹣(x﹣1)2+4,∴顶点坐标为(1,4),∵点(1,4)向上平移1个单位后的坐标为(1,5),∴将图像向上平移1个单位后与直线y=5有3个交点,故④正确;故选:D.2、(2022•资阳)如图是二次函数y=ax2+bx+c的图像,其对称轴为直线x=﹣1,且过点(0,1).有以下四个结论:①abc>0,②a﹣b+c>1,③3a+c<0,④若顶点坐标为(﹣1,2),当m≤x≤1时,y有最大值为2、最小值为﹣2,此时m的取值范围是﹣3≤m≤﹣1.其中正确结论的个数是()A.4个B.3个C.2个D.1个【分析】①:根据二次函数的对称轴,c=1,即可判断出abc>0;②:结合图像发现,当x=﹣1时,函数值大于1,代入即可判断;③:结合图像发现,当x=1时,函数值小于0,代入即可判断;④:运用待定系数法求出二次函数解析式,再利用二次函数的对称性即可判断.【解答】解:∵二次函数y=ax2+bx+c的图像,其对称轴为直线x=﹣1,且过点(0,1),∴,c=1,∴ab>0,∴abc>0,故①正确;从图中可以看出,当x=﹣1时,函数值大于1,因此将x=﹣1代入得,(﹣1)2⋅a+(﹣1)⋅b+c>1,即a﹣b+c>1,故②正确;∵,∴b=2a,从图中可以看出,当x=1时,函数值小于0,∴a+b+c<0,∴3a+c<0,故③正确;∵二次函数y=ax2+bx+c的顶点坐标为(﹣1,2),∴设二次函数的解析式为y=a(x+1)2+2,将(0,1)代入得,1=a+2,解得a=﹣1,∴二次函数的解析式为y=﹣(x+1)2+2,∴当x=1时,y=﹣2;∴根据二次函数的对称性,得到﹣3≤m≤﹣1,故④正确;综上所述,①②③④均正确,故有4个正确结论,故选A.3、(2022•黄石)已知二次函数y=ax2+bx+c的部分图像如图所示,对称轴为直线x=﹣1,有以下结论:①abc<0;②若t为任意实数,则有a﹣bt≤at2+b;③当图像经过点(1,3)时,方程ax2+bx+c ﹣3=0的两根为x1,x2(x1<x2),则x1+3x2=0,其中,正确结论的个数是()A.0 B.1 C.2 D.3【分析】利用抛物线开口方向得到a>0,利用抛物线的对称轴方程得到b=2a>0,利用抛物线与y轴的交点位置得到c<0,则可对①进行判断;利用二次函数当x=﹣1时有最小值可对②进行判断;由于二次函数y=ax2+bx+c与直线y=3的一个交点为(1,3),利用对称性得到二次函数y=ax2+bx+c与直线y=3的另一个交点为(﹣3,3),从而得到x1=﹣3,x2=1,则可对③进行判断.【解答】解:∵抛物线开口向上,∴a>0,∵抛物线的对称轴为直线x=﹣1,即﹣=﹣1,∴b =2a >0,∵抛物线与y 轴的交点在x 轴下方,∴c <0,∴abc <0,所以①正确;∵x =﹣1时,y 有最小值,∴a ﹣b +c ≤at 2+bt +c (t 为任意实数),即a ﹣bt ≤at 2+b ,所以②正确;∵图像经过点(1,3)时,得ax 2+bx +c ﹣3=0的两根为x 1,x 2(x 1<x 2),∴二次函数y =ax 2+bx +c 与直线y =3的一个交点为(1,3),∵抛物线的对称轴为直线x =﹣1,∴二次函数y =ax 2+bx +c 与直线y =3的另一个交点为(﹣3,3),即x 1=﹣3,x 2=1,∴x 1+3x 2=﹣3+3=0,所以③正确.故选:D .4、(2022•日照)已知二次函数y =ax 2+bx +c (a ≠0)的部分图像如图所示,对称轴为x =23,且经过点(﹣1,0).下列结论:①3a +b =0;②若点(21,y 1),(3,y 2)是抛物线上的两点,则y 1<y 2;③10b ﹣3c =0;④若y ≤c ,则0≤x ≤3.其中正确的有( )A.1个B.2个C.3个D.4个【分析】由对称轴为x=即可判断①;根据点(,y1),(3,y2)到对称轴的距离即可判断②;由抛物线经过点(﹣1,0),得出a﹣b+c=0,对称轴x=﹣=,得出a=﹣b,代入即可判断③;根据二次函数的性质以及抛物线的对称性即可判断④.【解答】解:∵对称轴x=﹣=,∴b=﹣3a,∴3a+b=0,①正确;∵抛物线开口向上,点(,y1)到对称轴的距离小于点(3,y2)的距离,∴y1<y2,故②正确;∵经过点(﹣1,0),∴a﹣b+c=0,∵对称轴x=﹣=,∴a=﹣b,∴﹣b﹣b+c=0,∴3c=4b,∴4b﹣3c=0,故③错误;∵对称轴x=,∴点(0,c)的对称点为(3,c),∵开口向上,∴y≤c时,0≤x≤3.故④正确;故选:C.5、(2022•荆门)抛物线y=ax2+bx+c(a,b,c为常数)的对称轴为x=﹣2,过点(1,﹣2)和点(x0,y0),且c>0.有下列结论:①a<0;②对任意实数m都有:am2+bm≥4a﹣2b;③16a+c>4b;④若x0>﹣4,则y0>c.其中正确结论的个数为()A.1个B.2个C.3个D.4个【分析】根据抛物线y=ax2+bx+c(a,b,c为常数)的对称轴为x=﹣2,过点(1,﹣2)且c>0,即可判断开口向下,即可判断①;根据二次函数的性质即可判断②;根据抛物线的对称性即可判断③;根据抛物线的对称性以及二次函数的性质即可判断④.【解答】解:∵抛物线y=ax2+bx+c(a,b,c为常数)的对称轴为x=﹣2,过点(1,﹣2),且c>0,∴抛物线开口向下,则a<0,故①正确;∵抛物线开口向下,对称轴为x=﹣2,∴函数的最大值为4a﹣2b+c,∴对任意实数m都有:am2+bm+c≤4a﹣2b+c,即am2+bm≤4a﹣2b,故②错误;∵对称轴为x=﹣2,c>0.∴当x=﹣4时的函数值大于0,即16a﹣4b+c>0,∴16a+c>4b,故③正确;∵对称轴为x=﹣2,点(0,c)的对称点为(﹣4,c),∵抛物线开口向下,∴若﹣4<x0<0,则y0>c,故④错误;故选:B.6、(2022•绵阳)如图,二次函数y=ax2+bx+c的图像关于直线x=1对称,与x轴交于A (x1,0),B(x2,0)两点.若﹣2<x1<﹣1,则下列四个结论:①3<x2<4;②3a+2b >0;③b2>a+c+4ac;④a>c>b,正确结论的个数为()A.1个B.2个C.3个D.4个【分析】根据二次函数的对称性,即可判断①;由开口方向和对称轴即可判断②;根据抛物线与x轴的交点以及x=﹣1时的函数的取值,即可判断③;根据抛物线的开口方向、对称轴,与y轴的交点以及a﹣b+c<0,即可判断④.【解答】解:∵对称轴为直线x=1,﹣2<x1<﹣1,∴3<x2<4,①正确,∵﹣=1,∴b=﹣2a,∴3a+2b=3a﹣4a=﹣a,∵a>0,∴3a+2b<0,②错误;∵抛物线与x轴有两个交点,∴b2﹣4ac>0,由题意可知x=﹣1时,y<0,∴a﹣b+c<0,∴a+c<b,∵a>0,∴b=﹣2a<0,∴a+c<0,∴b2﹣4ac>a+c,∴b2>a+c+4ac,③正确;∵抛物线开口向上,与y轴的交点在x轴下方,∴a>0,c<0,∴a>c,∵a﹣b+c<0,b=﹣2a,∴3a+c<0,∴c<﹣3a,∴b=﹣2a,∴b>c,所以④错误;故选:B.7、(2022•牡丹江)如图,抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=﹣2,并与x 轴交于A,B两点,若OA=5OB,则下列结论中:①abc>0;②(a+c)2﹣b2=0;③9a+4c <0;④若m为任意实数,则am2+bm+2b≥4a,正确的个数是()A.1 B.2 C.3 D.4【分析】根据函数图像的开口方向、对称轴、图像与y轴的交点即可判断①;根据对称轴x =﹣2,OA=5OB,可得OA=5,OB=1,点A(﹣5,0),点B(1,0),当x=1时,y =0即可判断②;根据对称轴x=﹣2,以及,a+b+c=0得a与c的关系,即可判断③;根据函数的最小值是当x=﹣2时,y=4a﹣2b+c,即可判断④;【解答】解:①观察图像可知:a>0,b>0,c<0,∴abc<0,故①错误;②∵对称轴为直线x=﹣2,OA=5OB,可得OA=5,OB=1,∴点A(﹣5,0),点B(1,0),∴当x=1时,y=0,即a+b+c=0,∴(a+c)2﹣b2=(a+b+c)(a+c﹣b)=0,故②正确;③抛物线的对称轴为直线x=﹣2,即﹣=﹣2,∴b=4a,∵a+b+c=0,∴5a+c=0,∴c=﹣5a,∴9a+4c=﹣11a,∵a >0,∴9a +4c <0,故③正确;④当x =﹣2时,函数有最小值y =4a ﹣2b +c ,由am 2+bm +c ≥4a ﹣2b +c ,可得am 2+bm +2b ≥4a ,∴若m 为任意实数,则am 2+bm +2b ≥4a ,故④正确;故选:C .8、(2022•烟台)二次函数y =ax 2+bx +c (a ≠0)的部分图像如图所示,其对称轴为直线x =﹣21,且与x 轴的一个交点坐标为(﹣2,0).下列结论:①abc >0;②a =b ;③2a +c =0;④关于x 的一元二次方程ax 2+bx +c ﹣1=0有两个相等的实数根.其中正确结论的序号是( )A .①③B .②④C .③④D .②③【分析】根据对称轴、开口方向、与y 轴的交点位置即可判断a 、b 、c 与0的大小关系,然后将由对称轴可知a =b .图像过(﹣2,0)代入二次函数中可得4a ﹣2b +c =0.再由二次函数最小值小于0,从而可判断ax 2+bx +c =1有两个不相同的解.【解答】解:①由图可知:a >0,c <0,<0,∴b >0,∴abc <0,故①不符合题意.②由题意可知:=﹣,∴b =a ,故②符合题意.③将(﹣2,0)代入y =ax 2+bx +c ,∴4a ﹣2b +c =0,∵a =b ,∴2a +c =0,故③符合题意.④由图像可知:二次函数y =ax 2+bx +c 的最小值小于0,令y =1代入y =ax 2+bx +c ,∴ax 2+bx +c =1有两个不相同的解,故④不符合题意.故选:D .9、(2022•广安)已知抛物线y =ax 2+bx +c 的对称轴为x =1,与x 轴正半轴的交点为A (3,0),其部分图像如图所示,有下列结论:①abc >0; ②2c ﹣3b <0; ③5a +b +2c =0;④若B (34,y 1)、C (31,y 2)、D (﹣31,y 3)是抛物线上的三点,则y 1<y 2<y 3.其中正确结论的个数有( )A .1B .2C .3D .4【分析】①正确,根据抛物线的位置,判断出a ,b ,c 的符号,可得结论;②③错误,利用对称轴公式,抛物线经过A (3,0),求出b ,c 与a 的关系,判断即可; ④正确.利用图像法判断即可.【解答】解:∵抛物线开口向上,∴a>0,∵抛物线的对称轴是直线x=1,∴1=﹣,∴b=﹣2a,∴b<0,∵抛物线交y轴于负半轴,∴c<0,∴abc>0,故①正确,∵抛物线y=ax2﹣2ax+c经过(3,0),∴9a﹣6a+c=0,∴c=﹣3a,∴2c﹣3b=﹣6a+6a=0,故②错误,5a+b+2c=5a﹣2a﹣6a=﹣3a<0,故③错误,观察图像可知,y1<y2<y3,故④正确,故选:B.10、(2022•辽宁)抛物线y=ax2+bx+c的部分图像如图所示,对称轴为直线x=﹣1,直线y=kx+c与抛物线都经过点(﹣3,0).下列说法:①ab>0;②4a+c>0;③若(﹣2,y 1)与(21,y 2)是抛物线上的两个点,则y 1<y 2;④方程ax 2+bx +c =0的两根为x 1=﹣3,x 2=1;⑤当x =﹣1时,函数y =ax 2+(b ﹣k )x 有最大值.其中正确的个数是( )A .2B .3C .4D .5【分析】利用图像的信息与已知条件求得a ,b 的关系式,利用待定系数法和二次函数的性质对每个结论进行逐一判断即可得出结论.【解答】解:∵抛物线的开口方向向下,∴a <0.∵抛物线的对称轴为直线x =﹣1,∴﹣=﹣1,∴b =2a ,b <0.∵a <0,b <0,∴ab >0,∴①的结论正确;∵抛物线y =ax 2+bx +c 经过点(﹣3,0),∴9a ﹣3b +c =0,∴9a ﹣3×2a +c =0,∴3a +c =0.∴4a+c=a<0,∴②的结论不正确;∵抛物线的对称轴为直线x=﹣1,∴点(﹣2,y1)关于直线x=﹣1对称的对称点为(0,y1),∵a<0,∴当x>﹣1时,y随x的增大而减小.∵>0>﹣1,∴y1>y2.∴③的结论不正确;∵抛物线的对称轴为直线x=﹣1,抛物线经过点(﹣3,0),∴抛物线一定经过点(1,0),∴抛物线y=ax2+bx+c与x轴的交点的横坐标为﹣3,1,∴方程ax2+bx+c=0的两根为x1=﹣3,x2=1,∴④的结论正确;∵直线y=kx+c经过点(﹣3,0),∴﹣3k+c=0,∴c=3k.∵3a+c=0,∴c=﹣3a,∴3k=﹣3a,∴k=﹣a.∴函数y=ax2+(b﹣k)x=ax2+(2a+a)x=ax2+3ax=a﹣a,∵a<0,∴当x=﹣时,函数y=ax2+(b﹣k)x有最大值,∴⑤的结论不正确.综上,结论正确的有:①④,故选:A.11、(2022•内蒙古)如图,抛物线y=ax2+bx+c(a≠0)与x轴的一个交点坐标为(﹣1,0),抛物线的对称轴为直线x=1,下列结论:①abc<0;②3a+c=0;③当y>0时,x 的取值范围是﹣1≤x<3;④点(﹣2,y1),(2,y2)都在抛物线上,则有y1<0<y2.其中结论正确的个数是()A.1个B.2个C.3个D.4个【分析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.【解答】解:根据函数的对称性,抛物线与x轴的另外一个交点的坐标为(3,0);①函数对称轴在y轴右侧,则ab<0,而c=3>0,故abc<0,故①正确,符合题意;②∵x=﹣=1,即b=﹣2a,而x=﹣1时,y=0,即a﹣b+c=0,∴a+2a+c=0,∴3a+c=0.∴②正确,符合题意;③由图像知,当y>0时,x的取值范围是﹣1<x<3,∴③错误,不符合题意;④从图像看,当x=﹣2时,y1<0,当x=2时,y2>0,∴有y1<0<y2,故④正确,符合题意;故选:C.12、(2022•枣庄)小明在学习“二次函数”内容后,进行了反思总结.如图,二次函数y =ax2+bx+c(a≠0)图像的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图像他得出下列结论:①ab>0且c>0;②a+b+c=0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1;④若点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图像上,则y1<y2<y3;⑤3a+c<0,其中正确的结论有.(填序号,多选、少选、错选都不得分)【分析】由抛物线的对称轴的位置以及与y轴的交点可判断①;由抛物线过点(1,0),即可判断②;由抛物线的对称性可判断③;根据各点与抛物线对称轴的距离大小可判断④;对称轴可得b=2a,由抛物线过点(1,0)可判断⑤.【解答】解:∵抛物线对称轴在y轴的左侧,∴ab>0,∵抛物线与y轴交点在x轴上方,∴c>0,①正确;∵抛物线经过(1,0),∴a+b+c=0,②正确.∵抛物线与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,∴另一个交点为(﹣3,0),∴关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1,③正确;∵﹣1﹣(﹣2)<﹣1﹣(﹣4)<3﹣(﹣1),抛物线开口向下,∴y2>y1>y3,④错误.∵抛物线与x轴的一个交点坐标为(1,0),∴a+b+c=0,∵﹣=﹣1,∴b =2a ,∴3a +c =0,⑤错误.故答案为:①②③.13、(2022•内江)如图,抛物线y =ax 2+bx +c 与x 轴交于两点(x 1,0)、(2,0),其中0<x 1<1.下列四个结论:①abc <0;②a +b +c >0;③2a ﹣c >0;④不等式ax 2+bx +c >﹣1x c x +c 的解集为0<x <x 1.其中正确结论的个数是( )A .4B .3C .2D .1【分析】利用二次函数的图像和性质依次判断即可.【解答】解:∵抛物线开口向上,对称轴在y 轴右边,与y 轴交于正半轴, ∴a >0,b <0,c >0,∴abc <0,∴①正确.∵当x =1时,y <0,∴a +b +c <0,∴②错误.∵抛物线过点(2,0),∴4a+2b+c=0,∴b=﹣2a﹣,∵a+b+c<0,∴a﹣2a﹣+c<0,∴2a﹣c>0,∴③正确.如图:设y1=ax2+bx+c,y2=﹣x+c,由图值,y1>y2时,x<0或x>x1,故④错误.故选:C.14、(2022•鄂州)如图,已知二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)的图像顶点为P(1,m),经过点A(2,1).有以下结论:①a<0;②abc>0;③4a+2b+c=1;④x>1时,y随x的增大而减小;⑤对于任意实数t,总有at2+bt≤a+b,其中正确的有()A.2个B.3个C.4个D.5个【分析】①根据抛物线的开口方向向下即可判定;②先运用二次函数图像的性质确定a、b、c的正负即可解答;③将点A的坐标代入即可解答;④根据函数图像即可解答;⑤运用作差法判定即可.【解答】解:①由抛物线的开口方向向下,则a<0,故①正确;②∵抛物线的顶点为P(1,m),∴﹣=1,b=﹣2a,∵a<0,∴b>0,∵抛物线与y轴的交点在正半轴,∴c>0,∴abc<0,故②错误;③∵抛物线经过点A(2,1),∴1=a•22+2b+c,即4a+2b+c=1,故③正确;④∵抛物线的顶点为P(1,m),且开口方向向下,∴x>1时,y随x的增大而减小,即④正确;⑤∵a<0,∴at2+bt﹣(a+b)=at 2﹣2at ﹣a +2a=at 2﹣2at +a=a (t 2﹣2t +1)=a (t ﹣1)2≤0,∴at 2+bt ≤a +b ,则⑤正确综上,正确的共有4个.故选:C .15、(2022•达州)二次函数y =ax 2+bx +c 的部分图像如图所示,与y 轴交于(0,﹣1),对称轴为直线x =1.下列结论:①abc >0;②a >31;③对于任意实数m ,都有m (am +b )>a +b 成立;④若(﹣2,y 1),(21,y 2),(2,y 3)在该函数图像上,则y 3<y 2<y 1;⑤方程|ax 2+bx +c |=k (k ≥0,k 为常数)的所有根的和为4.其中正确结论有( )个.A .2B .3C .4D .5【分析】①正确,判断出a ,b ,c 的正负,可得结论;②正确.利用对称轴公式可得,b =﹣2a ,当x =﹣1时,y >0,解不等式可得结论; ③错误.当m =1时,m (am +b )=a +b ;④错误.应该是y 2<y 3<y 1,;⑤错误.当有四个交点或3个时,方程|ax 2+bx +c |=k (k ≥0,k 为常数)的所有根的和为4,当有两个交点时,方程|ax 2+bx +c |=k (k ≥0,k 为常数)的所有根的和为2.【解答】解:∵抛物线开口向上,∴a>0,∴抛物线与y轴交于点(0,﹣1),∴c=﹣1,∵﹣=1,∴b=﹣2a<0,∴abc>0,故①正确,∵y=ax2﹣2ax﹣1,当x=﹣1时,y>0,∴a+2a﹣1>0,∴a>,故②正确,当m=1时,m(am+b)=a+b,故③错误,∵点(﹣2,y1)到对称轴的距离大于点(2,y3)到对称轴的距离,∴y1>y3,∵点(,y2)到对称轴的距离小于点(2,y3)到对称轴的距离,∴y3>y2,∴y2<y3<y1,故④错误,∵方程|ax2+bx+c|=k(k≥0,k为常数)的解,是抛物线与直线y=±k的交点,当有3个交点时,方程|ax2+bx+c|=k(k≥0,k为常数)的所有根的和为3,当有4个交点时,方程|ax2+bx+c|=k(k≥0,k为常数)的所有根的和为4,当有2个交点时,方程|ax2+bx+c|=k(k≥0,k为常数)的所有根的和为2,故⑤错误,故选:A.。
中考数学专题训练---二次函数的综合题分类含答案

中考数学专题训练---二次函数的综合题分类含答案一、二次函数1.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y 轴交于点N,其顶点为D.(1)求抛物线及直线AC的函数关系式;(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P 的坐标;(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.【答案】(1)y=﹣x2﹣2x+3;y=﹣x+1;(2)当x=﹣12时,△APC的面积取最大值,最大值为278,此时点P的坐标为(﹣12,154);(3)在对称轴上存在一点M(﹣1,2),使△ANM的周长最小,△ANM周长的最小值为102【解析】【分析】(1)根据点A,C的坐标,利用待定系数法即可求出抛物线及直线AC的函数关系式;(2)过点P作PE∥y轴交x轴于点E,交直线AC于点F,过点C作CQ∥y轴交x轴于点Q,设点P的坐标为(x,﹣x2﹣2x+3)(﹣2<x<1),则点E的坐标为(x,0),点F的坐标为(x,﹣x+1),进而可得出PF的值,由点C的坐标可得出点Q的坐标,进而可得出AQ的值,利用三角形的面积公式可得出S△APC=﹣32x2﹣32x+3,再利用二次函数的性质,即可解决最值问题;(3)利用二次函数图象上点的坐标特征可得出点N的坐标,利用配方法可找出抛物线的对称轴,由点C,N的坐标可得出点C,N关于抛物线的对称轴对称,令直线AC与抛物线的对称轴的交点为点M,则此时△ANM周长取最小值,再利用一次函数图象上点的坐标特征求出点M的坐标,以及利用两点间的距离公式结合三角形的周长公式求出△ANM周长的最小值即可得出结论.【详解】(1)将A(1,0),C(﹣2,3)代入y=﹣x2+bx+c,得:10423b c b c -++=⎧⎨--+=⎩,解得:23b c =-⎧⎨=⎩, ∴抛物线的函数关系式为y =﹣x 2﹣2x +3; 设直线AC 的函数关系式为y =mx +n (m ≠0), 将A (1,0),C (﹣2,3)代入y =mx +n ,得:023m n m n +=⎧⎨-+=⎩,解得:11m n =-⎧⎨=⎩, ∴直线AC 的函数关系式为y =﹣x +1.(2)过点P 作PE ∥y 轴交x 轴于点E ,交直线AC 于点F ,过点C 作CQ ∥y 轴交x 轴于点Q ,如图1所示.设点P 的坐标为(x ,﹣x 2﹣2x +3)(﹣2<x <1),则点E 的坐标为(x ,0),点F 的坐标为(x ,﹣x +1),∴PE =﹣x 2﹣2x +3,EF =﹣x +1,EF =PE ﹣EF =﹣x 2﹣2x +3﹣(﹣x +1)=﹣x 2﹣x +2. ∵点C 的坐标为(﹣2,3), ∴点Q 的坐标为(﹣2,0), ∴AQ =1﹣(﹣2)=3, ∴S △APC =12AQ •PF =﹣32x 2﹣32x +3=﹣32(x +12)2+278. ∵﹣32<0, ∴当x =﹣12时,△APC 的面积取最大值,最大值为278,此时点P 的坐标为(﹣12,154). (3)当x =0时,y =﹣x 2﹣2x +3=3, ∴点N 的坐标为(0,3). ∵y =﹣x 2﹣2x +3=﹣(x +1)2+4, ∴抛物线的对称轴为直线x =﹣1. ∵点C 的坐标为(﹣2,3), ∴点C ,N 关于抛物线的对称轴对称.令直线AC 与抛物线的对称轴的交点为点M ,如图2所示. ∵点C ,N 关于抛物线的对称轴对称, ∴MN =CM ,∴AM +MN =AM +MC =AC , ∴此时△ANM 周长取最小值. 当x =﹣1时,y =﹣x +1=2, ∴此时点M 的坐标为(﹣1,2).∵点A 的坐标为(1,0),点C 的坐标为(﹣2,3),点N 的坐标为(0,3),∴AC=,AN ,∴C△ANM=AM+MN+AN=AC+AN=32+10.∴在对称轴上存在一点M(﹣1,2),使△ANM的周长最小,△ANM周长的最小值为32+10.【点睛】本题考查待定系数法求一次函数解析式、待定系数法求二次函数解析式、二次函数图象上点的坐标特征、一次函数图象上点的坐标特征、二次函数的性质、三角形的面积以及周长,解题的关键是:(1)根据点的坐标,利用待定系数法求出抛物线及直线AC的函数关系式;(2)利用三角形的面积公式找出S△APC=﹣32x2﹣32x+3的最值;(3)利用二次函数图象的对称性结合两点之间线段最短找出点M的位置.2.如图,已知抛物线y=x2+bx+c与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,-3),对称轴是直线x=1,直线BC与抛物线的对称轴交于点D.(1)求抛物线的函数表达式;(2)求直线BC的函数表达式;(3)点E为y轴上一动点,CE的垂直平分线交CE于点F,交抛物线于P、Q两点,且点P 在第三象限.①当线段PQ=34AB时,求tan∠CED的值;②当以点C、D、E为顶点的三角形是直角三角形时,请直接写出点P的坐标.【答案】(1)抛物线的函数表达式为y =x 2-2x -3.(2)直线BC 的函数表达式为y =x -3.(3)①23.①P 1(122),P 2(1-62,74). 【解析】 【分析】已知C 点的坐标,即知道OC 的长,可在直角三角形BOC 中根据∠BCO 的正切值求出OB 的长,即可得出B 点的坐标.已知了△AOC 和△BOC 的面积比,由于两三角形的高相等,因此面积比就是AO 与OB 的比.由此可求出OA 的长,也就求出了A 点的坐标,然后根据A 、B 、C 三点的坐标即可用待定系数法求出抛物线的解析式. 【详解】(1)∵抛物线的对称轴为直线x=1,∴− 221bba -⨯==1 ∴b=-2∵抛物线与y 轴交于点C (0,-3), ∴c=-3,∴抛物线的函数表达式为y=x 2-2x-3; (2)∵抛物线与x 轴交于A 、B 两点, 当y=0时,x 2-2x-3=0. ∴x 1=-1,x 2=3. ∵A 点在B 点左侧, ∴A (-1,0),B (3,0)设过点B (3,0)、C (0,-3)的直线的函数表达式为y=kx+m ,则033k m m ==+⎧⎨-⎩,∴13k m ⎧⎨-⎩==∴直线BC 的函数表达式为y=x-3; (3)①∵AB=4,PQ=34AB ,∴PQ=3∵PQ⊥y轴∴PQ∥x轴,则由抛物线的对称性可得PM=32,∵对称轴是直线x=1,∴P到y轴的距离是12,∴点P的横坐标为−12,∴P(−12,−74)∴F(0,−74),∴FC=3-OF=3-74=54∵PQ垂直平分CE于点F,∴CE=2FC=5 2∵点D在直线BC上,∴当x=1时,y=-2,则D(1,-2),过点D作DG⊥CE于点G,∴DG=1,CG=1,∴GE=CE-CG=52-1=32.在Rt△EGD中,tan∠CED=23 GDEG=.②P1(2,-2),P2(1-62-52).设OE=a,则GE=2-a,当CE为斜边时,则DG2=CG•GE,即1=(OC-OG)•(2-a),∴1=1×(2-a),∴a=1,∴CE=2,∴OF=OE+EF=2∴F、P的纵坐标为-2,把y=-2,代入抛物线的函数表达式为y=x2-2x-3得:x=1+2或1-2∵点P在第三象限.∴P1(1-2,-2),当CD为斜边时,DE⊥CE,∴OE=2,CE=1,∴OF=2.5,∴P和F的纵坐标为:-52,把y=-52,代入抛物线的函数表达式为y=x2-2x-3得:x=1-6,或1+6,∵点P在第三象限.∴P2(1-6,-52).综上所述:满足条件为P1(1-2,-2),P2(1-6,-52).【点睛】本题是二次函数的综合题型,其中涉及到的知识点有抛物线的顶点公式和三角形的面积求法.在求有关动点问题时要注意分析题意分情况讨论结果.3.如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.(1)求抛物线的解析式;(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.【答案】(1)抛物线的解析式为y=﹣x 2﹣2x+3;(2)当△CEF 与△COD 相似时,P 点的坐标为(﹣1,4)或(﹣2,3). 【解析】 【分析】(1)根据正切函数,可得OB ,根据旋转的性质,可得△DOC ≌△AOB ,根据待定系数法,可得函数解析式;(2)分两种情况讨论:①当∠CEF =90°时,△CEF ∽△COD ,此时点P 在对称轴上,即点P 为抛物线的顶点;②当∠CFE =90°时,△CFE ∽△COD ,过点P 作PM ⊥x 轴于M 点,得到△EFC ∽△EMP ,根据相似三角形的性质,可得PM 与ME 的关系,解方程,可得t 的值,根据自变量与函数值的对应关系,可得答案. 【详解】(1)在Rt △AOB 中,OA =1,tan ∠BAO OBOA==3,∴OB =3OA =3. ∵△DOC 是由△AOB 绕点O 逆时针旋转90°而得到的,∴△DOC ≌△AOB ,∴OC =OB =3,OD =OA =1,∴A ,B ,C 的坐标分别为(1,0),(0,3),(﹣3,0),代入解析式为09303a b c a b c c ++=⎧⎪-+=⎨⎪=⎩,解得:123a b c =-⎧⎪=-⎨⎪=⎩,抛物线的解析式为y =﹣x 2﹣2x +3;(2)∵抛物线的解析式为y =﹣x 2﹣2x +3,∴对称轴为l 2ba=-=-1,∴E 点坐标为(﹣1,0),如图,分两种情况讨论:①当∠CEF =90°时,△CEF ∽△COD ,此时点P 在对称轴上,即点P 为抛物线的顶点,P (﹣1,4);②当∠CFE =90°时,△CFE ∽△COD ,过点P 作PM ⊥x 轴于M 点,∵∠CFE=∠PME=90°,∠CEF=∠PEM ,∴△EFC ∽△EMP ,∴13EM EF OD MP CF CO ===,∴MP =3ME . ∵点P 的横坐标为t ,∴P (t ,﹣t 2﹣2t +3).∵P 在第二象限,∴PM =﹣t 2﹣2t +3,ME =﹣1﹣t ,t <0,∴﹣t 2﹣2t +3=3(﹣1﹣t ),解得:t 1=﹣2,t 2=3(与t <0矛盾,舍去).当t =﹣2时,y =﹣(﹣2)2﹣2×(﹣2)+3=3,∴P (﹣2,3).综上所述:当△CEF 与△COD 相似时,P 点的坐标为(﹣1,4)或(﹣2,3).【点睛】本题是二次函数综合题.解(1)的关键是利用旋转的性质得出OC ,OD 的长,又利用了待定系数法;解(2)的关键是利用相似三角形的性质得出MP =3ME .4.已知,m ,n 是一元二次方程x 2+4x +3=0的两个实数根,且|m |<|n |,抛物线y =x 2+bx +c 的图象经过点A (m ,0),B (0,n ),如图所示. (1)求这个抛物线的解析式;(2)设(1)中的抛物线与x 轴的另一个交点为抛物线的顶点为D ,求出点C ,D 的坐标,并判断△BCD 的形状;(3)点P 是直线BC 上的一个动点(点P 不与点B 和点C 重合),过点P 作x 轴的垂线,交抛物线于点M ,点Q 在直线BC 上,距离点P为2个单位长度,设点P 的横坐标为t ,△PMQ 的面积为S ,求出S 与t 之间的函数关系式.【答案】(1)223y x x =--;(2)C (3,0),D (1,﹣4),△BCD 是直角三角形;(3)2213(03)2213(03)22t t t S t t t t ⎧-+⎪⎪=⎨⎪-⎪⎩<<<或>【解析】试题分析:(1)先解一元二次方程,然后用待定系数法求出抛物线解析式;(2)先解方程求出抛物线与x 轴的交点,再判断出△BOC 和△BED 都是等腰直角三角形,从而得到结论;(3)先求出QF=1,再分两种情况,当点P 在点M 上方和下方,分别计算即可. 试题解析:解(1)∵2+430x x +=,∴11x =-,23x =-,∵m ,n 是一元二次方程2+430x x +=的两个实数根,且|m|<|n|,∴m=﹣1,n=﹣3,∵抛物线223y x x =--的图象经过点A (m ,0),B (0,n ),∴10{3b c c -+==-,∴2{3b c =-=-,∴抛物线解析式为223y x x =--;(2)令y=0,则2230x x --=,∴11x =-,23x =,∴C (3,0),∵223y x x =--=2(1)4x --,∴顶点坐标D (1,﹣4),过点D 作DE ⊥y 轴,∵OB=OC=3,∴BE=DE=1,∴△BOC 和△BED 都是等腰直角三角形,∴∠OBC=∠DBE=45°,∴∠CBD=90°,∴△BCD 是直角三角形;(3)如图,∵B (0,﹣3),C (3,0),∴直线BC 解析式为y=x ﹣3,∵点P 的横坐标为t ,PM ⊥x 轴,∴点M 的横坐标为t ,∵点P 在直线BC 上,点M 在抛物线上,∴P (t ,t ﹣3),M (t ,223t t --),过点Q 作QF ⊥PM ,∴△PQF 是等腰直角三角形,∵PQ=2,∴QF=1.①当点P 在点M 上方时,即0<t <3时,PM=t ﹣3﹣(223t t --)=23t t -+,∴S=12PM×QF=21(3)2t t -+=21322t t -+,②如图3,当点P 在点M 下方时,即t <0或t>3时,PM=223t t --﹣(t ﹣3)=23t t -,∴S=12PM×QF=12(23t t -)=21322t t -.综上所述,S=2213(03)22{13 (03)22t t t t t t t 或-+<<-.考点:二次函数综合题;分类讨论.5.如图,过()A 1,0、()B 3,0作x 轴的垂线,分别交直线y 4x =-于C 、D 两点.抛物线2y ax bx c =++经过O 、C 、D 三点.()1求抛物线的表达式;()2点M 为直线OD 上的一个动点,过M 作x 轴的垂线交抛物线于点N ,问是否存在这样的点M ,使得以A 、C 、M 、N 为顶点的四边形为平行四边形?若存在,求此时点M 的横坐标;若不存在,请说明理由;()3若AOC V 沿CD 方向平移(点C 在线段CD 上,且不与点D 重合),在平移的过程中AOC V 与OBD V 重叠部分的面积记为S ,试求S 的最大值.【答案】(1)2413y x x 33=-+;(2)32332+332-;(3)13. 【解析】 【分析】(1)利用待定系数法求出抛物线的解析式;(2)由题意,可知MN ∥AC ,因为以A 、C 、M 、N 为顶点的四边形为平行四边形,则有MN =AC =3.设点M 的横坐标为x ,则求出MN =|43x 2﹣4x |;解方程|43x 2﹣4x |=3,求出x 的值,即点M 横坐标的值;(3)设水平方向的平移距离为t (0≤t <2),利用平移性质求出S 的表达式:S 16=-(t ﹣1)213+;当t =1时,s 有最大值为13. 【详解】(1)由题意,可得C (1,3),D (3,1).∵抛物线过原点,∴设抛物线的解析式为:y =ax 2+bx ,∴3931a b a b +=⎧⎨+=⎩,解得43133a b ⎧=-⎪⎪⎨⎪=⎪⎩,∴抛物线的表达式为:y 43=-x 2133+x . (2)存在.设直线OD 解析式为y =kx ,将D (3,1)代入,求得k 13=,∴直线OD 解析式为y 13=x . 设点M 的横坐标为x ,则M (x ,13x ),N (x ,43-x 2133+x ),∴MN =|y M ﹣y N |=|13x ﹣(43-x 2133+x )|=|43x 2﹣4x |. 由题意,可知MN ∥AC ,因为以A 、C 、M 、N 为顶点的四边形为平行四边形,则有MN =AC =3,∴|43x 2﹣4x |=3.若43x 2﹣4x =3,整理得:4x 2﹣12x ﹣9=0,解得:x 32+=或x 32-= 若43x 2﹣4x =﹣3,整理得:4x 2﹣12x +9=0,解得:x 32=,∴存在满足条件的点M ,点M 的横坐标为:32或32+或32-. (3)∵C (1,3),D (3,1),∴易得直线OC 的解析式为y =3x ,直线OD 的解析式为y 13=x . 如解答图所示,设平移中的三角形为△A 'O 'C ',点C '在线段CD 上.设O 'C '与x 轴交于点E ,与直线OD 交于点P ;设A 'C '与x 轴交于点F ,与直线OD 交于点Q .设水平方向的平移距离为t (0≤t <2),则图中AF =t ,F (1+t ,0),Q (1+t ,1133+t ),C '(1+t ,3﹣t ).设直线O 'C '的解析式为y =3x +b ,将C '(1+t ,3﹣t )代入得:b =﹣4t ,∴直线O 'C '的解析式为y =3x ﹣4t ,∴E (43t ,0). 联立y =3x ﹣4t 与y 13=x ,解得:x 32=t ,∴P (32t ,12t ). 过点P 作PG ⊥x 轴于点G ,则PG 12=t ,∴S =S △OFQ ﹣S △OEP 12=OF •FQ 12-OE •PG 12=(1+t )(1133+t )12-•43t •12t 16=-(t ﹣1)213+ 当t =1时,S 有最大值为13,∴S 的最大值为13.【点睛】本题是二次函数压轴题,综合考查了二次函数的图象与性质、待定系数法、函数图象上点的坐标特征、平行四边形、平移变换、图形面积计算等知识点,有一定的难度.第(2)问中,解题的关键是根据平行四边形定义,得到MN =AC =3,由此列出方程求解;第(3)问中,解题的关键是求出S 的表达式,注意图形面积的计算方法.6.已知抛物线2(5)6y x m x m =-+-+-.(1)求证:该抛物线与x 轴总有交点;(2)若该抛物线与x 轴有一个交点的横坐标大于3且小于5,求m 的取值范围;(3)设抛物线2(5)6y x m x m =-+-+-与y 轴交于点M ,若抛物线与x 轴的一个交点关于直线y x =-的对称点恰好是点M ,求m 的值.【答案】(1)证明见解析;(2)1?<?m?3<;(3)56m m ==或【解析】【分析】(1)本题需先根据判别式解出无论m 为任何实数都不小于零,再判断出物线与x 轴总有交点.(2)根据公式法解方程,利用已有的条件,就能确定出m 的取值范围,即可得到结果. (3)根据抛物线y=-x 2+(5-m )x+6-m ,求出与y 轴的交点M 的坐标,再确定抛物线与x 轴的两个交点关于直线y=-x 的对称点的坐标,列方程可得结论.【详解】(1)证明:∵()()()222454670b ac m m m ∆=-=-+-=-≥∴抛物线与x 轴总有交点.(2)解:由(1)()27m ∆=-,根据求根公式可知, 方程的两根为:257m m x ()-±-= 即1216x x m =-=-+,由题意,有 3<-m 6<5+1<?m 3∴<(3)解:令 x = 0, y =6m -+∴ M (0,6m -+)由(2)可知抛物线与x 轴的交点为(-1,0)和(6m -+,0),它们关于直线y x =-的对称点分别为(0 , 1)和(0, 6m -),由题意,可得:6166m m m 或-+=-+=-56m m ∴==或【点睛】本题考查对抛物线与x 轴的交点,解一元一次方程,解一元一次不等式,根的判别式,对称等,解题关键是熟练理解和掌握以上性质,并能综合运用这些性质进行计算.7.如图,抛物线y=ax 2+6x+c 交x 轴于A ,B 两点,交y 轴于点C .直线y=x ﹣5经过点B ,C .(1)求抛物线的解析式;(2)过点A 的直线交直线BC 于点M .①当AM ⊥BC 时,过抛物线上一动点P (不与点B ,C 重合),作直线AM 的平行线交直线BC 于点Q ,若以点A ,M ,P ,Q 为顶点的四边形是平行四边形,求点P 的横坐标; ②连接AC ,当直线AM 与直线BC 的夹角等于∠ACB 的2倍时,请直接写出点M 的坐标.【答案】(1)抛物线解析式为y=﹣x 2+6x ﹣5;(2)①P 点的横坐标为45+41或5-412;②点M 的坐标为(136,﹣176)或(236,﹣76). 【解析】分析:(1)利用一次函数解析式确定C (0,-5),B (5,0),然后利用待定系数法求抛物线解析式;(2)①先解方程-x 2+6x-5=0得A (1,0),再判断△OCB 为等腰直角三角形得到∠OBC=∠OCB=45°,则△AMB 为等腰直角三角形,所以,接着根据平行四边形的性质得到,PQ ⊥BC ,作PD ⊥x 轴交直线BC 于D ,如图1,利用∠PDQ=45°得到PQ=4,设P (m ,-m 2+6m-5),则D (m ,m-5),讨论:当P 点在直线BC 上方时,PD=-m 2+6m-5-(m-5)=4;当P 点在直线BC 下方时,PD=m-5-(-m 2+6m-5),然后分别解方程即可得到P 点的横坐标;②作AN ⊥BC 于N ,NH ⊥x 轴于H ,作AC 的垂直平分线交BC 于M 1,交AC 于E ,如图2,利用等腰三角形的性质和三角形外角性质得到∠AM 1B=2∠ACB ,再确定N (3,-2), AC 的解析式为y=5x-5,E 点坐标为(12,-52),利用两直线垂直的问题可设直线EM 1的解析式为y=-15x+b ,把E (12,-52)代入求出b 得到直线EM 1的解析式为y=-15x-125,则解方程组511255y x y x -⎧⎪⎨--⎪⎩==得M 1点的坐标;作直线BC 上作点M 1关于N 点的对称点M 2,如图2,利用对称性得到∠AM 2C=∠AM 1B=2∠ACB ,设M 2(x ,x-5),根据中点坐标公式得到3=13+62x ,然后求出x 即可得到M 2的坐标,从而得到满足条件的点M 的坐标.详解:(1)当x=0时,y=x ﹣5=﹣5,则C (0,﹣5),当y=0时,x ﹣5=0,解得x=5,则B (5,0),把B (5,0),C (0,﹣5)代入y=ax 2+6x+c 得253005a c c ++=⎧⎨=-⎩,解得15a b =-⎧⎨=-⎩, ∴抛物线解析式为y=﹣x 2+6x ﹣5;(2)①解方程﹣x 2+6x ﹣5=0得x 1=1,x 2=5,则A (1,0),∵B (5,0),C (0,﹣5),∴△OCB 为等腰直角三角形,∴∠OBC=∠OCB=45°,∵AM ⊥BC ,∴△AMB 为等腰直角三角形,∴AM=2AB=2, ∵以点A ,M ,P ,Q 为顶点的四边形是平行四边形,AM ∥PQ ,∴PQ ⊥BC ,作PD ⊥x 轴交直线BC 于D ,如图1,则∠PDQ=45°,∴PD=2PQ=2×22=4,设P(m,﹣m2+6m﹣5),则D(m,m﹣5),当P点在直线BC上方时,PD=﹣m2+6m﹣5﹣(m﹣5)=﹣m2+5m=4,解得m1=1,m2=4,当P点在直线BC下方时,PD=m﹣5﹣(﹣m2+6m﹣5)=m2﹣5m=4,解得m1=5+412,m2=5-412,综上所述,P点的横坐标为4或5+41或5-41;②作AN⊥BC于N,NH⊥x轴于H,作AC的垂直平分线交BC于M1,交AC于E,如图2,∵M1A=M1C,∴∠ACM1=∠CAM1,∴∠AM1B=2∠ACB,∵△ANB为等腰直角三角形,∴AH=BH=NH=2,∴N(3,﹣2),易得AC的解析式为y=5x﹣5,E点坐标为(12,﹣52,设直线EM1的解析式为y=﹣15x+b,把E(12,﹣52)代入得﹣110+b=﹣52,解得b=﹣125,∴直线EM1的解析式为y=﹣15x﹣125解方程组511255y xy x=-⎧⎪⎨=--⎪⎩得136176xy⎧=⎪⎪⎨⎪=-⎪⎩,则M1(136,﹣176);作直线BC上作点M1关于N点的对称点M2,如图2,则∠AM2C=∠AM1B=2∠ACB,设M2(x,x﹣5),∵3=13+ 62x∴x=236,∴M2(236,﹣76).综上所述,点M的坐标为(136,﹣176)或(236,﹣76).点睛:本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质、等腰直角的判定与性质和平行四边形的性质;会利用待定系数法求函数解析式;理解坐标与图形性质;会运用分类讨论的思想解决数学问题.8.已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.(1)求抛物线的解析式;(2)当点P运动到什么位置时,△PAB的面积有最大值?(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.【答案】(1)抛物线解析式为y=﹣12x 2+2x+6;(2)当t=3时,△PAB 的面积有最大值;(3)点P (4,6).【解析】 【分析】(1)利用待定系数法进行求解即可得;(2)作PM ⊥OB 与点M ,交AB 于点N ,作AG ⊥PM ,先求出直线AB 解析式为y=﹣x+6,设P (t ,﹣12t 2+2t+6),则N (t ,﹣t+6),由S △PAB =S △PAN +S △PBN =12PN•AG+12PN•BM=12PN•OB 列出关于t 的函数表达式,利用二次函数的性质求解可得; (3)由PH ⊥OB 知DH ∥AO ,据此由OA=OB=6得∠BDH=∠BAO=45°,结合∠DPE=90°知若△PDE 为等腰直角三角形,则∠EDP=45°,从而得出点E 与点A 重合,求出y=6时x 的值即可得出答案.【详解】(1)∵抛物线过点B (6,0)、C (﹣2,0),∴设抛物线解析式为y=a (x ﹣6)(x+2),将点A (0,6)代入,得:﹣12a=6,解得:a=﹣12, 所以抛物线解析式为y=﹣12(x ﹣6)(x+2)=﹣12x 2+2x+6; (2)如图1,过点P 作PM ⊥OB 与点M ,交AB 于点N ,作AG ⊥PM 于点G ,设直线AB 解析式为y=kx+b ,将点A (0,6)、B (6,0)代入,得:660b k b =⎧⎨+=⎩, 解得:16k b =-⎧⎨=⎩, 则直线AB 解析式为y=﹣x+6,设P (t ,﹣12t 2+2t+6)其中0<t <6, 则N (t ,﹣t+6),∴PN=PM﹣MN=﹣12t2+2t+6﹣(﹣t+6)=﹣12t2+2t+6+t﹣6=﹣12t2+3t,∴S△PAB=S△PAN+S△PBN=12PN•AG+12PN•BM=12PN•(AG+BM)=12 PN•OB=12×(﹣12t2+3t)×6=﹣32t2+9t=﹣32(t﹣3)2+272,∴当t=3时,△PAB的面积有最大值;(3)如图2,∵PH⊥OB于H,∴∠DHB=∠AOB=90°,∴DH∥AO,∵OA=OB=6,∴∠BDH=∠BAO=45°,∵PE∥x轴、PD⊥x轴,∴∠DPE=90°,若△PDE为等腰直角三角形,则∠EDP=45°,∴∠EDP与∠BDH互为对顶角,即点E与点A重合,则当y=6时,﹣12x2+2x+6=6,解得:x=0(舍)或x=4,即点P(4,6).【点睛】本题考查了二次函数的综合问题,涉及到待定系数法、二次函数的最值、等腰直角三角形的判定与性质等,熟练掌握和灵活运用待定系数法求函数解析式、二次函数的性质、等腰直角三角形的判定与性质等是解题的关键.9.如图,对称轴为直线x 1=-的抛物线()2y ax bx c a 0=++≠与x 轴相交于A 、B 两点,其中A 点的坐标为(-3,0).(1)求点B 的坐标;(2)已知a 1=,C 为抛物线与y 轴的交点.①若点P 在抛物线上,且POC BOC S 4S ∆∆=,求点P 的坐标;②设点Q 是线段AC 上的动点,作QD ⊥x 轴交抛物线于点D ,求线段QD 长度的最大值.【答案】(1)点B 的坐标为(1,0).(2)①点P 的坐标为(4,21)或(-4,5).②线段QD 长度的最大值为94. 【解析】【分析】(1)由抛物线的对称性直接得点B 的坐标.(2)①用待定系数法求出抛物线的解析式,从而可得点C 的坐标,得到BOC S ∆,设出点P 的坐标,根据POC BOC S 4S ∆∆=列式求解即可求得点P 的坐标.②用待定系数法求出直线AC 的解析式,由点Q 在线段AC 上,可设点Q 的坐标为(q,-q-3),从而由QD ⊥x 轴交抛物线于点D ,得点D 的坐标为(q,q 2+2q-3),从而线段QD 等于两点纵坐标之差,列出函数关系式应用二次函数最值原理求解.【详解】解:(1)∵A 、B 两点关于对称轴x 1=-对称 ,且A 点的坐标为(-3,0), ∴点B 的坐标为(1,0).(2)①∵抛物线a 1=,对称轴为x 1=-,经过点A (-3,0), ∴2a 1b 12a 9a 3b c 0=⎧⎪⎪-=-⎨⎪-+=⎪⎩,解得a 1b 2c 3=⎧⎪=⎨⎪=-⎩.∴抛物线的解析式为2y x 2x 3=+-.∴B 点的坐标为(0,-3).∴OB=1,OC=3.∴BOC 13S 1322∆=⨯⨯=. 设点P 的坐标为(p,p 2+2p-3),则POC 13S 3p p 22∆=⨯⨯=. ∵POC BOC S 4S ∆∆=,∴3p 62=,解得p 4=±. 当p 4=时2p 2p 321+-=;当p 4=-时,2p 2p 35+-=,∴点P 的坐标为(4,21)或(-4,5).②设直线AC 的解析式为y kx b =+,将点A ,C 的坐标代入,得:3k b 0b 3-+=⎧⎨=-⎩,解得:k 1b 3=-⎧⎨=-⎩. ∴直线AC 的解析式为y x 3=--.∵点Q 在线段AC 上,∴设点Q 的坐标为(q,-q-3).又∵QD ⊥x 轴交抛物线于点D ,∴点D 的坐标为(q,q 2+2q-3).∴()22239QD q 3q 2q 3q 3q q 24⎛⎫=---+-=--=-++ ⎪⎝⎭. ∵a 10<=-,-3302<<-∴线段QD 长度的最大值为94.10.如图,在平面直角坐标系中,抛物线y=ax 2+2ax ﹣3a (a <0)与x 轴相交于A ,B 两点,与y 轴相交于点C ,顶点为D ,直线DC 与x 轴相交于点E .(1)当a=﹣1时,求抛物线顶点D 的坐标,OE 等于多少;(2)OE 的长是否与a 值有关,说明你的理由;(3)设∠DEO=β,45°≤β≤60°,求a 的取值范围;(4)以DE 为斜边,在直线DE 的左下方作等腰直角三角形PDE .设P (m ,n ),直接写出n 关于m 的函数解析式及自变量m 的取值范围.【答案】(1)(﹣1,4),3;(2)结论:OE 的长与a 值无关.理由见解析;(3)﹣≤a≤﹣1;(4)n=﹣m﹣1(m<1).【解析】【分析】(1)求出直线CD的解析式即可解决问题;(2)利用参数a,求出直线CD的解析式求出点E坐标即可判断;(3)求出落在特殊情形下的a的值即可判断;(4)如图,作PM⊥对称轴于M,PN⊥AB于N.两条全等三角形的性质即可解决问题.【详解】解:(1)当a=﹣1时,抛物线的解析式为y=﹣x2﹣2x+3,∴顶点D(﹣1,4),C(0,3),∴直线CD的解析式为y=﹣x+3,∴E(3,0),∴OE=3,(2)结论:OE的长与a值无关.理由:∵y=ax2+2ax﹣3a,∴C(0,﹣3a),D(﹣1,﹣4a),∴直线CD的解析式为y=ax﹣3a,当y=0时,x=3,∴E(3,0),∴OE=3,∴OE的长与a值无关.(3)当β=45°时,OC=OE=3,∴﹣3a=3,∴a=﹣1,当β=60°时,在Rt△OCE中,∴﹣∴a=,∴45°≤β≤60°,a≤a≤﹣1.(4)如图,作PM⊥对称轴于M,PN⊥AB于N.∵PD=PE ,∠PMD=∠PNE=90°,∠DPE=∠MPN=90°,∴∠DPM=∠EPN ,∴△DPM ≌△EPN ,∴PM=PN ,PM=EN ,∵D(﹣1,﹣4a),E(3,0),∴EN=4+n=3﹣m ,∴n=﹣m ﹣1,当顶点D 在x 轴上时,P(1,﹣2),此时m 的值1,∵抛物线的顶点在第二象限,∴m <1.∴n=﹣m ﹣1(m <1).故答案为:(1)(﹣1,4),3;(2)OE 的长与a 值无关;(3)3﹣1;(4)n=﹣m ﹣1(m <1).【点睛】本题是二次函数综合题,考查了二次函数的图象与性质。
备战中考数学二次函数(大题培优 易错 难题)含答案
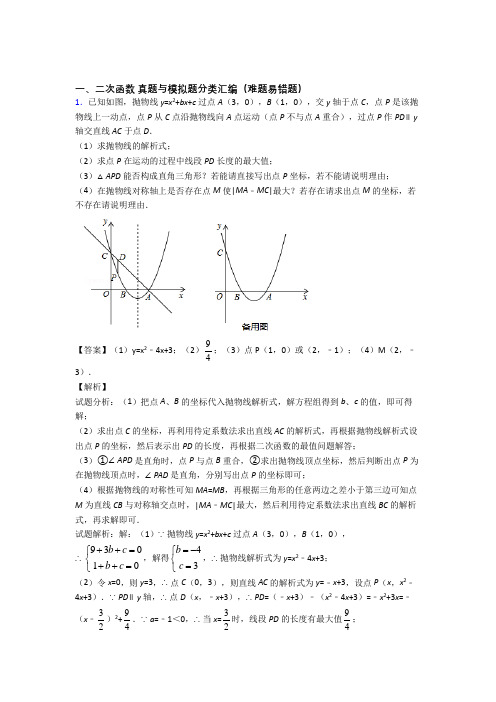
一、二次函数真题与模拟题分类汇编(难题易错题)1.已知如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与点A重合),过点P作PD∥y 轴交直线AC于点D.(1)求抛物线的解析式;(2)求点P在运动的过程中线段PD长度的最大值;(3)△APD能否构成直角三角形?若能请直接写出点P坐标,若不能请说明理由;(4)在抛物线对称轴上是否存在点M使|MA﹣MC|最大?若存在请求出点M的坐标,若不存在请说明理由.【答案】(1)y=x2﹣4x+3;(2)94;(3)点P(1,0)或(2,﹣1);(4)M(2,﹣3).【解析】试题分析:(1)把点A、B的坐标代入抛物线解析式,解方程组得到b、c的值,即可得解;(2)求出点C的坐标,再利用待定系数法求出直线AC的解析式,再根据抛物线解析式设出点P的坐标,然后表示出PD的长度,再根据二次函数的最值问题解答;(3)①∠APD是直角时,点P与点B重合,②求出抛物线顶点坐标,然后判断出点P为在抛物线顶点时,∠PAD是直角,分别写出点P的坐标即可;(4)根据抛物线的对称性可知MA=MB,再根据三角形的任意两边之差小于第三边可知点M为直线CB与对称轴交点时,|MA﹣MC|最大,然后利用待定系数法求出直线BC的解析式,再求解即可.试题解析:解:(1)∵抛物线y=x2+bx+c过点A(3,0),B(1,0),∴93010b cb c++=⎧⎨++=⎩,解得43bc=-⎧⎨=⎩,∴抛物线解析式为y=x2﹣4x+3;(2)令x=0,则y=3,∴点C(0,3),则直线AC的解析式为y=﹣x+3,设点P(x,x2﹣4x+3).∵PD∥y轴,∴点D(x,﹣x+3),∴PD=(﹣x+3)﹣(x2﹣4x+3)=﹣x2+3x=﹣(x﹣32)2+94.∵a=﹣1<0,∴当x=32时,线段PD的长度有最大值94;(3)①∠APD是直角时,点P与点B重合,此时,点P(1,0),②∵y=x2﹣4x+3=(x ﹣2)2﹣1,∴抛物线的顶点坐标为(2,﹣1).∵A(3,0),∴点P为在抛物线顶点时,∠PAD=45°+45°=90°,此时,点P(2,﹣1).综上所述:点P(1,0)或(2,﹣1)时,△APD能构成直角三角形;(4)由抛物线的对称性,对称轴垂直平分AB,∴MA=MB,由三角形的三边关系,|MA﹣MC|<BC,∴当M、B、C三点共线时,|MA﹣MC|最大,为BC的长度,设直线BC的解析式为y=kx+b(k≠0),则3k bb+=⎧⎨=⎩,解得:33kb=-⎧⎨=⎩,∴直线BC的解析式为y=﹣3x+3.∵抛物线y=x2﹣4x+3的对称轴为直线x=2,∴当x=2时,y=﹣3×2+3=﹣3,∴点M (2,﹣3),即,抛物线对称轴上存在点M(2,﹣3),使|MA﹣MC|最大.点睛:本题是二次函数综合题,主要利用了待定系数法求二次函数解析式,二次函数的最值问题,二次函数的对称性以及顶点坐标的求解,(2)整理出PD的表达式是解题的关键,(3)关键在于利用点的坐标特征作出判断,(4)根据抛物线的对称性和三角形的三边关系判断出点M的位置是解题的关键.2.童装店销售某款童装,每件售价为60元,每星期可卖100件,为了促销该店决定降价销售,经市场调查发现:每降价1元,每星期可多卖10件,已知该款童装每件成本30元,设降价后该款童装每件售价x元,每星期的销售量为y件.(1)降价后,当某一星期的销售量是未降价前一星期销售量的3倍时,求这一星期中每件童装降价多少元?(2)当每件售价定为多少元时,一星期的销售利润最大,最大利润是多少?【答案】(1)这一星期中每件童装降价20元;(2)每件售价定为50元时,一星期的销售利润最大,最大利润4000元.【解析】【分析】(1)根据售量与售价x(元/件)之间的关系列方程即可得到结论.(2)设每星期利润为W元,构建二次函数利用二次函数性质解决问题.【详解】解:(1)根据题意得,(60﹣x)×10+100=3×100,解得:x=40,60﹣40=20元,答:这一星期中每件童装降价20元;(2)设利润为w,根据题意得,w=(x﹣30)[(60﹣x)×10+100]=﹣10x2+1000x﹣21000=﹣10(x﹣50)2+4000,答:每件售价定为50元时,一星期的销售利润最大,最大利润4000元.【点睛】本题考查二次函数的应用,一元二次不等式,解题的关键是构建二次函数解决最值问题,利用图象法解一元二次不等式,属于中考常考题型.3.如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+n与x轴、y轴分别交于B、C两点,抛物线y=ax2+bx+3(a≠0)过C、B两点,交x轴于另一点A,连接AC,且tan∠CAO=3.(1)求抛物线的解析式;(2)若点P是射线CB上一点,过点P作x轴的垂线,垂足为H,交抛物线于Q,设P点横坐标为t,线段PQ的长为d,求出d与t之间的函数关系式,并写出相应的自变量t的取值范围;(3)在(2)的条件下,当点P在线段BC上时,设PH=e,已知d,e是以y为未知数的一元二次方程:y2-(m+3)y+14(5m2-2m+13)="0" (m为常数)的两个实数根,点M在抛物线上,连接MQ、MH、PM,且.MP平分∠QMH,求出t值及点M的坐标.【答案】(1) y=-x2+2x+3;(2)223(03){3(3)d t t td t t t=-+<<=->;(3)t=1,2,2)和(12,2).【解析】【分析】(1)当x=0时代入抛物线y=ax2+bx+3(a≠0)就可以求出y=3而得出C的坐标,就可以得出直线的解析式,就可以求出B的坐标,在直角三角形AOC中,由三角形函数值就可以求出OA的值,得出A的坐标,再由待定系数法建立二元一次方程组求出其解就可以得出结论;(2)分两种情况讨论,当点P在线段CB上时,和如图3点P在射线BN上时,就有P点的坐标为(t,-t+3),Q点的坐标为(t,-t2+2t+3),就可以得出d与t之间的函数关系式而得出结论;(3)根据根的判别式就可以求出m 的值,就可以求出方程的解而求得PQ 和PH 的值,延长MP 至L ,使LP=MP ,连接LQ 、LH ,如图2,延长MP 至L ,使LP=MP ,连接LQ 、LH ,就可以得出四边形LQMH 是平行四边形,进而得出四边形LQMH 是菱形,由菱形的性质就可以求出结论.【详解】(1)当x=0,则y=-x+n=0+n=n ,y=ax 2+bx+3=3,∴OC=3=n .当y=0,∴-x+3=0,x=3=OB ,∴B (3,0).在△AOC 中,∠AOC =90°,tan ∠CAO=33OC OA OA==, ∴OA=1,∴A (-1,0).将A (-1,0),B (3,0)代入y=ax2+bx+3,得 9330{30a b a b ++=-+=, 解得:1{2a b =-= ∴抛物线的解析式:y=-x 2+2x+3;(2) 如图1,∵P 点的横坐标为t 且PQ 垂直于x 轴 ∴P 点的坐标为(t ,-t+3),Q 点的坐标为(t ,-t 2+2t+3).∴PQ=|(-t+3)-(-t 2+2t+3)|="|" t 2-3t |∴223(03){3(3)d t t t d t t t =-+<<=->; ∵d ,e 是y 2-(m+3)y+14(5m 2-2m+13)=0(m 为常数)的两个实数根,∴△≥0,即△=(m+3)2-4×1(5m2-2m+13)≥04整理得:△= -4(m-1)2≥0,∵-4(m-1)2≤0,∴△=0,m=1,∴ PQ与PH是y2-4y+4=0的两个实数根,解得y1=y2=2∴ PQ=PH=2,∴-t+3=2,∴t="1,"∴此时Q是抛物线的顶点,延长MP至L,使LP=MP,连接LQ、LH,如图2,∵LP=MP,PQ=PH,∴四边形LQMH是平行四边形,∴LH∥QM,∴∠1=∠3,∵∠1=∠2,∴∠2=∠3,∴LH=MH,∴平行四边形LQMH是菱形,∴PM⊥QH,∴点M的纵坐标与P点纵坐标相同,都是2,∴在y=-x2+2x+3令y=2,得x2-2x-1=0,∴x12,x2=12综上:t值为1,M点坐标为2,2)和(12,2).4.已知,抛物线y=x2+2mx(m为常数且m≠0).(1)判断该抛物线与x轴的交点个数,并说明理由.(2)若点A(-n+5,0),B(n-1,0)在该抛物线上,点M为抛物线的顶点,求△ABM的面积.(3)若点(2,p),(3,g),(4,r)均在该抛物线上,且p<g<r,求m的取值范围.【答案】(1)抛物线与x轴有2个交点,理由见解析;(2)△ABM的面积为8;(3)m 的取值范围m>-2.5【解析】【分析】(1)首先算出根的判别式b2-4ac的值,根据偶数次幂的非负性,判断该值一定大于0,从而根据抛物线与x轴交点个数与根的判别式的关系即可得出结论;(2)根据抛物线的对称性及A,B两点的坐标特点求出抛物线的对称轴直线为x=2.从而再根据抛物线对称轴直线公式建立方程,求解算出m的值,进而求出抛物线的解析式,得出A,B,M三点的坐标,根据三角形的面积计算方法,即可算出答案;(3)方法一(图象法):根据抛物线的对称轴直线及开口方向判断出当对称轴在直线x=3的右边时,显然不符合题目条件;当对称轴在直线x=2的左边时,显然符合题目条件(如图2),从而列出不等式得出m 的取值范围;当对称轴在直线x=2和x=3之间时,满足3-(-m)>-m-2即可(如图3),再列出不等式得出m 的取值范围,综上所述,求出m 的取值范围;方法二(代数法):将三点的横坐标分贝代入抛物线的解析式,用含m 的式子表示出p,g,r ,再代入 p<g<r 即可列出关于m 的不等式组,求解即可。
中考数学压轴题专题二次函数的经典综合题及答案解析

一、二次函数真题与模拟题分类汇编(难题易错题)1.如图,某足球运动员站在点O处练习射门,将足球从离地面0.5m的A处正对球门踢出(点A在y轴上),足球的飞行高度y(单位:m)与飞行时间t(单位:s)之间满足函数关系y=at2+5t+c,已知足球飞行0.8s时,离地面的高度为3.5m.(1)足球飞行的时间是多少时,足球离地面最高?最大高度是多少?(2)若足球飞行的水平距离x(单位:m)与飞行时间t(单位:s)之间具有函数关系x=10t,已知球门的高度为2.44m,如果该运动员正对球门射门时,离球门的水平距离为28m,他能否将球直接射入球门?【答案】(1)足球飞行的时间是85s时,足球离地面最高,最大高度是4.5m;(2)能.【解析】试题分析:(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),于是得到,求得抛物线的解析式为:y=﹣t2+5t+,当t=时,y最大=4.5;(2)把x=28代入x=10t得t=2.8,当t=2.8时,y=﹣×2.82+5×2.8+=2.25<2.44,于是得到他能将球直接射入球门.解:(1)由题意得:函数y=at2+5t+c的图象经过(0,0.5)(0.8,3.5),∴,解得:,∴抛物线的解析式为:y=﹣t2+5t+,∴当t=时,y最大=4.5;(2)把x=28代入x=10t得t=2.8,∴当t=2.8时,y=﹣×2.82+5×2.8+=2.25<2.44,∴他能将球直接射入球门.考点:二次函数的应用.2.抛物线2y x bx c =-++(b ,c 为常数)与x 轴交于点()1,0x 和()2,0x ,与y 轴交于点A ,点E 为抛物线顶点。
(Ⅰ)当121,3x x =-=时,求点A ,点E 的坐标;(Ⅱ)若顶点E 在直线y x =上,当点A 位置最高时,求抛物线的解析式;(Ⅲ)若11,0x b =->,当(1,0)P 满足PA PE +值最小时,求b 的值。
初三中考数学专题复习:二次函数综合题(相似三角形问题)含答案

中考数学专题复习:二次函数综合题(相似三角形问题)1.如图①,二次函数y =﹣x 2+bx +c 的图象与x 轴交于点A (﹣1,0)、B (3,0),与y 轴交于点C ,连接BC ,点P 是抛物线上一动点.(1)求二次函数的表达式.(2)当点P 不与点A 、B 重合时,作直线AP ,交直线BC 于点Q ,若①ABQ 的面积是①BPQ 面积的4倍,求点P 的横坐标.(3)如图①,当点P 在第一象限时,连接AP ,交线段BC 于点M ,以AM 为斜边向①ABM 外作等腰直角三角形AMN ,连接BN ,①ABN 的面积是否变化?如果不变,请求出①ABN 的面积;如果变化,请说明理由.2.如图,二次函数2314y x bx =++的图像经过点()8,3A ,交x 轴于点B ,C (点B 在点C 的左侧),与y 轴交于点D .(1)填空:b = ______;(2)点P 是第一象限内抛物线上一点,直线PO 交直线CD 于点Q ,过点P 作x 轴的垂线交直线CD 于点T ,若PQ QT =,求点P 的坐标;(3)在x 轴的正半轴上找一点E ,过点E 作AE 的垂线EF 交y 轴于F ,若AEF 与EFO △相似,求OE 的长.3.如图,已知抛物线2y ax bx c =++与x 轴相交于点()1,0A -,()3,0B ,与y 轴的交点()0,6C .(1)求抛物线的解析式;(2)点(),P m n 在平面直角坐标系第一象限内的抛物线上运动,设PBC 的面积为S ,求S 关于m 的函数表达式(指出自变量m 的取值范围)和S 的最大值;(3)点M 在抛物线上运动,点N 在y 轴上运动,是否存在点M 、点N 使得①CMN =90°,且∆CMN 与OBC ∆相似,如果存在,请求出点M 和点N 的坐标.4.如图,抛物线L 1:y =ax 2﹣2x +c (a ≠0)与x 轴交于A 、B (3,0)两点,与y 轴交于点C (0,﹣3),抛物线的顶点为D .抛物线L 2与L 1关于x 轴对称.(1)求抛物线L 1与L 2的函数表达式;(2)已知点E 是抛物线L 2的顶点,点M 是抛物线L 2上的动点,且位于其对称轴的右侧,过M 向其对称轴作垂线交对称轴于P ,是否存在这样的点M ,使得以P 、M 、E 为顶点的三角形与△BCD 相似,若存在请求出点M 的坐标,若不存在,请说明理由.5.如图,在平面直角坐标系中,已知直线4y x =+与x 轴、y 轴分别相交于点A 和点C ,抛物线21y x kx k =++-的图象经过点A 和点C ,与x 轴的另一个交点是点B .(1)求出此抛物线的解析式; (2)求出点B 的坐标;(3)若在y 轴的负半轴上存在点D .能使得以A ,C ,D 为顶点的三角形与①ABC 相似,请求出点D 的坐标.6.如图1,已知抛物线23y ax bx =++经过点()1,5D ,且交x 轴于A ,B 两点,交y 轴于点C ,已知点()1,0A -,(),P m n 是抛物线在第一象限内的一个动点,PQ BC ⊥于点Q .(1)求抛物线的解析式;(2)当PQ =m 的值;(3)是否存在点P ,使BPQ 与BOC 相似?若存在,请求出P 点的坐标;若不存在,请说明理由.7.如图,在平面直角坐标系中,直线y =12x +2与x 轴交于点A ,与y 轴交于点C .抛物线y =ax 2+bx +c的对称轴是x=-32且经过A、C两点,与x轴的另一交点为点B.(1)求二次函数y=ax2+bx+c的表达式;(2)点P为线段AB上的动点,求AP+2PC的最小值;(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A,M,N为顶点的三角形与①ABC 相似?若存在,求出点M的坐标;若不存在,请说明理由.8.如图,抛物线y=−x2+bx+c与x轴相交于A(−1,0),B(3,0)两点,与y轴交于点C,顶点为点D,抛物线的对称轴与BC相交于点E,与x轴相交于点F.(1)求抛物线的函数关系式;(2)连结DA,求sin A的值;(3)若点H线段BC上,BOC与BFH△相似,请直接写出点H的坐标.9.如图,抛物线y=1-2x2+bx+c与x轴交于点A(﹣2,0)和点B(8,0),与y轴交于点C,顶点为D,连接AC,BC,BC与抛物线的对称轴l交于点E.(1)求抛物线的表达式;(2)点P 是第一象限内抛物线上的动点,连接PB ,PC ,当S △PBC =720S △ABC 时,求点P 的坐标; (3)点N 是对称轴l 右侧抛物线上的动点,在射线ED 上是否存在点M ,使得以点M ,N ,E 为顶点的三角形与①OBC 相似?若存在,求点M 的坐标;若不存在,请说明理由.10.如图,抛物线23y ax bx =++与x 轴交于1,0A 、()3,0B -两点,与y 轴交于点C ,设抛物线的顶点为D .(1)求该抛物线的表达式与顶点D 的坐标; (2)试判断BCD △的形状,并说明理由;(3)探究坐标轴上是否存在点P ,使得以P 、A 、C 为顶点的三角形与BCD △相似?若存在,请求出点P 的坐标;若不存在,请说明理由.11.如图,抛物线y =ax 2﹣2ax ﹣3a (a ≠0)与x 轴交于点A ,B .与y 轴交于点C .连接AC ,BC .已知ABC 的面积为2.(1)求抛物线的解析式;(2)平行于x 轴的直线与抛物线从左到右依次交于P ,Q 两点.过P ,Q 向x 轴作垂线,垂足分别为G ,H .若四边形PGHQ 为正方形,求正方形的边长;(3)抛物线上是否存在一点N ,使得①BCN =①CAB ﹣①CBA ,若存在,请求出满足条件N 点的横坐标,若不存在请说明理由.12.如图,二次函数2y x bx c =-++的图像与x 轴交于点A (-1,0),B (2,0),与y 轴相交于点C .(1)求这个二次函数的解析式;(2)若点M 在此抛物线上,且在y 轴的右侧.①M 与y 轴相切,过点M 作MD ①y 轴,垂足为点D .以C ,D ,M 为顶点的三角形与①AOC 相似,求点M 的坐标及①M 的半径长.13.如图,在平面直角坐标系中,抛物线2()0y ax bx c ac =++≠与x 轴交于点A 和点B (点A 在点B 的左侧),与y 轴交于点C .若线段OA OB OC 、、的长满足2OC OA OB =⋅,则这样的抛物线称为“黄金”抛物线.如图,抛物线22(0)y ax bx a =++≠为“黄金”抛物线,其与x 轴交点为A ,B (其中B 在A 的右侧),与y 轴交于点C .且4OA OB =(1)求抛物线的解析式;(2)若P 为AC 上方抛物线上的动点,过点P 作PD AC ⊥,垂足为D . ①求PD 的最大值;①连接PC ,当PCD 与ACO △相似时,求点P 的坐标.14.如图,在平面直角坐标系xOy 中,已知抛物线2y x bx c =++与x 轴交于点A 、B 两点,其中1,0A ,与y 轴交于点()0,3C .(1)求抛物线解析式;(2)如图1,过点B 作x 轴垂线,在该垂线上取点P ,使得①PBC 与①ABC 相似,请求出点P 坐标;(3)如图2,在线段OB 上取一点M ,连接CM ,请求出12CM BM +最小值.15.如图,抛物线y =ax 2+k (a >0,k <0)与x 轴交于A ,B 两点(点B 在点A 的右侧),其顶点为C ,点P 为线段OC 上一点,且PC =14OC .过点P 作DE ①AB ,分别交抛物线于D ,E 两点(点E 在点D 的右侧),连接OD ,DC .(1)直接写出A ,B ,C 三点的坐标;(用含a ,k 的式子表示) (2)猜想线段DE 与AB 之间的数量关系,并证明你的猜想;(3)若①ODC =90°,k =﹣4,求a 的值.16.如图,抛物线223y x bx c =++与x 轴交于A ,B 两点,与y 轴交于C 点,连接AC ,已知B (﹣1,0),且抛物线经过点D (2,﹣2).(1)求抛物线的表达式;(2)若点E 是抛物线上第四象限内的一点,且2ABES=,求点E 的坐标;(3)若点P 是y 轴上一点,以P ,A ,C 三点为顶点的三角形是等腰三角形,求P 点的坐标.17.如图,在直角坐标系xOy 中,抛物线y =ax 2+bx +2(a ≠0)与x 轴交于点A (﹣1,0)和B (4,0),与y 轴交于点C ,点P 是抛物线上的动点(不与点A ,B ,C 重合).(1)求抛物线的解析式;(2)当点P 在第一象限时,设①ACP 的面积为S 1,①ABP 的面积为S 2,当S 1=S 2时,求点P 的坐标; (3)过点O 作直线l ①BC ,点Q 是直线l 上的动点,当BQ ①PQ ,且①BPQ =①CAB 时,请直接写出点P 的坐标.18.如图,在平面直角坐标系xOy中,直线y=﹣x+3与两坐标轴交于A、B两点,抛物线y=x2+bx+c 过点A和点B,并与x轴交于另一点C,顶点为D.点E在对称轴右侧的抛物线上.(1)求抛物线的函数表达式和顶点D的坐标;(2)若点F在抛物线的对称轴上,且EF①x轴,若以点D,E,F为顶点的三角形与①ABD相似,求出此时点E的坐标;(3)若点P为坐标平面内一动点,满足tan①APB=3,请直接写出①P AB面积最大时点P的坐标及该三角形面积的最大值.19.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于点A、B,与y轴交于点C,且OC=2OB=6OA=6,点P是第一象限内抛物线上的动点.(1)求抛物线的解析式;(2)连接BC与OP,交于点D,当S△PCD:S△ODC的值最大时,求点P的坐标;(3)点M在抛物线上运动,点N在y轴上运动,是否存在点M、点N.使①CMN=90°,且①CMN与①BOC 相似,若存在,请求出点M、点N的坐标.20.如图,抛物线y=x2+bx+12(b<0)与x轴交于A,B两点(A点在B点左侧),且OB=3OA.(1)请直接写出b=,A点的坐标是,B点的坐标是;(2)如图(1),D点从原点出发,向y轴正方向运动,速度为2个单位长度/秒,直线BD交抛物线于点E,若BE=5DE,求D点运动时间;(3)如图(2),F点是抛物线顶点,过点F作x轴平行线MN,点C是对称轴右侧的抛物线上的一定点,P 点在直线MN上运动.若恰好存在3个P点使得①P AC为直角三角形,请求出C点坐标,并直接写出P点的坐标.答案1.(1)y =﹣x 2+2x +3.(2)P 352或 (3)①ABN 的面积不变,为4.2.(1)2-(2)5⎛ ⎝⎭或5⎛ ⎝⎭(3)4或493.(1)2246y x x =-++(2)S 关于m 的函数表达式为239(03)S m m m =-+<<,S 的最大值是274 (3)存在,M (1,8),N (0,172)或M (74,558),N (0,838)或M (94,398),N (0,38)或M (3,0),N (0,﹣32)4.(1)抛物线L 1:223y x x =--,抛物线L 2:2y x 2x 3=-++;(2)435(,)39M 或(4,5)M -.5.(1)254y x x =++(2)点B 的坐标为(-1,0)(3)点D 的坐标是(0,-203) 6.(1)215322y x x =-++ (2)1或5(3)存在;P (53,529)7.(1)抛物线表达式为:213222y x x =--+;(2)AP +2PC 的最小值是4;(3)存在M(0,2)或(-3,2)或(2,-3)或(5,-18),使得以点A 、M 、N 为顶点的三角形与ABC 相似.8.(1)y =-x 2+2x +3(3)点H 的坐标为(1,2)或(2,1)9.(1)21382y x x =++ (2)P 1(1,10.5),P 2(7,4.5)(3)存在,(3,8)或(3,5或(3,11)30.(1)y =﹣x 2﹣2x +3,(﹣1,4);(2)直角三角形,理由见解析;(3)存在,(0,0)或(0,﹣13)或(-9,0)11.(1)y =﹣13x 2+23x +1(2)﹣6﹣(3)存在,5或11712.(1)22y x x =-++; (2)M 的坐标为(12,94),(32, 54 ),(3,-4),①M 的半径长为12或32或313.(1)213222y x x =--+(2)①PD ①P 坐标为(3,2)-或325()28,-14.(1)243y x x =-+(2)P 点坐标为()3,9或()3,215.(1)点A 、B 、C 的坐标分别为(、、(0,k ) (2)DE =12AB(3)a =1316.(1)224233y x x =--(2)E ,-1)(3)P 点的坐标(0,2)或(02)或(0,﹣2或(0,54)17.(1)213222y x x =-++ (2)点P 的坐标为(103,139)(3)点P 的坐标为(32,﹣2)或(32,﹣2)或(173,﹣509)18.(1)y =x 2﹣4x +3,(2,﹣1)(2)(5,8)或(73,89-)(3)①P AB ,此时P )19.(1)y =﹣2x 2+4x +6 (2)点P 的坐标为(32,152) (3)存在,M 、N 的坐标分别为(3,0)、(0,﹣32)或(94,398)、(0,38)或(1,8)、(0,172)或(74,558)、(0,838)20.(1)﹣8,(2,0),(6,0)(2)3秒或212秒 (3)C 点坐标为(143,﹣329),P 点的坐标为(103,﹣4)或(﹣103,﹣4)或(11027,﹣4)。
备战中考数学专题训练---一元二次方程的综合题分类及答案

一、一元二次方程 真题与模拟题分类汇编(难题易错题)1.已知关于x 的二次函数22(21)1y x k x k =--++的图象与x 轴有2个交点.(1)求k 的取值范围;(2)若图象与x 轴交点的横坐标为12,x x ,且它们的倒数之和是32-,求k 的值. 【答案】(1)k <-34 ;(2)k=﹣1 【解析】试题分析:(1)根据交点得个数,让y=0判断出两个不相等的实数根,然后根据判别式△= b 2-4ac 的范围可求解出k 的值;(2)利用y=0时的方程,根据一元二次方程的根与系数的关系,可直接列式求解可得到k 的值.试题解析:(1)∵二次函数y=x 2-(2k-1)x+k 2+1的图象与x 轴有两交点,∴当y=0时,x 2-(2k-1)x+k 2+1=0有两个不相等的实数根.∴△=b 2-4ac=[-(2k-1)]2-4×1×(k 2+1)>0.解得k <-34; (2)当y=0时,x 2-(2k-1)x+k 2+1=0.则x 1+x 2=2k-1,x 1•x 2=k 2+1,∵=== 32-, 解得:k=-1或k= 13-(舍去),∴k=﹣12.已知为正整数,二次方程的两根为,求下式的值:【答案】【解析】由韦达定理,有,.于是,对正整数,有原式=3.关于x的方程(k-1)x2+2kx+2=0(1)求证:无论k为何值,方程总有实数根.(2)设x1,x2是方程(k-1)x2+2kx+2=0的两个根,记S=++ x1+x2,S的值能为2吗?若能,求出此时k的值.若不能,请说明理由.【答案】(1)详见解析;(2)S的值能为2,此时k的值为2.【解析】试题分析:(1)本题二次项系数为(k-1),可能为0,可能不为0,故要分情况讨论;要保证一元二次方程总有实数根,就必须使△>0恒成立;(2)欲求k的值,先把此代数式变形为两根之积或两根之和的形式,代入数值计算即可.试题解析:(1)①当k-1=0即k=1时,方程为一元一次方程2x=1,x=有一个解;②当k-1≠0即k≠1时,方程为一元二次方程,△=(2k)²-4×2(k-1)=4k²-8k+8="4(k-1)" ²+4>0方程有两不等根综合①②得不论k为何值,方程总有实根(2)∵x ₁+x ₂=,x ₁ x ₂=∴S=++ x1+x2=====2k-2=2,解得k=2,∴当k=2时,S的值为2∴S 的值能为2,此时k 的值为2.考点:一元二次方程根的判别式;根与系数的关系.4.沙坪坝区各街道居民积极响应“创文明城区”活动,据了解,某街道居民人口共有7.5万人,街道划分为A ,B 两个社区,B 社区居民人口数量不超过A 社区居民人口数量的2倍. (1)求A 社区居民人口至少有多少万人?(2)街道工作人员调查A ,B 两个社区居民对“社会主义核心价值观”知晓情况发现:A 社区有1.2万人知晓,B 社区有1.5万人知晓,为了提高知晓率,街道工作人员用了两个月的时间加强宣传,A 社区的知晓人数平均月增长率为m %,B 社区的知晓人数第一个月增长了45m %,第二月在第一个月的基础上又增长了2m %,两个月后,街道居民的知晓率达到92%,求m 的值.【答案】(1)A 社区居民人口至少有2.5万人;(2)m 的值为50.【解析】【分析】(1)设A 社区居民人口有x 万人,根据“B 社区居民人口数量不超过A 社区居民人口数量的2倍”列出不等式求解即可;(2)A 社区的知晓人数+B 社区的知晓人数=7.5×92%,据此列出关于m 的方程并解答.【详解】解:(1)设A 社区居民人口有x 万人,则B 社区有(7.5-x )万人,依题意得:7.5-x ≤2x ,解得x ≥2.5.即A 社区居民人口至少有2.5万人;(2)依题意得:1.2(1+m %)2+1.5×(1+45m %)+1.5×(1+45m %)(1+2m %)=7.5×92%, 解得m =50答:m 的值为50.【点睛】本题考查了一元二次方程和一元一次不等式的应用,解题的关键是读懂题意,找到题中相关数据的数量关系,列出不等式或方程.5.已知关于x 的一元二次方程()220x m x m -++=(m 为常数) (1)求证:不论m 为何值,方程总有两个不相等的实数根;(2)若方程有一个根是2,求m 的值及方程的另一个根.【答案】(1)见解析;(2) 即m 的值为0,方程的另一个根为0.【解析】【分析】(1)可用根的判别式,计算判别式得到△=(m+2)2−4×1⋅m=m 2+4>0,则方程有两个不相等实数解,于是可判断不论m 为何值,方程总有两个不相等的实数根;(2)设方程的另一个根为t ,利用根与系数的关系得到2+t=21m + ,2t=m,最终解出关于t 和m 的方程组即可.【详解】(1)证明:△=(m+2)2−4×1⋅m=m 2+4,∵无论m 为何值时m 2≥0,∴m 2+4≥4>0,即△>0,所以无论m 为何值,方程总有两个不相等的实数根.(2)设方程的另一个根为t , ()220x m x m -++=根据题意得2+t=21m + ,2t=m , 解得t=0,所以m=0,即m 的值为0,方程的另一个根为0.【点睛】本题考查根的判别式和根于系数关系,对于问题(1)可用根的判别式进行判断,在判断过程中注意对△的分析,在分析时可借助平方的非负性;问题(2)可先设另一个根为t ,用根于系数关系列出方程组,在求解.6.关于x 的方程()2204k kx k x +++=有两个不相等的实数根. ()1求实数k 的取值范围;()2是否存在实数k ,使方程的两个实数根之和等于两实数根之积的算术平方根?若存在,求出k 的值;若不存在,说明理由.【答案】(1)1k >-且0k ≠;(2)不存在符合条件的实数k ,使方程的两个实数根之和等于两实数根之积的算术平方根.【解析】【分析】()1由于方程有两个不相等的实数根,所以它的判别式0>,由此可以得到关于k 的不等式,解不等式即可求出k 的取值范围. ()2首先利用根与系数的关系,求出两根之和与两根之积,再由方程的两个实数根之和等于两实数根之积的算术平方根,可以得出关于k 的等式,解出k 值,然后判断k 值是否在()1中的取值范围内.【详解】解:()1依题意得2(2)404k k k =+-⋅>, 1k ∴>-,又0k ≠,k ∴的取值范围是1k >-且0k ≠;()2解:不存在符合条件的实数k ,使方程的两个实数根之和等于两实数根之积的算术平方根,理由是:设方程()2204k kx k x +++=的两根分别为1x ,2x , 由根与系数的关系有:1212214k x x k x x +⎧+=-⎪⎪⎨⎪=⎪⎩, 又因为方程的两个实数根之和等于两实数根之积的算术平方根,212k k +∴-=, 43k ∴=-, 由()1知,1k >-,且0k ≠,43k ∴=-不符合题意, 因此不存在符合条件的实数k ,使方程的两个实数根之和等于两实数根之积的算术平方根.【点睛】本题重点考查了一元二次方程的根的判别式和根与系数的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、二次函数真题与模拟题分类汇编(难题易错题)1.如图,已知抛物线y=﹣x2+bx+c与一直线相交于A(1,0)、C(﹣2,3)两点,与y 轴交于点N,其顶点为D.(1)求抛物线及直线AC的函数关系式;(2)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值及此时点P 的坐标;(3)在对称轴上是否存在一点M,使△ANM的周长最小.若存在,请求出M点的坐标和△ANM周长的最小值;若不存在,请说明理由.【答案】(1)y=﹣x2﹣2x+3;y=﹣x+1;(2)当x=﹣12时,△APC的面积取最大值,最大值为278,此时点P的坐标为(﹣12,154);(3)在对称轴上存在一点M(﹣1,2),使△ANM的周长最小,△ANM周长的最小值为102【解析】【分析】(1)根据点A,C的坐标,利用待定系数法即可求出抛物线及直线AC的函数关系式;(2)过点P作PE∥y轴交x轴于点E,交直线AC于点F,过点C作CQ∥y轴交x轴于点Q,设点P的坐标为(x,﹣x2﹣2x+3)(﹣2<x<1),则点E的坐标为(x,0),点F的坐标为(x,﹣x+1),进而可得出PF的值,由点C的坐标可得出点Q的坐标,进而可得出AQ的值,利用三角形的面积公式可得出S△APC=﹣32x2﹣32x+3,再利用二次函数的性质,即可解决最值问题;(3)利用二次函数图象上点的坐标特征可得出点N的坐标,利用配方法可找出抛物线的对称轴,由点C,N的坐标可得出点C,N关于抛物线的对称轴对称,令直线AC与抛物线的对称轴的交点为点M,则此时△ANM周长取最小值,再利用一次函数图象上点的坐标特征求出点M的坐标,以及利用两点间的距离公式结合三角形的周长公式求出△ANM周长的最小值即可得出结论.【详解】(1)将A(1,0),C(﹣2,3)代入y=﹣x2+bx+c,得:10423b c b c -++=⎧⎨--+=⎩,解得:23b c =-⎧⎨=⎩, ∴抛物线的函数关系式为y =﹣x 2﹣2x +3; 设直线AC 的函数关系式为y =mx +n (m ≠0), 将A (1,0),C (﹣2,3)代入y =mx +n ,得:023m n m n +=⎧⎨-+=⎩,解得:11m n =-⎧⎨=⎩, ∴直线AC 的函数关系式为y =﹣x +1.(2)过点P 作PE ∥y 轴交x 轴于点E ,交直线AC 于点F ,过点C 作CQ ∥y 轴交x 轴于点Q ,如图1所示.设点P 的坐标为(x ,﹣x 2﹣2x +3)(﹣2<x <1),则点E 的坐标为(x ,0),点F 的坐标为(x ,﹣x +1),∴PE =﹣x 2﹣2x +3,EF =﹣x +1,EF =PE ﹣EF =﹣x 2﹣2x +3﹣(﹣x +1)=﹣x 2﹣x +2. ∵点C 的坐标为(﹣2,3), ∴点Q 的坐标为(﹣2,0), ∴AQ =1﹣(﹣2)=3, ∴S △APC =12AQ •PF =﹣32x 2﹣32x +3=﹣32(x +12)2+278. ∵﹣32<0, ∴当x =﹣12时,△APC 的面积取最大值,最大值为278,此时点P 的坐标为(﹣12,154). (3)当x =0时,y =﹣x 2﹣2x +3=3, ∴点N 的坐标为(0,3). ∵y =﹣x 2﹣2x +3=﹣(x +1)2+4, ∴抛物线的对称轴为直线x =﹣1. ∵点C 的坐标为(﹣2,3), ∴点C ,N 关于抛物线的对称轴对称.令直线AC 与抛物线的对称轴的交点为点M ,如图2所示. ∵点C ,N 关于抛物线的对称轴对称, ∴MN =CM ,∴AM +MN =AM +MC =AC , ∴此时△ANM 周长取最小值. 当x =﹣1时,y =﹣x +1=2, ∴此时点M 的坐标为(﹣1,2).∵点A 的坐标为(1,0),点C 的坐标为(﹣2,3),点N 的坐标为(0,3),∴AC=,AN ,∴C△ANM=AM+MN+AN=AC+AN=32+10.∴在对称轴上存在一点M(﹣1,2),使△ANM的周长最小,△ANM周长的最小值为32+10.【点睛】本题考查待定系数法求一次函数解析式、待定系数法求二次函数解析式、二次函数图象上点的坐标特征、一次函数图象上点的坐标特征、二次函数的性质、三角形的面积以及周长,解题的关键是:(1)根据点的坐标,利用待定系数法求出抛物线及直线AC的函数关系式;(2)利用三角形的面积公式找出S△APC=﹣32x2﹣32x+3的最值;(3)利用二次函数图象的对称性结合两点之间线段最短找出点M的位置.2.某市实施产业精准扶贫,帮助贫困户承包荒山种植某品种蜜柚.已知该蜜柚的成本价为6元/千克,到了收获季节投入市场销售时,调查市场行情后,发现该蜜柚不会亏本,且每天的销售量y(千克)与销售单价x(元)之间的函数关系如图所示.(1)求y与x的函数关系式,并写出x的取值范围;(2)当该品种蜜柚定价为多少时,每天销售获得的利润最大?最大利润是多少?(3)某村农户今年共采摘蜜柚12000千克,若该品种蜜柚的保质期为50天,按照(2)的销售方式,能否在保质期内全部销售完这批蜜柚?若能,请说明理由;若不能,应定销售价为多少元时,既能销售完又能获得最大利润?【答案】(1)y =﹣20x +500,(x ≥6);(2)当x =15.5时,w 的最大值为1805元;(3)当x =13时,w =1680,此时,既能销售完又能获得最大利润. 【解析】 【分析】(1)将点(15,200)、(10,300)代入一次函数表达式:y =kx +b 即可求解; (2)由题意得:w =y (x ﹣6)=﹣20(x ﹣25)(x ﹣6),∵﹣20<0,故w 有最大值,即可求解;(3)当x =15.5时,y =190,50×190<12000,故:按照(2)的销售方式,不能在保质期内全部销售完;由50(500﹣20x )≥12000,解得:x ≤13,当x =13时,既能销售完又能获得最大利润. 【详解】解:(1)将点(15,200)、(10,300)代入一次函数表达式:y =kx +b 得:2001530010k bk b =+⎧⎨=+⎩, 解得:20500k b =-⎧⎨=⎩,即:函数的表达式为:y =﹣20x +500,(x ≥6);(2)设:该品种蜜柚定价为x 元时,每天销售获得的利润w 最大, 则:w =y (x ﹣6)=﹣20(x ﹣25)(x ﹣6), ∵﹣20<0,故w 有最大值, 当x =﹣2b a =312=15.5时,w 的最大值为1805元; (3)当x =15.5时,y =190, 50×190<12000,故:按照(2)的销售方式,不能在保质期内全部销售完; 设:应定销售价为x 元时,既能销售完又能获得最大利润w , 由题意得:50(500﹣20x )≥12000,解得:x ≤13, w =﹣20(x ﹣25)(x ﹣6), 当x =13时,w =1680,此时,既能销售完又能获得最大利润. 【点睛】本题考查了二次函数的性质在实际生活中的应用.最大销售利润的问题常利函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.其中要注意应该在自变量的取值范围内求最大值(或最小值).3.如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.(1)求抛物线的解析式;(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.【答案】(1)y=38x2﹣34x﹣3(2)运动1秒使△PBQ的面积最大,最大面积是9 10(3)K1(1,﹣278),K2(3,﹣158)【解析】【详解】试题分析:(1)把点A、B的坐标分别代入抛物线解析式,列出关于系数a、b的解析式,通过解方程组求得它们的值;(2)设运动时间为t秒.利用三角形的面积公式列出S△PBQ与t的函数关系式S△PBQ=﹣9 10(t﹣1)2+910.利用二次函数的图象性质进行解答;(3)利用待定系数法求得直线BC的解析式为y=34x﹣3.由二次函数图象上点的坐标特征可设点K的坐标为(m,38m2﹣34m﹣3).如图2,过点K作KE∥y轴,交BC于点E.结合已知条件和(2)中的结果求得S△CBK=94.则根据图形得到:S△CBK=S△CEK+S△BEK=12EK•m+12•EK•(4﹣m),把相关线段的长度代入推知:﹣34m2+3m=94.易求得K1(1,﹣278),K2(3,﹣158).解:(1)把点A(﹣2,0)、B(4,0)分别代入y=ax2+bx﹣3(a≠0),得423016430a ba b--=⎧⎨+-=⎩,解得3834ab⎧=⎪⎪⎨⎪=-⎪⎩,所以该抛物线的解析式为:y=38x2﹣34x﹣3;(2)设运动时间为t秒,则AP=3t,BQ=t.∴PB=6﹣3t.由题意得,点C的坐标为(0,﹣3).在Rt△BOC中,BC=2234+=5.如图1,过点Q作QH⊥AB于点H.∴QH∥CO,∴△BHQ∽△BOC,∴HBOCBGBC=,即Hb35t=,∴HQ=35t.∴S△PBQ=12PB•HQ=12(6﹣3t)•35t=﹣910t2+95t=﹣910(t﹣1)2+910.当△PBQ存在时,0<t<2∴当t=1时,S△PBQ最大=910.答:运动1秒使△PBQ的面积最大,最大面积是910;(3)设直线BC的解析式为y=kx+c(k≠0).把B (4,0),C (0,﹣3)代入,得403k c c +=⎧⎨=-⎩, 解得3k 4c 3⎧=⎪⎨⎪=-⎩,∴直线BC 的解析式为y=34x ﹣3. ∵点K 在抛物线上.∴设点K 的坐标为(m ,38m 2﹣34m ﹣3). 如图2,过点K 作KE ∥y 轴,交BC 于点E .则点E 的坐标为(m ,34m ﹣3).∴EK=34m ﹣3﹣(38m 2﹣34m ﹣3)=﹣38m 2+32m .当△PBQ 的面积最大时,∵S △CBK :S △PBQ =5:2,S △PBQ =910. ∴S △CBK =94. S △CBK =S △CEK +S △BEK =12EK•m+12•EK•(4﹣m ) =12×4•EK =2(﹣38m 2+32m ) =﹣34m 2+3m . 即:﹣34m 2+3m=94.解得 m 1=1,m 2=3.∴K 1(1,﹣278),K 2(3,﹣158).点评:本题是二次函数的综合题型,其中涉及到的知识点有待定系数法求二次函数解析式和三角形的面积求法.在求有关动点问题时要注意该点的运动范围,即自变量的取值范围.4.如图1,二次函数234y ax ax a =--的图像与x 轴交于,A B 两点(点A 在点B 的左侧),与y 轴交于点()0,3C-.(1)求二次函数的表达式及点A 、点B 的坐标;(2)若点D 在二次函数图像上,且45DBC ABC S S =△△,求点D 的横坐标;(3)将直线BC 向下平移,与二次函数图像交于,M N 两点(M 在N 左侧),如图2,过M 作ME y ∥轴,与直线BC 交于点E ,过N 作NF y ∥轴,与直线BC 交于点F ,当MN ME +的值最大时,求点M 的坐标.【答案】(1)y =239344x x --,A (﹣1,0),B (4,0);(2)D 点的横坐标为22﹣2,2;(3)M (13,﹣113) 【解析】 【分析】(1)求出a ,即可求解;(2)求出直线BC 的解析式,过点D 作DH ∥y 轴,与直线BC 交于点H ,根据三角形面积的关系求解;(3)过点M 作MG ∥x 轴,交FN 的延长线于点G ,设M (m ,34m 2﹣94m ﹣3),N(n ,34n 2﹣94n ﹣3),判断四边形MNFE 是平行四边形,根据ME =NF ,求出m +n =4,再确定ME +MN =﹣34m 2+3m +5﹣52m =﹣34(m ﹣13)2+6112,即可求M ;【详解】(1)y=ax2﹣3ax﹣4a与y轴交于点C(0,﹣3),∴a=34,∴y=34x2﹣94x﹣3,与x轴交点A(﹣1,0),B(4,0);(2)设直线BC的解析式为y=kx+b,∴403k bb+=⎧⎨=-⎩,∴343kb⎧=-⎪⎨⎪=-⎩,∴y=34x﹣3;过点D作DH∥y轴,与直线BC交于点H,设H(x,34x﹣3),D(x,34x2﹣94x﹣3),∴DH=|34x2﹣3x|,∵S△ABC=1155323⨯⨯=,∴S△DBC=41552⨯=6,∴S△DBC=2×|34x2﹣3x|=6,∴x=2+22,x=2﹣22,x=2;∴D点的横坐标为2+22,2﹣22,2;(3)过点M作MG∥x轴,交FN的延长线于点G,设M(m,34m2﹣94m﹣3),N(n,34n2﹣94n﹣3),则E(m,34m﹣3),F(n,34n﹣3),∴ME=﹣34m2+3m,NF=﹣34n2+3n,∵EF∥MN,ME∥NF,∴四边形MNFE是平行四边形,∴ME=NF,∴﹣34m2+3m=﹣34n2+3n,∴m+n=4,∴MG=n﹣m=4﹣2m,∴∠NMG=∠OBC,∴cos∠NMG=cos∠OBC=MG OBMN BC,∵B(4,0),C(0,﹣3),∴OB=4,OC=3,在Rt△BOC中,BC=5,∴MN=54(n﹣m)=54(4﹣2m)=5﹣52m,∴ME+MN=﹣34m2+3m+5﹣52m=﹣34(m﹣13)2+6112,∵﹣34<0,∴当m=13时,ME+MN有最大值,∴M(13,﹣113)【点睛】本题考查二次函数图象及性质,一次函数图象及性质;熟练掌握待定系数法求函数解析式的方法,结合三角形的性质解题.5.温州茶山杨梅名扬中国,某公司经营茶山杨梅业务,以3万元/吨的价格买入杨梅,包装后直接销售,包装成本为1万元/吨,它的平均销售价格y(单位:万元/吨)与销售数量x(2≤x≤10,单位:吨)之间的函数关系如图所示.(1)若杨梅的销售量为6吨时,它的平均销售价格是每吨多少万元?(2)当销售数量为多少时,该经营这批杨梅所获得的毛利润(w)最大?最大毛利润为多少万元?(毛利润=销售总收入﹣进价总成本﹣包装总费用)(3)经过市场调查发现,杨梅深加工后不包装直接销售,平均销售价格为12万元/吨.深加工费用y(单位:万元)与加工数量x(单位:吨)之间的函数关系是y=12x+3(2≤x≤10).①当该公司买入杨梅多少吨时,采用深加工方式与直接包装销售获得毛利润一样? ②该公司买入杨梅吨数在 范围时,采用深加工方式比直接包装销售获得毛利润大些?【答案】(1)杨梅的销售量为6吨时,它的平均销售价格是每吨10万元;(2)当x =8时,此时W 最大值=40万元;(3)①该公司买入杨梅3吨;②3<x ≤8. 【解析】 【分析】(1)设其解析式为y =kx +b ,由图象经过点(2,12),(8,9)两点,得方程组,即可得到结论;(2)根据题意得,w =(y ﹣4)x =(﹣12x +13﹣4)x =﹣12x 2+9x ,根据二次函数的性质即可得到结论;(3)①根据题意列方程,即可得到结论;②根据题意即可得到结论. 【详解】(1)由图象可知,y 是关于x 的一次函数. ∴设其解析式为y =kx +b ,∵图象经过点(2,12),(8,9)两点,∴21289k b k b +=⎧⎨+=⎩,解得k =﹣12,b =13, ∴一次函数的解析式为y =﹣12x +13, 当x =6时,y =10,答:若杨梅的销售量为6吨时,它的平均销售价格是每吨10万元; (2)根据题意得,w =(y ﹣4)x =(﹣12x +13﹣4)x =﹣12x 2+9x , 当x =﹣2ba=9时,x =9不在取值范围内, ∴当x =8时,此时W 最大值=﹣12x 2+9x =40万元;(3)①由题意得:﹣12x 2+9x =9x ﹣(12x +3) 解得x =﹣2(舍去),x =3, 答该公司买入杨梅3吨;②当该公司买入杨梅吨数在 3<x ≤8范围时,采用深加工方式比直接包装销售获得毛利润大些.故答案为:3<x ≤8. 【点睛】本题是二次函数、一次函数的综合应用题,难度较大.解题关键是理清售价、成本、利润三者之间的关系.6.如果一条抛物线y =ax 2+bx +c (a ≠0)与x 轴有两个交点,那么以抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”,[a ,b ,c ]称为“抛物线系数”. (1)任意抛物线都有“抛物线三角形”是 (填“真”或“假”)命题;(2)若一条抛物线系数为[1,0,﹣2],则其“抛物线三角形”的面积为 ;(3)若一条抛物线系数为[﹣1,2b ,0],其“抛物线三角形”是个直角三角形,求该抛物线的解析式;(4)在(3)的前提下,该抛物线的顶点为A ,与x 轴交于O ,B 两点,在抛物线上是否存在一点P ,过P 作PQ ⊥x 轴于点Q ,使得△BPQ ∽△OAB ?如果存在,求出P 点坐标;如果不存在,请说明理由.【答案】(1)假;(2)3)y =-x 2+2x 或y =-x 2-2x ;(4)P (1,1)或P (-1,-3)或P (1,-3)或(-1,1). 【解析】分析:(1)当△>0时,抛物线与x 轴有两个交点,由此可得出结论;(2)根据“抛物线三角形”定义得到22y x =-,由此可得出结论;(3)根据“抛物线三角形”定义得到y =-x 2+2bx ,它与x 轴交于点(0,0)和(2b ,0);当抛物线三角形是直角三角形时,根据对称性可知它一定是等腰直角三角形, 由抛物线顶点为(b ,b 2),以及直角三角形斜边上的中线等于斜边的一半得到2122b b =⨯,解方程即可得到结论; (4)分两种情况讨论:①当抛物线为y =-x 2+2x 时,②当抛物线为y =-x 2-2x 时. 详解:(1)当△>0时,抛物线与x 轴有两个交点,此时抛物线才有“抛物线三角形”,故此命题为假命题;(2)由题意得:22y x =-,令y =0,得:x=,∴ S=122⨯=12x x ;(3)依题意:y =-x 2+2bx ,它与x 轴交于点(0,0)和(2b ,0); 当抛物线三角形是直角三角形时,根据对称性可知它一定是等腰直角三角形.∵y =-x 2+2bx =22()x b b --+,∴顶点为(b ,b 2),由直角三角形斜边上的中线等于斜边的一半得到:2122b b =⨯,∴2b b =,解得:b =0(舍去)或b =±1, ∴y =-x 2+2x 或y =-x 2-2x .(4)①当抛物线为y =-x 2+2x 时.∵△AOB 为等腰直角三角形,且△BPQ ∽△OAB ,∴△BPQ 为等腰直角三角形,设P (a ,-a 2+2a ),∴Q ((a ,0),则|-a 2+2a |=|2-a |,即(2)2a a a -=-.∵a -2≠0,∴1a =,∴a =±1,∴P (1,1)或(-1, -3). ②当抛物线为y =-x 2-2x 时.∵△AOB 为等腰直角三角形,且△BPQ ∽△OAB ,∴△BPQ 为等腰直角三角形,设P (a ,-a 2-2a ),∴Q ((a ,0), 则|-a 2-2a |=|2+a |,即(2)2a a a +=+.∵a +2≠0,∴1a =,∴a =±1,∴P (1,-3,)或(-1,1). 综上所述:P (1,1)或P (-1,-3)或P (1,-3,)或(-1,1).点睛:本题是二次函数综合题.考查了二次函数的性质以及“抛物线三角形”的定义.解题的关键是弄懂“抛物线三角形”的定义以及分类讨论.7.如图,在平面直角坐标系xOy 中,A 、B 为x 轴上两点,C 、D 为y 轴上的两点,经 过点A 、C 、B 的抛物线的一部分C 1与经过点A 、D 、B 的抛物线的一部分C 2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C 的坐标为(0,),点M 是抛物线C 2:2y mx 2mx 3m =--(m <0)的顶点.(1)求A 、B 两点的坐标;(2)“蛋线”在第四象限上是否存在一点P ,使得△PBC 的面积最大?若存在,求出△PBC 面积的最大值;若不存在,请说明理由; (3)当△BDM 为直角三角形时,求m 的值. 【答案】(1)A (,0)、B (3,0).(2)存在.S △PBC 最大值为2716(3)2m 2=-或1m =-时,△BDM 为直角三角形. 【解析】 【分析】(1)在2y mx 2mx 3m =--中令y=0,即可得到A 、B 两点的坐标.(2)先用待定系数法得到抛物线C 1的解析式,由S △PBC = S △POC + S △BOP –S △BOC 得到△PBC 面积的表达式,根据二次函数最值原理求出最大值.(3)先表示出DM 2,BD 2,MB 2,再分两种情况:①∠BMD=90°时;②∠BDM=90°时,讨论即可求得m 的值. 【详解】解:(1)令y=0,则2mx 2mx 3m 0--=,∵m <0,∴2x 2x 30--=,解得:1x 1=-,2x 3=. ∴A (,0)、B (3,0).(2)存在.理由如下:∵设抛物线C 1的表达式为()()y a x 1x 3=+-(a 0≠),把C (0,32-)代入可得,12a =. ∴C1的表达式为:()()1y x 1x 32=+-,即213y x x 22=--.设P (p ,213p p 22--), ∴ S △PBC = S △POC + S △BOP –S △BOC =23327p 4216--+(). ∵3a 4=-<0,∴当3p 2=时,S △PBC 最大值为2716. (3)由C 2可知: B (3,0),D (0,3m -),M (1,4m -), ∴BD 2=29m 9+,BM 2=216m 4+,DM 2=2m 1+. ∵∠MBD<90°, ∴讨论∠BMD=90°和∠BDM=90°两种情况:当∠BMD=90°时,BM 2+ DM 2= BD 2,即216m 4++2m 1+=29m 9+, 解得:12m 2=-,22m 2=(舍去). 当∠BDM=90°时,BD 2+ DM 2= BM 2,即29m 9++2m 1+=216m 4+, 解得:1m 1=-,2m 1=(舍去) . 综上所述,2m =或1m =-时,△BDM 为直角三角形.8.在平面直角坐标系xOy 中(如图),已知抛物线y =x 2-2x ,其顶点为A . (1)写出这条抛物线的开口方向、顶点A 的坐标,并说明它的变化情况; (2)我们把一条抛物线上横坐标与纵坐标相等的点叫做这条抛物线的“不动点” ①试求抛物线y =x 2-2x 的“不动点”的坐标;②平移抛物线y =x 2-2x ,使所得新抛物线的顶点B 是该抛物线的“不动点”,其对称轴与x 轴交于点C ,且四边形OABC 是梯形,求新抛物线的表达式.【答案】(l)抛物线y =x 2-2x 的开口向上,顶点A 的坐标是(1,-1),抛物线的变化情况是:抛物线在对称轴左侧的部分是下降的,右侧的部分是上升的;(2)①(0,0)、(3,3); ②新抛物线的表达式是y =(x +1)2-1. 【解析】 【分析】 (1)10a =>,故该抛物线开口向上,顶点A 的坐标为()1,1-;(2)①设抛物线“不动点”坐标为(),t t ,则22t t t =-,即可求解;②新抛物线顶点B 为“不动点”,则设点(),B m m ,则新抛物线的对称轴为:x m =,与x 轴的交点(),0C m ,四边形OABC 是梯形,则直线x m =在y 轴左侧,而点()1,1A -,点(),B m m ,则1m =-,即可求解. 【详解】(l)10a =>,抛物线y =x 2-2x 的开口向上,顶点A 的坐标是(1,-1),抛物线的变化情况是:抛物线在对称轴左侧的部分是下降的,右侧的部分是上升的. (2)①设抛物线y =x 2-2x 的“不动点”坐标为(t ,t). 则t =t 2-2t ,解得t 1=0,t 2=3.所以,抛物线y =x 2-2x 的“不动点”的坐标是(0,0)、(3,3). ②∵新抛物线的顶点B 是其“不动点”,∴设点B 的坐标为(m ,m) ∴新抛物线的对称轴为直线x =m ,与x 轴的交点为C(m ,0) ∵四边形OABC 是梯形, ∴直线x =m 在y 轴左侧.∵BC与OA不平行∴OC∥AB.又∵点A的坐标为(1,一1),点B的坐标为(m,m),m=-1.∴新抛物线是由抛物线y=x2-2x向左平移2个单位得到的,∴新抛物线的表达式是y=(x+1)2-1.【点睛】本题为二次函数综合运用题,涉及到二次函数基本知识、梯形基本性质,此类新定义题目,通常按照题设顺序,逐次求解即可.9.如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.(1)求抛物线的函数关系式;(2)判断△ABM的形状,并说明理由;(3)把抛物线与直线y=x的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点.【答案】(1)抛物线解析式为y=x2﹣1;(2)△ABM为直角三角形.理由见解析;(3)当m≤时,平移后的抛物线总有不动点.【解析】试题分析:(1)分别写出A、B的坐标,利用待定系数法求出抛物线的解析式即可;根据OA=OM=1,AC=BC=3,分别得到∠MAC=45°,∠BAC=45°,得到∠BAM=90°,进而得到△ABM是直角三角形;(3)根据抛物线的平以后的顶点设其解析式为,∵抛物线的不动点是抛物线与直线的交点,∴,方程总有实数根,则≥0,得到m的取值范围即可试题解析:解:(1)∵点A是直线与轴的交点,∴A点为(-1,0)∵点B在直线上,且横坐标为2,∴B点为(2,3)∵过点A、B的抛物线的顶点M在轴上,故设其解析式为:∴,解得:∴抛物线的解析式为.(2)△ABM是直角三角形,且∠BAM=90°.理由如下:作BC⊥轴于点C,∵A(-1,0)、B(2,3)∴AC=BC=3,∴∠BAC=45°;点M是抛物线的顶点,∴M点为(0,-1)∴OA=OM=1,∵∠AOM=90°∴∠MAC=45°;∴∠BAM=∠BAC+∠MAC=90°∴△ABM是直角三角形.(3)将抛物线的顶点平移至点(,),则其解析式为.∵抛物线的不动点是抛物线与直线的交点,∴化简得:∴==当时,方程总有实数根,即平移后的抛物线总有不动点∴.考点:二次函数的综合应用(待定系数法;直角三角形的判定;一元二次方程根的判别式)10.如图,抛物线交轴于点,交轴于点,已知经过点的直线的表达式为.(1)求抛物线的函数表达式及其顶点的坐标;(2)如图①,点是线段上的一个动点,其中,作直线轴,交直线于,交抛物线于,作∥轴,交直线于点,四边形为矩形.设矩形的周长为,写出与的函数关系式,并求为何值时周长最大;(3)如图②,在抛物线的对称轴上是否存在点,使点构成的三角形是以为腰的等腰三角形.若存在,直接写出所有符合条件的点的坐标;若不存在,请说明理由.图① 图②【答案】(1)抛物线的表达式为y=-x2-2x+3,顶点C坐标为(-1,4);(2)L=-4m2-12m=-4(m+)2+9;当m=-时,最大值L=9;(3)点Q的坐标为(-1,),(-1,-),(-1,3+),(-1,3-).【解析】试题分析:(1)由直线经过A、B两点可求得这两点的坐标,然后代入二次函数解析式即可求出b、c的值,从而得到解析式,进而得到顶点的坐标;(2)由题意可表示出D、E的坐标,从而得到DE的长,由已知条件可得DE=EF,从而可表示出矩形DEFG的周长L,利用二次函数的性质可求得最大值;(3)分别以点A、点B为圆心,以AB长为半径画圆,圆与对称轴的交点即为所求的点.试题解析:(1)直线y=x+3与x轴相交于A(-3,0 ),与y轴相交于B(0,3)抛物线y=-x2+bx+c经过A(-3,0 ),B(0,3),所以,,∴,所以抛物线的表达式为y=-x2-2x+3,∵y=-x2-2x+3=-(x+1)2+4,所以,顶点坐标为C(-1,4).(2)因为D在直线y=x+3上,∴D(m,m+3).因为E在抛物线上,∴E(m,-m2-2m+3).DE=-m2-2m+3-(m+3)=-m2-3m.由题意可知,AO=BO,∴∠DAP=∠ADP=∠EDF=∠EFD=45°,∴DE=EF.L=4DE=-4m2-12m.L=-4m2-12m=-4(m+)2+9.∵a=-4<0,∴二次函数有最大值当m=-时,最大值L=9.(3)点Q的坐标为(-1,),(-1,-),(-1,3+),(-1,3-).考点:1、待定系数法;2、正方形的判定;3、二次函数的性质的应用;4、等腰三角形.。
