解直角三角形的应用导学案
《1.5 解直角三角形的应用》导学案(一)

九年级数学《1.5 解直角三角形的应用》导学案(一)执笔人贺新春参与人唐慧玉曲阿芳李业新高淑香李永义●学习目标:知识技能目标:会用解直角三角形的有关知识解某些简单的实际问题;过程方法目标:进一步了解数学建模思想,能将实际问题中的数量关系转化为直角三角形中元素之间的关系;情感态度目标:感受数学与生活的密切联系,丰富数学学习的成功体验。
●重点难点:重点:准确作辅助线并选择适当的关系解直角三角形;把实际问题转化为数学问题.难点:直角三角形的解法及其实际应用.●学习过程【自主学习】1.导入:自学课本P20做一做的内容,解决下面的几个问题:(1)我们在日常生活中能接触到许多这样类似的问题,它们都能够转化为___________________问题来解决。
(2)缆车垂直上升的距离是_____________.(3)可以通过计算得到的结果是____________________________________________________(根据平面图,利用解直角三角形的相关知识求出某些线段的长度,如BC,DE,BE的长度等)【合作交流】1.探究[例1]一个钟面,钟摆长度为2.5厘米,当钟摆转动时,摆角恰好为60°,且左右摆动的角度相同。
求它摆至最高位置时与其摆至最低位置时的高度之差2.探究:想一想利用解直角三角形的知识解决实际问题的一般过程是什么?【应用拓展】A类:1.长为4m的梯子搭在墙上与地面成45°角,作业时调整为60°角,则梯子的顶端沿墙面升高了 m2.一个人由山底爬到山顶,需先爬45°的山坡300 m,再爬30°的山坡100 m,求山高(精确到1m)B类:1.某楼梯侧面视图如图,其中AB=4m, ∠BAC=30°,∠C=90°,因某种活动,要求铺设红色地毯,则在AB段楼梯所铺地毯的长应。
2.如图,小明要测量河内小岛B到河边公路L的距离,在A点测得∠BAD=30°,在C点测得∠BCD=60°,又测得AC=50米,则小岛B到公路L的距离为()A、25米B、325米 C、225米 D、(32525 )米【课堂小结】1.本节课你掌握了哪些知识?2.还有哪些困惑?3.掌握了哪些数学思想?【达标检测】A类:完成课本P21 随堂练习第2题(部分数据有改动)B类: 1.完成课本P21 习题第1题2.如图所示,电工李师傅借助梯子安装天花板上距地面2.90m的顶灯。
人教版初三第一轮复习《解直角三角形的应用》导学案

解直角三角形的应用初三( )班 第 组 姓名 学习目标:能用解直角三角形的相关知识解决实际问题。
学习过程: 一、温故知新1、Rt △ABC 中,∠C=900, ∠A=450,AB=4, 则BC= 。
2、Rt △ABC 中,∠C=900, ∠B=300,BC=120, 则AC= 。
3、一个人从山下沿300角的山坡登上山顶,一共走了300m ,那么这座山的高度为。
4、如图,AC 是电线杆AB 的一根拉线,测得BC=6, ∠ACB=520,则拉线AC 长为() (A )06sin 45(B )06tan45(C )06cos52 (D )06cos 45二、新课学习1、仰角、俯角:如图,∠1、∠2都 是视线与水平线的夹角,∠1的视线 在水平线上方,叫 角,∠2的视线 在水平线下方,叫 角。
2、例:热气球的探测器显示,从热气球刊一栋高楼顶部的仰角为300,看这栋高楼底部的俯角为600,热气球与高楼的水平距离为150m ,这栋高楼有多高(结果保留小数点后1位)? 解:如图,α= ,β= ,AD= 在Rt △ABD 中,tan α= BD ∴BD=AD tan α= 在Rt △ACD 中,tan β=【归纳】利用解直角三角形的知识解决实际问题的一般过程(书本90页)三、题组训练:A 组1、如图,小明在地面上的A 点,小红在高 山上的B 点,小明与小红对望,则仰角是,俯角是 ;若小明看到高山上的小红的仰角是300,则小红看到小明的俯角是度。
2、如图,从C 测得树的顶端的仰角是300, (即∠ =300),若BC=20,则树高AB= 。
3、某飞机在离地面1200m 的上空测得 地面控制点A 的俯角为300(即∠ =300),此时飞机与该控制点之间的距 离AB 是 m 。
4、如图,在水平地面上,由点A 测得棋杆 BC 的顶点C 的仰角是600,点A 到棋杆的 距离AB=10m ,则棋杆BC 的长为 。
5、如图,为测量某塔AB 的高度,在离塔底部20米的E 处目测其顶A ,仰角为600,目高1.5米,试求该塔的高度(结果精确到0.1米)。
数学人教版九年级下册28.2.2解直角三角形的应用举例(1)导学案

28.2.2 解直角三角形的应用举例(1)【学习目标】1.了解仰角、俯角概念,提高计算能力,能应用解直角三角形解决观测中的实际问题.2.学会把实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题).3.经历用解直角三角形解决实际问题的过程,体会数学与生活的密切联系. 【重点难点】重点:应用解直角三角形的有关知识解决观测中的实际问题.难点:能够准确分析问题并将实际问题转化为数学模型.预习案(一)温故知新1.如图1,在直角三角形中,除直角外的五个元素之间有哪些关系?(1)锐角之间的关系:边之间的关系:角与边之间的关系(以∠A为例):(2)至少知道五个元素中的几个,就可以求其余元素?图12.请写出30°、45°、60°角的正弦值、余弦值和正切值:(二)问题导学1.如图2,当从低处观测高处的目标时,视线与水平线所成的锐角称为________.当从高处观测低处的目标时,视线与水平线所成的锐角称_________.图22.如图3,2016年10月19日,“神舟”十一号载人航天飞船与“天宫”二号目标飞行器成功实现交会对接. “神舟”十一号与“天宫”二号的组合体在离地球表面393km的圆形轨道上运行.如图,当组合体运行到地球表面上P点的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与P点的距离是多少?(地球半径约为6 400 km,π取3.142,结果取整数,参考数据:cos18.16°≈0.9502,cos19.59°≈0.9421,cos21.35°≈0.9314)?图3探究案探究:利用视角解直角三角形例: 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为100m ,这栋高楼有多高(结果取整数)?变式:直升飞机在高为63米的郑州二七纪念塔AB 斜上方P 点处,从塔的顶部和底部测得飞机的仰角为31°和42°,求飞机的高度PO (参考数据sin31°≈0.52,cos31°≈0.86,tan31°≈0.60, sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)训练案(C 级做1~4题,B 级、A 级全做)1.如图1所示,已知楼房AB 高为50m ,铁塔塔基距楼房地基间的水平距离BD •O B为100m,塔高CD为(50)3m,则下面结论中正确的是().A.由楼顶望塔顶仰角为60° B.由楼顶望塔基俯角为60°C.由楼顶望塔顶仰角为30° D.由楼顶望塔基俯角为30°图1 图2 图32.如图2所示,从地面上的C,D两点测得树顶的仰角分别是45°和30°,已知CD=200m,点C在BD上,则树高AB等于(根号保留).3.如图3所示,在离铁塔BE120m的A处,用测角仪测量塔顶的仰角为30°,•已知测角仪高AD=1.5m,则塔高BE=_________(根号保留).4.如图4所示,要在宽为28m的海堤公路的路边安装路灯.路灯的灯臂长为3m,且与灯柱成120°,路灯采用圆锥形灯罩,灯罩的轴线与灯臂垂直.当灯罩的轴线通过公路路面的中线时,照明效果最理想.问:应设计多高的灯柱,才能取得最理想的照明效果?5.如图5所示,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面成60°角,在离电线杆6米的B处安置测角仪,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果保留根号).图4tan310.6,sin310.52,cos310.86︒≈︒≈︒≈图56.如图6所示,某校九年级3班的一个学习小组进行测量小山高度的实践活动.部分同学在山脚点A 测得山腰上一点D 的仰角为30°,并测得AD 的长度为180米;另一部分同学在山顶点B 测得山脚点A 的俯角为45°,山腰点D 的俯角为60°.请你帮助他们计算出小山的高度BC (计算过程和结果都不取近似值).图67.(2012河南中考)某宾馆为庆祝开业,在楼前悬挂了许多宣传条幅,如图所示,一条幅从楼顶A 处放下,在楼前点C 处拉直固定,小明为了测量此条幅的长度,他先在楼前D 处测得楼顶A 点的仰角为31°,再沿DB 方向前进16米到达E 处,测得点A 的仰角为45°,已知点C 到大厦的距离BC =7米,,请根据以上数据求条幅的长度(结果保留整数.参考数据 ).图7。
《解直角三角形》导学案4

24.4解直角三角形(1)【学习目标】使学生理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的能力.渗透数形结合的数学思想,培养学生良好的学习习惯.【学习重点】直角三角形的解法.【学习难点】三角函数在解直角三角形中的灵活运用【课标要求】能利用三角函数的知识解决实际问题【知识回顾】1.在三角形中共有几个元素?2.直角三角形ABC中,∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?(1)边角之间关系(2)三边之间关系(3)锐角之间关系【自主学习】1、如图所示,一棵大树在一次强烈的地震中于离地面10米处折断倒下,树顶落在离树根24米处.大树在折断之前高多少?【例题学习】2、一个公共房屋门前的台阶共高出地面1.2米.台阶被拆除后,换成供轮椅行走的斜坡.根据这个城市的规定,轮椅行走斜坡的倾斜角不得超过9°.从斜坡的起点至楼门的最短的水平距离该是多少?(sin9°≈0.16,cos9°≈0.99,tan9°≈0.16,精确到0.1米)【巩固训练】3、如图,从点C测得树的顶角为33º,BC=20米,则树高AB多少米?(参考数据:sin33°≈0.54,cos33°≈0.84,tan33°≈0.65,结果精确到0.1米)4、小明放一个线长为125米的风筝,他的风筝线与水平地面构成39°角.他的风筝有多高?(sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,精确到1米)【归纳小结】【作业】、在△2 A BC 中,∠C=90°,sinA= ,则 cosA 的值是( ) A . B . C . 3 D . 4 3△1、在 ABC 中,∠C=90°,AC=6,BC=8,那么 sinA=________.3 53 4 9 16 D . 5 5 25 25 3、如图是某商场一楼与二楼之间的手扶电梯示意图.其中 AB .CD 分别表示一楼.二 楼地面的水平线,∠ ABC =150°,BC 的长是 8 m ,则乘电梯从点 B 到点 C 上升的高度 h 是( )CD150° h AA .8 3 B 3 m B .4 m C . 4 3 m D .8 m 4、某人想沿着梯子爬上高 4 米的房顶,梯子的倾斜角(梯子与地面的夹角)不能大于 60°, 否则就有危险,那么梯子的长至少为( )A .8 米B . 8 3 米C . 8 3 米 3 米5、在平静的湖面上,有一枝红莲,高出水面1 米,阵风吹来,红莲被风吹到一 边,花朵齐及水面,已知红莲移动的水平距离为 2 米,问这里水深多少?6、如图,在一棵树的 10 米高 B 处有两只猴子,一只猴子爬下树走到离树 20 米处的池塘 A 处.另一只爬到树顶 D 后直接跃到 A 处,距离以直线计算,如 果两只猴子所经过的距离相等,求这棵树的高度.7、若河岸的两边平行,河宽为900米,一只船由河岸的A处沿直线方向开往对岸的B处,AB与河岸的夹角是600,船的速度为5米/秒,求船从A到B处约需时间几分。
(人教版)九年级数学下册精品导学案:28.2.3 解直角三角形的应用(2)导学案

人教版九年级下册第28章《锐角三角函数》导学案[28.2.3 解直角三角形的应用(2)]1.能运用解直角三角形知识解决仰角和俯角有关的实际问题. (重点)2.在解题过程中进一步体会数形结合、转化、方程的数学思想,并从这些问题中归纳出常见的基本模型及解题思路. (难点)情境引入某探险者某天到达如图所示的点A 处时,他准备估算出离他的目的地,海拔为3 500 m的山峰顶点B处的水平距离.他能想出一个可行的办法吗?通过这节课的学习,相信你也行.知识精讲解与仰俯角有关的问题如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角.典例解析【例1】热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).【针对练习】建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).【例2】如图,小明想测量塔AB的高度.他在D处仰望塔顶,测得仰角为30°,再往塔的方向前进50m至C处.测得仰角为60°,小明的身高1.5 m.那么该塔有多高?(结果精确到1 m),你能帮小明算出该塔有多高吗?【针对练习】如图,直升飞机在长400米的跨江大桥AB的上方P点处,在大桥的两端测得飞机的仰角分别为37°和45 °,求飞机的高度 .(结果取整数. 参考数据:sin37°≈0.8,cos37 °≈0.6,tan 37°≈0.75)达标检测1. 如图①,在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=_________米.2. 如图②,两建筑物AB和CD的水平距离为30米,从A点测得 D点的俯角为30°,测得C 点的俯角为60°,则建筑物CD的高为_____米.3. 为测量松树AB的高度,一个人站在距松树15米的E 处,测得仰角∠ACD=52°,已知人的高度是1.72米,则树高 (精确到0.1米).4. 如图,在电线杆上离地面高度5m的C点处引两根拉线固定电线杆,一根拉线AC和地面成60°角,另一根拉线BC和地面成45°角.则两根拉线的总长度为m(结果用带根号的数的形式表示).5. 目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°.(tan39°≈0.81)(1) 求大楼与电视塔之间的距离AC;(2) 求大楼的高度CD(精确到1米).6. 如图,直升飞机在高为200米的大楼AB上方P点处,从大楼的顶部和底部测得飞机的仰角为30°和45°,求飞机的高度PO .。
《解直角三角形的应用》 导学案

《解直角三角形的应用》导学案一、学习目标1、能够运用解直角三角形的知识解决与测量、航海、工程等实际问题相关的数学问题。
2、通过将实际问题转化为数学问题,提高分析问题和解决问题的能力。
3、体会数学知识在实际生活中的广泛应用,增强应用意识和数学建模能力。
二、学习重难点1、重点(1)掌握解直角三角形在实际问题中的应用方法。
(2)能够准确地将实际问题中的数量关系转化为直角三角形中的元素关系。
2、难点(1)如何从实际问题中构建出合适的直角三角形模型。
(2)理解并灵活运用三角函数值来求解实际问题。
三、知识回顾1、直角三角形的边角关系在直角三角形中,若\(∠C =90°\),\(∠A\)、\(∠B\)、\(∠C\)的对边分别为\(a\)、\(b\)、\(c\),则有:(1)三边关系:\(a^2 + b^2 = c^2\)(勾股定理)(2)锐角关系:\(∠A +∠B = 90°\)(3)边角关系:\(\sin A =\frac{a}{c}\),\(\cos A =\frac{b}{c}\),\(\tan A =\frac{a}{b}\)\(\sin B =\frac{b}{c}\),\(\cos B =\frac{a}{c}\),\(\tan B =\frac{b}{a}\)2、解直角三角形由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形。
四、实际应用类型(一)测量物体的高度例 1:如图所示,为测量某建筑物的高度\(AB\),在离该建筑物底部\(B\)点\(30\)米的\(C\)处,测得建筑物顶端\(A\)的仰角为\(α\),且\(\tanα = 15\),求建筑物的高度。
分析:在\(Rt\triangle ABC\)中,已知\(BC = 30\)米,\(\tanα =\frac{AB}{BC} = 15\),则可求出\(AB\)的长度。
解:在\(Rt\triangle ABC\)中,\(\tanα =\frac{AB}{BC}\)因为\(\tanα = 15\),\(BC = 30\)米所以\(AB = BC \times \tanα = 30×15 = 45\)(米)答:建筑物的高度为\(45\)米。
解直角三角形导学案

- - 1 - -§28.2解直角三角形应用导学案一、知识要点解直角三角形的应用题是建立在解直角三角形的基础之上,分为两个大的类型:一是在一个Rt △中;二是在两个Rt △中。
本节只讲在两个Rt △中。
二、概念:1、仰角和俯角:视线与水平线的夹角,如图所示。
2、方位角:目标方向与南北方向所夹的小于90°的角,如图所示点A 位于北偏东45°方向,点B 位于南偏西30°方向。
三、模板固化如图1在R t △ABC 中有:AC=BCctan α 在R t △DBC 中有:CD= BCctan βtan tan AD xc xc αβ=- (此处用减法)即:tan tan y xc xc αβ=- 也可写成:tan tan yx c c αβ=-如图2:在R t △ABC 中有:AC=BCctan α 在R t △DBC 中有:CD= BCctan βtan tan AD hc hc αβ=+ (此处用加法)今后我们将图1称做模式1,将图2称做模式2。
解直角三角形应用题多数情况下都能化归到以上两种情形,注意在解题中要有方程意识,如模式1中那样。
解题步骤一般分三步:1、将题中所给数据在图中标示出来;2、寻找或者构造直角三角形,构造就是通过作辅助线构成直角三角形,此处常用的辅助线就是作高;3、套用模式1、模式2解答。
下面通过两个例子说明两种模式在中考中的运用。
四、典例引导例1如图某高速公路建设中需要确定隧道AB 的长度.已知在离地面1500m 高度水平线- 2 -C 处的飞机上,测量人员测得正前方A 、BAB 的长. 1.73) 分析:做此类题第一步是将已知数据标在图中,此图中各个已知数据已标明。
由于CD ∥OB,所以有∠OBC=45°,∠OAC=60°第二步寻找或构造(作高)Rt △,此题已有Rt △CBO 和Rt△CAO第三步与模式比对,显然属于模式1。
冀教版九年级数学上册26.4解直角三角形的应用导学案
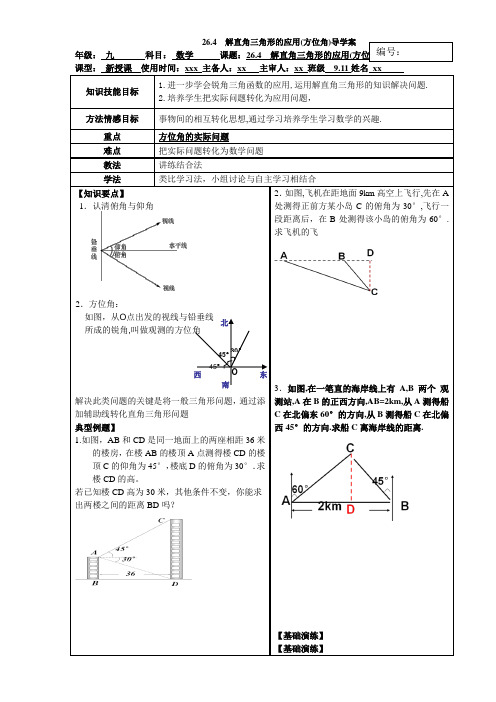
26.4解直角三角形的应用(方位角)导学案年级:九科目:数学课题:26.4 解直角三角形的应用(方位角)课型:新授课使用时间:xxx 主备人:xx 主审人:xx 班级9.11姓名xx 知识技能目标1.进一步学会锐角三角函数的应用,运用解直角三角形的知识解决问题.2.培养学生把实际问题转化为应用问题,方法情感目标事物间的相互转化思想,通过学习培养学生学习数学的兴趣.重点方位角的实际问题难点把实际问题转化为数学问题教法讲练结合法学法类比学习法,小组讨论与自主学习相结合【知识要点】1.认清俯角与仰角解决此类问题的关键是将一般三角形问题,通过添加辅助线转化直角三角形问题典型例题】1.如图,AB和CD是同一地面上的两座相距36米的楼房,在楼AB的楼顶A点测得楼CD的楼顶C的仰角为45°,楼底D的俯角为30°.求楼CD的高。
若已知楼CD高为30米,其他条件不变,你能求出两楼之间的距离BD吗?2.如图,飞机在距地面9km高空上飞行,先在A处测得正前方某小岛C的俯角为30°,飞行一段距离后,在B处测得该小岛的俯角为60°.求飞机的飞3.如图,在一笔直的海岸线上有A,B两个观测站,A在B的正西方向,AB=2km,从A测得船C在北偏东60°的方向,从B测得船C在北偏西45°的方向.求船C离海岸线的距离.【基础演练】【基础演练】编号:2.方位角:如图,从O点出发的视线与铅垂线所成的锐角,叫做观测的方位角30°45°45°北东西O南4.气象局发出预报:如图, 沙尘暴在A市的正东方向400km的B处以40km/h的速度向北偏西600的方向转移,距沙尘暴中心300km的范围内将受到影响,A市是否受到这次沙尘暴的影响?如果受到影响,将持续多长时间?5.如图, 海上有一灯塔P, 在它周围3海里处有暗礁. 一艘客轮以9海里/时的速度由西向东航行, 行至A点处测得P在它的北偏东60度的方向, 继续行驶20分钟后, 到达B处又测得灯塔P在它的北偏东45度方向. 问客轮不改变方向继续前进有无触礁的危险?5.海上有一小岛A,它周围8.7海里内有暗礁,某海船跟踪鱼群由西向东航行,在B点测得小岛在北偏东60°,航行10海里后到达C点,这时测得小岛A在北偏东30°,如果渔船不改变航向,继续1.如图,一座塔的高度TC=120m,甲、乙两人分别站在塔的西、东两侧的点A、B处,测得塔顶的仰角分别为28º、15º。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
桃溪中学师生共用导学案内容:解直角三角形(1) 执笔:【学习目标】⑴: 使学生理解直角三角形中五个元素的关系,会使用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形⑵: 通过综合使用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的水平.⑶: 渗透数形结合的数学思想,培养学生良好的学习习惯. 【学习重点】直角三角形的解法. 【学习难点】三角函数在解直角三角形中的灵活使用 【导学过程】 一、自学提纲: 知识回顾:在Rt △ABC 中,∠C =900,a ,b ,c ,分别为∠A,∠B,∠C 所对的边,则边之间的关系为 ,角之间的关系为 , 角与边之间的关系为 , 自主预习:1.在三角形中共有几个元素? 2、解直角三角的概念:有直角三角形中 求出 元素的过程,叫做解直角三角形。
3、解直角三角形的两种情况。
(1)已知 ,求第三边及两锐角。
(2)已知 和一个 ,求其它两边及另一锐角。
导学探究:1、在Rr △ABC 中,共有六个量,三条边a ,b ,c ,三个角∠A ,∠B ,∠C ,其中∠C 是已知的,其它的五个量都是未知的。
(1) 已知∠A ,∠B ,能求出其它的三个量a ,b ,c 吗? (2) 已知两条边的长,能求出其它的三个量吗? (3) 已知一角和一边,能求出其它的三个量吗? 你有什么发现?2、直角三角形ABC 中,∠C=90°,a 、b 、c 、∠A 、∠B 这五个元素间有哪些等量关系呢? (1)边角之间关系如果用α∠表示直角三角形的一个锐角,那上述式子就能够写成.(2)三边之间关系 (3)锐角之间关系∠A+∠B=90°. a 2 +b 2 =c 2 (勾股定理) 以上三点正是解直角三角形的依据.二、合作交流:要想使人安全地攀上斜靠在墙面上的梯子的顶端.梯子与地面所成的角一般要满足, (如图).现有一个长6m 的梯子,问:(1)使用这个梯子最高能够安全攀上多高的墙(精确到0. 1 m)(2)当梯子底端距离墙面2.4 m 时,梯子与地面所成的角等于多少(精确到1o ) 这时人是否能够安全使用这个梯子b aA c b A c a A = = = ;tan ; cos ; sin abB c a B c b B = = = ;tan ; cos ; sin ; 的邻边的对边; 斜边 的邻边 ; 斜边 的对边α α α α α α α∠ ∠ = ∠ = ∠ =tan cos sin三、教师点拨:例1在△ABC 中,∠C 为直角,∠A 、∠B 、∠C 所对的边分别为a 、b 、c ,且,解这个三角形.例2在Rt △ABC 中, ∠B =35o ,b=20,解这个三角形.四、学生展示: 完成课本87页练习 补充题1、 在△ABC 中,∠C 为直角,AC=6,BAC 的平分线AD=43,解此直角三角形。
2、Rt △ABC 中,若sinA=45,AB=10,那么BC=_____,tanB=______. 3、在△ABC 中,∠C=90°,AC=6,BC=8,那么sinA=________.4、在△ABC 中,∠C=90°,sinA=35,则cosA 的值是( ) A .35 B .45 C .916.2525D五 当堂达标;1已知Rt △ABC 中,∠C =900,∠A =300,斜边上的高为1,则△ABC 三边的长分别为( )A a =22 ,b =2, c =4,B a =3, b =2, c =7C a =332,b =2,c =334, D a =2,b =332,c =334 2已知在Rt △ABC 中,∠C =900,a ,b ,c ,分别为∠A,∠B,∠C 所对的边,由下列条件解直角三角形。
(1)已知a =65,b =65,求c , (2)已知a =20,c =202,求∠B ; (3)已知c =30,∠A=600,求a ;六 课后提升1.ΔABC 中,∠A ,∠B 都是锐角,且sinA =21,tanB =3,AB =10,求ΔABC 的面积。
2、Rt ΔABC 中,∠C =90°,D 是BC 中点,DE ⊥AB 于E ,tanB =21,AE =7,求DE 。
3、 如图,已知Rt ⊿ABC 中,斜边BC 上的高AD=4,cosB=54,则AC=4 如图,⊿ABC中,∠C=900,∠B=300,AD是⊿ABC的角平分线,若AC=3,求线段AD的长。
B5、某型号飞机的翼形状如图所示,根据图中数据计算AC、BD和CD的长度(精确到0.1米).七、课堂小结:八、自我反思:本节课我的收获于港初中师生共用导·学案A B年级:九学科:数学课型:新授课内容:解直角三角形(2)【学习目标】⑴:使学生了解仰角、俯角的概念,使学生根据直角三角形的知识解决实际问题.⑵:逐步培养学生分析问题、解决问题的水平.⑶:渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识【学习重点】将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决.【学习难点】实际问题转化成数学模型【导学过程】一、自学提纲:1.解直角三角形指什么?2.解直角三角形主要依据什么?(1)勾股定理:(2)锐角之间的关系:(3)边角之间的关系:二、合作交流:仰角、俯角当我们实行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角.三、教师点拨:例3 2003年10月15日“神舟”5号载人航天飞船发射成功.当飞船完成变轨后,就在离地球表面350km的圆形轨道上运行.如图,当飞船运行到地球表面上P点的正上方时,从飞船上最远能直接看到的地球上的点在什么位置?这样的最远点与P点的距离是多少?(地球半径约为6 400 km,结果精确到0. 1 km)例4热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30o,看这栋离楼底部的俯角为60o,热气球与高楼的水平距离为120 m.这栋高楼有多高(结果精确到0.1m)?四、学生展示:一、课本89页 练习 第1 、2题二、 1.热气球的探测器显示,从热气球看一栋高楼顶部的仰角为,看这栋楼底部的俯角为600,热气球与高楼的水平距离为120m ,这栋高楼有多高(结果精确到0.1`m )2.如图6-17,某海岛上的观察所A 发现海上某船只B 并测得其俯角α=60°.已知观察所A 的标高(当水位为0m 时的高度)为43m ,当时水位为+2m ,求观察所A 到船只B 的水平距离BC(精确到1m)3、如图,河旁有一座小山,从山顶A 处测得河对岸点C 的俯角为30º,测得岸边点D 的俯角为45º,又知河宽CD 为50米,现需从山顶A 到河对岸点C 拉一条笔直的缆绳AC 求缆绳AC 的长(答案可带根号).五、课堂小结:六、作业设置: 《课时作业本》 七、自我反思:本节课我的收获: 。
于港初中师生共用导·学案年级:九 学科:数学 课型:新授课 内容:解直角三角形(3)【学习目标】⑴: 使学生了解方位角的命名特点,能准确把握所指的方位角是指哪一个角 ⑵: 逐步培养学生分析问题、解决问题的水平;渗透数形结合的数学思想和方法. ⑶: 巩固用三角函数相关知识解决问题,学会解决方位角问题. 【学习重点】山用三角函数相关知识解决方位角问题【学习难点】学会准确分析问题并将实际问题转化成数学模型【导学过程】一、自学提纲:处理八个方向外还有南偏东x°、南偏西x°、北偏东x°、北偏西x°这个关系在实际问题中经常用到。
二、教师点拨:例5如图,一艘海轮位于灯塔P的北偏东60方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30方向上的B处.这时,海轮所在的B处距离灯塔P有多远?例6、《中华人民共和国道路交通管理条例》规定:“小汽车在城市街道上的行驶速度不得超过70km/h”,一辆小汽车在一条城市街道上由西向东行驶,在距路边25m处有“车速检测仪O”,测得该车从北偏西60°的A点行驶到北偏西30•°的B点,所用时间为1.5s.(1)试求该车从A点到B点的平均速度;(2)试说明该车是否超过限速.四、学生展示:完成课本91页练习1补充练习1、一艘船由港口A出发向东偏北20°方向航行,这艘船航行的速度是每小时66海里,1小时后到达B处,发现一灯塔在西偏北70°,该船就朝灯塔开去,到达灯塔后,发现港口在灯塔的西偏南50°,问灯塔与港口的距离是多少?(精确到0.1海里,已知数据=1.73)2、海中有一小岛,它的周围8海里内有暗礁,轮船由西向东航行,在B点测得小岛在北偏东60°方向上,航行10海里后到达C点,此时测得小岛在北偏东45°方向上,如果不改变航向,继续向东航行,有无触礁的危险?3、如图,某海防哨所(o)发现在它的北偏西30°距离500cm的A该船向正东方向航行,经过3分钟到达哨所东北方向的B每时多km?(3取1.7)五、课堂小结:六、作业设置:《课时作业本》七、自我反思:本节课我的收获:。
于港初中师生共用导·学案年级:九学科:数学课型:新授课内容:解直角三角形(3)【学习目标】⑴:使学生了解坡度与坡角⑵:逐步培养学生分析问题、解决问题的水平;渗透数形结合的数学思想和方法.⑶:巩固用三角函数相关知识解决问题,学会解决方位角问题.【学习重点】用三角函数相关知识解决方位角问题【学习难点】学会准确分析问题并将实际问题转化成数学模型【导学过程】一、自学提纲:坡度与坡角坡面的铅直高度h和水平宽度l的比叫做坡度(或叫做坡比),一般用i表示。
即i=,常写成i=1:m的形式如i=1:2.5 把坡面与水平面的夹角α叫做坡角.结合图形思考,坡度i与坡角α之间具有什么关系?这个关系在实际问题中经常用到。
二、教师点拨:例7同学们,如果你是修建三峡大坝的工程师,现在有这样一个问题请你解决:如图6-33水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求斜坡AB的坡面角α,坝底宽AD和斜坡AB的长(精确到0.1m)例8如图,MN表示某引水工程的一段设计路线,从M到N的走向为南偏东30°. 在M的南偏东60°方向上有一点A,以A为圆心、500m为半径的圆形区域为居民区.取MN上另一点B,测得BA的方向为南偏东75°.已知MB = 400m,通过计算回答,如果不改变方向,输水路线是否会穿过居民区?四、学生展示:完成课本91页练习2补充练习(1)一段坡面的坡角为60°,则坡度i=______;______,坡角 ______度.2、利用土埂修筑一条渠道,在埂中间挖去深为0.6米的一块(图阴影部分是挖去部分),已知渠道内坡度为1∶1.5,渠道底面宽BC为0.5米,求:①横断面(等腰梯形)ABCD的面积;②修一条长为100米的渠道要挖去的土方数.ABNM东北3、如图,水库大坝的截面是梯形ABCD.坝顶AD=6m,坡长CD=8m.坡底BC=30m,∠ADC=135°.(1)求∠ABC的大小:(2)如果坝长100 m.那么建筑这个大坝共需多少土石料?(结果精确到0.01 m3)五、课堂小结:六、作业设置:《课时作业本》七、自我反思:本节课我的收获:。
