解直角三角形的应用导学案
初中数学九年级下册《解直角三角形的简单应用》导学案

28.2.2 应用举例第1课时 解直角三角形的简单应用【学习目标】1.使学生根据直角三角形的知识解决实际问题.2. 逐步培养学生分析问题、解决问题的能力.3.渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识【学习重点】将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决.【学习难点】实际问题转化成数学模型【导学过程】一、课前热身:1.解直角三角形的类型:已知____________;已知___________________.2.如图解直角三角形的公式:(1)三边关系:__________________.(2)角关系:∠A+∠B=_____,(3)边角关系:sinA=___,sinB=____,cosA=_______.cosB=____,tanA=_____ ,tanB=_____.3.已知,如图,在△ABC 中,∠B = 45°,∠C = 60°,AB = 6.求BC 的长. (结果保留根号).c b a A CB二、合作交流:要想使人安全地攀上斜靠在墙面上的梯子的顶端.梯子与地面所成的角一般要满足,(如图).现有一个长6m的梯子,问:(1)使用这个梯子最高可以安全攀上多高的墙(精确到0. 1 m)(2)当梯子底端距离墙面2.4 m时,梯子与地面所成的角等于多少(精确到1o) 这时人是否能够安全使用这个梯子?(可用计算器)数学选择题解题技巧1、排除法。
是根据题设和有关知识,排除明显不正确选项,那么剩下唯一的选项,自然就是正确的选项,如果不能立即得到正确的选项,至少可以缩小选择范围,提高解题的准确率。
排除法是解选择题的间接方法,也是选择题的常用方法。
2、特殊值法。
即根据题目中的条件,选取某个符合条件的特殊值或作出特殊图形进行计算、推理的方法。
用特殊值法解题要注意所选取的值要符合条件,且易于计算。
此类问题通常具有一个共性:题干中给出一些一般性的条件,而要求得出某些特定的结论或数值。
解直角三角形导学案

《解直角三角形》学案一、学习目标1、了解解直角三角形的定义,能通过已知条件解直角三角形。
2、通过本节课的学习,培养自己知识的运用能力和计算能力。
二、重点难点学习重点:对解直角三角形的理解。
学习难点:对解直角三角形的应用。
三、前置学习1、计算:︒︒+︒+︒-︒46tan 44tan 45tan 60cos 230sin 22、在ABC ∆中,若0)cos 23(|1sin |2=-+-B A ,则∠C=_______度 3、如图,在ABC Rt ∆中,∠C 为直角,其余5个元素之间有以下关系:(1)三边之间关系:222c b a =+ (勾股定理)(2)锐角之间的关系:∠A+∠B=90°(直角三角形的两个锐角互余) (3)边角之间的关系:c a A =sin 、c b A =cos 、baA =tan 。
利用以上关系,如果知道其中的2个元素(其中至少有一个是边),那么就可以求出其余的3个未知元素。
由直角三角形中的已知元素,求出所有未知元素的过程,叫做解直角三角形。
例1、在ABC Rt ∆中,∠C=90°,∠A=30°,5=a ,解这个直角三角形。
例2、在ABC Rt ∆中,∠C=90°,3=a ,3=b ,求:(1)c 的大小;(2)∠A 、∠B 的大小。
四、展示交流在ABC Rt ∆中,CD 是斜边上的高,若AC=8,cosB=0.6,求ABC ∆的面积。
五、达标拓展在ABC Rt ∆中,∠C=90°,根据下列条件解直角三角形:(1)32=b ,4=c ; (2)8=c ,∠A=60°;(3)7=b ,∠A=45°; (4)24=a ,38=b 。
六、学习评价在ABC Rt ∆中,∠C=90°,∠A=60°,13+=+b a ,解这个直角三角形。
七、合作探究如图是小朋友玩的“滚铁环”游戏的示意图,⊙O 向前滚动时,铁棒DE 保持与OE 垂直。
解直角三角形及应用导学案

新人教九年级数学(下)导学案主备人:叶小凤审核人:唐海霞杨栓祥解直角三角形及其应用(1)学案班级姓名得分【学习目标】理解直角三角形中五个元素的关系,会运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形【学习重点】灵活运用知识点,准确解直角三角形【学习难点】三角函数在解直角三角形中的灵活运用一、自学课本,完成下列知识点1.Rt△ABC中,∠C=90°,∠A=30°,BC=8,则可求出AB= ,AC= 。
∠B= 。
2 结合上面题目的解决,归纳:(1)在三角形中共有几个元素(边、角):(2)Rt△ABC中,∠C=90°,a、b、c、∠A、∠B这五个元素间有哪些等量关系呢?①三边之间关系:②两锐角之间关系:③边角之间关系:3.解直角三角形概念:二、合作探究例1:在△ABC中,∠C为直角,∠A、∠B、∠C所对的边分别为a、b、c,且b=,例2:在Rt△ABC中,∠C=90°,∠B =45o,b=20,解这个直角三角形.三、课堂检测1.根据直角三角形的__________元素(至少有一个边),求出________•其它所有元素的过程,即解直角三角形.352、Rt △ABC 中,若sinA=54,AB=10,那么BC=_____,tanB=______.3、在△ABC 中,∠C=90°,AC=6,BC=8,那么sinA=________.4、在△ABC 中,∠C=90°,sinA=则cosA 的值是5、在Rt △ABC 中,∠C=90°,a=3,b=3,解这个三角形.6、 在△ABC 中,∠C 为直角,AC=6,BAC ∠的平分线AD=43,解此直角三角形。
四、达标检测2.在Rt △ABC 中,∠C =90°.(1)已知:a =35,235=c ,求∠A 、∠B ,b ;(2)已知:32sin =A ,6=c ,求a 、b ;(3)已知:,9,23tan ==b B 求a 、c ;(4)已知:∠A =60°,△ABC 的面积,312=S 求a 、b 、c 及∠B .新人教九年级数学(下)导学案 主备人:叶小凤 审核人:唐海霞 杨栓祥解直角三角形及其应用(2)学案班级 姓名 得分学习目标:能将解斜三角形的问题转化为解直角三角形. 学习重难点:灵活构造直角三角形解决问题 导学过程:一、自主学习1.直角三角形的边角关系是 2.已知:如图,△ABC 中,∠A =30°,∠B =60°,AC =10cm .求AB 及BC 的长.3.已知:如图,Rt △ABC 中,∠D =90°,∠B =45°,∠ACD =60°.BC =10cm .求AD 的长.4.已知:如图,△ABC 中,∠A =30°,∠B =135°,AC =10cm .求AB 及BC 的长.5.已知:如图,△ABC 中,∠A =60°,∠B =45°,AB =8cm .求△ABC 的面积A CB二、课堂练习1.已知:如图,Rt △ABC 中,∠A =30°,∠C =90°,∠BDC =60°,BC =6cm . 求AD 的长.2.已知:如图,△ABC 中,∠A =45°,∠B =120°,AB =10cm .求AC 及BC 的长.三、达标检测1.△ABC 中,∠A =120°,∠B =30°,AC =2cm .求AB 及BC 的长.2.已知:如图,△ABC 中,∠C =60°,∠B =45°,AB =6cm .求BCCA BB AC新人教九年级数学(下)导学案 主备人:叶小凤 审核人:唐海霞 杨栓祥解直角三角形及其应用(3)学案 仰角、俯角班级 姓名 得分学习目标:1.认识仰角、俯角,并能结合实际标准角度。
解直角三角形及其应用导学案
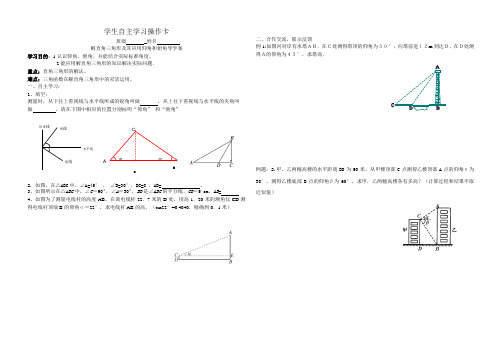
学生自主学习操作卡班级 _姓名解直角三角形及其应用仰角和俯角导学案学习目的:1.认识仰角、俯角,并能结合实际标准角度。
2.能应用解直角三角形的知识解决实际问题.重点:直角三角形的解法。
难点:三角函数在解直角三角形中的灵活运用。
一、自主学习: 1、填空:测量时,从下往上看视线与水平线所成的锐角叫做 ,从上往下看视线与水平线的夹角叫做 。
请在下图中相应的位置分别标明“仰角” 和“俯角”2. 如图,在△ABC 中,∠A=45° , ∠B=30°,BC=8 ,AB= 。
3、如图所示在△ABC 中,∠C =90°,∠A =30°,BD 是∠ABC 的平分线,CD =5 cm ,AB = 4、如图为了测量电线杆的高度AB ,在离电线杆22.7米的D 处,用高1.20米的测角仪CD测得电线杆顶端B 的仰角α=22°,求电线杆AB 的高.(tan22°=0.4040,精确到0.1米)二、合作交流,展示反馈例1:如图河对岸有水塔AB.在C处测得塔顶的仰角为30°,向塔前进12m 到达D,在D处测得A的仰角为45°,求塔高.例题:2.甲、乙两幢高楼的水平距离BD 为90米,从甲楼顶部C 点测得乙楼顶部A 点的仰角α为30°,测得乙楼底部B 点的仰角β为60°,求甲,乙两幢高楼各有多高?(计算过程和结果不取近似值)A三、分层训练:1. 如图,某飞机于空中A 处探测到目标C ,此时飞行高度AC =1200米,从飞机上看地面控制点B 的俯角α=30°,求飞机A 到控制点B 的距离.(精确到1米)2. 两座建筑AB 与CD ,其地面距离AC 为50米,从AB 的顶点B 测得CD 的顶部D 的仰角β=30°,测得其底部C 的俯角α=60°,求两座建筑物AB 与CD 的高.(精确到0.1米) 3、如图,小明想测量塔CD 的高度。
《解直角三角形在生活中的应用》导学案1

24.4《解直角三角形在生活中的应用》 新授课 知识目标
课时安排 1 执笔人 朱文泽 上课时间 2014 年 11 月
学习目标
能力目标
熟练掌握解直角三角形的基本条件和方法, 能运用解直角三角形的方法或构 造直角三角形的方法来解决生活实践中的实际问题。 通过情境问题的训练,体会建模思想、转化思想和数形结合的思想方法,提 高学生分析问题的能力。使学生从中体会到学数学的价值和用数学的乐趣。
0 0
拓展延伸
小组交流,展示相异构想: 你能用不同的方 复习题:A 层:A 组题;
B 层:B 组 第 11、12、13、14 题
教学后记
情感态度价 学生在数学问题抽象为数学模型过程中体会学数学的价值和用数学的乐趣。 值观 学习方法 小组合作学习 学习内容 学 习 活 动 二 备
【情境导学】 放风筝的时候,同学们总喜欢比一比,看看谁的风筝飞的高? 现有身高相近的甲、 乙、 丙三位同学放风筝, 各人放出的线长分别为 60m、 50m、 40m,线与地平面所成的角分别为 30°、45°、60°(假设风筝线是拉直的)。请你 们当回裁判:三人所放的风筝谁的飞得最高?为什么?
【回顾链接】 1、抢答:根据图中所给的条件,分别求出图中的 x :
500
13
x
13 500 x
x
500
8
6
x
3
2、思考:利用解直角三角形的知识解决实际问题的一般过程是什么?
【合作探索】
3、当前,我国新农村正如火如荼地进行,某村计划在建设区 B 的北偏东 30°方向 修一条新路,小明所在的教室 A 在该建设区 B 的正北方向 240m 处。如果拖拉机行 驶 时,150m 的范围内为受其噪音影响区域,问拖拉机经过该路时,教室 A 是否受 到噪音影响?为什么?
《解直角三角形的应用》导学案第三课时.doc

《解直角三角形的应用》导学案第三课时学习目标:1.知道坡角、破比(坡度)的意义.2.能将有关实际问题转化为解直角三角形的问题.3.培养严谨致学的学习态度.重点:把实际问题转化为解直角三角形的问题.难点:将实际问题中的数屋关系抽象为直角三角形中元素间的关系. 学法指导:讲练结合坡度的定义h 定义:坡面的铅垂高度(力)与水平宽度(厶)的比叫做坡面的坡度(或坡比),记作i,即/=-.坡度通常写成1 :m的形式.定义:坡而与水平而的夹角叫做坡角,记作a •h坡度与坡角的关条心厂例1.如图所示,水坝的横断面是梯形ABCD,迎水坡DA的坡度为1:25背水坡CB的坡度为1:2,坝高DE为8米,坝顶宽DC为6米.求(1)坝底的宽AB;(2) 1米长的堤坝所需的土石方(体积).例2•如图所示,从塔底同一水平线上的测量仪上,测得塔顶的仰角为45。
,向塔前进了10X (两次测量在塔的同侧),乂测得塔顶的仰角为60。
,测最仪器的高为1.5米,求塔窩(精确到0・1米).B巩固练习【课堂练习】—>选择题:形的面积为( )A 、1B 、——C 、V3 24. 某人上坡走了 60米,他升高了 30佢米,这坡的坡度是(A 、 30° Bx 1:1 C 、 45° 5. 在距电视塔S 米的地而测得塔顶的仰角是则塔高是(S S A^ -------- B 、 ----------------- C> 5 • cot 6Tsin© cos a6. 方程4兀2_2(加+ 1)兀+加=0,的两根恰好是某点角三角形的两锐角的正弦,则m 的值二>填空题: 2在\ABC 中,ZC = 90°, sin A =-,那么 tanfi=( ) 3A 、百B 、百c 、巫 D 、2 5 2 55 菱形的边长为4, 有一个内角为40°, 则较短的对角线长是()A 、4 sin 40°B 、4sin20( 〉C 、8 sin 20°D 、 8cos20° 1.2.3. 一个三角形的一边长为2,这边上的屮线长为1,另两边长之和为1 + V3,则这个三角A 、V2B 、V3C 、±V2D 、±7321 .已知在\ABC中,ZC = 90°, ZA>ZB , R tan A和tanB的值是方程x2--V3x + l = 0的两个根,则ZA= ______________________________________ ・32.已知在等腰AABC屮,顶角A的平分线与对边交于D点,若AB:BC=13:1(),则cos ADAC - _________ .3.三角形三边的长分别为腭,2巧,717 ,则此三角形最大内角的度数是 _____________ .三、解答题:1.如图所示,己知:在山脚C处测得岀顶A的仰角是45。
《解直角三角形的应用》 导学案

《解直角三角形的应用》导学案一、学习目标1、能够运用解直角三角形的知识解决与测量、航海、工程等实际问题相关的数学问题。
2、通过将实际问题转化为数学问题,提高分析问题和解决问题的能力。
3、体会数学知识在实际生活中的广泛应用,增强应用意识和数学建模能力。
二、学习重难点1、重点(1)掌握解直角三角形在实际问题中的应用方法。
(2)能够准确地将实际问题中的数量关系转化为直角三角形中的元素关系。
2、难点(1)如何从实际问题中构建出合适的直角三角形模型。
(2)理解并灵活运用三角函数值来求解实际问题。
三、知识回顾1、直角三角形的边角关系在直角三角形中,若\(∠C =90°\),\(∠A\)、\(∠B\)、\(∠C\)的对边分别为\(a\)、\(b\)、\(c\),则有:(1)三边关系:\(a^2 + b^2 = c^2\)(勾股定理)(2)锐角关系:\(∠A +∠B = 90°\)(3)边角关系:\(\sin A =\frac{a}{c}\),\(\cos A =\frac{b}{c}\),\(\tan A =\frac{a}{b}\)\(\sin B =\frac{b}{c}\),\(\cos B =\frac{a}{c}\),\(\tan B =\frac{b}{a}\)2、解直角三角形由直角三角形中的已知元素,求出其余未知元素的过程,叫做解直角三角形。
四、实际应用类型(一)测量物体的高度例 1:如图所示,为测量某建筑物的高度\(AB\),在离该建筑物底部\(B\)点\(30\)米的\(C\)处,测得建筑物顶端\(A\)的仰角为\(α\),且\(\tanα = 15\),求建筑物的高度。
分析:在\(Rt\triangle ABC\)中,已知\(BC = 30\)米,\(\tanα =\frac{AB}{BC} = 15\),则可求出\(AB\)的长度。
解:在\(Rt\triangle ABC\)中,\(\tanα =\frac{AB}{BC}\)因为\(\tanα = 15\),\(BC = 30\)米所以\(AB = BC \times \tanα = 30×15 = 45\)(米)答:建筑物的高度为\(45\)米。
《解直角三角形的应用(3)》导学案.doc

教师寄语:悟性的高低取决于有无悟,沁”,其实人与人的差别就在于你是否去思考,去发现。
2・5解直角三角形的应用(3)学习目标:1.会用解直角三角形的有关知识解某些简单的实际问题。
2.了解些常用的测量名词方位角、坡度、坡角的意义,能根据及测量术语绘出示意图。
学习重点、难点:理解坡度、坡角的概念,利用解直角三角形解决实际问题。
课前预习案1、如图,建筑学中把斜坡起止点A, B的________________ 与它们的______________ 的比叫做坡度(或坡比)2、表示:通常用字母i表示,即匸_____________ ,表示坡度时,一般吧比的前项取作1.3、如上图,斜坡AB与水平线AC的夹角记作a,那么i= __________ = _______ ,这就是说,坡度等于锐角a的____________________ o课中探究案探究]某地计划在河流的上游修建一条拦水大坝.大坝的横断面/fBG)是梯形(图9-21 ),坝顶宽306米,坝高25米.迎水坡朋的坡度21 :3,背水坡CQ的坡度l :2.5.(1)求斜坡AB和CD的长(精确到0.01米);(2 )求拦水大坝的底面*»的宽.方法指导:解决此类问题往往会遇到梯形,--般会过上底的两个顶点作出梯形的两条高,将梯形问题转化为直角三角形和矩形的问题探究2:如图,要测量铁塔的高AB,在地面上选取一点C,在A 、C 两点间选取一点D,测得CD=14米,在C 、D 两点处分别用测角仪测得铁塔顶端B 的仰角为a=30。
和卩=45。
.测角 仪支架的高为1.2米,求铁塔的高(精确到0」米).巩固练习1. mm 运希员从坡度为1:5的山城上滑下.如果这名运动员nr 行的距育是iso*, 那么他下降的离度是多少(m»o.i 米)?2如图.拦水現的湎为郴MGS 根摇图中数据•求,(1) 角“和0的大小(楮确到10(2) 坝JWD 和斜城的的长(精确到 0・1米)・B A D 图422B4jtC(第2电)能力提升1、在我市迎接奥运圣火的活动中,某校教学楼上悬挂着宣传条幅DC,小丽同学在点A处, 测得条幅顶端D的仰介为30。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解直角三角形的应用(1)导学案
一、 学习目标:
1、会用解直角三角形的有关知识解某些简单的实际问题。
2、了解俯角、仰角的意义,能根据测量术语会出示意图,培养学生把实际问题转化为数学问题的能力 二、 课前准备:
1、直角三角形的边角关系:
(1)角之间的关系: (2)边之间的关系: (3)角与边之间的关系: 2. 如果知道直角三角形的几个元素就可以求其他的元素?有几种情况?
巩固练习
3.若( 3 tanA-3)2
+│2cosB- 3 │=0,则△ABC ( ). A .是直角三角形 B .是等边三角形
C .是含有60°的任意三角形
D .是顶角为钝角的等腰三角形
4.已知∠A 为锐角,且cosA ≤1
2
,那么( )
A .0°<∠A ≤60°
B .60°≤∠A<90°
C .0°<∠A ≤30°
D .30°≤∠A<90° 计算
.
1
12)4cos 30||
3-⎛⎫
-++- ⎪
⎝⎭
°2
1
)15sin(A .10=
-A 满足若锐角度则__________=∠A 32,
3tan ,30.20===∠∆BC B A ABC 中,在.
AB ________=则0
2009
1(1).2sin 603tan 30(1)3⎛⎫
-++- ⎪⎝⎭
°
°2
2009
1)6sin 45(1)-+-°
三、 课内探究:
1、看课本P76页,知道什么是仰角、俯角?
2 坡度与坡角:坡面的铅直高度h 和水平宽度l 的比叫做坡度(或叫做坡比),
一般用i 表示。
即i=,常写成i=1:m 的形式如i=1:2.5 把坡面与水平面的夹角α叫做坡角.
结合图形思考,坡度i 与坡角α之间具有什么关系?
这一关系在实际问题中经常用到。
2、例题解析:
[例1] 如图,厂房屋顶人字架的跨度为10 米,上弦AB =BD ,∠A = 26°.求中柱BC 和上弦AB 的长(精确到0.01米).
例2:热气球的探测器显示,从热气球看一栋高楼顶部的仰角为α=30°,看这栋高
楼底部的俯角为β=60°, 热气球与高楼的水平距离为120m,这栋高楼有多高?(结果保留根号)
总结:
把实际问题转化为解直角三角形的问题的一般思路:。
3、巩固训练:
(1)如图,在电线杆上离地面6 米处用拉线固定电线杆,拉线和地面之间的夹
角为60, 求拉线AC 的长和拉线下端点A 与线杆底部D 的距离(精确到0 . 1 米)
A
D
26º
中上弦 B
(2)建筑物BC 上有一旗杆AB,由距BC 40m 的D 处观察旗杆顶部A 的仰角为
60°,观察底部B 的仰角为45°,求旗杆的高度。
(结果保留根号)
例3
同学们,如果你是修建三峡大坝的工程师,现在有这样一个问题请你解决:如图
6-33
水库大坝的横断面是梯形,坝顶宽6m ,坝高23m ,斜坡AB 的坡度i=1∶3,斜坡CD 的坡度i=1∶2.5,求斜坡AB 的坡面角α,坝底宽AD 和斜坡AB 的长(精确到0.1m)
练习.
1 如图所示,某公司入口处原有三级台阶,每级台阶高为20cm ,台阶面的宽为30cm ,为了方便残疾人士,拟将台阶改为坡角为12°的斜坡,设原台阶的起点为A ,斜坡的起点为C ,
A
B
D
B
C
求AC的长度(精确到1cm).
:
2、已知:如图,在1998年特大洪水时期,要加固全长为10000m的河堤.大堤高5m,坝顶宽4m,迎水坡和背水坡都是坡度为1∶1的等腰梯形.现要将大堤加高1m,背水坡坡度改为1∶1.5.已知坝顶宽不变,求大坝横截面面积增加了多少平方米,完成工程需多少立方米的土石?
3.已知:如图,小明准备测量学校旗杆AB的高度,当他发现斜坡正对着太阳时,旗杆AB 的影子恰好落在水平地面和斜坡的坡面上,测得水平地面上的影长BC=20m,斜坡坡面上的影长CD=8m,太阳光线AD与水平地面成26°角,斜坡CD与水平地面所成的锐角为30°,求旗杆AB的高度(精确到1m).
课后检测
1 海中有一个小岛A,它的周围8海里范围内有暗礁,渔船跟踪鱼群由西向东航行,在B点测得小岛A在北偏东60°方向上,航行12海里到达D点,这时测得小岛A在北偏东30°方向上,如果渔船不改变航线继续向东航行,有没有触礁的危险?
2:
如图所示,甲楼在乙楼的西面,它们的设计高度是若干层,每层高均为3m,冬天太阳光与水平面的夹角为30°.
(1)若要求甲楼和乙楼的设计高度均为6层,且冬天甲楼的影子不能落在乙楼上,那么建筑时两楼之间的距离BD至少为多少米?(保留根号)
(2)由于受空间的限制,甲楼和乙楼的距离BD=21m,若仍要求冬天甲楼的影子不能落在乙楼上,那么设计甲楼时,最高应建几层?
3.已知:如图,在一次越野比赛中,运动员从营地A 出发,沿北偏东60°方向走了500m 3到达B
点,然后再沿北偏西30°方向走了500m ,到达目的地C 点.求
(1)A 、C 两地之间的距离;
(2)确定目的地C 在营地A 的什么方向?
4、我校的46
10米/秒的速度沿北偏西A 是否在
5.如图,一艘渔船正以30海里/小时的速度由西向东赶鱼群,在A 处看小岛C 在船北偏东60度。
40分钟后,渔船行至B 处,此时看见小岛C 在船的北偏东30度。
已知以小岛C 为中心周围18海里以内为我军导弹部队军事演习的着弹危险区。
问:
(1)这艘渔船继续向东追赶鱼群,是否有进入危险区的可能?为什么? (2)若有危险,渔船在距离A 处多少海里前就要改变方向? (3)渔船经过多少分钟可侥幸脱离危险?
6、(2010 湖北孝感)如图,一艘船向正北航行,在A 处看到灯塔S 在船的北偏东30°的方向上,航行12海里到达B 点,在B 处看到灯塔S 在船的北偏东60°的方向上,此船继续沿正北方向航行过程中距灯塔S 的最近距离是 海里(不作近似计算)。
处
7 (2010广东深圳)如图,某渔船在海面上朝正方方向匀速航行,在A 处观测到灯塔M 在北偏东60°方向上,航行半小时后到达B 处,此时观测到灯塔M 在北偏东30°方向上,那么该船继续航行多长时间可使渔船到达离灯塔距离最近的位置?
8:(2010江苏南通)光明中学九年级(1)班开展数学实践活动,小李沿着东西方向的公路以50 m/min 的速度向正东方向行走,在A 处测得建筑物C 在北偏东60°方向上,20min 后他走到B 处,测得建筑物C 在北偏西45°方向上,求建筑物C 到公路AB 的距离.
1.732)
A B
东
M
北
北。
