六年级用比例解决问题
六年级数学 用比例解决问题
03
解:设王大爷家上个月用水x吨， 19.2：x=12.8：8 x=19.2×8÷12.8 x=12 答:王大爷家上个月用水12吨。
04
2.一批书如果每包20本，要捆18 包。如果每包30本，要捆多少包？
因为书的总数一定,所以包数和每包的本数成反 比例.也就是说,每包的本数和包数的乘积相等。
解:设要捆x包， 30x=20×18 x=360÷30 x=12 答：要捆12包。
用比例 解决问题
Template
WINTER
01
02
1.张大妈上个月用了8吨水，水费12.8元， 李奶奶家用了10吨水，李奶奶家上个月 的水费是多少钱？
因为每吨水的价钱一定,所以水费和用水的吨数成正比 例，也就是说,两家的水费和用水吨数的的比值相等。
解:设李奶奶家上个月的水费是x元， 12.8：8=x：10 王大爷家上个月的 8x=12.8×10 水费是19.2元，他 x=128÷8 们家上个月用了多 x=16 少吨水? 答:李奶奶家上个月的水费是16元。
05
1.500千克的海水中含盐25千克， 6800吨的海水含盐几吨？
2.服装厂2天加工西装120套， 照这样计算，加工540套西装 需要多少天？
谢谢观赏Biblioteka
六年级数学用比例解决问题试题
六年级数学用比例解决问题试题1.甲乙丙三人共同生产100个零件，甲完成了三成，乙和丙完成的数量比是2:5，乙和丙各完成多少个?【答案】乙完成20个，丙完成50个。
【解析】现已知乙丙完成的数量之比，只要找到他们两个完成的总数，就很容易“按比例分配”了。
解：100×（1-）=70（个），2+5=7，70×=20（个），70×=50（个）答：乙完成20个，丙完成50个。
【考点】比的应用。
2.某工厂采用最新技术，每天用料14吨，这样原来7天的用料，现在可用10天，原来每天用料几吨？【答案】20吨【解析】先求出木料的总量，再用这个总量除以原来使用的天数即可。
解：14×10=140（吨）140÷7=20（吨）答：原来每天用料20吨。
3.师徒两人加工一种零件．用同样的时间，徒弟可以加工3个，师傅可以加工5个。
如果两人共同加工200个这样的零件，师傅、徒弟分别要加工多少个？【答案】师傅加工125个，徒弟加工75个【解析】根据“用同样的时间，徒弟可以加工3个，师傅可以加工5个，”知道徒弟和师傅的工作效率的比是3：5，由此知道徒弟的工作效率是两人工作效率的和的，再根据在时间一定时，工作量与工作效率成正比例，即徒弟的工作量是两人工作量和的，进而解决问题。
解：他们的效率之比是3：5。
徒弟加工零件的个数：200×=200×=75（个）师傅加工零件的个数：200-75=125（个）答：师傅加工125个，徒弟加工75个。
4.某俱乐部男、女会员的人数之比是，分为甲、乙、丙三组．已知甲、乙、丙三组的人数比是，甲组中男、女会员的人数之比是，乙组中男、女会员的人数之比是．求丙组中男、女会员人数之比．【答案】5:9【解析】以总人数为1，则甲组男会员人数为，女会员为，乙组男会员为，女会员为；丙组男会员为，女会员为；所以，丙组中男、女会员人数之比为．5.一班和二班的人数之比是，如果将一班的名同学调到二班去，则一班和二班的人数比变为．求原来两班的人数．【答案】48 42【解析】原来一班的人数为两班总人数的，调班后一班的人数是两班人数的，调班前后一班人数的比值为，所以一班原来的人数为人，二班原来的人数为人.6.甲本月收入的钱数是乙收入的，甲本月支出的钱数是乙支出的，甲节余240元，乙节余480元．甲本月收入多少元？【答案】600【解析】甲、乙本月收入的比是，分别节余240元和480元，支出的钱数之比是．如果乙节余480元，甲节余元，那么两人支出的钱数之比也是，现在甲只节余240元，多支出了60元，结果支出的钱数之比从变成了(即)，所以这60元就对应份，那么甲支出了元，所以甲本月收入为元．7.甲、乙两车分别从、两地同时相向开出，甲车速度是千米／小时，乙车速度是千米／小时，当甲车驶过、距离的多千米时与乙车相遇，、两地相距（）千米．【答案】225【解析】在相同的时间内，两车行驶的路程比等于两车的速度之比，由于两车的速度之比等于，那么、距离的多千米即是、距离的，所以千米的距离相当于全程的，全程的距离为(千米)．8.甲、乙、丙三个数，已知，，求。
六年级下册 用比例解决问题应用题
用比例解决问题
班级： 姓名：
1．李叔叔开车从甲地到乙地一共用了5小时，每小时行60km ，返回时每小时行75km ，返回时用了多少时间？
2．六年级同学进行广播操表演，如果每排站15人，正好站8排，如果要站成10排，每排应站多少人？
3．一个晒盐场用100克海水可以晒出3克盐，照这样计算，多少吨海水可以晒出180吨盐？
4．修一条路，如果每天修120米，8天可以修完；如果每天多修30米，几天可以修完？
5．一个客厅，用边长3dm 的方砖铺地，需要112块，如果用边长4dm 的方砖铺地，需要多少块？
6．一个手机组装车间完成一批生产任务，若每天组装手机500台，需要24天完成．现在要求15天完成任务，每天需要组装多少台？
7．火车从甲站开往乙站，4.2小时行了全程的
9
7，照这样的速度，火车行完剩下的路程还需几小时？
8．加工一批零件，刘叔叔前3小时加工了135个零件．照这样的速度，刘叔叔加工完这批零件一共需要8小时．这批零件共有多少个？
9．李阿姨家装修房间，如果用边长为0.4m的方砖来铺，350块刚好铺满；如果用边长为0.5m的方砖来铺，需要多少块刚好铺满？
10．有一项工作，原计划40个人工作18天正好完成任务，如果每个人的工作效率相同，现在增加5个人，可以提前几天完成任务？
11．装订一本书，如果每页排500个字，可以排180页，如果改为每页排600个字，可以少排多少页？
12．有一项工作，原计划40个人工作18天正好完成任务，如果每个人的工作效率相同，现在增加5个人，可以提前几天完成任务？
13．榨油厂用300千克花生可以榨出39千克花生油，照这样计算，要榨出104千克油需要多少千克的花生？。
六年级数学下册用比例解决问题
用比例解决问题班级姓名1、在比例尺是1：30000000的地图上量得甲乙两面地相距12厘米，一架飞机从早上的8：30以每小时800千米的速度从甲地飞往乙地。
到达乙地的时间是几时几分？2、甲乙两地相距300千米，在比例尺是的地图上应画多少厘米？如果画在比例尺是1：6000000的地图上应画多少厘米？3、在比例尺是1：4000的图纸上量得一个圆形运动场的直径是8厘米，这个圆形运动场的实际面积是多少平方米？4、在比例尺是1：2000的图纸上量得一块长方形菜地的周长是25厘米，且长与宽的比是3：2，这块长方形菜地的实际面积是多少平方米？5、一个篮球场的长是28米，宽是15米。
请选择一个合适的比例尺画出这个篮球场的平面图？6、一辆汽车5小时行驶140千米，照这样的速度，从甲地到乙地行了8小时，甲乙两地相距多少千米？（用比例解）7、用一批纸装订同样的练习本，每本40页，可装订90本，现在要装订100本，每本多少页？（用比例解）8、一个自来水龙头3天要浪费600升水，照这样计算六月份要浪费多少升水？（用比例解）9、一本书3天看了51，照这样计算剩下的还要多少天看完？（用比例解）10、一辆汽车从甲地到乙地去时每小行40千米，10小时到达，返回时，速度提高41，可节约几小时？（用比例解）11、给教室铺方砖，用面积是4平方分米的方砖需要200块，若改用面积是5平方分米的方砖需要多少块？（用比例解）0 40 80km12、给教室铺方砖，用边长是4分米的方砖需要200块，若改用面积是8平方分米的方砖需要多少块？（用比例解）13、给教室铺方砖，用边长是4分米的方砖需要200块，若改用边长是5分米的方砖需要多少块？（用比例解）14、一件商品原价80元，现打七五折出售，原来买12件商品的钱，现在可以买多少件？（用比例解）15、两个圆柱体积相等，一个圆柱的底面积是30平方米，高6米，另一个圆柱的底面积是45平方米，它的高是多少米？（用比例解）16、一段木料锯成3段要12分钟，照这样，锯成8段要多少分钟？（用比例解）17、一个服装店的所有服装都打同样的折扣销售①、李阿姨买了一件上衣，原价250元，现价150元，李阿姨还想买一条裤子，原价180元，现价多少钱？（用比例解）②、张伯伯有一笔钱，如果买现价90元一件的衬衫，正好买4件，如果想买原价200元一件的夹克衫，能买多少件？（用比例解）18、一个长方形长8厘米，宽6厘米，按3:1放大后，它的面积是多少平方厘米？19、在一幅比例尺是1:2000000的地图上，量得甲乙两地的距离是厘米，如果画在比例尺是1:5000000的地图上，应画多少厘米？20、希望小学装修多媒体教室。
六年级下4.3用比例解决问题
六年级下4.3用比例解决问题《六年级下 43 用比例解决问题》在六年级的数学学习中，用比例解决问题是一个非常重要的知识点。
它不仅能够帮助我们更轻松地解决一些实际的数学问题，还能培养我们的逻辑思维和分析能力。
比例，简单来说，就是两个比相等的式子。
比如，2:3 ＝ 4:6，这就是一个比例。
而用比例解决问题，就是根据题目中给出的条件，找出其中的比例关系，然后通过设未知数、列比例式、解比例等步骤来求出答案。
我们先来看一个常见的例子。
比如，一辆汽车 2 小时行驶了 100 千米，按照这样的速度，5 小时可以行驶多少千米？在这个问题中，我们知道汽车行驶的速度是一定的，也就是路程和时间的比值是不变的。
那么，我们可以设5 小时行驶的路程为x 千米。
因为速度＝路程÷时间，所以第一次行驶的速度为 100÷2 ＝ 50（千米/小时），第二次行驶的速度为 x÷5。
由于速度不变，所以可以列出比例式：100:2 ＝ x:5接下来，我们就可以根据比例的性质来解这个比例。
在比例里，两个内项的积等于两个外项的积。
所以 2x ＝ 100×5，2x ＝ 500，x ＝ 250。
这就求出了 5 小时行驶的路程是 250 千米。
再来看另一个例子。
小明买 5 本同样的练习本用了 10 元，那么买 8 本这样的练习本需要多少钱？同样的，我们设买 8 本需要 x 元。
因为练习本的单价是一定的，所以可以列出比例式：5:10 ＝ 8:x根据比例的性质，5x ＝ 10×8，5x ＝ 80，x ＝ 16所以买 8 本练习本需要 16 元。
用比例解决问题的时候，关键是要找到题目中不变的量，以及与之相关的两个变量，然后判断它们是成正比例还是反比例关系。
正比例关系是指两个量的比值一定，比如上面汽车行驶的例子，速度一定，路程和时间成正比例。
反比例关系则是指两个量的乘积一定，比如做一项工作，工作总量一定，工作效率和工作时间成反比例。
苏教版数学六年级下册专项～比例解决问题【含答案】
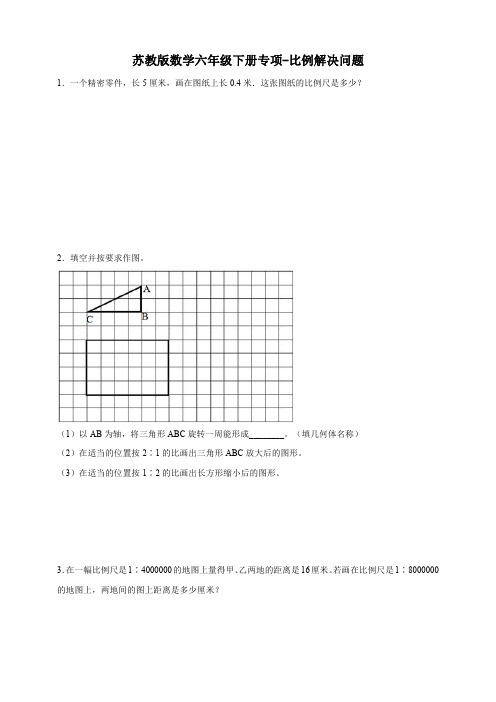
苏教版数学六年级下册专项-比例解决问题1．一个精密零件，长5厘米，画在图纸上长0.4米．这张图纸的比例尺是多少？2．填空并按要求作图。
（1）以AB为轴，将三角形ABC旋转一周能形成________。
（填几何体名称）（2）在适当的位置按2∶1的比画出三角形ABC放大后的图形。
（3）在适当的位置按1∶2的比画出长方形缩小后的图形。
3．在一幅比例尺是1∶4000000的地图上量得甲、乙两地的距离是16厘米。
若画在比例尺是1∶8000000的地图上，两地间的图上距离是多少厘米？4．画一画，填一填。
（1）按3∶1的比画出图形A放大后得到的图形B。
（2）按1∶2的比画出图形B缩小后得到的图形C。
我发现：放大或缩小前后的图形（）变了，但（）没有变，而且图形各部分长度是按一定的比变化的。
5．在一张比例尺是1∶150的建筑图纸上，量得一座大楼的长是6分米，这座大楼的实际长与宽的比是3∶1，这座大楼的实际宽是多少米？6．下图中小平行四边形按比放大后得到大平行四边形，求大平行四边形的高。
（单位：分米）12．根据图中提供的信息，完成下列问题。
（1）自来水厂要从水库取水，取水管道怎样铺最短，请在图中画出来。
（2）自来水厂到城区的送水管道经测算最短是2000米，请你测算：自来水厂到水库的取水管道最短需多少米？13．在一幅地图上，用5厘米长的线段表示实际距离100千米，这幅地图的比例尺是多少？如果甲市至乙市的铁路线路长150千米，那么这段铁路线路在这幅地图上的长度是多少厘米？14．江苏省云龙湖景区杏花坞广场是人们夏天避暑纳凉的佳处。
广场绿地面积与铺装面积的比是6∶5，其中铺装面积共5000平方米，绿地面积有多少平方米？15．甲乙两城相距150千米，在一幅地图上量得甲乙两城之间的距离是5厘米，同时在这幅地图上量得乙丙两城之间的距离是8厘米。
乙丙两城之间的实际距离是多少千米？20．下图中A点是游乐场所在的位置，B点是电影院所在的位置，两地实际距离相距2千米。
数学六年级下册《用比例解决问题》教案
数学六年级下册《用比例解决问题》教案一、教学目标1.知识与技能:理解比例意义，掌握解比例的方法，能够运用比例解决简单的实际问题。
能够区分正比例和反比例关系，并能根据实际问题选择合适的比关系进行解答。
2.过程与方法:通过观察、分析、比较、归纳等活动，经历用比例解决问题的过程体会数学与生活的联系，发展学生的分析问题和解决问题的能力。
能够运用多种方法（例如：方程法、比例法）解决同一个问题，并比较不同方法的优缺点。
3.情感态与价值观:培养学生认真细致的学习态度，增强学生运用数学知识解决实际问题的自信心，体会数学的应用价值。
二、教学重点运用比例解决实际问题，区分正比和反比例关系。
三、教学难点分析实际问题中的数量关系，选择合适的比例式列式解答。
四、教学准备多媒体课件、练习题、比例尺模型、实物投影仪五、教学过程(一复习旧知 (5分钟)1.什么是比例？比例的基本性质是什么？2.如何解比例？举例说明。
3.举例说明正比例和反比例的意义。
(二) 导入新课 (5分钟)教师展示一些生活中的图片例如：地图、比例模型、工程进度图等，引导学生思考这些图片中蕴含的数学知识，引出比例的应用。
(三) 探究新知 (30分钟)1.例题讲解:选择几个不同类型的例题进行讲解，例如：•例题1 (正比例):如果5个苹果重1千克，那么15个苹果重多少千克？引导学生分析题意，找出题中的数量关系，列出比例式并解答。
讲解解题步骤，并强调单位的统一。
•例题2 (反比例): 5个人完成一项工程需要10天，如果增加到10个人，完成这项工程需要多少天？引导学生分析题意，找出题中的数量关系，列出比例式并解答。
比较正比例和反比例的区。
o例题3 (稍复杂的应用题):某地图的比例尺是1:50000，地图上两地相距4厘米，实际距离是多少千米？引导学生理解比例尺的意义，并运用比例解决问题。
2.*小组合作:** 将学生分成小组，让学生尝试解决课本上的练习题，教师巡视指导，帮助学生解决遇到的问题。
人教版小学数学六年级下学期第4单元—用比例解决问题
用比例解决问题
班级：姓名：
一、判断两种相关联的量是否成比例？成什么比例？
1、总路程一定，速度和时间。
（）
2、总页数一定，看了的页数和剩下的页数。
（）
3、购买铅笔的单价一定，总价和数量。
（）
4、汽车行驶的速度一定，所走的路程和时间。
（）
二、解决问题。
1、小明买4支圆珠笔用了6元，小刚想买3支同样的圆珠笔，要用多少钱？
2、小兰的身高1.5m，她的影长是2.4m，如果同一时间、同一地点测得一棵树的影子长4m，这棵树有多高？
3、王叔叔开车从甲地到乙地、前2小时行了100km照这样的速度从甲地到乙地一共要用3小时，甲乙两地相距多远？
4、一辆货车前往灾区运送救灾物资，2小时行驶了30千米。
从出发地点到灾区有90千米，按照这样的速度，全程需要多少小时？
5、一个办公楼原来平均每天照明用电100千瓦时。
改用节能灯以后，平均每天只用电25千瓦时。
原来5天的用电量现在可以用多少天？
6、学校小商店有两种圆珠笔，小明带的钱刚好可以买4支单价是1.5元的，如果他只买单价是2元的，可以买多少支？
7、小明家用收割机收割小麦。
如果每小时收割0.3公顷，40小时能完成任务。
（1）现在想用30小时收割完，那么每小时应收割多少公顷？
（2）每公顷产小麦8t，这块地共产小麦多少吨？
8、一间房子要用方砖铺地，用边长0.6m的方砖铺地，需要100块。
如果改用边长是0.5m的方砖铺地，需要多少块？
9、中国发射的科学气象卫星，在太空中绕地球运行6周需10.6小时，如果运行15周需要多少小时？。
六年级-人教版-数学-下册-[教学设计]用比例解决问题(二)
![六年级-人教版-数学-下册-[教学设计]用比例解决问题(二)](https://img.taocdn.com/s3/m/2591f0684b7302768e9951e79b89680203d86b9a.png)
用比例解决问题（二）教学内容教科书第60页例6及相关内容。
教学目标1．能正确判断情境中的两种量是否成反比例关系，并利用反比例的意义解决实际问题。
掌握用反比例知识解决问题的解题思路。
2．能够类比正比例的相关知识，学习反比例的对应内容，培养学生的知识迁移能力。
3．在数学活动的深度体验中，体会解决问题的成功和喜悦，感受数学的无穷魅力，激发学生学习数学的热情。
教学重点能够利用反比例的意义解决问题。
教学难点能够正确利用反比例关系列出含有未知数的等式。
教学准备多媒体课件。
教学过程一、复习旧知师：我们已经能够判断什么叫作成正比例的量，什么叫作成反比例的量，也学会了用正比例的知识解决问题，下面看这几道题。
课件出示：1．判断下面每题中的两种量成什么比例关系。
（1）一根线截成同样的小段，截成的段数和每段的长度。
（2）每块地砖的面积一定，所需地砖的块数和所铺面积。
（3）给一间教室铺地砖，每块地砖的面积与所需的块数。
2．小花买5支圆珠笔用了8元，明明想买3支同样的圆珠笔，要用多少钱？（用比例的知识解答）教师指名学生逐题汇报，注意引导学生说出为什么。
在学生汇报完第2题之后，引导学生回顾用正比例知识解决问题的步骤：（1）找：找出题目中相关联的两种量。
（2）判：判断它们是否成正比例关系。
（3）列：根据正比例的意义列出比例式。
（4）解：解比例。
（5）检：检验、写答语。
师：这节课我们继续学习运用比例知识来解决实际问题。
二、探究新知（一）教学例61．阅读与理解。
课件出示：某办公楼原来平均每天照明用电100千瓦时。
改用节能灯以后，平均每天只用电25千瓦时。
原来5天的用电量现在可以用多少天？师：从题目中你知道了哪些数学信息？要解决的问题是什么？预设：知道了原来平均每天照明用电100千瓦时，改用节能灯以后，现在平均每天只用电25千瓦时。
要解决的问题是原来5天的用电量现在可以用多少天。
根据学生回答，课件出示表格：师：要解决这个问题必须要知道什么？预设：要求“原来5天的用电量现在可以用多少天”，就要知道现在每天的用电量和总用电量。
《用比例解决问题》说课稿(通用10篇)
《用比例解决问题》说课稿（通用10篇）《用比例解决问题》说课稿篇1教学目标：1、使学生掌握用比例知识解答以前学过的用归一、归总方法解答的应用题的解题思路，能进一步熟练地判断成正、反比例的量，加深对正、反比例概念的理解，沟通知识间的联系。
2、提高学生对应用题数量关系的分析能力和对正、反比例的判断能力。
3、培养学生良好的解答应用题的习惯。
教学重点：用比例知识解答比较容易的归一、归总应用题。
教学难点：正确分析题中的比例关系，列出方程。
教学过程：一、复习铺垫，引入新课。
（课件出示）1、判断下面每题中的两种量成什么比例？（1）速度一定，路程和时间．（2）路程一定，速度和时间．（3）单价一定，总价和数量．（4）每小时耕地的公顷数一定，耕地的总公顷数和时间．（5）全校学生做操，每行站的人数和站的行数．2、下面各题中各有哪三种量？那种量一定？哪两种量是变化的？变化的规律怎样？它们成什么比例？你能列出等式吗？（1）用一批纸装订练习本，每本30页，可装订200本，每本50页，可装订120本。
（2）一列火车从甲地到乙地，2小时行驶60千米，照这样的速度，8小时可行240千米。
（3）读一本书，每天读20页，6天可以读完，如果每天读5页，需要x天读完。
3、课件出示例5情境图，问：你能说出这幅图的意思吗？（指名回答）李奶奶家上个月的水费是多少钱？想请我们帮她算一算，你们能帮这个忙吗？（1）学生自己解答，然后交流解答方法。
（2）引入新课：象这样的问题也可以用比例的知识来解决，我们今天这节课就来讨论如何运用比例的知识来解决这类问题。
板书课题：用比例解决问题二、探究新知。
1、教学例5（1）学生再次读题，理解题意。
思考和讨论下面的问题：①问题中有哪三种量？哪一种量一定？哪两种量是变化的？②它们成什么比例关系？你是根据什么判断的？③根据这样的比例关系，你能列出等式吗？（2）根据上面三个问题，概括：因为水价一定，所以水费和用水的吨数成正比例。
六年级数学下册用比例解决问题
六年级数学下册用比例解决问题姓名：班级：1、学校食堂买来900千克大米，6天吃了180千克，照这样计算，剩下的还能吃几天？2、两根同样长的钢筋，其中一根锯成3段用了12分钟，另一根要锯成6段，需要多少分钟？3、电信公司要铺设一条通信光缆线，计划由20人工作12天完成。
因任务紧急，现在必须提前2天完成，如果工作效率不变，应增加多少人才能按时完成任务？4、某小区维修线路，需停电半小时，妈妈找来一根长20厘米的蜡烛，蜡烛燃烧8分钟后，还剩15厘米，请问：这根蜡烛能够燃烧到来电吗？5、一块圆柱形钢坯的底面半径是3cm，高是36cm。
如果把它熔铸成一个底面积是113.04平方厘米的圆锥，那么高是多少厘米？6、如果教室要用方砖铺地，用边长为3分米的方砖，需要96块，如果改用边长是4分米的方砖，需要多少块？7、如果教室要用方砖铺地，用面积为9平方分米的方砖，需要96块，如果改用面积是16平方分米的方砖，需要多少块？8、8、如果教室要用方砖铺地，用面积为9平方分米的方砖，需要96块，如果改用边长是4分米的方砖，需要多少块？9、聪聪在图书馆借到了《三体》第三册，计划每天看10页，需要51天刚好全部看完。
如果聪聪最后还书时共交了0.4元的延时服务费，那么他平均每天看了多少页？10、某工程队铺一段铁路，原计划每天铺3.6千米，实际每天比原计划多铺25%，实际铺完这段铁路用了8天。
原计划用多少天铺完？11、加工一批零件，若每天加工200个，则比原计划提前3天就能完成任务；若每天加工150个，则比原计划延迟5天才能完成任务。
原计划多少天完成任务？这批零件一共有多少个？12、甲乙两人骑自行车从A，B两地同时出发，相向而行。
甲行完全程要6小时，甲、乙相遇时所行的路程比是3：2，乙行完全程要多少小时？（甲、乙速度均保持不变）13、如图，平行四边形ABCD的周长为50厘米，以AD为底边时，高CE是8厘米；以AB 为底边时，高CF是12厘米，那么平行四边形ABCD的面积是多少平方厘米？14、甲、乙两车同时从A，B两城相对开出，经过8小时相遇，相遇后甲车继续开到B城还要4小时。
六年级数学用比例解决问题练习
六年级数学用比例解决问题练习学校：姓名：用比例知识解决下面问题：1、用边长40厘米的方砖给教室铺地，需要432块，如果用边长60厘米的方砖铺地，需要多少块方砖？解答：由于铺地面积不变，所以两种方砖的面积成比例。
设用60厘米边长的方砖需要x块，则有：40×40×432=60×60×x解得：x=192，所以需要192块60厘米边长的方砖。
2、一辆客车3小时行135千米，照这样计算，如果行315千米，需要多少小时？解答：客车的行驶速度不变，所以行驶时间与行驶距离成反比例。
设需要的时间为x，则有：3×135=315×x解得：x=1.35，所以需要1.35小时。
3、一种农药，用药液和水按1:1500配制而成。
如果只有3千克的药液，应加水多少千克？解答：药液和水的重量成比例。
设应加水x千克，则有：3:1500=x:(3+x)解得：x=4497，所以应加4497千克水。
4、运一批药品，每箱装36瓶，需要40只箱子，如果每箱装24瓶，需要多少只箱子？解答：药品的总瓶数不变，所以需要的箱子数与每箱装瓶数成反比例。
设需要的箱子数为x，则有：36×40=24×x解得：x=60，所以需要60只箱子。
5、一块长方形地长120米，宽90米。
把它画在比例尺是1:1000的图纸上，长和宽各应画多少厘米？解答：地的长度和宽度与图纸上的长度和宽度成比例。
设地在图纸上的长度为x厘米，则有：120:1000=x:1解得：x=12，所以地在图纸上的长度为12厘米。
同理可得，地在图纸上的宽度为9厘米。
6、在一幅比例尺是1:的地图上，量得甲乙两地的距离是12厘米，甲乙两地的实际距离是多少千米？解答：地图上的长度与实际长度成比例。
设甲乙两地的实际距离为x千米，则有：1:=12:x解得：x=420，所以甲乙两地的实际距离为420千米。
7、___用24元买了6本笔记本，___也想买几本，可是他妈妈只给他16元，他最多可以买到多少本笔记本？解答：笔记本的数量与钱数成正比例。
奥数班六年级第10讲 用比例解决问题
第4讲用比例解决问题【知识点拨】比例的意义：表示两个比相等的式子叫做比例。
比例的认识：比例有四个项，分别是两个内项和两个外项。
在3：4=9：12中，其中3与12叫做比例的外项，4与9叫做比例的内项。
比例的四个数均不能为0。
比例的基本性质：在一个比例中，两个外项的积等于两个内项的积。
比例尺：表示图上距离和实际距离的比，叫这幅地图的比例尺。
【典型例题】例1：一桶盐水200克，盐和水的质量比是1:24.要是盐水中，盐和水的质量比是1:29，要加入多少克水？例2：学校里有一些球，其中红球与总球数的比是1:3，当再买来8个红球后，红球与总球数的比是5:14,问现在共有多少个球？例3：张家与李家的收入钱数之比是8:5，支出的钱数之比是8:3，结果张家结余240元，李家结余270元。
问每家各收入多少元？例4：甲乙两人各有若干元，若甲拿出他所有钱的20%给乙,则两人所有的钱正好相等,原来甲乙两人所有钱的最简整数比是多少?例5：一个长方形长与宽的比是14：5，如果长减少13厘米，宽增加13厘米，则面积增加182平方厘米，那么原长方形面积是多少平方厘米？【课堂精练】1. A、B两人的钱数比是5：3，A给B拿去15元后，两人的钱同样多，原来两人共有多少钱？2. 一桶8升，一桶13升，往两个桶中加进同样多的水后，两桶中水量之比是5：7，那么往每个桶中加进去的水量是多少升？3. 一班和二班的人数之比是8:7，如果将一班的8名同学调到二班去，则一班和二班的人数比变为4:5．求原来两班的人数4. 有两桶大米共27千克，从大桶中吃掉2千克后，剩下的大米与小桶内大米的比是3：2，求大桶里原有多少千克大米？5. 圆珠笔和铅笔的价格比是4：3，20支圆珠笔和21支铅笔共用71．5元．问圆珠笔的单价是每支多少元?6. 幼儿园大班和中班共有32名男生，18名女生。
已知大班男生数与女生数的比为5:3，中班中男生数与女生数的比为2:1，那么大班有女生多少名？7. 车库中停放若干辆双轮摩托车和四轮小轿车，已知车的辆数与车轮数的比是2:5，摩托车与四轮小轿车的辆数比是多少？8.甲乙两人同时从A 地到B 地，骑车的速度比是8:9，已知甲每小时行15千米，行完全程比乙多用125小时，两地相距多少千米？9.袋子里红球与白球数量之比是19：13。
六年级用比例解决问题
用比例解决问题教学目标1、知道图形的变化和用所学知识解决生活中的问题2、理解一些较复杂的问题的解题方法。
3、让学生感受到数学的乐趣。
教学衔接1、 表示两个比相等的式子叫做比例。
2、 组成比例的四个数叫做比例的项，两端的两项叫做比例的外项，中间的两项叫做比例的内项。
3、 在比例里，两个外项的积等于两个内项的积，这叫做比例的基本性质。
4、 求比例中的未知项，叫做解比例。
5、 如果用字母x 和y 表示相关联的量，用k 表示他们的比值（一定）,这样的关系叫做正比例关系。
如果用字母x 和y 表示相关联的量，用k 表示他们的乘积（一定）这样的关系叫做反比例关系。
6、 图上距离：实际距离=比例尺一、 教学内容例一、用边长0.4米的方砖给房间铺地，需要方砖7200块。
若改用边长0.3米的方砖铺，要多少块砖？（用比例方法解答）例二、纸箱里有红绿黄三色球，红色球的个数是绿色球的43，绿色球的个数与黄色球个数的比是4：5，已知绿色球与黄色球共81个，问三色球各有多少个？例三、修一条路，如果每天修120米，8天可以修完；如果每天多修30米，几天可以修完？（用比例方法解）教学练习一、 1、解比例（1）0.4：0.8=9:x （2）0.24 :x=4:1.5 (3)8.4:1.4=x: 1.2（2）21∶51＝41∶X 25X ＝752.1 25.025.1＝2、一对互相啮合的齿轮，主动轮有60个齿，每分转80转。
从动轮有20个齿，每分转多少转？（用比例方法解）2、用同样的地砖铺地，铺完36平方米的房间用了方砖180块地砖，如果再铺个48平方米的房间，还要用地砖多少砖？（用比例解）3、按要求画一画。
⑴按1∶3的比例画出长方形缩小后的图形。
例四、甲、乙两个同学放学回家，甲要比乙多走1/5的路，而乙走的时间比甲少1/11，求甲、乙两人的速度的比。
例五、制造一个零件，甲需要6分钟，乙需5分钟，丙需4.5分钟，现在又1590个零件的制造任务分给他们三个人，要求在相同时间内完成，每人应该分配到多少个零件？例六、有甲、乙两杯含盐率不同的盐水，甲杯盐水重120克，乙杯盐水重80克，现在从两杯中倒出等量的盐水，分别交换倒入两杯中，这时两杯新盐水的含盐率相同，从每杯中倒出的盐水是多少克？分析：因为得到的两杯新盐水的含盐率相同，，所以新盐水的含盐率就是、乙两杯盐水合在一起的含盐率。
人教版六年级下册“用比例解决问题”(一题型多练,适合基础中等学生)
5．在比例尺是 的地图上，量得乐昌到清远的距离是4.5厘米。一辆汽车以每小时60千米的速度从乐昌开往清远，几时可以到达？
6．某工作小组装订一批课外读物，计划每天装订80本，20天可装订完；实际每天装订200本，照这样计算，多少天可以完成任务？（用比例解）
20．学校食堂的阿姨到超市买了28个同样的塑料桶，需要付448元。照这样计算，如果想买48个塑料桶，需要付多少元？（用比例解）
参考答案：
1．30平方米
【分析】设360块方砖能铺地x平方米，根据方砖数量∶铺的面积＝每平方米方砖数量（一定），列出正比例算式解答即可。
【详解】解：设360块方砖能铺地x平方米。
2x＝9×0.8
2x÷2＝7.2÷2
x＝3.6
答：大树有3.6米高。
【点睛】用比例解决问题只要等号两边的比统一即可。
3．2小时
【分析】根据比例尺的意义可知：实际距离＝图上距离÷比例尺，求出实际距离，然后再化成千米即可；再根据关系式：距离÷速度和＝相遇时间，解决问题。
【详解】A、B两地的实际距离：
16÷
17．一辆运货车从甲地到乙地，平均每小时行72千米，10小时到达。回来时空车原路返回，每小时可行80千米。多长时间能够返回原地？
18．工厂四月份组装一批产品，原计划每天组装2.7万台正好完成任务。受新冠疫情影响，实际每天只能组装1.5万台，实际需要多少天才能完成四月份任务？（用比例解）
19．某区用条形统计图表示各小学一周接受核酸检测的人数。纵轴4格表示阳光小学本周一测试人数为1000人，那么如果春晖小学有2375人，纵轴上应该用多少格表示？（用比例解答）
人教新课标六年级下册数学教案：4.3.6用比例解决问题
人教新课标六年级下册数学教案：4.3.6用比例解决问题本节课的教学内容来自于人教新课标六年级下册数学教材的第4.3.6节，主要内容是用比例解决问题。
具体来说，我们将学习如何利用比例关系来解决实际问题，包括如何设置比例尺、如何根据已知条件求解未知量等。
教学目标是让学生掌握比例解决问题的基本方法，能够独立设置比例尺，并利用比例关系求解实际问题。
同时，通过解决实际问题，培养学生的逻辑思维能力和解决问题的能力。
在教学过程中，我们将遇到一些难点和重点。
难点在于学生需要理解比例尺的概念，并能够灵活运用比例关系来解决问题。
重点则是学生能够通过实际问题，理解和掌握比例解决问题的方法。
为了更好地进行教学，我们需要准备一些教具和学具，如黑板、粉笔、教学课件等。
同时，学生也需要准备一些学习用品，如笔记本、尺子、圆规等。
在板书设计方面，我会利用黑板和粉笔来展示比例尺的设置方法，以及利用比例关系解决问题的步骤。
在作业设计方面，我会布置一些有关比例解决问题的题目，让学生独立完成，然后我会对作业进行批改，并对学生进行反馈。
在课后反思及拓展延伸方面，我会对本次课程的教学效果进行反思，看是否达到了预期的教学目标。
同时，我也会给学生提供一些拓展延伸的材料，让学生进一步深入学习比例解决问题。
重点和难点解析：在上述教案中，有几个关键的细节是需要我们重点关注的。
学生需要理解比例尺的概念，并能够灵活运用比例关系来解决问题，这是本节课的重点。
比例尺是图上距离与实际距离的比例关系，学生需要明白比例尺的设置方法，以及如何通过比例关系求解未知量。
教学过程中的例题讲解和随堂练习是非常重要的环节，通过解决实际问题，学生可以更好地理解和掌握比例解决问题的方法。
作业设计也是学生巩固所学知识的重要途径，通过独立完成作业，学生可以进一步提高自己的解题能力。
课后反思及拓展延伸环节可以帮助学生进一步深入学习比例解决问题，提高自己的思维能力和解决问题的能力。
对于这些重点细节，我需要进行详细的补充和说明。
西师大版六年级数学上册《用比例解决问题》教学PPT课件(4篇)
甲
乙
100 km
两地相距 100 km，甲乙两辆汽车从两地相
对开出，4小时相遇。甲乙两车速度比是 3∶2，
甲乙两车速度各是多少？
甲乙两车的总速度为：100÷4=25（km/h）
总份数：3 + 2 = 5
甲
乙
100 km
状元成才路
两地相距 100 km，甲乙两辆汽车从两地相
对开出，4小时相遇。甲乙两车速度比是 3∶2，
智力闯关：第三关
三角形最长边的边长是35厘米，三条边 的长度比是3：4：5。三角形的另两条边长多 少厘米？
用比例解决问题
第3课时
引入
1∶9
有20g糖水，糖与水的比是1∶9，其 中糖有（ 2 ）g，水有（18）g。
引入
1∶1∶2
一个三角形三个内角度数比是1∶1∶2， 这个三角形一定是（等腰直角三角形）。
（1）题目中要分配什么？ （2）平均分合理吗？为什么？ （3）你认为怎样分合理？ （4）陈红、赵青拿出钱数的比是（ ）：（ ）。 （5）怎样理解3:2?
理解
3:2就是陈红分得本数占（ 3 ）份，赵青 分得本数占（ 2 ）份，一共是（ 5 ）份。
陈红分得本数占总数的（ 3 ）。 5 2
赵青分得本数占总数的（ 5 ）。
星级挑战
分配水费问题 分配运费问题 分配租金问题
星级挑战
小李、小郭、小高、小张四家人7月份共付水 费180元，请结合下表所出示的信息，将水费 分摊到每家。
住户 人口数 应付水费
小李 5
小郭 3
小高 2
小张 2
星级挑战
甲、乙、丙三人合租一辆车运同样多的货 物处，卸从 货A，地乙到在B全地程需的付运43 费处5卸00货元，。只甲有在丙全到程B的地。31 他们如何分摊运费？
六年级用比例解决问题
六年级比例知识应用题1、甲地到乙地的实际距离是120千米，在一幅比例尺是1:6000000的地图上，应画多少厘米？2、修一条路，如果每天修120米，8天可以修完；如果每天修150米，几天可以修完？（用比例方法解）3、一台织补袜机2小时织袜26双，照这样计算，7小时可以织补多少双？4、一种铁丝长30米，重量是7 千克，现有这种铁丝950千克，长多少米？5.用同样的砖铺地，铺18平方米用砖618砖，如果铺24平方米，要用砖多少块？6、一个晒盐场用100克海水可以晒出3克盐，如果一块盐用一次放入585000吨海水，可以晒出多少吨盐？7、一篮苹果，如果8个人分，每人正好分6个，如果12个人来分，每人可以分几个？8、同学们排队做操，每行站20人，正好站8行，如果每行站24人，可以站多少行？9、一间房子要用砖铺地，用面积是9平方分米的方砖，需要96块，如果用面积是6平方分米的方砖，需要多少块?10、一艘轮船3小时航行80千米，照这样的速度航行200千米需要多少小时？11、一间房五铺地砖，用面只是9平方分米的方砖需要96块，如果改用面积是4平方分米的方砖，需要多少块？12、农场收小麦，前3天收割了16公顷，照这样计算，8天可以收割多少公顷小麦？13、一辆汽车2小时行驶64千米，用这样的速度从甲地到乙地行驶5小时，甲、乙两地之间的公路长多少千米?14、一个榨油厂用100千克黄豆可以榨出13千克豆油，照这样计算，用3吨黄豆可以榨出多少吨豆油？15.同学们做操，每行站20人，正好站18行。
如果每行站24人，可以站多少行？（用比例方法解）16.飞机每小时飞行480千米，汽车每小时行60千米。
飞机行4小时的路程，汽车要行多少小时？（用比例方法解）17.修一条公路,每天修0.5千米，36天完成。
如果每天修0.6千米，多少天可修完？（用比例方法解）18.一个晒盐场用500千克海水可以晒15千克盐；照这样的计算，用100吨海水可以晒多少吨盐？（用比例方法解答）19.一个车间装配一批电视机，如果每天装50台，60天完成任务，如果要用40天完成任务，每天应装多少台？（用比例方法解）20.生产一批零件，计划每天生产160个，15天可以完成，实际每天超产80个，可以提前几天完成？（用比例方法解）21.小明买4本同样的练习本用了4.8元,3.6元可以买多少本这样的练习本? （用比例方法解）22.配制一种农药,药粉和水的比是1:500(1) 现有水6000千克,配制这种农药需要药粉多少千克?(2) 现有药粉3.6千克,配制这种农药需要水多少千克?。
人教版数学六年级下册《用比例解决问题》教案
人教版数学六年级下册《用比例解决问题》教案
一、教学目标
1.了解比例的概念，能够应用比例解决实际问题；
2.能够运用比例的知识计算物体的实际尺寸；
3.提高学生的逻辑思维和问题解决能力。
二、教学重点
1.比例的概念理解；
2.比例的运用能力提升；
3.实际问题的计算能力。
三、教学难点
1.将实际问题转化为比例关系；
2.确定比例的应用范围。
四、教学准备
1.教材《人教版数学六年级下册》教科书；
2.课堂板书工具；
3.习题练习题目。
五、教学过程
1. 导入（5分钟）
通过展示两个不同尺寸的相似图形，引导学生思考如何确定它们之间的比例关系。
2. 讲解比例概念（10分钟）
解释比例的定义、比例的表示方法和如何应用比例解决实际问题。
3. 练习比例运用（20分钟）
让学生自主完成一些比例运用的练习题，检测他们对比例概念的掌握程度。
4. 教学拓展（15分钟）
提供一些实际问题，让学生运用比例的知识解决问题，并引导他们思考比例的应用场景。
5. 练习巩固（15分钟）
布置一些拓展性练习，帮助学生巩固比例的运用能力。
六、课堂作业
1.完成课堂练习题；
2.针对一些实际场景，尝试应用比例解决问题。
七、教学反思
本节课通过引导学生探究比例的概念与应用，增强了学生的运用能力和逻辑思维能力。
在以后的课堂教学中，可以注重更多实际问题的应用，提高学生解决问题的能力。
以上是人教版数学六年级下册《用比例解决问题》教案的相关内容，希望能够对您的教学工作有所帮助。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
六年级比例知识应用题
1、甲地到乙地的实际距离是120千米，在一幅比例尺是1:6000000的地图上，应画多少厘米？
2、修一条路，如果每天修120米，8天可以修完；如果每天修150米，几天可以修完？（用比例方法解）
3、一台织补袜机2小时织袜26双，照这样计算，7小时可以织补多少双？
4、一种铁丝长30米，重量是7 千克，现有这种铁丝950千克，长多少米？
5.用同样的砖铺地，铺18平方米用砖618砖，如果铺24平方米，要用砖多少块？
6、一个晒盐场用100克海水可以晒出3克盐，如果一块盐用一次放入585000吨海水，可以晒出多少吨盐？
7、一篮苹果，如果8个人分，每人正好分6个，如果12个人来分，每人可以分几个？
8、同学们排队做操，每行站20人，正好站8行，如果每行站24人，可以站多少行？
9、一间房子要用砖铺地，用面积是9平方分米的方砖，需要96块，如果用面积是6平方分米的方砖，需要多少块?
10、一艘轮船3小时航行80千米，照这样的速度航行200千米需要多少小时？
11、一间房五铺地砖，用面只是9平方分米的方砖需要96块，如果改用面积是4平方分米的方砖，需要多少块？
12、农场收小麦，前3天收割了16公顷，照这样计算，8天可以收割多少公顷小麦？
13、一辆汽车2小时行驶64千米，用这样的速度从甲地到乙地行驶5小时，甲、乙两地之间的公路长多少千米?
14、一个榨油厂用100千克黄豆可以榨出13千克豆油，照这样计算，用3吨黄豆可以榨出多少吨豆油？
15.同学们做操，每行站20人，正好站18行。
如果每行站24人，可以站多少行？（用比例方法解）
16.飞机每小时飞行480千米，汽车每小时行60千米。
飞机行4小时的路程，汽车要行多少小时？（用比例方法解）
17.修一条公路,每天修0.5千米，36天完成。
如果每天修0.6千米，多少天可修完？（用比例方法解）
18.一个晒盐场用500千克海水可以晒15千克盐；照这样的计算，用100吨海水可以晒多少吨盐？（用比例方法解答）
19.一个车间装配一批电视机，如果每天装50台，60天完成任务，如果要用40天完成任务，每天应装多少台？（用比例方法解）
20.生产一批零件，计划每天生产160个，15天可以完成，实际每天超产80个，可以提前几天完成？（用比例方法解）
21.小明买4本同样的练习本用了4.8元,3.6元可以买多少本这样的练习本? （用比例方法解）
22.配制一种农药,药粉和水的比是1:500
(1) 现有水6000千克,配制这种农药需要药粉多少千克?
(2) 现有药粉3.6千克,配制这种农药需要水多少千克?。