合肥168高中部招生条件2020
安徽省高中排名

合肥市第一中学位于安徽省合肥市,是安徽省重点中学、联合国教科文组织俱乐部成员、安徽省示范性普通高级中学。
二、合肥168中学合肥一六八中学位于安徽省合肥市,是一所由合肥市教育局主管的公立全日制完全中学,安徽省示范普通高中。
三、六安第一中学2020年高考成绩揭晓,经过全体毕业班师生的辛勤努力,六安一中高考取得优异成绩,具体情况如下:1467人报考,达一本线1289人;600分以上591人,全省名列前茅。
四、安徽师范大学附属中学安徽师范大学附属中学是安徽省教育厅唯一直属省示范高中,原安徽省25所重点中学和6所安徽省理科实验班承办学校之一,是安徽省第一所“中国科协青少年科技创新项目实验学校”。
五、马鞍山第二中学是全国文明单位、全国精神文明建设先进单位、全国中小学德育工作优秀案例单位、教育部全国百所重点联系学校之一、全国绿色学校、全国中小学现代教育技术实验学校、全国消防安全教育示范学校、安徽省重点中学、安徽省首所示范高中、北大“中学校长实名推荐制”推荐资质学校、清华大学“新百年领军计划”推荐资质学校、复旦大学“望道计划”推荐资质学校。
六、安庆第一中学是联合国教科文组织俱乐部成员、安徽省首批重点中学、安徽省示范高中、安徽省高中理科实验班承办学校。
以全面科学的评价模式开展生涯规划教育和信息化教学手段来推动和保障课程的实施,以保证课程质量。
让学校走上了特色化发展之路。
八、淮北第一中学淮北一中是首批省重点中学,全国现代教育技术实验学校,省级示范高中,安徽省新课程实验样本校,教育部特色高中建设项目培育校。
九、芜湖第一中学芜湖一中是安徽省老牌重点中学和省首批示范高中。
具有悠久办学历史和光荣革命传统,先后被评为省和国家级体卫工作先进学校、省教育干训实践考察基地、省科普工作先进集体等。
十、铜陵第一中学安徽省重点中学,安徽省示范高中,中科大基础教育理科实验基地。
先后被评为全国体育卫生工作先进单位、全国现代教育技术实验学校、省第四、第五届文明单位、省爱国主义教育示范学校、省绿色学校。
合肥168高中作息时间表

合肥168高中作息时间表
大部分高中的作息时间表都是相似的,但实际的具体作息时间可能会因学校而异。
以下是一种可能的合肥168高中的作息时间表:
周一至周五:
7:00 - 7:30:早自习
7:40 - 8:20:第一节课
8:30 - 9:10:第二节课
9:20 - 10:00:第三节课
10:10 - 10:50:第四节课
10:50 - 11:10:课间休息
11:10 - 11:50:第五节课
12:00 - 12:40:第六节课
12:40 - 13:30:午饭休息
13:30 - 14:10:午休
14:20 - 15:00:第七节课
15:10 - 15:50:第八节课
16:00 - 16:40:第九节课
16:40 - 17:00:放学
周六:
7:00 - 7:30:早自习
7:40 - 8:20:第一节课
8:30 - 9:10:第二节课
9:20 - 10:00:第三节课
10:10 - 10:30:课间休息
10:30 - 11:10:第四节课
11:20 - 12:00:第五节课
12:00 - 13:30:午饭休息
13:30 - 15:30:实验课/选修课/活动课
15:30 - 16:00:放学
这仅仅是一种可能的作息时间表,具体的作息时间可能因学校和年级而有所不同。
如果您对特定学校的作息时间有详细要求,建议您向该学校咨询。
安徽合肥一六八中学(168)2018年高考成绩录取结果
16
同济大学
软件工程
109
10
同济大学
工业设计
110
8
北京航空航天大学
工科试验班类(航空H航天类)
111
13
北京航空航天大学
工科试验班类(航空H航天类)
112
19
南方科技大学
7
北京航空航天大学
科试验班类(信息类)
88
706
19
浙江大学医学院
医学试验班类(5+3一体化培养)
89
722
17
北京航空航天大学 工科试验班类(国际通用工程学院) 90
746
6
同济大学
土木工程
91
758
12
北京航空航天大学
工科试验班类(信息类)
92
760
18
同济大学
土木工程
93
765
13
北京航空航天大学
子学院)
26 27
然科学试验班(拔尖人才培养计划) 28
微电子科学与工程(国家示范性微电 工科试验班(竺子可学桢院学)院交叉创新平
自然科学试验班台()拔尖人才培养计 划)
29 30 31
省排名 0 4 8 10 11 16 20 43 61 64 70 72 76 77 81 85 87 89 92 95 97
划)
35 36
200 218
2
浙江大学
工科试验班(电气与自动化)
37
224
6
中国科学技术大学
理科试验班类
38
229
6
浙江大学
理科试验班类
39
235
18
中国科学技术大学
合肥华兴职业高级中学招生章程

合肥华兴职业高级中学招生章程学校全称:合肥职业技术学院办学层次:高职(专科)办学类型:公办普通高等职业学校办学地址:合肥市新站区关井路与烈山路交汇处(合肥汇心湖校区)合肥市巢湖市姥山南路(巢湖鼓山校区)一、录取规则及要求:1.按照教育部要求,实行“学校负责、考试院监督”的录取体制,坚持公平、公正、公开的原则。
2.除助产专业只招女生外,其他专业不限制男女生比例。
3.体检要求:依照教育部、卫生部、中国残疾人联合会颁布的《普通高等学校招生体检工作指导意见》及有关补充规定执行。
新生入学三个月内进行身体健康复查,对不符合标准的,按相关规定处理。
4.外语不限。
大一新生入学后,学校开设英语课和日语、韩语等选修课。
5.投档成绩相同时:(1)优先录取学业水平测试和综合素质评价水平高的考生。
(2)优先考虑在文体方面有特长的考生。
6.各专业无年级差异,无相关科目成绩或额外考试要求。
7.按“专业清”的办法进行录取。
对各轮进档考生,根据考生专业顺序和招生计划数,从高分到低分录取。
若不能满足专业志愿,对服从调剂的考生,则录取到未满计划的专业;对不服从调剂的考生,则予以退档。
8.旅游管理专业要求考生有端正的体貌,清晰的吐字,灵敏的听力和辨别力。
9.轨道交通类专业要求考生无色盲、色弱、弱视,其中城市轨道交通运营管理专业要求男生身高170cm 及以上,女生身高 160cm 及以上,身体健康,五官端正。
10.新生报到入学后,学校会在三个月内审核其入学资格。
复审不合格者,由学校根据不同情况进行处理,直至取消资格。
凡发现弄虚作假者,取消其录取资格,并向学生所在省(自治区、直辖市)招生办公室举报。
二、其他:⒈ 奖助措施:设立国家奖学金、国家励志奖学金、国家助学金、生源地助学贷款(国家开发银行生源地信用助学贷款,安徽省农信社生源地信用助学贷款),并设立校内奖学金、特困学生补助、勤工助学等。
⒉ 推荐就业。
坚持实行学校推荐、双向选择、自主择业的就业原则,优先推荐合肥地区就业。
2023-2024学年安徽省合肥168中学等名校联考高三(上)期末数学试卷【答案版】

2023-2024学年安徽省合肥168中学等名校联考高三(上)期末数学试卷一、单选题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.)1.已知集合U ={1,2,3,4,5},A ={2,3},B ={x |x =2k ,k ∈Z },则B ∩∁U A =( ) A .{4}B .{2,4}C .{1,2}D .{1,3,5}2.复数(i −1i)3的虚部是( )A .﹣8B .﹣8iC .8D .8i3.已知向量a →=(0,−2),b →=(1,t),若向量b →在向量a →上的投影向量为−12a →,则a →⋅b →=( )A .﹣2B .−52C .2D .1124.在△ABC 中,“C =π2”是“sin 2A +sin 2B =1”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件5.过点(0,﹣2)与圆x 2+y 2﹣4x ﹣1=0相切的两条直线的夹角为α,则cos α( ) A .14B .√154C .−14D .√1046.A ,B ,C ,D ,E 五人站成一排,如果A ,B 必须相邻,那么排法种数共有( ) A .24B .120C .48D .607.若系列椭圆C n :a n x 2+y 2=1(0<a n <1,n ∈N *)的离心率e n =(12)n ,则a n =( )A .1−(14)nB .1−(12)nC .√1−(12)nD .√1−(14)n8.已知等差数列{a n }(公差不为0)和等差数列{b n }的前n 项和分别为S n 、T n ,如果关于x 的实系数方程1003x 2﹣S 1003x +T 1003=0有实数解,那么以下1003个方程x 2﹣a i x +b i =0(i =1,2,…1003)中,有实数解的方程至少有( )个. A .499B .500C .501D .502二、多选题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对得6分,部分选对得部分,有选错的得0分)9.已知一组数据:12,31,24,33,22,35,45,25,16,若去掉12和45,则剩下的数据与原数据相比,下列结论正确的是( ) A .中位数不变 B .平均数不变 C .方差不变D .第40百分位数不变10.双曲线C :x 2a 2−y 2b2=1(a >0,b >0),左、右顶点分别为A ,B ,O 为坐标原点,如图,已知动直线l 与双曲线C 左、右两支分别交于P ,Q 两点,与其两条渐近线分别交于R ,S 两点,则下列命题正确的是( )A .存在直线l ,使得AP ∥ORB .l 在运动的过程中,始终有|PR |=|SQ |C .若直线l 的方程为y =kx +2,存在k ,使得S △ORB 取到最大值D .若直线l 的方程为y =−√22(x ﹣a ),RS →=2SB →,则双曲线C 的离心率为√311.如图所示,有一个棱长为4的正四面体P ﹣ABC 容器,D 是PB 的中点,E 是CD 上的动点,则下列说法正确的是( )A .直线AE 与PB 所成的角为π2B .△ABE 的周长最小值为4+√34C .如果在这个容器中放入1个小球(全部进入),则小球半径的最大值为√63D .如果在这个容器中放入4个完全相同的小球(全部进入),则小球半径的最大值为2√6−25三、填空题(本大题共3小题,每小题5分,共15分) 12.小于300的所有末尾是1的三位数的和等于 . 13.已知函数f(x)=ln(x +1)−axx+1,若f (x )⩾0恒成立,则a = . 14.已知抛物线C :y 2=2px (p >0),点P 为抛物线上的动点,点A(4−p2,0)与点P 的距离|AP |的最小值为2,则p = .四、解答题(本大题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步骤)15.(13分)在△ABC中,A,B,C的对边分别为a,b,c,已知b=√2,c=4,acosC+b=0.(1)求a;(2)已知点D在线段BC上,且∠ADB=3π4,求AD长.16.(15分)甲、乙两人进行射击比赛,每次比赛中,甲、乙各射击一次,甲、乙每次至少射中8环.根据统计资料可知,甲击中8环、9环、10环的概率分别为0.7,0.2,0.1,乙击中8环、9环、10环的概率分别为0.6,0.2,0.2,且甲、乙两人射击相互独立.(1)在一场比赛中,求乙击中的环数少于甲击中的环数的概率;(2)若独立进行三场比赛,其中X场比赛中甲击中的环数多于乙击中的环数,求X的分布列与数学期望.17.(15分)如图,圆台O1O2的轴截面为等腰梯形A1ACC1,AC=2AA1=2A1C1=4,B为底面圆周上异于A,C的点.(1)在平面BCC1内,过C1作一条直线与平面A1AB平行,并说明理由;(2)设平面A1AB∩平面C1CB=l,Q∈l,BC1与平面QAC所成角为α,当四棱锥B﹣A1ACC1的体积最大时,求sinα的取值范围.18.(17分)已知函数f(x)=lnx﹣ax(x﹣1).(1)当a<0时,探究f′(x)零点的个数;(2)当a>0时,证明:f(x)⩽2+a√a+8a−a −3 2.19.(17分)阿波罗尼斯是古希腊著名数学家,他的主要研究成果集中在他的代表作《圆锥曲线》一书中.阿波罗尼斯圆是他的研究成果之一,指的是已知动点M与两定点Q,P的距离之比|MQ||MP|=λ(λ>0,λ≠1),λ是一个常数,那么动点M的轨迹就是阿波罗尼斯圆,圆心在直线PQ上.已知动点M的轨迹是阿波罗尼斯圆,其方程为x2+y2=4,定点分别为椭圆C:x2a2+y2b2=1(a>b>0)的右焦点F与右顶点A,且椭圆C的离心率为e=12.(1)求椭圆C的标准方程;(2)如图,过右焦点F斜率为k(k>0)的直线l与椭圆C相交于B,D(点B在x轴上方),点S,T 是椭圆C上异于B,D的两点,SF平分∠BSD,TF平分∠BTD.(ⅰ)求|BS||DS|的取值范围;(ⅱ)将点S、F、T看作一个阿波罗尼斯圆上的三点,若△SFT外接圆的面积为81π8,求直线l的方程.2023-2024学年安徽省合肥168中学等名校联考高三(上)期末数学试卷参考答案与试题解析一、单选题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.)1.已知集合U ={1,2,3,4,5},A ={2,3},B ={x |x =2k ,k ∈Z },则B ∩∁U A =( ) A .{4}B .{2,4}C .{1,2}D .{1,3,5}解:因为U ={1,2,3,4,5},A ={2,3},B ={x |x =2k ,k ∈Z }, 所以∁U A ={1,4,5},则B ∩∁U A ={4}. 故选:A .2.复数(i −1i)3的虚部是( )A .﹣8B .﹣8iC .8D .8i解:(i −1i )3=(i −1i )(i −1i )2=−4(i −1i )−4(i +i )=﹣8i ,则复数(i −1i)3的虚部是:﹣8.故选:A .3.已知向量a →=(0,−2),b →=(1,t),若向量b →在向量a →上的投影向量为−12a →,则a →⋅b →=( )A .﹣2B .−52C .2D .112解:a →=(0,−2),b →=(1,t),则向量b →在向量a →上的投影为a →⋅b →|a →|×a→|a →|=−2t 4a →=−12a →, 解得t =1,所以a →⋅b →=−2. 故选:A .4.在△ABC 中,“C =π2”是“sin 2A +sin 2B =1”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件解:在△ABC 中,当C =π2时,则A +B =π2,故sin 2A +sin 2B =sin 2A +sin 2(π2−A)=sin 2A +cos 2A =1,故充分性成立,当A =120°,B =30°,满足sin 2A +sin 2B =1,但C ≠π2,故必要性不成立,综上所述,在△ABC 中,“C =π2”是“sin 2A +sin 2B =1”的充分不必要条件.故选:A .5.过点(0,﹣2)与圆x 2+y 2﹣4x ﹣1=0相切的两条直线的夹角为α,则cos α( ) A .14B .√154C .−14D .√104解:圆x 2+y 2﹣4x ﹣1=0可化为(x ﹣2)2+y 2=5,则圆心C (2,0),半径为r =√5; 设P (0,﹣2),切线为P A 、PB ,则PC =√22+22=2√2,△P AC 中,sin ∠APB 2=√52√2,所以cos ∠APB =1﹣2sin 2∠APB 2=1﹣2×58=−14,所以cos α=14.故选:A .6.A ,B ,C ,D ,E 五人站成一排,如果A ,B 必须相邻,那么排法种数共有( ) A .24B .120C .48D .60解:根据题意,将A ,B 看成一个整体,A ,B 的排列方法有A 22种方法,然后将这个整体与其他三个人一共4个元素进行全排列,即不同的排列方式有A 44,根据分步计数原理可知排法种数为A 22A 44=48.故选:C .7.若系列椭圆C n :a n x 2+y 2=1(0<a n <1,n ∈N *)的离心率e n =(12)n ,则a n =( )A .1−(14)nB .1−(12)nC .√1−(12)nD .√1−(14)n解:由系列椭圆C n :a n x 2+y 2=1(0<a n <1,n ∈N *),可得a 2=1a n,b =1, ∴离心率e n =√1−b 2a 2=√1−a n ,∴1﹣a n =[(12)n ]2,∴a n =1﹣(14)n .故选:A .8.已知等差数列{a n }(公差不为0)和等差数列{b n }的前n 项和分别为S n 、T n ,如果关于x 的实系数方程1003x 2﹣S 1003x +T 1003=0有实数解,那么以下1003个方程x 2﹣a i x +b i =0(i =1,2,…1003)中,有实数解的方程至少有( )个. A .499B .500C .501D .502解:根据题意,方程1003x 2﹣S 1003x +T 1003=0有实数解, 而S 1003=(a 1+a 1003)×10032=1003a 502,T 1003=(b 1+b 1003)×10032=1003b 502,则原方程等价于x 2﹣a 502x +b 502=0,若其有解,必有Δ=a 5022−4b 502≥0,设方程x 2﹣a 1x +b 1=0与方程x 2﹣a 1003x +b 1003=0的判别式分别为Δ1和Δ1003,则有Δ1+Δ1003=(a 12−4b 1)+(a 10032−4b 1003)=a 12+a 10032−4(b 1+b 1003)≥12(a 1+a 1003)2﹣4(b 1+b 1003)=12(2a 502)2﹣8b 502=2(a 5022−4b 502)≥0, 其中等号成立的条件是a 1=a 1003, 所以Δ1<0和Δ1003<0至多一个成立, 同理可证:Δ2<0和Δ1002<0至多一个成立, …,Δ501<0和Δ503<0至多一个成立,且Δ502≥0,故在所给的1003个方程x 2﹣a i x +b i =0中,有实数解的方程至少有502个. 故选:D .二、多选题(本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对得6分,部分选对得部分,有选错的得0分)9.已知一组数据:12,31,24,33,22,35,45,25,16,若去掉12和45,则剩下的数据与原数据相比,下列结论正确的是( ) A .中位数不变 B .平均数不变 C .方差不变D .第40百分位数不变解:将原数据按从小到大的顺序排列为12,16,22,24,25,31,33,35,45, 其中位数为25,平均数是(12+16+22+24+25+31+33+35+45)÷9=27,方差是19×[(−15)2+(−11)2+(−5)2+(−3)2+(−2)2+42+62+82+182]=8249,由40%×9=3.6,得原数据的第40百分位数是第4个数24. 将原数据去掉12和45,得16,22,24,25,31,33,35, 其中位数为25,平均数是(16+22+24+25+31+33+35)÷7=1867,方差是17×[(−747)2+(−327)2+(−187)2+(−117)2+(317)2+(457)2+(597)2]=191649,由40%×7=2.8,得新数据的第40百分位数是第3个数24,故中位数和第40百分位数不变,平均数与方差改变,故A ,D 正确,B ,C 错误. 故选:AD .10.双曲线C :x 2a 2−y 2b2=1(a >0,b >0),左、右顶点分别为A ,B ,O 为坐标原点,如图,已知动直线l 与双曲线C 左、右两支分别交于P ,Q 两点,与其两条渐近线分别交于R ,S 两点,则下列命题正确的是( )A .存在直线l ,使得AP ∥ORB .l 在运动的过程中,始终有|PR |=|SQ |C .若直线l 的方程为y =kx +2,存在k ,使得S △ORB 取到最大值D .若直线l 的方程为y =−√22(x ﹣a ),RS →=2SB →,则双曲线C 的离心率为√3解:对于A 项:与渐近线平行的直线不可能与双曲线有两个交点,故A 项错误;对于B 项:设直线l :y =kx +t ,与双曲线联立{y =kx +tx 2a 2−y 2b 2=1,得:(b 2﹣a 2k 2)x 2﹣2a 2ktx ﹣(a 2t 2+a 2b 2)=0,设P (x 1,y 1),Q (x 2,y 2),由根与系数关系得:x 1+x 2=2a 2kt b 2−a 2k 2,x 1x 2=−a 2b 2+a 2t 2b 2−a 2k2,所以线段PQ 中点N(x 1+x 22,y 1+y 22)=(a 2kt b 2−a 2k 2,a 2k 2tb 2−a 2k2+t), 将直线l :y =kx +t 与渐近线y =b a x 联立得点S 坐标为S(at b−ak ,bt b−ak ),将直线l :y =kx +t 与渐近线y =−b a x 联立得点R 坐标为R(−at b+ak ⋅btb+ak ),所以线段RS 中点M(a 2kt b 2−a 2k 2,a 2k 2tb 2−a 2k2+t),所以线段PQ 与线段RS 的中点重合,所以|PR|=|PQ|−|RS|2=|SQ|,故B 项正确; 对于C 项:由B 项可得R(−2a b+ak ,2b b+ak ),S △ORB =12|OB|×|y R |=12|OB||2bb+ak|,因为|OB |为定值,当k 越来越接近渐近线y =−b a x 的斜率−b a 时,|2bb+ak|趋向于无穷,所以S △ORB 会趋向于无穷,不可能有最大值,故C 项错误; 对于D 项:联立直线l 与渐近线y =b a x ,解得S(a 2√2b+a ab√2b+a ),联立直线l 与渐近线y =−b a x ,解得R(a 2−√2b+a ab√2b−a),由题可知,RS →=2SB →,所以y S ﹣y R =2(y B ﹣y S ),即3y S =y R +2y B , √2b+a=√2b−a,解得b =√2a ,所以e =√3,故D 项正确.故选:BD .11.如图所示,有一个棱长为4的正四面体P ﹣ABC 容器,D 是PB 的中点,E 是CD 上的动点,则下列说法正确的是( )A .直线AE 与PB 所成的角为π2B .△ABE 的周长最小值为4+√34C .如果在这个容器中放入1个小球(全部进入),则小球半径的最大值为√63D .如果在这个容器中放入4个完全相同的小球(全部进入),则小球半径的最大值为2√6−25解:A 选项,连接AD ,由于D 为PB 的中点,所以PB ⊥CD ,PB ⊥AD ,又CD ∩AD =D ,AD ,CD ⊂平面ACD , 所以直线PB ⊥平面ACD ,又AE ⊂平面ACD ,所以PB ⊥AE ,故A 正确;B 选项,把△ACD 沿着CD 展开与平面BDC 同一个平面内,连接AB 交CD 于点E ,则AE+BE的最小值即为AB的长,由于AD=CD=2√3,AC=4,cos∠ADC=CD 2+AD2−AC22CD⋅AD=(2√3)2+(2√3)2−422×23×23=13,cos∠ADB=cos(π2+∠ADC)=−sin∠ADC=−13,所以AB2=BD2+AD2﹣2BD•AD cos∠ADB=22+(2√3)2﹣2×2×2√3(−2√23)=16+16√63,故AB=√16+1663=4√1+63,△ABE的周长最小值为4+4√1+√63,B错误;C选项,要使小球半径最大,则小球与四个面相切,是正四面体的内切球,设球心为O,取AC的中点M,连接BM,PM,过点P作PF垂直于BM于点F,则F为△ABC的中心,点O在PF上,过点O作ON⊥PM于点N,因为AM=2,AB=4,所以BM=√AB2−AM2=2√3,同理PM=2√3,则MF=13BM=2√33,故PF=√PM2−MF2=4√6 3,设OF=ON=R,故OP=PF−OF=4√63−R,因为△PNO∽△PFM,所以ONFM=OPPM,即2√33=4√63−R2√3,解得R=√63,C正确;D选项,4个小球分两层(1个,3个)放进去,要使小球半径最大,则4个小球外切,且小球与三个平面相切,设小球半径为r,四个小球球心连线是棱长为2r的正四面体Q﹣VKG,由C选项可知,其高为2√63r,由C选项可知,PF是正四面体P﹣ABC的高,PF过点Q且与平面VKG交于S,与平面HIJ交于Z,则QS=2√63r,SF=r,由C选项可知,正四面体内切球的半径是高的14,如图正四面体P﹣HJI中,QZ=r,QP=3r,正四面体Q﹣VKG高为3r+2√63r+r=√63×4,解得r=2√6−25,D正确.故选:ACD.三、填空题(本大题共3小题,每小题5分,共15分)12.小于300的所有末尾是1的三位数的和等于3920.解:小于300的所有末尾是1的三位数是101,111,121, (291)是以101为首项,以10为公差的等差数列,所以小于300的所有末尾是1的三位数的和为S20=20×(101+291)2=3920.故答案为:3920.13.已知函数f(x)=ln(x+1)−axx+1,若f(x)⩾0恒成立,则a=1.解:由f(x)=ln(x+1)−axx+1,得f′(x)=1x+1−a(x+1)2=x−(a−1)(x+1)2,当a>0时,当x∈(﹣1,a﹣1)时,f′(x)<0,f(x)单调递减,当x∈(a﹣1,+∞)时,f′(x)>0,f(x)单调递增,∴f(x)min=f(a﹣1)=lna﹣(a﹣1),∵f(x)⩾0恒成立,∴lna﹣(a﹣1)⩾0,记g(a)=lna−(a−1),g′(a)=1a−1=1−aa,当a∈(0,1)时,g′(a)>0,g(a)单调递增,当a∈(1,+∞)时g′(a)<0,g(a)单调递减,∴g(a)max=g(1)=0,∴lna﹣(a﹣1)⩽0,又lna﹣(a﹣1)⩾0,∴lna﹣(a﹣1)=0,∴a=1.当a⩽0时,f′(x)>0,∴f(x)在(﹣1,+∞)上单调递增,∴当x∈(﹣1,0)时,f(x)<f(0)=0,与f(x)⩾0矛盾.综上,a的值为1.故答案为:1.14.已知抛物线C:y2=2px(p>0),点P为抛物线上的动点,点A(4−p2,0)与点P的距离|AP|的最小值为2,则p=2−√2,4,12.解:设P(x,y),|AP|2=[x−(4−p2)]2+y2=x2−2(4−p2)x+(4−p2)2+2px=x2−(8−3p)x+(4−p2)2=[x−(4−3p2)]2+8p−2p2,(i)当4−3p2⩾0,即0<p⩽83时,|AP|2有最小值8p﹣2p2,即|AP|有最小值√8p−2p2=2,解得p=2±√2,由于2+√2>83,故p=2−√2,(ii)当4−3p2<0,即p>83时,|AP|2有最小值(4−p2)2,即|AP|有最小值|4−p2|=2,解得p=4或12,综上,p的值为2−√2,4,12.故答案为:2−√2,4,12.四、解答题(本大题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步骤)15.(13分)在△ABC中,A,B,C的对边分别为a,b,c,已知b=√2,c=4,acosC+b=0.(1)求a;(2)已知点D在线段BC上,且∠ADB=3π4,求AD长.解:(1)因为在△ABC中,A,B,C的对边分别为a,b,c,a cos C+b=0,由余弦定理得a⋅a2+b2−c22ab+b=0,即a2+3b2﹣c2=0,又b=√2,c=4,则可得a=√10;(2)由余弦定理cosC=b2+a2−c22ab=2+10−162×√2×√10=−√55,所以sinC=√1−cos2C=2√5 5,因为∠ADB=3π4,所以∠ADC=π4,则在△ADC中,由正弦定理可得AD=AC⋅sinCsin∠ADC=√2×2√55√22=4√55.16.(15分)甲、乙两人进行射击比赛,每次比赛中,甲、乙各射击一次,甲、乙每次至少射中8环.根据统计资料可知,甲击中8环、9环、10环的概率分别为0.7,0.2,0.1,乙击中8环、9环、10环的概率分别为0.6,0.2,0.2,且甲、乙两人射击相互独立.(1)在一场比赛中,求乙击中的环数少于甲击中的环数的概率;(2)若独立进行三场比赛,其中X场比赛中甲击中的环数多于乙击中的环数,求X的分布列与数学期望.解:(1)设乙击中的环数少于甲击中的环数为事件A,则事件A包括:甲击中9环乙击中8环,甲击中10环乙击中8环,甲击中10环乙击中9环,则P(A)=0.2×0.6+0.1×0.6+0.1×0.2=0.2.(2)由题可知X的所有可能取值为0,1,2,3,由(1)可知,在一场比赛中,甲击中的环数多于乙击中的环数的概率为0.2,则P(X=0)=C30×0.20×(1−0.2)3=0.512,P(X=1)=C31×0.2×(1−0.2)2=0.384,P(X=2)=C32×0.22×(1−0.2)=0.096,P(X=3)=C33×0.23×(1−0.2)0=0.008,故X的分布列为所以E(X)=3×0.2=0.6.17.(15分)如图,圆台O1O2的轴截面为等腰梯形A1ACC1,AC=2AA1=2A1C1=4,B为底面圆周上异于A,C的点.(1)在平面BCC1内,过C1作一条直线与平面A1AB平行,并说明理由;(2)设平面A1AB∩平面C1CB=l,Q∈l,BC1与平面QAC所成角为α,当四棱锥B﹣A1ACC1的体积最大时,求sinα的取值范围.解:(1)取BC中点P,作直线C1P,则直线C1P即为所求,取AB中点H,连接A1H,PH,则有PH∥AC,PH=12AC,如图,在等腰梯形A 1ACC 1中,A 1C 1=12AC ,∴HP ∥A 1C 1,HP =A 1C 1, ∴四边形A 1C 1PH 为平行四边形,∴C 1P ∥A 1H ,又A 1H ⊂平面A 1AB ,C 1P ⊄平面A 1AB , ∴C 1P ∥平面A 1AB ;(2)延长AA 1,CC 1交于点O ,作直线BO ,则直线BO 即为直线l ,如图,过点B 作BO '⊥AC 于O ',∵平面A 1ACC 1⊥平面ABC ,平面A 1ACC 1∩平面ABC =AC ,BO '⊂平面ABC , ∴BO '⊥平面A 1ACC 1,即BO '为四棱锥B ﹣A 1ACC 1的高,在Rt △ABC 中,∠ABC =90°,BO ′=BA⋅BC AC ≤BA 2+BC 22AC =12AC ,当且仅当BA =BC 时取等号,此时点O '与O 2重合,∴梯形A 1ACC 1的面积S 为定值,四棱锥B ﹣A 1ACC 1的体积V B−A 1ACC 1=13S ⋅BO′,∴当BO '最大,即点O '与O 2重合时四棱锥B ﹣A 1ACC 1的体积最大, 又BO 2⊥AC ,BO 2=2,以O 2为原点,射线O 2A ,O 2B ,O 2O 1分别为x ,y ,z 轴的非负半轴,建立空间直角坐标系,在等腰梯形A 1ACC 1中,AC =2AA 1=2A 1C 1=4,此梯形的高ℎ=√AA 12−(AC−A 1C 12)2=√3, 显然A 1C 1为△OAC 的中位线,∴O(0,0,2√3),A(2,0,0),B(0,2,0),C 1(−1,0,√3), BC 1→=(−1,−2,√3),AB →=(−2,2,0),BO →=(0,−2,2√3),O 2A →=(2,0,0), 设BQ →=λBO →,λ∈R ,则AQ →=AB →+BQ →=AB →+λBO →=(−2,2−2λ,2√3λ),设平面QAC 的一个法向量n →=(x ,y ,z),则{n →⋅O 2A →=2x =0n →⋅AQ →=−2x +(2−2λ)y +2√3λz =0,取n →=(0,√3λ,λ−1), ∴sinα=|cos〈n →,BC 1→〉|=|n →⋅BC 1→||n →||BC 1→|=|−2×√3λ+√3(λ−1)|√(√3λ)2+(λ−1)×√(−1)+(−2)+(√3)2=√3|λ+1|2√2×√4λ−2λ+1,令t =λ+1,则sinα=√3|t|2√2×√4t −10t+7,当t =0时,sin α=0,当t ≠0时,0<sinα=√32√2×√7t2−10t +4=√32√2×√7(1t −57)+37≤√144,当且仅当t =75,即λ=25时取等号, 综上得0≤sinα≤√144,∴sin α的取值范围是[0,√144].18.(17分)已知函数f (x )=lnx ﹣ax (x ﹣1). (1)当a <0时,探究f ′(x )零点的个数; (2)当a >0时,证明:f(x)⩽2+a√a +8a−a−32. 解:(1)已知f (x )=lnx ﹣ax (x ﹣1),函数定义域为(0,+∞), 可得f ′(x)=1x −2ax +a =−2ax 2+ax+1x, 因为二次函数y =﹣2ax 2+ax +1的判别式的对称轴为x =14,且Δ=a 2+8a ,当a >0时,二次函数y =﹣2ax 2+ax +1的图象开口向下,此时Δ>0, 所以f ′(x )在(0,+∞)上有1个零点, 当a =0时,f ′(x)=1x在(0,+∞)上无零点;当a <0时,二次函数y =﹣2ax 2+ax +1的图象开口向上, 当Δ<0,即﹣8<a <0时,f ′(x )在(0,+∞)上无零点, 当Δ=0,即a =﹣8时,f ′(x )在(0,+∞)上有1个零点14,当Δ>0,即a <﹣8时,f ′(x )在(0,+∞)有2个不同的零点, 综上,当﹣8<a <0时,f ′(x )在(0,+∞)上无零点; 当a =﹣8时,f ′(x )在(0,+∞)上有1个的零点; 当a <﹣8时,f ′(x )在(0,+∞)有2个不同的零点;(2)证明:由(1)得,当a >0时,f ′(x )在(0,+∞)上有1个零点,不妨设零点为x0,此时ax02=ax0+12,解得x0=a+√a2+8a4a,当0<x<x0时,f′(x)>0,f(x)单调递增;当x>x0时,f′(x)<0,f(x)单调递减,所以f(x)≤f(x0)=lnx0−ax0(x0−1)=lnx0−ax02+ax0=lnx0−ax0+12+ax0=lnx0+ax0−12,不妨设g(x)=lnx﹣(x﹣1),函数定义域为(0,+∞),可得g′(x)=1x−1=1−xx,当0<x<1时,g′(x)>0,g(x)单调递增;当x>1时,g′(x)<0,g(x)单调递减,所以当x=1时,函数g(x)取得最大值,最大值g(1)=0,则lnx﹣(x﹣1)≤0成立,此时lnx0+ax0−12≤(x0﹣1)+ax0−12=(a+2)x02−32=(2+a)a+√a2+8a4a2−32=2+a√a+8a−a32.故f(x)⩽√a2+8a−a 3 2.19.(17分)阿波罗尼斯是古希腊著名数学家,他的主要研究成果集中在他的代表作《圆锥曲线》一书中.阿波罗尼斯圆是他的研究成果之一,指的是已知动点M与两定点Q,P的距离之比|MQ||MP|=λ(λ>0,λ≠1),λ是一个常数,那么动点M的轨迹就是阿波罗尼斯圆,圆心在直线PQ上.已知动点M的轨迹是阿波罗尼斯圆,其方程为x2+y2=4,定点分别为椭圆C:x2a2+y2b2=1(a>b>0)的右焦点F与右顶点A,且椭圆C的离心率为e=12.(1)求椭圆C的标准方程;(2)如图,过右焦点F斜率为k(k>0)的直线l与椭圆C相交于B,D(点B在x轴上方),点S,T 是椭圆C上异于B,D的两点,SF平分∠BSD,TF平分∠BTD.(ⅰ)求|BS||DS|的取值范围;(ⅱ)将点S、F、T看作一个阿波罗尼斯圆上的三点,若△SFT外接圆的面积为81π8,求直线l的方程.解:(1)设M(x,y),由题意|MF||MA|=√(x−c)2+y2√(x−a)2+y2=λ(常数),整理得x2+y2+2x−2aλ2λ2−1x+λ2a2−c2λ2−1=0,故{2c−2aλ2λ2−1=0λ2a2−c2λ2−1=−4,又ca=12,解得a=2√2,c=√2.∴b2=a2﹣c2=6,椭圆C的方程为x28+y26=1.(2)(ⅰ)由S△SBFS△SDF=12|SB|⋅|SF|⋅sin∠BSF12|SD|⋅|SF|⋅sin∠DSF=|SB||SD|,又S△SBFS△SDF=|BF||DF|,∴|BS||DS|=|BF||DF|,(或由角平分线定理得)令|BF||DF|=λ,则BF→=λFD→,设D(x0,y0),则有3x02+4y02=24,又直线l的斜率k>0,则x0∈(−2√2,√2),{x B=√2(λ+1)−λx0y B=−λy0,代入3x2+4y2﹣24=0,得3[√2(1+λ)−λx0]2+4λ2y02−24=0,即(λ+1)(5λ−3−√2λx0)=0,∵λ>0,∴λ=35−√2x0∈(13,1).(ⅱ)由(ⅰ)知,|SB||SD|=|TB||TD|=|BF||DF|,由阿波罗尼斯圆定义知,S,T,F在以B,D为定点得阿波罗尼斯圆上,设该圆圆心为C1,半径为r,与直线l的另一个交点为N,则有|BF||DF|=|NB||ND|,即|BF||DF|=2r−|BF|2r+|DF|,解得r=11|BF|−1|DF|.又S圆C1=πr2=818π,故r=922,∴1|BF|−1|DF|=2√29,又|DF|=√(x0−√2)2+y02=√(x0−√2)2+6−34x02=2√2−12x0,∴1|BF|−1|DF|=1λ|DF|−1|DF|=√2x03(2√2−12x0)−2√2−12x0=√2x03(2√2−12x0)=2√29,解得x0=−√22,y0=−√6−34x02=−3√104,∴k=0√2−x0=√52,∴直线l的方程为y=√52x−√102.。
合肥所有私立高中排名一览表
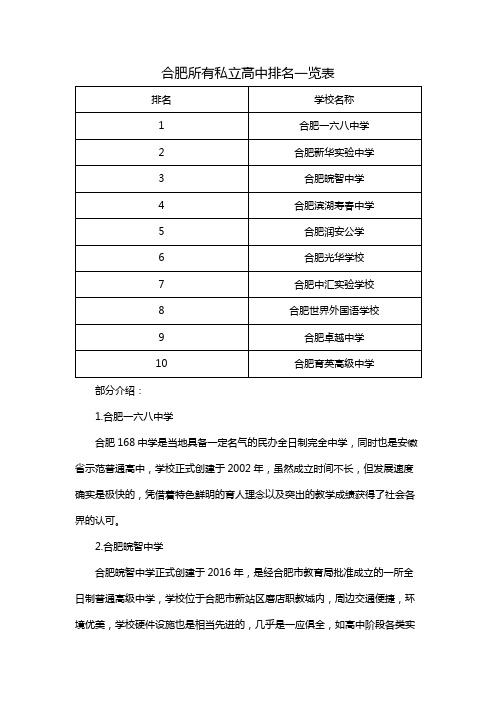
合肥所有私立高中排名一览表部分介绍:1.合肥一六八中学合肥168中学是当地具备一定名气的民办全日制完全中学,同时也是安徽省示范普通高中,学校正式创建于2002年,虽然成立时间不长,但发展速度确实是极快的,凭借着特色鲜明的育人理念以及突出的教学成绩获得了社会各界的认可。
2.合肥皖智中学合肥皖智中学正式创建于2016年,是经合肥市教育局批准成立的一所全日制普通高级中学,学校位于合肥市新站区磨店职教城内,周边交通便捷,环境优美,学校硬件设施也是相当先进的,几乎是一应俱全,如高中阶段各类实验室、图书室、音乐、美术室、心理咨询室、塑胶跑道绿茵球场和篮、排球场等,及专用功能教室都是具备的。
在师资力量方面,校内高薪聘请师德高尚、学术精湛的特级教师为教学督导,成功打造了一支务实高效执行力强的行政管理团队和以青年教师为主的精英教师团队,成立至今始终为人才的培养不懈努力着。
3.合肥滨湖寿春中学合肥滨湖寿春中学正式创建于2010年,学校共设有初中部与高中部,在校生达到了6000多人,并拥有着一支有500余名优秀教师组建而成的优秀教学团队。
教育教学设施设备配套先进,在住宿方面男女独立寝室各一栋,每间寝室均配有空调,也真正做到了孩子们在学校吃住学三合一,让家长们放心并安心。
4.合肥润安公学合肥润安公学正式创建于1993年,是一所集托育、幼儿园、小学、初中、高中五位一体的民办全日制寄宿制学校。
通过多年来的稳健发展,早已成为具备知名度与认可度的学校之一,在教学方面也形成了一定的特色,课程上,接轨BPYP、IBMYP、IGCSE、A-LEVEL、剑桥英语,整合国内外课程优势,形成了润安特色的中西合璧课程;在硬件设施方面也是相当完善的,建有教学楼、宿舍楼、实验室、图书馆、艺体中心、信息技术中心、运动场、游泳馆、文体馆、餐厅等,不仅如此更在2018年的合肥市教育教学质量综合评价中,荣获合肥市普通高中教育教学质量综合评价二等奖、四项进步奖。
合肥初中择校信息

1、名称:合肥市第四十二中学(合肥42中)性质:公办创校时间:1906年现任校长:郭艳华所属地区:合肥市庐阳区学校地址:合肥市庐阳区长江中路64号(市内乘1路、3路公交车到小东门站下)学校简介合肥四十二中是一所有百年历史的老校,整个校园环境很有古韵、文化气息,整个校园内的标识、标语,给人感觉走的是一种勤奋踏实、艰苦奋斗、励精图治的道路,每个楼层都有一曲诗篇。
学校也先后获得安徽省首批省级示范初中,安徽省体育传统项目学校,国家体育后备人才试点学校,全国布局调整示范初中等荣誉称号。
教育教学质量名列合肥市前茅,庐阳区重点中学之一。
学校现有47个教学班,学生总数3300余人,学校现有在岗教职工151人,其中全国体育教育先进工作者1名,全国初中信息技术优质课评比一等奖获得者1名,省级优秀教师1名,省级教坛新星6名,省级优质课评比一等奖获得者4名,市、区教坛新星及骨干教师43人,高级教师42人,占教师队伍的28%,一级教师78人。
2初中基本信息:班级设置:13年合肥四十二中初一分14个班级,班级人数最少的46人有2个班,最多52人的班级有4个班,招生人数共招收694名新生。
12年初一新生共分了18个班,每班约有55-60人左右。
有重点班。
根据历届在校家长评说,陈国昭老师,一直带的是重点班,老师为人也受到学生和家长的比较高的评价。
收费情况:今年42中择校费2万。
部分优秀学生有减免。
住宿情况:走读制作业量:根据班级、老师以及学生情况的不同,完成作业的时间也不同。
根据42中在校生反映,42中七年级作业语、数、外基本上要写到9点半-10点。
3 名师评说:陈国召:英语老师,上届14班班主任,42中名师,上届带2个班英语,除课本知识外,补充了大量课外知识,2个班英语平均成绩每次均名列年级1、2位,认真负责,深受学生爱戴,连续几届所带班级整体成绩名列前茅,带过2007届合肥市中考状元;。
阚汪洋:数学老师,上届3班班主任,数学教学能力强,和语文老师刘辉连续搭配几届,所带班级成绩优异;周宜奎:数学老师,上届7班班主任),上届第一次带班主任,普通班,数学教学水平高,所带班级成绩优秀。
合肥新华艺术高中招生简章

合肥新华艺术高中招生简章摘要:一、学校简介二、招生专业及计划三、报考条件及要求四、录取方式及优惠政策五、报名时间及地点六、联系方式正文:一、学校简介合肥新华艺术高中,位于美丽的安徽省合肥市,是一所具有丰富艺术教育底蕴的全日制普通高中。
学校创建于1998年,多年来致力于为学生提供优质的艺术教育,培养学生德、智、体、美全面发展。
我校秉持“以人为本,特色兴校,质量强校”的办学理念,努力打造艺术教育品牌。
二、招生专业及计划我校2023年招生专业包括:美术、音乐、舞蹈、戏剧影视表演等专业。
根据安徽省教育部门批准的计划,我校计划招生200人,其中美术专业50人,音乐专业50人,舞蹈专业50人,戏剧影视表演专业50人。
三、报考条件及要求1.报考美术、音乐、舞蹈、戏剧影视表演等专业的考生,需具备一定的艺术特长。
2.报考美术专业的考生,需参加我校组织的美术专业测试,测试内容包括素描、色彩等。
3.报考音乐、舞蹈、戏剧影视表演等专业的考生,需参加我校组织的专业测试,测试内容包括基本功、作品展示等。
4.考生需具备初中毕业及以上学历。
5.报考我校的考生,需参加全国普通高考。
四、录取方式及优惠政策1.根据考生艺术专业测试成绩,按照招生计划从高分到低分择优录取。
2.艺术专业测试成绩优异的考生,可获得不同程度的优惠政策,包括减免学费、发放奖学金等。
3.对于家庭经济困难的优秀学生,我校将提供助学金资助。
五、报名时间及地点1.报名时间:2023年4月1日至4月30日。
2.报名地点:合肥新华艺术高中招生办公室。
3.报名材料:考生身份证、户口本、学历证明、艺术特长证明等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
合肥168高中部招生条件2020
合肥一六八中学是合肥市教育局于2002年创办的一所现代化寄宿制中学,包含合肥一六八中学南校区(始信路校区)、合肥一六八中学东校区(淮海大道校区)和合肥一六八玫瑰园学校。
学校办学理念先进,管理科学,质量优秀,已成为省内前茅、国内一流、国际知名的多元化、集团化优质学校。
自2005年首届高考取得杰出成绩后,学校连续七年荣获合肥市“普通高中教学质量综合评价一等奖”;中考平均成绩2010年位居合肥13名、2011年位居合肥市前6;复读年级以绝对优势稳居安徽第一。
学校坚持科学发展观,全面贯彻党的教育方针,在“立足于升学预备教育,着眼于学生终身可持续发展”办学理念的指导下,大处着眼,小处着手,大力转变教育思想,努力提升办学品位,坚持走内涵发展之路,激活了自主创新欲望,激发了文化创造活力,推进了学校科学和谐发展。
学校先后获得“全国依法治校示范校”“北京2008奥林匹克教育示范校”、“全国和谐校园先进学校”“国家汉办汉语国际推广中小学基地”、“安徽省体育专项特色学校”、“安徽省花园式单位”、“合肥市平安校园”、“合肥市绿色学校”、“合肥市花园单位”、“合肥市卫生先进单位”、“合肥市维护社会稳定工作先进单位”、“合肥市德育工作先进单位”、“廉政文化建设示范单位”、“五四红旗团委”等多项殊荣。
学校以学生健康和谐发展为本,着力培养学生自主学习的意识与能力,培养学生自律的意识与能力。
学校通过社团活动,培养学生各类特长;通过开设各类校本课程,拓展学生的知识面;通过开展主题丰富的研究性学习和形式多样的社会实践活动,培养学生的创新意识和实践能力;通过开展德育主题教育,丰富学生德育体验,完善学生人格。
系列教育活动的开展,满足了不同兴趣爱好和个性特长学生的发展需求,培养了文理兼长、全面发展、具有国际视野的现代中学生。
学校先进的办学理念和前瞻性的教育创新,使大批优秀学生脱颖而出。
一六八中学素质教育的舞台上群星灿烂,光彩夺目。
近年来,300多名学生以其杰出的创造力和优异的成绩在数、理、化、生奥赛、国际模拟联合国比赛、省航模比赛、科技创新大赛等各类竞赛中取得了令人瞩目的成绩,其获奖级别之高、数量之多、科类之全,均位居安徽省前列。
2010年,夺取全国机器人大赛获国家金奖,填补了安徽省此项奖励空白。
自2005年首届高考取得杰出成绩后,学校连续七年荣获合肥市“普通高中教学质量综合评价一等奖”,2009年摘取安徽省理科状元;2011年高考升学率居全市榜首,全省高考文理科前50名中,一六八中学各占据五席。
合肥市高考文理科前十名中,一六八中学学生共占八席。
今年,学校荣获北京大学“中学校长实名制推荐”资质。
学校通过专家引领、同伴互助、行动研究、外出培训、在岗进修、自觉内省、蓝青工程、“四子工程”、“六个一工程”、名师工程等多种途径与方式促使教师转变教育教学观念,改善教育教学行为,提高教育教学水平。
学校逐步建立起一支献身教育事业、具有高尚品德、教育观念先进、治学精神严谨、基础知识宽厚、专业知识精深、教学水平一流、育人艺术精湛、不断创新的教师队伍。
一六八中学正以饱满的精神面貌,与时俱进,开拓创新,向着全国一流名校的既定目标奋力前进!。
