寿险精算 第三讲 人寿保险趸缴纯保费共78页文档
合集下载
保险精算课程三(寿险精算)
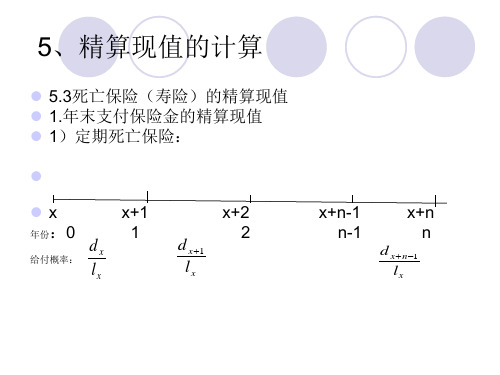
N N Dx
x
xn
x
xh
2.终身寿险的年缴纯保费
h Px
Ax ax:h|
Mx Nx Nxh
3.两全保险的年缴纯保费
P h x:n|
Ax:n| ax:h |
Mx
M xn Dxn Nx Nxh
课堂练习:
1.某人30岁投保20年期,延期10年,5年限期缴费的定期 人寿险,保险金额为100000元,求年缴纯保险费?
N x N x1 Dx
S x N x N x1
(Ia) x
Sx Dx
( Ia) x
S x 1 Dx
( Ia) x:n |
S x 1
S x n1 Dx
nN x n1
作业:
1.某人30岁(女)时投保寿险,约定45岁前死亡给付保险金 150000元,40岁至60岁之间死亡给付保险金为100000 元,60岁以后给付保险金50000元,求趸缴纯保险费?
(In| A)x (IA)1x:n| n|Ax
Rx Rxn nM xn N M xn
Dx
Dx
标准递减也可以看作:
A1 x:n |
A1 x:n 1|
A1 x:n 2|
A1 x:1|
nM x [Rx1 Rxn1 ] Dx
课堂练习
(x)=30,定期寿险保单。第一年死亡给付1000元, 第二年死亡给付1200元,第三年1400元,这样依次按 200元比例递增,n=20,求保险金的精算现值:
x:n |
Dx
Ax:n|
Mx
M xn Dx
Dxn
Ax
Mx Dx
m| Ax
M xm Dx
A1 x :n|
Mx
M Dx
x
xn
x
xh
2.终身寿险的年缴纯保费
h Px
Ax ax:h|
Mx Nx Nxh
3.两全保险的年缴纯保费
P h x:n|
Ax:n| ax:h |
Mx
M xn Dxn Nx Nxh
课堂练习:
1.某人30岁投保20年期,延期10年,5年限期缴费的定期 人寿险,保险金额为100000元,求年缴纯保险费?
N x N x1 Dx
S x N x N x1
(Ia) x
Sx Dx
( Ia) x
S x 1 Dx
( Ia) x:n |
S x 1
S x n1 Dx
nN x n1
作业:
1.某人30岁(女)时投保寿险,约定45岁前死亡给付保险金 150000元,40岁至60岁之间死亡给付保险金为100000 元,60岁以后给付保险金50000元,求趸缴纯保险费?
(In| A)x (IA)1x:n| n|Ax
Rx Rxn nM xn N M xn
Dx
Dx
标准递减也可以看作:
A1 x:n |
A1 x:n 1|
A1 x:n 2|
A1 x:1|
nM x [Rx1 Rxn1 ] Dx
课堂练习
(x)=30,定期寿险保单。第一年死亡给付1000元, 第二年死亡给付1200元,第三年1400元,这样依次按 200元比例递增,n=20,求保险金的精算现值:
x:n |
Dx
Ax:n|
Mx
M xn Dx
Dxn
Ax
Mx Dx
m| Ax
M xm Dx
A1 x :n|
Mx
M Dx
寿险精算学3..讲课讲稿

▪ 净均衡原则的实质是在统计意义上的收支平衡。是在大数场合下, 收费期望现时值等于支出期望现时值 。
净保费厘定的基本假定
❖ 三个基本假定条件:
▪ 同性别、同年龄、同时参保的被保险人的剩余寿命是独立同分布 的。
▪ 被保险人的剩余寿命分布可以用经验生命表进行拟合。 ▪ 保险公司可以预测将来的最低平稳收益(即预定利率)。
xtdt
趸缴纯保费的方差
❖ 方差公式
V ( z ta ) E ( r z t 2 ) E ( z t) 2 0 n e 2 tfT ( t) d E t ( z t) 2
❖记
2A1 x:n
ne2t
0
fT(t)dt
(相当于利息力翻倍以后求N年期寿险的趸缴保费)
❖ 所以方差等价为
Va(ztr)2Ax1:n(Ax1:n)2
寿险产品趸缴净保费的厘定
1 厘定原则和建模假设 2 建模思想 3 死亡即刻赔付趸缴净保费 4 死亡年末赔付趸缴净保费 5 不同时刻赔付的换算关系
建模思想
折算到保单签订日得到期望赔付值
要有一条共同的线索 将这些因素综合在一起考虑
什么时候 发生赔付
赔付额 等于多少
钱的 时间价值
赔付事件 发生概率
基本符号
❖ 假定:( x )岁的人,保额为1元,N年定期寿险
❖ 基本函数关系
1 , t n bt 0 , t n
vt vt , t 0
vt , t n
zt
btvt
0
,
t
n
趸缴纯保费的厘定
❖ 符号:
1
A x:n
❖ 厘定:
1
n
Ax:n E(zt) 0 zt fT(t)dt
nvt 0
净保费厘定的基本假定
❖ 三个基本假定条件:
▪ 同性别、同年龄、同时参保的被保险人的剩余寿命是独立同分布 的。
▪ 被保险人的剩余寿命分布可以用经验生命表进行拟合。 ▪ 保险公司可以预测将来的最低平稳收益(即预定利率)。
xtdt
趸缴纯保费的方差
❖ 方差公式
V ( z ta ) E ( r z t 2 ) E ( z t) 2 0 n e 2 tfT ( t) d E t ( z t) 2
❖记
2A1 x:n
ne2t
0
fT(t)dt
(相当于利息力翻倍以后求N年期寿险的趸缴保费)
❖ 所以方差等价为
Va(ztr)2Ax1:n(Ax1:n)2
寿险产品趸缴净保费的厘定
1 厘定原则和建模假设 2 建模思想 3 死亡即刻赔付趸缴净保费 4 死亡年末赔付趸缴净保费 5 不同时刻赔付的换算关系
建模思想
折算到保单签订日得到期望赔付值
要有一条共同的线索 将这些因素综合在一起考虑
什么时候 发生赔付
赔付额 等于多少
钱的 时间价值
赔付事件 发生概率
基本符号
❖ 假定:( x )岁的人,保额为1元,N年定期寿险
❖ 基本函数关系
1 , t n bt 0 , t n
vt vt , t 0
vt , t n
zt
btvt
0
,
t
n
趸缴纯保费的厘定
❖ 符号:
1
A x:n
❖ 厘定:
1
n
Ax:n E(zt) 0 zt fT(t)dt
nvt 0
保险精算第三讲

1 死亡即刻赔付
1.1 n年期定期寿险 1.2 终身寿险 1.3 延期m年 终身寿险
1.4 n年期生存保险
1.5 n年期两全保险
1.6 延期m年的 n年期两全保险
1.7 递增寿险 1.8 递减寿险
1 , t m bt 0 , t m
v , t m zt bt vt 0 , t m
e2 t fT (t )dt E ( zt )2
m
1.4 n年期生存保险
1.5 n年期两全保险
记
2 m
Ax e2 t fT (t )dt
m
1.6 延期m年的 n年期两全保险
1.7 递增寿险 1.8 递减寿险
所以方差等价于
Var ( zt ) A ( m Ax )
,x 0
1.6 延期m年的 n年期两全保险
1.7 递增寿险 1.8 递减寿险
求: (1)
10
Ax
(2)Var(zt )
2 计算基数
例3.3答案
S ( x t ) (1) fT (t ) 0.04e0.04t S ( x) A e m x
10 0.06 t
1 死亡即刻赔付
1.1 n年期定期寿险 1.2 终身寿险 1.3 延期m年 终身寿险
10
0.04e
0.04 t
dt 0.04 e0.1t dt 0.147 0.04e0.16t
10
1.4 n年期生存保险
1.5 n年期两全保险
(2) Ax e
2 m 10
0.12 t
0.16 Var ( zt ) m2 Ax ( m Ax )2 0.0288
保险精算学趸缴纯保费

一年递增m次
将每一个保单年度分为均等的m个时间段, 如被保险人在第一保单年度的第一个1/m年内死
亡,则在死亡时立即给付保险金1/m元, 如被保险人在第一保单年度的第二个1/m年内死
亡,则在死亡时立即给付保险金2/m元, 。。。。。 如被保险人在第二保单年度的第一个1/m年内死
亡,则在死亡时立即给付保险金1+1/m元, 如被保险人在第二保单年度的第二个1/m年内死
趸缴纯保费的厘定
符号:Ax:1n
趸缴纯保费厘定
1
Ax:n
E(zt ) vn n px
e n n px
现值随机变量的方差:
Var(zt ) v2n n px (vn n px )2
21
Ax:n
1
( Ax:n
)2
5、n年定期两全保险
定义
被保险人投保后如果在n年期内发生保险责任范围内的死 亡,保险人即刻给付保险金;如果被保险人生存至n年期 满,保险人在第n年末支付保险金的保险。它等价于n年生 存保险加上n年定期寿险的组合。
m
e2 t
fT
(t)dt
所以方差等价于
Var(zt )
2 m
Ax
(m
Ax )2
例4.3.3
假设(x)投保延期10年的终身寿险, 保额1元。
保险金在死亡即刻赔付。 已知
0.06,S (x) e0.04x , x 0
求:
(1) 10 Ax (2)Var(zt )
例4.3.3答案
(1)
保险利益: 如被保险人在第一保单年度内死亡,
则在死亡时立即给付保险金1元, 如被保险人在第二保单年度内死亡,
则在死亡时立即给付保险金2元, 。。。。。
寿险精算学课件-(3)精选全文

费用分类
成分
投资费用
(1)投资分析成本(2)购买、销售及服务成本
1、新契约费 (1)销售费用,包括代理人佣金及宣传广告费(2)风
保
险分类,包括体检费用(3)准备新保单及记录
险 2、维持费 (1)保费收取及会计
费
(2)给付变更及理陪选择权准备
用
(3)与保单持有人进行联络
3、营业费用 (1)研究、开发新险种费用(2)精算及一般法律服务 (3)普通会计(4)税金、许可证等费用
0
Ax
P( Ax )ax
0
P( Ax )
Ax ax
方差确定
Var(L)
Var[vt
P(
Ax
)
1
v d
k
1
]
Var[v(k 1)(s1)
P
(
Ax
)
1
v d
k
1
]
Var[(vs1 P( Ax ) )vk1] d
记Z s
vs1
P( Ax d
)
,Z
k
vk 1
由于分数剩余寿命和整值剩余寿命相互独立,
(
Z
k
)
方差的确定
终身寿险场合有
E
(Z
2 k
)
2 Ax,Var(Zk
)
2 Ax
-
Ax
2
在分数期死亡服从均匀分布的假定下,有
E(Zs )
E
v
s-1
P( Ax )
d
i
P( Ax ) d
Var(Zs
)
Var
v
s-1
P( Ax d
)
Var (v s -1 )
寿险精算学(第3版)课件:期缴保费

• 以例5.8进行讲解,每年的净保费等于133.07元,每年的 毛保费等于178.47元,也就是说每年缴纳的毛保费里面有 45.4元是覆盖费用的费用保费。但实际上第一年的真实费 用等于:
40.5+205+78%178.47=279.71
• 第一年收取的费用45.4元是完全不够支付第一年的真实费 用的。费用不够的部分是由保险公司现行垫付。这就产生 了寿险产品的新业务压力(new business strain)。也就 是说寿险公司只要新卖出一份保险产品,第一年就要承担 初年费用不够的资金压力。
毛保费的构成图示
经营费用
• 所谓经营费用是指保险公司支出的除了风险赔付之外, 其他维持 保险公司正常运作的所有费用支出的统称。
• 经营费用包括管理费用和佣金两大部分, 其中, 管理费用通常由 投资费用和保险费用两部分构成。
– 投资费用包括与投资相关的分析、 购买、 销售及服务成本。 由 于这些费用直接与投资收入的产生有关, 所以投资费用通常从总投 资收入中扣除, 在传统寿险产品保费计算时通常不单独考虑。
缴费频率与赔付频率不一致时, 期缴净保费的厘定
• 实务中, 有时保费的缴纳频率会和赔付的给付频率不一致
– 比如有可能保费每年期初缴纳, 但死亡即刻给付; – 再比如保费每年缴纳m 次, 而死亡年末赔付或死亡即刻赔付。
• 这时,期缴净保费的厘定, 通常需要借助不同频率之间精 算函数的变换来实现。
例5.6
未来损失变量
• 未来损失变量(Future Loss),t时刻的未来损失变量记作Lt
Lt =未来支出贴现到t 时刻的现值 - 未来收入贴现到t 时刻的现值
– 如果Lt >0, 意味着对保险人而言未来收不抵支, 将会产生亏损 (loss) – 如果Lt <0, 意味着对保险人而言未来收入会大于支出, 将会产生利润
40.5+205+78%178.47=279.71
• 第一年收取的费用45.4元是完全不够支付第一年的真实费 用的。费用不够的部分是由保险公司现行垫付。这就产生 了寿险产品的新业务压力(new business strain)。也就 是说寿险公司只要新卖出一份保险产品,第一年就要承担 初年费用不够的资金压力。
毛保费的构成图示
经营费用
• 所谓经营费用是指保险公司支出的除了风险赔付之外, 其他维持 保险公司正常运作的所有费用支出的统称。
• 经营费用包括管理费用和佣金两大部分, 其中, 管理费用通常由 投资费用和保险费用两部分构成。
– 投资费用包括与投资相关的分析、 购买、 销售及服务成本。 由 于这些费用直接与投资收入的产生有关, 所以投资费用通常从总投 资收入中扣除, 在传统寿险产品保费计算时通常不单独考虑。
缴费频率与赔付频率不一致时, 期缴净保费的厘定
• 实务中, 有时保费的缴纳频率会和赔付的给付频率不一致
– 比如有可能保费每年期初缴纳, 但死亡即刻给付; – 再比如保费每年缴纳m 次, 而死亡年末赔付或死亡即刻赔付。
• 这时,期缴净保费的厘定, 通常需要借助不同频率之间精 算函数的变换来实现。
例5.6
未来损失变量
• 未来损失变量(Future Loss),t时刻的未来损失变量记作Lt
Lt =未来支出贴现到t 时刻的现值 - 未来收入贴现到t 时刻的现值
– 如果Lt >0, 意味着对保险人而言未来收不抵支, 将会产生亏损 (loss) – 如果Lt <0, 意味着对保险人而言未来收入会大于支出, 将会产生利润
第三章 寿险的趸缴净保费

1
1
延期m年n年两全险
m|
Ax:n
m|
A
1 x:n
m| Ax:n Ax:m Ax m:n
1
1
例.已知: 计算20| Ax
1) 2.5%; 2)死亡力恒定; 3) e x 10.0.
0
7. 递增寿险 假定赔付金额为剩余寿命的线性递增函数 一年递增一次(n年定期寿险)
趸缴净保费
1 x:m
A
1 x:m n
A
1 x m:n
A x:m
1
( x) 岁的人,保额1元,延期m年n年生存险 假定:
T mn 0, ZT bT vT m n v , T mn
趸缴净保费
m|
Ax:n E ( Z ) v
1
mn
m n px A x:m Ax m:n m Ex n Ex m
基本函数关系
0, T n 0 , T n bT ZT bT vT n 1 , T n v , T n 趸缴净保费 1 n n 1
Ax:n ( Ax:n ) E(ZT ) v n px e
n px
随机变量现值方差
Var ( Z ) E ( Z 2 ) E 2 ( Z ) v 2 n n px (v n n px ) 2 v n px n qx A ( A )
净均衡原理 保险人收取的净保费应该恰好等于未来支出的保险赔付金。 (Arrow:风险转移公平原则) 趸缴纯保费=未来保险金给付的精算现值 死亡赔付方式:(1)死亡即刻赔付;(2)死亡年末赔付。
第一节 连续型寿险的趸缴纯保费
死亡即刻赔付就是指如果被保险人在保障期内发生保险责任 范围内的死亡 ,保险公司将在死亡事件发生之后,立刻给予 保险赔付。它是在实际应用场合,保险公司通常采用的理赔 方式。 由于死亡可能发生在被保险人投保之后的任意时刻,所以死 亡即刻赔付时刻是一个连续随机变量,它距保单生效日的时 期长度就等于被保险人签约时的剩余寿命。
寿险精算 第三讲 人寿保险趸缴纯保费78页文档

寿险精算 第三讲 人。——马·格林 47、在一千磅法律里,没有一盎司仁 爱。— —英国
48、法律一多,公正就少。——托·富 勒 49、犯罪总是以惩罚相补偿;只有处 罚才能 使犯罪 得到偿 还。— —达雷 尔
50、弱者比强者更能得到法律的保护 。—— 威·厄尔
61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
谢谢!
48、法律一多,公正就少。——托·富 勒 49、犯罪总是以惩罚相补偿;只有处 罚才能 使犯罪 得到偿 还。— —达雷 尔
50、弱者比强者更能得到法律的保护 。—— 威·厄尔
61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
谢谢!
