2018届人教A版算法初步单元测试13
2018秋新版高中数学人教A版必修3习题：第一章算法初步 1.1.1
1.1.1 算法的概念课时过关·能力提升一、基础巩固1.算法的每一步都应该是确定的,能有效执行的,并且得到的结果是确定的,而不是模棱两可的.这是指算法的( )A.确定性B.普遍性C.有限性D.不唯一性2.下列各式中,T的值不能用算法求解的是( )A.T=12+22+32+42+…+1 002B.T=12+13+14+15+…+150C.T=1+2+3+4+5+…D.T=1-2+3-4+5-6+…+99-100C中的求和不符合算法的有限性,∴C中T的值不能用算法求解.3.一个算法的步骤如下,若输入x的值为-3,则输出z的值为( )第一步,输入x的值.第二步,计算x的绝对值y.第三步,计算z=2y-y.第四步,输出z的值.A.4B.5C.6D.8x=-3,∴y=|x|=3.∴z=23-3=5.4.已知直角三角形两直角边长分别为a,b,求斜边长c的一个算法分下列三步:①计算c=a2+b2;②输入直角三角形两直角边长a,b的值;③输出斜边长c的值.其中正确的顺序是( )A.①②③B.②③①C.①③②D.②①③,再计算,最后输出的顺序执行.5.有如下算法:第一步,输入x的值.第二步,若x≥0成立,则y=x;否则,y=x2.第三步,输出y的值.若输入x=-2,则输出y= .x=-2后,x=-2≥0不成立,则计算y=x2=(-2)2=4,输出y=4.6.完成解不等式2x+2<4x-1的算法:第一步,移项并合并同类项,得 .第二步,在不等式的两边同时除以x的系数,得 .2x<-3 x >327.给出算法:第一步,输入n=6.第二步,令i=1,S=0.第三步,判断i≤n是否成立.若不成立,则输出S,结束算法;若成立,则执行下一步.第四步,令S的值加i,仍用S表示,令i的值加1,仍用i表示,返回第三步.该算法的功能是 .:n=6,i=1,S=0,i=1≤6成立;S=0+1=1,i=1+1=2,i=2≤6成立;S=1+2,i=2+1=3,i=3≤6成立;S=1+2+3,i=3+1=4,i=4≤6成立;S=1+2+3+4,i=4+1=5,i=5≤6成立; S=1+2+3+4+5,i=5+1=6,i=6≤6成立;S=1+2+3+4+5+6,i=6+1=7,i=7≤6不成立,输出S=1+2+3+4+5+6.1+2+3+4+5+6的值8.给出下列算法:第一步,输入x的值.第二步,当x>1时,计算y=x+2;否则计算y=4-x.第三步,输出y.当输出y=4时,x= .,y ={x+2,x>1,4-x,x≤1.当x>1时,令x+2=4,得x=2.当x≤1时,x=-12.令4-x=4,解得12或29.试写出判断圆(x-a)2+(y-b)2=r2(r>0)和直线Ax+By+C=0(A2+B2≠0)位置关系的算法.:第一步,输入圆心的坐标(a,b)、直线方程的系数A,B,C和半径r.第二步,计算z1=Aa+Bb+C.第三步,计算z2=A2+B2.第四步,计算d =|z1|z2.第五步,若d>r,则输出“相离”;若d=r,则输出“相切”;若d<r,则输出“相交”.10.有蓝和黑两个墨水瓶,但现在却错把蓝墨水装在了黑墨水瓶中,黑墨水装在了蓝墨水瓶中,要求将其互换,请你设计算法解决这一问题.:第一步,取一只空的墨水瓶,设其为白色.第二步,将黑墨水瓶中的蓝墨水装入白瓶中.第三步,将蓝墨水瓶中的黑墨水装入黑墨水瓶中.第四步,将白瓶中的蓝墨水装入蓝墨水瓶中,交换结束.二、能力提升1.阅读下面的四段话,其中不是算法的是( )A.求1×2×3的值,先计算1×2=2,再计算2×3=6,最终结果为6B.解一元一次方程的步骤是去分母、去括号、移项、合并同类项、系数化为1C.今天,我上了8节课,真累D.求1+2+3+4+5的值,先计算1+2=3,再计算3+3=6,6+4=10,10+5=15,最终结果为15项中,都是解决问题的步骤,故A,B,D项中所叙述的是算法;C项中是说明一个事实,不是算法.2.阅读下面的算法:第一步,输入两个实数a,b.第二步,若a<b,则交换a,b的值;否则,不交换a,b的值.第三步,输出a.这个算法输出的是( )A.a,b中较大的数B.a,b中较小的数C.原来的a的值D.原来的b的值,若a<b,则交换a,b的值,那么a是a,b中较大的数;否则a<b不成立,即a≥b,那么a也是a,b中较大的数.3.小明中午放学回家自己煮面条吃,有下面几道工序:①洗锅盛水2分钟;②洗菜6分钟;③准备面条及佐料2分钟;④用锅把水烧开10分钟;⑤煮面条3分钟.以上各道工序,除了④之外,一次只能进行一道工序.小明要将面条煮好,最少要用的分钟数为( )A.13B.14C.15D.23洗锅盛水2分钟、④用锅把水烧开10分钟(同时②洗菜6分钟、③准备面条及佐料2分钟)、⑤煮面条3分钟,共为15分钟.4.给出如下算法:第一步,输入a,b,c的值.第二步,当a>b时,令“最小值”为b;否则,令“最小值”为a.第三步,当“最小值”大于c时,令“最小值”为c;否则,“最小值”不变.第四步,输出“最小值”.若输入a=3,b=1,c=-2,则输出的“最小值”是 .a,b,c的值,输出其中的最小值,由于c<b<a,则输出-2.2★5.一个算法如下:第一步,令S=0,i=1.第二步,若i不大于10,则执行下一步;否则执行第五步.第三步,计算S+i且将结果代替S.第四步,用i+2代替i,返回第二步.第五步,输出S.则运行以上步骤输出的结果为 .1,第二次运算的结果为S=1+3,依此类推,此算法的功能为计算S=1+3+5+7+9的值,故输出S=25.6.已知球的表面积为16π,求球的体积.写出解决该问题的算法.R,再由球的体积公式可求得体积.:第一步,取S=16π.第二步,计算R =S4π.第三步,计算V =43πR3.第四步,输出V的值.★7.某班共有50人,要找出在一次数学测试中及格(60分及60分以上)的成绩.试设计一个算法.:第一步,把计数变量n的初始值设为1.第二步,输入一个成绩r,比较r与60的大小,若r≥60,则输出r,然后执行下一步;若r<60,则直接执行下一步.第三步,使计数变量n的值增加1.第四步,判断计数变量n与学生个数50的大小,若n≤50,则返回第二步;若n>50,则结束算法.。
2018届人教A版 算法 检测卷
专题12 算法
一．基础题组
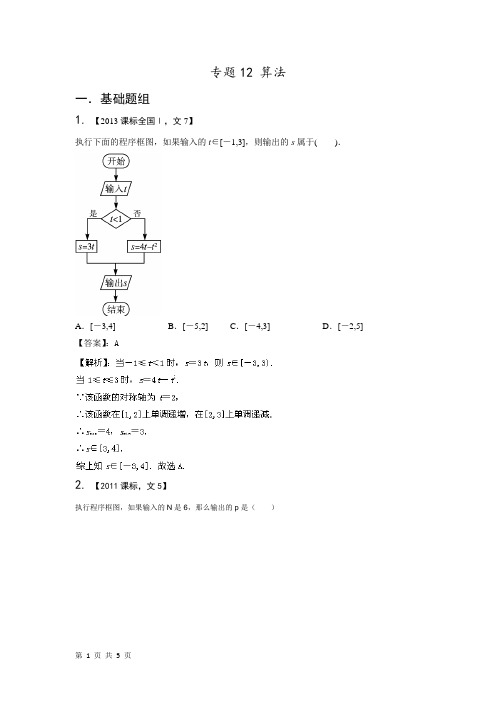
1.【2013课标全国Ⅰ，文7】
执行下面的程序框图，如果输入的t∈[－1,3]，则输出的s属于()．
A．[－3,4] B．[－5,2] C．[－4,3] D．[－2,5] 【答案】：A
2.【2011课标，文5】
执行程序框图，如果输入的N是6，那么输出的p是（）
A. 120
B.720
C.1440
D.5040
【答案】B
3.【2016高考新课标1，文10】执行右面的程序框图,如果输入的0,1,x y ==n =1,则输出,x y 的值满足
（A ）2y x =
（B ）3y x =
（C ）4y x =
（D ）5y x =
【答案】C
【解析】
试题分析：第一次循环：0,1,2x y n ===,
第二次循环：1,2,32
x y n ===, 第三次循环：3,6,32x y n =
==,此时满足条件2236x y +≥,循环结束,3,62x y ==,满足4y x =．故选C
考点：程序框图与算法案例
【名师点睛】程序框图基本是高考每年必考知识点,一般以客观题形式出现,难度不大,求解此类问题一般是把人看作计算机,按照程序逐步列出运行结果.
二．能力题组
1. 【2014全国1，文9】执行右面的程序框图，若输入的,,a b k 分别为1,2,3，则输出的M =( )
A.203
B.72
C.165
D.158
【答案】D
t=，则输出的n= 2. 【2015高考新课标1，文9】执行右面的程序框图，如果输入的0.01
（）
（A）5（B）6（C）10（D）12
【答案】C
考点：程序框图。
2018年高中数学人教A版必修3第1章算法初步1.1.2.3习题含解析
第3课时循环结构课时过关能力提升、基础巩固i •下列关于循环结构的说法正确的是 A. 可能不含顺序结构 B. 可能不含条件结构 C.含有顺序结构和条件结构 D.以上说法都不正确 答答案1CA.i < 19?B.i > 19? D.i<21?2.执行如图所示的程序框图，输出的 S 的值为（）D.15C.7 A.1 B.3 解析：开始时k=0,S=0. 第一次循环,k=0<3,S=0+20=1,k= 0+1 = 1, 第二次循环,k=1<3,S=1 + 21= 3,k= 1+1 = 2,第三次循环，k=2<3,S=3+22=7,k= 2+1 = 3.此时不满足条件k<3,输出结果S,即输出7.故选 答案：|C C. 3•某同学设计的程序框图如图所示 ,用来计算和式12 + 22+ 32+…+ 202的值,则在判断框中应填写（） C.i>21?,y= 12 X )= 60,x= 5+1 = 6;,y= 60 X )= 360,x= 6+1 = 7;x=7 < 6不成立 输出y=360. 答案：|D5•执行如图所示的程序框图，输出的k 的值为（ ）A.4B.5C.6D.7解析］第一次循环得S=0+2°=1,k=1; 第二次循环得S=1 + 21 = 3,k=2; 第三次循环得S=3+23=11,k=3, 第四次循环得S=11 + 211= 2059,k=4,但此时不满足条件，退出循环，输出k=4. 答案：|A6•执行如图所示的程序框图，输出的S 的值为 _____________解析］该程序框图中含有当型循环结构 止循环，则在判断框中应填写i< 21?.，判断框内的条件不成立时循环终止•由于是当i= 21时开始终答案:D A.3 4•执行如图所示的程序框图 B.12解析:x= 3,y= 1; x= 3 < 6成立,y= 1 X3= 3,x=3+1 =4; x=4 < 6成立 ,y= 3 X 4= 12,x= 4+1=5;x= 5 < 6成立 x=6 < 6成立解析］该程序框图的运行过程是：i= 1,S=1i= 1+ 1 = 2S=2 >(1 + 1)= 4i= 2> 5不成立i= 2+ 1 = 3S=2 ><4+1)=10i= 3> 5不成立i= 3+ 1 = 4S=2 ><10 + 1)=22i= 4> 5不成立i= 4+ 1 = 5S=2 <22 + 1)=46i= 5> 5不成立i= 5+ 1 = 6S=2 <46 + 1)=94i= 6> 5 成立答案：|947•如图是一个算法的程序框图，若此程序运行结果为S=720，则在判断框中应填入关于是 __________ .解析:k=10,S=1,判断条件成立,S=10X1=10,k=10-1=9;k的判断条件判断条件成立，S=10X9=90,k=9-1=8; 判断条件成立,S=90X8=720,k= 8-仁7;判断条件不成立，输出S=720,从而关于k 的条件是k > 8?”. 答案：k >8?8•执行如图所示的程序框图 若输入n 的值为4,则输出s 的值为 ______________解析:由程序框图可知 M 表示及格人数,N 表示不及格人数，所以q答案:q!=1¥1解析］第一步运算结果第二步运算结果 第三步运算结果 第四步运算结果:s=1,i= 2（i < 4 成立）; :s=2,i= 3（i < 4 成立）; :s=4,i= 4（i < 4 成立）;:s=7,i= 5（i < 4不成立），程序结束，故输出s 的值为9•如图是计算某年级 入 500名学生期末考试（满分为100分）及格率q 的程序框图，则图中空白框内应填 （=1 ]gfi ■:10.画出计算1 -- 的值的一个程序框图人教版2018-2019学年高中数学必修3习题（方法一）当型循环结构如图①（方法二）直到型循环结构如图②1•执行如图所示的程序框图，则输出S=（图①图②、能力提升A.2B.6C.15D.31解析：第一次满足条件，循环，S=1+仁2,k=2;第二次满足条件，循环，S=2+22=6,k=3;第三次满足条件，循2 环，S=6+3 =15，k=4;第四次不满足条件，退出循环，输出S=15选C.2•执行如图所示的程序框图，如果输入a=4,那么输出n的值为（）A.2B.3C.4D.5解析：若输入a=4,则执行P=0，Q= 1,判断0<1成立，进行第一次循环；P=1，Q= 3,n=1,判断1<3成立，进行第二次循环；P=5,Q=7,n=2,判断5<7成立，进行第三次循环；P=21,Q=15,n=3,判断21<15不成立，故输出n =3.3•阅读如图的程序框图，若输出S的值为52,则判断框内可填写（）A.i> 10?B.i<10?C.i>9?D.i< 9?4•阅读如图的程序框图，则输出的S等于（）答案:B 5•执行两次如图所示的程序框图 ，若第一次输入的a 的值为-1.2，第二次输入的a 的值为 输出a 的值是 _______ ，第二次输出a 的值是 ______ .解析：|根据输入的a 的值的不同而执行不同的程序 •由程序框图可知：当 a=-1.2 时,•/ a< 0, ••• a=-1.2+ 1=-0.2,a<0,a=- 0.2+1 = 0.8,a> 0. •/ 0.8<1,二输出 a=0.8.当 a=1.2 时，•/ a > 1,.・.a= 1.2-1= 0.2. •/ 0.2<1,「.输出 a=0.2. 答案 :|0.8 0.2★ 6.执行如图所示的程序框图，若输入x=- 5.2，则输出y 的值为 _________ .A.40B.38C.32 1.2，则第一次/ 辑Ai/In|/ ttlliy /解析］输入x=-5.2后，该程序框图的运行过程是：x=- 5.2,y=0,i=0,y=|- 5.2-2|=7.2,i= 0+ 1=1,x= 7.2,i= 1 > 5不成立；y=|7.2-2|=5.2,i= 1+ 1 = 2,x= 5.2,i= 2> 5不成立；y=|5.2-2|=3.2,i= 2+ 1 = 3,x= 3.2,i= 3>5不成立；y=|3.2-2|=1.2,i= 3+ 1 = 4,x=1.2,i= 4>5不成立；y=|1.2-2|=0.8,i= 4+ 1 = 5,x= 0.8,i= 5> 5成立;输出y=0.8.7•求使1 + 2+3+4+5+…+n < 100成立的最大自然数n的值，画出程序框图分析：由题目可获取以下主要信息：① 1 + 2+3+4+5+…+n < 100为关于n的不等式；②设计求n的最大自然数的算法.解答本题可先思考如何设计循环变量及循环体，再关注每一次循环后输出的变量的情况是否符合题目的要求• 解：|程序框图：★ 8•相传古代印度国王舍罕要褒赏他聪明能干的宰相达依尔（国际象棋的发明者），问他需要什么，达依尔说：国王只要在国际象棋的棋盘第一个格子上放一粒麦子，第二个格子上放两粒，第三个格子上放四粒,以后按此比例每一格加一倍，一直放到第64格（国际象棋8疋=64格）,我就感恩不尽，其他什么也不要了•”国王想：这有多少，还不容易！”让人扛来一袋小麦，但不到一会儿就全用没了，再扛来一袋很快又没有了，结果全印度的粮食用完还不够，国王很奇怪•一个国际象棋棋盘一共能放多少粒小麦？试用程序框图表示其算法• 分析］根据题目可知：第一格放1粒，1 = 20，第二格放2粒，2=21，第三格放4粒，4=22，第四格放8粒，8=23，第六十四格放263粒•则此题就转化为求1 + 21 + 22+ 23+ 24+…+ 263的和的问题•我们可弓I入一个累加变量S,—个计数变量i，累加64次就能算出一共有多少粒小麦•解一个国际象棋棋盘一共能放1+21+22+23+24+ - + 263粒小麦•程序框图：。
算法初步单元测试题
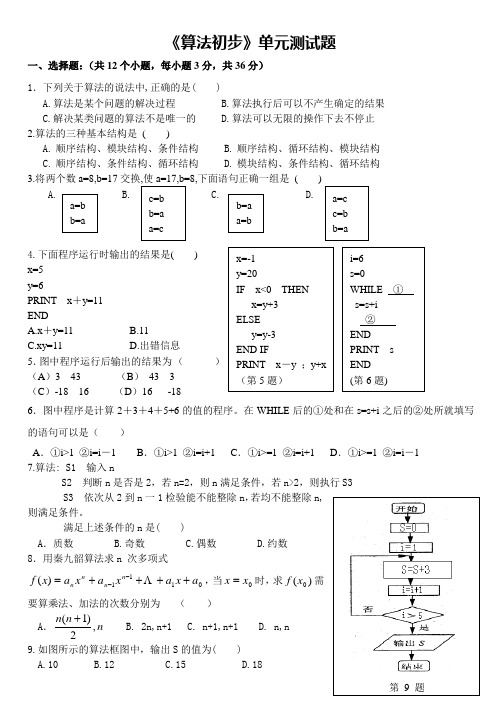
《算法初步》单元测试题一、选择题：（共12个小题，每小题3分，共36分）1．下列关于算法的说法中,正确的是( )A.算法是某个问题的解决过程B.算法执行后可以不产生确定的结果C.解决某类问题的算法不是唯一的D.算法可以无限的操作下去不停止2.算法的三种基本结构是( )A. 顺序结构、模块结构、条件结构B.顺序结构、循环结构、模块结构C.顺序结构、条件结构、循环结构D. 模块结构、条件结构、循环结构3.将两个数a=8,b=17下面语句正确一组是(A. B.C.D.4.下面程序运行时输出的结果是( )x=5y=6PRINTx＋y=11ENDA.x＋y=11B.11C.xy=11D.出错信息5．图中程序运行后输出的结果为（）（A）3 43 （B）43 3（C）-18 16 （D）16 -186．图中程序是计算2＋3＋4＋5+6的值的程序。
在WHILE后的①处和在s=s+i之后的②处所就填写的语句可以是（）A．①i>1 ②i=i－1 B．①i>1 ②i=i+1 C．①i>=1 ②i=i+1 D．①i>=1 ②i=i－17.算法: S1 输入nS2 判断n是否是2，若n=2，则n满足条件，若n>2，则执行S3S3 依次从2到n一1检验能不能整除n，若均不能整除n,则满足条件。
满足上述条件的n是( )A．质数 B.奇数 C.偶数 D.约数8．用秦九韶算法求n 次多项式111)(axaxaxaxf nnnn++++=--，当xx=时，求)(xf需要算乘法、加法的次数分别为（）A．nnn,2)1(+B. 2n,n+1C. n+1,n+1D. n,n9.如图所示的算法框图中，输出S的值为( )10.下列各数中最小的数是 ( )A.)9(85B.)6(210C.)4(1000D. )2(111111111.如右图所示的程序是用来( )A ．计算3×10的值B ．计算93的值C ．计算103的值 D ．计算1×2×3×…×10的值12．为了在运行程序之后得到输出16，键盘输入x 应该是( )A ． 3或-3B ． -5C ．5或-3D ．5或-5 二、填空题(共4小题，每小题3分，共12分)13.两个正整数120与252的最小公倍数为 ;14.下列各数)8(75．)7(210．(3)1200．)2(111111中最小的数是_________；15.该程序输出的n 的值是________；16．一个算法如下：第一步，S 取值0，i 取值1.第二步，若i 不大于12，则执行下一步；否则执行第六步．第三步，计算S ＋i 并将结果代替S.第四步，用i ＋2的值代替i.第五步，转去执行第二步．第六步，输出S.则运行以上步骤输出的结果为__________．三、解答题：17．试分别用辗转相除法和更相减损术求840与1764、440与556的最大公约数。
2018届人教A版 算法 单元测试
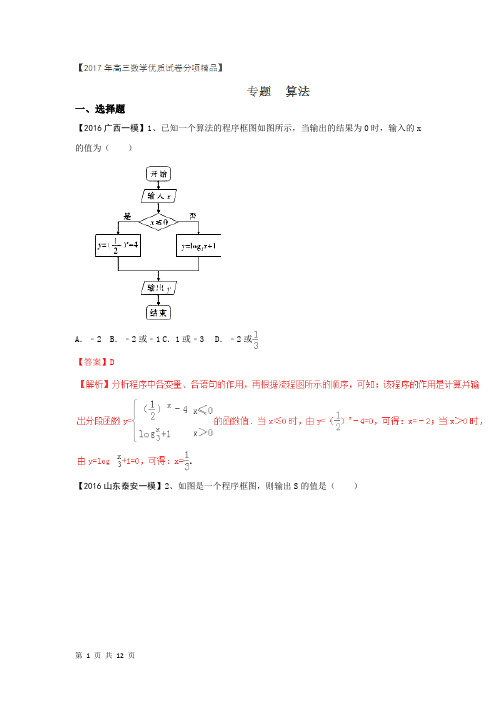
一、选择题【2016广西一模】1、已知一个算法的程序框图如图所示，当输出的结果为0时，输入的x 的值为（）A．﹣2 B．﹣2或﹣1 C．1或﹣3 D．﹣2或【答案】D【2016山东泰安一模】2、如图是一个程序框图，则输出S的值是（）A．84 B．35 C．26 D．10【答案】B【解析】当k=1时，不满足退出循环的条件，执行循环后，S=1，k=3；当k=3时，不满足退出循环的条件，执行循环后，S=10，k=5；当k=5时，不满足退出循环的条件，执行循环后，S=35，k=7；当k=7时，满足退出循环的条件，故输出的S值为35.【2016山东日照一模】3、执行如图所示的程序框图，输出的i为（）A．4 B．5 C．6 D．7【答案】C【2016山东济宁一模】4、执行如图所示的程序框图，若输入的x， y∈R，那么输出的S 的最大值为（）A．0 B．1 C．2 D．3【答案】C【2016山东滨州二模】5、执行如图所示的程序框图，如果输入的2016=N ，那么输出的=S （ ）A ．2015131211+⋅⋅⋅+++B ．!20151!31!211+⋅⋅⋅+++C ．2016131211+⋅⋅⋅+++D ．!20161!31!211+⋅⋅⋅+++ 【答案】D【2016宁夏吴忠模拟】6、执行如图所示的程序框图，若输出的结果为21，则判断框中应填（ ）A ．i ＜5B ．i ＜6C ．i ＜7D ．i ＜8【答案】C【2015吉林长春三模】7、阅读如图所示的程序框图，运行相应的程序，若输出的S为，则判断框中填写的内容可以是（）A．n=6 B．n＜6 C．n≤6 D．n≤8【答案】C【2016四川绵阳三诊】8、执行如图所示程序框图，则输出的n为（）A ．4B ．6C ．7D ．8【答案】D【2016山东济南3月模拟】9、公元263年左右，我国数学家刘徽发现当圆内接多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了割圆术。
2018年高中数学人教A版必修3第1章算法初步1.3.2习题含解析
人教版2018-2019学年高中数学必修 3习题第2课时进位制课时过关能力提升13.33 ⑷是（ ）A.十进制数 C.三进制数2•下列写法正确的是 A.858（8）B.865（7）C.121（3）D.68（6）解析:k 进制中各位上的数字均小于k,故A,B,D 错误•3•已知k 进制数32501 （k ）,则k 不可能是（ ）A.5B.6C.7D.84.101（2）转化为十进制数是（ ）A.2B.5C.20D.1012105.下列各数中最大的是（ ）A.110（2）B.18C.16（8）D.20（5）解析：| 110（2）=1 X22+ 1 X21 + 0疋0= 6;16（8）=1 ^81+6X8°= 14;20（5）= 2^51+0X5°= 10.则最大数是 答案：|B6.312⑷化为十进制数后的个位数字是_________ . 2107.把十进制数93化为二进制数为 _______ 解析］以2作为除数相应得出的除法算式为、基础巩固B.四进制数 D.二进制数18.I即93=1011101 (2) 答案：| 1011101 (2)8.二进制数中的最大四位数化为十进制数是_____________解析：最大的四位二进制数是 1111（2），化为十进制数为1怎3+ 1怎2+ 1 >2+1 = 15. 答案：| 159•把98（5）转化为九进制数为 __________ .—鞘---------- 11o解析：98（5）= 9拓 +8拓=53,故 98（5）=58（9）. 答案:58（9）10.求将127（8）化为六进制数时，最高数位上的数字• 解：T 127（沪1 X82+2 X8+7=87,「. 127（8）=223（6）.解析:3|血殛3] 63 A 21 0 3TT Q 3]T 10 1答案：|D3.已知k 进制数132与十进制数30相等，那么k 等于（ ）A.-7B.4C.-7 或 4D.7解析：|由题意得1乂2+3 *+2 >°=30，即k 2+ 3k-28=0,解得k=4或k=- 7（舍）.故选B. 答案：B 4.计算机中常用的十六进制是逢16进1的数制，采用数字0— 9和字母A — F 共16个记数符号，这些十八进制 0 1 2 3 4 56789 A B C D E F 十进制0 1 2 3 4 5 6 7 8 9101112131415例如，用十六进制表示：E+D = 1B ，则A X B = （ ） A.6EB.72C.5FD.B0•••127（ 8）化为六进制数后的最高数位上的数字是 2.二、能力提升11.01（9）化为十进制数为（） A.9B.11C.82解析：101（9）=1 X92+0 X91+1 >90= 82. 答案：|C2.把十进制数189化为三进制数，则末位数是（D.1010 25.21（7）+ 個4）= ___ .1010★ 6.古时候，当边境有敌人入侵时，守边的官兵通过在烽火台上点火向国内报告.如图，烽火台上点火表示二进制数1,不点火表示数字0,约定二进制数对应十进制的单位是 1 000,请你计算一下，这组烽火台表示有 ___________________ 名敌人入侵.解析:：由题图可知这组烽火台表示的二进制数为11011,它表示的十进制数为11011（2）= 27,因为对应十进制的单位是1000，所以入侵敌人的人数为27000.答案 :|27 0007.已知175（8）=120+r,求正整数r. 解：|175（8）=1 X82+7 X81 + 5 X8°=125,••• 125=120+r. ••• r= 5,即所求正整数r 为5.★ 8.已知44（紆=36把67（k）转化为十进制数. 解：|由题意得36=4>k1 + 4>k0,^ k= 8.故67（k）= 67（8）=6 4+7 X°=55.。
2018学年高中数学必修三人教A版 )练习：第一章 算法初
第一章算法初步1.1 算法与程序框图1.1.1 算法的概念A级基础巩固一、选择题1．下列四种自然语言叙述中，能称作算法的是()A．在家里一般是妈妈做饭B．做米饭需要刷锅、淘米、添水、加热这些步骤C．在野外做饭叫野炊D．做饭必须要有米解析：算法是做一件事情或解决一类问题的程序或步骤，故选B.答案：B2．下列关于算法的说法正确的是()A．一个算法的步骤是可逆的B．描述算法可以有不同的方式C．算法可以看成是按照要求设计好的有限的确切的计算序列，并且这样的步骤或序列只能解决当前问题D．算法只能用一种方式显示解析：由算法的定义可知A、C、D错．答案：B3．给出下面一个算法：第一步，给出三个数x，y，z.第二步，计算M＝x＋y＋z.第三步，计算N＝13M.第四步，得出每次计算结果．则上述算法是()A．求和B．求余数C．求平均数D．先求和再求平均数解析：由算法过程知，M为三数之和，N为这三数的平均数．答案：D4．一个算法步骤如下：S1，S取值0，i取值1；S2，如果i≤10，则执行S3；否则，执行S6；S3，计算S＋i并将结果代替S；S4，用i＋2的值代替i；S5，转去执行S2；S6，输出S.运行以上步骤后输出的结果S＝()A．16 B．25C．36 D．以上均不对解析：由以上计算可知：S＝1＋3＋5＋7＋9＝25.答案：B5．有如下算法：第一步，输入不小于2的正整数n.第二步，判断n是否为2.若n＝2，则n满足条件；若n>2，则执行第三步．第三步，依次从2到n－1的检验能不能整除n，若不能整除，则n满足条件．则上述算法满足条件的n是()A．质数B．奇数C．偶数D．约数解析：根据质数、奇数、偶数、约数的定义可知，满足条件的n 是质数．答案：A二、填空题6．给出下列算法：第一步，输入x的值．第二步，当x>4时，计算y＝x＋2；否则执行下一步．第三步，计算y＝4－x.第四步，输出y.当输入x＝0时，输出y＝________．解析：因为0<4，执行第三步，所以y＝4－0＝2.答案：27．下面是作y＝|x|图象的算法，请将算法补充完整．第一步，当x>0时，作出第一象限的角平分线．第二步，当x＝0时，即为原点．第三步，______________________________________________.解析：依据算法解决的问题知，第三步应为“当x<0时，作出第二象限的角平分线．”答案：当x<0时，作出第二象限的角平分线8．如下算法：第一步，输入x的值；第二步，若x≥0，则y＝x；第三步，否则，y ＝x 2；第四步，输出y 的值．若输出的y 值为9，则x ＝________．解析：根据题意可知，此为求分段函数y ＝⎩⎪⎨⎪⎧x ，x ≥0，x 2，x <0的函数值的算法，当x ≥0时，x ＝9；当x <0时，x 2＝9，所以x ＝－3.答案：9或－3三、解答题9．写出求1×2×3×4×5×6的算法．解：第一步，计算1×2得到2.第二步，将第一步的运算结果2乘3，得到6.第三步，将第二步的运算结果6乘4，得到24.第四步，将第三步的运算结果24乘5，得到120.第五步，将第四步的运算结果120乘6，得到720.10．设计一个解方程x 2－2x －3＝0的算法．解：算法如下：第一步，移项，得x 2－2x ＝3.①第二步，①式两边加1，并配方得(x －1)2＝4.②第三步，②式两边开方，得x －1＝±2.③第四步，解③得x ＝3或x ＝－1.第五步，输出结果x ＝3或x ＝－1.B 级 能力提升1．结合下面的算法：第一步，输入x .第二步，判断x 是否小于0，若是，则输出x ＋2；否则，执行第三步．第三步，输出x －1.当输入的x 的值为－1，0，1时，输出的结果分别为( )A ．－1，0，1B ．－1，1，0C ．1，－1，0D ．0，－1，1解析：根据x 值与0的关系选择执行不同的步骤．答案：C2．求过P (a 1，b 1)，Q (a 2，b 2)两点的直线斜率有如下的算法，请将算法补充完整：S 1 取x 1＝a 1，y 1＝b 1，x 2＝a 2，y 2＝b 2.S 2 若x 1＝x 2，则输出斜率不存在；否则，________． S 3 输出计算结果k 或者无法求解信息．解析：根据直线斜率公式可得此步骤．答案：k ＝y 2－y 1x 2－x 13．鸡兔同笼问题：鸡和兔各若干只，数腿共100条，数头共30只，试设计一个算法，求鸡和兔各有多少只．解：第一步，设有x 只鸡，y 只兔，列方程组⎩⎪⎨⎪⎧x ＋y ＝30，①2x ＋4y ＝100.② 第二步，②÷2－①，得y ＝20.第三步，把y ＝20代入①，得x ＝10.第四步，得到方程组的解⎩⎪⎨⎪⎧x ＝10，y ＝20. 第五步，输出结果，鸡10只，兔20只．。
最新-2018学年高中数学 第一章 算法初步单元测试 新人教A版必修3 精品
4.读程序
甲:
INPUT i s=0 WHILE i<=1000 s=s+i i=i+1 WEND PRINT s END
乙:
INPUT i s=0 DO s=s+i i=i-1 LOOP UNTIL i<1 PRINT s END'
其中输入甲中i=1,乙中i=1000,输出结果判断正确的是( ) A.程序不同,结果不同 B.程序不同,结果相同 C.程序相同,结果不同 D.程序相同,结果相同 答案:B
解析:图甲中用的是当型循环结构,输出结果是 s=1+2+3+…+1000;
而图乙中用的是直到型循环结构,输出结果是 s=1000+999+…+3+2+1.可见这两图的程序不同,但输出结果
19.(12分)已知平面内A,B两点的坐标分别为A(x1,y1)､ B(x2,y2),求A､B两点间的距离,写出算法,并画出程序框图.
解:算法如下:
第一步,输入x1,y1,x2,y2. 第二步,计算z1=(x1-x2)2. 第三步,计算z2=(y1-y2)2. 第四步,计算 d z12 z22 . 第五步,输出d,算法结束.
相同,故选B.
5.程序框图(如下图所示)能判断任意输入的数x的奇偶性,其 中判断框内的条件是( )
A.m=0? B.x=0? C.x=1? D.m=1? 解析:阅读程序易知,判断框内应填m=1?,应选D. 答案:D
6.840和1764的最大公约数是( )
A.84
B.12
C.168
D.252
2018届人教A版 算法初步与程序框图 单元测试
算法初步与程序框图一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．下列程序运行的结果是( )A ． 1, 2 ,3B ． 2, 3, 1C ． 2, 3, 2D ． 3, 2, 1【答案】C2．把十进制73化成四进制后，其末位数字是( )A ．０B ．１C ．２D ．3【答案】B3．阅读下列程序： 输入x ；if x ＜0， then y ＝32x π+； else if x ＞0， then y ＝52x π-；else y ＝0；输出 y ．如果输入x ＝－2，则输出结果y 为( )A ．π－5B ． －π－5C ． 3＋πD ． 3－π 【答案】D4．计算机中常用十六进制，采用数字0～9和字母A ～F 共16个计数符号与十进制得对应关系如下表：例如用十六进制表示有D+E ＝1B ，则A ×B=( )A ． 6EB ． 7C C ． 5FD ． B0【答案】A5．把11化为二进制数为( )A ．1 011(2)B ．11 011(2)C ．10 110(2)D ．0 110(2)【答案】A6．为了在运行下面的程序之后得到输出y ＝16，键盘输入x 应该是( )A ．3或3-B ．5-C ．5-或5D ．5或3-【答案】C 7．读程序对甲乙两程序和输出结果判断正确的是( )A ．程序不同结果不同B ．程序不同,结果相同C ．程序相同结果不同D ．程序相同,结果相同 【答案】B8．已知一个算法：第一步，；第二步，如果，则，输出；否则执行第三步；第三步，如果，则，输出，否则输出“无解” 如果，那么执行这个算法的结果是( ) A ．3 B ．6 C ．2 D ． 无解 【答案】C9．用秦九韶算法求多项式()543254321f x x x x x x =+++++, 当2x =时的值的过程中，做的乘法和加法次数分别为( ) A ．4，5 B ．5，4 C ．5，5 D ．6，5 【答案】C10．在程序框图中，算法中间要处理数据或计算，可分别写在不同的( )A ．处理框内B ．判断框内C ．输入、输出框内D ．终端框内 【答案】A11．将八位数135（8）化为二进制数为( )A．1110101（2）B．1010101（2）C．1011101（2）D．1111001（2）【答案】C12．根据右边的结构图，总经理的直接下属是( )A．总工程师和专家办公室B．开发部C．总工程师、专家办公室和开发部D．总工程师、专家办公室和所有七个部【答案】C二、填空题(本大题共4个小题，每小题5分，共20分，把正确答案填在题中横线上) 13．已知某算法的流程图如图所示，则程序运行结束时输出的结果为．【答案】（27，－5）14．228与1995的最大公约数是。
2018届人教A版算法初步单元测试10
2017-2018学年度xx学校xx月考卷一、选择题(共15小题,每小题5.0分,共75分)1.下列对赋值语句的描述正确的是()①可以给变量提供初值；②可以将表达式的值赋给变量；③可以给一个变量重复赋值；④不能给同一变量重复赋值．A．①②③B．①②C．②③④D．①②④2.程序框图符号“”可用于()A．输出a＝10B．赋值a＝10C．判断a＝10D．输入a＝13.下列关于算法的说法正确的是()A．一个算法的步骤是可逆的B．描述算法可以有不同的方式C．算法可以看成按照要求设计好的有限的确切的计算序列，并且这样的步骤或序列只能解决当前问题D．算法只能用一种方式显示4.在画程序框图时，如果一个框图需要分开来画，要在断开处画上()A．流程线B．注释框C．判断框D．连接点5.根据指定条件决定是否重复执行一条或多条指令的控制结构称为() A．条件结构B．循环结构C．递归结构D．顺序结构6.给出下列程序：若输出的A的值为120，则输入的A的值为()A． 1B． 5C． 15D． 1207.利用秦九韶算法求多项式7x3＋3x2－5x＋11在x＝23的值时，下列数中用不到的是()A． 164B． 3 767C． 86 652D． 85 1698.下列关于程序框的功能描述正确的是()A． (1)是处理框；(2)是判断框；(3)是终端框；(4)是输入、输出框B． (1)是终端框；(2)是输入、输出框；(3)是处理框；(4)是判断框C． (1)和(3)都是处理框；(2)是判断框；(4)是输入、输出框D． (1)和(3)的功能相同；(2)和(4)的功能相同9.把十进制数73化成四进制数后，其末位数字是()A． 0B． 1C． 2D． 310.下列各数中，最小的是()A． 101 010(2)B． 111(5)C． 32(8)D． 54(6)11.给出下面4个问题：①输入一个数x，输出它的绝对值；②求函数f(x)＝的函数值；③求面积为6的正方形的周长；④求三个数a，b，c中的最大数．其中可以用条件语句来描述其算法的有()A． 1个B． 2个C． 3个D． 4个12.如图所示的程序运行后输出的结果为()A． 9B． 11C． 13D． 1513.下列程序的功能是()A．求1×2×3×4×…×10 000的值B．求2×4×6×8×…×10 000的值C．求3×5×7×9×…×10 001的值D．求满足1×3×5×…×n＞10 000的最小正整数n14.在循环语句中，下列说法正确的是()A． UNTIL型循环可以无限循环B． WHILE型循环可以无限循环C．循环语句中必须有判断D． WHILE型循环不能实现UNTIL型循环的功能15.已知程序如图，若输入x，y的值分别为6,6，则输出的结果为()A． 6,6B．－2,10C． 2,10D． 6,10二、填空题(共5小题,每小题5.0分,共25分)16.将八进制数5 027(8)化成十进制数为________17.已知一个三角形的三边边长分别为2,3,4，将求其面积的一个算法补充完整：第一步，取a＝2，b＝3，c＝4；第二步，计算p＝________；第三步，计算S＝第四步，输出S的值等于________.18.当a的值为10时，“PRINT “a＝”；a”在屏幕上的输出结果为________．19.已知两点A(7，－4)，B(－5,6)，完成求线段AB的垂直平分线的算法：S1求线段AB的中点C的坐标，得C点坐标为________________；S2求直线AB的斜率，得________；S3求线段AB的垂直平分线的斜率，得________；S4求线段AB的垂直平分线的方程，得________.20.完成下列进位制之间的转化：101 101(2)＝______＝________(7)．三、解答题(共0小题,每小题12.0分,共0分)答案解析1.【答案】A【解析】根据赋值语句的特点判定．选A.2.【答案】B【解析】图形符号“”是处理框，它的功能是赋值、计算，不是输出、判断和输入，故选B.3.【答案】B【解析】由算法的定义可知A、C、D错，B对.4.【答案】D【解析】程序框图的概念.5.【答案】B【解析】根据循环结构的定义可知.6.【答案】A【解析】该程序的功能是计算A×2×3×4×5的值，则120＝A×2×3×4×5，故A＝1，即输入A的值为1.7.【答案】D【解析】f(x)＝((7x＋3)x－5)x＋11，v1＝7×23＋3＝164，v2＝164×23－5＝3 767，v3＝3 767×23＋11＝86 652，所以选项D中的值用不到．8.【答案】B【解析】根据程序框图的规定，(1)是终端框，(2)是输入、输出框，(3)是处理框，(4)是判断框.9.【答案】B【解析】73÷4＝18…1，18÷4＝4…2，4÷4＝1…0，1÷4＝0…1，把余数从下往上排序：1 021.即：73＝1 021(4)．其末位数字是1.10.【答案】C【解析】101 010(2)＝1×25＋0×24＋1×23＋0×22＋1×21＋0×20＝32＋8＋2＝42，111(5)＝1×52＋1×51＋1×50＝31，32(8)＝3×81＋2×80＝26，54(6)＝5×61＋4×60＝34.又42＞34＞31＞26，故最小的是32(8)．11.【答案】C【解析】在算法中需要逻辑判断的都要用到条件语句，其中①②④都需要进行逻辑判断，故都要用到条件语句，③只要顺序结构就能描述其算法．12.【答案】C【解析】当运行到第三次时，i＝5，S＝13，此时i＝4，不满足条件结束循环，故S＝13.13.【答案】D【解析】方法一S是累乘变量，i是计数变量，每循环一次，S乘以i一次且i增加2.当S＞10 000时停止循环，输出的i值是使1×3×5×…×n＞10 000成立的最小正整数n.方法二最后输出的是计数变量i，而不是累乘变量S.14.【答案】C【解析】UNTIL型循环和WHILE型循环实现的功能是一样的，只是看不同条件下哪种方便而已．15.【答案】D【解析】由于x＞0，所以执行ELSE后面的语句．16.【答案】2 583【解析】将八进制数5 027(8)化成十进制数＝5×83＋0＋2×81＋7×80＝2 583.17.【答案】【解析】由计算三角形的面积的海伦—秦九韶公式，得p＝，S＝＝.18.【答案】a＝10【解析】PRINT语句可将用双引号括起来的字符串显示在屏幕上，从而应输出“a＝10”．19.【答案】(1,1)－y－1＝(x－1)【解析】根据算法的步骤和相关的知识来解答本题.20.【答案】4563【解析】1×25＋0×24＋1×23＋1×22＋0×2＋1＝45.∵45/7＝6…3，6/7＝0…6，将余数从下到上连起来，即63.故答案为：45；63.。
2018单元滚动检测卷高考数学理人教A版全国通用：精练
单元滚动检测十三 推理与证明、算法、复数考生注意：1．本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共4页．2．答卷前，考生务必用蓝、黑色字迹的钢笔或圆珠笔将自己的姓名、班级、学号填写在相应位置上．3．本次考试时间120分钟，满分150分． 4．请在密封线内作答，保持试卷清洁完整．第Ⅰ卷(选择题 共60分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．(2016·青岛质检)设i 是虚数单位，复数1＋a i2－i为纯虚数，则实数a 的值为( ) A ．2B ．－2C ．－12D.122．观察下列各式：71＝7,72＝49,73＝343,74＝2401,75＝16807，…，则72016的末两位数字为( )A ．49B ．43C ．07D ．013．(2016·黄岗质检)已知某程序框图如图所示，则执行该程序后输出的结果是( )A ．2B ．－1C.12D.144．要证：a 2＋b 2－1－a 2b 2≤0，只要证明( ) A ．2ab －1－a 2b 2≤0 B ．a 2＋b 2－1－a 4＋b42≤0C.(a ＋b )22－1－a 2b 2≤0D ．(a 2－1)(b 2－1)≥05．(2016·安徽“江淮十校”第三次联考)我国古代数学名著《九章算术》中割圆术有：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣．”其体现的是一种无限与有限的转化过程，比如在2＋2＋2＋…中“…”即代表无限次重复，但原式却是个定值x ，这可以通过方程2＋x ＝x 确定x ＝2，则1＋11＋11＋…等于( ) A.－5－12B.5－12C.1＋52D.1－526．(2016·宝鸡质检)定义某种运算s ＝a b ，运算原理如程序框图所示，则2ln e＋2(13)－1的值为( )A ．12B ．11C ．8D ．47．平面内有n 条直线，最多可将平面分成f (n )个区域，则f (n )的表达式为( ) A ．n ＋1 B ．2n C.n 2＋n ＋22D ．n 2＋n ＋18．(2016·沈阳质检二)用数学归纳法证明不等式1＋12＋14＋…＋12n －1>12764 (n ∈N *)成立，其初始值至少应取( ) A ．7B ．8C ．9D ．109．(2016·西安地区八校联考)执行如图所示的程序框图，若输出的值是13，则判断框内应为( )A ．k ＜6?B ．k ≤6?C ．k ＜7?D ．k ≤7?10．(2016·陕西第三次质检)已知整数按如下规律排一列：(1,1)，(1,2)，(2,1)，(1,3)，(2,2)，(3,1)，(1,4)，(2,3)，(3,2)，(4,1)，…，则第60个数对是( ) A ．(4,8) B ．(5,7) C ．(6,6)D ．(7,5)11．(2016·湖南长郡中学月考二)某电商在“双十一”期间用电子支付系统进行商品买卖，全部商品共有n 类(n ∈N *)，分别编号为1,2，…，n ，买家共有m 名(m ∈N *，m ＜n )，分别编号为1,2，…，m .若a ij ＝⎩⎨⎧1，第i 名买家购买第j 类商品，0，第i 名买家不购买第j 类商品，1≤i ≤m,1≤j ≤n ，则同时购买第1类和第2类商品的人数是( ) A ．a 11＋a 12＋…＋a 1m ＋a 21＋a 22＋…＋a 2m B ．a 11＋a 21＋…＋a m 1＋a 12＋a 22＋…＋a m 2 C ．a 11a 12＋a 21a 22＋…＋a m 1a m 2 D ．a 11a 21＋a 12a 22＋…＋a 1m a 2m12．(2016·陕西质检二)小明用电脑软件进行数学解题能力测试，每答完一道题，软件都会自动计算并显示出当前的正确率(正确率＝已答对题目数÷已答题目总数)．小明依次共答了10道题，设正确率依次相应为a 1，a 2，a 3，…，a 10.现有三种说法： ①若a 1＜a 2＜a 3＜…＜a 10，则必是第一题答错，其余题均答对；②若a 1＞a 2＞a 3＞…＞a 10，则必是第一题答对，其余题均答错；③有可能a 5＝2a 10. 其中正确的个数是( ) A ．1B ．0C ．3D ．2第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上)13．已知i 为虚数单位，a ∈R .若a 2－1＋(a ＋1)i 为纯虚数，则复数z ＝a ＋(a －2)i 在复平面内对应的点位于第________象限．14．(2016·济南一模)执行如图所示的程序框图，如果输出的函数值在区间[14，12]内，则输入的实数x 的取值范围是________．15．(2016·湖南长郡中学月考)对于大于1的自然数m 的三次幂可用奇数进行以下方式的“分裂”：23＝⎩⎨⎧3，5，33＝⎩⎨⎧7，9，11，43＝⎩⎨⎧13，15，17，19，….依此，若m 3的“分裂数”中有一个是2015，则m ＝________.16．《孙子算经》卷下第二十六题：今有物，不知其数(shù)，三三数(shǔ)之剩二，五五数之剩三，七七数之剩二，问物几何？________.(只写出一个答案即可) 三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)17.(10分)(1)已知复数z ＝3＋i(1－3i )2，z 是z 的共轭复数，求z ·z 的值；(2)求满足z ＋iz ＝i(i 为虚数单位)的复数z ； (3)计算(21－i )2016＋(1＋i 1－i)6(i 是虚数单位).18.(12分)有一种密英文的明文(真实文)按字母分解，其中英文的a ，b ，c ，…，z 的26个字母(不分大小写)，依次对应1,2,3，…，26这26个自然数，见如下表格： 给出如下变换公式：x ′＝错误!将明文转换成密文，如8→82＋13＝17，即h 变成q ；如5→5＋12＝3，即e 变成c.(1)(2)按上述规定，若将某明文译成的英文是shxc ，那么原来的明文是什么？19.(12分)如图的程序可产生一系列随机数，其工作原理如下：①从集合D 中随机抽取1个数作为自变量x 输入；②从函数f (x )与g (x )中随机选择一个作为H (x )进行计算；③输出函数值y .若D ＝{1,2,3,4,5}，f (x )＝3x ＋1，g (x )＝x 2.(1)求y ＝4的概率；(2)将程序运行一次，求输出的结果是奇数的概率.20.(12分)用数学归纳法证明不等式2＋12·4＋14·…·2n ＋12n ＞n ＋1(n ∈N *)．21.(12分)在△ABC 中，若AB ⊥AC ，AD ⊥BC 于点D ，则1AD 2＝1AB 2＋1AC 2.类比上述结论，在四面体ABCD 中，你能得到怎样的猜想，并予以证明.22.(12分)已知a＝(cos x＋sin x，sin x)，b＝(cos x－sin x，2cos x)．(1)求证：向量a与向量b不可能平行；(2)若f(x)＝a·b，且x∈[－π4，π4]，求函数f(x)的最大值及最小值.答案精析1．A [∵1＋a i 2－i ＝(1＋a i )(2＋i )(2－i )(2＋i )＝2－a 5＋2a ＋15i ，∴2－a 5＝0，2a ＋15≠0，∴a ＝2.故选A.]2．D [71,72,73,74,75，…的末两位数字分别为07,49,43,01,07，…，周期性出现(周期为4)，而2 016＝4×504，所以72 016的末两位数字必定和74的末两位数字相同，故选D.]3．C [由于a ＝2，i ＝1；a ＝12，i ＝2；a ＝－1，i ＝3；a ＝2，i ＝4；…，由此规律可知，a ＝2，i ＝3k ＋1；a ＝12，i ＝3k ＋2；a ＝－1，i ＝3k ＋3，其中k ∈N *.从而可知当i ＝20时，退出循环，此时a ＝12.] 4．D [要证a 2＋b 2－1－a 2b 2≤0， 即证a 2b 2－a 2－b 2＋1≥0， 只要证(a 2－1)(b 2－1)≥0.] 5．C [设1＋11＋11＋…＝x ，则1＋1x ＝x ，即x 2－x －1＝0，解得x ＝1＋52(x ＝1－52舍)．故1＋11＋11＋…＝1＋52，故选C.]6．A [由程序框图知s ＝a b ＝⎩⎨⎧a (b ＋1)，a ≥b ，b (a ＋1)，a ＜b ，∴2ln e ＝212＝3,2(13)－1＝23＝9， ∴2ln e ＋2(13)－1＝12，故选A.]7．C [1条直线将平面分成1＋1个区域；2条直线最多可将平面分成1＋(1＋2)＝4个区域；3条直线最多可将平面分成1＋(1＋2＋3)＝7个区域；……；n 条直线最多可将平面分成1＋(1＋2＋3＋…＋n )＝1＋n (n ＋1)2＝n 2＋n ＋22个区域，故选C.]8．B [据已知可转化为1×(1－12n )1－12＞12764，整理得2n＞128，解得n ＞7，故原不等式的初始值为n ＝8，故选B.]9．A [依题意，执行题中的程序框图，进行第一次循环时，k ＝1，c ＝2，a ＝1，b ＝2；进行第二次循环时，k ＝2，c ＝3，a ＝2，b ＝3；进行第三次循环时，k ＝3，c ＝5，a ＝3，b ＝5；进行第四次循环时，k ＝4，c ＝8，a ＝5，b ＝8；进行第五次循环时，k ＝5，c ＝13，a ＝8，b ＝13；进行第六次循环时，k ＝6，因此当输出的值是13时，判断框内应为“k ＜6？”．]10．B [由已知数对得数对中两个数的和为2的有1对，和为3的有2对，和为4的有3对，…，和为n 的有n －1对，且和相等的数对的第一个数以1为公差递增，从n ＝2到n ＝11共有数对1＋2＋3＋…＋10＝55，n ＝12时有11个数对，分别是(1,11)，(2,10)，(3,9)，(4,8)，(5,7)，…，故第60个数对是(5,7)，故选B.]11．C [因为a ij ＝⎩⎨⎧1，第i 名买家购买第j 类商品，0，第i 名买家不购买第j 类商品，1≤i ≤m,1≤j ≤n ，所以若第i名买家同时购买第1类和第2类商品，则a i 1a i 2＝1，否则a i 1a i 2＝0，所以同时购买第1类和第2类商品的人数是a 11a 12＋a 21a 22＋…＋a m 1a m 2，故选C.]12．C [对于①，若第一题答对，则a 1＝1，a 1≥a 2，与题意不符，所以第一题答错，若剩余的9道题有答错的，不妨设第k (k ≥2)道题答错，则a k ≤a k －1，与题意不符，所以剩余的题均答对，①正确；对于②，若第一道题答错，则a 1＝0，a 1≤a 2，与题意不符，所以第一题答对，若剩余的9道题有答对的，不妨设第k (k ≥2)道题答对，则a k ≤a k －1，与题意不符，所以剩余的题均答错，②正确；对于③，设前5道题答对x 道题，后5道题答对y 道题，则由a 5＝2a 10得x5＝2·x ＋y 10，解得y ＝0，即当后5道题均答错时，a 5＝2a 10，③正确．综上所述，正确结论的个数为3，故选C.] 13．四解析 因为a 2－1＋(a ＋1)i 为纯虚数，所以a ＝1.所以z ＝1－i 对应的点在第四象限． 14．[－2，－1]解析 若x ∉[－2,2]，则f (x )＝2∉[14，12]，不合题意；当x ∈[－2,2]时，f (x )＝2x ∈[14，12]，得x ∈[－2，－1]． 15．45解析 由题意不难找出规律，23＝3＋5,33＝7＋9＋11,43＝13＋15＋17＋19，…，m 增加1，累加的奇数个数便多1，我们不难计算2015是第1008个奇数，若它是m 的分解，则1至m －1的分解中，累加的奇数一定不能超过1008个． ∴1＋2＋3＋…＋(m －1)<1008,1＋2＋3＋…＋(m －1)＋m ≥1008，即m (m －1)2<1008，m (m ＋1)2≥1008，解得m ＝45. 16．23(23＋105(n －1)，n ∈N *均可)解析 由题意可得物体的个数为3m ＋2＝5n ＋3＝7k ＋2，m ，n ，k ∈N *，所以物体的个数可以是23. 17．解 (1)∵z ＝3＋i (1－3i )2＝3＋i －2－23i ＝3＋i－2(1＋3i )＝(3＋i )(1－3i )－2(1＋3i )(1－3i )＝23－2i －8＝－34＋14i ，∴z ＝－34－14i ，∴z ·z ＝(－34＋14i)(－34－14i)＝316＋116＝14. (2)由已知得，z ＋i ＝z i ，则z (1－i)＝－i ， 即z ＝－i 1－i ＝－i (1＋i )(1－i )(1＋i )＝1－i 2＝12－i 2.(3)原式＝[(21－i )2]1008＋(1＋i 1－i )6＝(2－2i )1008＋i 6＝i 1008＋i 6＝i 4×252＋i 4＋2＝1－1＝0.18．解 (1)g →7→7＋12＝4→d ；o →15→15＋12＝8→h ；d →4→42＋13＝15→o. 则明文good 的密文为dhho. (2)逆变换公式为x ＝⎩⎨⎧2x ′－1(x ′∈N ，1≤x ′≤13)，2x ′－26(x ′∈N ，14≤x ′≤26)，则有s →19→2×19－26＝12→l ； h →8→2×8－1＝15→o ； x →24→2×24－26＝22→v ； c →3→2×3－1＝5→e. 故密文shxc 的明文为love.19．解 (1)∵D ＝{1,2,3,4,5}，f (x )＝3x ＋1，g (x )＝x 2.∴第一步：从集合D 中随机抽取1个数作为自变量x 输入，共有5种方法， 第二步：从函数f (x )与g (x )中随机选择一个作为H (x )进行计算，共有2种方法， ∴该运算共有f (1)，f (2)，f (3)，f (4)，f (5)，g (1)，g (2)，g (3)，g (4)，g (5)，10种方法， 而满足y ＝4的有f (1)，g (2)两种情况，∴由古典概型概率公式得y ＝4的概率P ＝210＝15.(2)输出结果是奇数有以下几种情况：f (2)，f (4)，g (1)，g (3)， g (5)，共5种，∴由古典概型概率公式得输出的结果是奇数的概率 P ＝510＝12.20．证明 ①当n ＝1时，左式＝32，右式＝2，左式＞右式，所以不等式成立． ②假设当n ＝k (k ≥1，k ∈N *)时不等式成立， 即2＋12·4＋14·…·2k ＋12k ＞k ＋1成立，则当n ＝k ＋1时，2＋12·4＋14·…·2k ＋12k ·2k ＋32(k ＋1)＞k ＋1·2k ＋32(k ＋1)＝2k ＋32k ＋1，要证当n＝k ＋1时不等式成立，只需证2k ＋32k ＋1≥k ＋2，即证2k ＋32≥(k ＋1)(k ＋2)，由基本不等式2k ＋32＝(k ＋1)＋(k ＋2)2≥(k ＋1)(k ＋2)成立，得2k ＋32k ＋1≥k ＋2成立，所以，当n ＝k ＋1时，不等式成立．由①②可知，当n ∈N *时，不等式2＋12·4＋14·…·2n ＋12n ＞n ＋1成立．21．解 猜想：在四面体ABCD 中，若AB ，AC ，AD 两两垂直，AE ⊥平面BCD ，则1AE 2＝1AB 2＋1AC 2＋1AD 2.证明：如图所示，连接并延长BE ，交CD 于点F ，连接AF .∵AB ⊥AC ，AB ⊥AD ，AC ∩AD ＝A ，AC ⊂平面ACD ，AD ⊂平面ACD ，∴AB ⊥平面ACD ，又AF ⊂平面ACD ，∴AB ⊥AF .在Rt △ABF 中，AE ⊥BF ，∴1AE 2＝1AB 2＋1AF 2.∵CD ⊂平面ACD ，∴AB ⊥CD ，又AE ⊥CD ，AB ∩AE ＝A ，AB ⊂平面ABF ，AE ⊂平面ABF ，∴CD ⊥平面ABF ，又AF ⊂平面ABP ，∴在Rt △ACD 中，AF ⊥CD ，∴1AF 2＝1AC 2＋1AD 2，∴1AE 2＝1AB 2＋1AC 2＋1AD 2.22．(1)证明 假设a ∥b ，则a ＝k b (k ≠0，k ∈R )，有⎩⎨⎧cos x ＋sin x ＝k (cos x －sin x )， ①sin x ＝2k cos x ，②将②代入①，整理得cos x (1＋2k )＝k cos x (1－2k )，即cos x (－2k 2－k －1)＝0，∵－2k 2－k －1＜0恒成立，∴cos x ＝0，代入②得sin x ＝0，与sin 2x ＋cos 2x ＝1矛盾．∴向量a 与向量b 不可能平行．(2)解 由题知f (x )＝a ·b ＝(cos x ＋sin x )·(cos x －sin x )＋sin x ·2cos x ＝cos 2x －sin 2x ＋2sin x cos x ＝cos2x ＋sin2x ＝2(22cos2x ＋22sin2x )＝2sin(2x ＋π4)，∵－π4≤x ≤π4，∴－π4≤2x ＋π4≤3π4，∴当2x ＋π4＝π2，即x ＝π8时，f (x )有最大值2； 当2x ＋π4＝－π4，即x ＝－π4时，f (x )有最小值－1.。
2018秋新版高中数学人教A版必修3习题：第一章算法初步 1.1.2.1
第1课时 程序框图与顺序结构课时过关·能力提升一、基础巩固1.对终端框叙述正确的是( )A.表示一个算法的起始和结束,程序框是B.表示一个算法输入和输出的信息,程序框是C.表示一个算法的起始和结束,程序框是D.表示一个算法输入和输出的信息,程序框是2.如图所示的程序框图中不含有的程序框是( )A.终端框B.输入、输出框C.判断框D.处理框,输入、输出框和处理框,不含有判断框.3.阅读如图所示的程序框图,若输入x=3,则输出y的值为( )A.33B.34C.40D.45x=3时,执行的过程是:x=3,a=2×32-1=17,b=a-15=2,y=ab=17×2=34,输出y=34.4.执行如图所示的程序框图后,输出的结果为5,则输入的x值为( )A.2B.3C.5D.9,当y=5时,2x-1=5,∴x=3.5.如图,若输出的结果为2,则①处的执行框内应填的是( )A.x=2B.b=2C.x=1D.a=5b=2,所以2=a-3,即a=5.所以5=2x+3,x=1.6.如图,若输入a=10,则输出a= .a=10,该程序框图的执行过程是:a=10,b=10-8=2,a=10-2=8,输出a=8.7.执行如图的程序框图,若R=8,则a= .:输入R=8,b a=4.=R 2=4=2,a =2b =4,输出8.如图是求长方体的体积和表面积的一个程序框图,将该程序框图补充完整,横线处应填 .:9.执行如图所示的程序框图后的结果为 .S=42+24=2.5..510.如图所示的程序框图,要使输出的y 的值最小,则输入的x 的值应为多少?此时输出的y 的值为多少?x的值,求函数y=x2+2x+3的值.将y=x2+2x+3配方,得y=(x+1)2+2,要使y的值最小,需x=-1,此时y min=2.故输入的x的值为-1时,输出的y的值最小为2.二、能力提升1.下列所画程序框图是已知三角形的一边a及这边上的高h,求三角形面积的算法,其中正确的是( )选项流程线没有箭头,故不正确;B选项输出框应为平行四边形,故不正确;D中没有输出框,故不正确.2.阅读如图所示的程序框图,若输入的a,b,c的值分别是21,32,75,则输出的a,b,c分别是( )A.75,21,32B.21,32,75C.32,21,75D.75,32,21:输入21,32,75.x=21.a=75.c=32.b=21.输出75,21,32.3.如图所示的是一个算法的程序框图,已知a 1=3,输出的b=7,则a 2的值是( )A.5B.7C.11D.13,该算法是计,a 2=11.算a 1+a 22的值故3+a 22=7,得4.阅读如图所示的程序框图,若输出y=3,则输入的x 的值为 .,当y=3时,log 2b=3,∴b=8.∴a ÷10=8.∴a=80.∴x 2-1=80.∴x=-9或x=9.9或95.根据下面的程序框图所表示的算法,输出的结果是 .1步分别将X ,Y ,Z 赋予1,2,3三个数,第2步使X 取Y 的值,即X 取值变成2,第3步使Y 取X 的值,即Y 的值也是2,第4步让Z 取Y 的值,即Z 取值也是2,从而第5步输出时,Z 的值是2.★6.图①是计算图②中阴影部分面积的一个程序框图,则图①中(1)处应填 .图①图②②中,正方形的面积为S 1=a 2,扇形的面积为S 2S=S 1-S 2=a 2=14πa 2,则阴影部分的面积为①中(1)处应填S ‒π4a 2=4-π4a 2.因此题图=4-π4a 2.=4-π4a 27.已知一个圆柱的底面半径为R ,高为h ,求圆柱的体积.设计解决该问题的一个算法,并画出相应的程序框图.R 、高h 代入圆柱的体积公式V=πR 2h ,最后输出结果即可,所以只用顺序结构就能解决该问题.:第一步,输入R ,h.第二步,计算V=πR 2h.第三步,输出V.程序框图:★8.一城市在法定工作时间内,每小时的工资为8元,加班工资为每小时10元,一人一周内工作60小时,其中加班20小时,写出这人一周内所得工资的算法,并画出算法的程序框图.:第一步,计算法定工作时间内工资a(a=8×(60-20)=320(元)).第二步,计算加班工资b(b=10×20=200(元)).第三步,计算一周内工资总数c(c=a+b=320+200=520(元)).第四步,输出c.程序框图:。
2018学年高中数学必修三人教A版 )练习：第一章 算法初
第一章算法初步1.1 算法与程序框图1.1.2 程序框图与算法的基本逻辑结构第1课时程序框图、顺序结构A级基础巩固一、选择题1．下列关于程序框图的说法正确的是()①程序框图只有一个入口，也只有一个出口；②程序框图中的每一部分都应有一条从入口到出口的路径通过它；③流程线只要是从上到下方向就表示上下执行，可以不要箭头；④连接点是用来连接两个程序框图的．A．①②③B．②③C．①④D．①②解析：由框图符号及作用可知③④错误，流程线表示算法步骤执行的顺序，用来连接程序框，是带箭头的直线或折线，应用时必须带箭头；连接点是连接同一个程序框图的不同部分的．答案：D2．下列是流程图中的一部分，表示恰当的是()解析：B选项应该用处理框而非输入、输出框，C选项应该用输入、输出框而不是处理框，D 选项应该在出口处标明“是”和“否”．答案：A3.下面的程序框图的运行结果是( )A.52 B.32 C ．－32D ．－1解析：因为a ＝2，b ＝4，所以S ＝a b －b a ＝24－42＝－32，故选C.答案：C4．在如图所示程序框图中，若R ＝8，运行结果也是8，则程序框图中应填入的内容是( )A ．a ＝2bB ．a ＝4bC.a4＝b D ．b ＝a4解析：因为R ＝8，所以b ＝4＝2. 又a ＝8，因此a ＝4b ，故选B. 答案：B5．下面的程序框图中，是已知直角三角形两直角边a ，b 求斜边c 的算法的是( )解析：A 项中，没有起始终端框，所以A 项不正确；B 项中，输入a ，b 和c ＝a 2＋b 2顺序颠倒，且程序框错误，所以B 项不正确；D 项中，赋值框中a 2＋b 2＝c 错误，应为c ＝a 2＋b 2，左右两边不能互换，所以D 项不正确；很明显C 项正确．答案：C 二、填空题6．下面程序框图输出的S 表示____________________．答案：半径为5的圆的面积7．如图所示的一个算法的程序框图，已知a 1＝3，输出的结果为7，则a 2的值为________．解析：由框图可知，b ＝a 1＋a 2，再将b2赋值给b ，所以7×2＝a 2＋3，所以a 2＝11.答案：118．阅读程序框图如图所示，若输入x ＝3，则输出y 的值为________．解析：输入x ＝3，则a ＝2×32－1＝17， b ＝a －15＝17－15＝2，y ＝a ·b ＝17×2＝34，则输出y 的值为34. 答案：34 三、解答题9．已知一个三角形的三边边长分别为2，3，4，设计一个算法，求出它的面积，并画出程序框图．解：第一步，取a ＝2，b ＝3，c ＝4.第二步，计算p＝a＋b＋c2.第三步，计算S＝p（p－a）（p－b）（p－c）.第四步，输出S的值．10.如图所示的程序框图，要使输出的y的值最小，则输入的x的值应为多少？此时输出的y的值为多少？解：此程序框图执行的功能是对于给定的任意x的值，求函数y ＝x2＋2x＋3的值．将y＝x2＋2x＋3配方，得y＝(x＋1)2＋2，要使y的值最小，需x ＝－1，此时y min＝2.故输入的x的值为－1时，输出的y的值最小为2.B级能力提升1.给出如图程序框图：若输出的结果为2，则①处的执行框内应填的是( ) A ．x ＝2 B ．b ＝2 C ．x ＝1 D ．a ＝5解析：因结果是b ＝2，所以2＝a －3，即a ＝5.当2x ＋3＝5时，得x ＝1.故选C.答案：C2．图1是计算图2中阴影部分面积的一个程序框图，则图1中①处应填________．解析：题干图2中，正方形的面积为S 1＝a 2，扇形的面积为S 2＝14πa 2，则阴影部分的面积为S ＝S 1－S 2＝a 2－π4a 2＝4－π4a 2.因此题干图1中①处应填入S ＝4－π4a 2.答案：S＝4－π4a23．“六一”儿童节这天，糖果店的售货员忙极了，请你设计一个程序，帮助售货员算账．已知水果糖每千克10元，奶糖每千克15元，巧克力糖每千克25元，那么依次购买这三种糖果a，b，c千克，应收取多少元钱？写出一个算法，画出程序框图．解：算法步骤如下：第一步，输入三种糖果的价格x，y，z.第二步，输入购买三种糖果的千克数a，b，c.第三步，计算Y＝xa＋yb＋zc.第四步，输出Y.程序框图如图所示．。
最新-2018高中数学 第一章 算法初步 同步练习 新人教A
第8题第11题高一试题《算法语言》一、选择题1、算法的有穷性是指A.算法必须包含输出B.算法中每个操作步骤都是可执行的C.算法的步骤必须有限 C.以上说法均不正确2、算法共有三种逻辑结构，即顺序结构，条件结构和循环结构，下列说法正确的是A.一个算法只能含有一种逻辑结构B. 一个算法最多可以包含两种逻辑结构C. 一个算法必须含有上述三种逻辑结构D. 一个算法可以含有上述三种逻辑结构的任意组合 3、下列给出的赋值语句中正确的是 A.4 = M B.M =－M C.B=A －3 D.x + y = 0 4、右边程序执行后输出的结果是 A.－1 B.0 C.1 D2 5、以下给出的各数中不可能是八进制数的是 A.312 B.10 110 C.82 D.7 457 6、如果右边程序执行后输出的结果是132，那么 在程序until 后面的“条件”应为A.i > 11B. i >=11C. i <=11D.i<117、840和1 764的最大公约数是 A.84 B.12 C.168 D.252 8、右图给出的是计算201614121+⋅⋅⋅+++的值的一个程序框图，其中判断框内应填入的条件是A.i>10B.i<10C.i>20D.i<209、右边程序运行的结果是A.1,2,3B.2,3,1C.2,3,2D.3,2,110.给出以下一个算法的程序框图（如图所示），该程序框图的功能是A.求输出a,b,c 三数的最大数B. 求输出a,b,c 三数的最小数C.将a,b,c 按从小到大排列D. 将a,b,c 按从大到小排列11、右边的程序框图（如图所示），能判断任意输入的数x 的奇偶性：其中判断框内的条件是 A.m=0 B.x=0C.x=1D.m=112、右边程序运行后的输出结果为A.17B.19（第16题） C.21 D.23二、填空题13、三个数72,120,168 的最大公约数是 14、若输入8时，则下列程序执行后输出的结果是 15.将二进制数101 101(2) 化为十进制结果为 ；再将该数化为八进制数，结果为 . 16、有如下程序框图（如右图所示），则该程序框图表示的算法的功能是 .三、解答题17、已知一个三角形的周长为a ，求这个三角形的面积.设计一个算法解决这个问题.18、（I ）用辗转相除法求840与1 764的最大公约数.（II ）用更相减损术求440 与556的最大公约数19、设计算法求100991431321211⨯+⋅⋅⋅+⨯+⨯+⨯的值.要求画出程序框图，写出用基本语句编写的程序.20、某电信部门规定：拨打市内电话时，如果通话时间不超过3分钟，则收取通话费0.2元，如果通话时间超过3分钟，则超过部分以每分钟0.1元收取通话费（通话不足1分钟时按1分钟计），试设计一个计算通话费用的算法.要求写出算法，画出程序框图，编写程序.21、给出30个数：1，2，4，7，……，其规律是：第1个数是1，第2个数比第1个数大1, 第3个数比第2个数大2，第4个数比第3个数大3，依此类推.要计算这30个数的和，现已给出了该问题算法的程序框图（如图所示），（I ）请在图中判断框内(1)处和执行框中的(2)处填上合适的语句，使之能完成该题算法功能；（II ）根据程序框图写出程序.22、青年歌手电视大赛共有10名选手参加，并请了12名评委，在计算每位选手的平均分数时，为了避免个别评委所给的极端分数的影响，必须去掉一个最高分和一个最底分后再求平均分.试设计一个算法，解决该问题，要求画出程序框图，写出程序（假定分数采用10分制，即每位选手的分数最高分为10分，最底分为0分）.第19题 程序框图算法初步参考答案二、填空题 13. 24 14. 0.7 15. 45, 55(8)16.计算并输出使1×3×5×7…× >10 000成立的最小整数.17、算法步骤如下：第一步，输入a 的值；第二步，计算3a l =的值；第三步，计算243l s ⨯=的值；第四步，输出S 的值.18、解 （I ）用辗转相除法求840与1 764 的最大公约数.1 764 = 840×2 + 84 840 = 84×10 +0所以840与1 764 的最大公约数是84( II)用更相减损术求440 与556的最大公约数.556－440 = 116 440－116 = 324 324－116 = 218 218－116 = 92 116－92 = 2492－24 = 68 68－24 = 44 44－24 = 20 24－20 = 4 20－4 = 16 16－4 = 12 12－4 = 8 8－4 = 4所以440 与556的最大公约数4.19、解 这是一个累加求和问题，共99项相加，可设计一个计数变量，一个累加变量，用循环结构实现这一算法.程序框图如下图所示20、解 我们用c （单位：元）表示通话费，t （单位：分钟）表示通话时间，则依题意有 ⎩⎨⎧>-+≤<=3),3(1.02.030,2.0t t t c 算法步骤如下：第一步，输入通话时间t ；第二步，如果t ≤3,那么c = 0.2 ;否则令 c = 0.2+0.1 (t －3);第三步，输出通话费用c ;程序框图如图所示21.解 （I ）该算法使用了当型循环结构，因为是求30个数的和，故循环体应执行30次，其中i 是计数变量，因此判断框内的条件就是限制计数变量i 的，故应为30≤i .算法中的变量p 实质是表示参与求和的各个数，由于它也是变化的，且满足第i 个数比其前一个数大1-i ，,第1+i 个数比其前一个数大i ，故应有i p p +=.故(1)处应填30≤i ；（2）处应填i p p += （II ）根据以上框图，可设计程序如下：22、由于共有12位评委，所以每位选手会有12个分数，我们可以用循环语句来完成这12个分数的输入，同时设计累加变量求出这12个分数的和，本问题的关键在于从这12个输入分数中找出最大数与最小数，以便从总分中减去这两个数.由于每位选手的分数都介于0分和10分之间，去我们可以先假设其中的最大数为0，最小数为10，然后每次输入一个评委的分数，就进行一次比较，若输入的数大于0,就将之代替最大数，若输入的数小于10，就用它代替最小数，依次下去，就能找出这12个数中的最大数与最小数，循环结束后，从总和中减去最大数与最小数，再除以10，就得到该选手最后的平均数.程序框图如图所示.。
2018-2019学年高中数学 第一章 算法初步 1.3 算法案例检测 新人教A版必修3
1.3 算法案例A级基础巩固一、选择题1．下列说法中正确的个数为( )①辗转相除法也叫欧几里得算法；②辗转相除法的基本步骤是用较大的数除以较小的数；③求最大公约数的方法除辗转相除法之外，没有其他方法；④编写辗转相除法的程序时，要用到循环语句．A．1 B．2 C．3 D．4解析：依据辗转相除法可知，①②④正确，③错误．答案：C2．用更相减损术求48和132的最大公约数时，需做减法的次数是( )A．2 B．3 C．4 D．5解析：132－48＝84，84－48＝36，48－36＝12，36－12＝24，24－12＝12.答案：D3．若用秦九韶算法求多项式f(x)＝4x5－x2＋2当x＝3时的值，则需要做乘法运算和加减法运算的次数分别为( )A．4，2 B．5，3 C．5，2 D．6，2解析：f(x)＝4x5－x2＋2＝((((4x)x)x－1)x)x＋2，所以需要做5次乘法运算和2次加减运算．答案：C4．已知一个k进制的数123与十进制的数38相等，那么k等于( )A．7或5 B．－7C．5 D．都不对解析：(123)(k)＝1×k2＋2×k＋3＝k2＋2k＋3，所以k2＋2k＋3＝38，即k2＋2k－35＝0.解得k＝5或k＝－7(舍去)．答案：C5．三位四进制数中的最大数等于十进制数的( )A．63 B．83C．189 D．252解析：三位四进制数中的最大数为333(4)，则333(4)＝3×42＋3×41＋3＝63.答案：A二、填空题6．用秦九韶算法求f (x )＝2x 3＋x －3当x ＝3时的值v 2＝________．解析：f (x )＝((2x ＋0)x ＋1)x －3， v 0＝2；v 1＝2×3＋0＝6；v 2＝6×3＋1＝19.答案：197．已知函数f (x )＝x 3－2x 2－5x ＋6，用秦九韶算法，则f (10)＝________．解析：f (x )＝x 3－2x 2－5x ＋6＝(x 2－2x －5)x ＋6＝[(x －2)x －5]x ＋6.当x ＝10时，f (10)＝[(10－2)×10－5]×10＋6＝(8×10－5)×10＋6＝75×10＋6＝756. 答案：7568．已知1 0b 1(2)＝a 02(3)，则(a ，b )＝________．解析：因为1 0b 1(2)＝1×23＋b ×2＋1＝2b ＋9， a 02(3)＝a ×32＋2＝9a ＋2，所以2b ＋9＝9a ＋2，即9a －2b ＝7.因为a ∈{1，2}，b ∈{0，1}，所以当a ＝1时，b ＝1符合题意，当a ＝2时，b ＝112不合题意， 所以a ＝1，b ＝1.所以(a ，b )＝(1，1)．答案：(1，1)三、解答题9．分别用辗转相除法和更相减损术求261，319的最大公约数．解：辗转相除法：319＝261×1＋58，261＝58×4＋29，58＝29×2.所以319与261的最大公约数是29.更相减损术：319－261＝58，261－58＝203，203－58＝145，145－58＝87，87－58＝29，58－29＝29，所以319与261的最大公约数是29.10．已知函数f(x)＝x3－3x2－4x＋5，试用秦九韶算法求f(2)的值．解：根据秦九韶算法，把多项式改写成如下形式：f(x)＝x3－3x2－4x＋5＝(x2－3x－4)x＋5＝((x－3)x－4)x＋5.把x＝2代入函数式得f(2)＝((2－3)×2－4)×2＋5＝－7.B级能力提升1．m是一个正整数，对于两个正整数a，b，如果a－b是m的倍数，则称a，b对模m同余，用符号ab(MOD m)表示，则下列各式中不正确的为( )A．127(MOD 5) B．2110(MOD 3)C．3420(MOD 2) D．477(MOD 40)解析：逐一验证，对于A，12－7＝5是5的倍数；对于B，21－10＝11不是3的倍数；对于C，34－20＝14是2的倍数；对于D，47－7＝40是40的倍数．答案：B2．324，243，135三个数的最大公约数是________．解析：324＝243×1＋81，243＝81×3，所以243与324的最大公约数是81.又135＝81×1＋54，81＝54×1＋27，54＝27×2＋0，所以135与81的最大公约数是27.答案：273．已知三个数12(16)，25(7)，33(4)，将它们按由小到大的顺序排列为________________．解析：将三个数都化为十进制数．12(16)＝1×16＋2＝18，25(7)＝2×7＋5＝19，33(4)＝3×4＋3＝15，所以33(4)＜12(16)＜25(7)．答案：33(4)＜12(16)＜25(7)。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2017-2018学年度xx学校xx月考卷
一、选择题(共15小题,每小题5.0分,共75分)
1.阅读下图所示的程序框图，运行相应的程序，输出的结果是()
A． 1
B． 2
C． 3
D． 4
2.如图程序中，输出的是4，则输入的x可以是()
A．－8
B． 4
C． 8
D．－16
3.下列关于算法的描述正确的是()
A．算法与求解一个问题的方法相同
B．算法只能解决一个问题，不能重复使用
C．算法过程要一步一步执行，每步执行的操作必须确切
D．有的算法执行后，可能无结果
4.早上从起床到出门需要洗脸刷牙(5 min)、刷水壶(2 min)、烧水(8 min)、泡面(3 min)、吃饭(10 min)、听广播(8 min)几个过程.则下列选项中最好的一种算法是()
A．第一步，洗脸刷牙.第二步，刷水壶.第三步，烧水.第四步，泡面.第五步，吃饭.第六步，听广播
B．第一步，刷水壶.第二步，烧水同时洗脸刷牙.第三步，泡面.第四步，吃饭.第五步，听广播C．第一步，刷水壶.第二步，烧水同时洗脸刷牙.第三步，泡面.第四步，吃饭同时听广播
D．第一步，吃饭同时听广播.第二步，泡面.第三步，烧水同时洗脸刷牙.第四步，刷水壶
5.下面程序运行的结果是()
A． 1,2，－1
B． 1,2,1
C． 1，－2，－1
D． 1，－2,1
6.将下列不同进位制下的数转化为十进制，这些数中最小的数是() A． 20(7)
B． 30(5)
C． 23(6)
D． 31(4)
7.下面的程序运行后，输出的结果为()
A． 13,7
B． 7,4
C． 9,7
D． 9,5
8.如图所示，程序的输出结果为S＝132，则判断框中应填()
A．i≥10?
B．i≥11?
C．i≤11?
D．i≥12?
9.下列说法正确的是()
A．算法是计算的方法
B．算法是计算机语言
C．算法是与计算机有关的问题的解决方法
D．算法通俗地讲是解决问题的程序与过程
10.如图所示，输出的n为()
A． 10
B． 11
C． 12
D． 13
11.程序框图是算法思想的重要表现形式，程序框图中不含() A．流程线
B．判断框
C．循环框
D．执行框
12.阅读下边的程序框图，若输出s的值为－7，则判断框内可填写()
A．i<3?
B．i<4?
C．i<5?
D．i<6?
13.2008年3月1日开始实施的《个人所得税法》规定：全月总收入不超过2 000元的免征个人工资、薪金所得税，超过2 000元部分需征税.设全月总收入金额为x元，前三级税率如下表所示：
当工资薪金所得不超过4 000元，计算个人所得税的一个算法框图如图，则输出①、输出②分别为()
A． 0.05x；0.1x
B． 0.05x；0.15x－250
C． 0.05x－100；0.1x－200
D． 0.05x－100；0.1x－225
14.在对16和12求最大公约数时，整个操作如下：(16,12)→(4,12)→(4,8)→(4,4)，由此可以看出12和16的最大公约数是()
A． 4
B． 12
C． 16
D． 8
15.根据如图的程序提示依次输入4,2，－5，则程序的运行结果是()
A． 2
B． max＝2
C． 4
D． max＝4
二、填空题(共5小题,每小题5.0分,共25分)
16.流程图中表示判断框的是________.
17.用更相减损术求98与63的最大公约数的第4步式子为______．
18.用秦九韶算法求函数f(x)＝1＋2x＋x2－3x3＋2x4，当x＝－1时的值时，v2的结果是________．
19.如下图所给出的是一个算法的程序．如果输出的y的值是20，则输入的x的值是________．
20.把111化为五进制数________．
三、解答题(共0小题,每小题12.0分,共0分)
答案解析
1.【答案】D
【解析】初值，S＝2，n＝1.
执行第一次后，S＝－1，n＝2，
执行第二次后，S＝，n＝3，
执行第三次后，S＝2，n＝4.
此时符合条件，输出n＝4.
2.【答案】D
【解析】本题考查条件语句的基本结构和功能．程序实现了函数y＝的功能．当输出4时，则
4＝，故输入的x＝±16，故选D.
3.【答案】C
【解析】算法与求解一个问题的方法既有区别又有联系，故A不对；算法能重复使用，故B不对；每个算法执行后必须有结果，故D不对；由算法的有序性和确定性可知C正确.
4.【答案】C
【解析】因为A选项共用时间36 min，B选项共用时间31 min，C选项共用时间23 min，D选项的算法步骤不符合常理.
5.【答案】C
【解析】第三步c＝1－2＝－1，
第四步b＝1＋(－1)－2＝－2.
∴结束时，a＝1，b＝－2，c＝－1.
6.【答案】D
【解析】A.20(7)＝2×71＋0×70＝14；
B．30(5)＝3×51＋0×50＝15；
C．23(6)＝2×61＋3×60＝15；
D．31(4)＝3×41＋1×40＝13.
7.【答案】C
【解析】直接根据当型循环语句的执行情况进行求解即可．该程序是当型循环，根据程序可知最后一次循环时，s＝2×5－1＝9，i＝5＋2＝7.故输出的结果为9,7.
8.【答案】B
【解析】对于选项可以逐个验证，当判断框中填写i≥10？时，输出结果为S＝1 320；当判断框中填写i≥11？时，输出结果为S＝132；当判断框中填写i≤11？时，输出结果为S＝1；当判断框中填写i≥12？时，输出结果为S＝12.
9.【答案】D
【解析】算法通俗地讲是解决问题的程序与过程.
10.【答案】D
【解析】该程序框图的运行过程是：
n＝0，S＝0，
n＝0＋1＝1，
S＝0＋＝－，
S＝－>0不成立；
n＝1＋1＝2，
S＝－＋＝－，
S＝－>0不成立；
……
由此可以看出，该程序框图的功能是求满足S＝(－)＋()＋…＋>0的最小正整数n的值，
可以验证当n＝10,11,12时，均有S<0，当n＝13时，S>0.
11.【答案】C
【解析】程序框图是由程序框和流程线组成.其中程序框包括起止框、输入、输出框、执行框、判断框.这里并没有循环框.
12.【答案】D
【解析】i＝1，s＝2；s＝2－1＝1，i＝1＋2＝3；
s＝1－3＝－2，i＝3＋2＝5；
s＝－2－5＝－7，i＝5＋2＝7.
因输出s的值为－7，循环终止，故判断框内应填“i<6？”.
13.【答案】D
【解析】当2 000<x≤2 500时，税收y＝(x－2 000)×5%＝0.05x－100，
当2 500<x≤4 000时，税收y＝500×5%＋(x－2 500)×10%＝0.1x－225.
14.【答案】A
【解析】利用更相减损术可得．
15.【答案】D
【解析】本程序的功能是求输入的三个数中的最大数，运行程序得max＝4.
16.【答案】菱形框
【解析】由框图的定义可知是菱形框.
17.【答案】28－7＝21
【解析】98－63＝35，
63－35＝28，
35－28＝7，
28－7＝21，
21－7＝14，
14－7＝7，
因此98和63的最大公约数是7.
其中第4步式子为28－7＝21.
18.【答案】6
【解析】此题的n＝4，a4＝2，a3＝－3，a2＝1，a1＝2，a0＝1，
由秦九韶算法的递推关系式(k＝1,2，…，n)，得v 1＝v0x＋a3＝2×(－1)－3＝－
5.
v2＝v1x＋a2＝－5×(－1)＋1＝6.
19.【答案】2或6
【解析】当x≤5时，10x＝20，即x＝2；
当x>5时，2.5x＋5＝20，解出x＝6.
20.【答案】421(5)
【解析】
∴111化为五进制数为421(5)．。