第三章剪切
第三章.剪切变形

F
F
Q
F
受力特点:
作用于构件两个侧面上且与构件轴线垂直的外力,可以简化成大小相等,方向相反,作用线相距很近的一对力,使构件两部分沿剪切面有发生相对错动的趋势。
变形特点:
以两力F 之间的横截面为分界面,构件的两部分沿该面发生相对错动。
剪切变形的定义:具有上述两个特点的变形,即为剪切变形
1、剪力
如图所示,沿截面mm 假想的把螺栓分成两部分,并取上一部分作为研究对象,如图:mm 面上的合力用Q 表示。
则:由
∑=⇒=-⇒=Q F Q F X 00F
由于Q 与mm 面相切,故形象的称Q 为mm 面上的剪力。
二、剪切的计算
F F F F
如图所示,两块厚度为的木板,被一个铆钉铆接在一起,在这两块板上分别作用着一对大小相等、方向相反的
的作用,使铆钉受到了如图所示的分布力系的作用,从而发生了剪切变形。
同时,由于铆钉与板
之间的相互挤压,使得原为图形的孔变成了长圆形,如果
这个变形过大,同样可使结构破坏。
因此,对于这样的构
件不反要进行剪切压强计算,同时也要进行挤压强度计算
(a) (c)
F
F
、扭转实验
实验结果:于截面mm对截面nn的相对转动,使方格的左右两边发生相对错动,但两对边之间的距离不变
的半径长度也不变。
与计算杆件拉伸或压缩时的变形能同样道理上述中,斜面线下面的面积就代表:在弹性范围内,扭转力矩M。
第三章—十字板剪切试验.

1、测定原位应力条件下软粘土的不排水抗剪强度; 2、评定软粘土的灵敏度; 3、计算地基的承载力; 4、判断软粘土的固结历史。
5、十字板剪切试验的适用范围:
适用范围:在沿海软土地区广泛使用,适用于灵敏度 St ≤ 10、固结系数cv ≤ 100(m2/a)的均质饱和软粘土。
稍硬土中,可用50mm×100mm的十字板头。
18
各种规格的十字板头
19
(3)轴杆 —般使用的轴杆直径为20mm。对于普通十字板仪,轴 杆与十字板头的连接方式,有国内广泛使用的离合式,也 有牙嵌式(套筒式)的。
十字板装配示意
20
(3)轴杆 离合式轴杆是利用一离合器装置,使轴杆与十字板
头能够离合,以便分别作十字板总剪力试验和轴杆摩
电缆的缠绕,甚至接头处被扭断,使该项技术要求难以很好地执行。
33
四、试验资料的整理
(一)试验资料整理的内容 (二)试验影响因素的分析 (三)试验结果修正方法
34
四、试验资料的整理
(一)试验资料整理的内容
(1)计算各试验点原状土的不排水抗剪强度、重塑土
抗剪强度和土的灵敏度; 计算土的抗剪强度 Cu:
用提土器逐段清孔至套管底部以上15cm处,并在套管内灌水,以防止 软土在孔底涌起及尽可能保持试验土层的天然结构和应力状态。
2.将十字板头、离合器、轴杆与试验钻杆及导杆等逐节接好下入
孔内至十字板与孔底接触。各杆件要直,各接头必须拧紧.以减少不
必要的扭力损耗。
30
(三)试验方法与步骤
3.用手摇套在导杆上向右转动,使十字板离合齿咬合。再将十字板徐 徐压入土中至预定试验深度,并静置2~3min。 4.装好底座和加力、测力装置,以约1°/10 s速度旋转转盘,每转 1°,测记钢环变形读数一次,直至读数不再增大或开始减小时.即表示 土体己被剪损。此时,施于钢环的作用力(以钢环变形值乘以钢环变形系 数算得)就是把原状土剪损的总作用力pf值。
第三章剪切讲稿同济大学材料力学

第三章剪切与挤压同济大学航空航天与力学学院顾志荣一、教学目标与教学内容一、教学目标解决联接件的强度计算,要求把握剪切与挤压的概念,熟练把握剪切与挤压的利用计算方式。
二、教学内容(1) 剪切与挤压的概念及工程实例;(2) 剪切的有效计算;(3) 挤压的有效计算;(4) 连接件的有效强度计算。
二、重点与难点一、重点:全数教学内容。
二、难点:剪切面和挤压面的确信。
通过讲解和模型演示来解决。
三、教学方式采纳启发式教学,通过提问,引导学生试探,让学生回答下列问题。
四、建议学时2学时五、实施学时六、讲课提纲一、铆钉的剪切强度计算一、剪切的概念⑴受力特点:(见图3-1,a)作用在垂直于构件双侧面上的外力的合力大小相等、方向相反,作用线相距很近。
(a) (b)图3-1⑵变形特点:(见图3-1,b)介于这两个作使劲中间部份的截面,有发生相对错动的趋势。
这种变形形式称为剪切。
⑶剪切面:发生相对错动的截面称为剪切面(见图3-1,b:截面m-m)。
注意:剪切面老是与作使劲平行,且居于相邻的一对外力作用线之间。
⑷单剪与双剪:只有一个剪切面的称为单剪(图3-2,b)有两个剪切面的称为双剪(图3-3,c)图3-3 二、剪切的有效计算⑴ 铆钉所受的外力F 1 指一个铆钉nF F P=1n 指铆钉的个数F P F P91PF =图3-4⑵ 铆钉剪切面上的内力F Q铆钉剪切面上的内力F Q 称为剪力。
单剪时: nF F F PQ ==1 双剪时: nF F F PQ 221==⑶ 剪切面上的名义剪应力τ ①何谓名义剪应力?τ在剪切面上各点的大小及散布规律很复杂,因为:a)铆钉的短跨弯曲;b)铆钉的冷却及螺帽的拧紧,使钉杆受拉; c)钢板孔壁与钉杆的相互挤压。
②τ的计算:QQ A F =τA Q —受剪面的面积③τ的单位:与σ一样:P a 、MP a ⑷剪切强度极限的测定图3-5①剪切实验装置依照联接件的的实际受剪情形,进行直接剪切实验来取得破坏荷载。
材料力学—剪切和挤压

2
785kN
n
4P nd
2 2
[ ] 62.5
4P
d [ ]
取 n = 64
D
2 连接筒壁和角铁铆钉个数 (1)剪切强度条件
n 4P nd
2 2
[ ] 35.7
4P
d t t
d [ ]
P ntd P td [ bs ]
(2)挤压强度条件
n [ bs ] 24.5
取 n = 36
p
t
N = 2(64+36) = 200(个)
ቤተ መጻሕፍቲ ባይዱP y Q x P y Q´ P x
Σy=0
P - Q´ = 0 Q´= P (数值上)
(实质上)
Q dA
A
Q和 Q´称为剪力。
2 剪应力和剪切强度条件
假设τ均布
Q dA dA A
A A
τ
dA
Q A
“名义”剪应力
剪应力强度条件
Q A
[ ]
[τ]--许用剪应力 [τ] =(0.6-0.8)[σ] (塑性材料) [τ] =(0.8-1.0)[σ] (脆性材料) 3 剪切破坏条件
Q A b
τb=(0.6-0.8)σb
§3.3 挤压实用计算 1 挤压的概念 受力特点: 变形特点: 挤压面:连接件和被连接 件之间相互压紧的面。
P P
第三章
剪切和挤压
§3.1剪切的概念 受力特点:作用于杆件上的外力是一 对大小相等、方向相反、作用线靠得 很近的集中力. 变形特点:杆件沿剪切面发生相对错动.
P
第三章剪切与挤压讲义

第三章剪切与挤压§3-1基本概念1、在轴、键、轮传动机构中,键埋入轴、轮的深度相等,三者的许用挤压应力为:[σbs1],[σbs2],[σbs3],三者之间应该有怎样的合理关系?2、在平板与螺栓之间加一垫片,可以提高的强度。
A:螺栓拉伸;B:螺栓挤压;C:螺栓的剪切;D:平板的挤压;3、在钢板、铆钉的连接接头中,有几种可能的破坏形式?4、“剪断钢板时,所用外力使钢板产生的应力大于材料的屈服极限。
”此说法对吗?5、判断剪切面和挤压面时应注意:剪切面是构件两部分发生的平面;挤压面是构件表面。
6、螺钉受力如图,其剪切面面积为,挤压面的面积为。
§3-2计算1、 P=100KN,螺栓的直径为D=30毫米,许用剪应力为[τ]=60MPa,校核螺栓的强度。
如果强度不够,设计螺栓的直径。
2、钢板厚t=10毫米,剪切极限应力为τ0=300MPa,欲冲出直径为D=25毫米的孔,求冲力P=?3、在厚t=10毫米的钢板上冲出如图所示的孔,钢板的剪切极限应力为τ0=300MPa,求冲力P=?4、凸缘联轴器传递的力偶矩为M=200Nm,四只螺栓的直径为d=10毫米,对称地分布在D=80毫米的圆周上,螺栓的许用剪应力为[τ]=60MPa,校核螺栓强度。
5、夹剪夹住直径为d=3毫米的铅丝,铅丝的剪切极限应力为:τ0=100MPa,求力P=?6、冲床的最大冲力为P=400KN,冲头材料的许用应力为[σ]=440MPa,钢板的剪切极限应力为τ0=360MPa。
求在最大冲力的作用下圆孔的最小直径和钢板的最大厚度。
7、用二个铆钉将140×140×12的等边角钢铆接在墙上构成支托,P=3KN,铆钉的直径为D=21毫米。
求铆钉内的剪应力τ与挤压应力σbs。
1.8、轴的直径为d=80毫米,用键连接。
键的尺寸为:宽b=24毫米,高h=14毫米,许用剪应力为[τ]=40MPa,许用挤压应力为[σbs]=90MPa。
第三章6 十字板剪切试验(岩土测试技术)
顶面的抗扭矩为: M3
D 12
3
D13 C H
Cv
D1 D D 3 M M 1 M 2 M 3 DH Cv D C H 2 6 2M C v C H Cu D 2 H D 3 M可以通过电测仪表测出 ,如下 M R
注意事项:
应先将电缆穿过施加扭力装置的中心孔,然后 再穿入探杆; 在扭剪前,应读取初始读数或将仪器调零; 匀速转动手摇柄,摇柄每转一圈,十字板头旋 转一度。 测试重塑土时,用扳手或管钳快速将探杆顺时 针方向旋转 6 圈,使十字板头周围的土充分扰 动后,立即拧紧钻杆夹具
四、测试数据处理
(1) 不用取样,特别是对难以取样的灵敏度高的 粘性土,可以在现场对基本上处于天然应力状 态下的土层进行扭剪。所求软土抗剪强度指标 比其他方法都可靠。 (2) 野外测试设备轻便,操作容易。 (3) 测试速度较快,效率高,成果整理简单。
其缺点是仅适用于江河湖海的沿岸地带的软土, 适应范围有限,对硬塑粘性土和含有砾石杂物 的土不宜采用,否则会损伤十字板头。
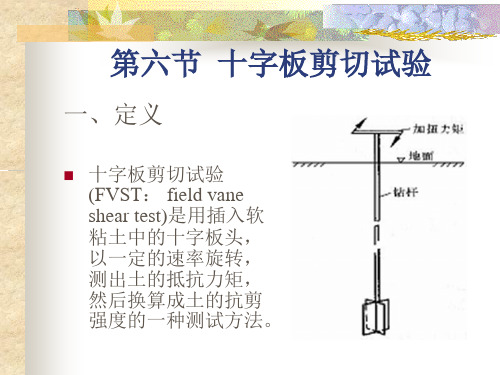
第六节 十字板剪切试验
一、定义
十字板剪切试验 (FVST: field vane shear test)是用插入软 粘土中的十字板头, 以一定的速率旋转, 测出土的抵抗力矩, 然后换算成土的抗剪 强度的一种测试方法。
FVST主要用于测定饱水软粘土的不排水抗剪强度。 它具有下列优点:
表格
计算重塑土的抗剪强度Cu/
Cu 10 K Re R e — 重塑土剪坏时表的读数
表格
计算土的灵敏度St
Cu St C
u
表格
纯剪切切应力互等定理剪切胡克定律
解:1.板的拉伸强度
2.板的剪切强度
Fs F 50103 A 4a 4 0.08 0.01
15.7106 15.7MPa [ ]
FN F A (b 2d )
50 103
(0.15 2 0.017) 0.01
43.1106 43.1MPa [ ]
15
§3-1 连接件的强度计算
d
b
a
3.铆钉的剪切强度
Fs A
4F 2πd 2
2F πd 2
2 50103 π 0.0172
110106 110MPa [ ]
4.板和铆钉的挤压强度
bs
Fbs Abs
F
2d
9
§3-1 连接件的强度计算
Fs F
A lb
bs
Fbs Abs
F cb
10
§3-1 连接件的强度计算
4F
d 2
F 2
dh
Fs A
4F
d 2
bs
Fbs Abs
F dh
2
为充分利用材
料切应力和挤压应
力均达到最大值。
27
§3-2 纯剪切 切应力互等定理 剪切胡克定律
三.剪切胡克定律
G
其中,比例常数G 称为切变模量。常用单位GPa
28
§3-2 纯剪切 切应力互等定理 剪切胡克定律
对各向同性材料可以证明,弹性常数E、G、 μ存在关系
G E
剪切和挤压工程力学
τ=Gγ
(3.5)
式(3.5)中,比例常数G与材料有关,称为材料的切变模量,是 表示材料抵抗剪切变形能力的物理量,它的单位与应力的单 位相同,常用GPa,其数值可由实验测得。一般钢材的G约为 80GPa,铸铁约为45GPa。
下一页 返回
3.3 剪切虎克定律 切应力互等定律
上一页 下一页 返回
3.3 剪切虎克定律 切应力互等定律
(τdy·dz)·dx= (τ´dy·dx)·dz
得
τ=τ´
(3.6)
为了明确切应力的作用方向,对其作如下号规定:使单元体 产生顺时针方向转动趋势的切应力为正,反之为负。则式 (3.6)应改写为
τ=-τ´
(3.7)
式(3.7)表明,单元体互相垂直两个平面上的切应力必定是同 时成对存在,且大小相等,方向都垂直指向或背离两个平面 的交线。这一关系称为切应力互等定理。
上一页 下一页 返回
6.2 剪切和挤压实用计算
当挤压面为平面时,挤压面面积即为实际接触面面积;当为 圆柱面时,挤压面面积等于半圆柱面的正投影面积,如图3-6
所示,Ajy=dl。
为了保证构件具有足够的挤压强度而正常工作,必须满足工
作挤压应力不超过许用挤压应力的条件。即挤压的强度条件
为
jy
F jy A jy
在承受剪切的构件中,发生相对错动的截面称为剪切面。剪
切面上与截面相切的内力称为剪力,用FQ表示 (图3-3d),其
大小可用截面法通过列平衡方程求出。 构件中只有一个剪切面的剪切称为单剪,如图3-3中的铆钉。
构件中有两个剪切面的剪切则称为双剪,拖车挂钩中螺栓所 受的剪切(图3-4)即是双剪的实例。
第3章 剪切与扭转(土木)资料
径为d=25mm的孔。 试求冲力P的大小。
13
解:
A dt 2510 785 (mm)2
Fs P
P
t
P
Fs A
P A
P 785 106
受剪面 d
P 785106 300106 236103 N
14
例: 两块矩形截面木杆用两块钢板连接如 图 所 示 , P=60kN , 木 材 顺 纹 剪 切 许 用 应 力 为
mA 12.73kN m mB mC 3.82kN m mD 5.09kN m
mB 1
T (kN·m) 3.82
mC 2
mA 3 mD + 5.09
- 7.64
55
§3.2.2 薄壁圆筒的扭转
先讨论比较简单的薄壁圆筒的扭转问题。
壁厚
1 t r
10 0
(r0:为平均半径)
一、实验:
1.实验前:
21
例: 挖掘机减速器的某轴上装一齿轮,齿轮与轴通 过平键连接。已知键所受的力为P=12.1kN,平键的宽、 高 、 长 分 别 为 b=6mm , h=10mm,l=70mm , 圆 头 半 径 R=14mm,键的许用剪应力[]=87MPa,轮毂的许用挤 压应力[bs]=100MPa,试校核键连接的强度。
A bL
L
Fs
b[
]
2
60 103 0.15 1106
P
P
LL
s1 s2 1
s1 1 Fs
0.2 m 16
3.1.2.挤压的实用计算 第二种破坏方式为铆钉与钢板间的局部接触,互相挤 压,导致破坏。接触面上的压力称为挤压力。记为Fbs 。
材料力学:第三章 拉压与剪切应变能
静定问题
一度静不定
静不定度 未知力数与有效平衡方程数之差
静不定问题分析
分析方法 求解思路 建立平衡方程 建立补充方程 联立求解
求解算例 平衡方程
E1A1= E2A2
变形几何关系
-变形协调方程
胡克定律
补充方程
联立求解平衡与补充方程
静不定问题求解与内力的特点: 静不定问题求解:
设计变量:在工程设计中可由设计者调整的量,例如构件 的截面尺寸
约束条件:设计变量必须满足的限制条件
目标函数:目标的设计变量表达式
单辉祖:材料力学Ⅰ
65
结构优化设计简单算例
已知:F=100 kN,l=500 mm,[st]150 MPa, [sc] 100 MPa, A1 = A3,密度 r 7.85103 kg/m3
2.内力能(应变能)
(1)用内力计算应变能 (2)用应力计算应变能
应变能 拉压
剪切
Dl FNl EA
应变能密度
3.功能等
应变能小结:解题思路
题目:求内力、位移、应力
功能守恒定律 截断法静力分析:求内力或应力
(1)用内力计 算应变能
计算内 力能
(2)用应力计算 应变能
计算外力功
(弹力作功)
功能等
例题
成立条件:载荷缓慢增大,动能、热能变化忽略不计。
单辉祖:材料力学Ⅰ
32
回顾:
轴向拉压应变能
(1) 外力功与弹性应变能计算
弹 性
回顾:
拉压与剪切应变能密度
(2) 由应力应变计算应变能 拉压应变能
拉压应变能密度
(单位体积内应变能)
剪切应变能
剪切应变能密度
34
