阵列除法器设计与实现
电路中的除法器设计

电路中的除法器设计在电路设计中,除法器是一种十分重要的组件。
它可以将输入的数字进行除法运算,将商和余数输出。
除法器在计算机和数字信号处理器等电子设备中被广泛使用,因此其设计和优化具有重要意义。
一、除法器的基本原理除法运算是一种复杂的运算,要实现除法器的设计,首先需要了解其基本原理。
除法器的基本原理是通过移位和减法实现的。
在将被除数和除数输入除法器后,除法器将被除数和除数进行比较,并开始迭代过程。
在每一次迭代中,被除数的位数向左移动,直到其高位与除数相等或超过除数。
然后,除法器进行减法操作,将除数减去被除数,结果作为商的一位。
此后,商持续左移,被减数保持不变,重复上述过程,直到所有的商位都得出。
二、除法器的设计策略在除法器的设计中,有几种常见的策略可以考虑。
1. 组合逻辑除法器:这种类型的除法器使用组合逻辑电路实现,通过减法器、比较器和移位器等组件的组合来实现除法运算。
组合逻辑除法器的优点是速度较快,但缺点是占用较多的电路资源。
2. 串行逻辑除法器:与组合逻辑除法器相反,串行逻辑除法器使用顺序逻辑电路实现。
它通过一个时钟信号,逐位地进行计算,因此典型的串行逻辑除法器速度较慢。
但串行逻辑除法器更节省电路资源,因此在一些资源有限的场景中得到了广泛应用。
3. 重复系列除法器:这种除法器通过多个并行的子除法器实现,并行计算多个位的商。
重复系列除法器具有较高的性能,但需要更多的电路资源和功耗。
三、除法器的优化方法为了提高除法器的性能和效率,可以采用一些优化方法。
1. 位级并行思路:通过将除法器分解为多位的子除法器,并行计算多个子除法器,可以大幅提高除法器的速度。
这种方法在重复系列除法器中得到了广泛应用。
2. 乘法相关技巧:利用乘法器计算除法运算,可以加速除法器的运算速度。
通过将除数进行逆运算,转化为乘法操作,可以利用乘法器的高速性能,提升除法器的效率。
3. 进制转换思想:将数字进行二进制到十进制的转换,然后进行简单的除法运算,可以减少运算的复杂程度,提高除法器的运算速度。
阵列除法器的FPGA实现

・ 备与 设旖・ 设
阵列除法器的 F G P A实现
口 孙 亮 周忠海 1廉 月仙 。 军礼 , 2 , , 刘
(. 1 中国海洋大学, 山东 青 岛 2 6 0; . 60 3 2山东省海洋仪器仪表研究所, 山东 青岛 2 60 ; 60 1 3西 日本株式会社. _ 山东 青岛 2 6 0 ) 60 1
口 SUN La g , in  ̄ZHOU Zh n - a , I e xa 。L U J n l o g h i LAN Yu - in , I u —i ’
( . c a i r i f i , n d o 2 6 0 , i ; . s tt f e n g a h sr me tt n S a d n 1O e n Un e s y o n Qi a 6 0 3 Ch a 2 I tueo a o r p i I t v t Ch a g n n i Oc c n u nai , h n o g o
除法器是 电子技术领 域的基础模 块 ,在 电子 电路设 计中
得多 , 但为了提升运算速度 , 就要 以硬件资源 的消耗为代价 。
2 除法 的运 算 的 分析
得到广泛地应用。然而相对于加法和乘法等其他操作 , 除法操 作的效率很低 。出现这种情况 的原 因除了除法本身 的复杂性
外, 还与人们普遍认为除法是不频繁的操作有关 。作为微处理 器的一个重要 的运 算单 元 , 除法器 的运 算速度 、 能 、 性 功耗 等 都会影 响系统 的整体性能 ,所 以对除法效率 的忽视会导致系
【 中图分类号】
T 62 N0
【 文献标 识码】
B Βιβλιοθήκη 【 文章编号】 1 0 — 5 8(0 8 0 — 1 0 0 7 4 3 , 0 ) 4 0 仃一 2 2
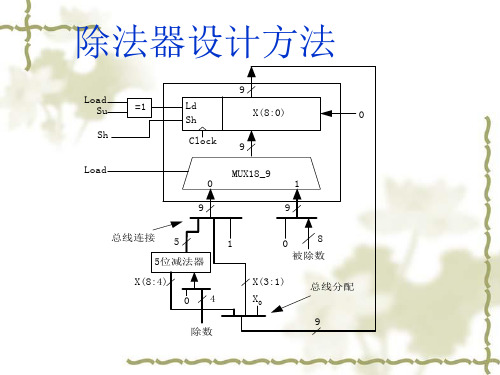
除法器设计方法
controlsignals:process(T,I,X,Y)
--状态控制进程
begin
Extern<='0';Done<='0';Ain<='0';Gin<='0';
Gout<='0';AddSub<='0';Rin<="0000";Rout<="0000";
case T is
when "00"=>
update:process(clk)
--同步数据更新进程
begin
if(clk='1'and clk'event) then
state<=nextstate;
if load='1' then
dividend<='0'÷nd_in;
end if;
if su='1' then
dividend(8 downto 4)<=subout;
end proc;
architecture Behavioral of proc is
component upcount
--计数器元件声明
Port ( Clear,Clock : in std_logic;
Q : buffer std_logic_vector(1 downto 0));
end component;
signal subout:std_logic_vector(4 downto 0);
signal dividend:std_logic_vector(8 downto 0);
阵列除法器

沈阳航空工业学院课程设计报告课程设计名称:计算机组成原理课程设计课程设计题目:阵列除法器的设计院(系):计算机学院专业:计算机科学与技术班级:7401101学号:*****************指导教师:***完成日期:2010年1月15日沈阳航空工业学院课程设计报告目录第1章总体设计方案 (1)1.1设计原理 (1)1.2设计思路 (2)1.3设计环境 (3)第2章详细设计方案 (6)2.1顶层方案图的设计与实现 (6)2.1.1创建顶层图形设计文件 (6)2.1.2器件的选择与引脚锁定 (7)2.1.3编译、综合、适配 (8)2.2功能模块的设计与实现 (8)2.3仿真调试 (10)第3章编程下载与硬件测试 (12)3.1编程下载 (12)3.2硬件测试及结果分析 (12)参考文献 (14)附录(电路原理图) (15)第1章总体设计方案1.1 设计原理阵列除法器的功能是利用一个可控加法/减法(CAS)单元所组成的流水阵列来实现的。
它有四个输出端和四个输入端。
当输入线P=0时,CAS作加法运算;当P=1时,CAS作减法运算。
可控加法/减法(CAS)单元的逻辑电路图如图1.1所示。
图1.1可控加法/减法(CAS)单元的逻辑图CAS单元的输入与输出关系可用如下一组逻辑方程来表示:S i=A i ⊕(B i ⊕P) ⨁CC i+1=(A i+C i) ∙(B i ⊕P)+A i C i当P=0时,就得到我们熟悉的一位全加器(FA)的公式:S i=A i ⊕B i ⊕C iC i+1=A i B i+B i C i+A i C i当P=1时,则得求差公式:S i=A i ⨁B i '⨁C iC i+1=A i B i '+B i 'C i+A i C i其中B i '=B i⨁1。
在减法情况下,输入C i称为借位输入,而C i+1称为借位输出。
不恢复余数的除法也称加减交替法。
组成原理课程设计报告-阵列乘法器的设计与实现

沈阳航空航天大学课程设计报告课程设计名称:计算机组成原理课程设计课程设计题目:阵列乘法器的设计与实现院(系):计算机学院专业:计算机科学与技术班级:学号:姓名:指导教师:施国君完成日期:2014年01月10日沈阳航空航天大学课程设计报告目录第1章总体设计方案 (2)1.1设计原理 (2)1.2设计思路 (2)1.3设计环境 (3)第2章详细设计方案 (5)2.1总体方案的设计与实现 (5)2.1.1创建顶层图形设计文件 (5)2.2功能模块的设计与实现 (6)2.2.1输入加法器模块的设计与实现 (6)2.3阵列乘法器的设计与实现 (8)第3章编程下载与硬件测试 (10)3.1编程下载 (10)3.2硬件测试及结果分析 (10)参考文献 (13)附录 (14)第1章 总体设计方案1.1 设计原理以COP2000实验仪、FPGA 实验板为硬件平台,采用Xilinx Foundation F3.1设计工具和COP2000仿真软件,采用自上而下的设计方法,设计并实现阵列乘法器功能。
阵列乘法器的设计原理如图1.1所示,X1,X2,X3,X4, Y1,Y2,Y3,Y4为阵列乘法器的输入端, S1~S8为阵列乘法器的输出端。
图中的排列形式和笔算乘法的位积排列形式相似。
阵列的每一行由乘数Y 的每一位数位控制,而各行错开形成的每一列由被乘数X 的每一位数位控制。
图中方框内的电路由一个与门和一个全加器组成。
由于采用阵列结构,虽然采用加法器数量较多,但内部结构规则,采用超大规模集成电路很容易实现,可大大提高运算速度。
图1.1 阵列乘法器原理图1.2 设计思路阵列乘法器是设计主要包含如下3个部分:S6S5S4S3S2S1乘 积 P = P 40P1P2P3部分积1、加法器的设计与实现;2、阵列乘法器的设计与实现;3、下载与硬件测试;阵列乘法器的设计与实现采用自上而下的设计方法,在这3个部分中分别设计实现相应功能的器件,在连接具体电路时配合相应脉冲和门电路以达到预期效果。
fpga除法运算

fpga除法运算FPGA(Field Programmable Gate Array)是用于数据处理、数字信号处理、调制解调、高速通讯等领域的一种可重构的现场可编程门阵列芯片。
它通过可编程的硬件逻辑资源来实现各种功能,包括了数字电路中的算数逻辑单元(ALU)。
在数字设计中,除法是一种非常重要的算术运算,而FPGA中的除法是属于整数除法。
因为浮点除法很难用硬件实现且复杂度很高,所以FPGA中的除法大多是整数除法。
在FPGA中实现除法有两种方法:1. 直接方法:直接使用除法器,这种方式的局限性比较大。
2. 迭代法:将除法转化为乘法,每次计算一位,比较灵活。
下文将详细介绍迭代法。
迭代法的基本思路是将被除数逐位移位,不断进行减法运算,直到除数小于被除数,就得到了商和余数。
因为每次只需要减去一个二进制数,因此运算速度会比使用除法器快一些。
FPGA中的除法可以使用两种方法:恒定除法和非恒定除法。
1. 恒定除法:被除数和除数的位数是恒定的,即所有数码相乘的结果按照一定规律进行加法运算。
2. 非恒定除法:被除数和除数的位数不确定,需要不断移位和相减以获得余数和商,这需要使用迭代方法。
原理介绍:FPGA中的迭代法除法通常采用的是高斯-约旦算法。
该算法的基本原理是使用几个数码相等的跨度,通过移位和加减运算进行迭代循环,将大数除以小数,得到除数和余数。
这个过程就是高斯-约旦算法,也被称为尾数规制法。
这种算法要求被除数和除数都是非负的,通过对两个正整数之间的无限不循环小数进行近似,将除法问题转化为乘法问题。
算法步骤:1. 消除除数最高位不为1的情况。
2. 对于每一位,将被除数左移一位并减去除数。
如果差值为负数,那么这一位就标记为0,否则标记为1,余数也会减去这个值。
3. 重复以上步骤,直到被除数小于除数,并得到商和余数。
举个例子来说明具体的计算过程:假设被除数为1101,除数为0110,如下所示。
- 首先从除数的最高位开始,找到最高的1(此例中是第二位)。
不恢复余数阵列除法器的FPGA实现

l
I
\
P
l
\
Y
I F l\ A
S i
减法. 也就是说 , 可作为1 图4 个单符号位的n l + 位补码加法/ 减法器 , 若考 虑n 1 C S + 个 A 的所有 输 出端 , 其符 号化 示 意图如 图5 示 . 则 所
圈 3 C S 逻 辑 结构 A的
2 不恢 复余 数 算 法
以定 点小 数 为 例 , 已知 【 和[] 为保 x Y补, 证 商也 是 定 点 小 数 ,故 规 定 I >XI为 了分 YII . 析 算 法 , 此 只考 虑 x Y 为 正 数 的情 况 , 因 和 均
则有 【 = .l …x, = .l " Y, Y 补 X 0 X 2 【 x Y 0 y 2 " [ ] = 0 y' 一
1YY…y, .。 设部 分余数 为 R, 为Q, 执 行下 商 则
列操 作 :
符号 位 ຫໍສະໝຸດ f l f n 图4 单 符号 位 的n l 补码 加/ 法器 +位 减
R= .x…x( 部分 余数 R , 做 减法 ) 00x 求 】 。 先 ,
21 0 0年 5 月
保 定 学 院 学 报
J 0URNAL 0F BA0DI NG UNI VERS T I Y
Ma ,01 y2 0
第2 3卷第 3 期
Vo 2 o3 L 3 N .
文章编 号 :6 42 9 (0 0 0 .0 60 17 .4 4 2 1 )30 5 .4
P
Ci + l
原码的阵列乘、除法运算器教学设计

( 1 ) 出一 道 十进 制 和一 道 二 进 制 的 乘 法 题 目 , 让 学生 在 黑 板 上运 算 , 然 后 总结 , 并 得 出结 论 : n位
另一方面是“ 操作系统” 、 “ 计算机系统结构” 等课程
的基 础 , 在课 程 体 系 中 起 着 承上 启 下 的作 用 。 学生
第3 8卷
第 6期
电气 电子教 学 学报
J O URNAL OF EE E
Vo 1 . 3 8 N o . 6
De C. 201 6
2 0 1 6年 l 2月
原 码 的 阵 列乘 、 除法 运 算 器 教 学 设 计
李社 蕾,杨婷婷 ,刘小飞
(三 亚 学院 理 工学 院 , 海 南 三亚 5 7 2 0 2 2 )
关 专业 的 核 心 专 业 基 础 课 , 它一 方 面 以 “ 模 拟 电 路 ”、 “ 数 字逻 辑 电路 ” 、 “ 汇编语言 法研 究
课 堂上 , 原码 陈列 乘法 器授 课可采 用 出题 、 解题 和 总结 的方 式进 行 。 例如 : 三道 实 例 题 的 授课 过程
Ab s t r ac t :Ac c o r d i n g t o t he c h a r a c t e r i s t i c s o f b r o a d s c o p e a n d a bs t r a c t i o n f o r a r r a y mu l t i p l i e r a n d a r r a y s d i v i d e r i n t h e Co mp u t e r Or g a n i z a t i o n Pr i nc i p l e s c o ur s e,t h e n e w wa y s o f c l a s s r o o m o r g a n i z a t i o n a n d a ra n g e me n t o f t e a c h i n g c o nt e n t i s d e s i g n e d,c l a s s r o o m t e a c h i n g a c t i v i t i e s h a s p r o v e d t ha t t hi s t e a c hi n g d e s i g n i s he l p f u l t o s t ud e n t s u n d e r - s t a n d i n g o f kn o wl e d g e p o i n t s,a n d b r i n g t h e c o nt e n t i n t o t h e i r o wn kn o wl e d g e s y s t e m ,a nd c u l t u r e d l e a r n i n g a b i l i t y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课程设计报告
课程设计名称:计算机组成原理课程设计课程设计题目:阵列除法器设计及实现
院(系):计算机学院
专业:
班级:
学号:
姓名:
指导教师:
完成日期:2016年1月12日
目录
第1章总体设计方案0
1.1设计原理0
1.2设计思路2
1.3设计环境3
第2章详细设计方案4
2.1功能模块的设计及实现4
2.1.1细胞模块的设计及实现5
2.1.2除法器模块的设计及实现7 2.2仿真调试9
参考文献11
附录(电路原理图)
1 2
第1章总体设计方案
1.1 设计原理
在原码除法中,原码除法符号位是单独处理的,商符由两数符号位进行异或运算求得,商值由两数绝对值相除求得。
原码除法中由于对余数的处理不同,又可分为恢复余数法和不恢复余数法(加减交替法)。
在机器操作中通常采用加减交替法,因为加减交替法机器除法时间短,操作规则。
加减交替法的运算规则如下:
(1)当余数为正时,上商1,余数左移一位后减去除数得下一
位余数。
(2)当余数为负时,上商0,余数左移一位后加上除数得下一位
余数。
阵列除法器是一种并行运算部件,采用大规模集成电路制造,及早期的串行除法器相比,阵列除法器不仅所需的控制线路少,而且能提供令人满意的高速运算速度。
阵列除法器有多种形式,如不恢复余数阵列除法器、补码阵列除法器等等。
本实验设计的是加减交替阵列除法器。
本实验利用的细胞单元是一个可控加法/减法CAS单元,利用它组成的流水阵列来实现四位小数的除法。
CAS单元有四个输入端、四个输出端。
其中有一个控制输入端P,当P=0时,CAS作加法运算;
当P=1时,CAS作减法运算。
逻辑结构图如图1.1所示。
图1.1 可控加法/减法(CAS)单元逻辑结构图CAS单元的输入及输出的关系可用如下逻辑方程来表示:Si=Ai⊕(Bi⊕P)⊕Ci
Ci+1=(Ai+Ci)(Bi⊕P)+AiCi
当P=0时,CAS单元就是一个全加器,如下:
Si=Ai⊕B⊕iCi
Ci+1=AiBi+BiCi+AiCi
当P=1时,则得求差公式:
Si=Ai⊕B⊕iCi
Ci+1=AiBi+BiCi+AiCi
其中有Bi=Bi⊕1
在减法中,输入称为借位输入,而称为借位输出。
不恢复余数法的除法即加减交替法。
在不恢复余数的除法阵列中,若前一行输出的符号及被除数的符号是一致的则这一行执行加法,如果不一致则这一行执行减法。
当出现不够减时,部分余数相对被除数来说要改变符号。
这时应该产生一个商位“0”,除数首先沿对角线右移,然后加到下一行的部分余数上,当部分余数不改变它的符号时,即产生商位“1”,下一行的操作应该是减法。
本实验就是要求用加减交替法设计阵列除法器。
如下图1.2所示的就是用加减交替法设计的阵列除法器,图中每一个方框代表一个CAS 单元,除数为Y0Y1Y2Y3Y4;
被除数为X0X1X2X3X4。
其中X0和Y0是被除数和除数的符号位,均为零,商的符号恒为零,商为0.S1S2S3S4,余数为0.000YU1YU2YU3YU4YU5。
被除数由顶部一行和最右边的对角线上的垂直输入线来提供,除数沿对角线方向进入阵列。
由控制信号P 来决定此行作加法还是除法,当P=0时,CAS作加法运算;当P=1时,CAS作减法运算。
1.2 设计思路
在本实验中要求输入得除数和被除数数据位均为四位,并用加减交替法来设计这个阵列除法器。
这个可以用CAS单元所组成的流水阵列来实现,四位数据位加上一个符号位,一个五位除五位的加减交替除
法阵列由5×5个CAS单元组成,其中两个操作数均为正。
流水逻辑框图如上图1.2所示
1.3 设计环境
(1)硬件环境
•伟福COP2000型计算机组成原理实验仪
COP2000计算机组成原理实验系统由实验平台、开关电源、软件三大部分组成。
实验平台上有寄存器组R0-R3、运算单元、累加器等组成。
COP2000计算机组成原理实验系统各单元部件都以计算机结构模型布局,系统在实验时即使不借助PC 机,也可实时监控数据流状态及正确及否, 实验系统的软硬件对用户的实验设计具有完全的开放特性,系统提供了微程序控制器和组合逻辑控制器两种控制器方式,系统还支持手动方式、联机方式、模拟方式三种工作方式,系统具备完善的寻址方式、指令系统和强大的模拟调试功能。
•COP2000集成调试软件
COP2000集成开发环境是为COP2000实验仪及PC机相连进行高层次实验的配套软件,它通过实验仪的串行接口和PC机的串行接口相连,提供汇编、反汇编、编辑、修改指令、文件传送、调试FPGA实验等功能,该软件在Windows下运行。
(2)EDA环境
•Xilinx foundation f3.1设计软件
Xilinx foundation f3.1是Xilinx公司的可编程期间开发工具,该平台功能强大,主要用于百万逻辑门设计。
该系统由设计入口工具、设计实现工具、设计验证工具三大部分组成。
第2章详细设计方案
2.1 功能模块的设计及实现
阵列除法器的底层设计包括25个CAS模块,这个CAS模块由2个或门、4个及门和3个异或门逻辑组合而成。
2.1.1细胞模块的设计及实现
(1)创建细胞模块设计原理图。
细胞模块原理结构图如图2.1所示。
图2.1 细胞块逻辑框图
(2)创建元件图形符号
为了能在图形编辑器中调用CAS芯片需要把它封装,可利Xilinx foundation f3.1编译器中的如下步骤实现:Tools=>Symbol Wizard=>下一步。
其中XIN、YIN、PIN、CIN为四个输入信号,YUOUT、YOUT、POUT、COUT为四个输出信号。
用其元件图形符号如图2.2所示:
图2.2 细胞元件图形符号
(3)功能仿真
对创建的取补模块进行功能仿真,验证其功能的正确性,可用Xilinx foundation f3.1编译器的Simulator模块实现。
仿真结果如图2.4所示:
图2.3 细胞模块仿真结果
表2.1 细胞模块真值表
输入信号输出信号
YOUT POUT COUT XIN YIN PIN CIN YUOU
T
11110111 00110011 10111011 11101110
00101010 10100011 11011101 00011000 10010001 11000101 00000000 10001000将仿真结果及细胞模块的输入、输出信号真值表相对比可知,细胞模块的仿真结果正确。
2.1.2除法器模块的设计及实现
(1)创建除法器模块设计原理图。
除法器模块原理结构如图2.4所示:
图2.54 除法器原理模块框图
(2)创建元件图形符号
为了能在图形编辑器中调用YANG芯片,需要为除法器模块创建一个元件图形符号,可利Xilinx foundation f3.1编译器中的如下步骤实现:Tools=>Symbol Wizard=>下一步。
其元件图形符号如图2.5所示:
图2.5 选择器元件图形符号
(3)功能仿真
对除法器模块进行功能仿真,验证其功能的正确性,可用Xilinx foundation f3.1编译器的Simulator模块实现。
仿真结果如图2.6
所示:
图2.6 除法器模块仿真结果图
(3)功能仿真
对创建的乘数补码移位寄存器模块进行功能仿真,验证其功能的正确性,可用Xilinx foundation f3.1编译器的Simulator模块实现。
仿真结果如图2.10所示:
2.2 仿真调试
仿真调试主要验证设计电路逻辑功能、时序的正确性,本设计中
主要采用功能仿真方法对设计的电路进行仿真。
(1)建立仿真波形文件及仿真信号选择
功能仿真时,首先建立仿真波形文件,选择仿真信号,对选定的输入信号设置参数,选定的仿真信号和设置的参数如表2. 2所示。
表2.2 仿真信号相关参数表
(2)功能仿真结果及分析
仿真结果分别如图2.6所示,仿真数据结果如表2.2所示。
对比图2.6和表2.2,多组功能仿真结果均正确,进而说明此电路设计的正确性。
参考文献
[1] 曹昕燕.EDA技术实验及课程设计[M].北京:清华大学出版社,2006
[2] 范延滨.微型计算机系统原理、接口及EDA设计技术[M].北京:
北京邮电大学出版社,2006
[3] 王爱英.计算机组成及结构(第三版)[M].北京:清华大学出版社,2006
[4] 白中英.计算机组成原理(第四版)[M].北京:科学出版社,2009
[5] 唐朔飞.计算机组成原理(第二版)[M].北京:高等教育出版社,2008
[6] 江国强.EAD技术习题及实验[M].北京:电子工业出版社,2005
附录(电路原理图)。
