信号与系统第一章练习题
信号与系统第一章习题答案

t 0 > 0 函数式的信号的波形如图 1.2(b)所示. 。
3
cos ωt
1 … …
−
5π 2ω
−
3π 2ω
−
π 2ω
-1
π 2ω
(a)
3π 2ω
5π 2ω
t
cos ωtε (t )
1
ε (t )
1
…
π 2ω
3π 2ω
5π 2ω
t
t
(b)
-1 (c ) 图 1.1
cos ωtε (t − t 0 )
1
P = lim
E =∞
1 T → ∞ 2T
1 ∫ [ε (t )] dt = 2
T 2 −T
(2) ε (t ) − ε (t − 1) 是脉冲信号,其为能量信号,能量为:
E = lim
[ε (t ) − ε (t − 1)]2 dt = ∫0 [ε (t ) − ε (t − 1)]2 dt =1 T →∞ ∫−T
T
2
(4) 3 cos (ω 0t + θ ) 是功率信号,其平均功率为:
P = lim
1 T → ∞ 2T
2 ∫−T [3 cos (ω0 t + θ )] dt = Tlim →∞ T
1 2T
2
∫
T
−T
9
cos 2(ω0 t + θ ) + 1 1 9 9 dt = lim ⋅ ⋅ 2T = T → ∞ 2 2T 2 2
T 2
2ω t 1 − cos 0 1 cos ω0 t + 1 9ω 0t ω t 5 dt = lim + sin − sin 0 + ∫ − T T →∞ 2T 2 20 20 2
信号与系统第一章习题及作业(1,2)

(2)(余弦序列是否为周期信号,取决于2л/Ω0是正整 (余弦序列是否为周期信号,取决于 Ω 有理数还是无理数。) 数、有理数还是无理数。) 因此, 因此, 2л/Ω0=2л·7/8л=7/4=N/m Ω =2л·7/8л 所以基波周期为N=7; 所以基波周期为N=7; N=7
因为2л/Ω =16л 为无理数, (4) 因为 Ω0=16л,为无理数,则此信号不是周期 信号. 信号. (5) 因为周期信号在[-∞,+∞]的区间上,而本题的重 因为周期信号在[ ∞,+∞]的区间上, 的区间上 复区间是[0, +∞],则此信号为非周期信号 则此信号为非周期信号, 复区间是[0, +∞],则此信号为非周期信号,
f(n) 1 0 3 6 … n
9、判断是否为线性系统?为什么? 、判断是否为线性系统?为什么?
( 3) ( 5) (7 )
y( t ) = ln y( t 0 ) + 3t 2 f ( t ) y( t ) = y( t 0 ) + f 2 ( t ) y( t ) = sin t ⋅ f ( t )
8、一个连续时间系统的输入-输出关系为 、一个连续时间系统的输入 输出关系为
1 t+T y ( t ) = T [ f ( t ) ] = ∫ T2 f (τ )d τ T t− 2 试确定系统是否为线性的?非时变的?因果的? 试确定系统是否为线性的?非时变的?因果的?
解:积分系统是线性的,因此系统是线性系统。 积分系统是线性的,因此系统是线性系统。
sin ω 0 tε ( t )
sin ω 0 ( t − t 0 )ε ( t )tt0 Nhomakorabeat
sin ω 0 tε ( t − t 0 )
信号与系统(西安工程大学)知到章节答案智慧树2023年

信号与系统(西安工程大学)知到章节测试答案智慧树2023年最新第一章测试1.周期信号,其周期为()参考答案:82.=( )参考答案:13.积分的值为()。
参考答案:24.已知,则等于()。
参考答案:5.已知某语音信号,对其进行运算得到信号,与信号相比,信号将发生什么变化( )参考答案:长度变长、音调变低第二章测试1.系统的零输入响应是指仅由系统的激励引起的响应。
()参考答案:错2.系统的零输入响应表达形式一定与其微分方程的通解形式相同,系统的零状态响应表达形式一定与其微分方程的特解形式相同。
()参考答案:错3.卷积的方法只适用于线性时不变系统的分析()。
参考答案:对4.单选题:单位阶跃信号作用于某线性时不变系统时,零状态响应为,则此系统单位冲激响应为()参考答案:5.判断题:两个线性时不变系统级联,其总的输入输出关系与它们在级联中的次序没有关系。
()参考答案:对第三章测试1.连续非周期信号频谱的特点是( )。
参考答案:连续;非周期2.若对进行理想取样,其奈奎斯特取样频率为,对进行取样,其奈奎斯特取样频率为 ( )。
参考答案:3.如图所示信号,其傅里叶变换=F [],等于()。
参考答案:24.如图:所示周期信号,该信号不可能含有的频率分量是()。
参考答案:1 Hz5.已知信号的频谱的最高角频率为,的频谱的最高角频率为,信号的最高角频率等于( )。
参考答案:第四章测试1.请判断下面说法是否正确:若连续时间信号是有限时宽信号,且绝对可积,则其拉氏变换的收敛域为整个s平面。
( )参考答案:对2.利用常用函数的象函数及拉普拉斯变换的性质,函数的拉普拉斯变换为()。
参考答案:3.描述某LTI系统的微分方程为,则激励下的零状态响应为()。
参考答案:4.如图所示的复合系统,由四个子系统组成,若各个子系统的系统函数或冲激响应分别为:则复合系统的冲激响应为()。
参考答案:5.描述某连续线性时不变系统的微分方程为,系统的冲激响应为(),阶跃响应为()。
《信号与系统》第一章知识要点+典型例题

y() 表示系统的输出。
1、线性系统与非线性系统 若系统满足下列线性性质: (1)可分解性 全响应 y () 可分解为零输入响应 y zi () 与零状态响应 y zs () 之和,即
y() y zi () y zs ()
(2)齐次性 零输入响应 y zi () 满足齐次性,零状态响应 y zs () 满足齐次性,即
( t ) 、 ( t ) 的重要性质
1
( t )dt 1 ,
t
( t )dt 0 , ( t )dt ( t ) ( k ) (k )
f ( k ) ( k ) f (0) ( k ) f ( k ) ( k k 0 ) f ( k 0 ) ( k k 0 )
f ( t ) ( t a )dt f (a )
k
f ( k ) ( k ) f (0)
(at )
5
1 (t ) a
1 b (at b) ( t ) a a f ( t ) ( t ) f (0) ( t ) f (0) ( t ) f ( t ) ( t ) f (0) ( t ) f (0) ( t )
2
。
而对离散的正弦(或余弦)序列 sin( k ) [或 cos( k ) ]( 称为数字角频率,单位为 rad ), 只有当
2
为有理数时才是周期序列,其周期 N M
2
, M 取使 N 为整数的最小整数。
如对信号 cos(6 k ) ,由于
2
2 1 为有理数,因此它是周期序列,其周期 N 1 。 6 3
(完整版)信号与系统第一章答案
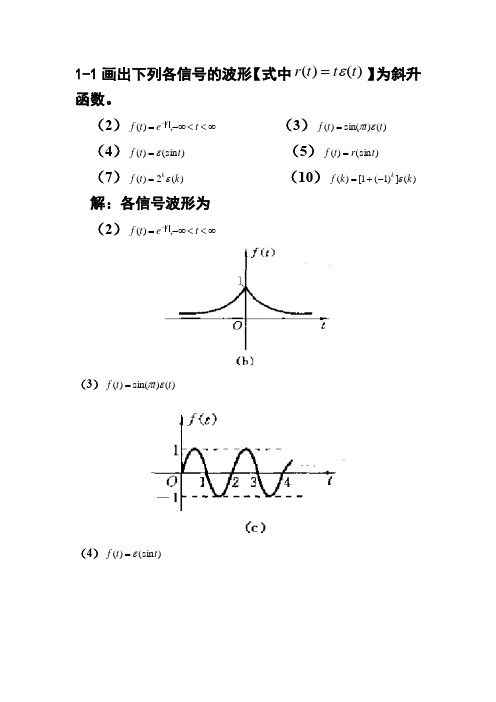
1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t et f t,)( (3))()sin()(t t t f επ=(4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f kε= (10))(])1(1[)(k k f kε-+=解:各信号波形为 (2)∞<<-∞=-t et f t,)((3))()sin()(t t t f επ=(4))(sin )(t t f ε=(5))f=rt)(sin(t(7))t=(kf kε(2)(10))f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε解:各信号波形为(1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f(5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与系统第一章习题解答

Problems Solution
xn
1
1
0
-4 -3 -2 -1 0 1 2 3 4
n
(a)
xe n
n
x0 n
1
-4 -3 -2 -1 0 1 2 3 4
n
Chapter 1
2
Problems Solution
3
xn
3 xe n
12
-2
12
1
-1 0
7
Chapter 1
Problems Solution
作业: 1.14 1.15 1.16 1.17
1.21 (d) (e) (f)
1.22 (d) (g)
1.23
1.24 (a) (b) 1.26 (a) (b) 1.27 1.31
Chapter 1 1.14
1 , 0 t 1 xt T 2 -2, 1t 2
xt
1
2 1 0
1
xe t
1
t
-2 -1 0 1 2
t
(b)
x t
1
xo t
-2 -1
1/ 2
1
0
1
2
t
1/ 2
0
1 2
t
Chapter 1 1.24 Determine and sketch the even and odd parts of the signals.
1
-2 -1 0 1
Problems Solution
xt
gt
k
t 2k
2
3
2
信号与系统第一、二、三章自测题解答

第一章自测题答案1.已知)()4()(2t u t t f +=,则)(''t f =(t)4δ2u(t)'+ 2.2(2)1()t t d t t δ∞-∞+⋅+-=⎰3=-⋅+⎰∞∞-dt t t t )1()2(2δ。
3.=-⎰∞∞-dt t t e tj )(0δωoj ωet 。
4.试画出下列各函数式表示的信号图形: (1)0 ),()(001>-=t t t u t f(2))]4()([3cos )(2--=t u t u t t f π在0到4区间内的6个周期的余弦波,余弦波的周期为2/3。
(3)][sin )(3t u t f π=5.已知f (t )的波形如图1.1所示,求f (2-t )与f (6-2t )的表达式,并画出波形。
答:函数表达式:f(2-t) = [u(t)-u(t-1)]+2[u(t-1)-u(t-2)] f(6-2t)=[u(t-2)-u(t-2.5)]+2[u(t-2.5)-u(t-3)]6.信号f (5-3t )的波形如图1.2所示,试画出f (t )的波形。
答:f(5-3t)左移5/3得到f(-3t),然后再扩展3倍得到f(-t),最后反褶可得到f(t)7.对于下述的系统,输入为e (t ), 输出为r (t ),T [e (t )]表示系统对e (t )的响应,试判定下述系统是否为: (1) 线性系统;(2)非时变系统;(3)因果系统;(4)稳定系统:(a) r (t )=T [e (t )]=e (t -2)线性、非时变、因果、稳定系统 (b) r (t )=T [e (t )]=e (-t )线性、时变、非因果、稳定系统 (c) r (t )=T [e (t )]=e (t )cos t 线性、时变、因果、稳定系统 (d) r (t )=T [e (t )]=a e (t )非线性、时不变、因果、稳定系统9. 一线性非时变系统,当输入为单位阶跃信号u (t )时,输出r (t )为 )1()()(t u t u e t r t --+=-,试求该系统对图1.3所示输入e (t )的响应。
信号与系统 陈后金版 第一章习题(部分)
21e
4 t
,t 0
(2)
y (0 ) 1 时
y zi ( t )
1 2
y zi1 ( t ) 3 e
4 t
,t 0
4 t 1
输 入 3 x ( t 1) 时
y zs ( t ) 3 5 e
4 t
t 1
21e
,t 1
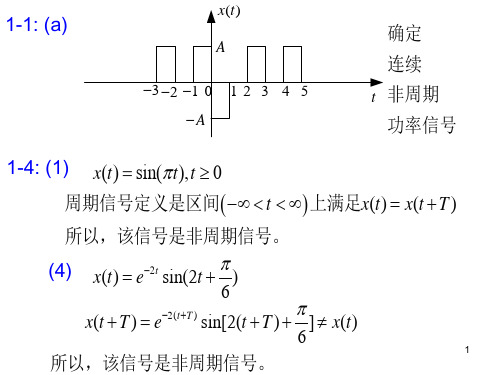
1-1: (a)
x(t )
3 2 1 0
A
A
12 3 4 5
确定 连续
t 非周期
功率信号
1-4: (1)
x(t ) sin( t ), t 0
周期信号定义是区间 t 上满足x(t ) x(t T ) 所以,该信号是非周期信号。
(4)
x(t ) e
yzs (t ) 2
d [ x1 (t ) x2 (t )] dt
2
dx1 (t ) dt
2
dx2 (t ) dt
yzs1 (t ) yzs 2 (t )
故系统为线性系统。
5
(5)
y[k ] 2 y[0] 6 x [k ]
2
1)具有可分解性,yzi [k ] 2 y[0];yzs [k ] 6 x [k ]
k k
1
1
1
k 1
2( ) 3
1
k 1
,k 1
9
y ( t ) y zi ( t ) y zs ( t ) 3e
5 e t 1 21e 4 t 1 , t 1 3
8
1-10:
线性非时变系统 y zi [ k ] 2 y zi1 [ k ] 3 y zi 2 [ k ] 8( ) 9( ) , k 0 2 3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 习题1.判断信号是否为周期的(1)(1)()cos(1)sin(1),2j t x t e t j t T πππ-==-+-=(2)11(){(cos 2)()}[(cos 2)()(cos 2)()]cos 2,122x t t u t t u t t u t t T ευππππ==+-== (3)1(){cos(2)()}[cos(2)()cos(2)()]4244x t t u t t u t t u t πππευπππ=+=++--, 非周期信号2.绘制下列信号波形(1)2()(36)()t t x t e e u t --=+ (3)()cos(10)[(1)(2)]t x t e t u t u t π-=---(5)()(1)(1)()(2)[()(1)](1)(2)x t t u t tu t u t t u t u t u t u t =+----=---+---(7)3()cos [()2()](cos )()22x t t u t u t t u t πππ=+--+-3cos [()()](cos )[()()]22t u t u t t u t u t ππππ=+--------另外一种情况12cos 2()3cos()232cos 2t t t x t t t t t ππππππ⎧<⎪⎪⎪<<⎪=⎨⎪-<<⎪⎪⎪>⎪⎩(8)()()t x t te u t -=(选讲,三点一限) ()(1),1t x t t e t -'=-=为极值点 ()(2),2t x t t e t -''=-= 为拐点 1lim ()lim lim0t t t t t x t te e-→∞→∞→∞=== 3.绘制波形(1)0(23)()tn e t n δ∞-=-⋅-∑ (5)1()(2)n t u t u t n ∞=⋅--∑(7)00[()]()()()()|()()|()tt t t t t d e t t e t t e t e t t dtδδδδδδδ---=='''=-+=-+--=(选讲)(8)()sgn(cos )x t t π=当322k t k πππππ+<<+,即1322k t k +<<+时,cos 0t π<当22k t k πππππ-<<+,即1122k t k -<<+时,cos 0t π>,其中k ∈4.画出下列信号波形的偶分量和奇分量解:根据()()()2e f t f t f t +-=和()()()2o f t f t f t --=求解,求解过程中注意()f t 与()f t -的定义域。
5.已知()f t 和()h t 的信号波形,求下列信号波形(1)()()f t h t - (3)(2)(4)2t f h t -+解:由()f t 求解()f at b +的过程中,简单方法是根据()f t 的关键点坐标0t ,按照公式01t at b =+求解()f at b +的关键点坐标1t ,然后画图。
6.已知()f t 的信号波形,求下列信号波形2(1)(4)f t + (3)2(12)f t -解:解法同第5题,只不过注意信号的幅度变化。
7.已知(2)3t f -的波形,求()f t 的波形图解:由()f at b +求解()f t 的过程中,简单方法是根据()f at b +的关键点坐标1t ,按照公式01t at b =+求解()f t 的关键点坐标0t ,然后画图。
并注意()t δ函数的幅度变化,按照该方法求解()f t 时,()t δ函数的幅度将倍乘a 。
8.求下列波形的直流分量和奇分量(1)()sin()f t t ω= 000112()sin()cos()|T D f ft t dt t T ππωωωωωπππ===-=⎰⎰,奇分量0o f = (3)()cos()sin())4f t t t t πωωω=+=+ 0D f =,1[()()]sin()2o f f t f t t ω=--=9.求下列函数积分(1)00()()()f t t t f t δ∞-∞-=-⎰ (3) 00()()()f t t t f t δ∞-∞-=⎰(5)2()(2)2te t t e δ∞--∞++=-⎰(7)0[2sin 2]()(2sin 2)|4t t t t t t δ∞=-∞''+=-+=-⎰10.求下列函数值(1)112111(9)[(3)(3)]03t dt t t dt δδδ---=++-=⎰⎰(2)222(43)t t dt δ--+⎰, 令2()430f t t t =-+=得到121,3t t ==,2()(43)24f t t t t ''-+=-(1)2,(3)2f f ''=-=2222222111(43)(3)(1)222t t dt t dt t dt δδδ----+=-+-=⎰⎰⎰(选讲) (3)12[(1)(1)(3)]1t e t t t dt e δδ∞---+-++=+⎰ (5)1102[(1)(1)][()]|2t t t e t t dt e e e δδ∞----=-''-+-=+-=⎰11.试求下列函数值 (1)22220[()]2()()|()2()tt t t t d e u t e u t e t t e u t dtδδ----==-+=- (2)22()()t e t e t δδ-+= (5)4(1)(1)2(1)u t t t δδ--=-(6)2()2()t t t δδ''=(选讲)在此处证明以下公式()()(0)()2(0)()(0)()f t t f t f t f t δδδδ''''''''=-+,证明如下00()()()()()()()()()|()[()()]0()()()()()()[()()]|[()()]|(0)(0)2(0)(0)(0)(0)[(0)t t f t t t dt f t t d t f t t t t f t t dtt f t t dt t f t t dt f t t f t t f f f f δϕϕδϕδδϕδϕδϕϕϕϕϕϕ∞∞-∞-∞∞∞-∞-∞∞∞-∞-∞=='''='''=-''''=--''''=+''''''=++''=⎰⎰⎰⎰⎰()2(0)()(0)()]()t f t f t t dtδδδϕ∞-∞''''-+⎰()()(0)()2(0)()(0)()f t t f t f t f t δδδδ''''''''∴=-+12.已知()f t 的波形图,求(32)f t --的波形图解:根据()f t 的关键点坐标0t ,按照0132t t =--公式求出(32)f t --的关键点坐标,然后画图。
13.已知()f t 的波形图,画出()()df t y t dt=的波形图解:()f t 可表示为()(1)()[()(2)]f t u t u t t u t u t =+-+--所以()()(1)()2(2)()(2)df t y t t t t u t u t dtδδδ==+---+--16.求广义导数(1)()(1)(1)()(2)x t t u t tu t u t =+----所以()(1)2(1)()(2)[()(1)]2(1)(2)dx t u t t u t t dt u t u t t t δδδδ=-+----=---+---(2)(24)(4)()()[1](2)(4)t t t t x t e u t e e u t e u t ----=+----(4)(4)()[](2)(4)t t t t e u t e e u t e u t ----=+----所以(4)22(4)(4)()()()[](2)[](2)(4)(4)[()(2)][(2)(4)]()(4)t t t t t t dx t e u t t e e u t e e t e u t t dt e u t u t e u t u t t t δδδδδ--------=-+++-+------=---+---+--17.判断下列系统是否为线性的、时不变的、因果的 (1)()()de t r t dt=,线性、时不变、因果 (3)()sin[()]()r t e t u t =,非线性、时变、因果 (5)()(2)r t e t =,线性、时变、非因果 (7)()()tr t e d ττ-∞=⎰,线性、时不变、因果 时不变性:00()()t t r t t e d ττ--∞-=⎰,当10()()e t e t t =-作用于系统时11000()()()()()()ttt t t t r t e d e t d T t e T dT e d r t t τττττττ---∞-∞-∞-∞==-=-==-⎰⎰⎰⎰令,为时不变 18.是否为可逆系统(1)()(5)r t e t =-,可逆,()(5)r t e t =+ (2)()()tr t e d ττ-∞=⎰,可逆 ,()()de t r t dt =但()()de t r t dt=不可逆,说明逆系统并不一定可逆。
19.判定系统的特性 系统微分方程为()()()sin ()f dv t Mk v t x t Mg t dtθ+=- (1) 如果()0t θ=,方程为线性常系数微分方程,系统为线性、时不变系统 (2) 如果()0t θ≠,方程为非线性常系数微分方程,系统为非线性、时变系统 (3) 如果()x t 为第一输入,sin ()t θ为第二输入,系统为线性、时不变系统20.判定系统特性(线性、时变、因果、稳定性) (2)()[()]()r t T e t te t ==,线性、时变、因果、非稳定 (4)()[()](3)r t T e t e t ==,线性、时变、非因果、稳定(6)(),1()[()]0,0(),1e t t r t T e t t e t t ≥⎧⎪===⎨⎪≤-⎩,线性、时变、因果、稳定 (8)()[()]{()}r t T e t e t ευ==可以表示成 ()()()2e t e t r t +-=,线性、时变、非因果、稳定 21.写出微分方程 (a) (c)()()()()()r t r t r t e t e t ''''''++=- ()3()2()5()4()r t r t r t e t e t ''''++=+22.画出下列微分方程的系统框图(2)322322()3()3()()()2()d d d d dr t r t r t r t e t e t dt dt dt dt dt+++=+23.某一线性时不变系统有下面的输入/输出关系:如果()()e t u t =,那么2()(1)()t r t e u t -=-;如果()cos(2)e t t =,那么()0.707cos(2/4)r t t π=-。
