20 斜弯桥荷载横向分布计算方法
桥梁上部计算教程--横向力分布系数计算
桥梁上部计算教程--横向力分布系数计算(转)总的来说，横向力分布系数计算归结为两大类（对于新手能够遇到的）：1、预制梁（板梁、T梁、箱梁）这一类也可分为简支梁和简支转连续2、现浇梁（主要是箱梁）首先我们来讲一下现浇箱梁（上次lee_2007兄弟问了，所以先讲这个吧）在计算之前，请大家先看一下截面这是一个单箱三室跨径27+34+27米的连续梁，梁高1.55米，桥宽12.95米！！支点采用计算方法为为偏压法（刚性横梁法）mi=P/n±P×e×ai/(∑ai x ai)跨中采用计算方法为修正偏压法（大家注意两者的公式，只不过多了一个β）mi=P/n±P×e×ai×β/(∑ai x ai)β---抗扭修正系数β=1/(1+L^2×G×∑It/(12×E×∑ai^2 Ii)其中：∑It---全截面抗扭惯距Ii ---主梁抗弯惯距 Ii=K Ii` K为抗弯刚度修正系数，见后L---计算跨径G---剪切模量 G=0.4E 旧规范为0.43EP---外荷载之合力e---P对桥轴线的偏心距ai--主梁I至桥轴线的距离在计算β值的时候，用到了上次课程/thread-54712-1-1.html我们讲到的计算截面几何性质中的抗弯惯矩和抗扭惯矩，可以采用midas计算抗弯和抗扭，也可以采用桥博计算抗弯，或者采用简化截面计算界面的抗扭，下面就介绍一下这种大箱梁是如何简化截面的：简化后箱梁高度按边肋中线处截面高度(1.55m)计算，悬臂比拟为等厚度板。
①矩形部分(不计中肋):计算公式:It1=4×b^2×h1^2/(2×h/t+b/t1+b/t2)其中：t,t1,t2为各板厚度h,b为板沿中心线长度h为上下板中心线距离It1=4×((8.096+7.281)/2)^2×1.34^2/(2×1.401/0.603+8.097/0 .22+7.281/0.2)=5.454 m4②悬臂部分计算公式: It2=∑Cibiti3其中：ti,bi为单个矩形截面宽度、厚度Ci为矩形截面抗扭刚度系数,按下式计算:Ci=1/3×(1-0.63×ti/bi + 0.052×(ti/bi)^5)=1/3×(1-0.63×0.26/2.2+0.052×(0.26/2.2)^5)=0.309It2=2×0.309×2.2×0.26^3=0.0239 m4③截面总的抗扭惯距It= It1+ It2=5.454+0.0239=5.4779 m4大家可以用midas计算对比一下看看简化计算和实际能差多少？？先计算一下全截面的抗弯和中性轴，下面拆分主梁需要用的到采用<<桥梁博士>>V2.9版中的截面设计模块计算全截面抗弯惯距，输出结果如下：<<桥梁博士>>---截面设计系统输出文档文件: D: \27+34+27.sds文档描述: 桥梁博士截面设计调试任务标识: 组合截面几何特征任务类型: 截面几何特征计算------------------------------------------------------------截面高度: 1.55 m------------------------------------------------------------计算结果:基准材料: JTJ023-85: 50号混凝土基准弹性模量: 3.5e+04 MPa换算面积: 7.37 m2换算惯矩: 2.24 m4中性轴高度: 0.913 m沿截面高度方向 5 点换算静矩(自上而下):主截面:点号: 高度(m): 静矩(m××3):1 1.55 0.02 1.16 1.773 0.775 1.834 0.388 1.585 0.0 0.0------------------------------------------------------------计算成功完成结果：I全= 2.24 m4 中性轴高度H=0.913m下面来讲一下主梁拆分的原则：将截面划分为τ梁和I梁,保持将两截面中性轴与全截面中性轴位置一致。
桥梁荷载横向分布系数的各种计算方法综述.
桥梁荷载横向分布系数的各种计算方法综述姓名：XXX学号：50XXXXXXX3摘要：公路桥梁荷载横向分布有多种计算模型，其中比较实用的有：1）杠杆原理法；2）偏心压力法、修正偏心压力法；3）铰接板（梁）法；4）刚接板（梁）法等。
这些理论方法有各自的适用范围，应按具体情况选用适当的方法来运用。
关键词：混凝土简支梁桥；荷载横向分布系数；影响线；影响因素1引言随着国民经济的发展，对交通的需求日益提高，众多的高速公路及城市快速干道相继修建。
公路桥梁上行驶车辆的轴重加重、速度提高，车流密度也相应提高。
使之在设计过程中如何确保桥梁结构在使用寿命期限内的安全性，准确计算各片梁所需承担的最大活载弯矩就显得尤为重要。
特别是对于中小跨多片梁型的桥梁，当跨数较多时，用测试横向分布状态的方法对桥梁运营状态进行评价，具有简洁、实用、可靠等优点，具有较高的推广价值。
所谓荷载横向分布系数（Lateral Distribution Factor of Live Load）是指公路车辆荷载在桥梁横向各主梁间分配的百分数。
普通简支桥梁中它和各主梁间的联结方式（铰接或刚接），有无内横梁及其数目，断面的抗弯刚度和抗扭刚度，以及车辆荷载在桥上的位置等有关。
它是一个复杂的空间结构问题，在桥梁设计中常简化为平面问题而引用荷载横向分布系数。
[1]目前广泛采用的是利用主梁的纵向影响线和它的荷载横向分布影响线相结合的方法，荷载横向分布系数是在荷载横向分布影响线的基础上按荷载的最不利位置布载，并将荷载位置相应的影响线竖标值求和得到的最后数值结果。
对于混凝土简支梁桥，荷载横向分布系数的影响因素主要有桥粱跨度(Z)、主梁间距(S)、桥面板的厚度(t0)、主梁刚度(K0)、横隔梁(板)的数量及位置、车载类型及布栽位置、车辆间距、栏杆及横跨比等。
[2][3][4][9]2计算方法及其适用范围荷载横向分布理论在桥梁设计中占有重要地位。
目前桥梁荷载横向分布系数常用的计算方法主要有杠杆原理法、偏心压力法（修正偏心压力法）、铰接板（梁）法、刚接梁法和比拟正交异性板法（G-M法）等。
桥梁荷载横向分布系数计算方法
桥梁荷载横向分布系数计算方法桥梁是交通系统中重要的基础设施，承载着大量的车辆和行人荷载。
桥梁荷载横向分布系数的计算对于桥梁设计和施工具有重要意义。
本文将详细介绍桥梁荷载横向分布系数的计算方法，包括计算原理、步骤和注意事项，并通过具体算例进行分析和说明。
桥梁荷载是指作用在桥梁上的各种力量，包括车辆荷载、人群荷载、风荷载等。
横向分布系数是用来描述桥梁荷载在桥面横向分布的系数，其大小与桥梁的形状、结构形式等因素有关。
桥梁荷载横向分布系数的计算是桥梁设计的重要环节，也是施工过程中的关键步骤。
计算桥梁荷载横向分布系数的方法可以分为理论计算和数值模拟两种。
理论计算方法包括集中力作用下的横向分布系数计算和均布力作用下的横向分布系数计算。
数值模拟方法则是利用计算机进行模拟分析，得到更精确的横向分布系数。
根据集中荷载作用下的弯矩和剪力，计算横向分布系数。
根据车道均布荷载的弯矩和剪力，计算横向分布系数。
数值模拟方法可以利用有限元软件进行模拟分析，得到更精确的横向分布系数。
具体步骤如下：通过对模型的应力、应变等进行分析，得出横向分布系数。
下面通过一个简单的算例来说明桥梁荷载横向分布系数的计算方法。
该桥梁为简支梁结构，跨度为20米，桥面宽度为10米。
车辆荷载为50吨的重车，速度为20公里/小时，作用在桥上长度为10米。
通过集中力作用下的横向分布系数计算方法，来计算该桥梁的横向分布系数。
计算桥梁单位长度的自重为5吨/米。
然后，确定车辆荷载的大小为50吨，位置为桥面中心线偏左1米处。
根据车辆荷载作用下的弯矩和剪力，可以得出横向分布系数为67。
根据横向分布系数的定义可知，该桥梁在车辆荷载作用下的横向分布系数为67。
桥梁荷载横向分布系数的计算是桥梁设计和施工中的重要环节，对于保证桥梁的安全性和正常使用具有重要意义。
本文详细介绍了桥梁荷载横向分布系数的计算方法，包括计算原理、步骤和注意事项，并通过具体算例进行了分析和说明。
随着计算机技术和数值模拟方法的发展，未来的研究方向将更加倾向于开发更加精确、便捷的计算方法和模型，以便更好地应用于实际工程中。
桥梁工程荷载横向分布计算简介
•由于跨中截面车轮加载值占总荷载的绝大多 数, 近似认为其它截面的横向分布系数与跨中 相同 •对于剪力
从影响线看跨中与支点均占较大比例 从影响面看近似影响面与实际情况相差较大
计算剪力时横向分布沿桥纵向的变化
与铰接板、梁的区别: 未知数增加一倍, 力法方程数增加一倍
5 .铰接板桥计算m举例:
如图所示，l＝12.60m的铰接空心板桥横截面布置。 桥面净空为净－7＋2x0.75m人行道。全桥由9块预应力混凝 土空心板组成，欲求1、3.5号板的公路-I级和人群荷载作用 的跨中横向分布系数？
分析: 荷载横向分布影响线竖标值与刚度参数γ ，板 块数n以及荷载作用位置有关。 5.8 I (b)2
4.目前常用的荷载横向分布计算方法： （1）梁格系模型
①杠杆原理法
②偏心压力法
③横向铰接梁（板）法
④ 横向刚接梁法 （2）平板模型——比拟正交异性板法（简称G—M法） 各计算方法的共同点: （1）横向分布计算得m （2）按单梁求主梁活载内力值
二、杠杆原理法 （一）计算原理 1.基本假定：
忽略主梁间横向结构的联系作用，假设桥面 板在主梁上断开，当作沿横向支承在主梁上的简 支梁或悬臂梁来考虑。
荷载横向分布计算
一、概述
荷载: 恒载: 均布荷载（比重×截面积）
活载: 荷载横向分布
1.活载作用下，梁式桥内力计算特点：
（1）单梁 （平面问题）
P
S=P·η1（x）
x
L/4
1
（2）梁式板桥或由多片主梁组成的梁桥（空间问题）: S＝Ｐ·η（x，ｙ） 实际中广泛使用方法: 将空间问题转化成平面问题
S P (x, y) P 2 (y) 1(x)
为求1号梁的荷载 假设: a、P＝1作用于1号梁梁轴， 跨中，偏心距为e； b、 各主梁惯性矩Ii不相等； c、横隔梁刚度无穷大。 则由刚体力学: 偏心力P=1 <====> 中心荷载 P=1+偏心力矩M=1·e
横向分布系数计算（多种方法计算）
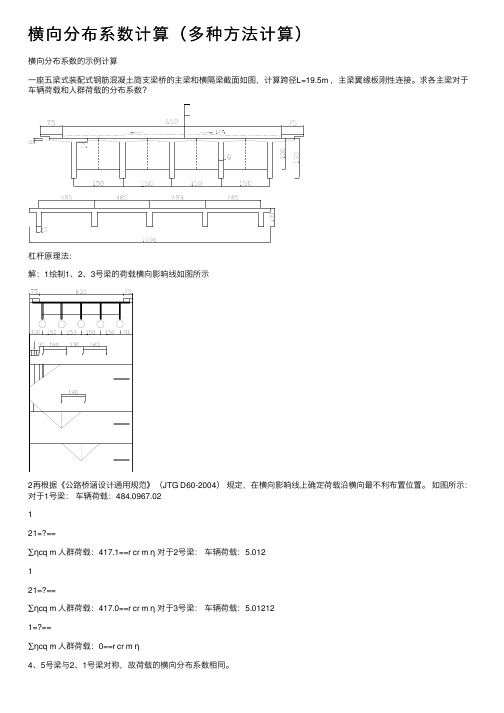
横向分布系数计算（多种⽅法计算）横向分布系数的⽰例计算⼀座五梁式装配式钢筋混凝⼟简⽀梁桥的主梁和横隔梁截⾯如图，计算跨径L=19.5m ，主梁翼缘板刚性连接。
求各主梁对于车辆荷载和⼈群荷载的分布系数？杠杆原理法：解：1绘制1、2、3号梁的荷载横向影响线如图所⽰2再根据《公路桥涵设计通⽤规范》（JTG D60-2004）规定，在横向影响线上确定荷载沿横向最不利布置位置。
如图所⽰：对于1号梁：车辆荷载：484.0967.02121=?==∑ηcq m ⼈群荷载：417.1==r cr m η对于2号梁：车辆荷载：5.012121=?==∑ηcq m ⼈群荷载：417.0==r cr m η对于3号梁：车辆荷载：5.012121=?==∑ηcq m ⼈群荷载：0==r cr m η4、5号梁与2、1号梁对称，故荷载的横向分布系数相同。
偏⼼压⼒法（⼀）假设：荷载位于1号梁 1长宽⽐为26.25.155.19>=?=b l ，故可按偏⼼压⼒法来绘制横向影响线并计算横向分布系数c m 。
本桥的各根主梁的横截⾯积均相等，梁数为5，梁的间距为1.5m ，则：5.220)5.11(2)5.12(2222524232221512=+?+?=++++=∑=a a a a a ai i2所以1号5号梁的影响线竖标值为：6.0122111=+=∑i a a n η 2.0122115-=-=∑i a a n η由11η和15η绘制荷载作⽤在1号梁上的影响线如上图所⽰，图中根据《公路桥涵设计通⽤规范》（JTG D60-2004）规定，在横向影响线上确定荷载沿横向最不利布置位置。
进⽽由11η和15η绘制的影响线计算0点得位置，设0点距离1号梁的距离为x ，则：4502.015046.0=?-?=x xx 0点已知，可求各类荷载相应于各个荷载位置的横向影响线竖标值3计算荷载的横向分布系数车辆荷载：()533.0060.0180.0353.0593.02121=-++?==∑ηcq m ⼈群荷载：683.0==r cr m η（⼆）当荷载位于2号梁时与荷载作⽤在1号梁的区别以下：4.0122112=+=∑i a a a n η0122552=-=∑ia a a n η其他步骤同荷载作⽤在1号梁时的计算修正偏⼼压⼒法（⼀）假设：荷载位于1号梁 1计算I 和T I ：2.3813018)2814(150)18150()2814(1301821)(2122221=?++?-+++??=+-++?=ch bd c b d ch y8.912.3813012=-=-=y y y[][]43333313132106543)112.38)(18150(2.381508.911831))((31cm d y c b by cy I ?=---?+??=---+?=对于翼板1.0073.01501111<==b t ，对于梁肋151.0119 1822==b t 查下表得所以：311=c ，301.02=c 433331027518119301.01115031cm t b c I i i i T ?=??+??==∑2计算抗扭修正系数β与主梁根数有关的系数ε则n=5，ε=1.042 G=0.425E875.055.15.1910654310275425.0042.111)(112332=??+=+=E E B l EI GI T εβ 3计算荷载横向影响线竖标值11η和15η55.0122111=+=∑i a a n βη 15.0122115-=-=∑ia a n βη由11η和15η绘制荷载作⽤在1号梁上的影响线如上图所⽰，图中根据《公路桥涵设计通⽤规范》（JTG D60-2004）规定，在横向影响线上确定荷载沿横向最不利布置位置。
桥梁工程荷载横向分布计算简介
2、横向分布系数（m）的概念：
• 多片式梁桥，在横向分布影响线上用规范规定的车轮 横向间距按最不利位置加载
说明：1）近似计算方法，但对直线梁桥，误差不大
2）不同梁，不同荷载类型，不同荷载纵向位置， 不同横向连接刚度，m不同。
3、横向连结刚度对荷载横向分布的影响
结论：横向分布的规律与结构横向连结刚度关系密切，
根据表中的横向影响线坐 标值绘制影响线图
公路－I级
七、横向分布系数沿桥纵向的变化
•对于弯矩
由于跨中截面车轮加载值占总荷载的绝大多数，近 似认为其它截面的横向分布系数与跨中相同
•对于剪力
从影响线看跨中与支点均占较大比例 从影响面看近似影响面与实际情况相差较大
计算剪力时横向分布沿桥纵向的变化
横向分布系数
横向分布系数 ：在横向分布影响线上加载
3. 铰接梁法
假定各主梁除刚体 位移外，还存在截 面本身的变形
与铰接板法的区别：变位系数中增加桥面板变形项
4.刚接梁法
假定各主梁间除传递剪力外，还传递弯矩
与铰接板、梁的区别： 未知数增加一倍，力法方程数增加一倍
5 .铰接板桥计算m举例：
如图所示，l＝12.60m的铰接空心板桥横截面布置。 桥面净空为净－7＋2x0.75m人行道。全桥由9块预应力混凝 土空心板组成，欲求1、3、5号板的公路-I级和人群荷载作用 的跨中横向分布系数？
值（ki）
1 ai ak 若各梁截面尺寸相同： ki Rki Rik n n 2 ai
i 1
（三） 计算举例
例2-5-3： 已知：l=19.50m，荷载位于跨中 试求：１#边梁，2＃中梁的mcq，mcr
作业
已知：l=29.16m, 38.88m，荷载位于跨中时 试求：2＃中梁的mcq，mcr
桥梁荷载横向分布系数的各种计算方法综述
桥梁荷载横向分布系数的各种计算方法综述姓名：XXX 学号：50XXXXXXX3摘要：公路桥梁荷载横向分布有多种计算模型，其中比较实用的有：1）杠杆原理法；2）偏心压力法、修正偏心压力法；3）铰接板（梁）法；4）刚接板（梁）法等。
这些理论方法有各自的适用范围，应按具体情况选用适当的方法来运用。
关键词：混凝土简支梁桥；荷载横向分布系数；影响线；影响因素1 引言随着国民经济的发展，对交通的需求日益提高，众多的高速公路及城市快速干道相继修建。
公路桥梁上行驶车辆的轴重加重、速度提高，车流密度也相应提高。
使之在设计过程中如何确保桥梁结构在使用寿命期限内的安全性，准确计算各片梁所需承担的最大活载弯矩就显得尤为重要。
特别是对于中小跨多片梁型的桥梁，当跨数较多时，用测试横向分布状态的方法对桥梁运营状态进行评价，具有简洁、实用、可靠等优点，具有较高的推广价值。
所谓荷载横向分布系数（Lateral Distribution Factor of Live Load）是指公路车辆荷载在桥梁横向各主梁间分配的百分数。
普通简支桥梁中它和各主梁间的联结方式（铰接或刚接），有无内横梁及其数目，断面的抗弯刚度和抗扭刚度，以及车辆荷载在桥上的位置等有关。
它是一个复杂的空间结构问题，在桥梁设计中常简化为平面问题而引用荷载横向分布系数。
[1]目前广泛采用的是利用主梁的纵向影响线和它的荷载横向分布影响线相结合的方法，荷载横向分布系数是在荷载横向分布影响线的基础上按荷载的最不利位置布载，并将荷载位置相应的影响线竖标值求和得到的最后数值结果。
对于混凝土简支梁桥，荷载横向分布系数的影响因素主要有桥粱跨度(Z)、主梁间距(S)、桥面板的厚度(t0)、主梁刚度(K0)、横隔梁(板)的数量及位置、车载类型及布栽位置、车辆间距、栏杆及横跨比等。
[2][3][4][9]2 计算方法及其适用范围荷载横向分布理论在桥梁设计中占有重要地位。
目前桥梁荷载横向分布系数常用的计算方法主要有杠杆原理法、偏心压力法（修正偏心压力法）、铰接板（梁）法、刚接梁法和比拟正交异性板法（G-M法）等。
荷载横向分布计算详细总结(全)
将式(a)与式(b)相加后，与式7-2联立，可得如下方程组：
= 式(7-2)
(式7-2)的具体推导过程见下图：
图6.6
⑦解上述方程组，解得：
(式7-3)
—第 片主梁的抗扭惯性矩。
G—材料的剪切模量，对于混凝土结构，G=0.425E。
注：修正偏心压力法作出的荷载横向分布影响线是一条直线。
5.铰接板（梁）法：（①中梁和边梁抗弯刚度相等或者接近②跨中）
☆适用条件：现浇砼纵向企口缝连结的装配式桥、仅在翼板间用钢板或钢筋连接的无中间横隔梁的装配式T梁桥。此类桥横向有一定连结构造，但刚性弱，板（梁）之间的连接可以看成是铰接。
矩阵B是 阶三对角方阵，其组成规律为：主对角线上的元素均为 ，剩余两条对角线元素均为 。
矩阵C为 阶方阵，组成规律为：主对角线上元素均为0，主对角线上侧第一条对角线上元素均为 ，主对角线下册第一条对角线上元素均为 （可以将矩阵C看成是一个主对角线元素为0的特殊三对角矩阵）。具有n片主梁时，矩阵C的一般形式见下图6.2：
注：铰接板（梁）法作出的荷载横向分布影响线是一条光滑曲线。
6.刚接板（梁）法：（①中梁和边梁抗弯刚度相等或者接近；②跨中）
☆适用条件：各种桥面板刚接的肋梁桥。对于整体式板桥，使用刚接梁法计算时，把整体式板划分成 块等宽度 的板（一般 ），当做彼此之间刚接的板桥来计算其荷载的横向分布。需要注意的是，将整体式板划分成 块等宽度为 的板时，每一块板的宽跨比 不宜大于1/4。
其中： —每片主梁的抗弯惯性矩。
—每片主梁的抗扭惯性矩。
—单位宽度翼缘板的抗弯惯性矩。
—梁（板）截面宽度。
—翼缘板的悬出长度。
荷载横向分布的计算
三、荷载横向分布的计算
2、荷载横向分布系数的计算方法 常用的计算方法： ◆ 杠杆原理法 ◆ 刚性横梁法 ◆ 修正的刚性横正交异性板法（G-M法） 从分析荷载在桥上的横向分布出发，求得各梁 的荷载横向分布影响线，再通过横向最不利加载来 计算荷载横向分布系数
多主梁桥的内力计算
S P ( x, y) P 2 ( y) 1 ( x)
三、荷载横向分布的计算
1、荷载横向分布系数的概念
荷载横向分布系数表示某根主梁所承担的最大荷载与轴 重的比值
车轮荷载的横向分布
三、荷载横向分布的计算
1、荷载横向分布系数的概念 荷载横向分布系数与各主梁之间的横向联系有直 接关系。
三、荷载横向分布的计算
2、荷载横向分布系数的计算方法 荷载横向分布影响线：P=1在梁上横向移动时，某 主梁所相应分配到的不同的荷载作用力。 对荷载横向分布影响线进行最不利加载Pi，可 求得某主梁可行最大荷载力
荷载横向分布系数：将Pi除以车辆轴重。
三、荷载横向分布的计算
2、荷载横向分布系数的计算方法 （1）杠杆分配法
二、行车道板的计算
1、车辆活载在板上的分布 公路汽车荷载
轮压一般作为分布荷载处理 车轮着地面积：a1×b1
桥面板荷载压力面：a2×b2
荷载在铺装层内按45°扩散 沿纵向：a2＝a1 +2h
沿横向：b2=b1+2h
桥面板的轮压局部分布荷载：
公路桥面板上车轮荷载的扩散
P p 2a2b2
三、荷载横向分布的计算
1、荷载横向分布系数的概念 公路桥梁桥面较宽，主梁片数往往较多并与桥 面板和横隔梁联结在一起。当桥上车辆处于横向不 同位置时，各主梁参与受力的程度不同，属空间问 题，求解难度大。 应将空间问题简化为平面问题。
《桥梁工程》荷载横向分布计算(偏心压力法)
3.偏心压力法 Method based on stiffness transverse connection
3）原理 Theory
P
Pe
L P Pe
w φ
P w
φ
Pe
3.偏心压力法 Method based on stiffness transverse connection
3）原理 Theory
当荷载P=1作用于第i号梁上时，
各主梁的荷载分布：
P=1
a1
ki Rik Rik ……（5）
R51
当各主梁截面尺寸相同时，
R11
ik
1 n
ai ak
5
ai2
……（6） η11
η15
i 1
3.偏心压力法 Method based on stiffness transverse connection
1）基本假设 横梁刚性极大,刚性横梁的微小变形可以忽略不计
PP
P/2
P/2
L
B
f
f
f’
f >>f’
3.偏心压力法 Method based on stiffness transverse connection
3.偏心压力法 Method based on stiffness transverse connection
i 1
i 1
ai wi’’
φ
MT1 R1’’
R2’’ MT2 MT3
R4’’ R5’’ MT4 MT5
4.修正偏心压力法
Modified method of the stiffness transverse connection
杠杆原理法计算桥梁荷载横向分布系数课件
杠杆原理法的应用范围
01
杠杆原理法适用于多跨连续梁桥 和连续刚构桥的荷载横向分布计 算。
02
该方法适用于等跨和不等跨的桥 梁，特别适用于等跨的桥梁。
杠杆原理法的计算步骤
01
确定各跨梁的计算跨径 和梁高。
02
根据桥梁的结构形式和 尺寸，将桥梁简化为一 系列的简支梁。
03
利用杠杆原理，计算各 跨梁的荷载横向分布系 数。
桥梁优化设计
利用杠杆原理法，可以计算出桥梁在 不同荷载作用下的横向分布系数，为 桥梁设计提供重要的数据支持。
杠杆原理法可以帮助设计人员对桥梁 进行优化设计，提高桥梁的使用性能 和寿命。
桥梁承载能力评估
通过杠杆原理法，可以对桥梁的承载 能力进行评估，确保桥梁在规定荷载 下的安全性和稳定性。
在桥梁设计中的注意事项
桥梁加固
当桥梁存在承载能力不足的问题时，可以通过对薄弱部位的加固处理， 提高其横向分布系数，从而提高整个桥梁的承载能力。
03
杠杆原理法计算桥梁荷载横向 分布系数
计算步骤
步骤一
确定计算跨径
步骤二
确定荷载类型
计算步骤
明确作用在桥梁上的荷载类型，如车辆、人群、风载等。 步骤三：建立杠杆模型
根据桥梁的结构形式，建立简化的杠杆模型，将实际结构简化为若干个杠杆单元。
与其他方法的计算精度比较
01
02
03
杠杆原法
在等跨径桥梁中，计算精 度较高，误差较小。
影响力系数法
在变跨径桥梁和桥面宽度 较大的桥梁中，计算精度 较高，误差较小。
弹性地基梁法
在桥面较宽、荷载较大的 桥梁中，计算精度较高， 误差较小。
05
杠杆原理法在桥梁设计中的应 用
荷载横向分布系数
荷载横向分布系数
荷载横向分布系数是指荷载和梁的宽度的比例关系的系数，它表明梁上的荷载是如何均匀地分布的。
它对于对梁及其抗压力能力的计算非常重要，主要决定着梁弯矩的大小。
另外，它还可以预测梁的变形程度以及梁的整体稳定性和结构安全性。
荷载横向分布系数可以通过梁的中心轴线来计算，可以用梁的节点距离来代表宽度，从而可以得到荷载横向分布系数的计算公式。
「b」和「h」分别代表梁的宽度和高度，而「P」代表点荷载，其公式如下：
荷载横向分布系数= (b/h) × (P/σ)
其中，「σ」是指梁应力，通常为允许应力。
荷载横向分布系数是梁的静健度和强度的重要决定因素。
正确的横向分布系数可以帮助梁承载最大的荷载，从而使梁受更少的变形和破坏。
荷载横向分布系数可以帮助梁充分利用载荷承受能力，可以有效减少结构成本。
桥梁工程课程设计--荷载横向分布系数计算
解得：
零点位置已知后，就可求出各类荷载相应于各个荷载位置的横向影响线竖标值 和 。
设行人道缘石至1号梁轴线的距离为 ，则：
于是，1号梁的荷载横向分布系数可以计算如下（以 分别表示影响线零点至汽车车轮和人群荷载集度的横坐标距离）：
车辆荷载：
人群荷载值为：
由 和 绘制1号梁横向影响线，如下图所示，图中按《公路桥涵设计通用规范》（JTG D60-2004）规定确定了汽车荷载的最不利荷载位置。
进而由 和 计算横向影响线的零点位置，在本梁中，零点至2号梁的距离
零点位置已知后，就可求出各类荷载相应于各个荷载位置的横向影响线竖标值 和 。
2
跨中
0.900
0.520
支点
0.500
0
3
跨中
0.900
0.520
支点
0.500
0
4
跨中
0.749
0.783
支点
0.550
1.500
荷载横向分布系数:
（1）用杠杆法计算 :
首先绘制1号梁和2号梁的荷载横向影响线，如上图所示。
再根据《公路桥涵设计通用规范》（JTGD60-2004）规定，在横向影响线上确定荷载沿横向最不利的布置位置。例如，对于车辆荷载，规定的车轮横向轮距为1.80m，两列汽车车轮的横向最小间距为1.30m，车轮距离人行道缘石最少为0.50m。求出相应于荷载位置的影响线竖标值后，就可得到横向所有荷载分布给1号梁的最大荷载值：
车辆荷载：
人群荷载：
式中， 相应为汽车荷载轴重和每延米跨长的人群荷载集度； 为对应于汽车车轮和人群荷载集度的影响线竖标。由此可得1号梁在车辆荷载和人群荷载作用下的最不利荷载横向分布系数分别为： 。
荷载横向分布系数的计算
适用情况 ①只有邻近两根主梁参与受力 ②虽为多主梁，但计算梁端支承处荷载 ③无中间横隔梁
2、荷载横向分布系数的计算方法
（1）杠杆分配法
作业1：画 及出单3车、辆4荷号载梁作的用荷下载3横、向4分号布梁影荷响载线横，向
0.75m
分布系数 7m
0.75m
1
2 2m
3
4
（2）刚性横梁法（偏心受压法） 假定 ①横梁是刚性的：宽跨比B/l≤0.5 ②忽略主梁抗扭刚度
▪ 计算假设： ①铰式键只传递竖
向剪力 gx ；
②桥上荷载近似作为一个沿桥连续分布的正弦荷 载 P sin x，且作用于梁轴上。
l
求出各铰处gx， 即可求出横向分布影响线
1号板 2号板 3号板 4号板 5号板
p11 1 g1
p21 p31
g1 g2
g2 g3
p41
g3
g4
p51 g4
(1 )g3 2(1 )g4 0
半波正弦荷载引起的变形
w pl4
4EI
pbl 2
2 2GIT
b
2
/w
b 2
pbl 2
2 2GIT
pl4
4
EI
2EI
4GIT
b l
2
5.8
I IT
b l
2
③ 刚结板（梁）法
▪ 在铰结板（梁）计算理论的基础上，在结合 缝处补充引入冗余弯矩m，得到考虑板的横 向刚性连接特点的变形协调方程，从而求解 各梁荷载横向分布的方法。
P
ai Iie
n
ai2 Ii
i 1
P
P
Ii
n
Ii
i 1
荷载横向分布系数的计算-杠杆法
02 杠杆法的计算步骤
确定计算跨度
计算跨度是桥梁横向分布系数计算的关键参数， 它决定了荷载在各片梁之间的分布情况。
计算跨度应考虑桥梁的结构形式、材料特性、施 工方法等因素，并根据桥梁设计规范进行确定。
在实际工程中，也可以通过实测和经验公式等方 法来确定计算跨度。
感谢您的观看
THANKS
案例三：其他工程领域中的应用
总结词
除桥梁和房屋建筑外，杠杆法还可应用于其他工程领域，如大型工业厂房、大跨度结构 等。
详细描述
在这些工程领域中，杠杆法同样通过将结构简化为一系列简支梁，利用杠杆原理计算各 简支梁的弯矩和剪力，从而得到结构的荷载横向分布系数。这种方法为这些复杂结构的
承载能力评估和设计提供了重要的技术支持。
荷载横向分布系数的 计算-杠杆法
目录
CONTENTS
• 杠杆法概述 • 杠杆法的计算步骤 • 杠杆法的优缺点 • 杠杆法与其他方法的比较 • 杠杆法的实际应用案例
01 杠杆法概述
杠杆法的定义
01
杠杆法是一种计算桥梁荷载横向 分布系数的方法，通过将桥梁的 总荷载分配到各个主梁上，以确 定各主梁所承受的荷载比例。
案例二：房屋建筑中的应用
总结词
况，以确保楼面承载能力满足设 计要求。
详细描述
在房屋建筑中，杠杆法通过将楼面简化为一系列简支梁，利用杠杆原理计算各简支梁的弯矩和剪力， 从而得到楼面荷载横向分布系数。这种方法在计算楼面活荷载、均布荷载等不同类型荷载作用下的楼 面承载能力时具有广泛的应用价值。
根据弯矩和剪力的计 算结果，可以进一步 分析梁的受力性能和 稳定性。
斜弯桥计算分析(2)
概述
一、斜弯桥的应用情况 1、高等级公路改变了原来路与桥的关系 2、城市立交的大量建设需要异性桥梁 3、设计手段的发展使设计水平提高 4、国外二十世纪六七十年代到达高峰，国内八九十年代是研究高潮
2021/4/22
2
某高速公路
2021/4/22
3
弯拱桥
2021/4/22
4
弯连续刚构
2021/4/22
5
天目路立交
2021/4/22
6
南浦大桥东引桥
2021/4/22
7
概述
二、计算方法 1、解析法 概念清晰 难以解决复杂问题 2、数值法 计算功能强 数据复杂，需要人工判断
2021/4/22
8
第一节 整体斜板桥的受力特点和构 造
主要用于小跨度桥梁 跨径通常在20米以下
全桥一般采用满樘支架整体浇筑
43
0 xz x 时：
Qx Tx M
Pl P x P
l (l
(l
x
l l
T ctg
l
x) D x tg
x) (xz Dx)
T[1 D(1 2kx
l
T l
[l
xz
D(l
tg 2 )]
2kx tg
2
)]
ctg
其中：
D
1
2(1 k tg 2 )
EI k
GI d
2021/4/22
1. 随着斜交角的增大，斜梁桥的纵梁弯矩减小，而横梁的弯矩则增大；弯矩 的减少，边梁比中梁明显，在均布荷载作用下比在集中荷载作用下明显；
2021/4/22
40
2. 正交横梁斜梁桥的横向分布性能比斜交横梁斜梁桥好，并且横向刚度 越大，横向分布性能越好；
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
竖向位移和扭角
（2）弯桥与正桥的比较 当荷载作用于跨中时，即
i
0
2
，有
C wpi
ri3 EIi
(0 sin 8 cos2 0
2
0
)
ki 80coss2in20 0
1 tg 0
2 2
0
4
梁系法[刚（铰）接板（梁）法] 比拟正交异性板法（G-M）等 对于变截面简支梁桥，连续梁桥，刚架桥等其它梁式
或梁式组合结构，可按等代刚度法将其换算为等代简支梁 进行横向分布计算，此方面内容可参阅文献[1]、[2]、[3]。
修正偏心压力法
在正交桥中，荷载横向分布的规律主要取决于纵横向
抗弯刚度的比值，而抗扭能力只影响分布系数的数值。因
C wpi源自l3 6EIi 1 2 1 2
1 2
2
2
l3 48EIi
Cpi cwTi 0(无弯扭耦合项)
C wTi
l 6EIi
3ki 2
3k
i
l 4EIi
ki
l
4GJi
就是正桥跨中作用单位竖向力和单位扭矩在跨中产生的
ki EIi / GIdi
i si / li
i 第 式中：、——分别
抗扭刚度
片梁截面的抗弯刚度和
2 ）曲梁桥
对于曲梁桥（后图），有
曲梁桥及其柔度系数计算图式
Cwpi
ri3 2EIi
{1 ki s in 0
[
0
s
in
2
i
s in 0
i
c os ( 0
4nGk
E
n
a
2 j
G
y
j 1
式；中：Gy
l 0
Dy
f
2
( x)dx
；Gk
l 0
Dk
f
2 (x)dx
P 对于等截面简支梁，若荷载 作用于 断面，取级数首
项时，有
f
(x)
2 pl3
bDz 4
sin
l
sin x
l
f ( ) 2 pl3 sin 2
bDz 4
l
若取泊松比为零，则 桥跨结构宽度，主梁相同时 B na
n
G ITi B 4Dk
aDy EI j
j 1
则林元培公式与郑考达公式相同
（4）日本国铁标准公式[6] 对于主梁相同的梁式桥有
荷载作用点至横 截面形心之距
i
1 n
a(n 1 2i) n(n2 1)
2 )考虑约束扭转的修正系数
（1）文献[8]公式
n
1
1
l2 12
G I dj
j 1
n
E
a
2 j
I
j 1
j
1
1
th
n
式中：1
G I di
j 1 n
； 1l / 2
E Ii
1j1
主梁扇性惯矩
(开口截面)
3 0
1
4
2 0
EI i
8 0 0
3
0
cos 2
0
2
l3 EIi
0
lim
0 0
0
3 0
3!
sin 0
8
3 0
c os2
0
2
l3
48EIi
CTi
ri EI i
0
lim
0 0
i )sini
0 s in 0
sin 2 i
sin(0
i )(i
cosi
s
in
i
)]
ki
s in i s in 0
s in( 0
i
)}
Cpi
CwTi
ri2 2EIi
{1 ki s in 0
[ 0 s in 0
sin 2 i
j
n
l 2G
I di
1
2E
i 1
n
a
2 j
Ii
j 1
i 1
（3）法印公式 苏联法印1962年提出开 口截面的修正式为
i
1 n
n
eai ai A
i 1
式中：
A
l2 6
1
1 th
GIdn EI
将 A代入可整理出与文献[8]公式相同的
（2）郑考达公式[4]
1
l2
n
1
G I dj
j 1
2
E
n
a
2 j
I
j
j 1
此式的 与荷载位置无关，是由于假定扭角与挠度在纵
向具有相同的变化规律。分母中的 2是由于取级数中的
首项而来的近似值。
（3）林元培公式[5]
1
1
对于直梁，有 ri 0 l, 0 0
则上列三式分别变为
Cwpi
ri3
EI i l3
3 0
lim
0 0
lim
80003cosssini2n200
0
k
i
0
8
3 0
sin cos2
0 0
2
1 2
tg0 / 2
0 0
8 0
cos2 0
2
l3 4EIi
ki
l 4GJi
CPi
C
l2 EIi
wTi
lim
0 0
08riE202Ici002os2li03m!20008(10 02kcsi )oins20(0无2弯0 扭(耦1合)
从以上公式不难看出，若I
扭转的 值。
或
I 为零时，得到的就是自由
3) 讨论
无论是从静力平衡条件（舒根公式等）还是从能量原
理（郑孝达公式等）所推导出的考虑自由扭转的修正系数
均为桥跨结构主梁几何参数的函数，由于能量法推导过程
中仅取了级数首项，致使其与静力平衡法的修正系数有一
定的偏差。考虑自由扭转的其它修正公式，只要略加变化
a
2 j
Ij
1
x(l
3
x)
n
G I dj
j 1
n
E
a
2 j
I
j
1
j 1
偏心压力法
可见 n
① G ITj 0 时， 1
③
j 1
l 2
min
；② x 0 、l, 1
；④ (0) (l) max 1
车轮荷载，即 轮重与轴重的比例数；汽车：(y) 1，挂车：( y) 1
n
2
4
m ( y)( y)
横向最不利布置车轮数
横向分布影响线竖标
荷载横向分布计算实际上是计算 (值y)。对于简支等截
面直梁桥，基于不同的计算假定，可有
支点剪力荷载横向分布计算的杠杆法，
跨中截面荷载横向分布计算的偏心压力
12(简支梁)
2478(.固4(端一梁端)固定另一端简支梁)
3(悬臂梁的悬臂端)
(1 )(简支外伸梁的悬臂端, 简支跨径为l, 外伸长l)
一般来说，考虑自由扭转的修正系数 适用于混凝土梁，
而考虑约束扭转的 适用于钢梁
斜弯梁的柔度系数
平面斜、弯梁存在弯曲和扭转耦合作用，为分析计算方 便，定义 ：
Cpi
li2 6EIi
i
(1 i
)
Ai C i 2Bi
(2 i )tg a
C wTi
li2 6EIi
Ai C i 2Bi
(2
i
)tg
a
)
i
(1
i
)
CTi
li 6EIi
Ci2 2Bi
2(3kii
1
n i 1
I di
/
n i 1
I i
(闭口截面)
主梁极惯矩
（2）杨国先公式[9]
文献[9]忽略了弯曲正应力，用能量法推导T梁的 为
1
l 2GId
2EI
1
若计及弯曲应变能，则
1
I n
n
a
2 j
I
i s s 弯桥径向水平力N 1.0作用于 号梁 截面，在该梁 截面引
起的径向水平位移CuN（i 此参数可用于水平荷载的横向分布计算[13]）。