Fractional Quantum Hall States in Graphene
“第17届凝聚态理论与统计物理学术会议”日程(初稿)

吴超(西安交通大学) 题目: The influence of local arrangements of oxygen adatoms on the energetics of O2 dissociation over Pt(111) 赵明文(山东大学) 题目: 新型碳材料结构设计和性能调控的理 论模型 李希茂(北京宏剑公司)(12:10-12:25) 题目: 第一原理计算材料的缺陷和掺杂特性
李文飞(南京大学) 题目: 蛋白质分子体系多尺度理论模拟
孙久勋(电子科技大学) 题目: Improvement of unified mobility model and electrical properties for organic diodes under dc and ac conditions
关丽(河北大学):Structural stability and electronic properties of two nonstoichiometric SrTiO3 phases
休息
报告厅 3(主题: 冷原子物理) 分会报告 ST3.3 主席:成 泽 教授(华中科技大学) (邀请报告) 周琦(香港中文大学) 题目:自旋轨道耦合下波色凝聚体的命运
主席:金国钧 教授(南京大学)
(邀请报告) 杨义峰(中国科学院物理研究所) (邀请报告) 孟胜(中国科学院物理研究所)
题目:重费米子物理中的演生现象
题目:Energy Conversion At Nanoscale
Room-Temperature Quantum Hall Effect in Graphene
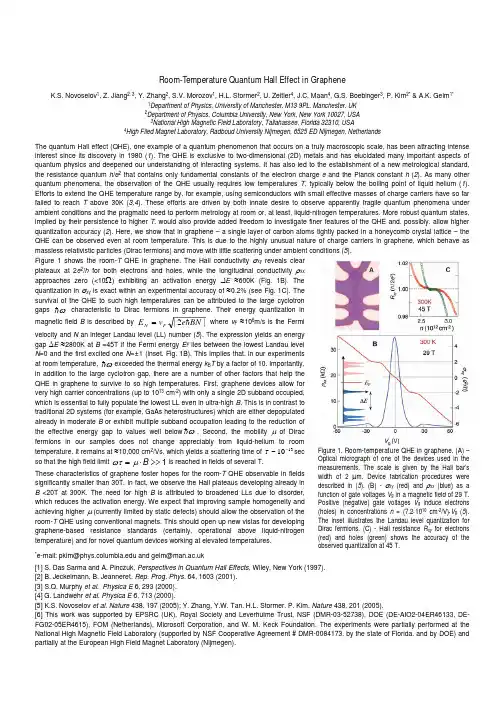
Room -Temperature Quantum Hall Effect in GrapheneK.S. Novoselov 1, Z. Jiang 2, 3, Y. Zhang 2, S.V. Morozov 1, H.L. Stormer 2, U. Zeitler 4, J.C. Maan 4, G.S. Boebinger 3, P. Kim 2* & A.K. Geim 1*1Department of Physics, University of Manchester, M13 9PL, Manchester, UK2Department of Physics, Columbia University, New York, New York 10027, USA3National High Magnetic Field Laboratory, Tallahassee, Florida 32310, USA4High Filed Magnet Laboratory, Radboud University Nijmegen, 6525 ED Nijmegen, NetherlandsThe quantum Hall effect (QHE), one example of a quantum phenomenon that occurs on a truly macroscopic scale, has been attracting intense interest since its discovery in 1980 (1). The QHE is exclusive to two-dimensional (2D) metals and has elucidated many important aspects of quantum physics and deepened our understanding of interacting systems. It has also led to the establishment of a new metrological standard, the resistance quantum h /e 2 that contains only fundamental constants of the electron charge e and the Planck constant h (2). As many other quantum phenomena, the observation of the QHE usually requires low temperatures T , typically below the boiling point of liquid helium (1). Efforts to extend the QHE temperature range by, for example, using semiconductors with small effective masses of charge carriers have so far failed to reach T above 30K (3,4). These efforts are driven by both innate desire to observe apparently fragile quantum phenomena under ambient conditions and the pragmatic need to perform metrology at room or, at least, liquid-nitrogen temperatures. More robust quantum states, implied by their persistence to higher T , would also provide added freedom to investigate finer features of the QHE and, possibly, allow higher quantization accuracy (2). Here, we show that in graphene – a single layer of carbon atoms tightly packed in a honeycomb crystal lattice – the QHE can be observed even at room temperature. This is due to the highly unusual nature of charge carriers in graphene, which behave as massless relativistic particles (Dirac fermions) and move with little scattering under ambient conditions (5).Figure 1 shows the room-T QHE in graphene. The Hall conductivity σxy reveals clearplateaux at 2e 2/h for both electrons and holes, while the longitudinal conductivity ρxxapproaches zero (<10Ω) exhibiting an activation energy ∆E ≈600K (Fig. 1B). Thequantization in σxy is exact within an experimental accuracy of ≈0.2% (see Fig. 1C). Thesurvival of the QHE to such high temperatures can be attributed to the large cyclotrongaps ωh characteristic to Dirac fermions in graphene. Their energy quantization inmagnetic field B is described by |2|BN e v E F N h = where v F ≈106m/s is the Fermivelocity and N an integer Landau level (LL) number (5). The expression yields an energygap ∆E ≈2800K at B =45T if the Fermi energy E F lies between the lowest Landau levelN =0 and the first excited one N =±1 (inset, Fig. 1B). This implies that, in our experimentsat room temperature, ωh exceeded the thermal energy k B T by a factor of 10. Importantly,in addition to the large cyclotron gap, there are a number of other factors that help theQHE in graphene to survive to so high temperatures. First, graphene devices allow forvery high carrier concentrations (up to 1013 cm -2) with only a single 2D subband occupied,which is essential to fully populate the lowest LL even in ultra-high B . This is in contrast totraditional 2D systems (for example, GaAs heterostructures) which are either depopulatedalready in moderate B or exhibit multiple subband occupation leading to the reduction ofthe effective energy gap to values well below ωh . Second, the mobility µ of Diracfermions in our samples does not change appreciably from liquid-helium to roomtemperature. It remains at ≈10,000 cm 2/Vs, which yields a scattering time of 1310~−τsecso that the high field limit 1>>⋅=B µωτ is reached in fields of several T.These characteristics of graphene foster hopes for the room-T QHE observable in fieldssignificantly smaller than 30T. In fact, we observe the Hall plateaus developing already inB <20T at 300K. The need for high B is attributed to broadened LLs due to disorder,which reduces the activation energy. We expect that improving sample homogeneity andachieving higher µ (currently limited by static defects) should allow the observation of theroom-T QHE using conventional magnets. This should open up new vistas for developing graphene-based resistance standards (certainly, operational above liquid-nitrogen temperature) and for novel quantum devices working at elevated temperatures. *e-mail: pkim@ and geim@[1] S. Das Sarma and A. Pinczuk, Perspectives in Quantum Hall Effects , Wiley, New York (1997).[2] B. Jeckelmann, B. Jeanneret. Rep. Prog. Phys. 64, 1603 (2001).[3] S.Q. Murphy et al . Physica E 6, 293 (2000).[4] G. Landwehr et al. Physica E 6, 713 (2000).[5] K.S. Novoselov et al . Nature 438, 197 (2005); Y. Zhang, Y.W. Tan, H.L. Stormer, P. Kim. Nature 438, 201 (2005).[6] This work was supported by EPSRC (UK), Royal Society and Leverhulme Trust, NSF (DMR-03-52738), DOE (DE-AIO2-04ER46133, DE-FG02-05ER4615), FOM (Netherlands), Microsoft Corporation, and W. M. Keck Foundation. The experiments were partially performed at the National High Magnetic Field Laboratory (supported by NSF Cooperative Agreement # DMR-0084173, by the state of Florida, and by DOE) and partially at the European High Field Magnet Laboratory (Nijmegen).Figure 1. Room-temperature QHE in graphene. (A ) – Optical micrograph of one of the devices used in the measurements. The scale is given by the Hall bar’s width of 2 µm. Device fabrication procedures were described in (5). (B ) - σxy (red) and ρxx (blue) as a function of gate voltages V g in a magnetic field of 29 T. Positive (negative) gate voltages V g induce electrons (holes) in concentrations n = (7.2⋅1010 cm -2/V)⋅V g (5). The inset illustrates the Landau level quantization for Dirac fermions. (C ) - Hall resistance R xy for electrons (red) and holes (green) shows the accuracy of the observed quantization at 45 T.。
Quantum Hall effect - Wikipedia, the free encyclopedia

Quantum Hall effectFrom Wikipedia, the free encyclopediaThe quantum Hall effect (or integer quantum Hall effect) is a quantum-mechanical version of the Hall effect, observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall conductance G undergoes certain quantum Hall transitions to take on the quantized valueswhere is the channel current, is the Hall voltage, e is the elementary charge and h is Planck's constant. The prefactor ν is known as the "filling factor", and can take on either integer (ν = 1, 2, 3, .. ) or fractional (ν = 1/3, 2/5, 3/7, 2/3, 3/5, 1/5, 2/9, 3/13, 5/2, 12/5 ...) values. The quantum Hall effect is referred to as the integer or fractional quantum Hall effect depending on whether ν is an integer or fraction respectively. The integer quantum Hall effect is very well understood, and can be simply explained in terms of single-particle orbitals of an electron in a magnetic field (see Landau quantization). The fractional quantum Hall effect is more complicated, as its existence relies fundamentally on electron–electron interactions. It is also very well understood as an integer quantum Hall effect, not of electrons but of charge-flux composites known as composite fermions. In 1988, it was proposed that there was quantum Hall effect without Landau levels. This quantum Hall effect is referred to as the quantum anomalous Hall (QAH) effect. There is also a new concept of the quantum spin Hall effect which is an analogue of the quantum Hall effect, where spin currents flow instead of charge currents.[1]Contents◾1 Applications◾2 History◾3 Integer quantum Hall effect – Landau levels◾4 Mathematics◾5 See also◾6 References◾7 Further readingApplicationsThe quantization of the Hall conductance has the important property of being incredibly precise. Actual measurements of the Hall conductance have been found to be integer or fractional multiples of e2/h to nearly one part in a billion. This phenomenon, referred to as "exact quantization", has been shown to be a subtle manifestation of the principle of gauge invariance.[2] It has allowed for the definition of a new practical standard for electrical resistance, based on the resistance quantum givenby the von Klitzing constant R K = h/e2 = 25812.807557(18) Ω.[3] This is named after Klaus von Klitzing, the discoverer of exact quantization. Since 1990, a fixed conventional value R K-90 is used in resistance calibrations worldwide.[4] The quantum Hall effect also provides an extremely precise independent determination of the fine structure constant, a quantity of fundamental importance in quantum electrodynamics.HistoryThe integer quantization of the Hall conductance was originally predicted by Ando, Matsumoto, and Uemura in 1975, on the basis of an approximate calculation which they themselves did not believe to be true. Several workers subsequently observed the effect in experiments carried out on the inversion layer of MOSFETs. It was only in 1980 that Klaus von Klitzing, working at the high magnetic field laboratory in Grenoble with silicon-based samples developed by Michael Pepper and Gerhard Dorda, made the unexpected discovery that the Hall conductivity was exactly quantized. For this finding, von Klitzing was awarded the 1985 Nobel Prize in Physics. The link between exact quantization and gauge invariance was subsequently found by Robert Laughlin. Most integer quantum Hall experiments are now performed on gallium arsenide heterostructures, although many other semiconductor materials can be used. In 2007, the integer quantum Hall effect was reported in graphene at temperatures as high as room temperature,[5] and in the oxide ZnO-Mg x Zn1-x O.[6] Integer quantum Hall effect – Landau levelsIn two dimensions, when classical electrons are subjected to a magnetic field they follow circular cyclotron orbits. When the system is treated quantum mechanically, these orbits are quantized. The energy levels of these quantized orbitals take on discrete values: , where ωc = eB/m is the cyclotron frequency. These orbitals are known as Landau levels, and at weak magnetic fields, their existence gives rise to many interesting "quantum oscillations" such as the Shubnikov–de Haas oscillations and the de Haas–van Alphen effect (which is often used to map the Fermi surface of metals). For strong magnetic fields, each Landau level is highly degenerate (i.e. there are many single particle states which have the same energy E n). Specifically, for a sample of area A, inmagnetic field B, the degeneracy of each Landau level is (where g s represents a factor of 2 for spin degeneracy, and is the magnetic flux quantum). ForHofstadter's butterfly sufficiently strong B-fields, each Landau level may have so many states that all of the free electrons in the system sit in only a few Landau levels; it is in this regime where one observes the quantum Hall effect.MathematicsThe integers that appear in the Hall effect are examples oftopological quantum numbers. They are known inmathematics as the first Chern numbers and are closelyrelated to Berry's phase. A striking model of much interest inthis context is the Azbel-Harper-Hofstadter model whosequantum phase diagram is the Hofstadter butterfly shown inthe figure. The vertical axis is the strength of the magneticfield and the horizontal axis is the chemical potential, whichfixes the electron density. The colors represent the integer Hall conductances. Warm colors represent positive integersand cold colors negative integers. The phase diagram isfractal and has structure on all scales. In the figure there is an obvious self-similarity.Concerning physical mechanisms, impurities and/or particular states (e.g., edge currents) are important for both the 'integer' and 'fractional' effects. In addition, Coulomb interaction is also essential in the fractional quantum Hall effect. The observed strong similarity between integer and fractional quantum Hall effects is explained by the tendency of electrons to form bound states with an even number of magnetic flux quanta, called composite fermions .See also◾quantum Hall transitions◾Fractional quantum Hall effect◾Composite fermions◾Hall effect◾Hall probe◾Graphene◾Quantum spin Hall effect◾Coulomb potential between two current loops embedded in a magnetic fieldReferences1.^ Ezawa, Zyun F. (2013). Quantum Hall Effects: Recent Theoretical and Experimental Developments (3rd ed.). World Scientific. ISBN 978-981-4360-75-3.2.^ Laughlin, R. (1981). "Quantized Hall conductivity in twodimensions" (/abstract/PRB/v23/i10/p5632_1). Physical Review B 23 (10): 5632–5633. Bibcode:1981PhRvB..23.5632L (/abs/1981PhRvB..23.5632L).doi:10.1103/PhysRevB.23.5632 (/10.1103%2FPhysRevB.23.5632). Retrieved 8 May 2012.3.^ Tzalenchuk, Alexander; Lara-Avila, Samuel; Kalaboukhov, Alexei; Paolillo, Sara; Syväjärvi, Mikael;Yakimova, Rositza; Kazakova, Olga; Janssen, T. J. B. M.; Fal'ko, Vladimir; Kubatkin, Sergey (2010)."Towards a quantum resistance standard based on epitaxialgraphene" (/nnano/journal/v5/n3/abs/nnano.2009.474.html). NatureNanotechnology5 (3): 186–189. arXiv:0909.1220 (https:///abs/0909.1220).Bibcode:2010NatNa...5..186T (/abs/2010NatNa...5..186T).doi:10.1038/nnano.2009.474 (/10.1038%2Fnnano.2009.474). PMID 20081845(https:///pubmed/20081845).4.^ "conventional value of von Klitzing constant" (/cgi-bin/cuu/Value?rk90). NIST.5.^ Novoselov, K. S.; Jiang, Z.; Zhang, Y.; Morozov, S. V.; Stormer, H. L.; Zeitler, U.; Maan, J. C.;Boebinger, G. S.; Kim, P.; Geim, A. K. (2007). "Room-Temperature Quantum Hall Effect in Graphene".Science315 (5817): 1379. arXiv:cond-mat/0702408 (https:///abs/cond-mat/0702408).Bibcode:2007Sci...315.1379N (/abs/2007Sci...315.1379N).doi:10.1126/science.1137201 (/10.1126%2Fscience.1137201). PMID 17303717(https:///pubmed/17303717).6.^ Tsukazaki, A.; Ohtomo, A.; Kita, T.; Ohno, Y.; Ohno, H.; Kawasaki, M. (2007). "Quantum Hall Effectin Polar Oxide Heterostructures". Science315 (5817): 1388–91. Bibcode:2007Sci...315.1388T(/abs/2007Sci...315.1388T). doi:10.1126/science.1137430(/10.1126%2Fscience.1137430). PMID 17255474(https:///pubmed/17255474).Further reading◾Ando, Tsuneya; Matsumoto, Yukio; Uemura, Yasutada (1975). "Theory of Hall Effect in a Two-Dimensional Electron System". J. Phys. Soc. Jpn.39 (2): 279–288.Bibcode:1975JPSJ...39..279A (/abs/1975JPSJ...39..279A).doi:10.1143/JPSJ.39.279 (/10.1143%2FJPSJ.39.279).◾Klitzing, K.; Dorda, G.; Pepper, M. (1980). "New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance". Phys. Rev. Lett.45 (6): 494–497. Bibcode:1980PhRvL..45..494K(/abs/1980PhRvL..45..494K). doi:10.1103/PhysRevLett.45.494(/10.1103%2FPhysRevLett.45.494).◾Laughlin, R. B. (1981). "Quantized Hall conductivity in two dimensions". Phys. Rev. B.23(10): 5632–5633. Bibcode:1981PhRvB..23.5632L(/abs/1981PhRvB..23.5632L). doi:10.1103/PhysRevB.23.5632(/10.1103%2FPhysRevB.23.5632).◾Yennie, D. R. (1987). "Integral quantum Hall effect for nonspecialists". Rev. Mod. Phys.59(3): 781–824. Bibcode:1987RvMP...59..781Y(/abs/1987RvMP...59..781Y). doi:10.1103/RevModPhys.59.781(/10.1103%2FRevModPhys.59.781).◾Hsieh, D.; Qian, D.; Wray, L.; Xia, Y.; Hor, Y. S.; Cava, R. J.; Hasan, M. Z. (2008). "A topological Dirac insulator in a quantum spin Hall phase". Nature452 (7190): 970–974.arXiv:0902.1356 (https:///abs/0902.1356). Bibcode:2008Natur.452..970H(/abs/2008Natur.452..970H). doi:10.1038/nature06843(/10.1038%2Fnature06843). PMID 18432240(https:///pubmed/18432240).◾25 years of Quantum Hall Effect, K. von Klitzing, Poincaré Seminar (Paris-2004). Postscript (http://parthe.lpthe.jussieu.fr/poincare/textes/novembre2004.html). Pdf(/PhysicsHorizon/25yearsQHE-lecture.pdf).◾Magnet Lab Press Release Quantum Hall Effect Observed at Room Temperature (/mediacenter/news/pressreleases/2007february15.html)◾Avron, Joseph E.; Osadchy, Daniel, Seiler, Ruedi (2003). "A Topological Look at the Quantum Hall Effect" (/resource/1/phtoad/v56/i8/p38_s1).Physics Today56 (8): 38. Bibcode:2003PhT....56h..38A(/abs/2003PhT....56h..38A). doi:10.1063/1.1611351(/10.1063%2F1.1611351). Retrieved 8 May 2012.◾Zyun F. Ezawa: Quantum Hall Effects - Field Theoretical Approach and Related Topics.World Scientific, Singapore 2008, ISBN 978-981-270-032-2◾Sankar D. Sarma, Aron Pinczuk: Perspectives in Quantum Hall Effects. Wiley-VCH, Weinheim 2004, ISBN 978-0-471-11216-7◾Baumgartner, A.; Ihn, T.; Ensslin, K.; Maranowski, K.; Gossard, A. (2007). "Quantum Hall effect transition in scanning gate experiments". Physical Review B76 (8).Bibcode:2007PhRvB..76h5316B (/abs/2007PhRvB..76h5316B).doi:10.1103/PhysRevB.76.085316 (/10.1103%2FPhysRevB.76.085316).◾E. I. Rashba and V. B. Timofeev, Quantum Hall Effect, Sov. Phys. - Semiconductors v. 20, pp.617-647 (1986).Retrieved from "/w/index.php?title=Quantum_Hall_effect&oldid=605304404"Categories: Hall effect Condensed matter physics Quantum electronics SpintronicsQuantum phases Mesoscopic physics◾This page was last modified on 22 April 2014 at 14:51.◾Text is available under the Creative Commons Attribution-ShareAlike License; additional terms may apply. By using this site, you agree to the Terms of Use and Privacy Policy.Wikipedia® is a registered trademark of the Wikimedia Foundation, Inc., a non-profitorganization.。
量子分数霍尔效应

量子分数霍尔效应量子分数霍尔效应(Quantum Fractional Hall Effect,简称QFHE)是指电子系统中,当在外加的磁场达到一个特定的值时,由于量子效应而产生的一种具有特殊性质的新型介质状态。
这种介质状态对外加的磁场的变化和电子的物理特性有着独特的响应,并表现出一种特殊的“分数”霍尔效应,因此得名。
QFHE是在1980年由K. von Klitzing首次发现的,根据国际单位系统(SI)提出的“霍尔定律”,当一个2D 电子系统受到外加的磁场时,在该系统中会出现一种特殊的“霍尔导电状态”,其电阻R的值为h/ne2(e为电子的电荷,n为电子的浓度,h为普朗克常数)。
但是,在1986年,Eisenstein等人发现,在低温时,在超低磁场强度下,2D电子系统会出现一种新的电阻状态,其电阻值不再是上述h/ne2,而是为h/me2,m为一个分数,因此,这种状态又被称为“分数霍尔效应” 。
QFHE也可以看作是一种模拟量子计算机系统,它能够模拟一个真正的量子计算机,有着相似的效应,而且它所考虑的是物理上的问题,因此,它可以很好地模拟出量子力学的运动。
在实验上,我们可以通过改变外加的磁场来控制QFHE,以调节QFHE的特性,从而模拟出一个真正的量子计算机系统。
QFHE还具有许多有趣的物理性质,例如它具有超流性和超导性,在低温下,它可以显示出一种有趣的“抗磁性”,这与普通霍尔效应的行为是完全不同的。
此外,QFHE的电阻也会呈非线性变化,这表明电子在外加磁场的作用下会受到一种强烈的量子效应。
QFHE的研究可以推动量子计算技术的发展,这不仅可以深入研究和理解量子力学的行为,而且还可以为量子计算技术提供一个可行的应用。
此外,QFHE也可以用于研究低温物理中的许多问题,这些问题一直是物理学家和工程师们努力去解决的,例如量子液体、量子气体等等。
综上所述,量子分数霍尔效应(QFHE)是一种由量子效应引起的特殊介质状态,它可以帮助我们更好地理解量子力学,也可以为量子计算技术提供可行的应用,是一种重要的物理现象。
The Physics of Quantum Hall Effect

The Physics of Quantum Hall Effect量子霍尔效应的物理学原理量子霍尔效应(Quantum Hall Effect)是量子力学中一个非常重要的现象。
它的发现和研究不仅对纳米科技、信息技术等领域具有重要的应用价值,而且对理解固态物理学的本质也有着重要的意义。
一、莫尔(Klaus von Klitzing)发现的量子霍尔效应1980年,德国物理学家莫尔通过研究二维电子气体,发现了量子霍尔效应。
因为他的发现,莫尔获得了1985年的诺贝尔奖。
莫尔通过实验观察到,在低温下,二维电子气体在强磁场中呈现出应变与电荷的非经典的关联,电阻率出现了奇特的分数倍量子化现象。
这个现象表明,在一个固定大小的电场中,电子所携带的负电荷在移动时产生的电荷分布与物质的特性相应地变化了。
这种现象被称为量子霍尔效应。
二、量子霍尔效应的物理学原理量子霍尔效应源自于量子化的电磁波动态。
它发生的表面是由电子在二维材料中受到两个垂直电场的影响,一个是外磁场,一个是表面势场。
背后的基本机理涉及到一个参数,即电子的荷质比,在二维材料中会产生一种平均的自由电场,被称为Lorentz力。
随着磁场的增强,这种力将越发强大。
这个力将会导致一种称为 Hall 电场的场的形成,它代表了在电子在磁场中的移动,因为在电子磁矩和磁场之间的相互作用会产生一个横向的电场。
电子在普通的材料中会受到散射。
在一个均匀的磁场下,这对电子的运动根本没有影响,但是在超出一定范围或者在密度较高的系统中,电子将会遇到一些携带着相反荷电的电子,因此会产生库伦相互作用。
当电子的速度增加时,不仅需要克服磁场导致的阻力,还需要克服由于原子核以及组成材料的其他电子的排斥所产生的力。
量子霍尔效应发生的原因是,当电子在固定的磁场下运动时,磁场的影响会将它们绑定在材料内部、数量有限的位置上。
当电子密度十分低时,电子将会分别占据这些位置,并将它们所携带的电荷向内部传递,导致出现整数量子霍尔效应。
Hamiltonian Theory of the Fractional Quantum Hall Effect Effect of Landau Level Mixing

arXiv:cond-mat/0201082v1 [cond-mat.mes-hall] 7 Jan 2002
73.50.Jt, 05.30.-d, 74.20.-z I. INTRODUCTION
The fractional quantum Hall effects (FQHE) [1,2] have demonstrated the existence of new states of matter for two-dimensional electron gases (2DEG’s) in high magnetic fields. When the fields are high enough that only a fraction of a Landau level (LL) is occupied, the system reorganizes itself at special fractions into incompressible ground states [3] with fractionally charged excitations. The current understanding of the FQHE is schematically expressed by saying that the quasiparticles are electrons dressed by an even number of units of statistical flux, called Composite Fermions (CF’s) [4,5]. The FQHE of electrons is then understood as the integer quantum Hall effect of CF’s. A fruitful approximation in the study of the FQHE has been the restriction of the single particle electronic wavefunctions to the LLL. This approximation becomes exact in the limit of very high magnetic fields (κ = (e2 /εl)/ωc → 0) and captures the essential physics underlying the FQHE. However, when one wishes to make detailed comparisons between the theory and experiment, say in the study of transport gaps, one must seek corrections due to the nonzero value of κ, that is, include the effects of Landau level mixing. Hitherto these effects have been studied numerically [6–8], with the latest results coming from a fixed-phase diffusion Monte Carlo study [9]. In this paper we present an analytical calculation of the effect of LL-mixing in two steps. First we deduce an effective hamiltonian within the LLL which incorporates the leading contribution in κ due to higher LL’s. This hamiltonian is written in terms of electronic coordinates. We then invoke results from our previous work on the hamiltonian formulation of the FQHE [10–12] which allows one to rewrite the hamiltonian in terms of composite fermion degrees of freedom. The advantage is that these particles see an effective field which is just right to fill an integer number of LL’s, thus yielding a nondegenerate ground state on which we can base a Hartree-Fock calculation of gaps. 1
第十八届全国凝聚态理论与统计物理学术会议
目录
1. 会议日程简表 2. 会议详细日程安排 3. 大会邀请报告、分会邀请报告、分会一般报告和张贴报告编码规则 4. 大会邀请报告: 题目与摘要 5. 分会邀请报告和一般报告: 题目与摘要 6. 张贴报告: 题目与摘要 7. 通讯录
第十八届全国凝聚态理论与统计物理学术会议
日
日期 2014 年 7 月 26 日 2014 年 7 月 27 日 时间 全天 签到、注册
午餐&小憩 地点:重庆大学学生第 1 食堂 2 楼大厅(见校园引导标识、或会 议相关地图)
2014 年 7 月 27 日第二单元:分会报告(第一分会场) 地点:民主湖报告厅 13:30-14:00 主题:1 主持人:罗洪刚(兰州大学)
分会邀请报告:Three Component Ultracold Fermi Gases Under Spin-orbit Coupling 报告人:易为(中国科技大学)
14:00-14:20
口 头 报 告 : Braiding of Majorana Edge States in One-dimensional Decorated
XY-model
报告人:董召阳(南京大学) 14:20-14:40 口头报告:Exotic Fractional Topological States in a Two-dimensional Organometallic
12:00-13:30 13:30-14:40
午餐、小憩 分会报告(含分会邀请报告)
14:40-15:00 15:00-16:10
茶歇 分会报告(含分会邀请报告)
16:10-17:30 17:30-18:30 18:30 20:00-21:00 2014 年 7 月 29 日 8:30 9:00-10:30 10:30-11:00 11:00-12:00
量子自旋霍尔效应的实验观测
量子自旋霍尔效应的实验观测量子自旋霍尔效应(Quantum Spin Hall Effect,简称QSHE)是量子力学中的一种现象,它引起了物理学界的广泛关注。
QSHE是指当材料处于二维平面时,电子在其表面上的自旋分裂成上、下自旋分量,同时,这两种自旋分量的电子会在材料内部形成两个相互独立的电流环路。
这种自旋分裂和电流环路相互作用的行为被称为QSHE,被认为是一种潜在的拓扑绝缘体状态。
在过去的几十年中,科学家们对QSHE进行了大量的理论研究,并提出了一些模型来解释这一现象。
其中最著名的是狄拉克费米子模型,该模型认为在二维零能隙材料中,存在两个相互悬殊的自旋极化的反常量子霍尔边缘态。
这些反常量子霍尔边缘态可通过QSHE的电导测量来观察和量化。
为了验证QSHE,科学家们进行了一系列的实验观测。
最早的实验观测是在2005年由Konig等人在汞镉碲(HgTe)量子阱中实现的,他们发现在一定的温度下,HgTe量子阱的二维电子气体的电导发生了突变,出现了QSHE的电导特征。
这一突变被称为QSHE的拓扑相变,成为QSHE研究的里程碑。
随后的实验观测表明,在更多的材料体系中,如砷化铟(InAs)和铋锗(Bi2Se3)等,也可以观察到QSHE的现象。
这些实验结果证实了QSHE的普遍性,使得科学家们对该现象更加感兴趣。
然而,虽然QSHE已经在实验中得到观察,但其机理和应用仍然是一个广泛的研究领域。
首先,科学家们正在努力理解QSHE的微观机制,例如自旋-轨道相互作用、拓扑绝缘体的表面态等等。
这些研究有助于揭示QSHE的本质,并为进一步的应用提供理论基础。
其次,QSHE还有许多重要的实际应用。
例如,QSHE在量子计算和量子通信中具有重要意义。
由于QSHE可以使电子在材料中传输时具有低能量损耗和高速度,因此可以用来构建高效的量子比特传输通道。
此外,QSHE还可以用于制备低功耗的拓扑自旋电子学器件。
为了进一步探索QSHE的应用前景,科学家们将不断寻找新的QSHE材料和量子器件。
1998年诺贝尔物理学奖——分数量子霍耳效应的发现
1998年诺贝尔物理学奖——分数量子霍耳效应的发现1998年诺贝尔物理学奖授予美国加州斯坦福大学的劳克林(Robert ughlin,195O—),美国纽约哥伦比亚大学与新泽西州贝尔实验室的施特默(Horst L.St rmer,1949—)和美国新泽西州普林斯顿大学电气工程系的崔琦(Daniel C.Tsui,1939—),以表彰他们发现了一种具有分数电荷激发状态的新型量子流体,这种状态起因于所谓的分数量子霍耳效应。
量子流体早在研究极低温状态下的液氦和超导体时就已有所了解。
在这些领域里,已经有好几位物理学家获得过诺贝尔物理学奖。
例如,卡末林-昂内斯由于液氦的研究和超导电性的发现获1913年诺贝尔物理学奖;朗道由于液氦和超流理论获1962年诺贝尔物理学奖;巴丁、库珀和施里弗由于提出超导电性的BCS 理论获1972年诺贝尔物理学奖;卡皮查由于发现氦的超流动性获1978年诺贝尔物理学奖;柏诺兹和缪勒由于发现高温超导获1987年诺贝尔物理学奖;戴维·李、奥谢罗夫和R.C.里查森则因发现氦-3的超流动性获1996年诺贝尔物理学奖。
这么多的物理学家受到如此殊荣,说明凝聚态物理学在20世纪有极大的发展,而低温和超导在这一领域内又具有特殊重要的地位。
分数量子霍耳效应正是继高温超导之后凝聚态物理学又一项崭新课题。
分数量子霍耳效应是继霍耳效应和量子霍耳效应①的发现之后发现的又一项有重要意义的凝聚态物质中的宏观量子效应。
冯·克利青由于在1980年发现了量子霍耳效应而于1985年获得诺贝尔物理学奖。
图98-1表示冯·克利青所得霍耳电阻随磁场变化的台阶形曲线。
台阶高度等于物理常数h/e2除以整数i。
e与h是自然的基本常数——e是电子的基本电荷,h是普朗克常数。
h/e2值大约为25kΩ。
图中给出了i=2,3,4,5,6,8,10的各层平台。
下面带峰的曲线表示欧姆电阻,在每个平台处趋于消失。
量子数i也可用填充因子f 代替,填充因子f由电子密度和磁通密度确定,可以定义为电子数N与磁通量子数Nφ(=φ/φ0)之比,即f=N/Nφ,其中φ为通过某一截面的磁通,φ0为磁通量子,φ0=h/e=4.1×10-15Vs.当f是整数时,电子完全填充相应数量的简并能级(朗道能级),这种情况的量子霍耳效应叫做整数量子霍耳效应,以与分数量子霍耳效应相区别。
Edge states for the n=0 Laudau level in graphene
a r X i v :0806.2429v 1 [c o n d -m a t .m e s -h a l l ] 15 J u n 2008Edge states for the n =0Laudau level in grapheneMitsuhiro Arikawa 1,Yasuhiro Hatsugai 1,Hideo Aoki 21Institute of Physics,University of Tsukuba,Tsukuba,305-8571,Japan2Department of Physics,University of Tokyo,Hongo,Tokyo 113-0033,JapanE-mail:arikawa@.tsukuba.ac.jpAbstract.In the anomalous quantum Hall effect (QHE),a hallmark of graphene,nature of the edge states in magnetic fields poses an important question,since the edge and bulk should be intimately related in QHE.Here we have theoretically studied the edge states,focusing on the E =0edge mode,which is unusual in that the mode is embedded right within the n =0bulk Landau level,while usual QHE edge modes reside across adjacent Landau levels.Here we show that the n =0Landau level,including the edge mode,has a wave function amplitude accumulated along zigzag edges whose width scales with the magnetic length,l B .This contrasts with the usual QHE where the charge is depleted from the edge.The implications are:(i)The E =0edge states in strong magnetic fields have a topological origin in the honeycomb lattice,so that they are outside the continuum (“massless Dirac”)model.(ii)The edge-mode contribution decays only algebraically into the bulk,but this is “topologically”compensated by the bulk contribution,resulting in the accumulation over l B .(iii)The real space behavior obtained here should be observable in STM experiments.Ever since the anomalous quantum Hall effect (QHE)was experimentally observed,[1,2]fascination with graphene is mounting.The interests have been focused on the “massless Dirac”dispersions around Brillouin zone corners in graphene,where the Dirac cone is topologically protected due to the chiral symmetry[3].The peculiar dispersion is responsible for the appearance of the n =0Landau level (n :Landau index)precisely around energy E =0in magnetic fields[4].For the ordinary integer QHE an important question is how the bulk and edge QHE conductions are related for finite samples.Many authors have addressed this question[5,6],and the bulk QHE conductivity,a topological quantity,is shown to coincide with the edge QHE conductivity,itself another topological quantity.This is an example of the phenomena that,when a bulk system has a topological order[7,8,9,10]that reflects the geometrical phase of the system[11],this should be reflected and become visible in the edge states in a bounded system.[12,13]This “bulk-edge correspondence”persists in graphene,as shown both from an analytic treatment of the topological numbers and numerical results for the honeycomb lattice[14,15].In this paper,we reveal the features in the real-space profile of the edges states in graphene in magnetic fields B in the one-body problem.A pecurier point on the graphene edge states is that the E =0edge mode,despite being embedded right within the n =0bulk Landau level in the energy spectrum,has a wave function whose charge is accumulated along zigzag edges.This is drastically different from the ordinary QHE,where edge modes reside,in energy,between adjacent Landau levels,and their charge is depleted toward an edge.The physics here indicates a topological origin in a honeycomb lattice,which is in fact totally outside continuum models.In B =0,a zigzag edge in graphene has been known to have a flat dispersion at E =0,[16]Figure 1.Honeycomb lattice with armchair(a)or zigzag(b)edges with e 1,e 2being respective unit translation vectors.Local charge density (∝area of each circle)in a magnetic field φ=1/41for the energy window −0.05<E <0.05around n =0Landau level is displayed.(c)Energy spectrum for a zigzag edge against k 2(momentum along the edge)in a magnetic field of φ=1/41for zigzag edges.(d)Blowup around the n =0Landau level for a zigzag edge,in a magnetic field of φ=1/5here for clarity,with shaded regions represent the bulk energy spectra,while red curves the modes localized on the zigzag edge.which is protected by the bipartite symmetry of the honeycomb lattice.Here we focus on the edge states in strong magnetic fields,which has a flat dispersion at E =0.We consider the tight-binding model on the honeycomb lattice with nearest-neighbor hopping t (which is taken to the the unit of energy hereafter).The magnetic field is introduced as a Peierls phase.The flux in units of the magnetic flux quantum is φ≡BS 6/(2π)=1/q in each hexagon with an area S 6=(3√2πE 2E 1dEdk 2|ψα(E,j 1,k 2)|2.(1)Here x is the distance from the edge (as related to j 1via e 1which is not normal to the edge),and E 1<E <E 2is the energy window to be included in the charge density (which is normalized to unitywhen the window covers the whole spectrum).Figure 1(c)shows the energy spectrum for a zigzag edge in a magnetic field φ=1/41.For this magnetic field the n =0Landau level around E =0,with a narrow energy width,almost looks like a line spectrum on this plot.We calculate the local charge density defined in eq.(1)for the armchair and zigzag edges.Figure 2(a)depicts the charge density I (x )normalized by thebulk value I0(=φ)against the distance from the edge x measured by the magnetic length l B for φ=1/41,with the energy window|E|<0.05set to cover the n=0Landau level(along with the embedded E=0edge mode).The charge density for an armchair edge decreases monotonically toward the edge,where the depletion occurs on the magnetic length scale(l B=33/4a/√π 1dtt2(n−1)(1−t2)1−t2/4.(2)Asymptotically p n has an algebraic decay as p n≃n−2/(π√(a) n=0 Landau level (near E=0)(b) Landau levels (near band botom)I (x )/I 0I (x )/I 0BFigure 2.(a)Scaled plot of the charge density I (x )for magntic flux φ=1/41against x/l B ,thedistance from the edge normalized by the magnetic length,for the n =0Landau level (marked with A in Fig.1(c)).(b)The same plot for the outermost Landau levels (marked with B and C in Fig.1(c)),for which I 0=φ/2.0 I (x )/I 0x/l B(a) E=0 contribution(b) n=0 Landau level and E=0 contributionFigure 3.Scaled plot of I (x )at E =0edge mode for φ(=1/q )=1/21and 1/41(a)and comparison with n =0Landau Level contribution for φ=1/41.[2]Zhang Y,Tan Y W,Stormer H L,and Kim P 2005Nature (London)438201[3]Ryu S and Hatsugai Y 2002Phys.Rev.Lett.89077002[4]Brey L and Fertig H A 2006Phys.Rev.B 73195408[5]Laughlin R B 1981Phys.Rev.B 235632[6]Halperin B I 1982Phys.Rev.B 252185[7]Wen X G 1989Phys.Rev.B 407387[8]Shapere A and Wilczek F ed.1989Geometric Phases in Physics (Singapore:World Scientific)[9]Hatsugai Y 2004J.Phys.Soc.Jpn.732604[10]Hatsugai Y 2004J.Phys.Soc.Jpn.741374[11]Berry M V 1984Proc.R.Soc.London,Ser.A 39245[12]Hatsugai Y 1993Phys.Rev.B 4811851[13]Hatsugai Y 1993Phys.Rev.Lett.713697[14]Hatsugai Y,Fukui T and Aoki H 2006Phys.Rev.B 74205414[15]Hatsugai Y,Fukui T and Aoki H 2007Eur.Phys.J.Special Topics 148133[16]Fujita M,Wakabayashi K,Nakada K and Kusakabe K 1996J.Phys.Soc.Jpn.651920;Wakabayashi K,Fujita M,Ajiki H and Sigrist M 1999Phys.Rev.B 598271[17]Arikawa M,Hatsugai Y and Aoki H 2008Preprint arXiv:0805.3240[18]Niimi Y et al 2006Phys.Rev.Lett.97236804has obtained STM and STS results for graphite.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
Introduction
Nowadays the observation of the famous quantum Hall effect (QHE) [1] does not remain at the stage of the semiconductors, but it can be seen in other materials. This is for example the case of graphene, which is a projected graphite of the group symmetry C3 into two-dimensional spaces. When such system is submitted to a perpendicular magnetic field, it appears an anomalous integer Hall conductivity [2, 3] that is a manifestation of the relativistic particle motions. It is originated from different sources, which are exactly the four-fold spin/valley and the Berry phase due to the pseudospin (or valley) precision when a massless (chiral) Dirac particle exercises cyclotron motion. This result was theoretically suggested by two groups [4, 5] independently. The emergence of QHE in graphene during 2005 offered a laboratory for different investigations and applications of some mathematical formalism. Many of them are brought from the QHE studies in semiconductors and used the Dirac operator as the cornstone instead of the Landau Hamiltonian as the starting point. Indeed, different questions have been partially or completely solved but still other attentions to be paid. This concerns an eventual fractional quantum Hall effect (FQHE) [6] in graphene and related issues. Such interest can be linked to the fact that FQHE is a fascinating subject because starting from its appearance is still capturing a great attention. This is due to its relations to different areas of physics and mathematics. There are many interesting theories have been appeared dealing with some problems related to the anomalous FQHE, for instance one may refer to the papers [7, 8, 9, 10]. In particular, based on different arguments some wavefunctions have been suggested as good candidates to describe the subject [11, 12, 13]. For instance, some of them used the composite fermion approach [14] and other made a straightforward generalization of the Halperin theory [15] for non-polarized spin. However, some of them can be linked to each other and recovered from some general proposals as has been seen in [13] as we will see in the present work. Another theory was proposed by the first author [13] who studied the effect exhibited by the relativistic particles living on two-sphere S2 and submitted to a magnetic monopole. In fact, he started by establishing a direct connection between the Dirac and Landau operators through the SP . This was helpful in the sense that the Dirac eigenvalues and Pauli–Schr¨ odinger Hamiltonian Hs SP spectrum, he showed that there is a composite eigenfunctions were easily derived. In analyzing Hs fermion nature supported by the presence of two effective magnetic fields. For the lowest Landau level (LLL), he argued that the basic physics of graphene is similar to that of two-dimensional electron gas, which is in agreement with the planar limit. For the higher Landau levels, he proposed a SU (N ) wavefunction for different filling factors that captures all symmetries. Focusing on the graphene case, i.e. N = 4, he gave different configurations those allowed to recover some known results. Motivated by different analysis concerning the anomalous FQHE and in particular [13], we develop a real approach in order to describe the subject. Taking advantage of our knowledge about the phenomena in semiconductors, we introduce some effective interactions as relevant ingredient in forming the Hamiltonian system. For this, we consider M -particles in the presence of a perpendicular magnetic field B where the interaction is taken to be two and three-body types. These have been successfully applied to the conventional FQHE, for instance one may see [16, 17]. Based on the connection between the Pauli-Schr¨ odinger and Dirac Hamiltonian’s, we construct an appropriate Dirac operator 1
UCDTPG 08-01 arXiv:0805.2388
Fractional Quantum Hall States in Graphene
Ahmed Jellala,b, ∗ and Bellati Malikab, †
arXiv:0805.2388v1 [hep-th] 15 May 2008
Abdus Salam International Centre for Theoretical Physics, Strada Costiera 11, 34014 Trieste, Italy b Theoretical Physics Group, Faculty of Sciences, Choua¨ ıb Doukkali University, Ibn Maˆ achou Road, PO Box 20, 24000 El Jadida, Morocco
a The
Abstract We quantum mechanically analyze the fractional quantum Hall effect in graphene. This will be done by building the corresponding states in terms of a potential governing the interactions and discussing other issues. More precisely, we consider a system of particles in the presence of an external magnetic field and take into account of a specific interaction that captures the basic features of the Laughlin series ν = 2l1 +1 . We show that how its Laughlin potential can be generalized to deal with the composite fermions in graphene. To give a concrete example, we consider the SU (N ) wavefunctions and give a realization of the composite fermion filling factor. All these results will be obtained by generalizing the mapping between the Pauli–Schr¨ odinger and Dirac Hamiltonian’s to the interacting particle case. Meantime by making use of a gauge transformation, we establish a relation between the free and interacting Dirac operators. This shows that the involved interaction can actually be generated from a singular gauge transformation.
