2012年温州中学高一自主招生笔试模拟试题数学试题
2012年温州中学自主招生综合练习(三)

2012年温州中学自主招生综合练习(三)物理部分1.如图,一不可伸长的轻质细绳跨过滑轮后,两端分别悬挂质量为m 1和m 2的物体A 和B 。
若滑轮有一定大小,质量为m 且分布均匀,滑轮转动时与绳之间无相对滑动,不计滑轮与轴之间的摩擦。
设细绳对A 和B 的拉力大小分别为T 1和T 2,已知下列四个关于T 1的表达式中有一个是正确的,请你根据所学的物理知识,通过一定的分析判断正确的表达式是( )2.如图所示,曲线M 、N 分别表示晶体和非晶体在一定压强下的熔化过程,图中横轴表示时间t ,纵轴表示温度0T 从图中可以确定的是( )A.晶体和非晶体均存在固定的熔点0TB.曲线M 的bc 段表示固液共存状态C.曲线M 的ab 段、曲线N 的ef 段均表示固态D.曲线M 的cd 段、曲线N 的fg 段均表示液态 3.一定量的理想气体在某一过程中,从外界吸收热量2.5×104J ,气体对外界做功1.0×104J ,则该理想气体的( )A.温度降低,密度增大B.温度降低,密度减小C.温度升高,密度增大D.温度升高,密度减小 4.下列说法正确的是( ) A.甲乙在同一明亮空间,甲从平面镜中看见乙的眼睛时,乙一定能从镜中看见甲的眼睛 B.我们能从某位置通过固定的注意透明的介质看见另一侧的所有景物 C.可见光的传播速度总是大于电磁波的传播速度 D.在介质中光总是沿直线传播5.一质量为m 的物块恰好静止在倾角为θ的斜面上。
现对物块施加一个竖直向下的恒力F ,如图所示。
则物块( ) A .仍处于静止状态 B .沿斜面加速下滑 C .受到的摩擦力不便 D .受到的合外力增大6.实验表明,可见光通过三棱镜时各色光的折射率n 随着波长λ的变化符合科西经验公式:24BCn A λλ=++,其中A 、B 、C 是正的常量。
太阳光进入三棱镜后发生色散的情形如下图所示。
则A .屏上c 处是紫光B .屏上d 处是红光C .屏上b 处是紫光D .屏上a 处是红光7.如图所示,甲、乙两人在冰面上“拔河”。
2012年温州中学自主招生模拟考试数学试卷

2012年温州中学自主招生模拟考试数学试卷(考试时间120分钟,满分150分)一.选择题(每小题5分,一共10题,满分50分,每小题只有一个选项符合题意)1.如果a ,b, c, d是非零实数,且满足a²+b²=1,c²+d²=1,ac+bd=0,下列结论中,(1)a²+c²=1(2)ab+cd=0(3)ad+bc=0,有几个命题成立()A.1B.2C.3D.02.一个三角形三边长为连续整数,且1个内角等于另一个内角的2倍,那他的三边长为a ,b, c试求abc的值( )A.120B.130C.60D.1403.已知x+1y=3,y+1z=1,z+1x=3,那么xyz=()A.1B.2C.3D.44.已知,那么m+1m的整数部分是()A.1B.2C.3D.45.如果m,n是正实数,方程x²+m x+2n=0和方程x²+2n x+m=0都有实数解,那么m+n 的最小值是()A.2B.4C.5D.66. 11145x y z++=的正整数解有()组A.0B.8C.12D.167.如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角AC相交于点E,且DE∥BC.已知AE=22,AC=23BC=6,则⊙O的半径是()A .32 B. 4 C. 34 D.38.整数x0,x1,x2,x3..... x10满足x0=0,1=x0+1x,2=x1+1x….. 10=x9+1x那么x1+x2+x3+.....+x10的最小值是()A.1B.0C.7D.49.已知实数p是一个三位数,也是一个质数,p的百位数为a ,十位数为b,个位数为c,那么一元二次方程20ax bx c++=的根的关系为()A. 有1个整数根B.有2个整数根C.无整数根D.无法确定10.△ABC中,∠A和∠B均为锐角,AC=6,BC=33,且sin A=33,则cosB的值为()A.3B.3C.1D.2二.填空题(一共6小题,每小题5分,满分30分)B第7题11.已知,p q 为实数,且满足p ³+q ³=2,那么p q +的最大值为___________.12.已知1, 2.....,7x x x 为自然数,且123.....7x x x x 〈〈〈〈,有123...7x x x x ++++=159, 那么123x x x ++的最大值是__________.13.在等腰三角形ABC 中,D 为腰AC 的中点,D,E 平分∠ADB 交AD 于E ,圆ADE 交BD于N ,BN=AE=__________.14.如图,矩形ABCD 中,点E ,F ,G ,H 分别在边AB ,BC ,CD ,DA 上,点P 在矩形ABCD 内.若AB =4cm ,BC =6cm ,AE =CG =3cm ,BF =DH =4cm ,四边形AEPH 的面积5cm 2,则四边形PFCG 的面积为_________cm 2.第14题15. 在正整数数列中,由1开始依次按如下规则取它的项:第一次取1,第二次取2个连续 偶数2、4;第三次取3个连续奇数5、7、9;第四次取4个连续偶数10、12、14、16; 第五次取5个连续奇数17、19、21、23、25.按此规则一直取下去,得到一个子数列1,2, 4,5,7,9,12,14,16,17,….则在这个子数列中,由1开始的第2008个数是 . 16.将1,2,3,4,5这5个数排成一排,最后一个是奇数,且使得其中任意连续三个数之 和都能被这三个数中的第一个整除,那么满足要求的排法有__________种.三.解答题(一共5小题,满分70分,每小题都要写出相应的解题过程,证明过程及演算步骤)17.(本题10分)解方程:x ³+3x ²+3x -7=0如图,梯形ABCD 中,AD ∥BC ,E 为线段AB 上的点,且满足AE =AD ,BE =BC ,过E 作EF ∥BC 交CD 于F ,设P 为线段CD 上任意一点,试说明2P D P C P F A DB CE F-=的理由.第18题 19.(本题14分)已知正三角形ABC ,AB = a ,点P ,Q 分别从A ,C 两点同时出发,以相同速度作 直线运动,且点P 沿射线AB 方向运动,点Q 沿射线BC 方向运动. 设AP 的长为x ,△PCQ 的面积为S ,(1)求S 关于x 的函数关系式;(2)当AP 的长为多少时?△PCQ 的面积和△ABC 的面积相等.EFDBAC在1,2,3,….n中,任取10个数,使得其中任意2数的比值大于23,小于32,求n的最大值.21.(本题16分)如图,点P为⊙O外一点,过点P作⊙O的两条切线,切点分别为A,B.过点A作PB的平行线,交⊙O于点C.连结PC,交⊙O于点E;连结AE,并延长AE交PB于点K.求证:PE·AC=CE·KB.第21题CN DB C2012年温州中学自主招生模拟考试数学试卷参考答案一.选择题二.填空题11.___2____ 12.____61_____ 13.____14.____8___ 15.___3593____ 16.______5_______ 三.解答题17.观察得x=1是原方程的根所以必有x-1这一因式移项可得(x-1)(x ²+5x+6)=(x-1)² 1.x-1=0,所以x=1 2.x-1≠0,所以x ²+4x+7=0 Δ=16-4×7<0所以无根,综合得,原方程的根为x=1.18. 解:如图,过E 作MN//CD ,交直线DA ,BC 于点M ,N ,过点P 作PQ//BC ,交AB 于点Q ,则MD=EF=NC 。
2012温州中学实验班招生模拟联考数学试卷

2012年温州中学实验班招生模拟联考试卷数学联考试题卷考生须知:1. 所有答案写在答题卷上,本试卷共2页,答题卷4页。
2. 满分150分,考试时间120分钟。
一. 选择题(本大题共8小题,每小题5分,满分40分)1.31231131144++-++的值是( )(A )1 (B )-1 (C )2 (D )-2 2. △ABC 中,22=AB ,2=AC ,2=BC,设P 为BC 边上任一点,则( )(A )PB PA <2·PC (B )PB PA =2·PC(C )PB PA >2·PC(D )PB PA 与2·PC 的大小关系并不确定3. 方程k k k x k x (02)13(722=--++-是实数)有两个实根α、β,且0<α<1,1<β<2,那么k 的取值范围是( )(A )3<k <4; (B )-2<k <-1; (C )3<k <4或-2<k <-1 (D )无解。
4. 若a ,c ,d 是整数,b 是正整数,且满足c b a =+,d c b =+,a d c =+,那么d c b a +++的最大值是( )(A)1- (B)5- (C)0 (D)15. 若M n 1210099321=⨯⨯⨯⨯⨯ ,其中M为自然数,n 为使得等式成立的最大的自然数,则M( )(A)能被2整除,但不能被3整除 (B)能被3整除,但不能被2整除 (C)能被4整除,但不能被3整除 (D)不能被3整除,也不能被2整除6. 2223,2,1,…,1234567892的和的个位数的数字是( )(A).2 (B).3 (C).4 (D).5 7. 在锐角△ABC 中,1=AC ,cAB =, 60=∠A ,△ABC 的外接圆半径R ≤1,则( )(A)21< c < 2 (B)0< c ≤21 (C )c >2 (D )c = 28. 如图ABCD 是边长为a 的正方形,以D 为圆心,DA 为半径的圆弧与以BC 为直径的圆交于另一点P ,延长AP 交BC 于点N ,则B NN C =( ) DAB(A).15323+(B)322 (C)0.5 (D)0.4二.填空题(本大题共6小题,每小题6分,满分36分)9. 已知关于x 的一元二次方程02=++c bx ax 没有实数解.甲由于看错了二次项系数,误求得两根为2和4;乙由于看错了某一项系数的符号,误求得两根为-1和4,那么,=+ac b 32 .10. 实数x 与y ,使得x + y ,x - y ,x y ,yx 四个数中的三个有相同的数值,求出所有具有这样性质的数对(x , y )_______________.11. n 是一个正整数,有一个天平以及n 个重量分别为0112,2,,2n - 的砝码。
2012温州中学提前招生模拟数学试卷

2012年温州中学自主招生模拟试题数 学一.选择题:一共8小题,每小题5分,满分40分1.如果关于x的方程至少有一个正根,则实数a的取值范围是()A、 B、 C、 D、2.如图AD是∠BAC的角平分线,AD的垂直平分线交BC的延长线于F,若,则………………… ()A、 B、 C、 D、3.对于素数,方程有整数解,则()A、1B、2C、3D、44.如图,正方形ABCD的边长为2,E,F分别是AB,BC的中点,AF 与DE,DB分别交于点M,N,则△DMN的面积是()A、 8B、12C、D、155.方程的实数根的个数为()A、1B、2C、3D、46.如果关于x的方程是正整数)的正根小于3,那么这样的方程个数是().A 、5 B、 6 C、 7 D 、87.x+y+z=3 x³+y³+z³=3,x²+y²+z²=()A、3B、4C、57D、非以上答案8.某城市的机动车牌照是从“10000”到“99999”连续编号,则在这90000个车牌照中数9至少出现一个,并且各数字之和是9的倍数的车牌照共有()个;A、2345B、9999C、4168 D.5014二.填空题:共6小题,每小题6分,满分36分9.设是给定的奇质数,正整数使得也是一个正整数,=________________。
10.黑板上写有共100个数字.每次操作先从黑板上的数中选取2个数,然后删去,并在黑板上写上数,则经过99次操作后,黑板上剩下的数是________________11.一次棋赛,有n个女选手和9n个男选手参赛,每位选手都与其余10n -1个选手各对局一次.计分方式为:胜者得2分,负者得0分,平局各得1分.比赛结束后统计发现,所有男选手的得分总和是所有女选手得分总和的4倍.则n的所有可能值是__________.12. 抛物线的图象与x轴有两个交点M(x1,0),N(x2,0),且经过点A(0,1),其中0<x1<x2.过点A的直线l与x轴交于点C,与抛物线交于点B(异于点A),满足△CAN是等腰直角三角形,且S△BMN=S△AMN.求该抛物线的解析式______________13.如图,矩形ABCD的对角线相交于O,AE平分∠BAD交BC于E.若∠CAE =15°,则∠BOE=____________14.方程组,的实数解(x,y)= 。
温州中学自主招生试题2012.9

温州中学自主招生模拟数学试题2012.9一试一. 选择题:本大题共8小题,每小题4分,满分32分1.已知,x y 均为正整数,且221997x y +=,则x y +=( )A.51B.63C.68D.722. 从混有5张假钞的20张百元钞票中任意抽取2张,将其中1张放在验钞机上检验发现是假钞.求两张都是假钞的概率( ) A.117 B. 217 C. 317 D. 4173. 若实数,,a b c满足等式3||6b =,9||6b c =,则c 可能取的最大值为 ( )A .0.B .1.C .2.D .3.4.若b a ,是两个正数,且,0111=+-+-ab b a 则 ( ) A .103a b <+≤. B .113a b <+≤. C .413a b <+≤. D .423a b <+≤.5.一个半径为r 的圆形纸片在边长为a(a ≥)的等边三角形内任意运动,则在该等边三角形内,这个圆形纸片“不能接触到的部分”的面积是( ).A.2π3r2C.2π)rD.2πr 6. 点D E ,分别在△ABC 的边A B A C ,上,B E C D ,相交于点F ,设1234BDF BCF CEF EADF S S S S S S S S ∆∆∆====四边形,,,,则13S S 与24S S 的大小关系为( ).A.1324S S S S <B.1324S S S S =C.1324S S S S >D.不能确定7.若方程2310x x --=的两根也是方程420x ax bx c +++=的根,则2a b c +-的值为 ( )A .-13.B .-9.C .6.D . 0. 8. 已知,x y 是实数,且满足224040x x y y y x ++=++=,有( )组不同的解。
A.12B.13C.14D.15二.填空题:本大题共6小题,每小题5分,满分30分9. 对于一切实数x ,抛物线2y ax bx c =++ (a <b )的值均为非负数,则b aa b c-++的最大值为________。
温一中自主招生模拟考试 数学试题

实验班招生数学模拟考试一、选择题(本大题满分42分,每小题6分)本题共有7道小题,请把正确的选项写在括号内。
1、已知抛物线y=ax 2+bx+c 经过点(1,4),点(2,7),对称轴为直线x=k ,且k ≤1,则a 的取) (A)353≤≤a (B) 3≥a (C)53≤a (D)a <0 2、已知方程x k x =-有两个不相等的实根,则实数k 的取值范围是( )(A)0≤k (B)410k ≤ (C)41 k (D)41≥k 3、已知c b a ,,为整数,且c b a c b a 126448222+++++ ,则代数式abc cb a )111(++的值是( ) (A) 0 (B) -1 (C) 1 (D) 84、在正△ABC 中,P 为AB 上一点,Q 为AC 上一点,且AP=CQ ,若点A 与PQ 的中点M 之间的距离为19cm ,则点P 到点C 的距离为( )(A) 19cm (B) 28cm (C) 38cm (D) 36cm 5、在直角扇形AOB 中,O 为圆心,OA=OB=1,C 为AB 上任一点,C D ⊥OB 于点D ,则OD+DC 的最大值为( ) (A) 3 (B) 1 (C) 2 (D) 56、已知锐角△ABC 的面积为30,由各边中点向其它两边引垂线,则这六条垂线所围成的面积是( ) (A) 20 (B) 15 (C) 10 (D)3207、任意△ABC ,内心为I ,当AB+A C ≥2BC 时,△ABC 的外接圆半径R1,与△IBC 外接圆半径R 2的大小关系为()(A) R 1 ≥R 2 (B) R 1 >R 2 (C) R 1 ≤3R 2 (D) R 2≤R 1 ≤2R 2 二、填空题(本大题满分42分,每小题7分)本题共有7道小题,请直接将答案写在横线上。
8、在梯形ABCD中,AB∥DC,AB=AC=ADBC则BD= . 9、如图在平行四边形ABCD 中,延长BC 到P ,延长DC 到Q ,使,m DCCQBC CP ==当 S △ABC =S ABCD 时,则m= 。
2012年自主招生考试数学试卷1

2012年高中自主招生考试理综试卷注意事项:1. 本试卷由数学、物理及化学三部分构成,数学1—8页;理化9—12页; 2.分值设置:数学100分,物理40分,化学40分,共180分; 3.考试时间:数学、物理及化学同场考试,时间为150分钟.4.答卷前,务必将自己的姓名、考号用钢笔(圆珠笔)写在每张试卷密封线内相应的位置上.5.考试结束后,考生须将第Ⅰ卷、第Ⅱ卷一并交回.数学部分第Ⅰ卷(选择题 共24分)一、选择题:(本大题共8个小题,每小题3分,共24分)在下列各小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号填入第Ⅱ卷选择题答题表中相应题号下的方格内,填错或不填均为零分. 1. 下列运算正确的是A .236(2)8a a -=-B .3362a a a +=C .632a a a ÷=D .3332a a a ⋅= 2. 若某三角形的两边长分别为6和8,则下列长度的线段能作为其第三边的是A .2B .10C .14D .163.实数aA . 7B . -7C . 2a -15D . 无法确定 4. 如图,在平面直角坐标系中,正方形ABCO 的顶点A 、C 分别 在y 轴、x 轴上,以AB 为弦的⊙M 与x 轴相切.若点A 的坐标 为(0,4),则圆心M 的坐标为A .(25,﹣2) B .(25-,2) C .(﹣2,25)D .(2,25-)(第3题图)(第4题图)5. 某水库大坝的横断面是梯形,坝内斜坡的坡度i =1i =1∶1,则两个坡角的和为A .o 60B .o 75C .o 90D .o 1056.如图,梯形ABCD 中,∠ABC 和∠DCB 的平分线相交于梯形中位线EF 上的一点P ,若EF =3,则梯形ABCD 的周长为 A .9B .10.5C .12D .157. 如图,函数x y =1和34312+=x y 的图象相交于(-1,1), (2,2)两点.当21y y <时,x 的取值范围是 A .x >-1 B .-1<x <2 C .x <2D . x <-1或x >28.如图,平面直角坐标系中,四边形OABC 是菱形,点C 的坐标为(4,0),∠AOC = 60°,垂直于x 轴的直线l 从y 轴出发,沿x 轴正方向以每秒1个单位长度的速度向右平移,设直线l 与菱形OABC 的两边分别交于点M ,N (点M 在点N 的上方),若△OMN 的 面积为S ,直线l 的运动时间为t 秒(0≤t ≤4),则能大致反映S 与t 的函数关系的图象是(第6题图)(第7题图)A BCDEF PA .B .C .D .A FCDBE (第12题图)2012年高中自主招生考试数 学 试 卷总 分 表选择题答题表第Ⅱ卷 (非选择题 共76分)二、填空题:(本大题共5个小题,每小题3分,共15分)将结果直接填写在每题的横线上. 9.分解因式:2224xy xy y -+-= .10.将二次函数2x y =的图象向右平移1个单位,再向上平移2个单位后,所得图象的函数表达式是 .11.已知扇形的圆心角为150°,它所对应的弧长为20πcm ,则此扇形的面积是 2cm (结果保留π). 12.如图,在ABC △中,点D 、E 、F 分别在边AB 、BC 、CA 上,且DE CA ∥,DF BA ∥.下列四种说法: ①四边形AEDF 是平行四边形;②如果90BAC ∠=,那么四边形AEDF 是矩形;③如果AD 平分BAC ∠,那么四边形AEDF 是菱形; ④如果AD BC ⊥且AB AC =,那么四边形AEDF是正方形.其中错误的是 (只填序号). 13.正方形A 1B 1C 1O ,A 2B 2C 2C 1,A 3B 3C 3C 2,…按如图所示的方式放置.点A 1,A 2,A 3,…和点C 1,C 2,C 3,…分别在直线y kx b =+(k >0)和x 轴上,已知点B 1(1,1),B 2(3,2),则直线y kx b =+的解析式为 .B n 的坐标是 .三、解答题:(本大题共8个小题,满分61分)14.(本题满分5分)化简:22222369x y x y yx y x xy y x y --÷-++++.15.(本题满分6分)已知关于x的一元二次方程x2 + 2(k-1)x + k2-1 = 0有两个不相等的实数根.(1)求实数k的取值范围;(2)0可能是方程的一个根吗?若是,请求出它的另一个根;若不是,请说明理由.16.(本题满分6分)在电视台举办的“超级女生”比赛中,甲、乙、丙三位评委对选手的综合表现,分别给出“淘汰”或“通过”的结论.(1)请用树状图表示出三位评委给出A选手的所有可能的结论;(2)比赛规则设定:三位评委中至少有两位评委给出“通过”的结论,那么这位选手才能进入下一轮比赛.试问:对于选手A,进行下一轮比赛的概率是多少?17.(本题满分6分)如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连结BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.EADB C18.(本题满分8分)如图,△ABC 内接于⊙O ,CA =CB ,CD ∥AB 与OA 的延长线交于点D . (1)求证:CD 是⊙O 的切线; (2)若∠ACB =120°,OA = 4,求CD 的长.19.(本题满分8分)如图,已知菱形OABC 的边长为6,O 点为坐标原点,C 点在x 轴上,D 为BC 边的中点,双曲线y =xk(k >0)经过A 、D 两点. (1)求反比例函数y =xk的解析式; (2)若点P 为x 轴上一点,且满足PD =AD ,求出点P 的坐标.ABC DO20.(本题满分10分)为迎新年,某公司用10台机器生产A、B两种不同的龙年吉祥玩具,每台机器只生产其中一种玩具,每天所需生产原料总数不超过950千克,每天生产的B种玩具不小于A种玩具的件数,每天连续工作10小时.下表是这种机器生产不同玩设生产A种玩具的机器x台,则生产B种玩具的机器有(10-x)台.(1)求x的取值范围.(2)若A种玩具每2件包装成一盒,B种玩具每4件包装成一盒,每天生产的各种玩具恰好包装完......A种玩具每盒可获利5元,B种玩具每盒可获利6元.(包装了才能销售)怎样安排机器生产使每天生产玩具获利最大.(3)若用6台机器生产A种玩具,4台机器生产B种玩具,且将A种玩具2件,B种玩具4件混合包装成一盒,这样安排后,每天生产出来的玩具不能成套包装的有多少件?21.(本题满分12分)如图,在平面直角坐标系中,已知点A 坐标为(2,4),直线2=x 与x 轴相交于点B ,连结OA ,抛物线2x y =从点O 沿OA 方向平移,与直线2=x 交于点P ,顶点M 到A 点时停止移动.(1)求线段OA 所在直线的函数解析式;(2)设抛物线顶点M 的横坐标为m ,①用m 的代数式表示点P 的坐标;②当m 为何值时,线段PB 最短;(3)当线段PB 最短时,相应的抛物线上是否存在点Q ,使△QMA 的面积与△PMA的面积相等,若存在,请求出点Q 的坐标;若不存在,请说明理由.。
温州中学自主招生数学模拟试题
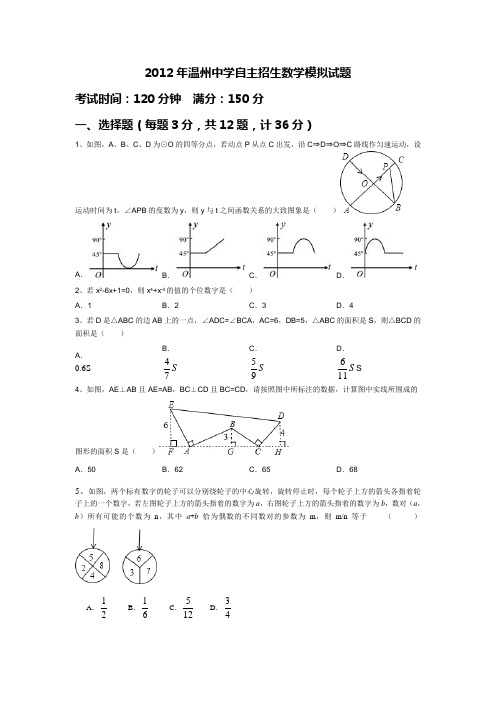
2012年温州中学自主招生数学模拟试题考试时间:120分钟 满分:150分一、选择题(每题3分,共12题,计36分)1、如图,A 、B 、C 、D 为⊙O 的四等分点,若动点P 从点C 出发,沿C ⇒D ⇒O ⇒C 路线作匀速运动,设运动时间为t ,∠APB 的度数为y ,则y 与t 之间函数关系的大致图象是( )A .B .C .D .2、若x 2-6x+1=0,则x 4+x -4的值的个位数字是( ) A .1B .2C .3D .43、若D 是△ABC 的边AB 上的一点,∠ADC=∠BCA ,AC=6,DB=5,△ABC 的面积是S ,则△BCD 的面积是( ) A .0.6SB .S 74 C .S 95 D .S 116S 4、如图,AE ⊥AB 且AE=AB ,BC ⊥CD 且BC=CD ,请按照图中所标注的数据,计算图中实线所围成的图形的面积S 是( )A .50B .62C .65D .685、如图,两个标有数字的轮子可以分别绕轮子的中心旋转,旋转停止时,每个轮子上方的箭头各指着轮子上的一个数字,若左图轮子上方的箭头指着的数字为a ,右图轮子上方的箭头指着的数字为b ,数对(a ,b )所有可能的个数为n ,其中a +b 恰为偶数的不同数对的参数为m ,则m/n 等于 ( )A .21 B .61 C .125 D .436、某一天的不同时刻老板把信交给秘书打字,每次都将信放在秘书信堆的最上面,秘书有时间就将信堆最上面的那封信取来打.假定共有5封信,且老板以1、2、3、4、5的顺序交来,在下列各顺序中,哪一顺序不可能是秘书打字的顺序?()A.12345 B.54321 C.23541 D.235147、如图,将△ADE绕正方形ABCD的顶点A顺时针旋转90°,得△ABF,连接EF交AB于H,则下列结论错误的是()A.AE⊥AFB.EF:AF=1:2C.AF2=FH•FE D.FB:FC=HB:EC8、在△ABC中,点D,E分别在AB,AC上,且CD与BE相交于点F,已知△BDF的面积为10,△BCF 的面积为20,△CEF的面积为16,则四边形区域ADFE的面积等于()A.22 B.24 C.36 D.449、如图,点A、D、G、M在半⊙O上,四边形ABOC、DEOF、HMNO均为矩形.设BC=a,EF=b,NH=c,则下列各式中正确的是()A.a>b>c B.b>c>a C.c>a>b D.a=b=c10、如图在梯形ABCD中,AD∥BC,AD⊥CD,BC=CD=2AD,E是CD上一点,∠ABE=45°,则tan ∠AEB的值等于()A.3 B.2 C.2.5D.1.511、两个不相等的正数满足a+b=2,ab=t-1,设S=(a-b)2,则S关于t的函数图象是()A.射线(不含端点)B.线段(不含端点)C.直线D.抛物线的一部分A .60°B .75°C .60°或45°D .15°或75°二、填空题(每空4分,共9空,计36分)13、若关于x 的方程(x-2)(x 2-4x+m )=0有三个根,且这三个根恰好可以作为一个三角形的三条边的长,则m 的取值范围是____________.14、如图,AB 是⊙O 的直径,AB=10cm ,M 是半圆AB 的一个三等分点,N 是半圆AB 的一个六等分点,P 是直径AB 上一动点,连接MP 、NP ,则MP+NP 的最小值是________cm.15、双曲线y=x1(x >0)与直线y=x 在坐标系中的图象如图所示,点A 、B 在直线上AC 、BD 分别平行y 轴,交曲线于C 、D 两点,若BD=2AC 则4OC 2-OD 2的值为_________.16、如图,在坐标平面上,沿着两条坐标轴摆着三个相同的长方形,其长、宽分别为4、2,则通过A ,B ,C 三点的拋物线对应的函数关系式是____________________________.17、设C 1,C 2,C 3,…为一群圆,其作法如下:C 1是半径为a 的圆,在C 1的圆内作四个相等的圆C 2(如图),每个圆C 2和圆C 1都内切,且相邻的两个圆C 2均外切,再在每一个圆C 2中,用同样的方法作四个相等的圆C 3,依此类推作出C 4,C 5,C 6,…,则(1)圆C 2的半径长等于________(用a 表示);(2)圆C k的半径为_________(k为正整数,用a表示,不必证明)18、已知正数a、b、c满足a2+c2=16,b2+c2=25,则k=a2+b2的取值范围为__________.19、已知x、y均为实数,且满足xy+x+y=17,x2y+xy2=66,则x4+x3y+x2y2+xy3+y4=___________.20、不论m取任何实数,抛物线y=x2+2mx+m2+m-1的顶点都在一条直线上,则这条直线的函数解析式是___________________________.三、简答题(共78分)21、如图1,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.(1)请在图中找出两对相似而不全等的三角形,并选取其中一对进行证明;(2)求m与n的函数关系式,直接写出自变量n的取值范围;(3)以△ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系(如图2).在边BC上找一点D,使BD=CE,求出D点的坐标,并通过计算验证BD2+CE2=DE2;(4)在旋转过程中,(3)中的等量关系BD2+CE2=DE2是否始终成立?若成立,请证明;若不成立,请说明理由.,∠BCM=.23、如图,BC是半圆⊙O的直径,D是弧AC的中点,四边形ABCD的对角线AC、BD交于点E.(1)求证:AC•BC=2BD•CD,(2)若AE=3,CD=25,求弦AB和直径BC的长.24、已知二次函数y=x2+bx-c的图象经过两点P(1,a),Q(2,10a).(1)如果a,b,c都是整数,且c<b<8a,求a,b,c的值.(2)设二次函数y=x2+bx-c的图象与x轴的交点为A、B,与y轴的交点为C.如果关于x的方程x2+bx-c=0的两个根都是整数,求△ABC的面积.的坐标;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年温州中学高一自主招生综合素质笔试卷模拟试题 数学试题注意事项:1、先将自己的姓名用钢笔或圆珠笔填写在答题卷的相应位置上。
考试结束后,应将草稿纸和答题卷一并交回。
2、本试题总分共150分,考试时间120分钟。
3、所有选择题的答案都必须从四个选项中挑选一个答案,选对给分;不答、错答或多选,均不给分。
4、所有答案用钢笔或圆珠笔写在答题卷上,注意字迹清楚,卷面整洁。
一. 选择题(本大题共8小题,每小题5分,满分40分,每题只有一个正确答案)1. 设,,x a b c y a c b z b c a =+-=+-=+-,其中a ,b ,c 为质数。
如果2x =,2=,则abc =( )A.561B.423C.356D.458 2. 设βα、是方程02322=--x x 的两个实数根,则βααβ+的值是( )A.-1B.1C.32-D.32 3.已知AD,BE,CF 为三角形ABC 的内角平分线,D,E,F 在边上。
若∠EDF=90°,∠BAC 的度数为( )A.120°B.135°C.150°D.165° 4.已知x ......+,那么x 的整数部分是( ) A.12 B.16 C.18 D.205.关于x 的方程a x x =-|1|2仅有两个不同的实根.则实数a 的取值范围是( ) A.a >0B.a≥4C.2<a <4D.0<a <46. 若干个棱长为2、3、5的长方体,依相同方向拼成棱长为90的正方体,则正方体的一条 对角线贯穿的小长方体的个数是( ) A.64 B.66 C.68 D.707. 已知a ,b ,c 为实数,函数212,y ax bx c y ax b =++=+(0)a >,当11x -≤≤时,有11y -≤≤,2y 有最大值为2,试求由212,y ax bx c y ax b =++=+所围成的封闭图形及其内部的所有格点顺次连结所得图形的面积为( ) A.4 B.2 C.1 D.88.有( )组非负整数对(,,)x y z 满足方程223xyz +=。
A.1 B.2 C.3 D.4二.填空题(本大题共6小题,每小题6分,满分36分)9. 已知q p 、均为正整数,且q p >,240)()(=+-+⋅++qpq p q p q p ,则q p ⋅所有可能值中的最大值是 .10. 已知二次函数1)12()1(2++-+=x a x a a y )0(>a 的图像顶点为A ,与x 轴交点为B 、C ,则tan ∠ABC= 。
11. 求所有的素数对(p ,q ),使得pq|5p +5q.________________.12. x 、y 为实数,则使)()(2222y x c xy y x +≥-+成立的最大常数c = 。
13. 已知:如图,以定线段AB 为直径作半圆O ,P 为半圆上任意一点(异于A 、B ),过点P 作半圆O 的切线分别交过A 、B 两点的切线于D 、C ,AC 、BD 相交于N 点,连接ON 、NP .下列结论:①四边形ANPD 是梯形;②ON=NP ;③PA 为∠NPD 的平分线.其中一定成立的是____________.14. 若抛物线222y x ax b =++-(其中a 、b 为实数)与x 轴交于相异的两点,其中一点 的横坐标在0与1之间,另一点的横坐标在1与2之间,则41b a --的取值是 。
2012年温州中学高一自主招生综合素质笔试卷模拟试题数学答题卷一.二.(本大题共6小题,每小题6分,满分36分)9._________________; 10._________________; 11._________________;12.________________; 13._________________; 14._________________;三.解答题(本大题共5小题,满分74分,每题必须写出相应的解题过程,证明过程及演算步骤)15.(12分)关于的方程322(2)(2)20x m x m x +--+-=有三个实数根分别为α、β、0x , 其中根0x 与m 无关。
(1)如0()3x αβ+=-,求实数m 的值。
(2)如a b αβ<<<,试比较:241a m a -+与241b mb -+的大小,并说明你的理由。
准考证号 考场座位号 姓名 学校16.(12分)实数0,,,≥≥≥≥w z y x w z y x 满足,且1006345=+++w z y x ,求w z y x +++的最大值和最小值.17.(15分)求最小实数M ,使得对一切实数 a ,b ,c 都成立不等式2222222222|()()()|()ab a b bc b c ca c a M a b c -+-+-++≤18.(15分)⊙O过△ABC顶点A,C,且与AB,BC交于K,N(K与N不同).△ABC 外接圆和△BKN外接圆相交于B和M.求证:∠BMO=90°.19.(20分)已知抛物线c bx ax y ++=232, (Ⅰ)若1==b a ,1-=c ,求该抛物线与x 轴公共点的坐标;(Ⅱ)若1==b a ,且当11<<-x 时,抛物线与x 轴有且只有一个公共点,求c 的取值范围;(Ⅲ)若0=++c b a ,且01=x 时,对应的01>y ;12=x 时,对应的02>y ,试判断当10<<x 时,抛物线与x 轴是否有公共点?若有,请证明你的结论;若没有,阐述理由.数学参考答案一.二.(本大题共6小题,每小题6分,满分36分)9.____ 135_________; 10._________ 21________;11. (2,3),(3,2),(2,5),(5,2),(5,5),(5,313)(313,5). 12.______1/2__________; 13.___ ①__③__ _______; 14._____143212b a -<-<_; 三.解答题(本大题共5小题,满分74分,每题必须写出相应的解题过程,证明过程及演算步骤)15. 解:(1)由322(2)(2)20x m x m x +--+-=得()()21220x x mx +--=,∴01x =-, 2分α、β是方程2220x mx --=的根∴ 2mαβ+=, 0()3x αβ+=-,所以6m = (2)设T=241b m b -+-241a ma -+=()()()()224411b a ab ma mb a b --++++ ,0,a b b a <∴-> 又2210,10a b +>+>,∴()()()2211b a a b -++>0设2()22f x x mx =-,所以α、β是2()22f x x mx =-与x 轴的两个交点,a b αβ<<<∴()0()0f a f b <⎧⎨<⎩,即22220220a mab mb ⎧--<⎨--<⎩ ∴ 22224ma mb a b +>+- ∴44ab ma mb -++>22()0a b -> ∴T>0,即241b m b -+>241a m a -+ 16. 解 设,,z w a y w ab x w a bc =+=++=+++,则,,0a b c ≥,且432x y z w w a b c +++=+++.所以 1005()4()3()w a b c w a b w a w =+++++++++181295w a b c =+++4(432)(2w a b c w b c =++++++4()x y z w ≥+++,所以 25x y z w +++≤,当25,03x y z w ====时等号成立,故w z y x +++的最大值为25.又 100181295w a b c =+++5(432)(23)w a b c w a b =+++-++5()x y z w ≤+++,所以 20x y z w +++≥,当20,0x y z w ====时等号成立,所以w z y x +++的最小值为2017. 解:222222()()()ab a b bc b c ca c a -+-+-()()()()a b b c c a a b c =----++.设a b x b c y c a z a b c s -=-=-=++=,,,,则22222221()3a b c x y z s ++=+++. 原不等式成为22222()9||(0)M x y z s xyzs x y z +++++=≥.x y z ,,中两个同号而与另一个反号.不妨设 x y ,≥0.则2221||()2z x y x y x y =+++,≥,2()4x y xy +≥.于是由算术-几何平均不等式222222223()(())2x y z s x y s +++++≥=22222111(()()())222x y x y x y s ++++++23)|||x y s xyzs =+≥(≥即32M =时原不等式成立.等号在1s x y ===,2z =-,即::3):3)a b c =时达到,故所求的最小的32M =. 18.证明:连接OC ,OK ,MC ,MK ,延长BM 到G , ∵△ABC 外接圆和△BKN 外接圆相交于B 和M , ∴∠GMC=∠BAC=∠BNK=∠BMK ,而∠COK=2•∠BAC=∠GMC+∠BMK=180°-∠CMK ,∴∠COK+∠CMK=180°, ∴C ,O ,K ,M 四点共圆, 在这个圆中,由OC=OK 得 OC =OK ,∴∠OMC=∠OMK ,但∠GMC=∠BMK ,∴∠BMO=90°.19. 解(Ⅰ)当1==b a ,1-=c 时,抛物线为1232-+=x x y , 方程01232=-+x x 的两个根为11-=x ,312=x . ∴该抛物线与x 轴公共点的坐标是()10-,和103⎛⎫ ⎪⎝⎭,. (Ⅱ)当1==b a 时,抛物线为c x x y ++=232,且与x 轴有公共点.对于方程0232=++c x x ,判别式c 124-=∆≥0,有c ≤31.①当31=c 时,由方程031232=++x x ,解得3121-==x x . 此时抛物线为31232++=x x y 与x 轴只有一个公共点103⎛⎫- ⎪⎝⎭,. ②当31<c 时, 11-=x 时,c c y +=+-=1231, 12=x 时,c c y +=++=5232.由已知11<<-x 时,该抛物线与x 轴有且只有一个公共点,考虑其对称轴为31-=x ,应有1200.y y ⎧⎨>⎩≤, 即1050.c c +⎧⎨+>⎩≤,解得51c -<-≤.综上,31=c 或51c -<-≤. (Ⅲ)对于二次函数c bx ax y ++=232,由已知01=x 时,01>=c y ;12=x 时,0232>++=c b a y , 又0=++c b a ,∴b a b a c b a c b a +=++++=++22)(23. 于是02>+b a .而c a b --=,∴02>--c a a ,即0>-c a . ∴0>>c a .∵关于x 的一元二次方程0232=++c bx ax 的判别式0])[(412)(4124222>+-=-+=-=∆ac c a ac c a ac b ,∴抛物线c bx ax y ++=232与x 轴有两个公共点,顶点在x 轴下方. 又该抛物线的对称轴abx 3-=, 由0=++c b a ,0>c ,02>+b a , 得a b a -<<-2, ∴32331<-<a b . 又由已知01=x 时,01>y ;12=x 时,02>y ,观察图象,可知在10<<x 范围内,该抛物线与x 轴有两个公共点.。
