四川省南溪二中2021届高三上学期期中考试数学(文)试卷

合集下载

四川省宜宾市南溪区第二中学校2022届高三上学期第3周周考数学(文)试题 Word版含答案

K2= =11.538＞10.828，
所以该争辩小组有99.9%的把握认为，中同学使用手机对学习有影响；
（2）记A组推选的两名同学分别为C、D，
B组推选的三名同学分别为a、b、c，则从这5人中任取两人有
CD、Ca、Cb、Cc、Da、Db、Dc、ab、ac、bc，共10种取法，
其中一人来自A组、另一人来自B组有6种取法，
2、若z=1﹣i，则复数z+z2在复平面上对应的点的坐标为（）
A．（1，﹣3）B．（﹣3，1）C．（1，1）D．（﹣1，1）
3、设x∈R，向量 =（x，1）， =（1，﹣2），且 ⊥ ，则| + |=（）
A． B． C．2 D．10
4、下列函数中，既是偶函数，又在区间单调递减的函数是（）
A. B. C. D.
14、【答案】【解析】由函数的解析式结合题意可得： .
15、【答案】- 解： =4×4×cos90°=0，
2 = ， = ，
则 =（ ﹣ ）（ + ）=（ ﹣ ）（ + ）
= 2﹣ 2﹣ = ×16﹣ ×16=﹣ ．
16、【答案】①③
【解析】命题① 命题①正确；命题②当时不满足“远离区间”的定义命题②错误；命题③由图一可得该命题正确；命题④由图二可得该命题错误.综上真命题的是①③.
所以x﹣2=0，所以 =（2，1），所以 =（3，﹣1），
所以| + |= ，故选B．
4、【答案】D【解析】逐一考查所给的函数：
A. ，函数是奇函数；
B. 函数是偶函数，在区间是增函数；
C. 函数是偶函数，在区间不具有单调性；
D. 函数是偶函数，在区间单调递减；
5、【答案】C

2021年高三上学期期中统考数学(文)试题含答案

2021年高三上学期期中统考数学（文）试题含答案本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分. 共 4页.满分150分，考试时间120分钟. 考试结束，将试卷答题卡交上，试题不交回.第Ⅰ卷选择题（共60分）注意事项：1.答卷前，考生务必将自己的姓名、准考证号、座号涂写在答题卡上.2.选择题每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，不能答在试题卷上.3.第Ⅱ卷试题解答要作在答题卡各题规定的矩形区域内，超出该区域的答案无效.一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合要求的.1.若，则＝A. B. C. D.2.已知集合，，则A. B. C. D.3.已知向量, ，如果向量与垂直，则的值为A. B. C. D.4.函数的图像为5.如果若干个函数的图象经过平移后能够重合，则称这些函数为“同簇函数”．给出下列函数：①；②；③；④．其中“同簇函数”的是A.①②B.①④C.②③D.③④6.若数列的前项和，则数列的通项公式A. B. C. D.7.已知命题；命题，则下列命题中为真命题的是A. B. C. D.8.已知，满足约束条件，若的最小值为，则A. B. C. D.9.在中,角的对边分别为,且.则A．B．C．D．10.函数是上的奇函数，,则的解集是A . B. C. D.11.定义在上的偶函数满足且，则的值为A. B. C. D.12.设函数，若实数满足则A． B．C． D．第Ⅱ卷非选择题（共90分）二、填空题：本大题共4小题，每小题4分，共16分．把答案填在答题卡中相应题的横线上．13.已知一元二次不等式的解集为,则的解集为. （）14. ．15.设正数满足, 则当 ______时, 取得最小值.16.在中，，，，则．三、解答题：本大题共6小题，共74分.把解答写在答题卡中.解答应写出文字说明，证明过程或演算步骤.17.(本小题满分12分）已知,.(Ⅰ)若,求的值;(Ⅱ)设,若,求的值.18.(本小题满分12分）已知函数和的图象关于轴对称，且.(Ⅰ)求函数的解析式；(Ⅱ)当时，解不等式.19. (本小题满分12分）设是首项为,公差为的等差数列,是其前项和.(Ⅰ) 若，求数列的通项公式；(Ⅱ) 记,，且成等比数列,证明:().20.(本小题满分12分）如图,游客在景点处下山至处有两条路径.一条是从沿直道步行到,另一条是先从沿索道乘缆车到,然后从沿直道步行到.现有甲、乙两位游客从处下山,甲沿匀速步行,速度为.在甲出发后,乙从乘缆车到,在处停留后,再从匀速步行到.假设缆车匀速直线运动的速度为,索道长为,经测量,,.(Ⅰ) 求山路的长;(Ⅱ) 假设乙先到，为使乙在处等待甲的时间不超过分钟,乙步行的速度应控制在什么范围内?21．（本小题满分12分）新晨投资公司拟投资开发某项新产品，市场评估能获得万元的投资收益.现公司准备制定一个对科研课题组的奖励方案：奖金（单位：万元）随投资收益（单位：万元）的增加而增加，且奖金不低于万元，同时不超过投资收益的.（Ⅰ）设奖励方案的函数模型为，试用数学语言表述公司对奖励方案的函数模型的基本要求.（Ⅱ）下面是公司预设的两个奖励方案的函数模型： C B A①；②试分别分析这两个函数模型是否符合公司要求.22．(本小题满分14分)设函数(Ⅰ)当时，求函数的最大值；(Ⅱ)令（），其图象上存在一点，使此处切线的斜率，求实数的取值范围；(Ⅲ)当，时，方程有唯一实数解，求的值．xx11文倾向数学参考答案及评分标准一、二、13. 14. 15. 16.三、17解: (Ⅰ)∵∴又∵,……3分 ∴ , ………………5分∴.…………………6分(Ⅱ)∵a 2b (2cos 2cos ,2sin 2sin )(2,0)αβαβ+=++= ∴即 …………………8分两边分别平方再相加得: ∴ ∴ ……10分∵且 ∴ …………………12分18.解：(Ⅰ)设函数图象上任意一点，由已知点关于轴对称点一定在函数图象上…………………2分代入，得 …………………4分（Ⅱ）由整理得不等式为等价……………………6分当，不等式为，解为………………7分当，整理为,解为……………………9分当，不等式整理为解为.……………………11分综上所述，当，解集为；当，解集为；当，解集为.…………12分19解(Ⅰ)因为是等差数列，由性质知，…………2分所以是方程的两个实数根，解得，………4分∴或即或.……………6分(Ⅱ)证明:由题意知∴∴ …………7分∵成等比数列，∴ ∴ …………8分∴ ∴ ∵ ∴ ∴…10分∴a n a n n na d n n na S n 222)1(2)1(=-+=-+= ∴左边= 右边=∴左边=右边∴()成立. ……………12分20解: (Ⅰ) ∵,∴∴, …………………2分∴[]6563sin cos cos sin sin sin sin =+=+=+-=C A C A C A C A B ）（）（π …………4分根据得所以山路的长为米. …………………6分(Ⅱ)由正弦定理得() …………8分甲共用时间：，乙索道所用时间：，设乙的步行速度为，由题意得，………10分整理得∴为使乙在处等待甲的时间不超过分钟,乙步行的速度应控制在内. …………………12分21．解：（Ⅰ）由题意知，公司对奖励方案的函数模型的基本要求是：当时，①是增函数；②恒成立；③恒成立………3分（Ⅱ）①对于函数模型：当时，是增函数，则显然恒成立 ……4分而若使函数在上恒成立，整理即恒成立，而，∴不恒成立．故该函数模型不符合公司要求． ……7分②对于函数模型：当时，是增函数，则．∴恒成立． ………8分设，则．当时，()24lg 12lg 1lg 10555e e e g x x --'=-≤=<，所以在上是减函数， ……10分从而．∴，即，∴恒成立．故该函数模型符合公司要求． ……12分22.解：(Ⅰ)依题意，的定义域为，当时，，……………………2分由，得，解得;由，得，解得或.，在单调递增，在单调递减；所以的极大值为，此即为最大值……………………4分(Ⅱ)，则有在上有解， ∴≥， ………6分所以当时，取得最小值……………8分(Ⅲ)因为方程有唯一实数解，所以有唯一实数解，……9分设，则，，所以由得，由得，所以在上单调递增，在上单调递减， . ……………11分若有唯一实数解，则必有11111()ln 011111m g e m m m m m e-=+=⇒=⇒=+---- 所以当时，方程有唯一实数解. ………14分38104 94D8 铘31576 7B58 筘27026 6992 榒•[22646 5876 塶z25325 62ED 拭27919 6D0F 洏237742 936E 鍮24070 5E06 帆33277 81FD 臽h+。

2021-2022学年高三上学期数学(文)期中试题及答案

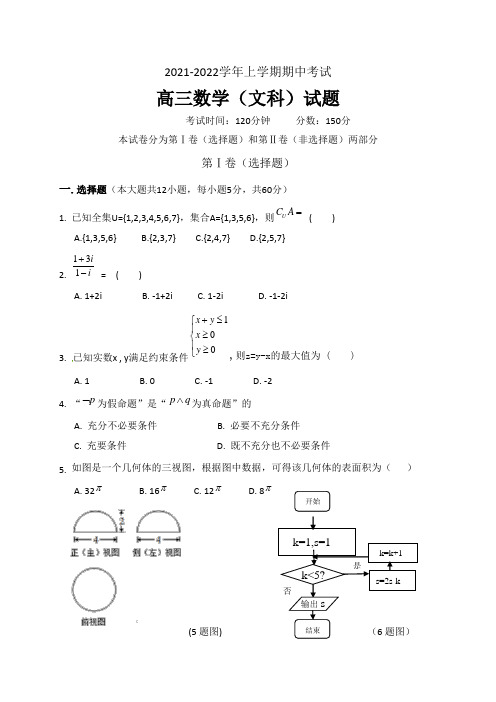
2021-2022学年上学期期中考试高三数学（文科）试题考试时间：120分钟分数：150分本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分第Ⅰ卷（选择题）一.选择题（本大题共12小题，每小题5分，共60分）1. 已知全集U={1,2,3,4,5,6,7}，集合A={1,3,5,6}，则U C A =( )A.{1,3,5,6}B.{2,3,7}C.{2,4,7}D.{2,5,7}2. 131ii +- = ( )A. 1+2iB. -1+2iC. 1-2iD. -1-2i3. 已知实数x , y 满足约束条件100x y x y +≤⎧⎪≥⎨⎪≥⎩,则z=y-x 的最大值为 ( )A. 1B. 0C. -1D. -2 4. “p ⌝为假命题”是“p q ∧为真命题”的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5. 如图是一个几何体的三视图，根据图中数据，可得该几何体的表面积为（） A. 32π B. 16π C. 12π D. 8π(5题图) （6题图）是否开始k=1,s=1k<5?输出s结束 k=k+1s=2s-k6. 执行如图所示的程序框图，输出的s 值为（） A. -10 B. -3 C. 4 D. 57. 已知x 与y 之间的几组数据如表：x 0 1 2 3 y267则y 与x 的线性回归方程y b x a ∧∧∧=+必过点 ( )A. (1,2)B. (2,6)C. (315,24) D. (3,7)8. 下列函数中，在定义域内与函数3y x =的单调性与奇偶性都相同的是（）A. sin y x =B. 3y x x =-C. 2x y =D.2lg(1)y x x =++9. 对于使()f x N ≥成立的所有常数N 中，我们把N 的最大值叫作()f x 的下确界．若,a b ∈(0, +∞),且2a b +=，则133a b +的下确界为（） A. 163 B. 83 C. 43 D. 2310.如图所示的数阵中，每行、每列的三个数均成等差数列．如果数阵中111213212223313233a a a a a a aa a ⎛⎫ ⎪ ⎪ ⎪⎝⎭所有数的和等于36，那么22a = （）A. 8B. 4C. 2D. 111.三棱锥P-ABC 的侧棱PA 、PB 、PC 两两垂直，侧面面积分别是6，4，3，则三棱锥的体积是（）A. 4B. 6C. 8D.1012.函数()f x 的定义域为R ，f(0)=2,对x R ∀∈，有()()1f x f x '+>，则不等式()1x xe f x e >+ 的解集为（） A. {}|0x x > B. {}|0x x < C. {}|11x x x <->或 D. {}|10x x x <->>或1第Ⅱ卷（非选择题）二．填空题（本大题共4小题，每小题5分，共计20分）13.已知-向量a 与b 的夹角为60°，且a =（-2，-6），10b =，则ab =14.已知数列{}n a 是等比数列，且1344,8a a a ==，则5a 的值为15.抛物线2(0)y ax a =<的焦点坐标为 16.将边长为2的等边∆ABC 沿x 轴正方向滚动，某时刻A 与坐标原点重合（如图），设顶点(,)A x y 的轨迹方程是y=f(x)，关于函数y=f(x)有下列说法：①f(x)的值域为[0，2]； ②f(x)是周期函数且周期为6 ; ③()(4)(2015)f f f π<<;④滚动后，当顶点A 第一次落在x 轴上时，f(x)的图象与x 轴所围成的面积为833π+．其中正确命题的序号为三．解答题(本大题共6道题,共70分,解答应写出文字说明，证明过程或演算步骤) 17.(本小题12分）在∆ABC 中，内角A,B,C 的对边分别为,,a b c .已知3cos 3cos c b C c B =+（I ）求sin sin C A 的值 (II)若1cos ,233B b =-=，求∆ABC 的面积。

2021年高三上学期期中联考数学(文)试题 Word版含答案

2021年高三上学期期中联考数学（文）试题 Word版含答案命题校：北京市六十五中学 xx年11月本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试用时120分钟。

考试结束后，将本试卷和答题卡一并交回。

祝各位考生考试顺利！第Ⅰ卷一、选择题：（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项符合题目要求。

）1. 设,, 则= （）A. B. C. D.2. 已知，则下列不等式正确的是（）A. B. C. D.3. 下列函数中，既是偶函数又在单调递增的函数是（）A . B. C. D.4. 已知，则等于（）A. B. C. D.5. 若,则“”是“”的（）A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件6. 若，当时，的大小关系为（）A. B. C. D.7. 已知正方形的边长为,为的中点,则（）A. B. C. D.8. 已知函数，满足，且在上的导数满足，则不等式的解为（）A. B. C. D.第Ⅱ卷二、填空题：（本大题共6小题，每小题5分，共30分。

）9．若曲线在原点处的切线方程是，则实数。

10．若向量a＝，，b＝(－，)，则a·bab＝。

11．设是周期为2的奇函数，当时，，则。

12．已知是公比为的等比数列，若，则；______________。

13．函数的值域为______________。

14. 关于函数，给出下列四个命题：①，时，只有一个实数根；②时，是奇函数；③的图象关于点，对称；④函数至多有两个零点。

其中正确的命题序号为______________。

三、解答题：（本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤。

）15. (本小题满分13分)已知函数，（Ⅰ）求的值；（Ⅱ）求的最大值和最小值。

16. (本小题满分13分)在中，角A、B，C，所对的边分别为，且（Ⅰ）求的值；（Ⅱ）若，求的面积。

四川省南溪二中高三数学上学期期中试题理-人教版高三全册数学试题

四川省南溪二中2021届高三数学上学期期中试题理一、选择题：本大题共12小题，每小题5分，共60分。

1．已知两点A （2，1），B （3，3），则直线AB 的斜率为（） A.2 B.C.54D.452.直线310x y ++=的倾斜角为（）A.30︒B.60︒C.120︒D.150︒ 3.过点()1,2，且与直线220x y ++=垂直的直线方程为（）A.20x y -=B.230x y -+=C.240x y +-=D.250x y +-= 4.已知圆1:22=+y x C ，直线:10l xy ，则l 被圆C 所截得的弦长为（）A. 22 D. 1 5.在三棱锥P ABC -中，PA ⊥平面ABC ，2ACB π∠=，且PA AC BC ==，则异面直线AB 与PC所成角的正切值为（）3 B.12 36.已知直线1l ：(1)20k x y -++=和直线2l ：8(1)10x k y k +++-=平行，则k 的值是（）A. 3B.3-C.3或3-D.7或7- 7.已知αβ，是两个平面，,m n 是两条直线，下列说法正确的是（）A.若,,m n αβαβ⊥⊂⊂，则m n ⊥B.若,,m n m n αβ⊥⊂⊂，则αβ⊥C.若n m //，β//n ，则β//mD.若α⊥m ，α//n ，则m n ⊥ 8.已知三棱柱111ABC A B C -的体积为24，则四面体11A B BC 的体积为（） A.12 B. 8 C. 4 D. 16 9. 如果AC<0且BC<0，那么直线Ax+By-C=0不通过（）A.第一象限B.第二象限C.第三象限D.第四象限10. 某四棱锥的三视图如右图所示，俯视图是等腰直角三角形，则该四棱锥的表面积是（）A.23+6+42B. 23+42+422侧视图俯视图第11题图C.D.11. 已知圆的方程为 ()()()22119,2,2x y P -+-=是该圆内一点，过点P 的最长弦和最短弦分别为AC 和BD ，则四边形ABCD 的面积是（）12. 在三棱锥S ABC -中，SA ⊥平面ABC ，212SA BC AB BAC π===∠≥，，，M 是线段BC上的动点，记直线SM 与平面ABC 所成角为θ，若tan θ，则三棱锥S ABC -外接球的表面积为（）A.2πB.4πC.8πD.16π二、填空题：本大题共4小题，每小题5分，共20分。

四川省南溪二中2021届高三上学期期中考试数学(文)试题

三．解答题（共 6 小题，共计 70 分）
17.（10 分）已知三角形的三个顶点是 A(4,0)，B(6,-7)，C(0,-3)．（1）求 BC 边上的中线所在直线的方程；（2）求 BC 边上的高所在直线的方程．
3
18.（12 分）如图，在四棱锥 P-ABCD 中，底面四边形 ABCD 满足 AD=2BC，且∠BAD= ∠ABC= 900 ，AB⊥PD，点 E 和 F 分别为棱 PD 和 AD 的中点．
9.直线 ax y a 0 与直线 x ay a 0 在同一坐标系中的图象可能是（）
A．
B．
C．
D．
10. 空间四边形 ABCD 中，AD=BC=2，E,F 分别为 AB,CD 的中点，EF= 3 ，则异面直线 AD 与 BC 所成的角为（）
A．120
B． 90
C． 60
D． 45
8
b a
16 a b
1 2
(8
2
b 16 a ) 1 (8 8) 8
ab 2
，
当且仅当，即 a 2 ， b 8 时取等号，
8
因此直线 l 的方程为为，即 4x y 8 0 ．
20、解：详解：（1）因为 P(1,-1)、Q(-1,1)．所以 PQ 中点坐标为(0,0)，直线 PQ 的斜率为,所以 PQ 的中垂线方程为 y=x，
2.直线 3x+my-1=0 与 4x+3y-n=0 的交点为(2，-1)，则 m+n 的值为 ( )
A．12
B．10
C．-8
D．-6
3.若 A(-2,3)，B(3,2)，C( 1 ,m)三点共线，则实数 m 的值为（） 2
A．2
B．

高三数学上学期第2周周考试题文试题

南溪区第二中2021届高三数学上学期第2周周考试题文制卷人：歐陽文化、歐陽理複；制卷時間：二O 二二年二月七日一、选择题{|0,}M x x x R =<∈，2{|20,}N x x x x R =+-=∈，那么MN =〔〕A ．φB ．{2}-C ．{1}D ．{2,1}-2. 复数z 满足方程i i z -=⋅2，那么z 在复平面上对应点位于〔〕 A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限3. 〕4. 0000sin 20sin 50cos160sin 40-的值是〔〕A ．B ．12- C. 12D 5.命题,p q ，“p ⌝为真〞是“p q ∧为假〞的 A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件ABC ∆中，,,a b c 分别是角,,A B C 的对边，4cos 5A =，2c =，ABC ∆的面积6S =，那么a 的值是〔〕A ．B ． D ．720.43a =，4log 0.3b =，4log 3c =，那么 ( )A ．a c b >>B ．b c a >> C. c a b >> D ．c b a >>8. 假设cos )4(απ-＝35，那么sin 2α＝( )A.725B.15C.－15D.－7259. 函数xx In x f 2)1()(-+=的零点所在的大致区间是〔〕 A ．〔0，1〕 B ．〔1，2〕 C ．〔2，e 〕 D ．〔3，4〕10.如图，从地面上C ，D 两点望山顶A ，测得它们的仰角分别为45°和30°，CD ＝100米，点C 位于BD 上，那么山高AB 等于( ) A ． 100米 B ．米 C ．米 D ．米11. 函数21()ln 12f x x x ax =+-+，以下结论中错误的选项是〔〕 A ．当2a =时，1x =是()f x 的一个极值点 B ．当22a -<<时，函数()f x 无极值C. 当2a >时，()f x 的极小值小于0 D ．,()a R f x ∀∈必有零点()()x f x xe k x R =-∈恰有两个零点，其中e 为自然对数的底数，那么实数k 的取值范围是〔〕A ． (,0)-∞B ．21(,2)e e - C. 1(,0)e- D ．2(0,2)e第二卷二、填空题〔每一小题5分，满分是20分，将答案填在答题纸上〕 13.函数f 〔x 〕=的定义域为14.设函数f 〔x 〕=x 3cosx+1，假设f 〔a 〕=11，那么f 〔﹣a 〕= ． 15.sin α＋2cos α＝0，那么2sin αcos α－cos 2α的值是________. 16.某同学在研究函数2()()1xf x x x =∈+R 时，分别得出如下几个结论：①等式()()0f x f x -+=在x ∈R 时恒成立；②函数()f x 的值域为〔-2，2〕；③假设12x x ≠，那么一定有12()()f x f x ≠；④函数x x f x h 2)()(-=在R 上有三个零点。

2021年高三上学期中段考试数学(文)试题含答案

2021年高三上学期中段考试数学（文）试题含答案选择题：本大题共10小题，每小题5分，满分50分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．的值为 ( ) A ．B ．C ．D ．2．设全集(){}{},30,1,U R A x x x B x x ==+<=<-集合集合则右图中阴影部分表示的集合为（） A. B. C. D.3. 条件P ：x <-1，条件Q ：x <-2，则P 是Q 的（）A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件4.．在复平面内为坐标原点, 复数与分别对应向量和,则=（） A. B. C. D.5. 函数的定义域是（） A ．（，） B ．(，） C ．(，1） D ．(，）6.. 已知函数，且，则的值是（） A. B. C. D.7.奇函数满足，且当时，，则的值为（）A. 8B.C.D.8．当时，下列大小关系正确的是( )A. B. D. D.9．客车从甲地以60km/h的速度匀速行驶1小时到达乙地，在乙地停留了半小时，然后以80km/h的速度匀速行驶1小时到达丙地．下列描述客车从甲地出发，经过乙地，最后到达丙地所经过的路程与时间之间关系的图象中，正确的是（）10．观察下列事实|x|+|y|=1的不同整数解（x,y）的个数为4 ， |x|+|y|=2的不同整数解（x,y）的个数为8， |x|+|y|=3的不同整数解（x,y）的个数为12 ….则|x|+|y|=20的不同整数解（x，y）的个数为（）A.76B.80C.86D.92二、填空题：本大题共4小题，考生作答4小题，每小题5分，满分20分．11．已知△ABC中，角A、B、C的对边分别为、、c且，，，则 .12．执行如右图所示的程序框图，若输入的值为6，则输出的值为13．已知满足约束条件，则的最大值是14.已知是内任意一点，连结，，并延长交对边于，，，则，这是平面几何中的一个命题，运用类比猜想，对于空间四面体中,若四面体内任意点存在什么类似的命题三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．15．（本小题满分12分）已知向量，（1）求向量与向量的夹角；（2）若向量满足：①；②，求向量.16．（本题满分13分）已知：函数，为实常数．(1) 求的最小正周期；(2)在上最大值为3，求的值.17．（本小题满分13分）如图6，某测量人员，为了测量西江北岸不能到达的两点A，B之间的距离，她在西江南岸找到一个点C，从C点可以观察到点A，B；找到一个点D，从D点可以观察到点A，C；找到一个点E，从E点可以观察到点B，C；并测量得到数据：，，，，，DC=CE=1（百米）. （1）求 CDE的面积；（2）求A，B之间的距离.18.（本小题满分14分）已知函数，曲线在点处的切线为:，且时,有极值.（1）求的值；（2）求函数在区间上的最大值和最小值.19.（本小题满分14分）（1）已知是公差为的等差数列，是与的等比中项，求该数列前10项和；（2）若数列满足，，试求的值.20．（本小题满分14分）已知是实数，函数，如果函数在区间上有零点，求的取值范围．五校联考xx学年高三第一学期期中考试文科数学试题答题卡一、选择题（每题5分,共40分）二．填空题（每题5分，共30分）11._____________________ 12.____________________ 13._____________________ 14.____________________三．解答题（共80分）15.解：(1)(2)(2)17.解：(1) (2)(2)19.解：（1）（2）（2）一．选择题（每题5分,共50分）三．解答题（共80分）16.解： .............2分.............4分.............6分（2）由（1）得且由可得 .............8分.............10分则 .............11分.............13分18.解：切线的斜率，，将代入切线方程可得切点坐标，根据题意可联立得方程解得（2）由（1）可得，令，得或.极值点不属于区间,舍去.分别将代入函数得.19.解:(1)设数列的首项为,公差为,则.根据题意,可知道,即(解得(2)解法一:由,经化简可得...........2分...........4分...........6分...........7分...........8分...........9分...........10分...........11分...........12分...........13分...........14分...........1分...........3分...........4分...........6分...........7分...........9分数列是首项为,公差为的等差数列..解法二:分别把代入可得:,,,,, 因此,猜想. . 20解: 若，，显然在上没有零点，所以 ...2分令得当时，恰有一个零点在上； ...5分当即时，也恰有一个零点在上；...8分当在上有两个零点时，则()()208244011121010a a a a f f >⎧⎪∆=++>⎪⎪-<-<⎨⎪≥⎪⎪-≥⎩ 或()()208244011121010a a a a f f <⎧⎪∆=++>⎪⎪-<-<⎨⎪≤⎪⎪-≤⎩ ..12分解得或 ..13分因此的取值范围是或； ..14分...........10分 ...........13分 ...........14分 ...........10分 ...........13分 ...........14分_; 20779 512B 儫31773 7C1D 簝 38555 969B 際39894 9BD6 鯖b F"236684 8F4C 轌o。

四川省南溪二中2021届高三上学期期中考试语文试卷

语文一、现代文阅读（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成1～3题。

（9分）宋朝是一个重视传统文化的朝代，每一个节日都被宋人发挥到极致。

清明节是当时一个非常重要的节日。

人们扫墓、踏青、荡秋千、蹴鞠、斗鸡、放风筝，各种民俗活动内容丰富、形式多样，寄托了人们美好的愿望。

宋朝的清明节的最大亮点应该是蹴鞠。

《水浒传》中写高俅球技高超，因陪侍宋徽宗踢球，被提拔当了殿前都指挥使。

诗圣杜甫《清明》诗中说，“十年蹴鞠将雏远，万里秋千习俗同”。

诗人陆游《感旧四首》诗中有“路入梁州似掌平，秋千蹴鞠趁清明”的诗句。

这说明从唐朝到宋朝清明节都有踢球娱乐的习俗。

蹴鞠在宋代获得了极大的发展。

上层踢球已经是成为时尚，上海博物馆馆藏一幅《宋太祖蹴鞠图》，描绘的就是当时皇帝和大臣在踢球的情景。

宋代社会上还有了专门靠踢球技艺维持生活的足球艺人。

宋代的足球有用球门的对抗性比赛和不用球门的“白打”，但书上讲的大多都是白打踢法。

所谓“脚头十万踢，解数百千般”，就是指踢球花样动作和由几个花样组成的成套动作，指用头、肩、背、胸、膝、腿、脚等一套完整的踢技，使“球终日不坠”。

由此看来，宋代的足球，由射门比准向灵巧和控制球技术方面发展。

为了维护自身利益和发扬互助精神，宋代的踢球爱好者还组织了自己的团体，叫做“齐云社”，又称“圆社”。

《水浒传》中写到宋徽宗也是“齐云社”的成员。

这是专门的蹴鞠组织，专事负责蹴鞠活动的比赛组织和宣传推广。

宋代清明节还有一个习俗，就是市民携带炊饼出游踏青。

宋代民间，习惯把无馅的食品称为饼，用火烤的叫烧饼，蒸的叫蒸饼，面条叫汤饼，油炸的叫油饼。

宋仁宗赵祯做皇帝之后，因为宋仁宗的名字叫赵祯，而蒸饼的“蒸”字和赵祯的“祯”字发音相似，那时说话写字都讲究避皇帝或长辈的名讳，所以，蒸饼就改称为“炊饼”。

在当时的汴梁城里，炊饼是一种大众食品，大街小巷都有卖炊饼的。

宋朝把有馅的食品叫做馒头。

《水浒传》中武大郎每天早起，挑起做好的一担炊饼出门叫卖。

四川省宜宾市南溪区第二中学校2021届高三零诊(摸底)数学(文)试题

2022.12高三数学（文史类）摸底测试（考试时间120分钟，满分150分）姓名＿＿＿＿＿＿＿班级＿＿＿＿＿＿＿得分＿＿＿＿＿＿＿一、选择题．本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．复数31i i -等于（A ）1122i + （B ）1122i -- （C ）1122i-+ （D ）1122i -2．设全集U={1，2，3，4}，集合S={l ，3}，T={4}，则（SC U ）T 等于（A ）{2，4} （B ）{4}（C ）∅（D ）{1,3,4}3．函数)2ln(1x x y -+-=的定义域是（A ）[)+∞,1 （B ）()2,∞- （C ）()2,1 （D ）[)2,1 4．已知命题p ：x ∀∈R ，2x =5，则⌝p 为（A ）x ∀∉R,2x=5 （B ）x ∃∈R ，20x≠5（C ）x ∃∈R ，20x=5（D ）x ∀∈R,2x≠55．计算21og 63 +log 64的结果是（A ）log 62 （B ）2 （C ）log 63 （D ）36．已知a ，b 是两条不同直线，α是一个平面，则下列说法正确的是（A ）若a ∥b ．b α⊂，则a//α （B ）若a//α，b α⊂，则a ∥b （C ）若a ⊥α，b ⊥α，则a ∥b （D ）若a ⊥b ，b ⊥α，则a ∥α7．函数12log 1()1x x x f x e x ≥⎧⎪=⎨⎪ <⎩的值域为（A ）(,)e -∞- （B ）(,)e +∞ （C ） (,)e -∞ （D ）(,)e -+∞ 8．函数y ＝2x －x 2的图象大致是9．已知双曲线22221x y a b -=（a>0,b>0）的一条渐近线与圆(x －3)2+y 2=9相交于A 、B 两点，若|AB|=2，则该双曲线的离心率为（A ）8（B ）22（C ）3（D ）3210．已知函数)(x f y =的周期为2，当x ∈时2)(x x f =，那么函数)(x f y = 的图象与函数xy lg =的图象的交点共有（A ）11个（B ）10个（C ）9个（D ）8个第Ⅱ卷（非选择题，共100分）二、填空题：本大题共5小题，每小题5分，共25分，答案填在答题卡上。

四川省宜宾市南溪第二中学2021年高三数学理期末试题含解析

四川省宜宾市南溪第二中学2020-2021学年高三数学理期末试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 已知等比数列公比为，其前项和为，若、、成等差数列，则等于（）A．B．1 C．或1 D．参考答案：A2. 设，则A. B. C. D.参考答案：B本题考查指数与对数的比较大小。

，，，所以；选B。

3. 若不等式对于一切正数、恒成立，则实数的最小值为（）A 2BC D参考答案：D4. 函数f（x）=xsinx的图象大致是（）A．B．C． D．参考答案：A【考点】函数的图象．【专题】函数的性质及应用．【分析】利用函数的奇偶性排除选项，然后利用特殊值判断即可．【解答】解：函数f（x）=xsinx满足f（﹣x）=﹣xsin（﹣x）=xsinx=f（x），函数的偶函数，排除B、C，因为x∈（π，2π）时，sinx＜0，此时f（x）＜0，所以排除D，故选：A．【点评】本题考查函数的图象的判断，函数的奇偶性以及函数值的应用，考查分析问题解决问题的能力．5. 的（）A．充分不必要条件Ｂ．必要不充分条件C．充分必要条件D．既不充分又不必要条件参考答案：A或，所以充分不必要条件，选A.6. 若x∈A则∈A，就称A是伙伴关系集合，集合M={－1，0，，，1，2，3，4}的所有非空子集中，具有伙伴关系的集合的个数为A．15 B．16 C．28D．25参考答案：A7. 设，则等于（）A． B． C．D．参考答案：D8. 复数在复平面上对应的点的坐标为( )A．B．C．D．参考答案：B9. 函数图象的对称轴为，则的值为A．B．C．D．参考答案：D10. 若a+bi=（1+i）（2﹣i）（i是虚数单位，a，b是实数），则a+b的值是（）A．1 B．2 C．3 D．4参考答案：D【考点】复数代数形式的乘除运算．【专题】计算题．【分析】利用复数的运算法则和模的计算公式即可得出．【解答】解：∵a+bi=（1+i）（2﹣i）=3+i，∴a=3，b=1．∴a+b=3+1=4．故选D．【点评】熟练掌握复数的运算法则和模的计算公式是解题的关键．二、填空题:本大题共7小题,每小题4分,共28分11. 已知、满足以下约束条件，使取得最小值的最优解有无数个，则的值为__________．参考答案：∵，则，为直线在轴上的截距，要使目标函数的最优解有无穷多个，则截距最小时的最优解有无数个，∵，把平移，使之与可行域的边界重合即可，∴，．12. 已知，，且，共线，则向量在方向上的投影为__________．参考答案：【分析】根据向量共线求得；再利用求得结果.【详解】由与共线得：，解得：向量在方向上的投影为：本题正确结果：【点睛】本题考查向量共线定理、向量在方向上的投影的求解问题，属于基础题.13. 已知函数.若对所有都有，则实数的取值范围为参考答案：14. 设偶函数的部分图象如图所示△KLM为等腰直角三角形，,KL=1，则的值为.参考答案：15. 若非零向量满足,则夹角的余弦值为_______参考答案：16. 已知A n={x|2n＜x＜2n+1，x=3m，m∈N+}，若|A n|表示集合A n中元素的个数则|A1|+|A2|+|A3|+…+|A10|= ．参考答案：682【考点】数列的求和．【专题】等差数列与等比数列．【分析】A n={x|2n＜x＜2n+1，x=3m，m∈N+}，可得A1═{x|2＜x＜22，x=3m，m∈N+}={3}，|A1|=1；A2={x|22＜x＜23，x=3m，m∈N+}={6}，|A2|=1；A3={x|23＜x＜24，x=3m，m∈N+}={9，12，15}，|A3|=3；…，A10={x|210＜x＜211，x=3m，m∈N+}={1026，1029，…，2046}，|A10|=301．由于3，6，9，…，2046，组成等差数列{a n}，首项为3，公差为3，即可得出个数．【解答】解：∵A n={x|2n＜x＜2n+1，x=3m，m∈N+}，∴A1═{x|2＜x＜22，x=3m，m∈N+}={3}，∴|A1|=1；A2={x|22＜x＜23，x=3m，m∈N+}={6}，∴|A2|=1；A3={x|23＜x＜24，x=3m，m∈N+}={9，12，15}，∴|A3|=3；A4={x|24＜x＜25，x=3m，m∈N+}={18，21，24，27，30}，∴|A2|=5；…，A10={x|210＜x＜211，x=3m，m∈N+}={1026，1029，…，2046}，∴|A10|=301．由于3，6，9，…，2046，组成等差数列{a n}，首项为3，公差为3，∴2046=3+3（n﹣1），解得n=682．∴|A1|+|A2|+|A3|+…+|A10|=682．故答案为：682．【点评】本题考查了等差数列的通项公式、指数幂的运算性质，考查了推理能力与计算能力，属于中档题．17. 在棱长为的正方体中,是的中点, 若都是上的点, 且，是上的点, 则四面体的体积是参考答案：三、解答题：本大题共5小题，共72分。

高中教学协作体高三数学上学期期中联考试题文试题(共10页)

局部(júbù)示范高中教学协作体2021年秋期中联考高三〔文科〕数学〔全卷满分是：150分考试用时：120分钟〕一．选择题：〔本大题一一共12小题，每一小题5分，一共60分．在每一小题给出的四个选项里面，只有一项是哪一项满足题目要求的．〕1.集合A＝{x|－1≤x≤1}，B＝{x|x2－2x<0}，那么A∪(∁R B)＝( )A．[0,1] B．(－∞，1]∪[2，＋∞)C．[－1,0]D．[1,2]2.条件p：x＋y≠2，条件q：x，y不都是1，那么q是p的( )A．充分不必要条件B．充要条件C．必要不充分条件D．既不充分也不必要条件f(x)＝x2-4x＋3，x∈[－4, 6]．那么f(x)的值域为〔〕A. [15,35]B. [-1,35]C. [-1,15]D. [3,15]4．如图，在直角坐标系xOy中，射线OP交单位圆O于点P，假设∠AOP＝θ，那么点P的坐标是( )A．(－，)B． (sinθ，cosθ)C．(－cosθ，sinθ)D． (cosθ，sinθ)5.在等差数列{a n}中，a2＋a4＝15－a3，S n表示数列{a n}的前n项和，那么S5＝( )A．5 B．15 C．25 D．756.函数(hánshù)＝sin(ωx ＋φ)+1(ω>0，|φ|<π2)的最小正周期为4π，且对任意x∈R ，都有()f x ≤成立，那么()f x 图象的一个对称中心的坐标是( )A. B. C. D.7.函数f (x )为奇函数，对任意x ∈R ，都有f (x ＋6)=f (x )，且f (2)＝4，那么f (2 014)＝( )A ．－4B ．－8C ．0D ．－168.△ABC 的三个内角A ，B ，C 的对边分别为a ，b ，c ，假设，那么该三角形的形状是( )A ．直角三角形或者等腰三角形B ．等腰直角三角形C ．等边三角形D ．直角三角形9.函数f (x )＝，那么该函数的单调递增区间为( ) A ．(－∞，1] B ．[-1，1) C ．(1，3]D ．[1，＋∞)10.y ＝f (x )为(0，＋∞)上的可导函数，且有＋>0，那么对于任意的a ，b ∈(0，＋∞)，当b >a 时，有( )A ． af (b )>bf (a )B ．af (b )<bf (a )C ． af (a )<bf (b )D ．af (a )>bf (b )11.函数(a >0，且a ≠1)，假设数列{a n }满足a n ＝f (n )(n ∈N *)，且是递增数列，那么实数a 的取值范围是( )A ．(1,3) B. (0,1) C ．D ．(2,3)12.设f (x )＝|ln x |，假设(jiǎshè)函数f (x )－ax=0在区间(0,4)上有三个根，那么实数a 的取值范围是( )A. ⎝ ⎛⎭⎪⎫ln 22，1eB. ⎝ ⎛⎭⎪⎫0，ln 22C. ⎝ ⎛⎭⎪⎫0，1eD. ⎝ ⎛⎭⎪⎫ln 22，e二、填空题〔本大题一一共4个小题，每一小题5分，一共计20分，将答案填在答题纸上〕 13.，是方程x 2-33x ＋4＝0的两根，且∈⎝ ⎛⎭⎪⎫－π2，π2，那么＝________.14.在数列{a n }中，a 1＝2，a n ＋1＝3a n ，S n 为{a n }的前n 项和．假设S n ＝242，那么n ＝________.15．命题p ：；命题q ：.假设命题“p ∨q 〞是真命题，那么实数a 的取值范围为________．16. 假设函数在区间上有极值点,那么实数a 的取值范围是 .三、解答题〔本大题一一共(y īg òng)70分. 解容许写出文字说明，证明过程或者演算步骤〕17. 〔本小题10分〕命题：函数()f x 为定义在上的单调递减函数，实数m 满足不等式. 命题：当x ∈时,方程有解.求使“p 且q 〞为真命题的实数m 的取值范围.18.〔本小题12分〕函数f (x )＝2sin x sin ⎝⎛⎭⎪⎫x ＋π6.(1)求函数f (x )的对称轴和单调递增区间； (2)当x ∈时，求函数f (x )的值域．19.〔本小题12分〕函数f (x )＝x +a ln x (a ∈R)．(1)当a ＝2时，求曲线y ＝f (x )在点A (1，f (1))处的切线方程； (2)求函数f (x )的极值．20.〔本小题12分〕设△ABC 的内角(nèi jiǎo)A ，B ，C 的对边分别为a ，b ，c ，b ＝a tanB ，且A 为钝角．(1)证明：A －B ＝π2；(2)求sin B ＋sin C 的取值范围．21.〔本小题满分是12分〕二次函数的图象经过坐标原点，其导函数为，数列{}n a 的前n 项和为S n ，点(n ，S n )(n ∈N *)均在函数()y f x =的图象上．(1)求数列{a n }的通项公式； (2)设b n ＝，试求数列{b n }的前n 项和T n .22．〔本小题12分〕函数(hánshù)f (x )＝x －(a ＋1)ln x －a x (a ∈R)，g (x )＝12x 2＋e x －x e x.(1)当x ∈[1，e 2]时，求f (x )的最小值；(2)当a <1时，假设存在x 1∈[e ，e 2]，使得对任意的x 2∈[－1,0]，f (x 1)<g (x 2)恒成立，求a 的取值范围．局部示范高中教学协作体2021年秋期中联考高三〔文科(w énk ē)〕数学参考答案一、选择题(本大题一一共12小题，每一小题5分，一共60分〕 1 2 3 4 5 6 7 8 9 10 11 12 BCBDCBADBCDA二、填空题(本大题一一共4小题，每一小题5分，一共20分〕 13、 2π314、5 15、(－∞，0]∪[1,+∞) 16、三．解答题(本大题一一共6小题，一共75分〕17.解：对于命题p :由函数f (x )为R 上的单调递减函数得解得………………………2分对于命题q :当x ∈时,sin x ∈[0,1],m=cos 2x-2sin x=-sin 2x-2sin x +1=-(sin x +1)2+2∈[-2,1], ………………………6分综上,要使“p 且q 〞为真命题,只需p 真q 真,即解得实数m 的取值范围是. ………………………10分18. 解：(1)f (x )＝2sin x ⎝ ⎛⎭⎪⎫32sin x ＋12cos x ＝3×1－cos 2x 2＋12sin 2x ＝sin ⎝ ⎛⎭⎪⎫2x －π3＋32. ………………2分所以函数f (x )的对称轴为x ＝. ………………………4分由－π2＋2k π≤2x －π3≤π2＋2k π，k ∈Z ，解得－π12＋k π≤x ≤5π12＋k π，k ∈Z ，所以函数f (x )的单调递增区间是⎣⎢⎡⎦⎥⎤－π12＋k π，5π12＋k π，k ∈Z. (7)分(2)当x ∈,62ππ⎡⎤⎢⎥⎣⎦时，2x －π3∈，sin ⎝⎛⎭⎪⎫2x －π3∈，………………………10分f (x )∈. ………………………11分故f (x )的值域为33,122⎡⎤+⎢⎥⎣⎦。

2021年高三上学期中段考试(数学文)

2021年高三上学期中段考试（数学文）一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.Ｍ＝，Ｎ＝，则集合ＭＮ＝ ( )A.{}B.{}C.{}D.{}2． =（）A． B． C． D．3.已知函数，则的值是 ( )A. 9B.C. -9D. -4.设且，则锐角x为( )A. B. C. D.5.已知等比数列的前三项依次为，，，则（）A．B．C．D．6．函数的零点一定位于下列哪个区间（）A. B. C. D.7，为得到函数的图像，只需将函数的图像（）A．向左平移个长度单位B．向右平移个长度单位C．向左平移个长度单位 D．向右平移个长度单位8.函数的图象大致是 ( )9. 已知定义在正整数集上的函数满足条件：，,,则的值为（）A．－2 B． 2 C．4 D．－4 10.设奇函数在上为增函数，且，则不等式的解集为( ) A．B．C ．D ．二、填空题：本大题共5小题，每小题5分，满分20分．其中14～15是选做题，考生只能选做一题，两题全答的，只计算前一题得分．11．设曲线在点处的切线与直线垂直，则． 12. 函数的最小正周期为____________.13. 观察下式：1=12，2+3+4=32，3+4+5+6+7=52，4+5+6+7+8+9+10=72，…，则可得出一般结论： _________________________________________.14．（坐标系与参数方程选做题）把极坐标方程化为直角坐标方程是____________________； 15．（几何证明选讲选做题）如图，梯形，，是对角线和的交点，，则__________ .三、解答题：本大题共6小题，满分80分．解答须写出文字说明、证明过程和演算步骤．16．（本小题满分12分）设函数)( 1cos sin 32cos 2)(2R x x x x x f ∈-+=（Ⅰ）化简函数的表达式，并求函数的最小正周期和单调递增区间；（Ⅱ）若，求函数的最大值与最小值．17、（本小题满分12分）在递增等差数列中，已知，且、、成等比数列，． (1) 求数列的公差；(2) 设数列的前项和为，求的最值．18、（本小题满分14分）在△ABC 中，已知．(1) 求AB 边的长度； (2)证明：；（3）若,求．19、（本题满分14分）运货卡车以每小时千米的速度匀速行驶130千米（单位：千米/小时）．假设汽油的价格是每升2元，而汽车每小时耗油升，司机的工资是每小时14元. （1）求这次行车总费用关于的表达式；（2）当为何值时，这次行车的总费用最低，并求出最低费用的值．20、（本题满分14分）观察下面由奇数组成的数阵，回答下列问题：（Ⅰ）求第六行的第一个数．（Ⅱ）求第20行的第一个数．（Ⅲ）求第20行的所有数的和．21．(本题满分14分)设函数8)(,42)(223-+=-++=x ax x g x x x x f （1）求函数极值；（2）当恒成立，求实数a 的取值范围.广东省恩城中学xx 届高三上学期中段考试（数学文）参考答案一、选择题(每小题5分，共50分)二、填空题(每小题5分，共20分)11、___2____ 12、___π_____13、2(1)(2)(32)(21)n n n n n +++++⋅⋅⋅⋅⋅⋅+-=-19171513119753114、 15、 1：6三、解答题(共80分，16、17题12分，18-21题每小题14分)16、（本小题满分12分）设函数)( 1cos sin 32cos 2)(2R x x x x x f ∈-+=（Ⅰ）化简函数的表达式，并求函数的最小正周期和单调递增区间；（Ⅱ）若，求函数的最大值与最小值．解：（Ⅰ）∵…………………………… 2 分∴函数的最小正周期 …………………………… 4 分222,26236()[]36k x k k x k f x k k πππππππππππππ-≤+≤+∴-≤≤+-+的单调递增区间为，………………… 6 分（Ⅱ）∵， ∴ ……………………………7分∴∴ …………………………… 8分∴当时，即时…………………………… 10分当时，即时…………………………… 12分17、（本小题满分12分）在递增等差数列中，已知，且、、成等比数列，． (I)求数列的公差；(Ⅱ)设数列的前项和为，求的最值．解：(I)、、成等比数列……………………………… 2分……………………………… 4分整理得：，解得或……………………………… 5分又递增……………………………… 6分 (Ⅱ)由，得……………………………… 8分令得：，且……………………………… 11分所以前6项或者前7项的和最小，无最大值……………………………… 12分18、（本小题满分13分）在△ABC 中，已知．(1) 求AB 边的长度； (2)证明：；（3）若,求．CB A解：（1）∵∴2()||2AB BC AB AC AB AB AC AB ⋅=-=⋅-=-∵ ∴, 即AB 边的长度为----------------4分 (2) 由得--------------------①即--------------------②-----6分由①②得, 由正弦定理得 ∴∴-----------------------------------------------9分 (3) ∵，由（2）中①得由余弦定理得222||||||2||||cos BC AB AC AB AC A =+-⋅=∴=--------------------------------------------------------------------------14分19、（本题满分14分）运货卡车以每小时千米的速度匀速行驶130千米（单位：千米/小时）．假设汽油的价格是每升2元，而汽车每小时耗油升，司机的工资是每小时14元. （1）求这次行车总费用关于的表达式；（2）当为何值时，这次行车的总费用最低，并求出最低费用的值．解：（1）行车所用时间为 ………1分2130141302(2),[50,100]360x y x x x⨯=⨯⨯++∈ ………5分所以，这次行车总费用y 关于x 的表达式是（或：）…7分（2） ………10分当且仅当时，上述不等式中等号成立 ………12分当时，这次行车的总费用最低，最低费用为元………14分20、（本题满分14分）观察下面由奇数组成的数阵，回答下列问题：（Ⅰ）求第六行的第一个数．（Ⅱ）求第20行的第一个数．（Ⅲ）求第20行的所有数的和．解：（Ⅰ）第六行的第一个数为31……………2分（Ⅱ）∵第行的最后一个数是，第行共有个数，且这些数构成一个等差数列，设第行的第一个数是 ……………5分 ∴ ……………7分 ∴ …………9分191715131197531∴第20行的第一个数为381 ……………10分（Ⅲ）第20行构成首项为381，公差为2的等差数列，且有20个数设第20行的所有数的和为 ………………12分则 ……………14分21．(本题满分14分)设函数8)(,42)(223-+=-++=x ax x g x x x x f （1）求函数极值；（2）当恒成立，求实数a 的取值范围. （1）∵f (x )=x 3+2x 2+x —4∴=3x 2+4x +1，………………………………………………2分令=0，得x 1= —1,x 2= —.（2）设F(x )=f (x )—g(x )=x 3+(2—a )x 2+4x a x x F a x F a x x F x F )2(23)(02804)(02),0[0)(,),0[0)(2min min -+='∴<->=≥-+∞∈≥∴+∞≥若分显然若上恒成立在上恒成立在4)342()2()342(:0)342()(),0[0)(,3420)(,3420342,00)(23min 21≥+-⋅---≥-=+∞∈∴>'-><'-<<-==='a a a a F x F x x F a x x F a x a x x x F 即即可时当时当时当解得令解得a ≤5 ∴2<a ≤5………10分，当x =0时，F(x )=4∴a 的范围为…………1４分32646 7F86 羆 35325 89FD 觽 23716 5CA4 岤 . z24524 5FCC 忌7$26757 6885 梅37558 92B6 銶b。

四川省南溪二中2021届高三上学期期中试题

四川省南溪二中2021届高三历史上学期期中试题第Ⅰ卷一、选择题：每小题2，共48分。

在所给的四个选项中,只有一个答案是正确的.1．《礼记》载：“故天子有田以处其子孙，诸侯有国以处其子孙，大夫有采以处其子孙,是谓制度。

"该材料主要反映的制度是A．分封制 B．宗法制 C．郡县制 D．禅让制2A. A B。

B C。

C D. D3.宁波天一阁是我国现存最古老的私人藏书楼。

1984年，离乡多年的世界船王包玉刚回到宁波访问，在天一阁看到了馆藏的《包氏家谱》，意外发现自己是包拯的第29代嫡孙。

这段材料反映的是中国古代的A。

禅让制 B。

分封制 C. 宗法制 D. 郡县制4．《左传·昭公七年》:“天有十日，人有十等。

下所以事上，上所以共神也。

故王臣公，公臣大夫，大夫臣士，士臣皂”.上材料反映西周社会结构的基本特点是A．通过垄断神权强化王权 B．嫡长子拥有继承特权C．严格的等级关系 D．血缘纽带和政治关系紧密结合5。

史学家许倬云根据对春秋时期在政治上活动的516人和战国时期在政治上活动的713人所做的统计研究，发现后一个时期出身微贱的人的百分比两倍于前一个时期：春秋时期为26％，战国时期为55%。

比例增加说明A。

更多儒家思想家得到重用 B. 宗法分封制逐渐走向解体C. 世卿世禄制度被彻底打破D. 战国时普遍推行军功爵制6．“元元黎民，得免于战国。

"这句出自班固《汉书》的话,表明了秦统一的意义是：A．建立我国第一个统一的多民族国家B．使人们脱离了弱小诸侯国的统治C．为我国的长期统一奠定了基础D．使人民的生产生活有了安定的社会环境7．传说古代先王在阴历一月决定一年的政事，所以阴历一月叫政月。

到了秦朝，由于嬴政出生于一月,所以就把政月改为正月，并且“正”字的读音也改为“征”了.这主要说明了A．中央集权 B．规范法度C．皇权至上 D．君权神授8．《史记》：“……上佐天子理阴阳、顺四时；下抚万民明庶物；外镇四夷诸侯，内使卿大夫各尽职务。

四川省宜宾市南溪第二中学高一数学文联考试题含解析

四川省宜宾市南溪第二中学高一数学文联考试题含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 右图是某个四面体的三视图,该四面体的体积为（）A．72 B．36 C．24 D．12参考答案：D2. 圆台侧面的母线长为2a，母线与轴的夹角为30°，一个底面的半径是另一个底面半径的2倍．求两底面的面积之和是（）A．3πa2 B．4πa2 C．5πa2 D．6πa2参考答案：C【考点】L5：旋转体（圆柱、圆锥、圆台）．【分析】根据相似三角形求出上底面半径和a的关系，再计算两底面积之和．【解答】解：设圆台的母线AA′与圆台的轴OO′交于点S，则∠ASO=30°，设圆台的上底面半径为r，则SA′=2r，OA=2r，SA=4r，∴AA′=SA﹣SA′=4r﹣2r=2r=2a，∴r=a，∴圆台的上下底面积S=πr2+π（2r）2=5πr2=5πa2．故选C．3. 由直线上的一点向圆引切线，则切线长的最小值为A． B． C．D．参考答案：B4. 与函数f（x）=|x|表示同一函数的是（）A．f（x）=B．f（x）=C．f（x）=（）2 D．f（x）=参考答案：B【考点】判断两个函数是否为同一函数．【分析】根据两个函数的定义域相同，对应关系也相同，即可判断它们是同一函数．【解答】解：对于A，函数f（x）==|x|（x≠0），与函数f（x）=|x|（x∈R）的定义域不同，所以不是同一函数；对于B，函数f（x）==|x|（x∈R），与函数f（x）=|x|（x∈R）的定义域相同，对应关系也相同，所以是同一函数；对于C，函数f（x）==x（x≥0），与函数f（x）=|x|（x∈R）的定义域不同，对应关系也不同，所以不是同一函数；对于D，函数f（x）==x（x∈R），与函数f（x）=|x|（x∈R）的对应关系不同，所以不是同一函数．故选：B．【点评】本题考查了判断两个函数是否为同一函数的应用问题，是基础题目．5. 的解集是（）A．（5,4） B．（5，-4） C．{（-5,4）} D．{（5，-4）}参考答案：D略6. 设奇函数在上为增函数，且，则不等式的解集为( ) A． B． C． D．参考答案：D略7. 正方体ABCD－A1B1C1D1中，M为棱AB的中点，则异面直线DM与D1B所成角的余弦值为()A． B． C． D．参考答案：B8. 已知函数，则方程的解的个数为（）A. 4B. 5C. 6D. 7参考答案：B【分析】绘制函数f(x)和函数g(x)的图像，据此讨论可得方程的解的个数. 【详解】原问题等价于函数f(x)和函数g(x)的交点的个数，在平面直角坐标系中绘制函数f(x)和函数g(x)的图像如图所示，注意到当时，，且观察可得，交点个数为5个，故方程的解的个数为5.故选：B.9. 如果一个几何体的三视图如图所示（单位长度：cm），则此几何体的体积是（）A．B．C．D．参考答案：B10. 设，，，则下列结论中正确的是（）A. B. C. D.参考答案：D【分析】根据子集的定义可排除；由交集定义排除；根据补集和交集的定义可知正确.【详解】，错误；，则错误；，正确.本题正确选项：【点睛】本题考查集合间的关系、集合运算中的交集和补集运算，属于基础题.二、填空题:本大题共7小题,每小题4分,共28分11. 已知函数f（x）满足f（x+1）=x2+2x+2，则f（x）的解析式为．参考答案：f（x）=x2+1【考点】函数解析式的求解及常用方法．【专题】函数的性质及应用．【分析】方法一：凑配法：先将函数f（x+1）=x2+2x+2的右侧凑配成用x+1表示的形式，然后用x替换x+1，可得答案．方法二：换元法：令t=x+1，则x=t﹣1，换元整理后，可得f（t）=t2+1，然后用x替换t，可得答案．【解答】解：方法一：凑配法：∵f（x+1）=x2+2x+2=（x+1）2+1，∴f（x）=x2+1方法二：换元法：令t=x+1，则x=t﹣1∵f（x+1）=x2+2x+2∴f（t）=（t﹣1）2+2（t﹣1）+2=t2+1∴f（x）=x2+1故答案为：f（x）=x2+1【点评】本题考查的知识点是函数解析式的求解及常用方法，熟练掌握凑配法及换元法的方法，步骤及适用范围是解答的关键．12. 等差数列中，则_________.参考答案：10略13. 已知直线经过点（2，5），则_____________参考答案：-5略14. 函数y=log2（x+1）的定义域A= ．参考答案：（﹣1，+∞）【考点】函数的定义域及其求法．【专题】计算题．【分析】根据对数函数真数大于0，列出x+1＞0，再解出不等式．【解答】解：根据题意得x+1＞0，解得x＞﹣1，∴函数的定义域A=（﹣1，+∞），故答案为：（﹣1，+∞）．【点评】本题考查了对数函数定义域的求法，即令真数大于零进行求解即可．15. 一个正三棱柱的侧棱长和底面边长相等，体积为2，它的三视图中的俯视图如下图所示，侧视图是一个矩形，则这个矩形的面积是________．参考答案：216. 求过直线A斜率是的直线的一般方程______参考答案：略17. 幂函数的图象过点，则的解析式是_____________________.参考答案：三、解答题：本大题共5小题，共72分。

2021年高三数学上学期期中联考试题文新人教A版

2021年高三数学上学期期中联考试题文新人教A版（满分150分，考试时间：120分钟）选择题（本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

）1.设集合U={1，2，3，4}，A=｛1，2｝，B={2，4}，则等于（）A.{1，4}B.{1，3，4}C.{2}D.{3}2.已知复数 z 满足，则（）A. B. C. D.23.点在第二象限是角的终边在第三象限的（）A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.设是两个不同的平面，是一条直线，以下命题正确的是（）A.若，则B.若，则C.若，则D.若，则5.已知是等差数列，其前项和为，若，则=（）A.15B.14C.13D.126.已知向量满足的夹角为与则向量且bbb a,a)a(,2||,1|a|⊥+==（）0150.120.60.30.DCBA7.同时具有性质“①最小正周期是，②图象关于直线对称”的一个函数是 ( )A. B. C. D．8.x，y满足约束条件若取得最大值的最优解不唯一，则实数的值为（）A.或-1B.2或C.2或1D.2或-19.已知函数当时，有解，则实数的取值范围为（）A. B. C. D.10.已知椭圆与圆，若在椭圆上不存在点P，使得由点P所作的圆的两条切线互相垂直，则椭圆的离心率的取值范围是（）A. B. C. D.二、填空题(本大题共7小题，每小题4分，共28分。

)11.已知角的终边经过点（-4,3），则cos=__________12.某几何体的三视图如图所示，则该几何体的体积为____________13.设，则的值为14.设直线过点其斜率为1，且与圆相切，则的值为________15.函数的定义域为______________16.已知，若，则17.已知为偶函数，当时，，则满足的实数的个数有________个三、解答题(本大题共5小题，共72分。

四川省宜宾市南溪区第二中学校2021-2022学年高一上学期期中考试数学试题 Word版含答案

2021.10南溪二中高一上期期中考试试卷数学姓名___________ 班级__________ 成果__________（考试时间120分钟，满分150分，答案填写在答题卷上，只交答题卷）第Ⅰ卷（选择题共60分）一、选择题：本大题共12题，每小题5分,共60分.在每个小题给出的四个选项中，只有一项是符合题目要求的.1．下列命题正确的是（） A ．很大的实数可以构成集合 B ．自然数集N 中最小的数是1C ．集合}{1|2-=x y y 与集合}{1|)(2-=x y y x ，是同一个集合D ．空集是任何集合的子集.2. 设集合}{8,6,53，=A ，集合}{8,7,54，=B ，则=B A （） A ．}{8,5 B ．}{8,7,6,5,43，C ．}{6,3D ．}{7,4 3．若()1f x x =+，则=)7(f （） A ．2 B. 4 C. 22 D. 104．设集合}{1|->∈=x Z x A ，则（） A ． A ∅∉ B ．A ∈2 C ．2A ∈ D ．{}2⊆A5. 已知全集R U =，集合}{212|≤-≤-=x x M ，则=M C U （）A ．}{31|<<-x xB ．}{31|≤≤-x xC ．}{31|>-<x x x 或 D.}{31|≥-≤x x x 或6．下列图像中表示函数图像的是（）A. B. C. D.7. 设U ＝Z ，}{9,7,3,1，=A ，}{54,3,2,1，=B , 则右图中阴影部分表示的集合是（）A ．}{5,3,1B ．}{4,2C ．}{9,7D ．}{54,3,2,1，8．下列各组函数中，表示同一个函数的是（）A ．112--=x x y 与1+=x y B ．x y=与||x y =C ．||x y =与2x y = D ．12-=x y 与1-=x y9.下列函数定义域是R 且在区间)1,0(是递增函数的（）A ．|1|+=x yB ．x y =C ．xy 1=D ．42+-=x y10. )(x f 为奇函数，)(x g 为偶函数，且23)()(2++=-x x x g x f ,则)1(f 的值为（） A ．1 B. 3 C.4 D. 6 11. 已知函数[]1,0,4-)(2∈++=x a x x x f ，若)(x f 有最小值-2，则)(x f 的最大值为（） A ．-1 B. 0 C.1 D. 212.定义在R 上的偶函数)(x f ，当0>x 时，xx x f 2)(2-=，则)(,)2(,)5(πf f f -- 的大小为（） A ． )()5()2(πf f f <-<- B ．)2()5()(-<-<f f f π C ． )()2()5(πf f f <-<- D ．)5()()2(-<<-f f f π 第Ⅱ卷（非选择题共90分）二、填空题：本大题共4小题，每小题5分，共20分. 13.函数123)(-+-=x xx x f 的定义域为_________________（用区间表示）.14．已知函数⎩⎨⎧>≤≤-=2,220,4)(2x x x x x f ,若00()8,f x x ==则_________________.15.定义域为R 的奇函数)(x f 在区间[]6,3上是增函数，在区间[]6,3上的最大值为8，最小值为-1，则)3(2)6(-+-f f 的值为_________________.16.已知函数⎩⎨⎧>+--≤+-=1,)1(1,4)1()(2x x a x x a x a x f 为R 上的减函数，则实数a 的取值范围为_________________.x y 0 x y 0 x y 0 x y 0三、解答题：本大题共6小题，共70分.解答应写出必要的计算步骤、解答过程. 17.（本题满分10分）已知全集R U =，}{33|<≤-=x x A ，}{1|-≤=x x B 求：（1）B A ；（2）A C U ；（3）)()(B C A C U U18.（本题满分12分）已知全集R U =，}{3|-==x y x A ，}{71|≤≤=x x B ，{}|1C x x a =≥-（1）求A B ；B A （2）若A A C = ，求实数a 的取值范围.19.（本题满分12分）已知函数12)(2+-=x x f ．（1）用定义证明()f x 是偶函数；（2）用定义证明()f x 在(,0]-∞上是增函数；（3）求函数()f x 在[1,2]x ∈-时的最大值与最小值．20．(本题满分12分)已知函数1|1|2)(--=x x f（1）用分段函数的形式表示该函数；（2）画出该函数的图像；（3）写出该函数的定义域，值域.21．(本题满分12分)已知)(x f 是定义在R 上的奇函数，且0<x 时，xx x f 2)(2-= （1）求)0(f ，)1(f 的值；（2）求)(x f 的解析式.22. (本题满分12分)已知函数)0()(2>-=m mx x x f 在区间[]2,0上的最小值记为)(m g . （1）若40≤<m ，求函数)(m g 的解析式。