matlab实验十周期函数
matlab信号与系统实验报告
实验一 基本信号的产生与运算一、 实验目的学习使用MATLAB 产生基本信号、绘制信号波形、实现信号的基本运算。
二、 实验原理MATLAB 提供了许多函数用于产生常用的基本信号:如阶跃信号、脉冲信号、指数信号、正弦信号和周期方波等等。
这些信号是信号处理的基础。
1、 利用MATLAB 产生下列连续信号并作图。
(1)51),1(2)(<<---=t t u t x (2)300),32sin()(3.0<<=-t t e t x t (3)1.01.0,3000cos 100cos )(<<-+=t t t t x (4)2000),8.0cos()1.0cos()(<<=t t t t x ππ 答:(1)、>> t=-1:0.02:5; >> x=(t>1);>> plot(t,-2*x);>> axis([-1,5,-3,1]);>> title('杨婕婕 朱艺星'); >> xlabel('x(t)=-2u(t-1)');(2)、>> t=0:0.02:30;>> x=exp(-0.3*t).*sin(2/3*t);>> plot(t,x);>> title('杨婕婕朱艺星');>> xlabel('x(t)=exp(-0.3*t).*sin(2/3*t)');因为原函数在t=15后x(t)取值接近于零,所以将横坐标改成0到15,看得更清晰axis([0,15,-0.2,0.6]);(3)>> t=-0.1:0.01:0.1;x=cos(100*t)+cos(3000*t);plot(t,x);>> title('杨婕婕朱艺星');>>xlabel('x=cos(100*t)+cos(3000*t)');因为t的间隔取太大,以至于函数不够准确,缩小t的间隔:t=-0.1:0.002:0.2;x=cos(100*t)+cos(3000*t);plot(t,x);title('杨婕婕')>> t=-0.1:0.0001:0.1;x=cos(100*t)+cos(3000*t);>> plot(t,x);title('杨婕婕朱艺星');>> xlabel('x=cos(100*t)+cos(3000*t)');(4)、t=0:0.01:200;>> x=cos(0.1*pi*t).*cos(0.8*pi*t);>> plot(t,x);>> title('杨婕婕朱艺星');>> xlabel('x=cos(0.1*pi*t).*cos(0.8*pi*t)');因为为周期函数,可以将横坐标t间隔扩大以便于观察图像>> axis([0,30,-1,1]);2、利用MATLAB 产生下列离散序列并作图。
matlab软件仿真实验(信号与系统)(1)
matlab软件仿真实验(信号与系统)(1)《信号与系统实验报告》学院:信息科学与⼯程学院专业:物联⽹⼯程姓名:学号:⽬录实验⼀、MATLAB 基本应⽤实验⼆信号的时域表⽰实验三、连续信号卷积实验四、典型周期信号的频谱表⽰实验五、傅⽴叶变换性质研究实验六、抽样定理与信号恢复实验⼀MATLAB 基本应⽤⼀、实验⽬的:学习MATLAB的基本⽤法,了解 MATLAB 的⽬录结构和基本功能以及MATLAB在信号与系统中的应⽤。
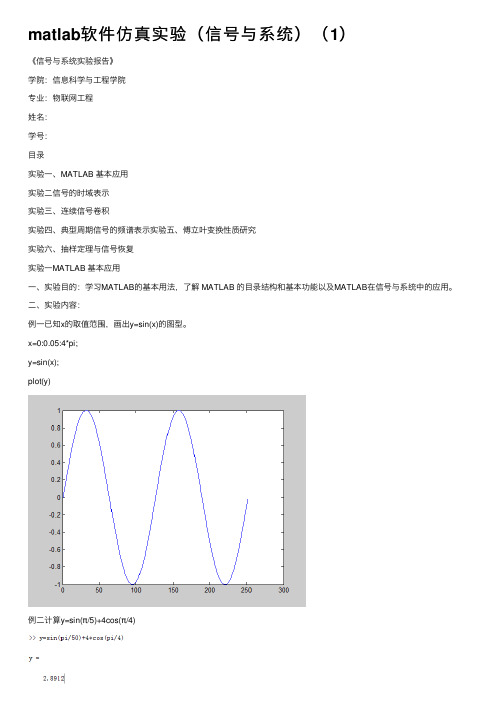
⼆、实验内容:例⼀已知x的取值范围,画出y=sin(x)的图型。
x=0:0.05:4*pi;y=sin(x);plot(y)例⼆计算y=sin(π/5)+4cos(π/4)例三已知z 取值范围,x=sin(z);y=cos(z);画三维图形。
z=0:pi/50:10*pi;x=sin(z);y=cos(z);plot3(x,y,z)xlabel('x')ylabel('y')zlabel('z')例四已知x的取值范围,⽤subplot函数绘图。
参考程序:x=0:0.05:7;y1=sin(x);y2=1.5*cos(x);y3=sin(2*x);y4=5*cos(2*x);subplot(2,2,1),plot(x,y1),title('sin(x)')subplot(2,2,2),plot(x,y2),title('1.5*cos(x)')subplot(2,2,3),plot(x,y3),title('sin(2*x)')subplot(2,2,4),plot(x,y4),title('5*cos(2*x)')连续信号的MATLAB表⽰1、指数信号:指数信号Ae at在MATLAB中可⽤exp函数表⽰,其调⽤形式为:y=A*exp(a*t) (例取 A=1,a=-0.4)参考程序:A=1;a=-0.4;t=0:0.01:10;ft=A*exp(a*t);plot(t,ft);grid on;2、正弦信号:正弦信号Acos(w0t+?)和Asin(w0t+?)分别由函数cos和sin表⽰,其调⽤形式为:A*cos(w0t+phi) ;A*sin(w0t+phi) (例取A=1,w0=2π,?=π/6) 参考程序:A=1;w0=2*pi; phi=pi/6; t=0:0.001:8;ft=A*sin(w0*t+phi);plot(t,ft);grid on ;3、抽样函数:抽样函数Sa(t)在MATLAB中⽤sinc函数表⽰,其定义为:sinc(t)=sin(πt)/( πt)其调⽤形式为:y=sinc(t)参考程序:t=-3*pi:pi/100:3*pi;ft=sinc(t/pi);plot(t,ft);grid on;4、矩形脉冲信号:在MATLAB中⽤rectpuls函数来表⽰,其调⽤形式为:y=rectpuls(t,width),⽤以产⽣⼀个幅值为1,宽度为width,相对于t=0点左右对称的矩形波信号,该函数的横坐标范围由向量t决定,是以t=0为中⼼向左右各展开width/2的范围,width的默认值为1。
matlab 数字信号处理 周期图 程序

1、假设一平稳随机信号为()()()0.81x n x n w n =-+,其中)(n w 是均值为0,方差为1的白噪声,数据长度为1024。
(1)、产生符合要求的)(n w 和)(n x ;(2)、给出信号x(n)的理想功率谱;(3)、编写周期图谱估计函数,估计数据长度N=1024及256时信号功率谱,分析估计效果。
(4)、编写Bartlett 平均周期图函数,估计当数据长度N=1024及256时,分段数L 分别为2和8时信号)(n x 的功率谱,分析估计效果。
解:思路在matlab 中提供的有 randn (m.n )函数,其为均值为零,方差为1的函数,所以w(n)可以通过随机序列randn(1,N)来产生,x(n)可以通过对 w(n)滤波产生,也可以直接由递推式迭代产生。
由于线性系统的输出功率谱等于输入功率谱乘以传递函数模的平方,X(n)可以看做w(n) 通过一线性系统的输出,H(z)=1/(1-0.8z)所以x(n)的理想功率谱2jw 2jw |)H(e |)P(e σ=直接产生Matlab 程序:>>clear;close all;F=500; %采样率N=1024; %观测数据>> subplot(2,1,1);w=sqrt(1)+randn(1,N);>> plot(w);>> xlabel ('观察次数');ylabel('功率db');title('白噪声w 的分布情况');>> subplot(2,1,2);>> x=[w(1) zeros(1,N-1)]; %初始化x(n),长度1024,x(1)=w(1)for i=2:Nx(i)=0.8*x(i-1)+w(i); %迭代产生观测数据x(n)end>> plot(x);>> xlabel('观测次数');ylabel('x 的分布情况');title('x的分布情况'); %% 理想功率谱cn=xcorr(x,x);%自相关函数Cn=fft(cn,N);%快速傅里叶变化Pxx=abs(Cn);%取绝对值index=0:round(N/2-1);k=index*Fs/N;pxx=10*log10(Pxx(index+1));%转换成dbfigure;plot(k,pxx);>> xlabel('频率');ylabel('功率db');>> title('理想功率谱');%%周期图谱%1024Pxx1=abs(fft(x)).^2/N;>> pxx1=10*log10(Pxx1(index+1));>> figure;>> plot(k,pxx1);>> title('周期图1024个点');>> xlabel('频率');ylabel('功率db');% 周期图256个观测点>> x1=x(1:4:N);>> Pxx2=abs(fft(x1,1024)).^2/N;>> pxx2=10*log10(Pxx2(index+1));>> figure;>> plot(k,pxx2);>> title('周期图256');xlabel('频率'); ylabel('功率db');%%L=2 N=1024>> L=2;>> x1=x(1:L:N);>> x2=x(2:L:N);>> pxx2_1=abs(fft(x1,1024)).^2/length(x1);>> pxx2_2=abs(fft(x2,1024)).^2/length(x2);>> pxx_2=(pxx2_1+pxx2_2)/L;>> figure;>> subplot(2,1,1);>> plot(k,10*log10(pxx_2(index+1)));>> title('N=1024,L=2时的周期图');>> xlabel('频率');>> ylabel('功率db');>> L1=8;%当数据长度为8时x3=zeros(L1,N/L1);for i=1:L1x3(i,:)=x(i:L1:N);end>> pxx3=zeros(L1,N);for i=1:L1pxx3(i,:)=abs(fft(x3(i,:),1024)).^2/length(x3(i,:)); end>> for i=1:1024Pxx3(i)=sum(pxx3(:,i))/L1;end>> subplot(2,1,2);plot(k,10*log10(Pxx3(index+1)));title('N=1024,L=8时的周期图');xlabel('频率');ylabel('功率db');当长度为256时,指针函数发生变化clear;close all;Fs=500; %采样率N=256; %观测数据w=sqrt(1)+randn(1,N); %x=[w(1) zeros(1,N-1)];for i=2:Nx(i)=0.8*x(i-1)+w(i);endindex=0:round(N/2-1);k=index*Fs/N;>> L=2;>> x1=x(1:L:N);>> x2=x(2:L:N);>> pxx2_1=abs(fft(x1,1024)).^2/length(x1); >> pxx2_2=abs(fft(x2,1024)).^2/length(x2); >> pxx_2=(pxx2_1+pxx2_2)/L;>> figure;>> subplot(2,1,1);>> plot(k,10*log10(pxx_2(index+1)));>> title('N=256,L=2时的周期图');>> xlabel('频率');>> ylabel('功率db');>> L1=8;%当数据长度为8时x3=zeros(L1,N/L1);for i=1:L1x3(i,:)=x(i:L1:N);end>> pxx3=zeros(L1,N);for i=1:L1pxx3(i,:)=abs(fft(x3(i,:),1024)).^2/length(x3(i,:)); end>> for i=1:1024Pxx3(i)=sum(pxx3(:,i))/L1;end>> subplot(2,1,2);plot(k,10*log10(Pxx3(index+1)));title('N=256,L=8时的周期图');xlabel('频率');ylabel('功率db');结果:理想功率谱:长度为256跟长度为1024时候的周期图谱:N=1024时,当L=2与L=8时的周期图当N 的长度为256时,L=2与L=8时的周期图谱从上面的图像可以看出, 周期图法得到的功率谱估计, 谱线的起伏较大, 即估计所得的均方误差较大。
最新matlab函数大全最完整版资料

MATLAB函数大全Matlab有没有求矩阵行数/列数/维数的函数?ndims(A)返回A的维数size(A)返回A各个维的最大元素个数length(A)返回max(size(A))[m,n]=size(A)如果A是二维数组,返回行数和列数nnz(A)返回A中非0元素的个数MATLAB的取整函数:fix(x), floor(x) :,ceil(x) , round(x) (1)fix(x) : 截尾取整.>> fix( [3.12 -3.12])ans =3 -3(2)floor(x):不超过x 的最大整数.(高斯取整)ans =3 -4(3)ceil(x) : 大于x 的最小整数>> ceil( [3.12 -3.12])ans =4 -3(4)四舍五入取整>> round(3.12 -3.12)ans =ans =3 -3>>如何用matlab生成随机数函数rand(1)rand(n):生成0到1之间的n阶随机数方阵rand(m,n):生成0到1之间的m×n的随机数矩阵(现成的函数)另外:Matlab随机数生成函数betarnd 贝塔分布的随机数生成器binornd 二项分布的随机数生成器chi2rnd 卡方分布的随机数生成器exprnd 指数分布的随机数生成器frnd f分布的随机数生成器gamrnd 伽玛分布的随机数生成器geornd 几何分布的随机数生成器hygernd 超几何分布的随机数生成器lognrnd 对数正态分布的随机数生成器nbinrnd 负二项分布的随机数生成器ncfrnd 非中心f分布的随机数生成器nctrnd 非中心t分布的随机数生成器ncx2rnd 非中心卡方分布的随机数生成器normrnd 正态(高斯)分布的随机数生成器poissrnd 泊松分布的随机数生成器raylrnd 瑞利分布的随机数生成器trnd 学生氏t分布的随机数生成器unidrnd 离散均匀分布的随机数生成器unifrnd 连续均匀分布的随机数生成器weibrnd 威布尔分布的随机数生成器一、MATLAB常用的基本数学函数abs(x):纯量的绝对值或向量的长度angle(z):复数z的相角(Phase angle)sqrt(x):开平方real(z):复数z的实部imag(z):复数z的虚部conj(z):复数z的共轭复数round(x):四舍五入至最近整数fix(x):无论正负,舍去小数至最近整数floor(x):地板函数,即舍去正小数至最近整数ceil(x):天花板函数,即加入正小数至最近整数rat(x):将实数x化为分数表示rats(x):将实数x化为多项分数展开sign(x):符号函数(Signum function)。
(完整版)MATLAB常用函数总结,推荐文档

MATLAB 常用函数总结Matlab 的内部常数pi 圆周率exp(1)自然对数的底数ei 或j虚数单位Inf 或 inf无穷大Matlab 的常用内部数学函数指数函数exp(x)以e 为底数log(x)自然对数,即以e 为底数的对数log10(x)常用对数,即以10为底数的对数对数函数log2(x)以2为底数的x 的对数开方函数sqrt(x)表示x 的算术平方根绝对值函数abs(x)表示实数的绝对值以及复数的模sin(x)正弦函数cos(x)余弦函数tan(x)正切函数cot(x)余切函数sec(x)正割函数三角函数(自变量的单位为弧度)csc(x)余割函数反三角函数asin(x)反正弦函数acos(x)反余弦函数atan(x)反正切函数acot(x)反余切函数asec(x)反正割函数acsc(x)反余割函数sinh(x)双曲正弦函数cosh(x)双曲余弦函数tanh(x)双曲正切函数coth(x)双曲余切函数sech(x)双曲正割函数双曲函数csch(x)双曲余割函数asinh(x)反双曲正弦函数acosh(x)反双曲余弦函数atanh(x)反双曲正切函数acoth(x)反双曲余切函数asech(x)反双曲正割函数反双曲函数acsch(x)反双曲余割函数求角度函数atan2(y,x)以坐标原点为顶点,x轴正半轴为始边,从原点到点(x,y)的射线为终边的角,其单位为弧度,范围为(,]gcd(a,b)两个整数的最大公约数数论函数lcm(a,b)两个整数的最小公倍数排列组合函数factorial(n)阶乘函数,表示n的阶乘real(z)实部函数imag(z)虚部函数复数函数abs(z)求复数z的模angle(z)求复数z 的辐角,其范围是( ,]conj(z)求复数z 的共轭复数ceil(x)表示大于或等于实数x 的最小整数floor(x)表示小于或等于实数x 的最大整数求整函数与截尾函数round(x)最接近x 的整数max([a ,b ,c ,...])求最大数最大、最小函数min([a ,b ,c ,..])求最小数符号函数sign(x)Matlab 中的数学运算符a+b 加法 a./b 数组右除a-b 减法 a.\b 数组左除a*b 矩阵乘法a^b 矩阵乘方a.*b 数组乘法 a.^b 数组乘方a/b 矩阵右除-a负号a\b矩阵左除' 共轭转置.'一般转置Matlab 的关系运算符 ==等于<小于>大于<=小于或等于>=大于或等于~=不等于如何用matlab求阶乘factorial(n) 求n的阶乘如何用matlab进行多项式运算(1)合并同类项 syms 表达式中包含的变量 collect(表达式,指定的变量)(2)因式分解 syms 表达式中包含的变量 factor(表达式)(3)展开syms 表达式中包含的变量 expand(表达式)(4)化简syms 表达式中包含的变量simplify(表达式) 如何用matlab进行复数运算 a+b*i 或 a +b*j表示复数a+bi 或 a+bjreal(z)求复数z的实部imag(z)求复数z的虚部abs(z)求复数z的模angle(z)求复数z的辐角,conj(z)求复数z的共轭复数exp(z)复数的指数函数,表示e^z如何用Matlab求集合的交集、并集、差集和补集 union(A,B)求集合A和B的并集intersect(A,B)求集合A和B的交集setdiff(A,B)求集合A和B的差集A-Bsetdiff(U,A)求集合A关于全集U的补集如何用matlab排序sort(v) 将向量v的元素从小到大排列(升序排列)sort(v,dim,’descend or ascend’)当dim=1时矩阵按列排序,descend or ascend用来控制升序还是降序当dim=2时矩阵按行排序,descend or ascend用来控制升序还是降序如何用Matlab求极限(1)极限:syms xlimit(f(x), x, a)求f(x)关于x趋于a时的极限(2)单侧极限:左极限:syms x limit(f(x), x, a,’left’)求f(x)关于x趋于a时的左极限右极限:syms x limit(f(x), x, a,’right’)求f(x)关于x趋于a时的右极限如何用Matlab求导数diff('f(x)') diff('f(x)','x') 求f(x)关于x的导数或者:syms x diff(f(x))syms x diff(f(x), x)如何用Matlab求高阶导数如何用Matlab求高阶导数diff('f(x)',n) diff('f(x)','x',n)求f(x)关于x的n阶导数syms x diff(f(x),n)syms x diff(f(x), x,n)如何用Matlab求不定积分int('f(x)') int ('f(x)','x')求f(x)关于x的积分syms x int(f(x))syms x int(f(x), x)如何用Matlab求定积分、广义积分int('f(x)',a,b) int ('f(x)','x',a,b)求f(x)关于x的积分,区间为a到b syms x int(f(x),a,b)syms x int(f(x), x,a,b)如何用Matlab展开级数syms x taylor(f(x), x, n,)a如何在Matlab中进行积分变换syms s tlaplace( f(t), t, s ) 拉普拉斯变换ilaplace( F(s), s, t ) 拉普拉斯变换的逆变换 syms t ωfourier( f(t), t, ω)傅立叶变换ifourier( F(ω), ω, t ) 傅立叶变换的逆变换 syms n zztrans( f(n), n, z) Z变换iztrans( F(z), z, n ) Z变换的逆变换 如何用Matlab解微分方程dsolve('微分方程','自变量')dsolve('微分方程','初始条件或边界条件','自变量') dsolve('D2x+2*x+x=sin(t)','x(0)=1','Dx(0)=1','t')如何用matlab求多变量函数的极限 以两个变量为例说明,多于两个变量的函数极限可以依次类推。
周期函数解读

实验十 周期函数【实验目的】1. 了解几周期函数的基本概念。
2. 了解周期函数经过四则运算、复合运算、求导运算、积分运算后的周期性。
3. 学习掌握MATLAB 软件有关的命令。
【实验内容】从图形上观测六个三角函数的周期性【实验准备】1.周期函数的基本概念函数)(x f 是以T 为周期的周期函数是指对任何x ,有)()(x f T x f =+.使得上式成立的最小正数T 称为函数的最小正周期。
2.周期函数的四则运算若)(),(x g x f 都是周期函数,一般地,他们的和(差)积商都未必再是周期函数。
例如][)(x x x f -=在),(+∞-∞以11=T 为最小正周期,x x g sin )(=在),(+∞-∞以π=2T 为最小正周期,但)()(x g x f +并非周期函数。
事实上,对任意实数0>a ,总有.0)0()0()()(=+>+g f a g a f但我们有如下具有一般意义的结论:若)(),(x g x f 都是周期函数,具有正周期21,T T ,且21T T 为有理数,则 )0)(()()(),()(),()(≠±x g x g x f x g x f x g x f 仍是周期函数。
事实上,设q p qpT T ,,21=是互质的自然数,则可以证明21pT qT T ==是)(),(x g x f 的周期,从而是经过四则运算后函数的周期。
3.周期函数的最小正周期一般说来,周期函数未必有最小正周期。
例如,常值函数c x f =)(显然是没有最小正周期的,事实上,容易证明任何实数T 都是)(x f 的周期。
然而,非常值的周期函数也未必有最小正周期,例如⎩⎨⎧-=是理数,是有理数x x x g 1,1)( 由于有理数与有理数(无理数)之和必为有理数(无理数),因此任何一个有理数都是)(x g 的周期,显然)(x g 没有最小正周期。
但我们有如下具有普遍意义的结论:非常值函数M x x f y ∈=),(,如果在M 的某聚点处有一单边有限或无限的极限,则)(x f 必有最小正周期。
MATLAB自相关编写及周期函数分析

MATLAB自相关编写及周期函数分析自相关是一种描述信号之间相似性的统计方法,主要用于分析时间序列数据。
在MATLAB中,可以使用`xcorr`函数来计算自相关。
周期函数是一种以固定时间间隔重复的函数,可以通过分析函数的振幅、相位和频率来研究其周期性。
下面我将介绍如何在MATLAB中编写自相关程序,并进行周期函数的分析。
首先,我们来编写一个自相关的程序。
考虑一个包含2个正弦波的信号,我们可以使用`sin`函数生成这个信号。
程序的步骤如下:1.定义一个时间向量t,表示信号的采样时间点。
例如,可以设置t 从0到10,采样间隔为0.01```t=0:0.01:10;```2. 定义两个正弦波信号,分别表示频率为2Hz和5Hz的信号。
可以使用`sin`函数生成这些信号。
```x1 = sin(2*pi*2*t);x2 = sin(2*pi*5*t);```3.将这两个信号相加,得到包含两个正弦波的信号。
```x=x1+x2;```4. 使用`xcorr`函数计算信号的自相关。
```[R, lags] = xcorr(x);```其中,`R`表示自相关系数,`lags`表示时间延迟。
接下来,我们将进行周期函数的分析。
考虑一个三角波函数,其周期为T,可以使用以下方式来表示:```t=0:0.01:10;T=2;f = sawtooth(2*pi/T*t);plot(t, f);```这段代码中,`sawtooth`函数用于生成三角波形,`plot`函数用于绘制信号。
为了了解周期函数的频域特性,我们可以使用傅里叶变换来获得其频谱。
在MATLAB中,可以使用`fft`函数进行快速傅里叶变换,并使用`abs`函数取绝对值得到频谱幅值。
代码如下:```Fs=100;%采样率N = length(f); % 信号长度frequencies = 0:Fs/N:Fs/2; % 频率向量transformed = fft(f); % 快速傅里叶变换amplitude = abs(transformed(1:N/2+1)); % 幅值谱plot(frequencies, amplitude);```这段代码中,`Fs`表示采样率,`N`表示信号长度,`frequencies`表示频率向量,`transformed`表示傅里叶变换结果,`amplitude`表示频谱幅值。
MATLAB函数的使用方法及示例详解

MATLAB函数的使用方法及示例详解引言:MATLAB是一种用于算法开发、数据可视化、数据分析和数值计算的强大工具。
它不仅具备丰富的内置函数库,还可由用户编写函数,以满足各种复杂的计算需求。
本文将详细介绍MATLAB函数的使用方法,并通过示例来解释其具体应用。
一、MATLAB函数的定义与调用在MATLAB中,函数是一段封装了特定操作的可重复使用的代码,它可以接受输入参数,并返回输出结果。
函数的定义与调用是使用MATLAB的重要基础。
函数的定义:MATLAB中函数的定义以关键词"function"开头,后面跟着函数名和一对圆括号。
函数名用于函数的调用,圆括号内可定义输入参数。
函数体代码位于圆括号之后,用于实现函数的具体功能。
举个例子,定义一个简单的函数用于计算两个数的和:```function result = add(a, b)result = a + b;end```在这个例子中,`add`是函数名,`a`和`b`是输入参数,`result`是输出结果。
函数的调用:函数的调用通过函数名和相应的参数实现。
调用函数时,需要提供参数的值。
调用函数后,函数会执行其功能,并返回结果。
我们使用上面定义的`add`函数来进行示例调用:```x = 3;y = 5;sum = add(x, y);disp(sum);```在这个例子中,我们定义了两个变量`x`和`y`,分别赋值为3和5,然后调用`add`函数,并将结果赋值给变量`sum`。
最后,使用`disp`函数显示`sum`的值。
二、MATLAB内置函数的使用方法MATLAB提供了丰富的内置函数库,涵盖了数学、统计、信号处理、图像处理等各个领域。
下面我们将介绍几个常用的内置函数及其使用方法。
1. `sin`函数:`sin`函数用于计算给定角度的正弦值。
其使用方法为:```result = sin(angle);```其中,`angle`为角度的值,`result`为计算得到的正弦值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验十周期函数
【实验目的】
1.了解周期函数的基本概念。
2.了解周期函数经过四则运算、复合运算、求导运算、积分运算后的周期性。
3.学习、掌握MATLAB软件有关命令。
【实验容】
从图形上观察六个三角函数的周期性。
【实验准备】
1.周期函数的基本概念
函数()
f x是以T为周期的周期函数是指对任何x,有
+=
()()
f x T f x
使得上式成立的最小正数T称为函数的最小正周期。
2.周期函数的四则运算
3.周期函数的最小正周期
【实验重点】
1、周期函数的四则运算与复合
2、周期函数的求导与积分运算
【实验难点】
1、最小正周期的确定
【实验方法与步骤】
练习 1 图形上观察六个三角函数
sinx,cosx,tanx,cotx,secx,cscx的周期性。
绘制正弦函数y=sinx 在区间[-6π,6π]的图形,相应的MATLAB代码为
>>x=-6*pi:2*pi/30:6*pi;
>>y=sin(x);
>>plot(x,y);
>>xlabel('x');ylabel('y');
运行结果见图10.1。
从图形中可以看出y=sinx为周期函数,最小正周期T≈6。
实际上,最小正周期T=2π=6.28…。
同样,可以画出余弦函数y=cosx的图形,见图10.2,其最小正周期也为T=2π。
画正切函数y=tanx 的图形时,要注意函数在,0,1,2,...2x k k π
π=+=±±是不连续,所以我们只能分别绘出函数在区间(,),0,1,2,...22k k k ππ
ππ-+=±±的图形。
相应的MATLAB 代码为 >>x=-1.5:0.01:1.5;
>>x1=x-pi;x2=x+pi;
>>y=tan(x);y1=tan(x1);y2=tan(x2);
>>plot(x,y,x1,y1,x2,y2);
>>xlabel('x');ylabel('y');
运行结果见图10.3。
从图
10.3可看出,函数y=tanx 在每个区间(,),0,1,2, (22)
k k k ππππ-+=±±的图形是相同的,故其最小正周期为π。
同样,注意到余切函数y=cotx 在,0,1,2,...x k k π==±±上不连续,可画出函数在各个区间(,(1)),0,1,2,...k k k ππ+=±±上的图形,这个函数是以π为最小正周期的奇函数。
图10.4 正割函数1sec cos
y x ==
在,0,1,2,...x k k π==±±上没有定义,它是个无界的偶函数。
图10.5 余割函数1c sin
y cs x ==在,0,1,2,...x k k π==±±上没有意义,它是个无界的奇函数,且是以2π为最小正周期的周期函数。
图10.6
练习2研究函数sin2sin23sin3
=++的周期性。
在区间[-6π,
y x x x
6π]绘图,相应的MATLAB代码为
>>x=-6*pi:2*pi/30:6*pi;
>>y=sin(x)+2*sin(2*x)+3*sin(3*x);
>>plot(x,y);
>>xlabel('x');ylabel('y');
从图10.7可见,函数sin2sin23sin3
y x x x
=++仍然为周期函数,
最小正周期T≈6。
【练习与思考】
1. 画图研究下列函数的周期性,并从理论上证明。
(1)sin2x;
(2)cos2cos23cos34cos4
+++
x x x x
(3)sin(cos(sin()));
x x x
++
(4)sin(sin(sin()));
x x x
++
(5)sin(2cos(sin()));
x x x
++。
