2015年苏科版八年级数学下册 第11章 反比例函数第2节《反比例函数的图像与性质(3)》参考课件
合集下载
苏科版八年级下册数学11.1反比例函数课件(共18张)

总结:一般地,形如 y= k (k为常数,k≠0)的函数 x
称为反比例函数,其中x是自变量,y是函数.
试一试
下列关系式中的y是x的反比例函数吗?如果 是,比例系数k是多少?如果不是,说明理由。
(1) y=-
1 2x
(2) y=
x 4
(3) y=1-x
(4) xy=2
(5) y=
2 x+3
(6) y=x-1
(1)体积是100 cm3 的圆锥,高 h (cm)随底面面积 S ( cm2 )的变化而变化. (2)现有一张100元人民币,如果把它换成其他面额的人民币
换成的每张面 值为 x(元)
50105Fra bibliotek21
换成的张数 y
(张)
2
10
20 50 100
换得的张数y随面值x的变化而变化.
实践探索
实验名称: 探索等积矩形中的函数关系
(7) y=x2
(8) y=
1 x
+1
思考:如何判断函数是反比例函数?
等价情势:(k ≠0)
y k x
y=kx-1
xy=k
y与x成反比例
实践探索
请写出2个反比例函数的表达式.
巩固练习
1. 在下列函数中,y是x的反比例函数的是( C )
(A)y
=
8
X+5
(B)y =
3 x
+7
(C)xy = 5
(D)y =
实验步骤:1、将附录6中的矩形纸片揭下来; 2、将所有矩形纸片贴在38页的平面直角坐标
系,使每个矩形纸片的一个顶点与原点O重合,相邻两边 分别放在对应x、y轴的正半轴上。
3、填写37页表格中实验数据,根据表格中的数 据,你有什么发现?
称为反比例函数,其中x是自变量,y是函数.
试一试
下列关系式中的y是x的反比例函数吗?如果 是,比例系数k是多少?如果不是,说明理由。
(1) y=-
1 2x
(2) y=
x 4
(3) y=1-x
(4) xy=2
(5) y=
2 x+3
(6) y=x-1
(1)体积是100 cm3 的圆锥,高 h (cm)随底面面积 S ( cm2 )的变化而变化. (2)现有一张100元人民币,如果把它换成其他面额的人民币
换成的每张面 值为 x(元)
50105Fra bibliotek21
换成的张数 y
(张)
2
10
20 50 100
换得的张数y随面值x的变化而变化.
实践探索
实验名称: 探索等积矩形中的函数关系
(7) y=x2
(8) y=
1 x
+1
思考:如何判断函数是反比例函数?
等价情势:(k ≠0)
y k x
y=kx-1
xy=k
y与x成反比例
实践探索
请写出2个反比例函数的表达式.
巩固练习
1. 在下列函数中,y是x的反比例函数的是( C )
(A)y
=
8
X+5
(B)y =
3 x
+7
(C)xy = 5
(D)y =
实验步骤:1、将附录6中的矩形纸片揭下来; 2、将所有矩形纸片贴在38页的平面直角坐标
系,使每个矩形纸片的一个顶点与原点O重合,相邻两边 分别放在对应x、y轴的正半轴上。
3、填写37页表格中实验数据,根据表格中的数 据,你有什么发现?
新苏科版八年级数学下册《11章 反比例函数 11.2 反比例函数的图象与性质》课件_0

连结OA,OB,OC, 记D OAA1, D OBB1, D OCC1的
面积分别为S1, S2 , S3,则有 _A_ .
y
A.S1 = S2 = S3
B. S1 < S2 < S3
ห้องสมุดไป่ตู้
A
C. S3 < S1 < S2 D. S1 > S2 >S3
解:由性质(1)得
S1
B C
S2 S3
o A1 B1 C1
=4+ 1 (2 8) 3-4=15 2
y
A(1,8 )
B (4,2 ) oC D x
探究1:反比例函数 y A(1,8 ) 和B (4,2),
m x
与一次函数y=kx+b交于点
求:⑴这两个函数的解析式;⑵三角形⊿AOB的面积。
⑵解法3: 如图,过A作AC⊥x轴于点C, 过B点作BD⊥x轴于点D, CA与 DB相交于E点, 由A(1,8 ) 和 B (4,2)的坐标可知点E的坐标
x
y6 x
↑y
D(-3,2)
由性质1可知,S △OBC=3
C
于是有,
S△AOC +3=S △AOB= 12
B
O →x
∴ S△AOC =9
探究1:反比例函数 y m 与一次函数y=kx+b交于点 A(1,8 ) 和B (4,n), x
求:⑴这两个函数的解析式;⑵三角形⊿AOB的面积。
解:⑴ 将A(1,8 )代入 y m
①△ODB与△OCA的面积相等; ②四边形PAOB的面积不会发生变化; ③ △OPB与△OPA的面积相等 ④ PA与PB始终相等 ⑤当点A是PC的中点时, 点B一定是 PD的中点. 其中一定正确的是
苏科版八年级下册数学:112 反比例函数的图象与性质 (4)

两个函数图像所在象限不同,图像的变化趋势相反;
(3)这两个图像有什么位置关系?
两个图像关于x轴对称,关于y轴对称.
苏科版八年级数学(下)
课堂练习 在同一平面直角坐标系中画出函数 y=4x和 y=-4x的图像.
苏科版八年级数学(下)
收获分享
你对反比例函数的图像及特征有 哪些认识?请谈一谈你收获和体会与 其他同学分享.
(3)连线.
.
.
苏科版八年级数学(下)
探索思考 反比例函数 y=6x的图像是怎样的图形?
苏科版八年级数学(下)
操作归纳
根据图像,你发现函数 y 6 的图像有哪些特征? x
有两条曲线组成(双曲线);
图像的两个分支分别在第一、三象限;
在每一个象限内,从左往右,图像的两个分支呈 下降趋势,两个分支无限接近坐标轴,与坐标轴 无交点;
作业: 习题11.2 第1题、第3题.
苏科版八年级数学(下)
苏科版八年级数学(下)
§11.2反比例函数的图像与性质(1)
苏科版八年级数学(下)
复习引入 一次函数y=x+1的图像是怎样的图形?
(1)列表;
y x 1.
x … -4 -3 -2 -1 0 1 2 3 4 … y=x+1 … -3 -2 -1 0 1 2 3 4 5 …
.
. .
.
(2)描点;
.
.
图像关于原点对称.
苏科版八年级数学(下)
探索思考
分析函数 y=-6x的图像特征.并在同一平面直角 坐标系中画出函数 y=-6x的图像.
苏科版八年级数学(下)
比较函数 y 6 与函数 y - 6 的图像特征:
x
x
(1)有哪些相同点?
苏科版八年级数学下册第十一章《11.2反比例函数的图象与性质(3)》公开课课件

Ø练习巩固 1、已知点P、Q在反比函数y= 3 的图象上。 x 若P(x1,y1),Q(x2,y2),x1< x2,你能比较 y1与 y2的 大小吗?
2、如图是三个反比例函数 y= ,y= ,y= ,在x轴的
学科网
k1
k2
k3
上方的图象,由此观察得到k1、xk2、k3的大x 小关系为x ( )
A. k1>k2>k3 B. k2>k3>k1
y
y
y
y
Ox
Ox
Ox
Ox
A
B
C
D
Ø中考链接
2.如图RtΔAOB的顶点A是直线 y=x+11-m 与双曲线
(1y)求mxm在的第值一;象限的交点,y且SΔAOB = 3。
(2)求点C坐标。
A
CO B
x
(2)已知:点P是双曲线
y
6 x
上任意一点,PA⊥OX于A,
PB⊥OY于B.求:矩形PAOB的面积. y
PB
x
AO
小结:
已知:点P是双曲线 y k 上任意一点,PA⊥OX于A, x
PB⊥OY于B.
则:矩形PAOB的面积= |k| .
y yk x
B
P(a,b)
O
A
x
Ø练习
已知反比例函数 y= Q(b,2.5).
2 反比例函数的图象与性质(
Ø回顾与思考
一、什么叫反比例函数?
一般地,形如 yk(k为常数 k, 0)
学科网
x
的函数叫做反比例函数.
学科网
其中x是自变量,y是x的函数,k是比例系数.
Ø回顾与思考
二、反比例函数的图象与性质 反比例函数 y k (k为常数,k≠0)的图象是双曲线
苏科版八年级下册数学课件 反比例函数

用函数表达式表示下列问题中两个变量之间的关系: 1、计划修建一条长为500km的高速公路,完成该项目的天数
y(天)随日完成量x(km)的变化而变化;
解:根据题意,得:xy=500
即 y 500
x
2、某银行为资助某社会福利厂,提供了20万元的 无息贷款,该厂的年平均还款额y(万元)随还款年限x(年) 的变化而变化;
(1)面积是50cm2的矩形,一边长y (cm)随另一边长 x(cm)的变化而变
化;
(2)体积是100cm3的圆锥,高h(cm)随底面面积S(cm2)的变化而变化.
(3)妈妈买菜已经用了25(元),还想买5元/斤的鱼a 斤,则总的花 费 y(元)随着所购买的斤数 a(斤)的变化而变化. (4)两条对角线长分别为a、b的菱形的面积为12,则一条对角线a随另 一条对角线b的变化而变化
解:根据题意,得:xy=20
即 y 20
x
3、游泳池的容积为5000 m3,向池内注水,注满水所需时间 t(h)随注水速度 v(m3 /h) 的变化而变化;
解:根据题意,得vt=5000 即 t 5000
v
4、实数m与n的积为-500,m随n的变化而变化;
解:根据题意,得mn= - 500 即 m 500
与x成正比例关系
x
两种相关联的量,一种量变化,另一种量也随着变化,如 果这两种量相对应的两个数的比值(也就是商)一定,这两 种量就叫做成正比例的量,它们的关系叫做成正比例关系.
如果用字母x和y表示两种相关联的量,用k表示它们的比值, 那么上面的这种数量关系可以用 y =k (k一定)来表示
x
这里的x,y可以表示 单项式也可以是多 项式
例如: 1、圆柱的底面积是10,体积v与高度h的函数关系式 2、有6个相同的本子,售价y与单价x的函数关系式
江苏8年级下册数学课件11.2反比例函数的图像与性质1 (共18张PPT)

X
-2
-4
-6
反比例函数
y=
6 X
的图像有哪些特征?
y
6 4 2
-6 -4 -2 O 2 4 6
X
-2
-4
-6
概略归纳
反比例函数的图像:
一般地,反比例函数
y=
k X
(k为常
数,k≠0)的图像是由两个分支组成的,
叫做双曲线。
自主探究
6
例2、反比例函数 y= - X 的图像在什么象限?
y
6 4 2
总结反思
数缺形时少直觉 形少数时难入微
图像的特征:
双曲线与坐标轴无限接近,但不能到达。
练习反馈 1、如果函数y=mxm的图像是双曲线,则m
的值是( A )
A、-1 B、0 C、1 D、2
练习反馈 2、属于反比例函数图像的是(D )
练习反馈
3、反比例函数 y= - 5 的图像大致是( D )
y
x
y
A
o
x
B
o
x
y
C
o
x
D
y
o x
练习反馈
-6 -4 -2 O 2 4 6
X
-2
-4
-6
自主探究
反比例函数 y=Байду номын сангаас
6 X
与
6 y= -
X
的图像有什么共同特征?
y
6 4 2
- -4 - O 2 4 6
X
6 2-
2-4
-6
y
6 4 2
- -4 - O 2 4 6
X
6 2-
2-4
-6
概略归纳 图像的位置:
苏科版八年级数学下_11.2反比例函数的图像与性质

进而可求反比例函数的表达式.
②过反比例函数的图像上任意一点作两坐标轴的垂线,这两
条垂线与坐标轴围成的矩形的面积是一个不变的值.
感悟新知
例 7 [中考·牡丹江] 如图11.2-5 所示,点A
在反比例函数y1=
18 x
(x>
0)的图像上,
过点A 作AB ⊥ x 轴,垂足为B,交
反比例函数y2= 6 (x> 0)的图像于点 x
感悟新知
知3-讲
方法点拨 : 确定反比例函数表达式的方法:
在明确两个变量为反比例函数关系的前提下,先设出 反比例函数的表达式,然后把满足反比例函数关系的一 组对应值代入设出的表达式中构造方程,解方程求出待 定系数,从而确定反比例函数的表达式.
感悟新知
知3-讲
解:(1)设反比例函数的表达式为y= k (k ≠ 0). x
<
0)的图像上有三点P1(x1,y1)、
P2(x2,y2)、P3(x3,y3),若x1< x2<0<x3,则下列结
论正确的是( B )
A. y1 < y2 < y3 B. y3 < y1 < y2 C. y3 < y2 < y1 D. y1 < y3 < y2
感悟新知
知1-讲
解题秘方:紧扣反比例函数的增减性及不同象限的 函数值的关系比较大小.
知1-讲
感悟新知
知识点 2 反比例函数的性质
知2-讲
反比例函数的性质主要研究它的图像的位置和函数值的增 减情况,如下 表所示.
感悟新知
特别提醒 :
知2-讲
在描述反比例函数的增减性时,必须指明“在每
一个象限内”.因为当k>0(k< 0) 时,整个函数不是y
随x 的增大而减小(增大),而是函数在每一个象限内,
八年级下册数学教学设计:反比例函数的图像与性质
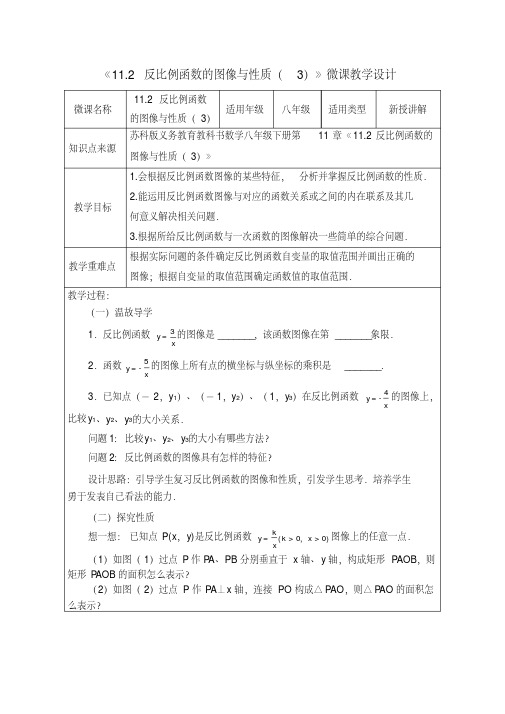
y= k 的图像经过点 A,则 k 的值是
(
x
A.2
B.-
C. 4
) D.- 4
A
C
BO
x
(第 1 题图)
2.若反比例函数
k-3 y = 的图像位于一、三象限内,正比例函数
x
y=(2k- 9)x
过二、四象限,则 k 的整数值是 _______.
x
2.函数 y = - 5 的图像上所有点的横坐标与纵坐标的乘积是 _______.
x
3.已知点(- 2,y1)、(- 1,y2)、( 1,y3)在反比例函数 y = - 4 的图像上,
x
比较 y1、y2、 y3的大小关系. 问题 1: 比较 y1、y2、 y3的大小有哪些方法? 问题 2: 反比例函数的图像具有怎样的特征?
矩形 PAOB 的面积怎么表示?
(2)如图( 2)过点 P 作 PA⊥ x 轴,连接 PO 构成△ PAO,则△ PAO 的面积怎
么表示?
y BP
y P
OA
x
OA
x
图( 1)
图( 2)
问题 3: 若不约束 k、 x的取值范围,则矩形 PAOB与△ PAO的面积应如何表示?
设计思路:引导学生通过探究体会如何根据反比例函数图像的某些特征,分析 并掌握反比例函数的性质.通过从特殊到一般的方法进行探究,增强学生对反比例
x
坐标是- 3. (1)求 k 的值,并画出这个反比例函数的图像;
(2)根据反比例函数图像,指出当 x <- 1 时, y 的取值范围.
设计思路:引导学生掌握根据点的坐标求函数表达式的一般方法,明白函数图
像在解题中的重要性,一切性质皆源于图像.
y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)根据反比例函数图像,指出当x<-1时, y的取值范围.
11.2 反比例函数的图像与性质(3)
解:(1)把x=-3代入y=x+1,得 y=-2. k 根据题意,可得反比例函数 y= 的图像与一次函 x 数y=x+1 的图像的一个交点的坐标是(-3,-2). k k y = 把x=-3 、y=-2代入 ,得 -2= , x -3 即k=6.
6 函数 y= 的图像如图11-4. x
(2)由函数图像可知,当x<-1时,-6<y<0.
11.2 反比例函数的图像与性质(3)
练习
n+3 1.已知反比例函数y= 的图像在同一象限内, x y随x增大而增大,求n的取值范围.
11.2 反比例函数的图像与性质(3)
练习
k y= (k<0)的图像上,比较y1、y2的大小. x
11.2 反比例函数的图像与性质(3)
例题教学
例2 设菱形的面积是5cm2,两条对角线的长 分别是xcm、ycm. (1)确定y与x的函数表达式; (2)画出这个函数的图像.
11.2 反比例函数的图像与性质(3)
解:(1)由“菱形的面积等于它的两条对角线长的 1 乘积的一半”,得 xy=5 . y与x的函数表达式为 2 10 ,y是x的反比例函数. y=
11.2反比例函数的图像与性质(3)
11.2 反比例函数的图像与性质(3)
课前热身
m-3 1.如图,是反比例函数 y= x 的图像的一支.
(1)函数图像的另一支在第几象限? (2)求常数m的取值范围. y
O
x
11.2 反比例函数的图像与性质(3)
3 2.已知点A、B在反比例函数 y 的图像上,若A x (3, y1 ),B (5, y2 ),比较 y1 (1,y2)在反比例函数
11.2 反比例函数的图像与性质(3)
课堂小结:
谈谈你这一节课有哪些收获.
x
(2)根据题意,可知x>0.
10 反比例函数 y= ( x>0)的图像是其在第一 x
象限的一支.如图11-3.
11.2 反比例函数的图像与性质(3)
例题教学
例3
y=x+1
k 已知反比例函数 y= 的图像与一次函数 x 的图像的一个交点的横坐标是-3 .
(1)求k的值,并画出这个反比例函数的图像;
11.2 反比例函数的图像与性质(3)
解:(1)把x=-3代入y=x+1,得 y=-2. k 根据题意,可得反比例函数 y= 的图像与一次函 x 数y=x+1 的图像的一个交点的坐标是(-3,-2). k k y = 把x=-3 、y=-2代入 ,得 -2= , x -3 即k=6.
6 函数 y= 的图像如图11-4. x
(2)由函数图像可知,当x<-1时,-6<y<0.
11.2 反比例函数的图像与性质(3)
练习
n+3 1.已知反比例函数y= 的图像在同一象限内, x y随x增大而增大,求n的取值范围.
11.2 反比例函数的图像与性质(3)
练习
k y= (k<0)的图像上,比较y1、y2的大小. x
11.2 反比例函数的图像与性质(3)
例题教学
例2 设菱形的面积是5cm2,两条对角线的长 分别是xcm、ycm. (1)确定y与x的函数表达式; (2)画出这个函数的图像.
11.2 反比例函数的图像与性质(3)
解:(1)由“菱形的面积等于它的两条对角线长的 1 乘积的一半”,得 xy=5 . y与x的函数表达式为 2 10 ,y是x的反比例函数. y=
11.2反比例函数的图像与性质(3)
11.2 反比例函数的图像与性质(3)
课前热身
m-3 1.如图,是反比例函数 y= x 的图像的一支.
(1)函数图像的另一支在第几象限? (2)求常数m的取值范围. y
O
x
11.2 反比例函数的图像与性质(3)
3 2.已知点A、B在反比例函数 y 的图像上,若A x (3, y1 ),B (5, y2 ),比较 y1 (1,y2)在反比例函数
11.2 反比例函数的图像与性质(3)
课堂小结:
谈谈你这一节课有哪些收获.
x
(2)根据题意,可知x>0.
10 反比例函数 y= ( x>0)的图像是其在第一 x
象限的一支.如图11-3.
11.2 反比例函数的图像与性质(3)
例题教学
例3
y=x+1
k 已知反比例函数 y= 的图像与一次函数 x 的图像的一个交点的横坐标是-3 .
(1)求k的值,并画出这个反比例函数的图像;
