浙教版数学九年级上册《两个三角形相似的判定》习题
浙教版九年级数学上册同步习题:4.4 两个三角形相似的判定

4.4 两个三角形相似的判定一、选择题(共10小题;共50分)1. 如图,四边形的对角线,相交于,且将这个四边形分成①②③④四个三角形.若,则下列结论中一定正确的是A. ①和②相似B. ①和③相似C. ①和④相似D. ②和④相似2. 下列判断中,不正确的是A. 两直角边长分别是,和,的两个直角三角形相似B. 斜边和一直角边长分别是,和,的两个直角三角形相似C. 两条边长分别是,和,的两个直角三角形相似D. 两个等腰直角三角形相似3. 如图所示,有点光源在平面镜上方,若点恰好在点光源的反射光线上,并测得,,,且,则点光源到平面镜的距离的长度为A. B. C. D.4. 如图,在正方形网格上有个三角形:① ;② ;③ ;④ ;⑤ ;⑥ .② ⑥中与①相似的是A. ②③④B. ③④⑤C. ④⑤⑥D.②③⑥5. 下列的正方形网格中,小正方形的边长均为,三角形的顶点都在格点上,则与相似的三角形所在的网格图形是A. B.C. D.6. 如图,小明在做选择题"如图,四边形中,,,,,则的长为多少"时遇到了困难.小明通过测量发现,试题给出的图形中,,,且各角度符合条件,因此小明猜想下列选项中最可能正确的是A. B. C. D.7. 如图,是的边上的一点,那么下列四个条件不能单独判定的是A. B.C. D.8. 如图,是的边上一点,,,.如果的面积为,那么的面积为A. B. C. D.9. 若两个扇形满足弧长的比等于它们的半径的比,则称这两个扇形相似.如图所示,如果扇形与扇形是相似扇形,且半径(为不等于的常数),那么下面的四个结论:① ;② ;③ ;④扇形与扇形的面积之比为.成立的个数为A. 个B. 个C. 个D. 个10. 如图,在中,,于点,于点,为边的中点,连接,,则下列结论:① ;② ;③ 为等边三角形;④当时,.其中正确的个数是( )A. 个B. 个C. 个D. 个二、填空题(共10小题;共50分)11. 两边且夹角的两个三角形相似.利用这种方法判定两个三角形相似时,寻找的条件必须满足“两边夹一角”,如果改为“两边与一组对应角相等”,这两个三角形就不一定相似了.12. 如图,在中,,点在上.要使,可添加的一个条件是.13. 的三边长分别为,,,的两边长分别为,,当的第三边长为时,.14. 如图,在四边形中,,,,,,如果边上的点,使得以,,为顶点的三角形与,,为顶点的三角形相似,这样的点有个.15. 在中,,是边上的高,并且,则的度数为.16. 如图,在平面直角坐标系中,点为轴上的一点,且点坐标为,过点的直线轴,点为直线上的一动点,连接,交直线于点,则的值为.17. 已知的三边长分别为,,,的两边长分别为和,要判定,那么的第三边长应为.18. 如下图,矩形纸片中,,,点是边上的动点.现将纸片折叠,使点与点重合,折痕与矩形边的交点分别为,.(1)当点恰好为的中点时,折痕的长度为;(2)设,要使折痕始终与边,有交点,的取值范围是.19. 如图,在中,,,,动点从点开始沿边向点以每秒个单位长度的速度运动,动点从点开始沿边向点以每秒个单位长度的速度运动,连接,点,分别从点,同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为秒().(1)当秒时,点,,所构成的三角形与相似.(2)在整个运动过程中,线段的中点所经过的路程长为.20. 如图,在平面直角坐标系中,已知点,的坐标分别,,是的中点,过作轴的垂线垂足为.动点从点出发,沿向匀速运动,过点做轴的垂线,垂足为,连接,.当所在直线与所在直线第一次垂直时,点的坐标为.三、解答题(共5小题;共65分)21. 如图,在锐角三角形中,,上的高,相交于点,写出图中的两对相似三角形.22. 如图,在中,,,是两条高.求证;.23. 如图,四边形和四边形都是矩形,且点恰好在上.若,,则.24. 网格图中每个方格都是边长为的正方形.若,,,,,都是格点,试说明.25. 阅读下面材料:小骏遇到这样一个问题:画一个和已知矩形面积相等的正方形.小骏发现:延长到,使得,以为直径作半圆,过点作的垂线,交半圆于点,以为边作正方形,则正方形即为所求.请回答:,和的数量关系为.参考小骏思考问题的方法,解决问题:画一个和已知平行四边形面积相等的正方形,并写出画图的简要步骤.答案第一部分1. B2. C3. C4. B5. B6. A7. C8. D9. D 10. D第二部分11. 成比例;相等12. 答案不唯一.如或等.13.14.15.16.17.18. (1);(2)19. ;20.第三部分21. ,.22. ,是两条高,,,,,,,,,,,.23.24. ,,,,,,,.25. .解决问题:方法一:过点作于点,延长到,使得,以为直径作半圆,过点作垂线,交半圆于点,以为边作正方形,正方形即为所求.方法二:如图,过点作于点,过点作交延长线于点,将平行四边形转化为等面积矩形,后同小骏的画法.。
浙教版数学九年级上册4.4.两个三角形相似的判定(一)

4.4.两个三角形相似的判定(一)一.选择题1.已知下列命题:①含有o 30角的直角三角形都相似;②所有等腰直角三角形都相似;③有一个角是o 60的等腰三角形都相似;④有一个角是o 45的等腰三角形都相似.其中真命题有( )A. 1个B.2个C.3个D.4个2.如图,在Rt △ABC 中,∠ACB=o 90,BC=3,AC=4,AB 的垂直平分线DE 交BC 的延长线于点E,则CE 的长为( )A. 23B. 67C. 625 D. 2 3.点E是□ABCD 的边BC 延长线上的一个点,AE 与CD 相交于G ,则图中相似三角形共有( )A. 2对B. 3对C. 4对D. 5对4.如图,在△ABC 中,∠ABC=o 90,BD ⊥AC, DE ⊥BC,垂足分别为D,E,则图中与△ABC 相似的三角形共有( )A. 4个B. 3个C. 2个D. 1个(第2题) (第3题) (第4题)5.如图,已知点E,F 分别是△ABC 中AC,AB 边的中点,BE,CF 相交于点G,FG=2,则CF 的长为 ( )A. 4B. 4.5C. 5D. 6二.填空题6.已知,如图四边形ABCD 是平行四边形,则图中相似三角形有_________对7. 如图,在锐角△ABC 中,高CE 和BF 相交于点D,请写出图中的两对相似三角形:_______________________(用相似符号连结)(第5题) (第6题) (第7题)8.如图,∠DAB=∠CAE,请补充一个条件:________________,使△ABC ∽△ADE9.如图,∠BAC=o 90,AD ⊥BC,则△ABC ∽________∽_________10.如图,点D 和E 分别在△ABC 的边AB 和AC 上,且∠AED=∠ABC,若DE=3,BC=6,AB=8,则AE 的长为__________,(第8题) (第9题) (第10题)三.解答题11.如图,已知□ABCD 中,EF//AB,DE:EA=2:3,EF=4,求CD 的长12.如图,△PMN 是等边三角形,∠APB=o 120,求证:AP PN PM AM ∙=∙13. 如图,在△ABC 中,AD 是中线,EF//BC,EF 交AD 于H,求证:EH=FH14.如图,M 为线段AB 的中点,AE 于BD 交于C, ∠DME=∠A=∠B,且DM 交AC 于F,ME 交BC 于G,写出图中三对相似三角形,并证明其中一对。
浙教版-数学-九年级上册-4.4 两个三角形相似的判定(2) 作业
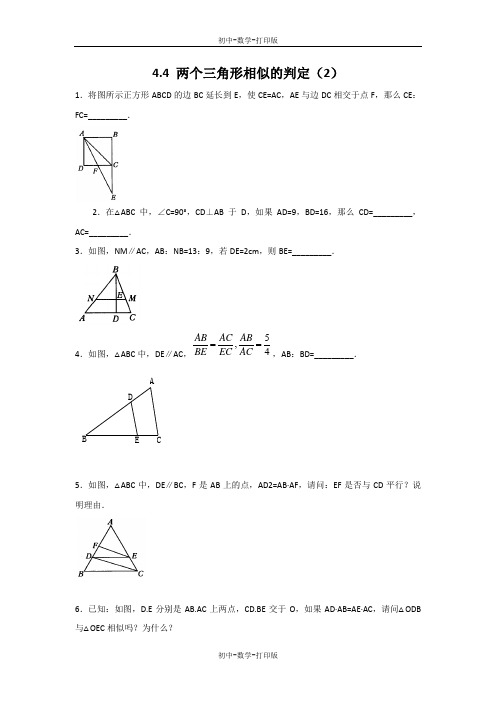
4.4 两个三角形相似的判定(2)1.将图所示正方形ABCD 的边BC 延长到E ,使CE=AC ,AE 与边DC 相交于点F ,那么CE :FC=_________.2.在△ABC 中,∠C=90°,CD ⊥AB 于D ,如果AD=9,BD=16,那么CD=_________,AC=_________.3.如图,NM ∥AC ,AB :NB=13:9,若DE=2cm ,则BE=_________.4.如图,△ABC 中,DE ∥AC ,5,4AB AC AB BE EC AC ==,AB :BD=_________.5.如图,△ABC 中,DE ∥BC ,F 是AB 上的点,AD2=AB·AF ,请问:EF 是否与CD 平行?说明理由.6.已知:如图,D.E 分别是AB.AC 上两点,CD.BE 交于O ,如果AD·AB=AE·AC ,请问△ODB 与△OEC 相似吗?为什么?DC BA7.如图,△ADE 与△ABC 有公共顶点A ,∠BAD=∠CAE .(1)请你写一个适当的条件,使△ADE ∽△ABC ,则需添加的条件可以是,并选择其中之一证明.(2)由(1)能否得出其他的相似三角形?如果能,请说明理由.参考答案1.): 12.12 153.924.8:55.平行.证明:∵DE ∥BC ,∴=,∵AD2=AB•AF ,∴=,∴,∴=,∴EF∥DC.6.△ODB∽△OEC证明:∵AD·AB=AE·AC,即AB:AE=AC:AD,∠A为公共角,∴△ACD∽△ABE,∴∠BDO=∠CEO,又∵∠BOD=∠COE,∴△ODB∽△OEC.7.解:(1)使△ADE∽△ABC,则需添加的条件可以是:∠ADC=∠ABC或∠AED=∠ACB,理由:∵∠BAD=∠CAE,∴∠BAD+∠BAE=∠BAE+∠CAE,即∠DAE=∠CAB,又∵∠ADC=∠ABC,∴△ADE∽△ABC,故答案为:∠ADC=∠ABC或∠AED=∠ACB;(2)△ABD∽△ACE.理由:∵△ADE∽△ABC,∠BAC=∠DAE,∴=,∠BAC﹣∠DAC=∠DAE﹣∠CAE,∴=,∠BAD=∠CAE,∴△ABD∽△ACE.。
浙教版-数学-九年级上册-4.4.2 两个三角形相似的判定(二) 练习

两个三角形相似的判定(二)1.下列条件中能判定△ABC ∽△A′B′C′的是 ( C )A .∠A =30°,∠B =40°,∠A ′=35°,∠B ′=105°B .∠A =30°,∠B =50°,∠B ′=30°,∠C ′=105°C .AB =AC ,∠A =∠A′,A ′B ′=A′C′D .∠A =30°,∠A ′=30°,AB A ′B ′=BC B ′C ′=122.在Rt △ABC 和Rt △DEF 中,∠C =∠F =90°,下列条件中不能判定这两个三角形相似的是 ( C )A .∠A =55°,∠D =35°B .AC =9,BC =12,DF =6,EF =8C .AC =3,BC =4,DF =6,DE =8D .AB =10,AC =8,DE =15,EF =93.如图4-4-18,D 是△ABC 的边AC 上一点,那么下面四个命题中错误的是( D )A .如果∠ADB =∠ABC ,那么△ADB ∽△ABCB .如果∠ABD =∠C ,那么△ABD ∽△ACBC .如果AB AC =AD AB,那么△ABC ∽△ADB D .如果AD AB =AB BC,那么△ADB ∽△ABC图4-4-184.如图4-4-19,若OA OB =__OC OD__,则△OAC ∽△OBD. 【解析】 ∵OA OB =OC OD,∠AOC =∠BOD , ∴△OAC ∽△OBD.图4-4-19 图4-4-205.如图4-4-20所示,在△ABC 中,D 是AB 边上一点,连结CD ,要使△ADC 与△ABC 相似,应添加的条件是__∠ACD =∠B 或∠ADC =∠ACB 或AD AC =AC AB__ (写出一个条件即可).6.如图4-4-21,已知△ABC ∽△DEF ,AM ,DN 是中线,试判断△ABM 与△DEN 是否相似,为什么?图4-4-21解:相似.∵△ABC ∽△DEF ,∴AB DE =BC EF =BM EN,∠B =∠E ,∴△ABM ∽△DEN. 7.如图4-4-22,已知∠DAE =∠BAC ,AD ∶AB =1∶2,点E 是AC 的中点.求证:△ADE ∽△ABC.图4-4-22证明:∵E 是AC 的中点,∴AE AC =12, 又∵∠DAE =∠BAC ,AD AB =AE AC =12, ∴△ADE ∽△ABC.。
4.4 两个三角形相似的判定 浙教版九年级数学上册同步练习(含答案)

4.4 两个三角形相似的判定一、选择题(共9小题)1. 如图所示,如果 ∠BAD =∠CAE ,那么添加下列一个条件后,仍不能判定 △ABC ∽△ADE 的是 ( )A. ∠B =∠DB. ∠C =∠AEDC. AB AD =DEBCD. AB AD =ACAE2. 如图所示,在方格纸中,△ABC 和 △EPD 的顶点均在格点上,要使 △ABC ∽△EPD ,则点 P 所在的格点为 ( )A. P 1B. P 2C. P 3D. P 43. 如图所示,在正方形 ABCD 中,E 是 CD 的中点,点 F 在 BC 上,且 FC =14BC ,则图中的相似三角形共有 ( )A. 4 对B. 3 对C. 2 对D. 1 对4. 如图所示,在等边三角形 ABC 中,点 D ,E 分别在 AC ,AB 上,且 ADAC =13,AE =BE ,则有 ( )A. △AED∽△BEDB. △AED∽△CBDC. △AED∽△ABDD. △BAD∽△BCD5. 如图所示,已知正方形ABCD,E是CD的中点,P是BC边上的一点,下列条件中不能推出△ABP与△ECP相似的是( )A. ∠APB=∠EPCB. ∠APE=90∘C. P是BC的中点D. BP:BC=2:36. 如图所示,在直角梯形ABCD中,AD∥BC,∠ABC=90∘,AB=8,AD=3,BC=4,P为AB边上一动点,若△PAD与△PBC是相似三角形,则满足条件的点P有( )A. 1个B. 2个C. 3个D. 4个7. 如图所示,已知P是边长为5的正方形ABCD内一点,且PB=3,BF⊥BP于点B,若在射线BF上找一点M,使以点B,M,C为顶点的三角形与△ABP相似,BM的值为( )A. 3B. 253C. 3或5 D. 3或2538. 如图所示,△ABC≌△ADE且∠ABC=∠ADE,∠ACB=∠AED,BC,DE交于点O.下列四个结论:①∠1=∠2;②BC=DE;③△ABD∽△ACE;④A,O,C,E四点在同一个圆上.一定成立的结论有( )A. 1个B. 2个C. 3个D. 4个9. 如图所示,AB是半圆O的直径,D,E是半圆上任意两点,连接AD,DE,AE与BD交于点C,要使△ADC与△ABD相似,可以添加一个条件.下列添加的条件中,错误的是( )A. ∠ACD=∠DABB. AD=DEC. AD2=BD⋅CDD. CD⋅AB=AC⋅BD二、填空题(共5小题)10. 如图所示,在边长为1的正方形网格中有点P,A,B,C,则图中所形成的三角形中,相似的三角形是.11. 如图所示,在两个直角三角形中,∠ACB=∠ADC=90∘,AC=6,AD=2,当AB=时,这两个直角三角形相似.12. 如图所示,已知,在四边形ABCD中,∠A=∠B=∠DEC,且E为AB边中点,则图中有对相似三角形.13. 如图所示,平行四边形ABCD中,AB=4,AD=6,∠ABC=60∘,P是射线AD上的一个动点(与点A不重合),BP与AC交于点E,设AP=x,当x=时,△ABP与△EBC相似.14. 如图所示,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为时,△ADP和△ABC相似.三、解答题(共7小题)15. 如图所示,在△ABC中,AB=AC,D为CB延长线上一点,E为BC延长线上一点,且AB2=DB⋅CE.求证:△ADB∽△EAC.16. 如图所示,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE.(1)写出图中两对相似三角形(不得添加字母和线);(2)请分别说明两对三角形相似的理由.17. 如图所示,AB=3AC,BD=3AE,BD∥AC,点B,A,E在同一条直线上.(1)求证:△ABD∽△CAE.(2)如果AC=BD,AD=22BD,设BD=a,求BC的长.18. 如图所示,已知△ABC,△DCE,△FEG是三个全等的等腰三角形,底边BC,CE,EG在同一条直线上,且AB=3,BC=1,连接BF分别交AC,DC,DE于点P,Q,R.(1)求证:△BFG∽△FEG,并求出BF的长.(2)观察图形,请你提出一个与点P相关的问题,并进行解答.19. △ABC和△DEF是两个等腰直角三角形,∠A=∠D=90∘,△DEF的顶点E位于边BC的中点上.(1)如图1所示,DE与AB交于点M,EF与AC交于点N,求证:△BEM∽△CNE;(2)如图2所示,将△DEF绕点E旋转,使得DE与BA的延长线交于点M,EF与AC交于点N,除(1)中的一对相似三角形外,再找出一对相似三角形并证明你的结论.20. 如图所示,四边形ABCD内接于⊙O,AB是⊙O的直径,AC,BD交于点E,DC2=CE⋅CA.(1)求证:BC=CD.(2)分别延长AB,DC交于点P,过点A作AF⊥CD交CD的延长线于点F,若PB=OB,CD=22,求DF的长.21. 如图所示,在矩形ABCD中,AB=12 cm,BC=8 cm.点E,F,G分别从点A,B,C三点同时出发,沿矩形的边按逆时针方问移动.点E,G的速度均为2 cm/s,点F的速度为4 cm/s,当点F追上点G(即点F与点G重合)时,三个点随之停止移动.设移动开始后第t(s)时,△EFG的面积为S(cm2).(1)当t=1(s)时,S的值是多少?(2)写出S关于t的函数表达式,并指出自变量t的取值范围.(3)若点F在矩形的边BC上移动,当t为何值时,以点E,B,F为顶点的三角形与以点F,C,G为顶点的三角形相似?请说明理由.答案1. C2. C3. B4. B5. C6. C7. D8. D9. D10. △APB∽△CPA11. 3或3212. 313. 814. 4或915. ∵AB=AC,∴∠ABC=∠ACB.∴∠ABD=∠ACE.∵AB2=DB⋅CE,∴ABCE =DBAB.∴ABCE =DBAC.∴△ADB∽△EAC.16. (1)△ABC∽△ADE,△ABD∽△ACE.(2)∵∠BAD=∠CAE,∴∠BAD+∠DAC=∠CAE+∠DAC,即∠BAC=∠DAE.∵∠ABC=∠ADE,∴△ABC∽△ADE.∴ABAD =ACAE.∵∠BAD=∠CAE,∴△ABD∽△ACE.17. (1)因为BD∥AC,点B,A,E在同一条直线上,因为 ABAC =BDAE =3,所以 △ABD ∽△CAE .(2) 因为 AB =3AC =3BD ,AD =22BD ,所以 AD 2+BD 2=8BD 2+BD 2=9BD 2=AB 2.所以 ∠D =90∘.因为 △ABD ∽△CAE ,所以 ∠E =∠D =90∘.因为 AE =13BD ,EC =13AD =232BD ,AB =3BD ,所以BC 2=(AB +AE )2+EC 2=3BD +13BD2+BD 2=12BD 2=12a 2.所以 BC =23a .18. (1) ∵ △ABC ≌△DCE ≌△FEG ,∴ BC =CE =EG =13BG =1,FG =AB =3.∴ BG =3. ∴ FGEG =BGFG =33=3.∵ ∠BGF =∠FGE , ∴ △BFG ∽△FEG . ∵ △FEG 是等腰三角形, ∴ △BFG 是等腰三角形. ∴ BF =BG =3.(2) 问题:求证 BP =PR .证明:∵ ∠ACB =∠REB , ∴ AC ∥DE .又 ∴ BC =CE , ∴ BP =PR .19. (1) ∵ △ABC 是等腰直角三角形, ∴ ∠MBE =45∘.∴ ∠BME +∠MEB =135∘. ∵ △DEF 是等腰直角三角形, ∴ ∠DEF =45∘.∴ ∠NEC +∠MEB =135∘.∵ ∠B =∠C =45∘, ∴ △BEM ∽△CNE . (2) △ECN ∽△MEN .证明:与(1)同理得 △BEM ∽△CNE , ∴ BECN =EMNE . ∵ BE =EC , ∴ ECCN =EMNE .∵ ∠ECN =∠MEN =45∘, ∴ △ECN ∽△MEN .20. (1) 因为 DC 2=CE ⋅CA ,所以 DCCE =CADC .所以 △CDE ∽△CAD .所以 ∠CDB =∠DAC .所以 BC =CD .所以 BC =CD .(2) 如图所示,连接 OC ,过点 O 作 OG ⊥CD 于点 G .因为 BC =CD ,所以 ∠BAD =∠BOC .所以 OC ∥AD .所以 △PCO ∽△PDA .所以 PCPD =POPA .因为 PB =OB ,CD =22,所以 PCPC +22=23.所以 PC =42.因为 OG ∥AF ,所以 △PGO ∽△PFA .所以 PGPF =POPA .所以 PC PD =PGPF .所以 4242+22=42+242+22+DF,解得 DF =322.21. (1) 当 t =1(s) 时,AE =2(cm),EB =10(cm),BF =4(cm),FC =4(cm),CG =2(cm),S =S 梯形GCBE ―S △EBF ―S △FCG=12(EB +CG )×BC ―12EB ×BF ―12FC ×CG =12×(10+2)×8―12×10×4―12×4×2=24(cm 2). (2) ①如图1所示,当 0 s ≤t ≤2 s 时,点 E ,F ,G 分别在边 AB ,BC ,CD 上移动,此时 AE =2t (cm),EB =(12―2t )(cm),BF =4t (cm),FC =(8―4t )(cm),CG =2t (cm), S =S 梯形GCBE ―S △EBF ―S △FCG=12(EB +CG )×BC ―12EB ×BF ―12FC ×CG =12×8×(12―2t +2t )―12×4t (12―2t )―12×2t (8―4t )=8t 2―32t +48. ②当点 F 追上点 G 时,4t =2t +8,解得 t =4(s).如图2所示,当 2 s <t ≤4 s 时,点 E 在边 AB 上移动,点 F ,G 都在边 CD 上移动,此时 CF =(4t ―8)(cm),CG =2t (cm),FG =CG ―CF =2t ―(4t ―8)=8―2t (cm),S =12FG ×BC =12(8―2t )×8=―8t +32.∴S =8t 2―32t +48,0≤t≤2―8t +32.2<t ≤4. (3) 如图1所示,当点F在矩形BC上移动时,0≤t≤2.在△EBF和△FCG中,∠B=∠C=90∘.①若EBFC =BFCG,即12―2t8―4t =4t2t,解得t=23.当t=23时,△EBF∽△FCG.②若EBGC =BFCF,即12―2t2t =4t8―4t,解得t=32.当t=32时,△EBF∽△GCF.综上所述,当t=23或t=32时,以点E,B,F为顶点的三角形与以F,C,G为顶点的三角形相似.。
新浙教版九年级数学上册课后练习:4.4 两个三角形相似的判定

新浙教版九年级数学上册课后练习:4.4两个三角形相似的判定(第1题)1. 如图,四边形ABCD是平行四边形,则图中与△DEF相似的三角形共有(B)A. 1个B. 2个C. 3个D. 4个2.如图,M是Rt△ABC的斜边BC上异于B,C的一个定点,过点M作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有(C)A.1条 B.2条C.3条 D.4条,(第2题)) ,(第3题)) 3.如图,点A,B,C,D,E,F,G,H,O都是5×7方格中的格点,为使△DEM∽△ACB,则点M应是F,G,H,O四点中的点(C)A.F B.GC.H D.O4.下列叙述中,不正确的是(C)A.在Rt△ABC中,∠C=90°,∠B=20°,在Rt△A′B′C′中,∠C′=90°,∠A′=20°,则△ABC与△A′B′C′相似B.△ABC的两个角分别是35°和100°,△A′B′C′的两个角分别是45°和35°,则这两个三角形相似C.等腰△ABC和等腰△A′B′C′都有一个角为25°,则△ABC与△A′B′C′相似D.等腰△ABC和等腰△A′B′C′都有一个角为105 °,则△ABC与A′B′C′相似(第5题)5.如图,已知∠1=∠2,可补充条件__∠E=∠C或∠D=∠B(不唯一)__(写出一个即可),使△ADE∽△ABC.6. 已知△ABC∽△A′B′C′,AB=2 cm,BC=3 c m,AC=4 cm,A′B′=5 cm,则△A ′B ′C ′的周长是__22.5__cm(第7题)7.如图,已知AC⊥CD,垂足为C ,BD ⊥CD ,垂足为D ,AB 与CD 交于点O.若AC =1,BD =2,CD =4,则AB =__5__.8. 如图,BE ,CF 是△ABC 的中线且交于点G .求证:BG =2EG .(第8题)【解】 连结EF.∵BE ,CF 为△ABC 的中线, ∴EF 为△ABC 的中位线, ∴EF∥BC,∴△EGF ∽△BGC , ∴EG BG =EF BC =12, ∴BG =2EG.9.如图,为了测量一个大峡谷的宽度,地质勘探人员在对面的岩石上观察到一个特别明显的标志点O ,再在他们所在的同一侧选点A ,B ,D 使得AB⊥AO,DB ⊥AB ,然后确定DO 和AB 的交点C.测得AC =120m ,CB =60m ,BD =50m ,你能帮助他们算出大峡谷的宽AO 吗?(第9题)【解】 ∵AB⊥AO,DB ⊥AB , ∴∠A =∠B=90°. 又∵∠OCA =∠DCB , ∴△ACO ∽△BCD ,∴AC BC =AO BD ,即12060=AO 50, ∴AO =100(m).(第10题)10.如图,△ABC 内接于⊙O,∠BAC 的平分线分别交⊙O,BC 于点D ,E ,连结BD ,则图中相似三角形有(C )A .1对B .2对C .3对D .4对【解】 ∵∠D=∠C,∠CAD =∠DB E , ∴△BDE ∽△ACE.∵AD 平分∠BAC,∴∠BAD =∠CAD. 又∵∠D=∠C, ∴△AB D∽△AEC.∵∠DBC =∠CAD=∠BA D ,∠D =∠D, ∴△BDE ∽△ADB.∴共有3对相似三角形.11.如图,点A ,B ,C ,D 在⊙O 上,AC ⊥BD 于点E ,过点O 作OF⊥BC 于点F.求证:(第11题)(1)△AEB∽△OFC; (2)AD =2OF.【解】 (1)连结OB ,则∠BAE=12∠BOC.∵OB =OC ,OF ⊥BC , ∴∠COF =12∠BOC.∴∠BAE =∠COF. ∵AC ⊥BD ,OF ⊥BC , ∴∠OFC =∠AEB=90°, ∴△AEB ∽△OFC . (2)∵△AEB ∽△OFC , ∴AE BE =OF CF.由圆周角定理,得∠D =∠BCE ,∠DAE =∠CBE , ∴△ADE ∽△BCE ,∴AD BC =AE BE,∴OF CF =ADBC.∵OB =OC ,OF ⊥BC ,∴BC =2CF , ∴AD =BC CF·OF =2OF , 即AD =2OF .12.如图,在⊙O 上,位于直径AB 的异侧有一个定点C 和一个动点P ,AC =12AB ,点P在半圆弧AB 上运动(不与A ,B 两点重合),过点C 作直线PB 的垂线CD 交PB 于点D .(1)如图①,求证:△PCD ∽△ABC ;(2)当点P 运动到什么位置时,△PCD ≌△ABC ?请在图②中画出此时的△PCD ,并说明理由.(第12题)【解】 (1)∵AB 是⊙O 的直径, ∴∠ACB =90°.∵PD ⊥CD ,∴∠D =90°, ∴∠D =∠ACB .∵∠A 与∠P 是BC ︵所对的圆周角,∴∠A =∠P , ∴△PCD ∽△ABC .(2)如图②,当PC 是⊙O 的直径时(此时B ,D 两点重合),△PCD ≌△ABC .理由如下: ∵AB ,PC 是⊙O 的直径,∴∠PDC =∠ACB =90°,AB =PC . 又∵∠A =∠P , ∴△PCD ≌△ABC .(第13题)13.如图,M 为线段AB 的中点,AE 与BD 交于点C ,∠DME =∠A=∠B=α,且DM 交AC 于F ,ME 交BC 于点G ,连结FG.(1)写出图中两对相似三角形,并证明其中的一对;(2)如果α=45°,AB =4 2,AF =3,求FG 的长.【解】 (1)△AMF ∽△BGM ,△DMG ∽△DBM ,△EMF ∽△EAM 等. 下面证明△AMF ∽△BGM :∵∠A =∠B =∠DME =α,∠AFM =∠DME +∠E , 又∵∠BMG =∠A +∠E ,∴∠AFM =∠BMG , ∴△AMF ∽△BGM .(2)由α=45°,可知AC ⊥BC 且AC =BC . ∵M 为AB 的中点,AB =4 2, ∴AM =BM =2 2,AC =BC =4. ∵△AMF ∽△BGM ,∴AF BM =AMBG, 即32 2=2 2BG ,∴BG =83.∵AC =BC =4,∴CG =4-83=43,CF =1,∴在Rt△CFG 中,FG =CG 2+CF 2=⎝ ⎛⎭⎪⎫432+12=53.14.如图,在△ABC 中,∠ABC =90°,AB =3,BC =4.点Q 是线段AC 上的一个动点,过点Q 作AC 的垂线交线段AB (如图①)或线段AB 的延长线(如图②)于点P .(1)当点P 在线段AB 上时,求证:△AQP ∽△ABC ; (2)当△PQB 为等腰三角形时,求AP 的长.,(第14题))【解】 (1)∵PQ⊥AC,∠ABC =90°, ∴∠AQP =∠ABC . 又∵∠A =∠A , ∴△AQP ∽△ABC .(2)在Rt△ABC 中,AB =3,BC =4,由勾股定理,得AC =AB 2+BC 2=5.当△PQB 为等腰三角形时,分情况讨论: ①当点P 在线段AB 上时,如图①. ∵∠QPB 为钝角,∴当△PQB 为等腰三角形时,只可能是PB =PQ . 由(1),得△AQP ∽△ABC ,∴AP AC =QP BC ,即3-PB 5=PB 4,解得PB =43,∴AP =AB -PB =3-43=53.②当点P 在线段AB 的延长线上时,如图②. ∵∠QBP 为钝角,∴当△PQB 为等腰三角形时,只可能是PB =BQ . ∵BP =BQ ,∴∠BQP =∠P .∵∠BQP +∠AQB =90°,∠A +∠P =90°, ∴∠AQB =∠A , ∴BQ =AB , ∴BP =AB ,∴AP =2AB =2×3=6.综上所述,当△PQB 为等腰三角形时,AP 的长为53或6.。
度浙教新版九年级数学上第4章相似三角形 4.4两个三角形相似的判定 同步练习(有答案)

度浙教新版九年级数学上第4章相似三角形4一.选择题〔共12小题〕1.如图,10×2网格中有一个△ABC,图中与△ABC相似的三角形的个数有〔〕A.1个B.2个C.3个D.4个2.以下条件不能判定△ADB∽△ABC的是〔〕A.∠ABD=∠ACB B.∠ADB=∠ABC C.AB2=AD•AC D.=3.如图,点P在△ABC的边AC上,假设添加一个条件后可以失掉△ABP∽△ACB,那么以下添加的条件中,不正确的选项是〔〕A.∠ABP=∠C B.∠APB=∠ABC C.AB2=AP•AC D.4.如图,在四边形ABCD中,对角线AC与BD相交于点O,AC平分∠DAB,且∠DAC=∠DBC,那么以下结论不一定正确的选项是〔〕A.△AOD∽△BOC B.△AOB∽△DOC C.CD=BC D.BC•CD=AC•OA 5.如图,在△ABC中,点D、E、F区分在边AB、AC、BC上,且∠AED=∠B,再将以下四个选项中的一个作为条件,不一定能使得△ADE和△BDF相似的是〔〕A.B.C.D..6.以下说法:①一切等腰三角形都相似;②有一个底角相等的两个等腰三角形相似;③有一个角相等的等腰三角形相似;④有一个角为60°的两个直角三角形相似,其中正确的说法是〔〕A.②④B.①③C.①②④D.②③④7.如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE 相似,还需满足以下条件中的〔〕A.=B.=C.=D.=8.如图,在△ABC中,D为AC边上一点,∠DBC=∠A,BC=,AC=3,那么CD 的长为〔〕A.1B.C.2D.9.如图,△ABC中,AD是中线,BC=4,∠B=∠DAC,那么线段AC的长为〔〕A.B.2C.3D.10.如图,在△ABC中,点D,E区分在边AB,AC上,且==,那么S△ADE:S四边形BCED的值为〔〕A.1:B.1:3C.1:8D.1:911.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,衔接AE交BD于点F,那么△DEF的面积与△BAF的面积之比为〔〕A.3:4B.9:16C.9:1D.3:112.如图,等边△ABC的边长为3,P为BC上一点,且BP=1,D为AC上一点,假定∠APD=60°,那么CD的长是〔〕A.B.C.D.二.填空题〔共8小题〕13.在△ABC中,AB=9,AC=6.点M在边AB上,且AM=3,点N在AC边上.当AN=时,△AMN与原三角形相似.14.如图,:∠ACB=∠ADC=90°,AD=2,CD=2,当AB的长为时,△ACB 与△ADC相似.15.如图,要使△ABC∽△ACD,需补充的条件是.〔只需写出一种〕16.如图,在平面直角坐标系中有两点A〔4,0〕、B〔0,2〕,假设点C在x轴上〔C与A不重合〕,当点C的坐标为或时,使得由点B、O、C组成的三角形与△AOB相似〔至少找出两个满足条件的点的坐标〕.17.如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP 相似时,DP=.18.如图,在▱ABCD中,AC是一条对角线,EF∥BC,且EF与AB相交于点E,与AC相交于点F,3AE=2EB,衔接DF.假=1,那么S△ADF的值为.定S△AEF19.如图,平行四边形ABCD中,E为AD的中点,△DEF的面积为1,那么平行四边形ABCD的面积为.20.如图,Rt△ABC中,∠BAC=90°,AD⊥BC,假定BD=1,AD=3,那么CD=.三.解答题〔共8小题〕21.如图,AB⊥BD,CD⊥BD,AB=6cm,CD=4cm,BD=14cm,点P在BD上由点B向点D方向移动,当点P移到离点B多远时,△APB和△CPD相似?22.如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,〔1〕求证:AC2=AB•AD;〔2〕求证:△AFD∽△CFE.23.如图,在矩形ABCD中,AB=24,BC=12,点E沿BC边从点B末尾向点C以每秒2个单位长度的速度运动;点F沿CD边从点C末尾向点D以每秒4个单位长度的速度运动,假设E、F同时动身,用t〔0≤t≤6〕秒表示运动的时间,当t为何值时,以点E、C、F为顶点的三角形与△ACD相似?24.如图,在平面直角坐标系中,OA=12厘米,点P从点O末尾沿OA边向点A 以1厘米/秒的速度移动.:点Q从点B末尾沿BO边向点O以1厘米/秒的速度移动.假设P、Q同时动身,用t〔秒〕表示移动的时间〔0≤t≤6〕,那么,当t为何值时,△POQ与△AOB相似?25.如图,△ABC中,AB=8厘米,AC=16厘米,点P从A动身,以每秒2厘米的速度向B运动,点Q从C同时动身,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应中止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是多少?26.如图,△ABC是等边三角形,点D、E区分在BC、AC上,且BD=CE,AD与BE相交于点F.〔1〕试说明△ABD≌△BCE;〔2〕△EAF与△EBA相似吗?说说你的理由.27.如图,在矩形ABCD中,AD=6,AB=8,M是AD的中点,N,E是BC的三等分点,P是AB上一动点.〔1〕当MP∥BD时,求MP的长;〔2〕能否存在点P,满足△AMP与一点B,N,P为顶点的三角形相似?假定存在,求出AP的长;假定不存在,说明理由.28.:在△ABC中∠ACB=90°,CD⊥AB于点D,点E在AC上,BE交CD于点G,EF⊥BE交AB于点F.如图甲,当AC=BC时,且CE=EA时,那么有EF=EG;〔1〕如图乙①,当AC=2BC时,且CE=EA时,那么线段EF与EG的数量关系是:EF EG;〔2〕如图乙②,当AC=2BC时,且CE=2EA时,请探求线段EF与EG的数量关系,并证明你的结论;〔3〕当AC=mBC时且CE=nEA时,那么线段EF与EG的数量关系,并直接写出你的结论〔不用证明〕.参考答案一.选择题1.C.2.D.3.D.4.D.5.C.6.A.7.C.8.C.9.A.10.C.11.B.12.C.二.填空题13.2或4.5.14.4.15.∠ACD=∠B或∠ADC=∠ACB或AD:AC=AC:AB时16.﹣1,0〕;〔1,0〕.17.1或4或2.5.18..19.12.20.9三.解答题21.解:∵AB⊥BD,CD⊥BD,∴∠B=∠D=90°,∴当或时,△PAB与△PCD是相似三角形,∵AB=6,CD=4,BD=14,∴或,解得:BP=2或12或,即PB=2或12或时,△PAB与△PCD是相似三角形.22.〔1〕证明:∵AC平分∠DAB,∴∠DAC=∠CAB,∵∠ADC=∠ACB=90°,∴△ADC∽△ACB,∴AD:AC=AC:AB,∴AC2=AB•AD;〔2〕证明:∵E为AB的中点,∴CE=BE=AE,∴∠EAC=∠ECA,∵∠DAC=∠CAB,∴∠DAC=∠ECA,∴CE∥AD,∴△AFD∽△CFE.23.解:依据题意,可分为两种状况:①假定△EFC∽△ACD,那么=,所以=,解得t=3,即当t=3时,△EFC∽△ACD.②假定△FEC∽△ACD,那么=,所以=,解得t=1.2,即当t=1.2时,△FEC∽△ACD.因此,当t为3或1.2时,以点E,C,F为顶点的三角形与△ACD相似.24.解:①假定△POQ∽△AOB时,=,即=,整理得:12﹣2t=t,解得:t=4.②假定△POQ∽△BOA时,=,即=,整理得:6﹣t=2t,解得:t=2.∵0≤t≤6,∴t=4和t=2均契合题意,∴当t=4或t=2时,△POQ与△AOB相似.25.解:设运动了ts,依据题意得:AP=2tcm,CQ=3tcm,那么AQ=AC﹣CQ=16﹣3t〔cm〕,当△APQ∽△ABC时,,即,解得:t=;当△APQ∽△ACB时,,即,解得:t=4;故当以A、P、Q为顶点的三角形与△ABC相似时,运动时间是:s或4s.26.〔1〕证明:∵△ABC是等边三角形,∴AB=BC,∠ABD=∠BCE=∠BAC,又∵BD=CE,∴△ABD≌△BCE;〔2〕答:相似;理由如下:∵△ABD≌△BCE,∴∠BAD=∠CBE,∴∠BAC﹣∠BAD=∠CBA﹣∠CBE,∴∠EAF=∠EBA,又∵∠AEF=∠BEA,∴△EAF∽△EBA.27.解:〔1〕∵PM∥BD,AM=MD,∴AP=PB,∴PM=BD,∵BD==10,∴PM=5.〔2〕存在点P使得两三角形相似.∵BN=4,设AP=x,那么PB=8﹣x,当△MAP∽△NBP时,解得x=.当△MAP∽△PBN时,解得x=2或6,∴存在点P使得两三角形相似,此时AP的长为或2或4.28.图甲:衔接DE,∵AC=BC,CD⊥AB,∴AD=BD,∠ACD=45°,∴CD=AD=AB,∵AE=EC,∴DE=AE=EC=AC,∴∠EDC=45°,DE⊥AC,∵∠A=45°,∴∠A=∠EDG,∵EF⊥BE,∵∠AEF+∠FED=∠EFD+∠DEG=90°,∴∠AEF=∠DEG,∴△AEF≌△DEG〔ASA〕,∴EF=EG.〔1〕EF=EG;〔2〕解:EF=EG.证明:作EM⊥AB于点M,EN⊥CD于点N,∵EM∥CD,∴△AEM∽△ACD,即EM=CD,同理可得,EN=AD,∵∠ACB=90°,CD⊥AB,∴tanA=,又∵EM⊥AB,EN⊥CD,∴∠EMF=∠ENG=90°,∵EF⊥BE,∴∠FEM=∠GEN,∴△EFM∽△EGN,即EF=EG;〔3〕由〔1〕当AC=2BC时,且CE=EA时,EF=EG,当AC=2BC时,且CE=2EA时,EF=EG,可以得出:当AC=mBC时且CE=nEA时,EF=EG.。
2019—2020年最新浙教版九年级数学上册《两个三角形相似的判定》同步练习及答案.docx

4.4 两个三角形相似的判定(二)1.如图,在△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是(C)(第1题) (第2题)2.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是(B)3.如图,在方格纸中,△ABC和△PED的顶点均在格点上,要使△ABC∽△PED,则点P所在的格点为(C)A. P1B. P2C. P3D. P4(第3题)4.如图,在△ABC 中,D ,E 分别是AB ,AC 上的点,有下列条件:①∠AED =∠B ;②AD AC =AE AB ;③DE BC =ADAC.其中能够判断△ADE 与△ACB 相似的有(A)A.①②B.①③C.①②③D.①(第4题) (第5题)5.如图,点P 在△ABC 的边AC 上,要判断△ABP ∽△ACB ,添加一个条件,不正确的是(D)A. ∠ABP =∠CB. ∠APB =∠ABCC. AP AB =AB ACD. AB BP =AC CB6.如图,在平面直角坐标系中,有两点A(4,0),B(0,2),点C在x轴上(点C 与点A不重合).当点C的坐标为(1,0)或(-1,0)或(-4,0)时,以B,O,C为顶点的三角形与△AOB相似(至少写出两个满足条件的点的坐标).(第6题)7.根据下列条件,判断△ABC与△A′B′C′是否相似,并说明理由.∠A=100°,AB=7cm,AC=14cm,∠A′=100°,A′B′=3cm,A′C′=6cm.【解】△ABC∽△A′B′C′.理由如下:∵ABA′B′=73,ACA′C′=146=73,∴ABA′B′=ACA′C′.又∵∠A=∠A′,∴△ABC∽△A′B′C′.(第8题)8.如图,AB·AD=AC·AE.求证:△ABC∽△AED. 【解】∵AB·AD=AC·AE,∴AB AE =AC AD. 又∵∠BAC =∠EAD , ∴△ABC ∽△AED.9.在△ABC 中,E 是AB 上一点,AE =2,BE =3,AC =4.在AC 上取一点D ,使△ADE 与△ABC 相似,则AD 的值是(C)A. 85B. 52C. 85或52D. 85或25(第9题解)【解】 如解图.①当△ADE ∽△ABC 时,有AD AE =AB AC.∵AE =2,BE =3,∴AB =5. ∴AD 2=54,∴AD =52.②当△AED ∽△ABC 时,有AE AD =ABAC,∴2AD =54,∴AD =85. 10.如图,在梯形ABCD 中,AD ∥BC ,∠D =90°,AD =2,BC =5,DC =8.若DC 边上有一点P ,使△PAD 与△PBC 相似,则符合条件的点P 有(C)(第10题)A.1个B.2个C.3个D.4个 【解】 设PD =x ,则PC =8-x. 在△PAD 与△PBC 中,∠D =∠C =90°.①若△PAD ∽△PBC ,则AD BC =PD PC ,即25=x 8-x,解得x =167,符合题意.②若△PAD ∽△BPC ,则AD PC =PD BC ,即28-x =x5,解得x =4±6,均符合题意.综上所述,符合条件的点P 有3个.(第11题)11.如图,在正方形ABCD 中,E 是CD 的中点,点F 在BC 上,且FC =14BC ,那么图中相似的三角形共有多少对?并证明.【解】 图中相似三角形共有3对.证明如下: ∵四边形ABCD 是正方形, ∴∠D =∠C =90°,AD =DC =CB.∵DE =EC ,FC =14BC ,∴EC =12BC =2CF ,∴AD DE =ECCF=2,∴△ADE ∽△ECF , ∴AE EF =ADEC,∠DAE =∠CEF , ∴AE EF =AD DE ,即AD AE =DE EF. ∵∠DAE +∠AED =90°, ∴∠CEF +∠AED =90°, ∴∠AEF =90°,∴∠D =∠AEF ,∴△ADE∽△AEF.由相似三角形的传递性,得△AEF∽△ADE∽△ECF,即△ADE∽△ECF,△ADE∽△AEF,△AEF∽△ECF.12.如图①,△ABC与△CDE是等腰直角三角形,直角边AC,CD在同一条直线上,M,N分别是斜边AB,DE的中点,P是AD的中点,连结AE,BD,PM,PN.(1)猜想PM与PN的数量关系及位置关系,请直接写出结论.(2)现将图①中的△CDE绕点C顺时针旋转α(0°<α<90°),得到图②,AE与MP,BD,BC分别交于点G,H,O.请判断(1)中的结论是否成立?若成立,请证明;若不成立,请说明理由.(3)若图②中的等腰直角三角形变成直角三角形,使BC=kAC,CD=kCE,如图③,写出PM与PN的数量关系,并加以证明.(第12题)【解】(1)PM=PN,PM⊥PN.理由如下:∵△ABC和△CDE是等腰直角三角形,∴AC=BC,EC=CD,∠ACB=∠ECD=90°.在△ACE 和△BCD 中, ∵⎩⎪⎨⎪⎧AC =BC ,∠ACE =∠BCD =90°,CE =CD ,∴△ACE ≌△BCD(SAS). ∴AE =BD ,∠EAC =∠CBD.∵M ,N 分别是斜边AB ,DE 的中点,P 是AD 的 中点,∴PM =12BD ,PN =12AE ,∴PM =PN.易得∠NPD =∠EAC ,∠MPA =∠BDC ,∠EAC +∠BDC =90°,∴∠MPA +∠NPD =90°, ∴∠MPN =180°-90°=90°,即PM ⊥PN. (2)成立.证明如下:同(1)可得△ACE ≌△BCD(SAS), ∴AE =BD ,∠CAE =∠CBD. 又∵∠AOC =∠BOE , ∴∠BHO =∠ACO =90°.∵P ,M ,N 分别是AD ,AB ,DE 的中点, ∴PM =12BD ,PN =12AE ,∴PM =PN.易得PM ∥BD ,PN ∥AE. ∴∠MGE +∠BHA =180°. ∴∠MGE =∠BHO =90°. ∴∠MPN =∠MGE =90°. ∴PM ⊥PN.(3)PM =kPN.证明如下: ∵△ABC 和△CDE 是直角三角形, ∴∠ACB =∠ECD =90°.∴∠ACB +∠BCE =∠ECD +∠BCE. ∴∠ACE =∠BCD. ∵BC =kAC ,CD =kCE , ∴BC AC =CDCE=k ,∴△BCD ∽△ACE , ∴BD =kAE.∵P ,M ,N 分别是AD ,AB ,DE 的中点, ∴PM =12BD ,PN =12AE.∴PM =kPN.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如图,为了估算河的宽度,我们可以在河对岸选定一点A,再在河的这一边选定点B和点C,使得AB⊥BC,然后选定点E,使EC⊥BC,确定BC与AE的交点D,若测得BD=180米,DC=60米,EC=50米,你能知道小河的宽是多少吗?
A.4∶5B.5∶4C.5∶9D.4∶9
(3)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=2,BD=1,则AD的长是()
A.1B. C.2D.4
三、开动脑筋哟
如图4-6-14,在四边形ABCD中,AC、BD相交于点O,∠ABD=∠ACD,试找出图中的相似三角形,并加以证明.
图4-6-14
(4)如图,正方形ABCD的边长为2,AE=EB,MN=1,线段MN的两端分别在CB、CD上滑动,那么当CM=________时,△ADE与△MNC相似.
二、认真选一选
(1)如图,下列条件不能判定△ABC与△ADE相似的是()
A. B.∠B=∠ADE
C. D.∠C=∠AED
(2)在□ABCD中,E在BC边上,AE交BD于F,若BE∶EC=4∶5,则BF∶FD等于()
《两个三角形相似的判定》习题
一、请你填一填
(1)如图,在△ABC中,AC是BC、DC的比例中项,则△ABC∽___Βιβλιοθήκη ____,理由是________.
(2)如图,D、E、F分别是△ABC各边的中点,则△DEF∽________,理由是________.
(3)如图,∠BAD=∠CAE,∠B=∠D,AB=2AD,若BC=3cm,则DE=________cm.
