1.4 等腰梯形的性质和判定 课件(苏科版九年级上)
1.4等腰梯形的性质与判定

§1.3.5等腰梯形的性质与判定(九年级上数学007)—— 研究课班级________姓名________一.学习目标:1.能证明等腰梯形的性质定理和判定定理,并能用之解决问题;2.经历证明的过程,不断感受证明的必要性、感受合情推理和演绎推理都是人们正确认识事物的重要途径;3.感受探索活动中所体现的转化的数学思想方法.二.学习重点:等腰梯形的性质和判定;学习难点:转化思想.以及正确的添加辅助线.三.教学过程(一)知识梳理:我们曾用等腰三角形剪出了等腰梯形并探索得到等腰梯形的性质和判定,请你回忆等腰梯形的相关知识.1.等腰梯形定义:_______________________________的图形叫做等腰梯形.2.根据上图,我们得知了等腰梯形的一个性质:______________________________.同样我们也可以通过图①、图②得到这样的性质,你知道这些线是如何添加的吗?有何帮助?图①______________________________.图②______________________________.3.若按照图③________________________的添法,我们又能得到一个性质:________ _____.4.等腰梯形性质:①________ _____;②________ _____.5.等腰梯形的判定:________________________________________________ ________________________(二)反馈讲练:1. 若等腰梯形的一个锐角为40°,则其他三个角的度数分别是________ _____.变式1:若等腰梯形两角之和为100°,则等腰梯形的四个角度数分别是________ _____. 思考:有两个内角..相等的梯形是________ _____. ①通过“平移一腰....”找寻等腰梯形的边角关系.(10 长沙)已知等腰梯形的上底是4cm ,下底是10cm ,一个底角是60°,则腰长为______ __. 变式1: 在梯形ABCD 中,AD ∥BC ,AD =1,BC =4,∠C =70°,∠B =40°,则AB 的长为______ . 变式2:如图1,在梯形ABCD 中,AD ∥BC ,AB =DC =5,AD =2,BC =7,则∠B =_____ 变式3:(10西安)如图2,在梯形ABCD 中,DC ∥AB ,∠A +∠B =90°.若AB =10,AD =4,DC =5,则梯形ABCD 的面积为 .图① 图② 图③ 的梯形..是等腰梯形 图1 图2②熟记一个常规的题型.(10 台州)梯形ABCD 中,AD ∥BC ,AB=CD=AD =2,∠B =60°,则下底BC 的长是 . 变式1:(10 宁波)如图1,在等腰梯形ABCD 中,AD ∥BC ,AB =AD =CD . 若∠ABC =60°,BC =12,则梯形ABCD 的周长为 .变式2:(10 攀枝花)如图2,在梯形ABCD 中,AB ∥DC ,DB ⊥AD ,AD =DC =BC =2cm ,那么梯形ABCD 的面积是 .变式3:(10 湖州)如图3,在梯形ABCD 中,DC ∥AB ,AD =BC ,BD 平分∠ABC ,∠A =60°.(1)求∠ABD 的度数;(2)若AD =2,求对角线BD 的长.变式4:(11 绵阳)如图4,在等腰梯形ABCD 中,AB//CD ,对角线AC 、BD 相交于O ,∠ABD =30°,AC ⊥BC , AB =8cm ,则△COD 的面积为 .③通过“平移..对角线...”找寻梯形两条对角线与两底和关系. 如右图,在梯形ABCD 中,AD ∥BC ,对角线AC ⊥BD ,AC =6,BD =8.Ⅰ.AD +BC = .Ⅱ.梯形ABCD 的高= .Ⅲ.S 梯形ABCD = .变式1.(10 威海)如图1,在梯形ABCD 中,AB ∥CD ,AD =BC ,对角线AC ⊥BD ,垂足为O .若CD =3,AB =5,则AC 的长为 .变式2.(10 黄冈)如图2,在等腰梯形ABCD 中,AC ⊥BD ,AC =6cm ,则等腰梯形ABCD 的面积为_____cm 2.变式3.(10 芜湖)如图3,在等腰梯形ABCD 中,AD ∥BC ,对角线AC ⊥BD 于点O ,AE ⊥BC ,DF ⊥BC ,垂足分别为E 、F ,AD =4,BC =8,则AE +EF 等于 .图1 图2 图 3图4图1 图2 图3(三)例题精讲:1.如图,等腰梯形ABCD 中,AD ∥BC ,点E 是AD 延长线上一点,DE =BC .(1)求证:∠E =∠DBC ; (2)判断△ACE 的形状(不需要说明理由).2.如图,已知在梯形ABCD 中,AD ∥BC ,AB =DC ,对角线AC 和BD 相交于点O ,E 是BC 边上的一个动点(点E 不于B 、C 两点重合),EF ∥BD 交AC 于点F ,EG ∥AC 交BD 于点G .(1)求证:四边形EFOG 的周长等于2OB ;(2)请将上述题目的条件“梯形ABCD 中,AD ∥BC ,AB =DC ”改为另一种四边形,其他条件不变,使得结论“四边形EFOG 的周长等于2OB ”仍成立,并将改编后的题目画出图形,写出已知、求证,不必证明3. (11 益阳)如图,是小红设计的钻石形商标,△ABC 是边长为2的等边三角形,四边形ACDE 是等腰梯形,AC ∥ED ,∠EAC =60°,AE =1.(1)证明:△ABE ≌△CBD ;(2)图中存在多对相似三角形,请你找出一对进行证明,并求出其相似比(不添加辅助线,不找全等的相似三角形);(3)小红发现AM =MN =NC ,请证明此结论;(4)求线段BD 的长.4.如图,等腰梯形ABCD 中,AD ∥BC ,AD =3cm ,BC =7cm ,∠B =60°,P 为下底BC 上一点(不与B 、C 重合),连结AP ,过P 点作PE 交DC 于E ,使得∠APE =∠B .(1)求证:△ABP ∽△PCE .(2)求等腰梯形的腰AB 的长.A BC DEDCBA 等腰梯形的判定:1 (11 盐城)将两个形状相同的三角板放置在一张矩形纸片上,按图示画线得到四边形ABCD ,则四边形ABCD 的形状是 .依据: . 2.如图,在梯形ABCD 中,AD ∥BC ,点E 是BC 边的中点,EM ⊥AB ,EN ⊥CD ,垂足分别为M 、N 且 EM =EN .求证:梯形ABCD 是等腰梯形3.如图,在梯形ABCD 中,AB ∥DC , DB 平分∠ADC ,过点A 作AE ∥BD ,交CD 的延长线于点E ,且∠C =2∠E .(1)求证:梯形ABCD 是等腰梯形.(2)若∠BDC =30°,AD =5,求CD 的长.4.如图,在梯形ABCD 中,AD ∥BC , ∠B =900,AD =24cm ,AB =8cm ,BC =26cm ,动点P 从A 点开始沿AD 边以1cm/秒的速度向D 运动,动点Q 从C 点开始沿CB 边以3cm/秒的速度向B 运动,P 、Q 分别从A 、C 同时出发,当其中一点到端点时,另一点也随之停止运动.设运动时间为t 秒,t 分别为何值时,四边形PQCD 是平行四边形、等腰梯形?5.如图,在直角梯形ABCD 中,∠ABC =90°,AD ∥BC ,AD =4,AB =5,BC =6,点P 是AB 上一个动点,当PC +PD 的和最小时,PB 的长为__________.。
数学高效课堂公开课1.4等腰梯形的性质与判定

B A D
O
C
例1:判断下列说法是否正确。 (1)一组对边平行的四边形是梯形. (2)等腰梯形的对角线相等. (3)等腰梯形的两个底角相等. (4)等腰梯形有一条对称轴.
例2、如图,等腰梯形ABCD中,AD∥BC,点E 是AD 延长线上一点,DE=BC. (1)求证:∠E=∠DBC; (2)判断△ACE的形状
A
D
E
B
C
1、将两个形状相同的三角板放置在一张 矩形纸片上,按图示画线得到四边形 ABCD,则四边形ABCD的形状是 等腰梯形 . 依据:在同一底上的两个角相等的梯形是等腰梯形。 .
A D
B
C
2.如图,在等腰梯形ABCD中,AB=CD=8, BC=15,∠B=60°, 则AD=
7 .
B
A
D
C
E
3、已知如图,等腰梯形ABCD的面积是4 ㎝2,M为CD中点,连AM,BM,则△ABM 2cm2 的面积是_______
A M D
说说你的证 明思路!
B
C
初 中 数 学
九 上
课外思考题: 请你画一个等腰梯形,使它的
两底的长分别为6cm和12cm,腰长
为5cm.你能否尝试用不同的方法来
画这个等腰梯形?
学有所获
新问题 转化 转化 等腰梯形 老问题
三角形或特 殊四边形
挑战自我
已知:在梯形ABCD中,AD∥BC, AB=DC,M、N分别是AD、BC的中点, AD=3,BC=9,∠B=450, 求MN的长。A M D
2.等腰梯形的判定: ______________________________ 3.等腰梯形的性质: _______________________________ _______________________________
§1.4等腰梯形的的性质与判定
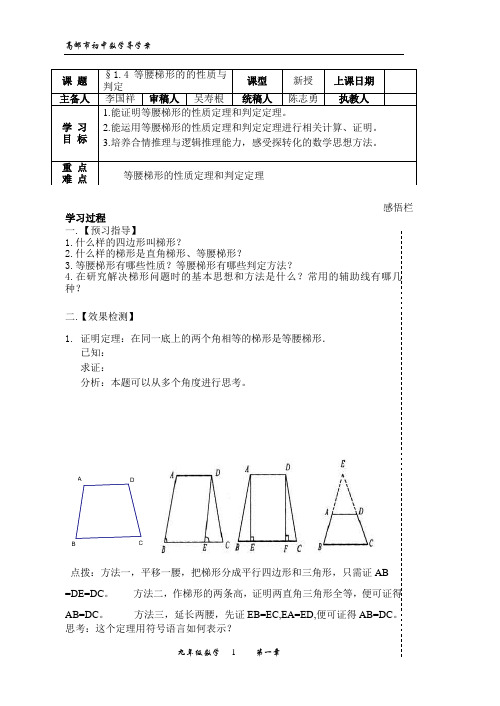
学习过程一.【预习指导】1.什么样的四边形叫梯形?2.什么样的梯形是直角梯形、等腰梯形?3.等腰梯形有哪些性质?等腰梯形有哪些判定方法?4.在研究解决梯形问题时的基本思想和方法是什么?常用的辅助线有哪几种?二.【效果检测】1. 证明定理:在同一底上的两个角相等的梯形是等腰梯形. 已知:求证:分析:本题可以从多个角度进行思考。
点拨:方法一,平移一腰,把梯形分成平行四边形和三角形,只需证AB=DE=DC 。
方法二,作梯形的两条高,证明两直角三角形全等,便可证得AB=DC 。
方法三,延长两腰,先证EB=EC,EA=ED,便可证得AB=DC 。
思考:这个定理用符号语言如何表示?感悟栏DC B A三.【小组检查】感悟栏小组内成员就上述习题进行讨论、修正。
四.【布置任务】师生互动探究问题1. “在同一底上的两个角相等的梯形是等腰梯形”的逆命题是什么?证明:等腰梯形同一底上的两底角相等。
思考:这个定理用符号语言如何表示?问题2. 等腰梯形的两条对角线相等。
思考:这个定理用符号语言如何表示?五.【小组交流】学生展示1.证明:等腰梯形同一底上的两底角相等。
2.证明:两条对角线相等的梯形是等腰梯形六.【课堂训练】拓展延伸问题3.如图等腰梯形ABCD 中,AD ∥BC ,AB=DC ,M 是AD 的中点, 求证:BM=CM思考:你能够用一个命题概括吗?拓展:(1)如图等腰梯形ABCD 中,AD ∥BC ,BM=CM 。
求证: M 是AD 的中点(2)如图梯形ABCD 中,AD ∥BC ,M 是AD 的中点,BM=CM 。
求证:四边形ABFE 是等腰梯形;七.【课堂小结】1.梯形性质和判定定理是什么?2.解决梯形问题的基本思想和方法有哪些?3.解决梯形问题时,常用的辅助线有哪几种?.4.你还有哪些困惑?B C A M D感悟栏八.【课堂反馈】 班级____________ 姓名________ 成绩____________1.四边形的四个内角的度数比是2∶3∶3∶4,则这个四边形是( )A.等腰梯形B.直角梯形C.平行四边形D.不能确定2.在等腰梯形ABCD 中,AD ∥BC ,AE ⊥BC 于E ,且AE=AD ,BC=3AD ,则∠B 等于( )A.30°B.45°C.60°D.135°3.梯形的上底长为6 cm ,将一腰平移到上底的另一端点位置后与另一腰和 下底所构成的三角形的周长为20 cm ,那么梯形的周长为_______.4.梯形ABCD 中,AD ∥BC ,∠B=50°,∠C=80°,AD=8,BC=11,则CD=____。
江苏省连云港市九年级数学上册《等腰梯形的性质和判定》课件苏科版PPT文档共16页

43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
江苏省连云港市九年级数念园林好,人间良可辞。 22、步步寻往迹,有处特依依。 23、望云惭高鸟,临木愧游鱼。 24、结庐在人境,而无车马喧;问君 何能尔 ?心远 地自偏 。 25、人生归有道,衣食固其端。
41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
九年级数学等腰梯形的性质和判定

还听老辈人讲过一个故事。说是解放初时,西安城开了不少新工厂,而许多西安人有房子有地不愿去进厂当工人,于是工厂就去别的穷困地方招了不少工人。在东大街上有这么家皮鞋厂,老板十分 仗义,从不亏待工人。说是有一天老板心一动想给工人们变变花样改善一下生活,于是,他就让厨房想办法给工人们蒸了些红薯。可谁知工人们吃饭时一见红薯就炸锅了,大吵大闹,说老板不把工人当 人。老板一脸的委曲问:“我好心给大家变个花样改善一下,怎么就没把大家当人了?”工人们却说:“我们离开老家过来给你当工人,就是再也不想吃红薯了,你今天却故意给我们吃那破东西,分明 是不拿我们当人么!”老板一听这,冲厨房一挥手说:“这还不简单?大米白面咱不有的是嘛!把红薯锅倒掉,跟以往一样烙锅盔、下面,再另添俩菜,一定让大家吃饱咥美!”工人们山呼万岁。如此, 一场风波平息了。
篮球论坛 我们的这个同学从来不会说西安城墙是假的,因为西安的城墙他不但见过、摸过,而且还住过。至于有人提出来用现代的砖整修过的问题,他会说:瞎扯淡!谁家祖先能盖出几百、几千年不烂的房
子?就如这城墙,后人若不及时整修恐修么?
1.4等腰梯形的性质和判定

B
C
B
E
C B E
F C
性质定理2、等腰梯形的两条对角线相等。 证明定理2: 已知:梯形ABCD中,AD∥BC. 求证:AC=BD.
A D
思路1:转化方向——全等三角形.
B
思路2:转化方向——平行四边形.
C
A
DБайду номын сангаас
A
D
B
C
B
C
例题1:
如图,等腰梯形ABCD中,AD∥BC,点E是AD 延长 线上一点,DE=BC. (1)求证:∠E=∠DBC; (2)判断△ACE的形状
解决梯形问题常用的方法:
(1)平移腰:构造平行四边形 (2)“作高”:使两腰在两个直角三角形中. (3)“平移对角线”:使两条对角线在同一个三角形 中 (4)“延长两腰”:构造具有公共角的两个等腰三角 形. (5)取一腰的中点:构造全等三角形,将上底下移
学有所获
转化
新问题
老问题
等腰梯形
转化
三角形或特 殊四边形
1.4 等腰梯形的性质和判定
1.等腰梯形概念: 有两腰相等的梯形叫做等腰梯形。 2.等腰梯形的判定: (1)定义(2)在同一底上的两个角相等的梯形是等腰 梯形。 3.等腰梯形的性质: 等腰梯形同一底上的两个角相等。 等腰梯形的两条对角线相等。
证明:在同一底上的两个角相等的梯形是等 腰梯形
已知:在梯形ABCD中,AD//BC, ∠B=∠C.
(2008年江苏省连云港市)如图,在直角梯形纸片 中, , , ,将纸片沿过点D的直线折 叠,使点A落在CD边上的E点处,折痕为DF.连接EF并展开纸 片. (1)求证:四边形ADEF是正方形; (2)取线段AF的中点G,连接EG,如果 ,试说明 四边形GBCE是等腰梯形.
江苏省灌南县实验中学九年级数学上册《等腰梯形的性质与判定》课件苏科版PPT文档23页

43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
江苏省灌南县实验中学九年级数学上册 《等腰梯形的性质与判定》课件苏科版
•
46、寓形宇内复几时,曷不委心任去 留。
•
47、采菊东篱下,悠然见南山。
•
48、啸傲东轩下,聊复得日 有所长 。
•
50、环堵萧然,不蔽风日;短褐穿结 ,箪瓢 屡空, 晏如也 。
41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
苏科版九年级上册 1.4等腰梯形的性质与判定(2)

是_____,还具备在_______相等; ▪ 书写格式;Fra bibliotek判定定理二
▪ _________相等的梯形是等腰梯形; ▪ 如何证明? ▪ 根据判定定理二,要证明一个图形是等腰梯形,首先它必须
是_____,还具备在_______相等; ▪ 书写格式;
▪ 例一; ▪ 例二;
典型例题
练习
▪ 见补充习题P12第1题;
小结
▪ ____相等的____叫做等腰梯形;
▪ 根据等腰梯形的定义,一个图形要成为等腰 梯形,首先它必须是_____,还要具备_____ 相等;
▪ 在________的两个角相等的梯形是等腰梯 形;
▪ 根据判定定理一,要证明一个图形是等腰梯 形,首先它必须是_____,还具备在_______ 相等;
▪ _________相等的梯形是等腰梯形;
1.4等腰梯形的性质和判定2
教学目标
▪ 1.会证明等腰梯形的判定定理; ▪ 2.会用判定定理来解决有关问题;
回忆
▪ 什么样的图形叫做等腰梯形? ▪ ____相等的____叫做等腰梯形; ▪ 根据等腰梯形的定义,一个图形要成为等腰梯形,首先它必
须是_____,还要具备_____相等;
判定定理一
▪ 在________的两个角相等的梯形是等腰梯形; ▪ 在解决有关梯形的问题时常见的辅助
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等腰梯形判定定理2
两条对角线相等的梯形是等腰梯形 已知:如图梯形ABCD,AD∥BC,AC=BD, 求证:梯形ABCD是等腰梯形
A D
B
1 E F
2
C
E
例题分析:
例1.如图, 梯形ABCD中,AB∥CD, M是CD的
中点, ∠1=∠2;
说明梯形ABCD是等腰梯形.
C M
D
B
A
例题分析:
例2. 如图,等腰梯形ABCD中,AD∥BC,点
E是AD 延长线上一点,DE=BC.
(1)求证:∠E=∠DBC;
(2)判断△ACE的形状
A
DEΒιβλιοθήκη BC小结与思考:
解决梯形问题常用的方法:
(1)平移腰:构造平行四边形 (2)“作高”:使两腰在两个直角三角形中. (3)“平移对角线”:使两条对角线在同一个三角形中 . (4)“延长两腰”:构造具有公共角的两个等腰三角 形. (5)取一腰的中点:构造全等三角形,将上底下移
等腰梯形是轴对称图形,过两底中点的 直线是它的对称轴
性质定理1
等腰梯形同一底上的两个底 角相等
已知:如图等腰梯形ABCD,AD∥BC,AB=CD, 求证:∠B=∠C
A D
它的逆命题是什么?
1
B
正确吗?
C
E
判定定理1
在同一底上的两个角相等的梯形是等腰梯形
已知:在梯形ABCD中,AD//BC, ∠B=∠C. 求证:梯形ABCD是等腰梯形.
思路1:转化方向——等腰三角形.
证明:延长BA,CD相交于点E. ∵∠B=∠C, ∴BE=CE.
∵四边形ABCD是梯形,
∴AD∥BC. ∴∠EAD=∠B,∠EDA=∠C. ∴∠EAD=∠EDA. ∴AE=DE.
∴AB=CD.
∴梯形ABCD是等腰梯形.
思路2:转化方向——平行四边形.
证明:过点A作AE∥DC,交BC 于点E. 此时四边形AECD是平行四边形. 则AE∥CD且AE=CD,
1.4 等腰梯形的性质和判定
知识回顾
1.等腰梯形概念: 两腰相等的梯形 _______________________________ 叫做等腰梯形
2.等腰梯形的性质:
等腰梯形在同一底上的两个底角相等 _______________________________ 等腰梯形的两条对角线相等
_______________________________
A D
B
C
等腰梯形的判定定理1
在同一底上的两个角相等的梯形是等 腰梯形.
等腰梯形的性质定理2
等腰梯形的两条对角线相等。 已知:如图等腰梯形ABCD, AD∥BC,AB=CD, 求证: AC=BD
A D A D
B
C
思路1:转化方向——全等三角形. 思路2:转化方向——平行四边形.
B
A
D C
它的逆命题是什么?正确吗?
∴∠AEB=∠C.
又∵∠B=∠C, ∴∠B=∠AEB. ∴AB=AE. ∴AB=CD. ∴梯形ABCD是等腰梯形.
思路3:转化方向——全等三角形.
证明:过点A作AE⊥BC, DF⊥BC,垂足分别为点E,F,
则有∠AEB=∠DFC.
∵AD∥BC,
∴AE=DF,
∵∠B=∠C, ∴△AEB≌△DFC(AAS). ∴AB=CD. ∴梯形ABCD是等腰梯形.
