2015年井冈山大学专升本高等数学考试大纲
专升本的数学考试大纲
专升本的数学考试大纲专升本的数学考试是高等教育自学考试中的重要组成部分，它旨在检验学生对高等数学基础知识的掌握程度和应用能力。
考试大纲通常包括以下几个主要部分：函数、极限与连续性、导数与微分、积分、无穷级数、多元函数微分学、常微分方程等。
以下是对这些部分的概述：# 函数、极限与连续性- 函数：理解函数的概念，包括定义域、值域、函数的表示方法等。
- 极限：掌握极限的基本概念，包括数列极限和函数极限，以及极限的运算法则。
- 连续性：理解连续函数的定义，连续函数的性质，以及间断点的分类。
# 导数与微分- 导数：掌握导数的定义、几何意义、基本求导公式和求导法则。
- 微分：理解微分的概念，微分与导数的关系，以及一阶微分的计算。
# 积分- 不定积分：掌握基本积分公式，换元积分法和分部积分法。
- 定积分：理解定积分的定义、性质和计算方法，包括几何意义和物理意义。
- 反常积分：了解反常积分的概念和计算方法。
# 无穷级数- 数项级数：掌握正项级数的收敛性判别方法，包括比较判别法、比值判别法等。
- 幂级数：理解幂级数的收敛半径和收敛区间，以及幂级数的运算。
# 多元函数微分学- 偏导数：理解偏导数的定义和计算方法。
- 全微分：掌握全微分的概念和计算。
- 多元函数的极值：了解多元函数极值的概念和求法。
# 常微分方程- 一阶微分方程：掌握可分离变量方程、一阶线性微分方程的解法。
- 高阶微分方程：理解高阶微分方程的基本概念，包括齐次和非齐次方程的解法。
- 微分方程的应用：了解微分方程在实际问题中的应用，如物理、工程等领域。
# 线性代数基础- 矩阵：理解矩阵的概念，矩阵的运算，包括加法、乘法、转置、求逆等。
- 行列式：掌握行列式的定义、性质和计算方法。
- 向量空间：了解向量空间的概念，基、维数、线性组合等。
- 线性变换：理解线性变换的定义和矩阵表示。
# 概率论与数理统计基础- 随机事件：掌握随机事件的概率计算，包括加法公式、乘法公式等。
(整理)江西专升本大纲.
江西理工大学2010年“专升本”考试自主命题课程考试大纲科目一、《高等数学》考试大纲一. 主要内容1。
函数与极限函数；数列的极限；函数的极限；无穷小与无穷大；极限运算法则极限存在准则，两个重要极限；无穷小的比较；函数的连续性；闭区间上连续函数的性质。
2．导数与微分导数的概念及其性质；函数的和、差、积、商的求导法则；复合函数的求导法则；高阶导数、隐函数的导数以及由参数方程所确定的函数的导数；函数的微分。
3、中值定理与导数的应用中值定理；洛必塔法则；函数的单调性和曲线的凹凸性；函数的极值和最大值、最小值；函数图形的描绘。
4、不定积分不定积分的概念与性质；换元积分法；分部积分法；有理函数的不定积分。
5、定积分及其应用定积分的概念与性质；微积分基本公式；定积分的换元法及分部积分法；定积分在几何上的应用；反常（广义）积分。
6、微分方程微分方程的基本概念；可分离变量的微分方程；齐次方程；一阶线性微分方程；二阶常系数齐次线性微分方程；二阶常系数非齐次线性微分方程。
7、向量代数与空间解析几何向量及其线性运算；点的坐标与向量的坐标；数量积、向量积；平面及其方程；空间直线及其方程。
8、多元函数微分法及其应用多元函数的基本概念；偏导数；全微分；多元复合函数的求导法则；隐函数的求导公式；多元函数微分法的几何应用举例；多元函数的极值及其求法。
9、重积分二重积分的概念与性质；二重积分的计算。
10、无穷级数常数项级数的概念与性质；常数项级数的审敛法；幂级数；函数展开成幂级数。
二. 基本要求1 。
函数与极限a．理解初等函数的概念。
熟练掌握函数的四种特性。
会建立简单问题的函数关系式。
b．理解数列极限的描述性定义。
熟练掌握数列极限的计算。
c．理解函数极限的描述性定义。
熟练掌握极限的四则运算法则。
理解无穷小与无穷大的概念，掌握无穷小的性质及阶的比较。
熟练掌握极限的收敛准则。
熟练掌握两个重要极限。
d．了解函数的连续性。
知道闭区间上连续函数的性质。
2015年江西普通专升本招生院校专业
2015年江西普通专升本招生院校专业按A—Z顺序排列对比大全（按专业名称的首写字的字母）目录B (2)C (3)D (6)F (9)G (11)H (15)J (19)K (24)L (25)M (26)N (27)Q (28)R (29)S (31)T (35)W (37)X (39)Y (41)Z (44)保险表演播音与主持艺术编辑出版学测绘工程材料科学与工程财政学财务管理材料成型及控制工程车辆工程城乡规划材料化学材料物理产品设计城市规划测控技术与仪器D电气工程及其自动化电子信息工程地质工程地理信息系统电子商务电子科学与技术动物医学动物科学动画地理科学道路桥梁与渡河工程电子信息科学与技术F房地产经营管理服装设计与工程飞行器制造工程服装与服饰设计法学G工程管理给水排水工程工商管理广告学公共事业管理学国民经济管理管理科学工艺美术工程造价广播电视学光电信息工程广播电视编导国际经济与贸易工业设计工业工程H环境设计化学工程与工艺汉语言文学环境工程化学护理学焊接技术与工程汉语国际教育绘画环境工程J机械设计制造及自动化交通工程建筑环境与设备工程机械电子工程建筑电气与智能化交通设备信息工程计算机科学与技术经济学金融学交通运输金属材料工程经济学经济犯罪侦查教育技术学建筑环境与能源应用工程建筑学康复治疗学口腔医学会计学旅游管理劳动和社会保障历史学临床医学美术学农业水利工程汽车服务工程人力资源管理软件工程人文地理与城乡规划日语热能与动力工程S商务英语视觉传达设计数学与应用数学数字媒体技术园林生物科学税务思想政治教育食品科学与工程生物工程市场营销生物技术审计学社会体育指导与管理水利水电工程水文与水资源工程水土保持与荒漠化防治社会学社会体育T统计学体育教育陶瓷艺术设计通信工程土木工程W舞蹈学物联网工程物理学文化产业管理物流管理网络工程X新闻学新能源科学与工程新能源材料与器件信息工程信息管理与信息系统信息与计算科学行政管理学前教育Y医学检验技术口腔医学园艺英语冶金工程音乐学应用化学园林药学医学影像技术药物制剂Z自动化资源勘查工程资源技术与工程侦查学治安学制药工程中医学中西医临床医学针灸推拿学中药学资源环境科学。
井冈山大学2020年普通专升本《数学与应用数学》专业基础科目考试大纲
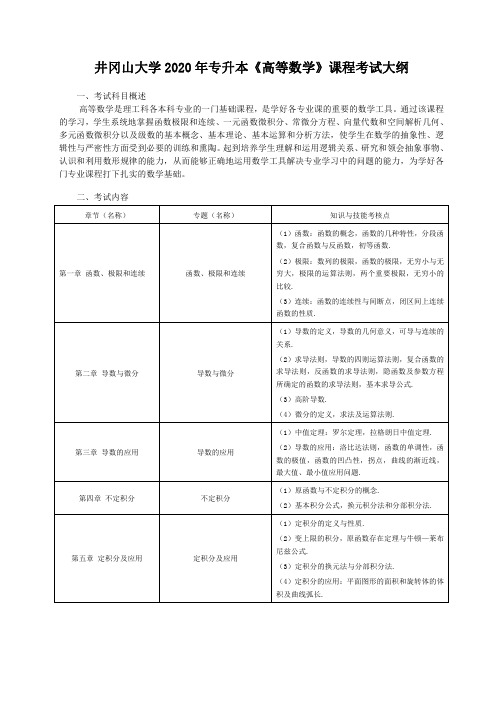
井冈山大学2020年专升本《高等数学》课程考试大纲一、考试科目概述高等数学是理工科各本科专业的一门基础课程，是学好各专业课的重要的数学工具。
通过该课程的学习，学生系统地掌握函数极限和连续、一元函数微积分、常微分方程、向量代数和空间解析几何、多元函数微积分以及级数的基本概念、基本理论、基本运算和分析方法，使学生在数学的抽象性、逻辑性与严密性方面受到必要的训练和熏陶。
起到培养学生理解和运用逻辑关系、研究和领会抽象事物、认识和利用数形规律的能力，从而能够正确地运用数学工具解决专业学习中的问题的能力，为学好各门专业课程打下扎实的数学基础。
二、考试内容三、考试方式与试卷结构1.考试方式：闭卷，笔试2.试卷分数：满分150分3.考试时间：120分钟4.题型比例：填空题，共7小题，每小题3分，计21分。
单项选择题，共7小题，每小题3分，计21分。
计算题，共8小题，每小题10分，计80分。
综合或应用解答题2题，计20分。
证明题1题，计8分.井冈山大学2020年专升本《线性代数》课程考试大纲一、考试科目概述线性代数是理工科各本科专业的一门基础课程，是学好各专业课的重要的数学工具。
通过本课程的学习，使学生不仅能较好地掌握行列式、矩阵特有的分析概念，并在一定程度上掌握用行列式、矩阵解决问题的方法，而且能使他们对线性代数的基本概念、基本方法、基本结果有所了解，并能运用其解决实际问题中的一些简单课题。
通过该课程的学习，使学生掌握线性代数的基本理论与方法，培养学生正确运用数学知识来解决实际问题的能力，并为进一步学习后续课程及相关课程打好基础。
二、考试内容章节（名称）专题（名称）知识与技能考核点第一章行列式行列式的性质行列式的性质及应用行列式的计算行列式的计算行列式按一行(列)展开行列式按一行(列)展开的应用第二章矩阵及其运算矩阵的概念与运算性质矩阵的运算性质矩阵的逆逆矩阵的性质、计算和应用矩阵的分块法运用分块矩阵思想解决矩阵相关计算问题第三章矩阵的初等变换与线性方程组矩阵的初等变换矩阵的初等变换的性质及应用矩阵的秩矩阵秩的性质及计算线性方程组的解线性方程组有解的判定及计算第四章向量组的线性相关性向量组线性相关与线性无关向量组线性相关与线性无关的概念与判定向量组的秩向量组的秩的判定线性方程组解的结构线性方程组通解的计算向量空间向量空间的性质第五章相似矩阵及二次型向量的内积、长度及正交性向量的内积、长度及正交性的概念与性质方阵的特征值与特征向量特征值与特征向量的计算相似矩阵利用相似变换化矩阵为对角矩阵对称矩阵的对角化利用对角变换化矩阵为对角矩阵二次型及其标准形二次型的矩阵及标准形的定义用配方法化二次型为标准形用配方法化二次型为标准形正定二次型正定二次型的判定三、考试方式与试卷结构1.考试方式：闭卷，笔试2.试卷分数：满分150分3.考试时间：120分钟4.题型比例：选择题30分；填空题30分；计算题75分；证明题15分。
2015年井冈山大学专升本工程力学考试大纲
2015年井冈山大学专升本工程力学考试大纲一、适用专业此考试大纲适用于建筑工程学院土木工程和工程管理二个本科专业的“专升本”考试。
二、参考教材1．邹昭文，程光均，张祥东编，建筑力学第一分册《理论力学》第4版，高等教育出版社。
2．干光瑜，秦惠民编，秦惠民，王秋生，刘钊修订，建筑力学第二分册《材料力学》第4版，高等教育出版社。
三、考试内容理论力学部分:第一章静力学公理和物体的受力分析考试内容：1-1静力学基本概念1-2静力学公理1-3约束与约束反力1-4物体的受力分析和受力图第二章汇交力系考试内容：2-1汇交力系合成与平衡的几何法2-1力在坐标轴上的投影2-3汇交力系合成与平衡的解析法第三章平面一般力系考试内容：3-1平面力对点之矩的概念与计算3-2力偶及其性质、平面力偶系的合成与平衡3-3力的平移定理3-4平面一般力系向作用面内一点简化3-5平面一般力系的平衡条件和平衡方程3-6物体系统的平衡、静定与超静定问题材料力学部分：第一章绪论和基本概念考试内容：1-1材料力学的任务1-2关于变形固体的概念1-3材料力学采用的基本假设1-4内力的概念截面法1-5应力的概念1-6位移和应变的概念1-7构件变形的基本形式第二章轴向拉伸和压缩考试内容：2-1轴向拉伸、压缩及工程实例2-2轴力和轴力图2-3横截面上的应力2-4斜截面上的应力2-5拉、压杆的变形2-6材料在拉伸、压缩时的力学性质2-7强度计算、许用应力和安全因素2-8拉伸和压缩超静定问题第三章剪切和扭转考试内容：3-1剪切及剪切的实用计算3-2拉（压）杆连接部分的强度计算3-3扭转、扭矩和扭矩图3-4薄壁圆杆的扭转3-5切应力互等定理和剪切胡克定律3-6圆杆扭转时的应力3-7圆杆扭转时的变形第四章梁的应力星原专升本扣扣：800，089,910考试内容：4-1工程中的弯曲问题4-2梁的荷载和支座反力4-3梁的内力及其求法4-4内力图—剪力图和弯力图4-5弯矩、剪力与荷载集度间的关系第五章截面的几何性质考试内容：5-1静矩和形心5-2惯性矩和惯性积5-3惯性矩的平行移轴公式主轴和主惯性距5-4组合截面惯性矩的计算第六章：梁的应力考试内容：6-1梁的正应力6-2梁的正应力强度条件及其应用6-3梁的合理截面形状及变截面梁6-4矩形截面梁的切应力6-6梁的切应力强度条件第七章梁的变形考试内容：7-1概述7-2梁的挠曲线的近似微分方程7-3积分法计算梁的位移7-4叠加法计算梁的位移7-5梁的刚度校核7-6超静定梁第八章应力状态和强度理论考试内容：8-1应力状态的概念8-2平面应力状态下任意斜截面上的应力8-3主应力和极值切应力8-4平面应力状态下的几种特殊情况8-6空间应力状态下任一点的主应力和最大切应力8-7广义胡克定律8-8强度理论第九章组合变形星原专升本扣扣：800,089,910考试内容：9-1组合变形的概念9-2斜弯曲9-3拉伸（压缩）与弯曲的组合变形9-4偏心拉伸（压缩）9-6弯曲与扭转的组合变形第十章压杆稳定考试内容：10-1压杆稳定的概念10-2铰支细长压杆的临界力10-3其他支承情况下细长压杆的临界力10-4临界应力、欧拉公式的适用范围10-5压杆的稳定计算10-6提高压杆稳定性的措施。
2015专升本考试大纲
2015专升本考试大纲2015年的专升本考试是中国高等教育中一个重要的选拔机制，它为专科生提供了一个继续深造的机会，使他们能够进入本科阶段学习。
考试大纲是指导考生复习和准备考试的重要文件，它规定了考试的内容、范围和要求。
以下是2015年专升本考试大纲的概述。
考试科目与内容2015年专升本考试通常包括公共基础课和专业课两个部分。
公共基础课一般包括语文、数学、英语等科目，而专业课则根据不同的专业要求有所不同，可能涵盖专业基础知识、专业技能等。
1. 语文：考试内容通常包括现代汉语的基础知识、阅读理解、写作能力等。
考生需要掌握一定的汉语词汇、语法，能够理解并分析不同文体的文章，并具备一定的写作能力。
2. 数学：数学考试内容可能包括高等数学、线性代数、概率论与数理统计等。
考生需要掌握数学的基本概念、原理和计算方法，能够解决实际问题。
3. 英语：英语考试通常包括英语听说读写四个方面的能力测试。
考生需要具备一定的词汇量、语法知识，能够进行基本的英语交流和理解英文材料。
考试形式与要求考试形式一般为笔试，可能包括选择题、填空题、简答题、论述题等。
考试要求考生在规定时间内完成所有题目，并且答案需要准确、清晰。
1. 选择题：考生需要从四个选项中选择最合适的答案。
这类题目考察考生对知识点的掌握程度和理解能力。
2. 填空题：考生需要根据题目要求填写正确的答案。
这类题目考察考生的记忆力和对知识点的熟练程度。
3. 简答题：考生需要对问题进行简要回答。
这类题目考察考生的分析和表达能力。
4. 论述题：考生需要对问题进行详细的论述。
这类题目考察考生的综合分析能力和表达能力。
复习建议1. 系统复习：考生应该系统地复习所有考试科目的知识点，确保没有遗漏。
2. 模拟练习：通过模拟考试来检验复习效果，熟悉考试流程和时间管理。
3. 重点突破：针对自己的薄弱环节进行重点复习和练习，提高解题能力。
4. 心理调适：保持良好的心态，避免过度紧张，确保在考试中能够发挥出最佳水平。
最新《高等数学(二)》专升本考试大纲资料
《高等数学（二）》专升本考试大纲《高等数学》专升本入学考试注重考察学生基础知识、基本技能和思维能力、运算能力、以及分析问题和解决问题的能力。
考试时间为2小时，满分150分。
考试内容和基本要求一、函数、极限与连续（一）考试内容函数的概念与基本特性；数列、函数极限；极限的运算法则；两个重要极限；无穷小的概念与阶的比较；函数的连续性和间断点；闭区间上连续函数的性质。
（二）考试要求1．理解函数的概念，了解函数的基本性态（奇偶性、单调性、周期性、有界性）。
了解反函数的概念，理解复合函数的概念，理解初等函数的概念。
会建立简单经济问题的函数关系。
掌握常用的经济函数（需求函数、成本函数、收益函数、利润函数）。
2．了解数列极限、函数极限的概念（不要求做给出ε，求N 或δ的习题）；了解极限性质（唯一性、有界性、保号性）。
3．掌握函数极限的运算法则；熟练掌握极限计算方法。
掌握两个重要极限，会用两个重要极限求极限；4．了解无穷小、无穷大、高阶无穷小、等价无穷小的概念，会用等价无穷小求极限。
5．理解函数连续的概念；了解函数间断点的概念，会判别间断点的类型（第一类与第二类）。
6．了解初等函数的连续性；了解闭区间上连续函数的性质，会用性质证明一些简单结论。
二、导数与微分（一）考试内容导数的概念及求导法则；隐函数所确定函数的导数；高阶导数；微分的概念与运算法则。
（二）考试要求1．理解导数的概念及几何意义和经济意义，了解函数可导与连续的关系，会求平面曲线的切、法线方程。
2．掌握基本初等函数的求导公式；掌握导数的四则运算法则和复合函数的求导法则；掌握隐函数及取对数求导法。
会熟练求函数的导数。
3．了解高阶导数的概念，掌握初等函数的一阶、二阶导数的求法。
4．理解微分的概念，了解微分的运算法则和一阶微分形式不变性，会求函数的微分。
三、中值定理与导数应用（一）考试内容罗尔中值定理、拉格朗日中值定理；洛必达法则；函数单调性与极值、曲线凹凸性与拐点。
2015井冈山大学专升本招生专业及考试科目
2015井冈山大学专升本招生专业及考试科目
井冈山大学2014年“专升本”招生专业、考试科目及参考书
序号 招生专业
招生 计划
专业考试科目
基础课
专业课 参考书
1
学前教育
50人(专业具体招生人数将根据报
考人数、英
语统考上线
人数和考试
总分等综合考虑来决定，但口腔医学专业最
多只招5x 星原专升本
扣：
800-089-910人。
退役士兵单独划
线录取，不占计划。
)
大学语文 刘晓鑫、淡中扬主
编的《大学语文新教程》，同济大学出版社2010年16
月出版。
教育学原理
《教育学基础》教育科学出版社20所重点师范大学联合编写
2
电子信息科学与技术 高等数学
刘忠东，罗贤强等编《微积分》（上、
下）中国传媒大学出版社
电子技术基础 （低频和数字）
《模拟电子技术基础》童诗白主编，《数字电子技术基础》（第四版）阎
育出版社
3
机械设计制造及其自动化
机械设计基础
《机械设计基础》，陈立德主编，高等教育出版社
4
土木工程
工程力学 1．邹昭文，程光均，张祥东编，建
《理论力学》第4版，高等教育出2．干光瑜，秦惠民编，秦惠民，王
建筑力学第二分册《材料力学》第版社。
5
工程管理
6
护理学
医学基础综合[《人
体解剖学》、《生理学》]
护理学基础 《护理学基础》崔焱主编，人卫出
7
口腔医学（最多只招5人）
医学基础综合[《口腔解剖生理学》、《口腔组织病理学》]
专业综合（口腔内科学、口腔修复学）
见考试大纲。
2015年井冈山大学专升本《高等数学》考试大纲
2015年井冈山大学专升本《高等数学》考试大纲1．高等数学是理工类本科专业后续课程的基础，是教学计划中的一门专业基础课.2．考试要求：本课程的考试要求既要考核知识，又要考核能力，因此要求考生复习本课程时应注意系统掌握本大纲所规定的基础知识，基本方法，提高运算能力和逻辑思维能力，并能运用数学知识分析，解决一些实际问题.3．本大纲中将基本要求分为由低到高的三个等级，对概念和理论性的知识，分别用“知道”、“了解”、“理解”三级区分，对运算方法的知识分别用“会或能”、“掌握”、“熟练掌握”三级区分.4．本课程考试方式为闭卷，答卷时间为120分钟，采用百分制，试题的难度按易、中、难三个层次的比例约为30：50：20.5．题型填空题，共5小题，每小题3分，计15分.单项选择题（四个备选答案中有且只有一个正确）共5小题，每小题3分，计15分.计算题，共5小题，每小题10分，计50分.综合或应用题1题，计10分.证明题1题，计10分.6．参考书目：刘忠东，罗贤强等编《微积分》（上、下）中国传媒大学出版社考试内容及要求一、函数、极限与连续1．考核知识点（1）函数：函数的概念，函数的几种特性，分段函数，复合函数与反函数，初等函数. （2）极限：数列的极限，函数的极限，无穷小与无穷大，极限的运算法则，两个重要极限，无穷小的比较.（3）连续：函数的连续性与间断点，闭区间上连续函数的性质.2．考核目标和要求（1）理解和掌握函数、极限与连续的概念.（2）能熟练地求函数的定义域，初等函数及分段函数的函数值.（3）熟练地应用极限的四则运算法则，两个重要极限求数列或函数极限.（4）了解无穷小量与无穷大的概念与关系，会对无穷小的阶进行比较.（5）掌握函数左、右极限与极限的关系.（6）了解函数连续性的概念，会判断分段函数在分段点处的连续性.（7）会求函数的间断点和连续区间以及会判断间断点的类型.（8）知道闭区间上连续函数的性质.二、导数与微分1．考核知识点（1）导数的定义，导数的几何意义，可导与连续的关系.（2）求导法则，导数的四则运算法则，复合函数的求导法则，反函数的求导法则，隐函数及参数方程所确定的函数的求导法则，基本求导公式.（3）高阶导数.（4）微分的定义，求法及运算法则.2．考核目标及要求（1）理解导数定义，了解微分的概念，会求曲线上一点处的切线斜率及切线方程，会用导数定义求一些简单函数的导数，知道可导与连续的关系.（2）熟练地运用求导法则求函数的导数，熟练地求函数的微分.（3）会求初等函数的高阶导数.三、导数的应用1．考核知识点（1）中值定理、罗尔定理、拉格朗的中值定理，柯西中值定理.（2）导数的应用，洛比达法则，函数的单调性，函数的极值，函数的凹凸性，拐点，曲线的渐近线（水平、垂直）简单函数图形的描绘，最大值、最小值应用问题.2．考核目标和要求（1）会叙述罗尔定理，拉格朗的中值定理，柯西中值定理，掌握用这三个定理作一些命题的证明.（2）熟练地运用洛比达法则求各种未定型的极限.（3）掌握用导数判定函数的单调性和极值点，会求函数的单调区间和极值，会用函数的单调性证明不等式.（4）会求函数的凹凸区间和拐点，会求曲线的水平和垂直浙近线.（5）会利用导数方法作简单函数的图形.（6）掌握用导数方法求解最值应用问题.四、不定积分1．考核知识点（1）原函数与不定积分的概念.（2）基本积分公式，换元积分法和分部积分法.（3）简单有理函数的积分.2．考核目标和要求（1）掌握原函数与不定积分的概念，能熟练地应用基本积分公式，知道求导与求不定积分两种运算的关系.（2）熟练地利用换元法与分部积分法求不定积分.（3）会求一些简单有理函数的不定积分.五、定积分及其应用1．考核知识点（1）定积分的定义与性质.（2）变上限的定积分，原函数存在定理与牛顿—莱布尼兹公式.（3）定积分的换元法与分部积分法.（4）广义积分.（5）定积分的应用，平面图形的面积和旋转体的体积.2．考核目标和要求（1）知道定积分的定义，了解定积分的性质和积分中值定理.（2）了解变上限的定积分，原函数存在定理，熟练地应用牛顿—莱布尼兹公式计算定积分. （3）熟练掌握用定积分的换元法和分部积分法求定积分.（4）会计算简单的广义积分.（5）掌握有关用积分性质，变上限的定积分或换元法作一些命题的证明.（6）了解微元法，掌握用定积分求平面图形的面积或旋转体的体积.六、向量代数与空间解析几何1．考核知识点（1）向量的概念及向量的线性运算.（2）空间直角坐标系，向量的坐标表示.（3）向量的数量积与向量积.（4）平面与空间直线的各种方程.（5）两平面间，两直线间，平面与直线间的位置关系.（6）曲面与空间曲线的方程.（7）柱面、旋转曲面、椭球面、椭圆抛物面、单叶双曲面及双叶双曲面.2．考核目标及要求（1）理解向量的定义，向量的模、方向的概念.（2）熟练掌握向量的加、减、数乘、数量积及向量积的运算.（3）知道向量平行与垂直的条件.（4）根据条件，熟练地建立平面和直线的各种形式的方程.（5）能正确判断平面与平面、直线与直线、平面与直线的位置关系.（6）能正确识别曲面的方程及形状.七、多元函数的微积分学1．考核知识点（1）多元函数的定义，二元函数的极限与连续.（2）偏导数的概念及计算，高阶偏导数，全微分的概念及计算.（3）多元复合函数的求导法则及隐函数的求导法.（4）偏导数的几何应用.（5）多元函数的极值，条件极值及拉格朗日乘数法.（6）二重积分的概念及性质.（7）二重积分的计算—直角坐标系及利用极坐标计算.（8）二重积分的简单应用—立体的体积及曲面的面积.2．考核目标及要求（1）知道二元函数和二元函数极限与连续的定义，会求二元函数的定义域.（2）熟练掌握求偏导数的方法，会求二元函数的二阶偏导数.（3）掌握二元复合函数及隐函数的求导法则，会求三元复合函数及隐函数的偏导数. （4）了解二、三元函数全微分的概念，会求二、三元函数的全微分.（5）会求空间曲线的切线与法平面、曲面的切平面与法线方程.（6）了解二元函数极值与条件极值的概念，会求二元函数的极值与条件极值.（7）知道二重积分的定义和性质.（8）熟练掌握化二重积分为二次积分求二重积分的方法，包括直角坐标系中及利用极坐标变换的方法.八、常微分方程1．考核知识点（1）微分方程的定义，阶及解的概念.（2）一阶微分方程：可分离变量的微分方程，齐次方程，一阶线性微分方程.（3）可降阶的高阶微分方程.型，型及型微分方程.（4）二阶常系数线性齐次和非齐次微分方程.2．考核目标及要求（1）了解微分方程的定义，阶及解的概念，熟练掌握可分离变量方程和一阶非齐次线性方程的解法，掌握齐次方程的解法.（2）掌握可降阶的三类微分方程的解法.（3）掌握二阶常系数齐次线性方程的解法.（4）掌握二阶常系数非齐次线性方程中和时通特及特解的求法.（这里为的次多项式）（5）掌握对实际问题建立微分方程并求解之.九、级数1．考核知识点（1）数项级数的概念，级数的敛散性及性质.（2）正项级数的定义及其判别法.（3）交错级数的定义及其收敛判别法，任意项级数的绝对收敛与条件收敛.（4）幂级数的定义，收敛半径、收敛域.（5）幂级数的运算和函数的连续性，和函数的求导与求积.（6）函数展开成幂级数.（7）几个常见函数的马克劳林级数.()2．考核目标和要求（1）理解无穷级数敛散性的定义，收敛的必要条件及基本性质.（2）熟练掌握正项级数敛散性的比较判别法，比值判别法.（3）了解交错级数的定义，掌握交错级数收敛的判别法.（4）理解任意项级数的绝对收敛与条件收敛.（5）知道幂级数的定义，会求幂级数的收敛半径和收敛域.（6）了解幂级数的四则运算，和函数的连续性，会求和函数的导数和积分.（7）掌握的幂级数展开式，并应用它们将一些简单函数展成的幂级数.。
数学与应用数学专业专升本专业课考试大纲
数学与应用数学专业专升本专业课考试大纲一、《数学分析》部分课程性质：数学分析是高等师范院校基础数学专业和应用数学专业的必修课。
本课程是进一步学习许多后继课程，如复变函数论，常微分方程，数理方程，微分几何，概率论，实变函数论等课程的必要的基础知识。
也为在更高层次上理解中学数学的相关内容打下必要的基础。
考核方式：专业课试卷数学分析部分占60%，采用闭卷考试。
考核内容：第一章 函数考核内容：函数定义，函数的四则运算；四类特殊函数的概念；复合函数、反函数的概念。
第二章 极限考核内容： N -ε定义证明一些数列极限；收敛数列的三个性质、四则运算和两边夹法则； Cauchy 收敛准则；两边夹定理的应用；函数极限定义；函数极限的三个性质，四则运算法则，两类重要极限；等价无穷小在计算极限中的应用。
第三章 函数连续考核内容：函数连续概念；间断点的定义及分类；函数的左连续与右连续；连续函数的运算及其性质；初等函数的连续性；闭区间上连续函数三个性质。
第四章 导数与微分考核内容：导数定义及几何意义；可导与连续的关系；求导法则及基本初等函数的求导公式，复合函数求导法则；隐函数与参数方程的求导方法；微分的定义； 初等函数的高阶导数。
第五章 微分学基本定理及其应用考核内容： Lagrange 中值定理， Rolle 中值定理，Lagrange 中值定理及其应用；洛必达法则；Taylor 公式及其应用； 导数在研究函数上的应用。
第六章 不定积分考核内容：不定积分的性质，不定积分公式表；分部积分法与换元积分法；有理函数的不定积分法；简单无理函数与三角函数的不定积分。
第七章 定积分考核内容：定积分的定义，可积准则；定积分的性质；定积分的分部积分法与换元积分法；定积分的应用（求面积旋转体体积）。
第八章 级数考核内容：数值级数及其敛散性以及判别，收敛级数的性质，条件收敛与绝对收敛，绝对收敛级数的性质；函数级数，函数级数一致收敛的概念及其判别，函数级数一致收敛时和函数的分析性质，函数列的一致收敛及其性质；幂级数的收敛半径和收敛域，幂级数和函数的分析性质，泰勒级数及其基本初等函数的幂级数展开。
《高等数学》(专升本)考试大纲
《高等数学》(专升本)考试大纲函数极值与极值点，最值；曲线的凹凸性、拐点；曲线的水平渐近线与垂直渐近线。
要求：会用罗尔中值定理证明方程根的存在性。
会用拉格朗日中值定理证明简单的不等式。
熟练掌握洛必达法则求未定式的极限方法。
掌握利用导数判定函数单调性的方法，会利用增减性证明简单的不等式。
掌握求函数的极值和最值的方法，并且会解简单的应用问题。
会判定曲线的凹凸性，会求曲线的拐点。
会求曲线的水平渐近线与垂直渐近线。
（三）一元函数积分学1.不定积分考试内容：不定积分的概念；换元积分法；分部积分法；一些简单有理函数的积分。
要求：理解原函数与不定积分概念及其关系。
熟练掌握不定积分换元法，分部积分法。
会求简单有理函数的不定积分。
2.定积分考试内容：定积分的概念；定积分的性质；定积分的计算；无穷区间的广义积分；定积分的应用：平面图形的面积、旋转体的体积。
要求：掌握定积分的基本性质。
理解变上限的定积分是变上限的函数，掌握对变上限定积分求导数的方法。
掌握牛顿—莱布尼茨公式。
掌握定积分的换元积分法与分部积分法。
掌握无穷区间广义积分的计算方法。
掌握直角坐标系下用定积分计算平面图形的面积以及平面图形绕坐标轴旋转所生成的旋转体体积。
（四）多元函数的微积分学及应用1.多元函数的微分学考试内容：多元函数的概念；二元函数的极限与连续的概念；多元函数偏导数的概念与几何意义；全微分的概念；全微分存在的必要条件和充分条件；多元复合函数，隐函数的求导方法；二阶偏导数。
要求：理解多元函数的概念；了解二元函数的几何意义；了解二元函数的极限与连续的概念。
理解多元函数偏导数和全微分的概念，知道全微分存在的必要条件和充分条件。
掌握偏导数与微分的四则运算法则，掌握复合函数的求导法则，会求一些函数的二阶偏导数。
2.多元函数的微分学的应用考试内容：多元函数极值的概念；多元函数极值的必要条件；二元函数极值的充分条件；多元函数极值和最值的求法及简单应用。
要求：了解多元函数极值和条件极值的概念，知道多元函数极值存在的必要条件。
专升本高等数学二课程考试大纲
专升本《高等数学（二）》课程考试大纲一、考试对象参加专升本考试的各经济类、管理类和文科专业专科学生。
二、考试目的《高等数学（二）》课程考试旨在考核学生对本课程知识的掌握和运用能力，包括必要的高等数学基础知识和基本技能，一定的抽象概括问题的能力、逻辑推理能力、空间想象能力、自学能力，比较熟练的运算能力和综合运用所学知识去分析问题和解决问题的能力等。
三、考试的内容要求第一章函数、极限与连续1. 函数（1）理解函数的概念，掌握函数的表示法，会建立简单应用问题中的函数关系。
（2）了解函数的有界性、单调性、周期性和奇偶性。
（3）理解复合函数及分段函数的概念，了解隐函数及反函数的概念。
（4）掌握基本初等函数的性质及其图形，理解初等函数的概念。
2．数列与函数的极限（1）理解数列极限和函数极限（包括左极限和右极限）的概念，了解极限的性质与极限存在的两个准则。
（2）掌握极限四则运算法则，会应用两个重要极限。
３．无穷小与无穷大（1）理解无穷小的概念，掌握无穷小的基本性质和比较方法。
（2）了解无穷大的概念及其与无穷小的关系。
４．函数的连续性（1）理解函数连续性的概念（含左连续与右连续），会判别函数间断点的类型。
（2）了解连续函数的性质和初等函数的连续性，了解闭区间上连续函数的性质（有界性、最大值和最小值定理、介值定理）及其简单应用。
第二章导数与微分1．导数概念理解导数的概念及可导性与连续性之间的关系，了解导数的几何意义与经济意义（含边际与弹性的概念）。
2．函数的求导法则掌握基本初等函数的导数公式、导数的四则运算法则及复合函数的求导法则，掌握反函数、隐函数及由参数方程所确定的函数的求导法，了解对数求导法。
3．高阶导数理解高阶导数的概念，会求简单函数的高阶导数。
4．函数的微分理解微分的概念，掌握导数与微分之间的关系以及一阶微分形式的不变性，会求函数的微分。
第三章微分中值定理与导数的应用1．微分中值定理理解罗尔定理和拉格朗日中值定理，了解柯西中值定理，掌握这三个定理的简单应用。
《高等数学(二)》专升本考试大纲
《高等数学（二）》专升本考试大纲《高等数学》专升本入学考试注重考察学生基础知识、基本技能和思维能力、运算能力、以及分析问题和解决问题的能力。
考试时间为 2 小时，满分 150 分。
考试内容和基本要求一、函数、极限与连续（一）考试内容函数的概念与基本特性；数列、函数极限；极限的运算法则；两个重要极限；无穷小的概念与阶的比较；函数的连续性和间断点；闭区间上连续函数的性质。
（二）考试要求1．理解函数的概念，了解函数的基本性态（奇偶性、单调性、周期性、有界性）。
了解反函数的概念，理解复合函数的概念，理解初等函数的概念。
会建立简单经济问题的函数关系。
掌握常用的经济函数（需求函数、成本函数、收益函数、利润函数）。
2．了解数列极限、函数极限的概念（不要求做给出，求 N 或的习题）；了解极限性质（唯一性、有界性、保号性）。
3．掌握函数极限的运算法则；熟练掌握极限计算方法。
掌握两个重要极限，会用两个重要极限求极限；4．了解无穷小、无穷大、高阶无穷小、等价无穷小的概念，会用等价无穷小求极限。
5．理解函数连续的概念；了解函数间断点的概念，会判别间断点的类型（第一类与第二类）。
6．了解初等函数的连续性；了解闭区间上连续函数的性质，会用性质证明一些简单结论。
二、导数与微分（一）考试内容导数的概念及求导法则；隐函数所确定函数的导数；高阶导数；微分的概念与运算法则。
（二）考试要求1．理解导数的概念及几何意义和经济意义，了解函数可导与连续的关系，会求平面曲线的切、法线方程。
2．掌握基本初等函数的求导公式；掌握导数的四则运算法则和复合函数的求导法则；掌握隐函数及取对数求导法。
会熟练求函数的导数。
3．了解高阶导数的概念，掌握初等函数的一阶、二阶导数的求法。
4．理解微分的概念，了解微分的运算法则和一阶微分形式不变性，会求函数的微分。
三、中值定理与导数应用（一）考试内容罗尔中值定理、拉格朗日中值定理；洛必达法则；函数单调性与极值、曲线凹凸性与拐点。
《高等数学》(专升本)考试大纲
《高等数学》(专升本)考试大纲《高等数学》（专升本）考试大纲一、考试内容与要求（一）函数、极限和连续1.函数考试内容：函数的简单性质；反函数；函数的四则运算与复合运算基本初等函数；初等函数。
要求：会求函数的定义域、表达式及函数值。
并会作出简单的分段函数图像。
理解和掌握函数的简单性质，会判断所给函数的类别。
会求单调函数的反函数。
掌握基本初等函数的简单性质及其图象。
2.极限考试内容：数列极限的概念，性质，收敛准则；函数极限的概念，函数极限的定理；无穷小量和无穷大量；两个重要极限。
要求：理解极限的概念。
会求函数在一点处的左极限与右极限。
了解极限的有关性质，掌握极限的四则运算法则。
掌握无穷小量的性质、无穷小量与无穷大量的关系。
会进行无穷小量阶的比较。
会运用等价无穷小量代换求极限。
熟练掌握用两函数极值与极值点，最值；曲线的凹凸性、拐点；曲线的水平渐近线与垂直渐近线。
要求：会用罗尔中值定理证明方程根的存在性。
会用拉格朗日中值定理证明简单的不等式。
熟练掌握洛必达法则求未定式的极限方法。
掌握利用导数判定函数单调性的方法，会利用增减性证明简单的不等式。
掌握求函数的极值和最值的方法，并且会解简单的应用问题。
会判定曲线的凹凸性，会求曲线的拐点。
会求曲线的水平渐近线与垂直渐近线。
（三）一元函数积分学1.不定积分考试内容：不定积分的概念；换元积分法；分部积分法；一些简单有理函数的积分。
要求：理解原函数与不定积分概念及其关系。
熟练掌握不定积分换元法，分部积分法。
会求简单有理函数的不定积分。
2.定积分考试内容：定积分的概念；定积分的性质；定积分的计算；无穷区间的广义积分；定积分的应用：平面图形的面积、旋转体的体积。
要求：掌握定积分的基本性质。
理解变上限的定积分是变上限的函数，掌握对变上限定积分求导数的方法。
掌握牛顿—莱布尼茨公式。
掌握定积分的换元积分法与分部积分法。
掌握无穷区间广义积分的计算方法。
掌握直角坐标系下用定积分计算平面图形的面积以及平面图形绕坐标轴旋转所生成的旋转体体积。
2015年井冈山大学专升本招生简章
2015年井冈山大学专升本招生简章为了增强专科生适应经济社会发展的能力，构建培养人才的“立交桥”，根据江西省教育厅《关于做好我省2015年普通高校专升本招生工作的通知》（赣教考字﹝2015﹞4号）的文件精神，我校决定面向贵校选拔符合条件的应届专科毕业生进入本科阶段学习，现将有关事项通知如下：1．我校2015年“专升本”招生选拔的专业有4个（详见附件一）。
2．推荐选拔的范围和条件①经统招入学、政治思想好、身体健康、成绩优秀，在校期间没有考试舞弊或受到纪律处分等不良记录的普通高职高专应届毕业生；②只能报考相同或相近专业。
3．推荐报名事项①推荐报名时间及地点：4月29日-5月9日由各推荐院校教务处向我校教务处集体报名；②推荐报名所须递交的材料：考生个人一寸免冠照片四张（《推荐表》贴三张、办准考证一张）；已加盖考生所在学校教务处公章的《推荐表》一式三份；已加盖考生所在学校教务处公章的身份证复印件一份；③考生报名：考试费130元/人，请各推荐学校代收后汇入我校指定的账户。
户名：井冈山大学开户银行：建设银行江西省吉安市青原支行；帐号：36001451020052501439，汇款时请在备注中注明报考学生姓名。
④上述材料连同《井冈山大学2015年“专升本”报名情况汇总表》（见附件三，相应电子文档发送到jwc@），经推荐学校审核盖章后，由推荐学校教务处于5月9日前统一交井冈山大学教务处（特快邮寄须在5月7日前寄出），并将报名考试费统一汇入指定账户（银行回执单和报名材料一并寄回），逾期或材料不全者不予办理报名手续。
4．考试安排①考试课程和考试时间：②领取准考证时间和地点：考生凭身份证、学生证于6月5日下午3:00~5:00在我校教务处教学管理科领取准考证，同时看考场，外地考生可在我校培训接待中心或宿管科安排食宿，费用自理。
5．学籍和编班：经过考试选入我校本科阶段学习的学生，学籍转入我校，编入我校2013级本科相关专业学习。
2015年专升本高数内部考试资料
2015年专升本高数内部考试资料第一章函数、极限与连续 (1)一、函数定义域的求法 (1)二、函数相等的判定 (1)三、函数表达式的求法 (2)四、函数的基本性质 (3)五、反函数的求法 (4)六、数列极限的求法 (4)七、函数存在极限的充要条件 (4)八、函数极限的求法 (5)九、无穷小量阶的比较 (7)十、关于函数极限的反问题 (8)十一、函数在一点处的连续性 (8)十二、求函数的间断点及其类型 (9)十三、闭区间上连续函数的性质 (11)第二章一元函数微分学及其应用 (12)一、根据导数的定义求极限或函数在某一点的导数 (12)二、利用导数的几何意义求切线或法线方程 (12)三、可导与连续的关系以及函数在一点可导性的判定 (13)四、求导法则及复合函数的导数与微分 (14)五、函数的高阶导数 (15)六、参数方程或隐函数方程的导数 (16)七、幂指函数的导数求法 (16)八、关于中值定理条件的验证 (16)九、利用拉格朗日中值定理证明不等式 (17)十、利用拉格朗日中值定理证明恒等式 (18)十一、关于中值命题的证明 (18)十二、利用洛必达法则求极限 (18)十三、单调性的判定与单调区间的求法 (19)十四、利用单调性证明不等式，以及数值不等式的证法 (20)十五、利用单调性判定根的存在性或唯一性 (20)十六、关于函数的极值问题 (20)十七、函数的最值问题 (21)十八、曲线凹凸性的判定 (22)十九、曲线的拐点求法 (23)二十、曲线的渐近线求法 (24)第三章一元函数积分学及其应用 (25)一、原函数与不定积分的概念及性质 (25)二、不定积分的直接积分法 (27)三、不定积分的第一类换元积分法（凑微分法） (27)四、不定积分的第二类换元积分法 (29)五、不定积分的分部积分法 (29)六、有理分式的不定积分 (30)七、定积分的概念与性质 (30)八、积分上限函数的导数 (31)九、定积分的常规计算 (32)十、使用定积分的性质和一些重要结果计算定积分 (34)十一、广义积分的计算与敛散性的判定 (35)十二、含定积分的函数表达式求法 (36)十三、利用定积分的几何意义求平面图形的面积 (36)十四、利用定积分求特殊的空间立体的体积 (38)第四章向量代数与空间解析几何 (39)一、向量代数 (39)二、空间直线与平面的方程求法 (40)三、两点间的距离、点到平面的距离以及空间中对称点的求法 (41)四、位置关系的判定及其夹角计算 (42)五、二次曲面与旋转曲面的特征 (43)六、旋转曲面与投影曲线的求法 (44)第五章多元函数微分学 (45)一、二元函数的表达式与定义域的求法 (45)二、二元函数的极限与函数的连续性 (45)三、二元函数的偏导数与全微分 (46)四、二元复合函数的偏导数与全微分 (47)五、可微、连续、偏导数之间的关系 (47)六、高阶偏导数 (48)七、多元抽象函数的偏导数与全微分 (48)八、多元隐函数的偏导数与全微分 (49)九、方向导数与梯度 (49)十、空间曲线的切线与曲面的切平面求法 (49)十一、二元函数的极值 (50)十二、多元函数的最值问题 (51)第六章多元函数积分学 (51)一、二重积分的概念与性质 (51)二、直角坐标系下二重积分的计算 (52)三、特殊被积函数的二重积分计算 (53)四、极坐标系下的二重积分计算 (54)五、含二重积分的函数表达式求法 (55)六、两坐标系下二重积分的相互转化与交换二重积分的积分次序 (55)七、利用二重积分计算空间立体的体积 (56)八、第一类曲线积分的计算 (56)九、利用定积分计算第二类曲线积分 (57)十、格林公式与曲线积分与路径无关 (57) 第七章无穷级数 (58)一、利用定义判定级数的敛散性 (58)二、利用级数的一般性质判定级数的敛散性 (59)三、利用级数收敛的必要条件判定级数敛散性 (60)四、正项级数的敛散性判别法 (60)五、交错级数与一般项级数的敛散性判定 (62)六、阿贝尔第一定理及其应用 (63)七、幂级数的收敛半径、收敛区间以及收敛域的求法 (64)八、幂级数的和函数与数项级数和的求法 (65)九、函数f(x)展开成幂级数的方法 (65)十、由函数的幂级数展开式，求函数的高阶导数 (66)第八章常微分方程 (66)一、微分方程的基本概念 (66)二、可分离变量的微分方程与一阶线性齐次微分方程的解法 (67)三、齐次方程的解法 (68)四、一阶线性非齐次微分方程的解法 (68)五、可降阶的高阶微分方程的解法 (69)六、线性微分方程解的结构定理应用 (70)七、二阶常系数线性齐次微分方程的解法 (71)八、二阶常系数线性非齐次微分方程的解法 (72)九、常系数线性微分方程的反问题 (73)十、已知一个变限积分方程，求函数表达式 (74)参考答案 (74)第一章函数、极限与连续 (74)第二章函数、极限与连续 (77)第三章一元函数积分学及其应用 (82)第四章向量代数与空间解析几何 (86)第五章多元函数微分学 (88)第八章常微分方程 (94) 第一章函数、极限与连续一、函数定义域的求法1.已知函数的表达式，求函数的定义域例1函数y=ln(x-1)+arcsin(x-3)的定义域是（）A.［2，+∞)B.(2,4)C.［2,4)D.［2,4］例2函数f(x)=ln(x-1)x+1的定义域是（）A.(-1,1)B.(-∞,-1)C.(1,+∞)D.(-∞,-1)∪(-1,1)∪(1，+∞)例3函数f(x)=16-x2ln(x+2)的定义域是.例4函数f(x)=2+x2-x的定义域是.例5函数y=x2-9x-3的定义域是.2.分段函数的定义域是各分段区间的并集.3.抽象函数定义域的求法例6设f(x)的定义域为（0，1），则函数f(lnx)的定义域为.例7设f(x)的定义域为［0,4］，则函数f(x+1)+f(x-1)的定义域为.例8设f(x+1)的定义域为［0，1］，则函数f(2x+3)的定义域为.例9设f(x)的定义域为（0，1），则f(ex)的定义域为（）A.（-∞,0)B.(1,e)C.(-∞,1)D.(-∞,e)二、函数相等的判定例1下列函数相同的是()A.f(x)=x2，g(x)=xB.f(x)=ddx∫x0sintdt,g(x)=sinxC.f(x)=lnx2,g(x)=2lnxD.y=x,y=sin(arcsinx)例2下列函数相同的是()A.y=1,y=xxB.y=x2-4,y=x-2·x+2C.y=x,y=cos(arccosx)D.y=x2,y=|x|例3下列函数相等的是()A.y=x2-x-2x-2与y=x+1B.y=sin2x与y=sinxC.f(x)=x2+sin2x+cos2x与g(t)=t2+1D.f(x)=sec2x-tan2x与f(x)=1三、函数表达式的求法1.已知f(x)和g(x)的表达式，求f［g(x)］或g［f(x)］的表达式例1f(x)=xx-1，则f1f(x)-1=.例2设f(x)=x，x≤0，x+x2,x>0，则f［f(x)］=.例3设g(x）=2-x,x≤0，x+2,x>0，f(x)=x2,x<0，-x,x≥0，则g［f(x)］=.例4设f(x)=x1+x2，求f［f……f(x)］n个f的表达式.2.已知f［g(x)］和g(x)，求f(x)的表达式例5设fx-2x=1+x，则f(x)=.例6设f(ex+1)=e2x+ex+x，则f(x)=.例7设fx-1x=x3-xx4+1（x≠0），求f(x).例8设f(lnx)=x3+1,则f(x)=.例9若函数fsinx2=1+cosx,则fcosx2=.3.已知f(x)和f［g(x)］的表达式，求g(x)的表达式例10已知f(x)=ln(1+x),f［g(x)］=x，求g(x).例11已知f(x)=3lnx,f［g(x)］=ln（1-2lnx），求g(x). 四、函数的基本性质掌握函数的单调性、奇偶性、有界性、周期性的概念及其性质.例1设f(x)为增函数，g(x)为减函数，则下列函数中为减函数的是()A.f［-g(x)］B.f［g(x)］C.f［f(x)］D.g［g(x)］例2函数f(x)=11+2x-12在其定义域内()A.奇函数B.偶函数C.非奇非偶函数D.无法判定例3函数f（x）=x7arcsin（tanx）在其定义域内()A.偶函数B.奇函数C.非奇非偶函数D.无法判定例4函数f(x)=cotx·3x-13x+1是()A.偶函数B.奇函数C.非奇非偶函数D.无法判定例5若f(x)在（-∞,+∞）内为奇函数,则F(x)=f(x)ln(x+x2+1)在(-∞,+∞)内为()A.奇函数B.偶函数C.既奇又偶函数D.非奇非偶函数例6设f(x)是奇函数,且处处可导，则f′(x)是()A.奇函数B.偶函数C.既奇又偶函数D.非奇非偶函数例7函数y=1-arctanx是()A.单调增加且有界函数B.单调减少且有界函数C.奇函数D.偶函数例8函数f(x)在(-∞，+∞)上是奇函数，当x≤0时，f(x)=x2-x，则当x>0时，f(x)的表达式是()A.x2-xB.-x2+xC.x2+xD.-x2-x例9函数y=1x在定义域内是()A.周期函数B.单调函数C.有界函数D.无界函数例10下列函数不是周期函数的是()A.y=3sin(x+π)B.y=sin2xC.y=1+sin5xD.y=xsinx例11设函数f(x)的定义域为(-∞,+∞)，若对x∈（-∞,+∞），有f(x+k)=1f(x)（k为常数）则函数f(x)具有()A.单调性B.奇偶性C.周期性D.有界性 五、反函数的求法例1设函数f(x)=log2x+8(x≥2)，则其反函数的定义域为()A.(-∞,+∞)B.［2,+∞)C.（0，2］D.［9，+∞)例2y=ax-bcx-d的反函数是()A.y=ax-bcx-dB. y=ax-dcx-bC.y=cx-dax-bD.y=dx-bcx-a六、数列极限的求法例1求下列极限:（1）limn→∞1n2+2n2+…+nn2;(2)limn→∞12n3+22n3+…+n2n3；(3)limn→∞11·2+12·3+…+1n（n+1）；(4)limn→∞1n2+1+1n2+2+…+1n2+n;（5）limn→∞1n2+n+1+2n2+n+2+…+nn2+n+n.例2极限limn→∞1+2+…+n2+n-n2的值为()A.14B.12C.-12D.-∞七、函数存在极限的充要条件1.函数f(x)在x→∞时极限存在的充要条件常见的几个极限式：limx→-∞arctanx=-π2，limx→+∞arctanx=π2,limx→+∞arccotx=0，limx→-∞arccotx=π,limx→-∞ex=0，limx→+∞ex=+∞(及其二者的推广)例1下列极限不存在的是：()A.limx→∞（2x-1）20(3x+2)30(5x+3)50B.limx→∞sinxnxnC. limx→∞xsin1xD.limx→∞ex2.函数f(x)且x→x0时极限存在的充要条件例2下列函数中，limx→0f(x)存在的是()A.f(x)=12-x,x<00,x=0 x+12,x>0B.f(x)=|x|x,x≠0x,x=0C.f(x)=x2+2,x<03,x=0sinx2x,x>0D.f(x)=e1x,x≠00,x=0例3函数f(x)=21x在x=0处()A.有定义B.极限存在C.左极限存在D.右极限存在例4下列极限存在的是()A.limx→∞4xB.limx→∞x3+13x3-1C.limx→0+lnxD.limx→1sin1x-1八、函数极限的求法1.利用极限的运算法则求极限例1求下列极限：（1）limx→-∞2x-3x2x+3x;（2）limx→+∞2x-3x2x+3x;（3）limx→∞（x+1）10（2x-1）20(3x+2)30；(4)limx→0x-sinxx+sinx.例2对任意x总有φ(x)≤f(x)≤g(x),且limx→∞［g(x)-φ(x)］=0,则limx→∞f(x)() A.存在且一定为0 B.存在且一定不为0C.一定不存在D.不一定存在例3已知limx→0xf(4x)=1,求limx→0f(2x)x.2.无理分式极限的求法例4求极限：(1)limx→02x+1-3x+2-2; (2)limx→0x+1-1x;（3）limx→∞nn2+1+n2-1; （4）limx→∞x4-3x2+1-12x2-3x.3.“∞-∞”型分式极限的求法例5求极限：(1)limx→01x-1ex-1;（2）limx→21x-2-1x2-4; (3)limx→01sin2x-cos2xx2;(4)limx→01+x1-e-x-1x.4.x→x0与x→∞时，有理分式极限的求法例6求极限：(1)limx→0ex2cosxarcsin(1+x); (2)limx→0x2+2x2+x;（3）limx→1x2-3x+21-x2.例7求极限：（1）limx→∞3x2+x-82x2+5x+1; （2）limx→∞3x2+x-82x3+5x+1;（3）limx→∞3x3+x-82x2+5x+1.5.利用重要极限求极限例8求极限:（1）limx→01-cosxxsinx; (2)limx→πsinxπ-x；(3)limn→∞nsinπn； (4)limx→1sin(x2-1)x-1.例9求极限：（1）limx→∞1-1x4x+3; (2)limx→03x1+2x;(3)limx→π2（1+cosx）3secx; (4)limn→∞1+1n+1n2n;（5）limx→∞x2-1x2+1x2; (6)limx→∞1+sin2x2x;（7）limx→0(1+x2)11-cosx; (8)limn→∞（1+2n+3n）1n(洛必达).例10设f(x)=limt→0x(1+3t)xt,则f′(x)=.6.利用无穷小量的性质求极限例11求下列极限:（1）limn→∞x2+x-sinxx3-4x+5（sinx+cosx）;（2）limx→+∞x3+x2+12x+x3(sinx+cosx).(3)limx→∞(sinn2+1π);（4）limx→+∞(sinx2+1-sinx).例12当x→∞时，下列变量不是无穷小量的是()A.x2sinx2x3-1B.(x2+1)sinxx2+1C.(x3+2x)sin1x3-2xD.11-x3sin1+x32x7.利用无穷小替换求极限 例13求下列极限:（1）limx→01-e3xtan2x; （2）limx→0ln（1+4x2）sinx2;（3）limx→∞x(e2x-1); (4)limx→∞x(e2sin1x-1);(5)limx→01+xsinx-1arctanx; (6)limx→0+1-cosxx(1-cosx)；（7）limx→1x2-1lnx; (8)limx→01+tanx-1+xarcsinxarctanx2.九、无穷小量阶的比较例1当x→0+时，与x等价的无穷小量是()A.1-exB.ln（1+x）C.1+x-1D.1-cosx例2当x→0时，下列无穷小量中是其他三个高阶无穷小的是()A.x2B.1-cosxC.1-x2-1D.x-tanx例3当x→0时，函数eax-1与1+x-1是等价无穷小量，则常数a的值为()A.2B.12C.-2D.-12例4设f(x)=∫1-cosx0sint2dt，g(x)=x55+x66，则当x→0时，f(x)是g(x)的()A.低阶无穷小量B.高阶无穷小量C.等价无穷小量D.同阶但不等价无穷小量例5当x→0时，函数f(x)=sinax与g(x)=ln（1-2x）为等价无穷小，则常数a的值为() A.-1 B.1 C.-2 D.2例6设f(x)=e-x2-1,g(x)=xtanx,当x→0时()A.f(x)是g(x)的高阶无穷小B.f(x)是g(x)的低阶无穷小C.f(x)与g(x)为同阶无穷小,但非等价无穷小D.f(x)与g(x)为等价无穷小例7当x→0时，无穷小量1-cosx2是x4()A.等价无穷小B.同阶无穷小C.较高阶无穷小D.较低阶无穷小例8下列陈述中正确的是()A.sinx22与x22是等价无穷小量（x→0）B.sinx22与x2sinx2是等价无穷小量（x→∞)C.sin2x2与1x2是等价无穷小量（x→∞） D.sin2x2与2xsin2x是等价无穷小量（x→∞）例9当x→0时,4x+5x-2是x的()A.等价无穷小B.同阶非等价无穷小C.高阶无穷小D.低阶无穷小例10当x→0时，与e-sinx-1比较是同阶非等价无穷小的是()A.-xB.x2C.x2D.-sinx例11当x→0时，ex-ax2-x-1是x2的高阶无穷小量，则a=.例12当x→0时，(1-cosx)ln(1+x2)是比xsinxn高阶的无穷小，而xsinxn是比ex2-1高阶的无穷小，则正整数n=()A.1B.2C.3D.4例13当x→0时，1+x2-ex2是x的阶无穷小量.例14当x→0+时，下列函数为无穷大量的是()A.2-x-1B.sinx1+secxC.e-xD.e1x十、关于函数极限的反问题例1若limx→01bx-sinx∫x0t2a+t2dt=1，则()A.a=4,b=1B.a=2,b=1C.a=4,b=0D.a=2,b=1例2已知limx→∞x2x+1-ax-b=0,求常数a,b.例3设limx→0ln(1+x)-(ax+bx2)x2=2,求常数a,b.十一、函数在一点处的连续性例1极限limx→x0f(x)存在是函数f(x)在x=x0处连续的()A.必要而非充分条件B.充分而非必要条件C.充要条件D.无关条件例2极限limx→x0f(x)存在是函数f(x)在x=x0处可导的()A.必要而非充分条件B.充分而非必要条件C.充要条件D.无关条件例3设f(x)=1+xsinx-cosxx2，当x≠0时，F(x)=f(x),且F(x)在x=0处连续，则F(0)=() A.-1 B.0 C.1 D.2例4函数f(x)=2x,x≥1,x2,x<1在点x=1处()A.不可导B.连续C.可导且f′(1)=2D.无法判断是否可导例5设f(x)=|x2-1|x-1,x≠1，2，x=1则f(x)在点x=1处()A.不连续B.连续但不可导C.可导但导数不连续D.可导且导数连续例6设函数f(x)=ex,x<0,x2+2a,x≥0在点x=0处连续，则a=()A.0B.1C.-1D.12例7设f(x)=sin3xx+b,x<0，a,x=0，2x，x>0在x=0处连续，则常数a与b的值为()A.a=0,b=-3B.a=-3,b=0C.a=0,b=3D.a=0,b=-13例8已知函数f(x)=a+bx2,x≤0，sinbxx,x>0在x=0处连续，则常数a和b满足()A.a>bB.a<bC.a=bD.a与b为任意实数十二、求函数的间断点及其类型例1x=0是函数f(x)=xsin1x的()A.可去间断点B.跳跃间断点C.振荡间断点D.无穷间断点例2x=0是函数f(x)=21x-1的()A.连续点B.可去间断点C.跳跃间断点D.第二类间断点例3设f(x)=1x-1x+11x-1-1x，则f(x)的可去间断点的个数为()A.3B.2C.1D.0 例4设f(x)=xsin1x,x≠0,0,x=0,则x=0是()A.可去间断点B.跳跃间断点C.第二类间断点D.连续点例5设函数f(x)=sinxx-x2，x≠0,0,x=0,则f(x)的间断点为()A.x=0B.x=1C.x=0和x=1D.不存在例6设函数f(x)在［-1，1］上连续，则x=0是函数g(x)=∫x0f(t)dtx的()A.连续点B.第二类间断点C.可去间断点D.跳跃间断点例7设函数f(x)=e1x-1，x<1,lnx，x≥1,则x=1是f(x)的()A.可去间断点B.跳跃间断点C.无穷间断点D.连续点例8函数f(x)=e1x,x>0,ln(x+1),-1<x≤0则x=0是()A.连续点B.可去间断点C.无穷间断点D.跳跃间断点例9设f(x)=x1+e1x2,x≠0,0,x=0则x=0是()A.连续点B.可去间断点C.跳跃间断点D.无穷间断点例10对于函数y=x2-4x(x-2),下列结论中正确的是()A.x=0是第一类间断点，x=2是第二类间断点B.x=0是第二类间断点，x=2是第一类间断点C.x=0是第一类间断点，x=2是第一类间断点D.x=0是第二类间断点，x=2是第二类间断点例11设函数f(x)=1exx-1-1,则()A.x=0,x=1都是第一类间断点B.x=0,x=1都是第二类间断点C.x=0是第一类间断点，x=1是第二类间断点D.x=0是第二类间断点，x=1是第一类间断点例12函数f(x)=1e-e1x的第二类间断点的个数()A.0B.1C.2D.3 例13函数f(x)=x2-2x|x|(x2-4)的第一类间断点的个数()A.0B.1C.2D.3十三、闭区间上连续函数的性质例1设函数f(x)在［a,b］上连续，且f(a)=f(b)，但f(x)不恒等于常数，则函数f(x)在（a,b）内()A.必有最大值或最小值B.既有最大值又有最小值C.既有极大值又有极小值D.至少存在一点ξ,使f′(ξ)=0例2下列方程在(0,1)内至少有一个实根的为()A.arctanx+x2+1=0B.x3-4x2+1=0C.x5-3x=1D.sinx+x+1=0例3下列区间中，使方程x4-x-1=0至少有一个根的区间是()A.(1,2)B.(2,3)C.12,1D.0,12例4已知函数f(x)在［0,+∞）上可导，且f′(x)<0，f(0)>0，则方程f(x)=0在（0，+∞）上()A.有唯一实根B.至少存在一个实根C.不能确定根D.没有根例5设a2-3b<0，则方程x3+ax2+bx+c=0的实根个数()A.1B.2C.3D.无法确实根的个数例6设函数f(x)在区间［0，1］上可导，f′(x)>0，且f(0)<0,f(1)>0，则f(x)在［0,1］内()A.至少有两个零点B.有且仅有一个零点C.没有零点D.零点的个数不能确定例7设函数f(x)在闭区间［0，2］上连续，且f(2)=0，f(1)=2,求证：存在ξ∈(1,2)，使得f(ξ)=ξ.提示：令g(x)=x-f(x)，∵f(x)在［0,2］上连续，所以g(x）在［0,2］上也连续，进而在［1,2］上也连续，又g(1)=1-f(1)<0，g(2)=2-f(2)>0，由零点定理，ξ∈(1,2) （0,2），使f(ξ)=ξ. 例8设函数f(x)在闭区间［0,1］上连续，且0≤f(x)≤1.证明：存在ξ∈［0,1］，使f(ξ)=ξ.第二章一元函数微分学及其应用一、根据导数的定义求极限或函数在某一点的导数例1已知f(0)=0，f′(0)=1，则limx→0f(x)x=()A.2B.1C.0D.+∞例2设f(x)在x=1处可导，且f′(1)=1,则limx→1f(x)-f(1)x2-1=.例3设函数f(x)在x=0处可导，且f(0)=0，则limx→0x2f(x)-2f(x3)x3=()A.-2f′(0)B.-f′(0)C.f′(0)D.0例4设函数f(x)在x=2处可导，且f′(2)=1，则limh→0f(2+h)-f(2-h)2h=()A.-1B.1C.-2D.2例5设f(x)=(x-a)g(x)，g(x)连续但不可导，且在x=a处有界，则f′(a)=()A.不存在B.0C.1D.g(a)例6设f(x)为可导的奇函数，且f′(x0)=6，则f′(-x0)=.例7设f(x)=x(x-1)(x-2)…（x-100），求f′(0),f′(50)和f′(100).例8设φ(x)在x=a处连续，f(x)=（x2-a2）φ(x),求f′(a).例9设f(x)在x=0处可导，且f(x)=f(0)-3x+α(x)，limx→0α(x)x=0,求f′(0).例10设f(x)在x=0处可导，且limx→0f(x)+1x+sinx=2,求f′(0).例11设函数f(x)满足下列条件：(1)f(x+y)=f(x)f(y)对x,y∈R都成立;（2）f(x)=1+xg(x)，而limx→0g(x)=1.试证明f(x)在R上处处可导，且f′(x)=f(x).二、利用导数的几何意义求切线或法线方程例1已知椭圆的参数方程为x=acost，y=bsint，（a>0，b>0），则椭圆在t=π4对应点处的切线斜率为()A.baB.abC.-baD.-ab 例2直线l与x轴平行且与曲线y=x-ex相切，则切点坐标为()A.（1，1）B.（-1，1）C.（0，-1）D.（0，1）例3已知函数f(x)为可导偶函数，且limx→0f(1+x)-f(1)2sinx=-2,则曲线y=f(x)在（-1，2）处的切线方程为()A.y=4x+6B.y=-4x-2C.y=x+3D.y=-x+1例4曲线y=∫x0（t-1）(t-2)dt在点（0,0）处的切线方程为.例5设函数y=f(x)在点x处可导且在点x0处取得极小值，则曲线y=f(x)在点（x0，f(x0)）处的切线方程为.例6某曲线在任一点处的切线斜率等于该点横坐标的倒数，且通过点（e2,3），则曲线方程为.例7求曲线tanx+y+π4=ey在点(0,0)处的切线方程与法线方程.例8证明：双曲线xy=a2上任一点处的切线与两坐标轴围成的三角形面积等于常数.例9已知f(x)是周期为5的连续函数，它在x=0的某个邻域内满足关系式f(1+sinx)-3f(1-sinx)=8x+α(x),其中α（x）是当x→0时比x高阶的无穷小量，且f(x)在x=0处可导，求曲线y=f(x)在点（6,f(6)）处的切线方程.三、可导与连续的关系以及函数在一点可导性的判定例1函数y=f(x)在点x0处可导是它在x0处连续的()A.充要条件B.必要条件C.充分条件D.以上都不对例2设f(x)在x0处存在左、右导数，则f(x)在x0点()A.可导B.连续C.不可导D.不一定连续例3设f(x)在x0点不连续，则()A.f′(x0)必存在B.f′(x0)必不存在C.limx→x0f(x)必不存在D.limx→x0f(x)必存在例4已知函数f(x)=ln（1+x），-1<x≤0，ex-1,0<x<1,则f(x)在x=0处()A.无极限B.有极限，但不连续C.连续但不可导D.可导例5下列函数在点x=0处可导的是() A.3x B.e-x C.|x| D.e3x2ln（1+x）例6下列函数在点x=0处可导的是()A.y=|x|B.y=x2sin1x,x≠00,x=0C.y=2xD.y=x,x≤0x2,x>0例7设f(x）=acosx+bsinx,x<0，ex-1，x≥0在点x=0处可导，则a和b的值分别为()A.a=0,b=0B.a=1,b=0C.a=1,b=1D.a=0,b=1例8若f(x)=eax,x≤0，1+sin2x,x>0在点x=0处可导，则a=.例9函数y=|x|+1在点x=0处()A.无定义B.不连续C.可导D.连续但不可导例10函数f(x)=(x2-x-2)|x3-x|的不可导点个数为()A.3B.2C.1D.0例11函数f(x)=e|x-a|在x=a处()A.不连续B.连续但不可导C.可导但导函数不连续D.导函数连续例12若f(x)在点x0处可导，则|f(x)|在点x0处()A.必可导B.连续但不一定可导C.一定不可导D.不连续例13设函数f(x)=|x2-1|φ(x)，其中φ(x)在x=1处连续，则φ（1）=0是f(x)在x=1处可导的()A.充分必要条件B.必要条件C.充分条件D.既非充分也非必要条件四、求导法则及复合函数的导数与微分例1设f(x)=sinx,则f′(x)=.例2设函数y=11+cosx，则y′=. 例3设函数f(x)=(x+1)1x-1，则f′(x)=.例4若f(x-1)=x2-1,则f′(x)=()A.2x+2B.x(x+1)C.x(x-1)D.2x-2例5已知ddxf1x2=1x，f′12=()A.22B.-22C.-1D.1例6设f′(lnx)=x,则ddxf(sinx)=()A.esinxcosxB.ecosxsinxC.esinxD. e cosx例7某企业每月生产Q（单位：t）产品时，总成本C是产量Q的函数,即C(Q)=Q2-10Q+20,则每月生产产品8 t时的边际成本是()A.4B.6C.10D.20例8设y=lncos(ex),求dydx.例9设y=e(arctanx)2，求y′.例10若y=sine-x，则有()A.dy=cose-xdxB.dy=e-xsine-xdxC.dy=-e-xcose-xdxD.dy=e-xcose-xdx例11设y=f(sec2x)，求dy.五、函数的高阶导数例1设函数f(x)=e2x-1，则函数f(x)在x=0处的二阶导数f″(0)等于()A.0B.e-1C.4e-1D.e例2设函数y=xlnx，则y10=()A.-1x9B.1x9C.8！x9D.-8!x9例3设函数f(x)=sinx,则f(2013)（x）=()A.sinxB.cosxC.-sinxD.-cosx例4设f(2013)（x)=x2+lnx，则f(2015)(x)=()A.2-1x2B.2+1x3C.1x2D.-1x2例5设函数f(x)在x=2的某邻域内可导，且f′(x)=ef(x),f(2)=1，则f(2)=.例6设f(x)=x3-cosx+lnx，n>3，则f(n)(x)=.例7设f(x)=x(x+1)(2x-1)（3x+1）（4x-1），求f(5)(0)，f(6)(x). 例8设f(x)=sin4x+cos4x,求f(n)(x).例9设函数y=13x+5,则y(n)(0)=.六、参数方程或隐函数方程的导数例1设x=ln(1+t2),y=arctant,则dydx=()A.12tB.2tC.1D.t例2设x=t-1t,y=12t2+lnt,则d2ydx2=()A.tB.t+1tC.1t2+1D.t2t2+1例3已知x=sint+1，y=∫t0cosudu，则d2ydx2=.例4设y=xey+1，则dydx=()A. ey2+yB.eyy-2C.eyxey+1D.ey1-xey例5y=y(x)是由方程arctanyx=lnx2+y2确定的隐函数，则dydx=()A.y-xy+xB.y+xy-xC.x-yx+yD.x+yx-y例6设y是由方程∫y0etdt+∫xπ2sintdt=0所确定的x的函数,则dydx=()A.sinxeyB.-sinxeyC.cosxeyD.-cosxey例7已知ex-x3ey=cos(xy),且y=f(x),求y′.七、幂指函数的导数求法例1设y=xxlnx-x,求dydx.例2设y=xsinx,求dydx.例3求函数y=x-1x+2·（3-x）4·3xln(1+x)的导数.八、关于中值定理条件的验证例1下列函数在闭区间［-1,1］上满足罗尔定理条件的是()A.y=|x|B.y=x3C.y=x2D.y=1x例2下列函数在指定区间上满足罗尔定理条件的是() A.f(x)=1x ,x∈［-2,0］ B.f(x)=(x-4)2,x∈［-2,4］C.f(x)=sinx,x∈-3π2,π2D.f(x)=|x|，x∈［-1,1］例3下列函数在给定的区间上满足罗尔定理条件的是()A.y=|x-1|,［0,2］B.y=13（x-2）2，［0,2］C.y=x3-3x+2,［1,2］D.y=xarcsinx,［0,1］例4下列函数在［1，e］上满足拉格朗日中值定理条件的是()A.ln［lnx］B.lnxC.1lnxD.ln(2-x)例5函数y=sinx在闭区间［0，2π］上符合罗尔定理条件的ξ=()A.0B.π2C.πD.2π例6若函数y=x3在闭区间［0，1］上满足拉格朗日中值定理的条件，则ξ＝()A.33B.-33C.±33D.±3例7设函数f(x)在闭区间［a,b］上连续，在开区间（a,b）内可导，则()A.至少存在一点ξ∈(a,b)，使f′(ξ)=0B.当ξ∈(a,b)时,必有f′（ξ）=0C.至少存在一点ξ∈(a,b)，使得f′(ξ)=f(b)-f(a)b-a成立D.当ξ∈(a,b)时，必有f′(ξ)=f(b)-f(a)b-a例8函数f(x)在开区间（a,b）上可导，且a<x1<x2<b,则至少存在一点ξ,使下式成立的是()A.f(b)-f(a)=f′(ξ)(b-a)(a<ξ<b)B.f(b)-f(x1)=f′(ξ)(b-x1)(x1<ξ<b)C.f(x2)-f(x1)=f′(ξ)(x2-x1)(x1<ξ<x2)D.f(x2)-f(a)=f′(ξ)(x2-a)(a<ξ<x2)例9不求函数f(x)=(x-2)(x-4)(x-7)的导数，说明方程f′(x)=0有几个实根，并指明其所在的区间.例10设f(x)=(x2-9)(x2-16)，则f′(x)=0的实根个数是()A.1B.2C.3D.4九、利用拉格朗日中值定理证明不等式例1证明：当x>0时，11+x<ln1+xx<1x. 例2证明不等式x1+x2<arctanx<x(x>0).例3证明不等式nan-1(b-a)<bn-an<nbn-1(b-a)(0<a<b,n>1).例4证明不等式|arctana-arctanb|≤|a-b|.十、利用拉格朗日中值定理证明恒等式例1证明下列恒等式:（1）sin2x+cos2x=1；(2)1+tan2x=sec2x；(3)1+cot2x=csc2x.例2证明:当x≥1时，arctanx+12arccos2x1+x2=π4.例3设f(x)在(-∞,+∞)内满足关系式f′(x)=f(x)，且f(0)=1，则f(x)=ex.例4证明：对于任意的实数a,有∫a+Taf(x)dx=∫T0f(x)dx,其中T为连续周期函数f(x)的周期.十一、关于中值命题的证明例1设函数f(x)，g(x)在［a,b］上连续，在（a,b）内可导，且f(b)-f(a)=g(b)-g(a)，试证明，在(a,b)内至少有一点c,使f′(c)=g′(c).例2设函数F(x)=∫x1sinx·f(t)dt，其中f(t)在［1,π］上连续，求F′（x）,并证明在（1，π)内至少存在一点ε,使得cosε·∫ε1f(x)dx+sinε·f(ε)=0.例3设函数f(x)在［a,b］上连续,在(a,b)内可导,且f(a)=f(b)=0,证明在(a,b)内至少存在一点ξ,使得f′(ξ)=f(ξ).例4设函数f(x)在［0,1］上有二阶导数,且f(0)=f(1)=0,又F(x)=x2f(x),证明:至少存在一点ξ∈(0,1),使得F″(ξ)=0.例5设a<c<b,f(x)和g(x)都在［a,b］上连续，在(a,b)内二阶可导，且f(a)=g(a),f(c)=g(c),f(b)=g(b),则在（a,b）内至少有一点ξ，使f″（ξ）=g″(ξ).十二、利用洛必达法则求极限例1极限limx→0∫x0tan2tdtx3等于() A.+∞B.16C.0D.13例2limx→0∫x0ln(1+t3)tdtx-sinx=.例3求极限limx→0∫x0et2sintdtln(1+x2).例4limx→∞ln1+x2+xx=.例5求极限limx→+∞x+x-x-x.例6求极限limx→∞xsin5x-15sin5x.例7求极限limx→0ax+bx+cx31x（a>0,b>0,c>0）.例8下列极限问题，不能使用洛必达法则的是()A.limx→0x2sin1xsinxB.limx→+∞xπ2-arctanxC.limx→∞1+kxxD.limx→∞x-sinxxsinx例9设F(x)=x2x-a∫xaf(t)dt，其中f(x)为连续函数，则limx→aF（x）=()A.a2B.a2f(a)C.0D.不存在例10求极限limx→0+1xtanx.例11若limx→01bx-sinx∫x0t2a+t2dt=1，则()A.a=4,b=1B.a=2,b=1C.a=4,b=0D.a=2,b=1十三、单调性的判定与单调区间的求法例1函数f(x)=x-ex+1在（0，+∞）内()A.是单调增加函数B.是单调减少函数C.有极大值D.有极小值例2函数f(x)=xlnx的单调增加区间是.例3设函数f(x)在［a,b］上连续，且单调增加，求证：F(x)=1x-a∫xaf(t)dt在［a,b］上单调增加.例4设在［0,1］上f″(x)>0，则f′(0)，f′(1)，f(1)-f(0)或f(0)-f(1)几个数的大小顺序为()A.f′(1)>f′(0)>f(1)-f（0）B.f′(1)>f(1)-f(0)>f′(0)C.f(1)-f(0)>f′(1)>f′(0)D.f′(1)>f(0)-f(1)>f′(0)例5函数F(x)=∫x0dt1+t2在(-∞,+∞)范围内()A.单调增加B.有无数多条铅直渐近线 C.图像是凹的 D.没有拐点十四、利用单调性证明不等式，以及数值不等式的证法例1证明:当x>0时，ln（x+1+x2）>x1+x2.例2证明：当0<x<1时，1-x2arcsinx<(1+x)ln（1+x）.例3证明：当x>0时，(x2-1)lnx≥(x-1)2.例4证明:当x>0时，1x>arctanx-π2.例5证明：当x>0时，有(1+x)ln(1+x)>arctanx.例6证明：当0<a<b时，lnba>2（b-a）a+b.例7求证:当0<a<b<π时，bsinb+2cosb+πb>asina+2cosa+πa.例8设f(x),g(x)都是可导函数,且|f′(x)|<g′(x),证明:当x>a时，f(x)-f(a)<g(x)-g(a).十五、利用单调性判定根的存在性或唯一性例1已知函数f(x)在［0，+∞)上可导，且f′(x)<0,f(0)>0,则方程f(x)=0在（0,+∞）上()A.有唯一根B.至少存在一个根C.不能确定有根D.没有根例2设函数f(x)在区间［0,1］上可导，f′(x)>0，且f(0)<0，f(1)>0,则f(x)在［0，1］内()A.至少有两个零点B.有且仅有一个零点C.没有零点D.零点的个数不能确定例3证明：方程ex-32-∫x0dt1+t2=0在开区间（0，1）内有唯一的实根.例4设f(x)在区间［0,1］上连续，且f(x)<1,证明：方程2x-∫x0f(t)dt=1在区间（0,1）内有且仅有一个实根.十六、关于函数的极值问题例1下列结论中正确的是()A.若x0是f(x)的驻点，则一定是f(x)的极值点B.若x0是f(x)的极值点，则一定是f(x)的驻点C.若f(x)在x0处可导，则一定在x0处连续D.若f(x)在x0处连续，则一定在x0处可导例2函数f(x)=xe-x2的极大值点为()A.x=22B.x=-22C.22，22e-12D.-22，22e-12例3函数f(x)=∫x0（1+t）arctantdt的极小值为.例4函数y=x3-3x2+1的单调增加区间是，单调减少区间是，极小值点是，极大值点是.例5设一个函数的导数为x2-2x-8，则该函数的极大值与极小值之差是()A.-36B.12C.36D.-1713例6设f(x)=xsinx+cosx，则正确的是()A.f(0)是极大值，fπ2是极小值B.f(0)是极小值，fπ2是极大值C.f(0)是极大值，fπ2是极大值D.f(0)是极小值，fπ2是极小值例7设f(x)的导数在x=2处连续，又limx→2f′(x)x-2=-1,则()A.x=2是f(x)的极小值点B.x=2是f(x)的极大值点C.（2,f(2)）是曲线y=f(x)的拐点D.x=2不是f(x)的极值点，(2,f(2))也不是曲线y=f(x)的拐点例8设f(x)的导数在x=a处连续，且limx→af′(x)x-a=1，则()A.x=a是f(x)的极小值点B.x=a是f(x)的极大值点C.（a,f(a)）是曲线f(x)的拐点D.x=a不是f(x)的极值点例9若f(1)=0，limx→1f(x)(x-1)2=5,则f(x)在x=1处()A.导数不存在B.不连续C.取得极大值D.取得极小值例10求f(x)=(x-1)eπ2+arctanx的单调区间和极值.例11利用第二充分条件求函数f(x)=x3-3x2-9x-5的极值.十七、函数的最值问题例1设函数f(x)在［a,b］上连续，且f(a)=f(b)，但f(x)不恒为常数，则函数f(x)在（a,b）内() A.必有最大值或最小值 B.既有最大值又有最小值C.既有极大值又有极小值D.至少存在一点ξ,使f′(ξ)=0例2设函数f(x)=13x3-x，则x=1为f(x)在［-2，2］上的()A.极小值点，但不是最小值点B.极小值点，也是最小值点C.极大值点，但不是最大值点D.极大值点，也是最大值点例3函数y=x+1-x在［-5，1］上的最大值为()A.6-5B.54C.6+5D.45例4函数f(x)=x+9x(x>0)的最小值为.例5函数y=x·2x的最小值点为.例6函数f(x)=x4-2x2在区间［0,2］上的最小值为.例7函数y=∫x02t-1t2-t+1dt在［0，1］上的最小值是.例8在斜边长为L的直角三角形中,求最大周长的直角三角形.例9一房地产公司有50套公寓要出租,当月租金每套定为2000元时,公寓会全部租出去,当月租金每增加100元时,就会多一套公寓租不出去,而租出去的公寓每套每月需花费200元的维修费,试问租金定为多少可获得最大收入?最大收入是多少?例10某厂生产某种产品,其固定成本为100元,每多生产一件产品成本增加6元,又知该产品的需求函数为Q=1000-100P.问产量为多少时可使利润最大,最大利润是多少?例11已知生产某零件Q单位时，总收入的变化率为R′(Q)=100-Q10.求:（1）求生产Q单位时的总收入R(Q);（2）如果已经生产了200个单位，求再生产200个单位时的总收入R(单位：万元).十八、曲线凹凸性的判定例1函数y=e-x在区间（-∞,+∞）内()A.单调递增且图像是凹的曲线B.单调递增且图像是凸的曲线C.单调递减且图像是凹的曲线D.单调递减且图像是凸的曲线例2曲线y=xe-x+3x+1的凹区间为()A.（-∞，2）B.（2，+∞）C.（-∞，-2）D.（-2，2）例3y=xarctanx的图形()A.在（-∞，+∞）内是凹的B.在（-∞，+∞）内是凸的C.在（-∞，0）内是凸的，在（0,+∞）内是凹的D.在（-∞，0）内是凹的，在（0，+∞）内是凸的例4下列曲线在其定义域内为凹的是()A.y=e-xB.y=ln(1+x2)C.y=arctanxD.y=sin(x2+2)例5设f(x)在（a,b）内二阶可导，且f′(x)>0,f″(x)<0，则f(x)在（a,b）内()A.单调增加且是凸的B.单调增加且是凹的C.单调减少且是凸的D.单调减少且是凹的例6在闭区间［-1，1］上有f′(x)=(x-1)2，则曲线f(x)在闭区间［-1，1］内是()A.单调减少且凹的B.单调减少且凸的C.单调增加且凸的D.单调增加且凹的例7下列函数对应的曲线在区间（0，+∞）内是凸函数的为()A.y=x3B.y=ln(1+x2)C.y=cos2xD.y=lnx十九、曲线的拐点求法例1曲线y=(x-2)53的拐点是()A.（0,2）B.(2,0)C.(1,0)D.(2,1)例2曲线y=x3-3x2的拐点为()A.（1，-2）B.（1，2）C.（0，0）D.（2，-4）例3设函数y=f(x)在区间（a,b）内有二阶导数，则()成立时，点（c,f(c)）(a<c<b)是曲线y=f(x)的拐点.A.f″(c)=0B.f″(x)在（a,b）内单调增加C.f″(x)在（a,b）内单调减少D.f″(c)=0且f″(x)在（a,b）内单调增加例4曲线y=x+2xx2-1的拐点坐标为.例5设f(x)=x3-3x2+2,则曲线y=f(x)的拐点是.例6已知f(x）=∫x0e-12t2dt（-∞<x<+∞），则曲线y=f(x)的拐点是. 例7已知点（0，1）是曲线y=x3+ax2+b的拐点，则a=,b=.例8点（1,2）是曲线y=ax3+bx2的拐点，则()A.a=-1,b=3B.a=0,b=1C.a为任意实数，b=3D.a=-1,b为任意实数例9若曲线y=x3+ax2+bx+1有拐点(-1,0)，则a=,b=.例10曲线y=e-x2的拐点是.例11设f′(x0)=f″(x0)=0,f(x0)>0，则下列正确的是()A.f′(x0)是f′(x)的极大值B.f(x0)是f(x)的极大值C.f(x0)是f(x)的极小值D.（x0，f(x0)）是曲线f(x)的拐点例12设函数f(x)有连续的二阶导数，且f′(0)=0,limx→0f″(x)x=2，则()A.f(0)是函数的极大值B.f(0)是函数的极小值C.(0,f(0))是曲线f(x)的拐点D.f(0)不是f(x)的极值例13f″(x0)=0是曲线f(x)的图形在x=x0处有拐点的()A.充分必要条件B.充分非必要条件C.必要非充分条件D.既非充分也非必要条件二十、曲线的渐近线求法例1下列曲线有水平渐近线的是()A.y=x2-3x+4xB.y=e1xC.y=ex1+xD.y=ln(1+x2)例2曲线y=x2+1x-1()A.有水平渐近线，无垂直渐近线B.无水平渐近线，有垂直渐近线C.无水平渐近线，也无垂直渐近线D.有水平渐近线，也有垂直渐近线例3曲线f(x)=2xsin13x()A.有且仅有水平渐近线B.有且仅有垂直渐近线C.既有水平渐近线又有垂直渐近线D.没有渐近线例4曲线y=ln(1+x)x()A.有水平渐近线，无垂直渐近线B.有水平渐近线，也有垂直渐近线C.无水平渐近线，有垂直渐近线D.无水平渐近线，也无垂直渐近线。
专升本入学考试数学考试大纲
专升本入学考试数学考试大纲考试形式和试卷结构一、答题方式答题方式为：闭卷、笔试．二、试卷题型结构试卷题型结构为：单选题、填空题、解答题：三、参考书籍高等数学（上、下册）（第二版）常迎香主编科学出版社专升本入学考试数学考试大纲一函数、极限、连续考试内容函数的概念及表示法：函数的有界性单调性周期性和奇偶性复合函数反函数分段函数和隐函数基本初等函数的性质及其图形初等函数函数关系的建立数列极限与函数极限的定义及其性质：函数的左极限与右极限无穷小量和无穷大量的概念及其关系无穷小量的性质及无穷小量的比较极限的四则运算极限存在的两个准则：单调有界准则和夹逼准则两个重要极限函数连续的概念函数间断点的类型初等函数的连续性闭区间上连续函数的性质考试要求1、理解函数的概念，掌握函数的表示法，会建立简单应用问题的函数关系.2、了解函数的有界性、单调性、周期性和奇偶性．3、理解复合函数及分段函数的概念，了解反函数及隐函数的概念．4、掌握基本初等函数的性质及其图形，了解初等函数的概念.5、理解极限的概念，理解函数左极限与右极限的概念以及函数极限存在与左、右极限之间的关系．6、掌握极限的性质及四则运算法则.7、掌握极限存在的两个准则，并会利用它们求极限，掌握利用两个重要极限求极限的方法．8、理解无穷小量、无穷大量的概念，掌握无穷小量的比较方法，会用等价无穷小量求极限．9、理解函数连续性的概念（含左连续与右连续），会判别函数间断点的类型．10、了解连续函数的性质和初等函数的连续性，理解闭区间上连续函数的性质（有界性、最大值和最小值定理、介值定理），并会应用这些性质．二一元函数微分学考试内容导数和微分的概念导数的几何意义和物理意义函数的可导性与连续性之间的关系平面曲线的切线和法线导数和微分的四则运算基本初等函数的导数复合函数反函数隐函数以及参数方程所确定的函数的导数高阶导数一阶微分形式的不变性微分中值定理洛必达（L’Hospital）法则函数单调性的判别函数的极值函数的最大值和最小值函数图形的凹凸性拐点及渐近线函数图形的描绘考试要求1、理解导数和微分的概念，理解导数与微分的关系，理解导数的几何意义，会求平面曲线的切线方程和法线方程，了解导数的物理意义，会用导数描述一些物理量，理解函数的可导性与连续性之间的关系．2、掌握导数的四则运算法则和复合函数的求导法则，掌握基本初等函数的导数公式．了解微分的四则运算法则和一阶微分形式的不变性，会求函数的微分．3、了解高阶导数的概念，会求简单函数的高阶导数．4、会求分段函数的导数，会求隐函数和由参数方程所确定的函数以及反函数的导数.5、理解并会使用罗尔(Rolle)定理，拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理.6、掌握用洛必达法则求未定式极限的方法．7、理解函数的极值概念，掌握用导数判断函数的单调性和求函数极值的方法，掌握函数最大值和最小值的求法及其应用．8、会用导数判断函数图形的凹凸性、会求函数图形的拐点以及水平、铅直渐近线，会描绘函数的图形．三一元函数积分学考试内容原函数和不定积分的概念不定积分的基本性质基本积分公式定积分的概念和基本性质定积分中值定理积分上限函数及其导数牛顿一莱布尼茨（Newton-Leibniz）公式不定积分和定积分的换元积分法与分部积分法有理函数、三角函数的有理式和简单无理函数的积分反常积分定积分的应用考试要求1、理解原函数的概念，理解不定积分和定积分的概念．2、掌握不定积分的基本公式，掌握不定积分和定积分的性质及定积分中值定理，掌握换元积分法与分部积分法．3、会求有理函数，三角函数有理式和简单无理函数的积分．4、理解积分上限的函数，会求它的导数，掌握牛顿－莱布尼茨公式．5、了解反常积分的概念，会计算反常积分．6、掌握利用定积分表达和计算一些几何量与物理量（平面图形的面积、平面曲线的弧长、旋转体的体积、平行截面面积为已知的立体体积等）及函数的平均值．四向量代数和空间解析几何考试内容向量的概念向量的线性运算向量的数量积和向量积两向量垂直、平行的条件两向量的夹角向量的坐标表达式及其运算单位向量方向余弦曲面方程和空间曲线方程的概念平面方程直线方程平面与平面、平面与直线、直线与直线的夹角以及平行、垂直的条件球面柱面旋转曲面等常用的二次曲面方程及其图形空间曲线的参数方程和一般方程空间曲线在坐标面上的投影曲线方程考试要求1、理解空间直角坐标系，理解向量的概念及其表示.2、掌握向量的运算（线性运算、数量积、向量积），了解两个向量垂直、平行的条件.3、理解单位向量、方向余弦、向量的坐标表达式，掌握用坐标表达式进行向量运算的方法.4、掌握平面方程和直线方程及其求法.5、会求平面与平面、平面与直线、直线与直线之间的夹角，并会利用平面、直线的相互关系（平行、垂直、相交等）解决有关问题.6、会求点到直线以及点到平面的距离.7、了解曲面方程和空间曲线方程的概念.8、掌握常用二次曲面的方程及其图形，会求简单的柱面和旋转曲面的方程.9、掌握空间曲线的参数方程和一般方程，了解空间曲线在坐标平面上的投影，并会求该投影曲线的方程.五多元函数微分学考试内容多元函数的概念二元函数的极限与连续的概念有界闭区域上多元连续函数的性质多元函数的偏导数和全微分全微分存在的必要条件和充分条件多元复合函数、隐函数（仅限一个方程的情形）的一阶偏导数二阶偏导数方向导数和梯度空间曲线的切线和法平面曲面的切平面和法线多元函数的极值和条件极值多元函数的最大值、最小值及其简单应用考试要求1、理解多元函数的概念，理解二元函数的几何意义.2、了解二元函数的极限与连续的概念以及有界闭区域上连续函数的性质.3、理解多元函数偏导数和全微分的概念，会求全微分，了解全微分存在的必要条件和充分条件，了解全微分形式的不变性.4、理解方向导数与梯度的概念，并掌握其计算方法.5、掌握多元复合函数一阶、二阶偏导数的求法.6、会求隐函数（仅限一个方程的情形）的一阶偏导数、二阶偏导数.7、掌握空间曲线的切线和法平面及曲面的切平面和法线的概念，会求它们的方程.8、理解多元函数极值和条件极值的概念，掌握多元函数极值存在的必要条件，了解二元函数极值存在的充分条件，会求二元函数的极值，会用拉格朗日乘数法求条件极值，会求简单多元函数的最大值和最小值，并会解决一些简单的应用问题.六多元函数积分学考试内容二重积分的概念、性质、计算和应用考试要求1、理解二重积分的概念，了解二重积分的性质，了解二重积分的中值定理.2、掌握二重积分的计算方法（直角坐标、极坐标），3、会用二重积分求一些几何量（平面图形的面积、立体的体积、曲面的面积）.七常微分方程考试内容常微分方程的基本概念可分离变量的微分方程齐次微分方程一阶线性微分方程贝努利方程二阶线性微分方程解的性质及解的结构定理二阶常系数齐次线性微分方程简单的二阶常系数非齐次线性微分方程考试要求1、了解微分方程及其阶、解、通解、初始条件和特解等概念.2、掌握可分离变量的微分方程及一阶线性微分方程的解法．3、会解齐次微分方程、贝努利方程，会用简单的变量代换解某些微分方程．4、理解线性微分方程解的性质及解的结构．5、掌握二阶常系数齐次线性微分方程的解法.6、会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程．。
高等数学考试大纲(适合专升本考生)
《高等数学I 》课程考试大纲一、课程基本信息1．课程性质：公共基础课2．适用对象：怀化学院专升本考生二、课程考试目的《高等数学》课程考试旨在考察学生对知识的掌握情况以及运用知识解决实际问题的能力.三、考试内容与要求第一章 函数极限与连续（一）考试内容一元函数的概念，函数的性质(有界性、单调性、奇偶性、周期性)，反函数，基本初等函数的概念、性质及其图形，复合函数，初等函数，数列极限，函数极限，无穷小与无穷大，无穷小与极限之间的关系，无穷小与无穷大之间的关系，极限的运算法则，极限存在准则，两个重要极限，无穷小的比较，函数的连续性，函数的间断点及其类型，连续函数的运算定理，初等函数的连续性，闭区间上连续函数的基本性质．（二）考试要求1．理解函数、初等函数的概念；2．了解函数的性质以及反函数的概念；3．掌握基本初等函数的性质及其图形；4．理解极限的概念，思想方法；5．了解极限的,,N X εεδε---定义；6．掌握左、右极限的概念，左、右极限与双边极限的关系；7．掌握极限四则运算法则；8．了解两个极限存在准则，熟练掌握两个重要极限；9．理解无穷小的概念及与极限的关系；10．了解无穷小的比较；11．理解连续的两种定义，掌握连续性的证明方法、连续函数的运算性质，会判定间断点的类型；12．知道闭区间上连续函数的性质，会用零点定理判别方程的根。
第二章 导数与微分（一）考试内容导数的概念，基本初等函数的导数，函数的和，差、积、商的导数，反函数和复合函数的导数，高阶导数，由隐函数、参数方程确定的函数的导数，微分的基本公式，微分形式不变性，微分在近似计算中的应用．（二）考试要求1．理解导数的概念，掌握利用概念求某些特殊极限的方法；2．掌握导数的几何意义，掌握求切线和法线方程的方法，明确可导与连续的关系；2．熟练掌握导数的运算；3．理解微分的概念、几何意义、微分形式不变性，明确可导与可微的关系；4．掌握微分在近似计算中的应用；第三章中值定理与导数的应用。
2015专接本考试大纲
2015专接本考试大纲2015年的专接本考试大纲是针对希望从专科学历提升到本科学历的学生所制定的一系列考试要求和标准。
专接本考试通常由各省教育考试院组织，旨在选拔优秀的专科毕业生进入本科阶段继续深造。
以下是2015年专接本考试大纲的主要内容概述。
# 一、考试目的专接本考试旨在考查学生是否具备进入本科学习的基本素质和能力，包括专业基础知识、专业技能、综合分析能力以及创新能力等。
# 二、考试科目专接本考试通常包括以下几个科目：1. 公共基础课：如政治、英语等。
2. 专业基础课：根据学生所报考的专业不同，可能包括数学、物理、化学等。
3. 专业课：针对学生所报考专业的核心课程。
# 三、考试形式考试形式可能包括：- 笔试：传统的书面考试，考查学生的理论知识掌握程度。
- 口试：部分专业可能需要进行面试，考查学生的实际操作能力和专业素养。
- 实践操作：针对某些专业，如医学、工程等，可能需要进行实践操作考核。
# 四、考试内容1. 公共基础课考试内容：- 政治：考查学生对政治理论的理解和分析能力。
- 英语：考查学生的英语阅读、写作、翻译等能力。
2. 专业基础课考试内容：- 数学：考查学生对高等数学、线性代数、概率论等基础知识的掌握。
- 物理/化学：根据专业要求，考查学生对物理或化学基础知识的掌握。
3. 专业课考试内容：- 根据学生所报考的专业，考查学生对专业核心知识的理解和应用能力。
# 五、考试要求1. 知识掌握：学生需要对所学专业知识有系统、深入的理解。
2. 分析能力：学生需要具备对复杂问题的分析和解决能力。
3. 实践能力：特别是对于需要实践操作的专业，学生需要有良好的实践操作技能。
# 六、考试准备1. 复习资料：学生应根据大纲要求，准备相应的复习资料，包括教材、参考书、历年真题等。
2. 时间管理：合理安排复习时间，确保各科目均衡复习。
3. 模拟考试：通过模拟考试来检验复习效果，及时调整复习策略。
# 七、考试技巧1. 答题技巧：掌握答题技巧，如快速阅读、关键词定位等，提高答题效率。
高等数学(专升本)考试大纲
《高等数学》（专升本）考试大纲一、考试内容与要求（一）函数、极限和连续1.函数考试内容：函数的简单性质；反函数；函数的四则运算与复合运算基本初等函数；初等函数。
要求：会求函数的定义域、表达式及函数值。
并会作出简单的分段函数图像。
理解和掌握函数的简单性质，会判断所给函数的类别。
会求单调函数的反函数。
掌握基本初等函数的简单性质及其图象。
2.极限考试内容：数列极限的概念，性质，收敛准则；函数极限的概念，函数极限的定理；无穷小量和无穷大量；两个重要极限。
要求：理解极限的概念。
会求函数在一点处的左极限与右极限。
了解极限的有关性质，掌握极限的四则运算法则。
掌握无穷小量的性质、无穷小量与无穷大量的关系。
会进行无穷小量阶的比较。
会运用等价无穷小量代换求极限。
熟练掌握用两个重要极限求极限的方法。
3.连续考试内容：函数连续的概念；函数在一点处连续的性质；闭区间上连续函数的性质；初等函数的连续性。
要求：理解函数连续与间断的概念，理解函数在一点连续与极限存在的关系。
会求函数的间断点及确定其类型。
掌握在闭区间上连续函数的性质，会运用介值定理推证一些简单命题。
会利用连续性求极限。
（二）一元函数微分学1.导数与微分考试内容：导数概念；求导法则，方法；高阶导数的概念；微分。
要求：了解可导性与连续性的关系，会用定义求函数在一点处的导数。
会求各类函数的导数。
会求简单函数的高阶导数。
理解函数的微分概念，掌握微分法则，了解可微与可导的关系，会求函数的一阶微分。
2.中值定理及导数的应用考试内容：中值定理；洛必达法则；函数增减性的判定法；函数极值与极值点，最值；曲线的凹凸性、拐点；曲线的水平渐近线与垂直渐近线。
要求：会用罗尔中值定理证明方程根的存在性。
会用拉格朗日中值定理证明简单的不等式。
熟练掌握洛必达法则求未定式的极限方法。
掌握利用导数判定函数单调性的方法，会利用增减性证明简单的不等式。
掌握求函数的极值和最值的方法，并且会解简单的应用问题。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2015年井冈山大学专升本《高等数学》考试大纲
关于考试大纲的几点说明
1．高等数学是理工类本科专业后续课程的基础，是教学计划中的一门专业基础课. 2．考试要求：本课程的考试要求既要考核知识，又要考核能力，因此要求考生复习本课程时应注意系统掌握本大纲所规定的基础知识，基本方法，提高运算能力和逻辑思维能力，并能运用数学知识分析，解决一些实际问题.
3．本大纲中将基本要求分为由低到高的三个等级，对概念和理论性的知识，分别用“知道”、“了解”、“理解”三级区分，对运算方法的知识分别用“会或能”、“掌握”、“熟练掌握”三级区分.
4．本课程考试方式为闭卷，答卷时间为120分钟，采用百分制，试题的难度按易、中、难三个层次的比例约为30：50：20.
5．题型
填空题，共5小题，每小题3分，计15分.
单项选择题（四个备选答案中有且只有一个正确）共5小题，每小题3分，计15分. 计算题，共5小题，每小题10分，计50分.
综合或应用题1题，计10分.
证明题1题，计10分.
6．参考书目：刘忠东，罗贤强等编《微积分》（上、下）中国传媒大学出版社
考试内容及要求
一、函数、极限与连续
1．考核知识点
（1）函数：函数的概念，函数的几种特性，分段函数，复合函数与反函数，初等函数. （2）极限：数列的极限，函数的极限，无穷小与无穷大，极限的运算法则，两个重要极限，无穷小的比较.
（3）连续：函数的连续性与间断点，闭区间上连续函数的性质.
2．考核目标和要求
（1）理解和掌握函数、极限与连续的概念.
（2）能熟练地求函数的定义域，初等函数及分段函数的函数值.
（3）熟练地应用极限的四则运算法则，两个重要极限求数列或函数极限.
（4）了解无穷小量与无穷大的概念与关系，会对无穷小的阶进行比较.
（5）掌握函数左、右极限与极限的关系.
（6）了解函数连续性的概念，会判断分段函数在分段点处的连续性.
（7）会求函数的间断点和连续区间以及会判断间断点的类型.
（8）知道闭区间上连续函数的性质.
二、导数与微分
1．考核知识点
（1）导数的定义，导数的几何意义，可导与连续的关系.
（2）求导法则，导数的四则运算法则，复合函数的求导法则，反函数的求导法则，隐函数及参数方程所确定的函数的求导法则，基本求导公式.
（3）高阶导数.
（4）微分的定义，求法及运算法则.
2．考核目标及要求
（1）理解导数定义，了解微分的概念，会求曲线上一点处的切线斜率及切线方程，会用导数定义求一些简单函数的导数，知道可导与连续的关系.
（2）熟练地运用求导法则求函数的导数，熟练地求函数的微分.
（3）会求初等函数的高阶导数.
三、导数的应用
1．考核知识点
（1）中值定理、罗尔定理、拉格朗的中值定理，柯西中值定理.
（2）导数的应用，洛比达法则，函数的单调性，函数的极值，函数的凹凸性，拐点，曲线的渐近线（水平、垂直）简单函数图形的描绘，最大值、最小值应用问题.
2．考核目标和要求星原专升本扣扣：800,089,910及重难点
（1）会叙述罗尔定理，拉格朗的中值定理，柯西中值定理，掌握用这三个定理作一些命题的证明.
（2）熟练地运用洛比达法则求各种未定型的极限.
（3）掌握用导数判定函数的单调性和极值点，会求函数的单调区间和极值，会用函数的单调性证明不等式.
（4）会求函数的凹凸区间和拐点，会求曲线的水平和垂直浙近线.
（5）会利用导数方法作简单函数的图形.
（6）掌握用导数方法求解最值应用问题.
四、不定积分
1．考核知识点
（1）原函数与不定积分的概念.
（2）基本积分公式，换元积分法和分部积分法.
（3）简单有理函数的积分.
2．考核目标和要求
（1）掌握原函数与不定积分的概念，能熟练地应用基本积分公式，知道求导与求不定积分两种运算的关系.
（2）熟练地利用换元法与分部积分法求不定积分.
（3）会求一些简单有理函数的不定积分.
五、定积分及其应用
1．考核知识点
（1）定积分的定义与性质.
（2）变上限的定积分，原函数存在定理与牛顿—莱布尼兹公式.
（3）定积分的换元法与分部积分法.
（4）广义积分.
（5）定积分的应用，平面图形的面积和旋转体的体积.
2．考核目标和要求
（1）知道定积分的定义，星原专升本扣扣：800,089,910了解定积分的性质和积分中值定理.
（2）了解变上限的定积分，原函数存在定理，熟练地应用牛顿—莱布尼兹公式计算定积分.
（3）熟练掌握用定积分的换元法和分部积分法求定积分.
（4）会计算简单的广义积分.
（5）掌握有关用积分性质，变上限的定积分或换元法作一些命题的证明.
（6）了解微元法，掌握用定积分求平面图形的面积或旋转体的体积.
六、向量代数与空间解析几何
1．考核知识点
（1）向量的概念及向量的线性运算.
（2）空间直角坐标系，向量的坐标表示.
（3）向量的数量积与向量积.
（4）平面与空间直线的各种方程.
（5）两平面间，两直线间，平面与直线间的位置关系.
（6）曲面与空间曲线的方程.
（7）柱面、旋转曲面、椭球面、椭圆抛物面、单叶双曲面及双叶双曲面.
2．考核目标及要求
（1）理解向量的定义，向量的模、方向的概念.
（2）熟练掌握向量的加、减、数乘、数量积及向量积的运算.
（3）知道向量平行与垂直的条件.
（4）根据条件，熟练地建立平面和直线的各种形式的方程.
（5）能正确判断平面与平面、直线与直线、平面与直线的位置关系.
（6）能正确识别曲面的方程及形状.
七、多元函数的微积分学
1．考核知识点
（1）多元函数的定义，二元函数的极限与连续.
（2）偏导数的概念及计算，高阶偏导数，全微分的概念及计算.
（3）多元复合函数的求导法则及隐函数的求导法.
（4）偏导数的几何应用.
（5）多元函数的极值，条件极值及拉格朗日乘数法.
（6）二重积分的概念及性质.
（7）二重积分的计算—直角坐标系及利用极坐标计算.
（8）二重积分的简单应用—立体的体积及曲面的面积.
2．考核目标及要求星原专升本扣扣：800,089,910及重难点
（1）知道二元函数和二元函数极限与连续的定义，会求二元函数的定义域.
（2）熟练掌握求偏导数的方法，会求二元函数的二阶偏导数.
（3）掌握二元复合函数及隐函数的求导法则，会求三元复合函数及隐函数的偏导数. （4）了解二、三元函数全微分的概念，会求二、三元函数的全微分.
（5）会求空间曲线的切线与法平面、曲面的切平面与法线方程.
（6）了解二元函数极值与条件极值的概念，会求二元函数的极值与条件极值.
（7）知道二重积分的定义和性质.
（8）熟练掌握化二重积分为二次积分求二重积分的方法，包括直角坐标系中及利用极坐标变换的方法.
八、常微分方程
1．考核知识点
（1）微分方程的定义，阶及解的概念.
（2）一阶微分方程：可分离变量的微分方程，齐次方程，一阶线性微分方程.
（3）可降阶的高阶微分方程.型，型及型微分方程.
（4）二阶常系数线性齐次和非齐次微分方程.
2．考核目标及要求
（1）了解微分方程的定义，阶及解的概念，熟练掌握可分离变量方程和一阶非齐次线性方程的解法，掌握齐次方程的解法.
（2）掌握可降阶的三类微分方程的解法.
（3）掌握二阶常系数齐次线性方程的解法.
（4）掌握二阶常系数非齐次线性方程中和时通特及特解的求法.（这里为的次多项式）
（5）掌握对实际问题建立微分方程并求解之.
九、级数
1．考核知识点
（1）数项级数的概念，级数的敛散性及性质.
（2）正项级数的定义及其判别法.
（3）交错级数的定义及其收敛判别法，任意项级数的绝对收敛与条件收敛.
（4）幂级数的定义，收敛半径、收敛域.
（5）幂级数的运算和函数的连续性，和函数的求导与求积.
（6）函数展开成幂级数.
（7）几个常见函数的马克劳林级数.()
2．考核目标和要求
（1）理解无穷级数敛散性的定义，收敛的必要条件及基本性质.
（2）熟练掌握正项级数敛散性的比较判别法，比值判别法.
（3）了解交错级数的定义，掌握交错级数收敛的判别法.
（4）理解任意项级数的绝对收敛与条件收敛.
（5）知道幂级数的定义，会求幂级数的收敛半径和收敛域.
（6）了解幂级数的四则运算，和函数的连续性，会求和函数的导数和积分.
（7）掌握的幂级数展开式，并应用它们将一些简单函数展成的幂级数.。