复数的有关概念-几何意义1
复数的几何意义是什么

复数的几何意义是什么复数的定义复数是形如a+bi的数。
式中a,b为实数,i是一个满足i=-1的数,因为任何实数的平方不等于-1,所以i不是实数,而是实数以外的新的数。
在复数a+bi中,a称为复数的实部,b称为复数的虚部,i称为虚数单位。
当虚部等于零时,这个复数就是实数;当虚部不等于零时,这个复数称为虚数,虚数的实部如果等于零,则称为纯虚数。
由上可知,复数集包含了实数集,因而是实数集的扩张。
复数常用形式z=a+bi叫做代数式。
我们把形如z=a+bi(a、b均为实数)的数称为复数。
其中,a称为实部,b称为虚部,i称为虚数单位。
当z的虚部b=0时,则z为实数;当z的虚部b≠0时,实部a=0时,常称z为纯虚数。
复数域是实数域的代数闭包,即任何复系数多项式在复数域中总有根。
复数是由意大利米兰学者卡当在16世纪首次引入,经过达朗贝尔、棣莫弗、欧拉、高斯等人的工作,此概念逐渐为数学家所接受。
复数的四则运算公式复数运算法则有:加减法、乘除法。
两个复数的和依然是复数,它的实部是原来两个复数实部的和,它的虚部是原来两个虚部的和。
复数的加法满足交换律和结合律。
此外,复数作为幂和对数的底数、指数、真数时,其运算规则可由欧拉公式e^iθ=cos θ+i sin θ(弧度制)推导而得。
加法法则:复数的加法按照以下规定的法则进行:设z1=a+bi,z2=c+di是任意两个复数,则它们的和是 (a+bi)+(c+di)=(a+c)+(b+d)i。
两个复数的和依然是复数,它的实部是原来两个复数实部的和,它的虚部是原来两个虚部的和。
复数的加法满足交换律和结合律,即对任意复数z1,z2,z3,有: z1+z2=z2+z1;(z1+z2)+z3=z1+(z2+z3)。
减法法则:复数的减法按照以下规定的法则进行:设z1=a+bi,z2=c+di是任意两个复数,则它们的差是 (a+bi)-(c+di)=(a-c)+(b-d)i。
两个复数的差依然是复数,它的实部是原来两个复数实部的差,它的虚部是原来两个虚部的差。
5.1复数的概念及其几何意义-【新教材】北师大版高中数学必修第二册课件

O 1 2
x
的圆(如图(1)).
|z|=2
图(1)
典型例题
例3:在复平面内,表示下列复数的点Z
的集合是什么图形?
(1)|z|=2;
(2) 2≤|z|≤3.
解: (2)不等式2≤|z|≤3可以化为不等式组
|z|≤3,
|z|≥2.
典型例题
例3:在复平面内,表示下列复数的点Z
y
b
Z
O
a x
课文精讲
➢ 复数的几何意义
虽然两个复数一般不能比较大小,
但它们的模是非负实数,可以比较大小.
典型例题
例3:在复平面内,表示下列复数的点Z
的集合是什么图形?
(1)|z|=2;
(2) 2≤|z|≤3.
解: (1)复数z的模等于2表明,向量的
模等于2,即点Z到原点O的距离等于2,
y
因此满足条件|z|=2的点Z的集合
典型例题
例2:设x,y∈R,(x+2)-2xi=-3y+(y-1)i,
求x,y的值.
解: 由复数相等的定义,得
x+2=-3y
-2x=y-1
解这个方程组,得
x=1
y=-1
课文精讲
➢ 复数的几何意义
问题提出
我们知道,实数与数轴上的点一一对
应,可以用数轴上的点来表示实数.复数
z=a+bi(a,b∈R)由实部a和虚部b两个实
故答案为:1+i.
本课小结
复数的概念
复数的概念及其
几何意义
复数的几何意义
再 见
它是实数.
课文精讲
➢ 复数的概念
两个复数a+bi 与c+di (a,b,c , d∈R)相等
复数的几何意义与三角形式

复数的几何意义与三角形式复数是数学中重要的概念,它包含了一个实部和一个虚部,可以表示为$a+bi$,其中$a$是实部,$b$是虚部,$i$是虚数单位,满足$i^2=-1$。
复数的几何意义是指将复数表示在复平面上的点。
复平面是一个平面直角坐标系,实轴表示实部,虚轴表示虚部。
复数$a+bi$在复平面上的位置可以由其实部和虚部决定。
例如,复数$3+4i$在复平面上的位置是实轴上3的位置,再向上移动4个单位。
使用复数的三角形式可以更方便地表示复数在复平面上的位置。
复数$a+bi$的三角形式可以表示为$r(\cos\theta+i\sin\theta)$,其中$r$是复数的模长,表示复数到原点的距离,$\theta$是复数的辐角,表示复数与实轴的夹角。
这种表示方法的优势在于可以使用三角函数来直接计算复数的运算,更加简洁和直观。
在三角形式中,可以使用指数形式进一步简化复数的运算。
根据欧拉公式,$e^{i\theta}=\cos\theta+i\sin\theta$,将三角形式中的$\cos\theta$和$\sin\theta$替换为指数形式可以得到$r \cdote^{i\theta}$。
这种形式方便了复数的乘法和幂运算。
例如,两个复数$r_1 \cdot e^{i\theta_1}$和$r_2 \cdot e^{i\theta_2}$的乘积可以表示为$r_1r_2 \cdot e^{i(\theta_1+\theta_2)}$,两个复数的幂可以表示为$(r \cdot e^{i\theta})^n=r^n \cdot e^{in\theta}$。
复数的几何意义在很多数学和工程应用中都非常重要。
首先,复数可以用来表示平面上的向量。
向量有大小和方向,复数的实部可以表示向量的大小,复数的虚部可以表示向量与实轴的夹角。
复数在向量运算中具有很好的性质,可以方便地进行加法、减法、乘法和除法。
其次,复数的几何意义在电路分析中扮演了重要角色。
复数的几何意义与运算规则

复数的几何意义与运算规则复数起源于解方程中无实数解的情况,它扩展了实数域,使得原本不可能的运算变得有解。
复数的几何意义和运算规则是理解和应用复数的基础。
本文将从几何角度解释复数,介绍复数的四则运算规则,并提供一些实例来进一步说明。
一、复数的几何意义复数可以表示为一个实数和一个虚数的和,其中实数部分代表复数在实轴上的位置,虚数部分代表复数在虚轴上的位置。
我们可以将复数表示为z=a+bi,其中a为实部,b为虚部。
从几何意义上看,复数可以在平面上表示为一个有序数对(a, b),其中a为复数的实部,b为复数的虚部,平面上的每个点都表示一个复数。
实部和虚部决定了复数在平面上的位置。
二、复数的运算规则1. 加法复数的加法满足交换律和结合律。
当两个复数相加时,实部与实部相加,虚部与虚部相加,得到新的复数。
2. 减法复数的减法可以通过加法和乘法来计算。
减去一个复数相当于加上这个复数的相反数。
3. 乘法复数的乘法满足交换律和结合律。
两个复数相乘时,实部和虚部分别相乘后相加,得到新的复数。
4. 除法复数的除法可以通过乘法和共轭复数来计算。
除以一个复数相当于乘以这个复数的倒数。
三、实例说明例子1:假设有两个复数z1=2+3i和z2=1-2i,求它们的和、差、积和商。
解:两个复数的和:z1+z2=2+3i+1-2i=3+i两个复数的差:z1-z2=2+3i-(1-2i)=1+5i两个复数的积:z1*z2=(2+3i)*(1-2i)=8-1i两个复数的商:z1/z2=(2+3i)/(1-2i)=0.8+1.6i例子2:在复平面上,给定两个复数z1=2+3i和z2=4-2i,求它们的距离和中点。
解:两个复数的距离可以计算为:|z1-z2|=|2+3i-(4-2i)|=|-2+5i|=√((-2)^2+(5^2))=√29两个复数的中点可以计算为:(z1+z2)/2=((2+3i)+(4-2i))/2=(6+1i)/2=3+0.5i以上例子说明了复数的几何意义和运算规则在实际问题中的应用。
复数的几何意义

复数的几何意义2篇复数的几何意义(一)复数是数学中的一个重要概念,它由实数和虚数构成,形如a+bi 的形式,其中a是实数部分,b是虚数部分,i是虚数单位。
虽然在实际生活中我们很少遇到复数,但是它在数学和物理学等学科中有着广泛的应用。
复数的几何意义就是描述复平面上的点,本文将从两个角度来探讨复数的几何意义。
首先,我们来看复数的几何意义与向量的关系。
复数可以表示为二维向量的形式(a,b),其中a和b分别是复数的实部和虚部。
将复数对应到二维平面上,可以将复数a+bi表示为点(x,y),其中x=a,y=b。
这样,复数就可以转化为二维平面上的一个点。
根据向量的性质,我们可以将复数相加、相减、相乘、相除等运算转化为向量的运算。
例如,两个复数相加就是将它们对应的点向量相加,两个复数相乘就是将它们对应的点向量进行缩放和旋转操作。
通过这种方式,复数的运算就可以直观地在二维平面上进行,这有助于我们更好地理解和掌握复数的运算规律。
其次,复数的几何意义还与极坐标系的相关性质有关。
复数可以用极坐标的形式来表示,即r(cosθ+ i sinθ),其中r为复数的模,θ为复数的幅角。
在复平面上,复数对应的点可以看作是从原点出发的一个向量,其长度为r,与x轴正向之间的夹角为θ。
这样,复数的加法、减法、乘法等运算也可以用极坐标形式来表示。
例如,两个复数的乘积可以表示为r1 r2 (cos(θ1+θ2)+ i sin(θ1+θ2)),即两个向量的长度相乘,夹角相加。
通过极坐标形式,我们可以更直观地描述和理解复数的乘法运算。
综上所述,复数的几何意义可以从向量和极坐标两个角度来理解。
复数可以对应到二维平面上的一个点,它可以应用于向量运算和极坐标形式的运算。
这种几何意义的理解有助于我们更好地理解和应用复数,而不仅仅将其看作是一个抽象的符号。
通过深入研究和探讨复数的几何意义,我们可以更好地应用复数的性质解决实际问题,拓展数学的应用领域。
复数的几何意义(二)在前文中我们已经了解了复数的几何意义与向量和极坐标的关系。
《复数的概念及其几何意义》示范公开课教学课件【高中数学北师大】

把新引进的数添加到实数集后,我们希望按照前面总结的数系扩充的“规则”,对实数系进行进一步扩充,那么,实数系经过扩充后,得到的新数系由哪些数组成?
,
,
.(如:,,,等)
所有新数集中的数都可以写成(,)的形式,因为,,,.
我们把形如(,)的数叫做复数.通常用字母表示,即
(,).
实数的绝对值和向量的模的几何意义分别是什么?通过类比,你能说出复数的模的几何意义吗?
数轴上表示数的点到原点的距离,就叫做这个数的绝对值.而向量的大小称为向量的长度,也称为向量的模. 类比可得, 复数的模:.
从几何上来看复数(,)的模表示点到原点的距离.
全体复数构成的集合为,,叫做复数集,用字母一般记作.
复数集与实数集有什么关系呢?
对于复数(,),当且仅当时,它是实数,当且仅当时,它是实数,当时,叫做虚数,当且时,叫做纯虚数.
复数集
虚数集
实数集
你能写出自然数集、整数集、有理数集、实数集和复数集的关系,并用图表示吗?
显然实数集是复数集的真子集,即.
我们知道复数集是由形如(,)的数组成的,为了保证集合中元素的互异性(确定性),我们需要明确集合中两个元素相等的含义,那么,两个复数和(,)相等的含义是什么呢?
复数由实部和虚部唯一确定,所以判断两个复数是否相等,就要考虑它们的实部和虚部是否分别相等.
两个实数可以比较大小,但是两个负数,如果不全是实数,它们之间就不能比较大小,只能说相等或不相等.
解:向量平移后得到向量,则,因而向量所对应的复数是.注意:(1)向量平移后,所得向量的坐标不变.(2)向量的横坐标、纵坐标分别是其对应复数的实部与虚部.
结构框图
教材第167页练习第1-4题.
Байду номын сангаас
复数的几何意义(优秀经典公开课课件)

[母题变式] 1.在例 3(2)中,B→A对应的复数是 z,则 z =________. 解析 由例 3(2)的解析可知B→A对应的复数是 5-5i,即 z=5-5i, 所以-z =5+5i.
答案 5+5i
2.在例 3(2)中,若点 A 关于实轴的对称点为点 C,则向量O→C对应的复数为 ________.
A.a=0 或 a=2
B.a=0
C.a≠1 且 a≠2
D.a≠1 或 a≠2
解析 ∵复数 z=(a2-2a)+(a2-a-2)i 对应的点在虚轴上,∴a2-2a=0, ∴a=0 或 a=2.
答案 A
4.已知复数 z 的实部为-1,虚部为 2,则|z|=____________. 解析 |z|= -12+22= 5. 答案 5
题型二 复数模的几何意义 [例 2] 设 z∈C,在复平面内对应点 Z,试说明满足下列条件的点 Z 的集合 是什么图形. (1)|z|=3;(2)1≤|z|≤2. [解析] (1) |z|=3 说明向量O→Z的长度等于 3,即复数 z 在复平面内对应的点 Z 到原点的距离为 3,这样的点 Z 的集合是以原点 O 为圆心,3 为半径的圆.
(2)若 z 对应的点在第三象限,则有
a2-1<0, 2a-1<0,
解得-1<a<21.
故 a 的取值范围是-1,21.
[规律方法] 按照复数和复平面内所有点所成的集合之间的一一对应关系,每一个复数都 对应着一个有序实数对,只要在复平面内找出这个有序实数对所表示的点,就可 根据点的位置判断复数实部、虚部的取值.
B.-5-5i
C.5+5i
D.5-5i
[解析] (1)由复数的几何意义, 可得O→Z1=(5,-4),O→Z2=(-5,4), 所以O→Z1+O→Z2=(5,-4)+(-5,4)=(0,0), 所以O→Z1+O→Z2对应的复数为 0.
复数的几何意义
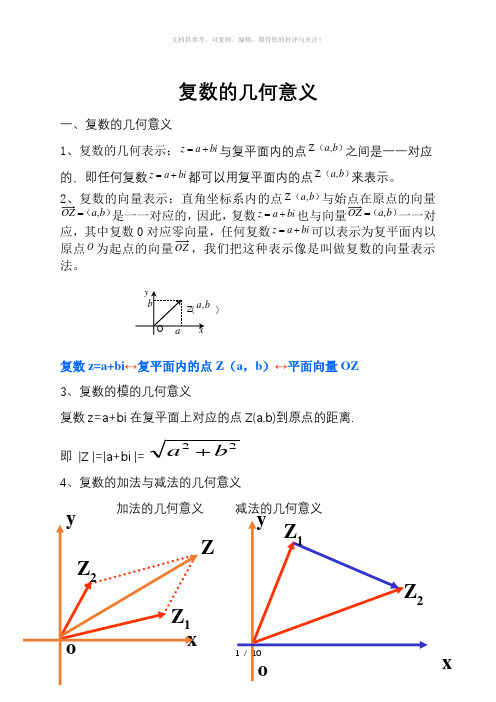
复数的几何意义一、复数的几何意义1、复数的几何表示:bi a z +=与复平面内的点)(b ,a Z 之间是一一对应的,即任何复数bi a z +=都可以用复平面内的点)(b ,a Z 来表示。
2、复数的向量表示:直角坐标系内的点)(b ,a Z 与始点在原点的向量)(b ,a OZ =是一一对应的,因此,复数bi a z +=也与向量)(b ,a OZ =一一对应,其中复数0对应零向量,任何复数bi a z +=可以表示为复平面内以原点O 为起点的向量OZ ,我们把这种表示像是叫做复数的向量表示法。
复数z=a+bi ↔复平面内的点Z (a ,b )↔平面向量OZ 3、复数的模的几何意义复数z=a+bi 在复平面上对应的点Z(a,b)到原点的距离. 即 |Z |=|a+bi |=22b a +4、复数的加法与减法的几何意义加法的几何意义 减法的几何意义)ZZ 2Z1yz 1z 2≠0时, z 1+z 2对应的向量是以OZ 1、OZ 2、为邻边的平行四边形OZ 1ZZ 2的对角线OZ , z 2-z 1对应的向量是Z 1Z 2 5、 复数乘法与除法的几何意义z 1=r 1(cos θ1+i sin θ1) z 2=r 2(cos θ2+i sin θ2)①乘法:z=z 1· z 2=r 1·r 2 [cos(θ1+θ2)+i sin(θ1+θ2)]如图:其对应的向量分别为oz oz oz 12→→→显然积对应的辐角是θ1+θ2 < 1 > 若θ2 > 0 则由oz 1→逆时针旋转θ2角模变为oz 1→的r 2倍所得向量便是积z 1·z 2=z 的向量oz →。
< 2 >若θ2< 0 则由向量oz 1→顺时针旋转θ2角模变为r 1·r 2所得向量便是积z 1·z 2=z 的向量oz →。
为此,若已知复数z 1的辐角为α,z 2的辐角为β求α+β时便可求出z 1·z 2=z a z 对应的辐角就是α+β这样便可将求“角”的问题转化为求“复数的积”的运算。
