三视图与立体几何练习
立体几何三视图经典练习及答案详解

A.4π B.8π C.12π D.16π 解析 由正弦定理得sin630°=2r(其中 r 为正三棱柱底面 三角形外接圆的半径),∴r=1,∴外接球的半径 R= 12+12 = 2,∴外接球的表面积 S=4πR2=8π.故选 B.
4
高考一轮总复习 ·数学[理](经典版)
解析 设圆柱底面圆半径为 r 尺,高为 h 尺,依题意, 圆柱体积为 V=πr2h=2000×1.62≈3×r2×13.33,所以 r2≈81,即 r≈9,所以圆柱底面圆周长为 2πr≈54,54 尺=5 丈 4 尺,则圆柱底面圆周长约为 5 丈 4 尺.故选 B.
10
高考一轮总复习 ·数学[理](经典版)
6.[2018·遵义模拟]一个几何体的三视图如图所示,其中 俯视图是菱形,则该几何体的侧面积为( )
A. 3+ 6 B. 3+ 5 C. 2+ 6 D. 2+ 5
11
高考一轮总复习 ·数学[理](经典版)
解析 由三视图还原为空间几何体,如图所示,则有 OA=OB=1,AB= 2.
23
高考一轮总复习 ·数学[理](经典版)
2.[2018·北京模拟]某三棱锥的三视图如图所示,则该三 棱锥的表面积是( )
A.2+ 5 C.2+2 5
24
B.4+ 5 D.5
高考一轮总复习 ·数学[理](经典版)
解析 由三视图分析知,该几何体是底面为等腰三角 形,其中一条侧棱与底面垂直的三棱锥(SA⊥平面 ABC),如 图,由三视图中的数据可计算得 S△ABC=21×2×2=2,S△SAC =12× 5×1= 25,S△SAB=21× 5×1= 25,S△SBC=21×2× 5 = 5,所以 S 表面积=2+2 5.故选 C.
高三数学空间几何体的三视图与直观图试题答案及解析
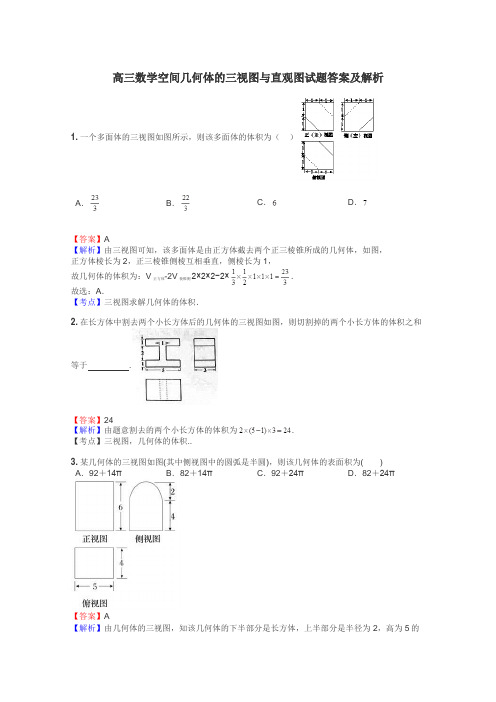
高三数学空间几何体的三视图与直观图试题答案及解析1.一个多面体的三视图如图所示,则该多面体的体积为()A.B.C.D.【答案】A【解析】由三视图可知,该多面体是由正方体截去两个正三棱锥所成的几何体,如图,正方体棱长为2,正三棱锥侧棱互相垂直,侧棱长为1,故几何体的体积为:V正方体-2V棱锥侧2×2×2−2×.故选:A.【考点】三视图求解几何体的体积.2.在长方体中割去两个小长方体后的几何体的三视图如图,则切割掉的两个小长方体的体积之和等于.【答案】24【解析】由题意割去的两个小长方体的体积为.【考点】三视图,几何体的体积..3.某几何体的三视图如图(其中侧视图中的圆弧是半圆),则该几何体的表面积为()A.92+14πB.82+14πC.92+24πD.82+24π【答案】A【解析】由几何体的三视图,知该几何体的下半部分是长方体,上半部分是半径为2,高为5的圆柱的一半.长方体中EH=4,HG=4,GK=5,所以长方体的表面积为(去掉一个上底面)2(4×4+4×5)+4×5=92.半圆柱的两个底面积为π×22=4π,半圆柱的侧面积为π×2×5=10π,所以整个组合体的表面积为92+4π+10π=92+14π,选A.4.在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为()【答案】D【解析】由题目所给的几何体的正视图和俯视图,可知该几何体为半圆锥和三棱锥的组合体,如图所示,可知左视图为等腰三角形,且轮廓线为实线,故选D.5.一个正方体截去两个角后所得几何体的正视图、侧视图如图所示,则其俯视图为()【答案】C【解析】依题意可知该几何体的直观图如图所示,故其俯视图应为C.6.某几何体的三视图如图所示,则该几何体的体积为A.12B.18C.24D.30【答案】C【解析】由三视图可知该几何体是一个底面为直角三角形的直三棱柱的一部分,其直观图如上图所示,其中,侧面是矩形,其余两个侧面是直角梯形,由于,平面平面,所以平面,所以几何体的体积为:故选C.【考点】1、空间几何体的三视图;2、空间几何体的体积.7.一块石材表示的几何体的三视图如图2所示,将石材切削、打磨、加工成球,则能得到的最大球的半径等于()A.1B.2C.3D.4【答案】B【解析】由图可得该几何体为三棱柱,因为正视图,侧视图,俯视图的内切圆半径最小的是正视图(直角三角形)所对应的内切圆,所以最大球的半径为正视图直角三角形内切圆的半径,则,故选B.【考点】三视图内切圆球三棱柱8. [2013·四川高考]一个几何体的三视图如图所示,则该几何体可以是()A.棱柱B.棱台C.圆柱D.圆台【答案】D【解析】由正视图和侧视图可知,该几何体不可能是圆柱,排除选项C;又由俯视图可知,该几何体不可能是棱柱或棱台,排除选项A、B.故选D.9.[2013·宁波质检]如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA1⊥平面A1B1C1,正视图是正方形,俯视图是正三角形,该三棱柱的侧视图面积为()A.2B.C.2D.4【答案】A【解析】由题意可知,该三棱柱的侧视图应为矩形,如图所示.在该矩形中,MM1=CC1=2,CM=C1M1=·AB=.所以侧视图的面积为S=2.10.某几何体的三视图如图所示,则该几何体的体积的最大值为 .【答案】【解析】该几何体是类似墙角的三棱锥,假设一条直角的棱长为x,则三条直角棱长分别为.所以体积为.当且仅当时取等号.【考点】1.三视图.2.函数最值问题.3.空间想象能力.11.(2012•广东)某几何体的三视图如图所示,它的体积为()A.12πB.45πC.57πD.81π【答案】C【解析】由三视图可知,此组合体上部是一个母线长为5,底面圆半径是3的圆锥,下部是一个高为5,底面半径是3的圆柱故它的体积是5×π×32+π×32×=57π故选C12. (2014·咸宁模拟)某几何体的三视图如图所示(其中侧视图中的圆弧是半圆),则该几何体的表面积为( )A.92+14πB.82+14πC.92+24πD.82+24π【答案】A【解析】由几何体的三视图知该几何体的下半部分是长方体,上半部分是半径为2,高为5的圆柱的一半.所以长方体的表面积为(去掉一个上底面)2(4×4+4×5)+4×5=92.半圆柱的两个底面积为π×22=4π,半圆柱的侧面积为π×2×5=10π,所以整个组合体的表面积为92+4π+10π=92+14π. 13.在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为【答案】D【解析】条件对应的几何体是由底面棱长为r的正四棱锥沿底面对角线截出的部分与底面为半径为r的圆锥沿对称轴截出的部分构成的。
小学数学 三视图练习题

小学数学三视图练习题三视图是指物体在正投影面上的三个视图分别为正视图、左视图和顶视图。
它是学习立体几何的基础,并且在工程制图中也有广泛的应用。
下面是一些小学数学的三视图练习题,帮助大家巩固相关知识。
题目一:根据下图的正视图、左视图和顶视图,确定物体的形状。
(插入图片,显示正视图、左视图和顶视图)要求:根据正视图、左视图和顶视图确定物体的形状,然后用文字描述出这个物体的形状。
注意描述要准确,并包括物体的名称和各个面的特征。
解答:根据正视图,我们可以看到物体是一个长方体形状的容器,其中有两个相对的长方形面。
根据左视图,我们可以看到物体的侧面有两个边相等的正方形面。
根据顶视图,我们可以看到物体的上面是一个定位的长方形,而下面则无法确定。
综合以上三个视图,我们可以确定这个物体是一个长方体形状的容器,上面和下面都是长方形面,两侧是正方形面。
题目二:根据下图的正视图、左视图和顶视图,求这个物体的体积,并单位是立方米。
(插入图片,显示正视图、左视图和顶视图)要求:根据三个视图计算出物体的体积,并将结果用文字描述出来,并附上计算过程。
解答:根据正视图和左视图,我们可以得出这个物体的长、宽、高分别为5米、3.5米和2米。
根据三个值,我们可以利用体积的计算公式V=长×宽×高来计算该物体的体积。
计算过程如下:V = 5米 × 3.5米 × 2米 = 35立方米。
综上所述,这个物体的体积为35立方米。
题目三:根据下图的正视图、左视图和顶视图,求这个物体的表面积,并单位是平方米。
(插入图片,显示正视图、左视图和顶视图)要求:根据三个视图计算出物体的表面积,并将结果用文字描述出来,并附上计算过程。
解答:根据正视图和左视图,我们可以得出物体的长、宽、高同题目二中一样,即5米、3.5米和2米。
根据这三个值,我们可以利用表面积的计算公式表面积=2×(长×宽+长×高+宽×高)来计算该物体的表面积。
立体几何专题
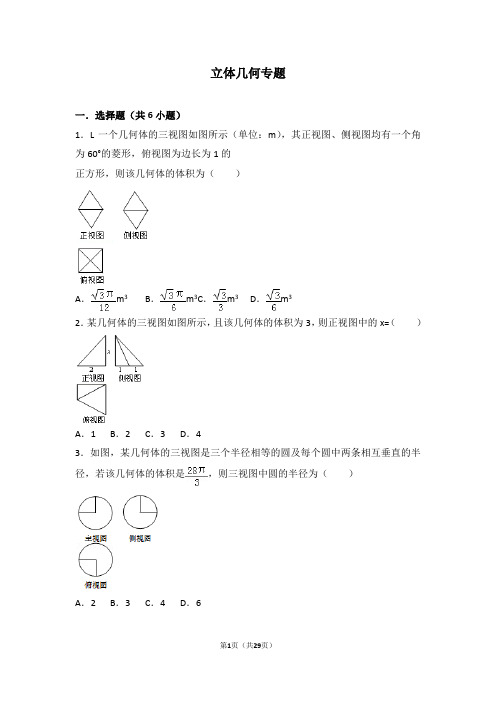
立体几何专题一.选择题(共6小题)1.L一个几何体的三视图如图所示(单位:m),其正视图、侧视图均有一个角为60°的菱形,俯视图为边长为1的正方形,则该几何体的体积为()A.m3B.m3C.m3D.m32.某几何体的三视图如图所示,且该几何体的体积为3,则正视图中的x=()A.1 B.2 C.3 D.43.如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径,若该几何体的体积是,则三视图中圆的半径为()A.2 B.3 C.4 D.64.一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为()A.+πB.+πC.+πD.1+π5.一个几何体的三视图如图所示,则该几何体的表面积为()A.24+πB.24﹣3πC.24﹣πD.24﹣2π6.已知四棱锥P﹣ABCD的三视图如图所示,则四棱锥P﹣ABCD的四个侧面中的最大面积是()A.6 B.8 C.2 D.3二.解答题(共10小题)7.如图,在三棱柱ABC﹣A 1B1C1中,AA1⊥底面ABC,AB=1,,∠ABC=60°.(1)证明AB⊥A1C;(2)求异面直线AB1和BC1所成角的余弦值;(3)求二面角A﹣A1C﹣B的平面角的余弦值.8.如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AC=AB=AA1,E是BC的中点,G是CC1的中点.(I)求异面直线AE与A1C所成的角;(II)求证EG⊥A1C;(III)求二面角C﹣AG﹣E的正切值.9.如图,在长方体ABCD﹣A1B1C1D1中,E、F分别是棱BC,CC1上的点,CF=AB=2CE,AB:AD:AA1=1:2:4,(1)求异面直线EF与A1D所成角的余弦值;(2)证明AF⊥平面A1ED;(3)求二面角A1﹣ED﹣F的正弦值.10.如图,在四棱柱ABCD﹣A1B1C1D1中,侧棱AA1⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=,且点M和N分别为B1C和D1D的中点.(Ⅰ)求证:MN∥平面ABCD(Ⅱ)求二面角D1﹣AC﹣B1的正弦值;(Ⅲ)设E为棱A1B1上的点,若直线NE和平面ABCD所成角的正弦值为,求线段A1E的长.11.如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.(1)求证:EG∥平面ADF;(2)求二面角O﹣EF﹣C的正弦值;(3)设H为线段AF上的点,且AH=HF,求直线BH和平面CEF所成角的正弦值.12.已知在直三棱柱ABC﹣A1B1C1中,AB⊥BC,且AA1=2AB=2BC=2,E,M分别是CC1,AB1的中点.(Ⅰ)证明:EM∥平面ABC;(Ⅱ)求直线A1E与平面AEB1所成角的正弦值;(Ⅲ)求二面角B﹣EM﹣B1的余弦值.13.如图,在四棱锥A﹣EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.(Ⅰ)求证:AO⊥BE;(Ⅱ)求二面角F﹣AE﹣B的余弦值;(Ⅲ)若直线CA与平面BEA所成的角的正弦值为,求实数a的值.14.如图四棱锥P﹣ABCD,三角形ABC为正三角形,边长为2,AD⊥DC,AD=1,PO垂直于平面ABCD于O,O为AC的中点,PO=1.(1)证明PA⊥BO;(2)证明DO∥平面PAB;(3)平面PAB与平面PCD所成二面角的余弦值.15.如图,在三棱锥S﹣ABC中,SA=AB=AC=BC=SC,0为BC的中点.(I)求证:SO⊥面ABC;(II)求异面直线SC与AB所成角的余弦值;(III)在线段AB上是否存在一点E,使二面角B﹣SC﹣E的平面角的余弦值为;若存在,求BE:BA的值;若不存在,试说明理由.16.已知在四棱锥P﹣ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,F,G分别是PA,PB,BC的中点.(Ⅰ)求证:EF⊥平面PAD;(Ⅱ)求平面EFG与平面ABCD所成锐二面角的大小;(Ⅲ)线段PD上是否存在一个动点M,使得直线GM与平面EFG所成角为,若存在,求线段PM的长度,若不存在,说明理由.立体几何专题参考答案与试题解析一.选择题(共6小题)1.L一个几何体的三视图如图所示(单位:m),其正视图、侧视图均有一个角为60°的菱形,俯视图为边长为1的正方形,则该几何体的体积为()A.m3B.m3C.m3D.m3【解答】解:由三视图知几何体为两个大小相同的正四棱锥的组合体,∵正视图、侧视图均有一个角为60°的菱形,俯视图为边长为1m的正方形,∴正四棱锥的高是正视图、侧视图中边长为1m的正三角形的高(m),∴该几何体的体积V=2×=(m3),故选:C.2.某几何体的三视图如图所示,且该几何体的体积为3,则正视图中的x=()A.1 B.2 C.3 D.4【解答】解:根据三视图判断几何体为四棱锥,其直观图是:V==3⇒x=3.故选:C.3.如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径,若该几何体的体积是,则三视图中圆的半径为()A.2 B.3 C.4 D.6【解答】解:由三视图可知:该几何体为球去掉,余下的几何体.设三视图中圆的半径为r,则=,解得r=2.故选:A.4.一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为()A.+πB.+πC.+πD.1+π【解答】解:由已知中的三视图可得:该几何体上部是一个半球,下部是一个四棱锥,半球的直径为棱锥的底面对角线,由棱锥的底底面棱长为1,可得2R=.故R=,故半球的体积为:=π,棱锥的底面面积为:1,高为1,故棱锥的体积V=,故组合体的体积为:+π,故选:C.5.一个几何体的三视图如图所示,则该几何体的表面积为()A.24+πB.24﹣3πC.24﹣πD.24﹣2π【解答】解:几何体为棱长为2的正方体挖去半径为2的球,所以几何体的表面积为:=24﹣π;故选:C.6.已知四棱锥P﹣ABCD的三视图如图所示,则四棱锥P﹣ABCD的四个侧面中的最大面积是()A.6 B.8 C.2 D.3【解答】解:因为三视图复原的几何体是四棱锥,顶点在底面的射影是底面矩形的长边的中点,底面边长分别为4,2,后面是等腰三角形,腰为3,所以后面的三角形的高为:=,所以后面三角形的面积为:×4×=2.两个侧面面积为:×2×3=3,前面三角形的面积为:×4×=6,四棱锥P﹣ABCD的四个侧面中面积最大的是前面三角形的面积:6.故选:A.二.解答题(共10小题)7.如图,在三棱柱ABC﹣A 1B1C1中,AA1⊥底面ABC,AB=1,,∠ABC=60°.(1)证明AB⊥A1C;(2)求异面直线AB1和BC1所成角的余弦值;(3)求二面角A﹣A1C﹣B的平面角的余弦值.【解答】证明:(1)在三棱柱ABC﹣A1B1C1中,∵AA1⊥ABC,∴AA1⊥AB,在△ABC中,AB=1,,∠ABC=60°,由正弦定理得∠ACB=30°,∴∠BAC=90°,即AB⊥AC.且AA1,AC为平面ACC1A1内两条相交直线,∴AB⊥平面ACC1A1,又A1C⊂ACC1A,∴AB⊥A1C.解:(2)如图,以A为坐标原点,AB为x轴,AC为y轴,AA1为z轴,建立空间直角坐标系,则A(0,0,0),B(1,0,0),,,,∴,,∴,∴异面直线AB1和BC1所成角的余弦值为(3)可取为平面AA 1C的法向量,设平面A 1BC的法向量为,则,又∵,,∴,不妨取y=1,则,因此有∴二面角A﹣A1C﹣B的平面角的余弦值为.8.如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AC=AB=AA1,E是BC的中点,G是CC1的中点.(I)求异面直线AE与A1C所成的角;(II)求证EG⊥A1C;(III)求二面角C﹣AG﹣E的正切值.【解答】解:(I)取B1C1的中点E1,连A1E1,E1C,E1C1,则AE∥A1E1,所以∠E1A1C是异面直线AE与A1C所成的角.设AC=AB=AA 1=2a,则,,..在△A1E1C中,.所以异面直线AE与A1C所成的角为.(II)由(I)可知,A1E1⊥B1C1,又因为三棱柱ABC﹣A1B1C1是直三棱柱,所以A1E1⊥面BCC1B1,得A1E1⊥EG;又由△E1CC1与△GEC相似,得又由A1E1∩CE1=E1,所以EG⊥面A1E1C,EG⊥A1C.(III)连接AG,设P是AC的中点,过点P作PQ⊥AG于Q,连EP,EQ,则EP⊥AC.又由平面ABC⊥平面ACC1A1,所以EP⊥平面ACC1A1.∠PQE是二面角C﹣AG﹣E的平面角,由,得所以二面角C﹣AG﹣E的平面角正切值是.9.如图,在长方体ABCD﹣A1B1C1D1中,E、F分别是棱BC,CC1上的点,CF=AB=2CE,AB:AD:AA1=1:2:4,(1)求异面直线EF与A1D所成角的余弦值;(2)证明AF⊥平面A1ED;(3)求二面角A1﹣ED﹣F的正弦值.【解答】解:(1)如图所示,建立空间直角坐标系,点A为坐标原点,设AB=1,依题意得D(0,2,0),F(1,2,1),A1(0,0,4),E(1,,0).(1)易得=(0,,1),=(0,2,﹣4).于是cos<,>==.所以异面直线EF与A1D所成角的余弦值为.(2)证明:连接ED,易知=(1,2,1),=(﹣1,,4),=(﹣1,,0),于是=0,=0.因此,AF⊥EA1,AF⊥ED.又EA1∩ED=E,所以AF⊥平面A1ED.(3)设平面EFD的一个法向量为u=(x,y,z),则即不妨令x=1,可得u=(1,2,﹣1).由(2)可知,为平面A1ED的一个法向量.于是cos<u,>==,从而sin<u,>=.二面角A1﹣ED﹣F的正弦值是10.如图,在四棱柱ABCD﹣A1B1C1D1中,侧棱AA1⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=,且点M和N分别为B1C和D1D的中点.(Ⅰ)求证:MN∥平面ABCD(Ⅱ)求二面角D1﹣AC﹣B1的正弦值;(Ⅲ)设E为棱A1B1上的点,若直线NE和平面ABCD所成角的正弦值为,求线段A1E的长.【解答】(Ⅰ)证明:如图,以A为坐标原点,以AC、AB、AA1所在直线分别为x、y、z轴建系,则A(0,0,0),B(0,1,0),C(2,0,0),D(1,﹣2,0),A1(0,0,2),B1(0,1,2),C1(2,0,2),D1(1,﹣2,2),又∵M、N分别为B1C、D1D的中点,∴M(1,,1),N(1,﹣2,1).由题可知:=(0,0,1)是平面ABCD的一个法向量,=(0,﹣,0),∵•=0,MN⊄平面ABCD,∴MN∥平面ABCD;(Ⅱ)解:由(I)可知:=(1,﹣2,2),=(2,0,0),=(0,1,2),设=(x,y,z)是平面ACD1的法向量,由,得,取z=1,得=(0,1,1),设=(x,y,z)是平面ACB1的法向量,由,得,取z=1,得=(0,﹣2,1),∵cos<,>==﹣,∴sin<,>==,∴二面角D1﹣AC﹣B1的正弦值为;(Ⅲ)解:由题意可设=λ,其中λ∈[0,1],∴E=(0,λ,2),=(﹣1,λ+2,1),又∵=(0,0,1)是平面ABCD的一个法向量,∴cos<,>===,整理,得λ2+4λ﹣3=0,解得λ=﹣2或﹣2﹣(舍),∴线段A1E的长为﹣2.11.如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.(1)求证:EG∥平面ADF;(2)求二面角O﹣EF﹣C的正弦值;(3)设H为线段AF上的点,且AH=HF,求直线BH和平面CEF所成角的正弦值.【解答】(1)证明:取AD的中点I,连接FI,∵矩形OBEF,∴EF∥OB,EF=OB,∵G,I是中点,∴GI∥BD,GI=BD.∵O是正方形ABCD的中心,∴OB=BD.∴EF∥GI,EF=GI,∴四边形EFIG是平行四边形,∴EG∥FI,∵EG⊄平面ADF,FI⊂平面ADF,∴EG∥平面ADF;(2)解:建立如图所示的坐标系O﹣xyz,则B(0,﹣,0),C(,0,0),E(0,﹣,2),F(0,0,2),设平面CEF的法向量为=(x,y,z),则,取=(,0,1)∵OC⊥平面OEF,∴平面OEF的法向量为=(1,0,0),∵|cos<,>|=∴二面角O﹣EF﹣C的正弦值为=;(3)解:AH=HF,∴==(,0,).设H(a,b,c),则=(a+,b,c)=(,0,).∴a=﹣,b=0,c=,∴=(﹣,,),∴直线BH和平面CEF所成角的正弦值=|cos<,>|==.12.已知在直三棱柱ABC﹣A1B1C1中,AB⊥BC,且AA1=2AB=2BC=2,E,M分别是CC1,AB1的中点.(Ⅰ)证明:EM∥平面ABC;(Ⅱ)求直线A1E与平面AEB1所成角的正弦值;(Ⅲ)求二面角B﹣EM﹣B1的余弦值.【解答】证明:(Ⅰ)在直三棱柱ABC﹣A1B1C1中,BB1⊥AB,BB1⊥BC,又∵AB⊥BC,∴AB⊥平面BCC1B1.…(1分)如图,以点B为原点,,,分别为x轴、y轴、z轴正方向,建立空间直角坐标系,则B(0,0,0),C(1,0,0),B1(0,2,0),A(0,0,1),C1(1,2,0),A1(0,2,1).…(3分)∵E,M分别是CC1,AB1的中点,∴E(1,1,0),M(0,1,),∴=(﹣1,0,).平面ABC的法向量为=(0,2,0),∵•=0,∴⊥.又∵EM⊄平面ABC,∴EM∥平面ABC.…(6分)(Ⅱ)=(0,2,﹣1),=(﹣1,1,0),=(﹣1,1,1).设=(x1,y1,z1)为面AEB1的法向量,则•=•=0,即取y1=1,则x1=1,z1=2,从而=(1,1,2),设直线A1E与平面AEB1所成角为θ,则sinθ=|cos<,>|===,即直线A1E与平面AEB1所成角的正弦值为.…(10分)(Ⅲ)=(1,1,0),=(0,1,).设=(x2,y2,z2)为面BEM的法向量,则•=•=0,即取z2=2,则x2=1,y2=﹣1,从而=(1,﹣1,2),∴cos<,>==,由图形可知所求二面角的平面角为钝角,∴二面角B﹣EM﹣B1的余弦值为﹣.…(13分)13.如图,在四棱锥A﹣EFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.(Ⅰ)求证:AO⊥BE;(Ⅱ)求二面角F﹣AE﹣B的余弦值;(Ⅲ)若直线CA与平面BEA所成的角的正弦值为,求实数a的值.【解答】证明:(Ⅰ)∵△AEF为等边三角形,O为EF的中点,∴AO⊥EF,又∵平面AEF⊥平面EFCB,平面AEF∩平面EFCB=EF,AO⊂平面AEF,∴AO⊥平面EFCB,又BE⊂平面EFCB,∴AO⊥BE.(Ⅱ)取CB的中点D,连接OD,则OD⊥EF,以O为原点,分别以OE、OA、OD为坐标轴建立空间直角坐标系,则O(0,0,0),E(a,0,0),F(﹣a,0,0),,,,∴,=(a,﹣a,0),设平面AEB的一个法向量,则,∴,令y=1,得=(,1,﹣1).平面AEF的一个法向量为,∴=﹣1,||=,||=1,∴,由二面角F﹣AE﹣B为钝二面角,∴二面角F﹣AE﹣B的余弦值为﹣.(Ⅲ),∴=4,||=,||=,∴cos<,>=,∴6a2﹣12a+16=10,解得a=1.14.如图四棱锥P﹣ABCD,三角形ABC为正三角形,边长为2,AD⊥DC,AD=1,PO垂直于平面ABCD于O,O为AC的中点,PO=1.(1)证明PA⊥BO;(2)证明DO∥平面PAB;(3)平面PAB与平面PCD所成二面角的余弦值.【解答】解:(1)证明:如图以A为原点建立空间直角坐标系A﹣xyz,则,A(0,0,0),B(,﹣1,0),C(,1,0),D(0,1,0),O(,,0),P(,,1)…(2分)=(,,1),=(1,,0),,∴PA⊥BO.…(5分)(2)证明:=(,,1),=(,﹣1,0),设平面APB法向量为=(x0,y0,z0)可得,令x°=1,则=(1,,)…(7分).=(,,0),,DO∥平面PAB…(9分)(3)=(,,1),=(,0,0)设平面DPC法向量为,可得,令y°=1,则=(0,1,)…(11分).平面PAB与平面PCD所成二面角的余弦值为 (13)15.如图,在三棱锥S﹣ABC中,SA=AB=AC=BC=SC,0为BC的中点.(I)求证:SO⊥面ABC;(II)求异面直线SC与AB所成角的余弦值;(III)在线段AB上是否存在一点E,使二面角B﹣SC﹣E的平面角的余弦值为;若存在,求BE:BA的值;若不存在,试说明理由.【解答】解:(Ⅰ)连接SO,显然∴SO⊥BC,设SB=a,则SO=,AO=,SA=a∴SO2+OA2=SA2,∴SO⊥OA,又∴BC∩OA=0,∴SO⊥平面ABC.(Ⅱ)以O为原点,以OC所在射线为x轴正半轴,以OA所在射线为y轴正半轴以OS所在射线为z轴正半轴建立空间直角坐标系.则有O(0,0,0),,,,,∴∴,∴,∴异面直线SC与AB所成角的余弦值为,(Ⅲ)假设存在E满足条件,设(0≤λ≤1),则,.设面SCE的法向量为=(x,y,z),由,得,.因为OA⊥面ABC,所以可取向量=(0,1,0)为面SBC的法向量.所以,,解得,.所以,当BE:BA=1:2时,二面角B﹣SC﹣E的余弦值为.16.已知在四棱锥P﹣ABCD中,底面ABCD是边长为4的正方形,△PAD是正三角形,平面PAD⊥平面ABCD,E,F,G分别是PA,PB,BC的中点.(Ⅰ)求证:EF⊥平面PAD;(Ⅱ)求平面EFG与平面ABCD所成锐二面角的大小;(Ⅲ)线段PD上是否存在一个动点M,使得直线GM与平面EFG所成角为,若存在,求线段PM的长度,若不存在,说明理由.【解答】(Ⅰ)证明:∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,AB ⊥AD∴AB⊥平面PAD,(2分)又∵EF∥AB∴EF⊥平面PAD,(3分)(Ⅱ)取AD中点O,连结PO∵平面PAD⊥平面ABCD,PO⊥AD∴PO⊥平面ABCD,(4分)如图以O点为原点分别以OG、OD、OP所在直线为x轴y轴z轴建立空间直角坐标系:∴O(0,0,0)A(0,﹣2,0)B(4,﹣2,0)C(4,2,0),D(0,2,0),G(4,0,0),,E(0,﹣1,),设平面EFG的法向量为,,∴,(6分)又平面ABCD的法向量为,(7分)设平面EFG与平面ABCD所成锐二面角为θ∴,∴平面EFG与平面ABCD所成锐二面角为.(9分)(Ⅲ)设,,∴,(10分),∴=,(12分)即2λ2﹣3λ+2=0,无解,∴不存在这样的M.(13分)。
高中数学 第一章立体几何初步 1.3 三视图练习 北师大版必修2-北师大版高一必修2数学试题
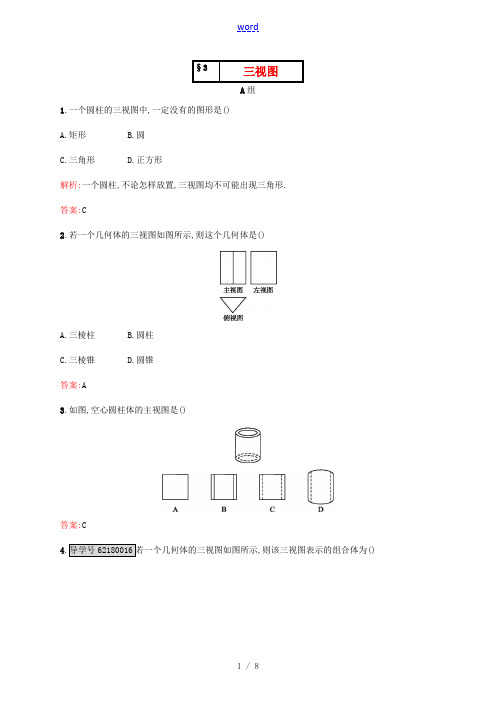
§3三视图A组1.一个圆柱的三视图中,一定没有的图形是()A.矩形B.圆C.三角形D.正方形解析:一个圆柱,不论怎样放置,三视图均不可能出现三角形.答案:C2.若一个几何体的三视图如图所示,则这个几何体是()A.三棱柱B.圆柱C.三棱锥D.圆锥答案:A3.如图,空心圆柱体的主视图是()答案:C4.导学号62180016若一个几何体的三视图如图所示,则该三视图表示的组合体为()A.圆柱与圆锥B.圆柱与三棱锥C.圆柱与四棱锥D.四棱柱与圆锥答案:C5.一个几何体的三视图如图所示,则该几何体的直观图可以是()解析:由俯视图易知,只有选项D符合题意.故选D.答案:D6.如图所示的立体图形,都是由相同的小正方体拼成的.(1)图①的主视图与图②的图相同;(2)图③的主视图与图④的主视图.(填“相同”或“不同”)答案:(1)俯视(2)不同7.如图所示是一个圆锥的三视图,则该圆锥的高为 cm.解析:由三视图知,圆锥的母线长为3 cm,底面圆的直径为3 cm,所以圆锥的轴截面是边长为3 cm 的等边三角形,所以圆锥的高为(cm).答案:8.已知某组合体的主视图与左视图相同(如图1所示,其中AB=AC,四边形BCDE为正方形),则该组合体的俯视图可以是如图2所示的.(把你认为正确的图的序号都填上)图1图2解析:由主视图与左视图可得该几何体可以是由正方体与底面边长相同的四棱锥组合而成的,则其俯视图为图①;可以是由正方体与底面直径与底面正方形边长相同的圆锥组合而成的,则其俯视图为图④;可以是由圆柱与底面相同的圆锥组合而成的,则其俯视图为图③;可以是由圆柱与底面正方形边长等于圆柱底面直径的四棱锥组合而成的,则其俯视图为图②.答案:①②③④9.一个几何体的三视图如图所示,请画出它的实物图.解:由三视图可知,该几何体由正方体和四棱柱组成,如图所示.10.导学号62180017如图所示是一个零件的实物图,画出这个几何体的三视图.解:该零件由一个长方体和一个半圆柱拼接而成,并挖去了一个小圆柱(形成圆孔).主视图反映了长方体的侧面和半圆的底面、小圆柱的底面,左视图反映了长方体的侧面、半圆柱的侧面、小圆柱的侧面,俯视图反映了长方体的底面、半圆柱的侧面和小圆柱的侧面投影后的形状.它的三视图如图所示.B组1.如图①②③分别为三个几何体的三视图,根据三视图可以判断这三个几何体依次分别为()图①图②图③A.三棱台、三棱柱、圆锥B.三棱台、三棱锥、圆锥C.三棱柱、正四棱锥、圆锥D.三棱柱、三棱台、圆锥解析:图①②③对应的原几何体分别是三棱柱、正四棱锥、圆锥,故选C.答案:C2.导学号62180018将正方体(如图1-(1)所示)截去两个三棱锥,得到图1-(2)中的几何体,则该几何体的左视图为(如图2所示)()图1图2解析:左侧被截去的三棱锥的底面三条边中,有两条与正方体的棱重合,另一条应为正方形自左上到右下的对角线,是可见的;右侧被截去的三棱锥的底面的三条边中,有两条与正方体的棱重合,另一条应为正方形自右上到左下(从左面看)的对角线,是不可见的.故选B.答案:B3.如图所示,已知正三棱柱ABC-A1B1C1的底面边长为2,高为3,则其左视图的面积为()A.6B.3C.3D.6解析:由三视图的画法可知,该几何体的左视图是一个矩形,其宽为2sin 60°=,长为3,故面积S=3.答案:C4.已知一几何体的主视图与左视图如图所示,则下列图形中,可以是该几何体的俯视图的图形有()A.①②③⑤B.②③④⑤C.①②④⑤D.①②③④解析:可以结合实物想象,对于①,可认为该几何体的最下部为棱柱,上部为两个圆柱;对于②,可认为该几何体的上部为两个棱柱,下部为圆柱;对于③,可认为该几何体的上部为圆柱,下部为两个棱柱;对于④,可认为该几何体的上部是底面为等腰直角三角形的棱柱,中间为一圆柱,底部为四棱柱;对于⑤,由原几何体最下部的两个视图可知,其俯视图不可能是一个三角形.答案:D5.如图所示,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为.解析:根据三视图还原成实物图,即四棱锥P-ABCD,所以最长的一条棱的长为PB=2.答案:26.已知三棱锥的直观图及其俯视图与左视图如图所示,俯视图是边长为2的正三角形,左视图是有一直角边长为2的直角三角形,则该三棱锥的主视图面积为.解析:三棱锥的主视图如图所示,故主视图的面积为×2×2=2.答案:27.下图是一个几何体的三视图,试画出其实物图.解:由几何体的三视图容易想到该几何体可以由正方体切割而得到,如图所示.俯视图8.导学号62180019一个棱长均为6的正三棱锥,其俯视图如图所示,求其主视图的面积和左视图的面积.解:作出正三棱锥的直观图如图所示,E为BD的中点,AO为三棱锥的高,由三棱锥的放置方式知,其主视图为三角形,底面边长为BD=6,其高等于AO,其左视图为三角形,底面边长等于CE(中线)的长,其高等于AO.在Rt△BCE中,BC=6,BE=3,得CE=3,CO=×CE=2.在Rt△ACO中,AC=6,CO=2,则AO==2,故主视图面积为×6×2=6,左视图的面积为×3×2=9.。
高三数学空间几何体的三视图与直观图试题
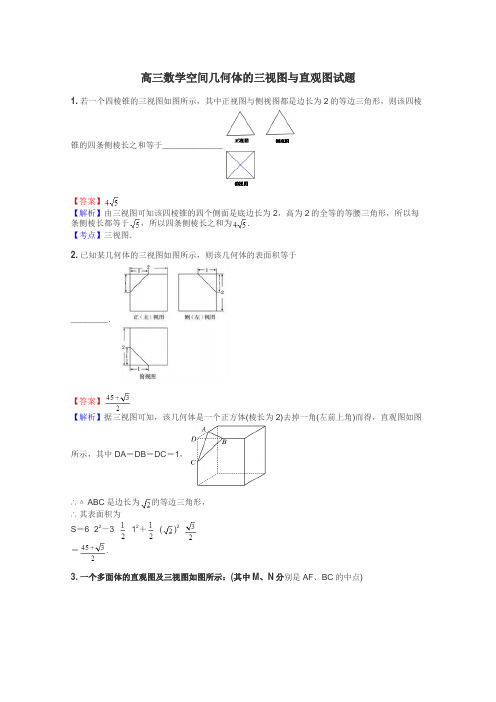
高三数学空间几何体的三视图与直观图试题1.若一个四棱锥的三视图如图所示,其中正视图与侧视图都是边长为2的等边三角形,则该四棱锥的四条侧棱长之和等于_____________【答案】【解析】由三视图可知该四棱锥的四个侧面是底边长为2,高为2的全等的等腰三角形,所以每条侧棱长都等于,所以四条侧棱长之和为.【考点】三视图.2.已知某几何体的三视图如图所示,则该几何体的表面积等于________.【答案】【解析】据三视图可知,该几何体是一个正方体(棱长为2)去掉一角(左前上角)而得,直观图如图所示,其中DA=DB=DC=1,∴△ABC是边长为的等边三角形,∴其表面积为S=6×22-3××12+×()2×=.3.一个多面体的直观图及三视图如图所示:(其中M、N分别是AF、BC的中点)(1)求证:MN∥平面CDEF;(2)求多面体A-CDEF的体积.【答案】(1)见解析(2)【解析】解:由三视图可知,AB=BC=BF=2,DE=CF=2,∠CBF=.(1)证明:取BF的中点G,连接MG、NG,由M、N分别为AF、BC的中点可得,NG∥CF,MG∥EF,∴平面MNG∥平面CDEF,又MN⊂平面MNG,∴MN∥平面CDEF.(2)取DE的中点H.∵AD=AE,∴AH⊥DE,在直三棱柱ADE-BCF中,平面ADE⊥平面CDEF,平面ADE∩平面CDEF=DE.∴AH⊥平面CDEF.∴多面体A-CDEF是以AH为高,以矩形CDEF为底面的棱锥,在△ADE中,AH=.S矩形=DE·EF=4,CDEF∴棱锥A-CDEF的体积为V=·S·AH=×4×=.矩形CDEF4.一个几何体的主视图和俯视图如图所示,主视图是边长为的正三角形,俯视图是边长为的正六边形,则该几何体左视图的面积是【答案】【解析】左视图的面积为.【考点】三视图.5.一空间几何体的三视图如图所示,该几何体的体积为12π+,则正视图中x的值为( )A.5B.4C.3D.2【答案】C【解析】三视图,由正四棱锥和圆柱组成,故选C.6.三棱柱的直观图和三视图如下图所示,其侧视图为正三角形(单位cm)⑴当x=4时,求几何体的侧面积和体积⑵当x取何值时,直线AB1与平面BB1C1C和平面A1B1C1所成角大小相等。
高三数学空间几何体的三视图与直观图试题答案及解析
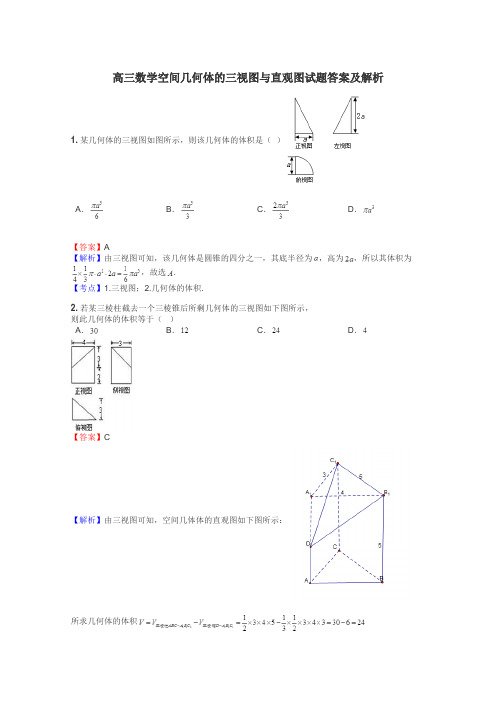
高三数学空间几何体的三视图与直观图试题答案及解析1.某几何体的三视图如图所示,则该几何体的体积是()A.B.C.D.【答案】A【解析】由三视图可知,该几何体是圆锥的四分之一,其底半径为,高为,所以其体积为,故选.【考点】1.三视图;2.几何体的体积.2.若某三棱柱截去一个三棱锥后所剩几何体的三视图如下图所示,则此几何体的体积等于()A.B.C.D.【答案】C【解析】由三视图可知,空间几体体的直观图如下图所示:所求几何体的体积故选C.【考点】1、三视图;2、空间几何体的体积.3.如图,一个几何体的三视图(正视图、侧视图和俯视图)为两个等腰直角三角形和一个边长为1的正方形,则其外接球的表面积为A.πB.2πC.3πD.4π【答案】C【解析】原几何体为有一条侧棱垂直于底面的四棱锥,且底面是边长为1的正方形,垂直于底面的侧棱长也为1,因此,该几何体可以补形为一个棱长为1的正方体,其外接球就是这个正方体的外接球,直径为正方体的对角线长,即2R=,故R=故外接球表面积为:4πR2=3π.【考点】三视图,几何体的外接球及其表面积4.如图所示,一个三棱锥的三视图是三个直角三角形(单位: cm),则该三棱锥的外接球的表面积为________cm2.【答案】29π【解析】从三棱锥的三视图可知,三棱锥有两侧面与底面垂直,把三棱锥补成长,宽,高分别为4,2,3的长方体,设外接球的半径为R,由42+22+32=4R2得,S=4πR2=29π(cm2).球5.某个长方体被一个平面所截,得到的几何体的三视图如图所示,则这个几何体的体积为()A.4B.2C.D.8【答案】D【解析】由三视图可知,该几何体如图所示,其底面为正方形,正方形的边长为2.HD=3,BF =1,将相同的两个几何体放在一起,构成一个高为4的长方体,所以该几何体的体积为×2×2×4=8.6.在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为()【答案】D【解析】由题目所给的几何体的正视图和俯视图,可知该几何体为半圆锥和三棱锥的组合体,如图所示,可知左视图为等腰三角形,且轮廓线为实线,故选D.7.一个几何体的三视图如图所示,已知这个几何体的体积为,= .【答案】【解析】由三视图知,原几何体是一个四棱锥,底面是面积为的矩形,高为,所以,解得.【考点】三视图,空间几何体的体积.8.如图,水平放置的正三棱柱的主视图是一边长为2的正方形,则该三棱柱的左视图的面积为.【答案】【解析】左视图为一个矩形,长宽分别为,因此面积为.【考点】三视图9.若一个正三棱柱的正视图如图所示,其顶点都在一个球面上,则该球的表面积为() A.B.C.D.【答案】B【解析】依题意得,该正三棱柱的底面正三角形的边长为2,侧棱长为1.设该正三棱柱的外接球半径为R,易知该正三棱柱的底面正三角形的外接圆半径是2sin 60°×=,所以R2=+=,则该球的表面积为4πR2=.10.图中的网格是边长为1的小正方形,在其上用粗线画出了某多面体的三视图,则该多面体的体积为________.【答案】16【解析】从三视图可知,这是一个四棱锥,.【考点】三视图.11.如图所示,一个空间几何体的正视图和左视图都是边长为的正方形,俯视图是一个直径为的圆,那么这个几何体的体积为 ( )A.B.C.D.【答案】B【解析】几何体是圆柱,.【考点】三视图,圆柱的体积.12.一个几何体的三视图如图所示,其中正视图是一个正三角形,则该几何体的体积为( )A.1B.C.D.【答案】B【解析】由三视图可知,此几何体为三棱锥,如图,其中正视图为,是边长为2的正三角形,,且,底面为等腰直角三角形,,所以体积为,故选B.13.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于()A.1B.C.D.【答案】C【解析】由题意知,正视图的最大面积为对角面的面积,最小面积为,而,故选C.【考点】三视图.14.已知某几何体的三视图如右图所示,其中俯视图是圆,且该几何体的体积为;直径为2的球的体积为.则()A.B.C.D.【答案】C【解析】由题意,该几何体是一个圆柱挖去一个圆锥得到的几何体,,,∴.选B.【考点】三视图,体积.15.三棱锥S-ABC及其三视图中的正视图和侧视图如图所示,则棱SB的长为()A.B.C.D.【答案】B【解析】过B作BD⊥AC于点D,则BD=2,CD=2,所以BC=,因为SC⊥平面ABC,所以SC⊥BC,所以SB=,故选B.【考点】三视图、直线与平面垂直的性质.16.一个几何体的三视图如图,则该几何体的体积为()A.B.C.D.【答案】A【解析】由三视图可知,该几何体是由一个半圆柱和一个三棱锥拼接而成,且半圆柱的底面是半径为的半圆,高为,其底面积为,故其体积为,三棱锥的底面是一个直角三角形,三棱锥的高也为,其底面积为,故其体积为,所以该几何体的体积为,故选A.【考点】1.三视图;2.组合体的体积17.右图为某几何体的三视图,则该几何体的体积为 .【答案】【解析】所求几何体为一个底面半径为1,高为1的圆柱与半径为1的四分之一的球的组合体,所以体积为【考点】三视图18.一个空间几何体的三视图如图所示,该几何体的体积为______.【答案】96【解析】几何体为一个三棱柱,底面为一个等腰三角形,底边长为6,底边上高为4,棱柱的高为8.因此所求体积为【考点】三视图19.把边长为1的正方形ABCD沿对角线BD折起,形成三棱锥C-ABD,它的主视图与俯视图如右上图所示,则二面角 C-AB-D的正切值为.【答案】【解析】如图所示,做BD,AB的中点分别为点E,F.则有CE面ABD,由于EF为等腰直角三角形ABD的中位线,故EF AB,则为二面角 C-AB-D的代表角,所以,故填.【考点】二面角三视图20.已知水平放置的△ABC的直观图△A′B′C′(斜二测画法)是边长为a的正三角形,则原△ABC 的面积为()A.a2B.a2C.a2D.a2【答案】D【解析】斜二测画法中原图面积与直观图面积之比为1∶,则易知S= ( a)2,∴S=a2.21.一个空间几何体的三视图如图所示,则该几何体的体积为()A.πcm3B.3πcm3C.πcm3D.πcm3【答案】D【解析】由三视图可知,此几何体为底面半径为1cm、高为3cm的圆柱上部去掉一个半径为1cm的半球,所以其体积为V=3π-π=π(cm 3).22. 右图为一简单组合体,其底面ABCD 为正方形,PD ⊥平面ABCD ,EC ∥PD ,且PD =AD =2EC =2.(1)请画出该几何体的三视图; (2)求四棱锥B-CEPD 的体积.【答案】(1)见解析 (2)2【解析】解:(1)该组合体的三视图如图所示.(2)∵PD ⊥平面ABCD , PD ⊂平面PDCE ,∴平面PDCE ⊥平面ABCD. ∵四边形ABCD 为正方形,∴BC ⊥CD ,且BC =DC =AD =2. 又∵平面PDCE∩平面ABCD =CD , BC ⊂平面ABCD. ∴BC ⊥平面PDCE.∵PD ⊥平面ABCD ,DC ⊂平面ABCD , ∴PD ⊥DC.又∵EC ∥PD ,PD =2,EC =1,∴四边形PDCE 为一个直角梯形,其面积: S 梯形PDCE = (PD +EC)·DC =×3×2=3, ∴四棱锥B-CEPD 的体积V B-CEPD =S 梯形PDCE ·BC =×3×2=2.23. 某几何体的三视图如图所示,则该几何体的体积为( ).A .16+8πB .8+8πC .16+16πD .8+16π【答案】A【解析】将三视图还原成直观图为:上面是一个正四棱柱,下面是半个圆柱体.所以V=2×2×4+×22×π×4=16+8π.24.某几何体的三视图如图所示,则其体积为________.【答案】【解析】由三视图还原几何体为半个圆锥,高为2,底面半圆的半径r=1.∴体积V=×(π×12×2)=.25.如图所示为一个几何体的直观图、三视图(其中正视图为直角梯形,俯视图为正方形,侧视图为直角三角形).(1)求四棱锥P-ABCD的体积;(2)若G为BC上的动点,求证:AE⊥PG.【答案】(1)(2)见解析【解析】(1)由几何体的三视图可知,底面ABCD是边长为4的正方形,PA⊥平面ABCD,PA∥EB,且PA=4 ,BE=2 ,AB=4.∴VP-ABCD =PA·S四边形ABCD=×4 ×4×4=.(2)∵=,∠EBA=∠BAP=90°,∴△EBA∽△BAP,∴∠BEA=∠PBA.∴∠BEA+∠BAE=∠PBA+∠BAE=90°,∴PB⊥AE又∵BC⊥平面APEB,∴BC⊥AE.∵BC∩PB=B,∴AE⊥平面PBC.∵PG⊂平面PBC,∴AE⊥PG.26.如图所示,网格上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为________.【答案】9【解析】由题意知,此几何体是三棱锥,其高h=3,相应底面面积为S=×6×3=9,∴V=Sh=×9×3=9.27.某几何体的三视图如图所示,主视图和侧视图为全等的直角梯形,俯视图为直角三角形.则该几何体的表面积为( )A. B. C. D【答案】B【解析】此几何体直观图如图所示。
高三立体几何三视图练习(带答案)

高三立体几何三视图练习(带答案)姓名:___________班级:___________考号:___________ 一、单选题1.某四棱锥的三视图如图所示,该四棱锥的体积是()A.32 B.323C.48 D.1632.已知某三棱柱的三视图如图所示,那么该几何体的表面积为()A.2B.C.D.3.已知一几何体的三视图如图所示,俯视图是一个等腰直角三角形和半圆,则该几何体的体积为4.已知某几何体的三视图如图所示,则该几何体的体积为()A.B.C.D.5.已知图中的网格是由边长为1的小正方形组成的,一个几何体的三视图如图中的粗实线和粗虚线所示,则这个几何体的体积为A.64B.C.D.1286.某几何体的三视图如右图所示,则该几何体的体积为()7.已知某棱锥的三视图如图所示,则该棱锥的体积为A.8B.C.3D.8.已知某几何体的三视图如下,根据图中标出的尺寸(单位:),可得这个几何体的体积是()A.B.C.D.9.一个几何体的三视图如图所示,则该几何体的体积为()A.143B.5 C.163D.610.某几何体的三视图单位:,如图所示,则此几何体的外接球的体积为A .B .C .D .11.某空间几何体的三视图如图所示,则该几何体的外接球的体积为A .B .C .D .12.已知长方体一个顶点上三条棱的长分别是3、4、5,且它的顶点都在同一球面上,则这个球的表面积是( )A .B .C .D .13.如图,圆柱内有一内切球(圆柱各面与球面均相切),若内切球的体积为43π,则圆柱的侧面积为A . πB . 2πC . 4πD . 8π14.用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为( ).A . 8π3B .C .D . 32π315.三棱锥的三条侧棱两两垂直,其长分别为,则该三棱锥的外接球的表面积( )A . 24πB . 18πC . 10πD . 6π16.一个四面体的三视图如图所示,则该四面体的外接球的表面积为( )A . 43πB . 4πC . 23π D . 2π 17.四棱锥P ABCD -的三视图如下图所示,四棱锥P ABCD -的五个顶点都在一个球面上,E 、F 分别是棱AB 、CD 的中点,直线EF 被球面所截得的线段长为该球表面积为( )A .12πB .24πC .36πD .48π参考答案1.B试题分析:由题意知本题是一个高为2,底面是一个长度为4正方形形的四棱锥,其体积为13244233 V=⨯⨯⨯=2.D由已知得到几何体如图:三棱柱的表面积为=5+;故选D.【点睛】本题考查了由几何体的三视图求几何体的表面积;关键是正确还原几何体.3.B由已知中的三视图可得:该几何体是一个三棱锥与半圆柱的组合体,三棱锥的长宽高分别为:4,2,4,故体积为:,半圆柱的底面半径为2,高为4,故体积为:,故组合体的体积,故选:B.4.D【解析】把三视图还原为几何体,此几何体是底面为直角梯形,一条侧棱垂直于底面的四棱锥,可以本卷由系统自动生成,请仔细校对后使用,答案仅供参考。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、 一个正方体内接于一个球,过球心作一截面,如图所示,则截面的可能图形是( ) A .①② B.②④ C.①②③ D.②③④
2、 给出下列命题: ① 如果一个几何体的三视图是完全相同的,则这个几何体是正方体; ② 如果一个几何体的正视图和俯视图都是矩形,则这个几何体是长方体; ③ 如果一个几何体的三视图都是矩形,则这个几何体是长方体; ④ 如果一个几何体的正视图和侧视图都是等腰梯形,则这个几何体是圆台. 其中正确命题的个数是( ) A.0 B.1 C.2 D.3
3、 若一个几何体的正视图和侧视图都是等腰三角形,俯视图是圆,则这个几何体可能是( ) A.圆柱 B.三棱柱 C.圆锥 D.球体
4、. 下列说法中正确的是( )
A.互相垂直的两条直线的直观图仍然是互相垂直的两条直线 B.梯形的直观图可能是平行四边形 C.矩形的直观图可能是梯形
D.正方形的直观图可能是平行四边形
5. 如下图为一个几何体的三视图,其中府视图为正三角形,A 1B 1=2,AA 1=4,则该几何体的表面积为 ( )
A.6+
B.324+
C.24+23
D.32
6、下列命题中:(1)、平行于同一直线的两个平面平行;(2)、平行于同一平面的两个平面平行;(3)、垂直于同一直线的两直线平行;(4)、垂直于同一平面的两直线平行.其中正确的个数有
A 、1
B 、2
C 、3
D 、4
7、a ,b ,c 表示直线,M 表示平面,给出下列四个命题:①若a ∥M ,b ∥M ,则a ∥b ;②若b ⊂M ,
a ∥
b ,则a ∥M ;③若a ⊥
c ,b ⊥c ,则a ∥b ;④若a ⊥M ,b ⊥M ,则a ∥b .其中正确命题的个数有
A 、0个
B 、1个
C 、2个
D 、3个
A B 1 C
正视图 侧视图 府视图 ① ② ③ ④
8、在棱长为1的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的凸多面体的体积是
A 、
23 B 、76 C 、45 D 、56
9、已知二面角AB αβ--的平面角是锐角θ,α内一点C 到β的距离为3,点C 到棱AB 的距离为4,那么tan θ的值等于
A 、34
B 、35
C
、7
D
、7
10、如图:直三棱柱ABC —A 1B 1C 1的体积为V ,点P 、Q 分别在侧棱AA 1和
CC 1上,AP=C 1Q ,则四棱锥B —APQC 的体积为
A 、2V
B 、3V
C 、4V
D 、5
V
二、填空题(每小题5分,共25分)
11、等体积的球和正方体,它们的表面积的大小关系是S 球_____S 正方体
(填”大于、小于或等于”).
12、正方体1111ABCD A BC D -中,平面11AB D 和平面1BC D 的位置关系为 13、已知PA 垂直平行四边形ABCD 所在平面,若PC BD ⊥,平行则四边形ABCD 一定
是 .
14. (12分) 如图,在四边形ABCD 中,
,
,
,
,AD=2,求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积. (12分)
15.如图在四棱锥P —ABCD 中,PA ⊥底面ABCD ,AB ⊥AD ,AC ⊥CD ,∠ABC=60°,PA=AB=BC ,
E 是PC 的中点。
(1)求证:CD ⊥AE ; (2)求证PD ⊥平面ABE 。
Q
P
C'B'
A'C
B
A
16、设A 、B 、C 、D 是不共面的四点,E 、F 、G 、H 分别是AC 、BC 、DB 、DA 的中点,
若AB CD ==四边形EFGE
的面积为AB 、CD 所成的角.
17、如图,四面体S -ABC 中,∠BAC =︒90,∠SAB =∠SAC =︒60,当SA =a 时,(1) 求SA 在平面ABC 中的射影长;(2) 求SA 与平面ABC 所成的角。
(13)
18、已知△BCD 中,∠BCD =90°,BC =CD =1,AB ⊥平面BCD ,
∠ADB =60°,E 、F 分别是AC 、AD 上的动点,且
(01).AE AF
AC AD
λλ==<< (Ⅰ)求证:不论λ为何值,总有平面BEF ⊥平面ABC ; (Ⅱ)当λ为何值时,平面BEF ⊥平面ACD ? (14分)
19.如图,直三棱柱ABC -A 1B 1C 1中,∠ACB =90°,M ,N 分别为A 1B ,B 1C 1的中点.
(1)求证BC ∥平面MNB 1;(2)求证平面A 1CB ⊥平面ACC 1A 1.
A B
C
M N
A 1
B 1
C 1
(第19题)
F
E
D
B
A
C
20.如图所示,在直三棱柱111C B A ABC -中,⊥=11,AC BB AB 平面D BD A ,1为AC 的中点。
(Ⅰ)求证://1C B 平面BD A 1;(Ⅱ)求证:⊥11C B 平面11A ABB ;
(Ⅲ)设E 是1CC 上一点,试确定E 的位置使平面⊥BD A 1平面BDE ,并说明理由。
21.在如图所示的几何体中,EA ⊥平面ABC ,DB ⊥平面ABC ,
AC BC ⊥,且2AC BC BD AE ===,M 是AB 的中点.
(I )求证:CM EM ⊥;(II )求CM 与平面CDE 所成的角.
E
D
C
M
A
(第21题)。
