最新重点中学小升初自主招生数学备考试卷3(含答案)
人教版2021年六年级下册数学小升初招生入学考试卷(3)(含解析答案)

⼈教版2021年六年级下册数学⼩升初招⽣⼊学考试卷(3)(含解析答案)⼩升初招⽣⼊学考试数学试卷⼀、思前想后,填补空⽩.(每⼩题2分,共24分)1.(2分)⼀个数由5个⼗,3个百分之⼀组成,这个数是,这个数精确到⼗分位是.2.(2分)如果某校获省级表彰的学⽣为1⼈.已知获省级表彰的学⽣⽐获市级表彰的学⽣少75%,那么获市级表彰的学⽣有⼈.3.(2分)当X=0.6时,5X+3的值是;当X=时,8X+3=7.4.(2分)如图中多边形的周长是厘⽶.5.(2分)分数,如果分母加上10,分⼦应加才能使分数⼤⼩不变.6.(2分)⼀个圆锥体底⾯周长是6.28厘⽶,体积是6.28⽴⽅厘⽶,⾼是厘⽶.7.(2分)在4、6、3、0、2这五个数中选出四个数组成⼀个能同时被2、3、5整除的最⼩四位数.8.(2分)有两个⾃然数相除,商是6,余数是2,已知被除数、除数、商与余数的和等于45,则被除数是.9.(2分)12个朋友见⾯,每两个都互相赠送⼀张名⽚,共赠出张名⽚.10.(2分)甲有132个玻璃球,⼄有84个同样的玻璃球.两⼈相互给球,16次后,甲有的个数是⼄的5倍,平均每次甲要少给⼄个.11.(2分)⽣活中⽤扑克牌“算24点”是⼤家喜爱的⼀种游戏,现有10,10,4,4,四张牌,你能算出24点吗?请写出你的综合算式:.12.(2分)如果×2014=+x成⽴,则x=.⼆、反复⽐较,慎重选择.(每⼩题2分,共10分)13.(2分)下⾯四个数中,最接近1的是()A.B.C.D.14.(2分)在含盐量是20%的盐⽔中,盐⽐⽔少()A.52% B.80% C.75% D.60%15.(2分)今年⼩明的爸爸A岁,⼩明(A﹣26)岁,再过X年后,爸爸⽐⼩明⼤()岁.A.X B.X+26 C.26 D.X﹣2616.(2分)甲商场以打8折优惠,⼄商场满100元送20元的购物券优惠.李阿姨打算花掉500元,在()商场购物更加合算.A.甲B.⼄C.都⼀样D.⽆法确定17.(2分)如图1是三个直⽴于⽔平⾯上的形状完全相同的⼏何体(下底⾯为圆⾯,单位:cm).将它们拼成如图2的新⼏何体,则该新⼏何体的体积⽤π表⽰,应为()A.64πcm3B.60πcm3C.56πcm3D.40πcm3三、分析数据,合理计算.(每⼩题4分,共16分)18.(4分)1042﹣384÷16×13.19.(4分)(66﹣32×1.2)÷0.25.20.(4分).21.(4分)5×11.8+4.75×11.8.四、仔细操作,⼼灵⼿巧.(共9分)22.(9分)如图请⽤三种⽅法,在已知图案上再添上⼀个⼩正⽅形后,使其成为轴对称图形,并画出对称轴.五、活⽤知识,解决问题.(第1题5分,其余每题6分,共41分)23.(5分)⼀辆客车2⼩时⾏驶100千⽶,照这样的速度,如果再⾏驶3.5⼩时就能⾏完全程,全程有多少千⽶?24.(6分)⼩康村修防洪堤,第⼀周修了全长的30%,第⼆周修了1500⽶,这两周修的总⽶数占全长的.这条防洪堤还有多少⽶没修?25.(6分)有⼀个边长为4厘⽶的等边三⾓形,现将它按下图所⽰滚动,请问B 点从开始到结束,经过的路线的总长度是多少厘⽶?26.(6分)计划⽣产⼀批零件,甲单独做需要6⼩时,⼄单独做需要8⼩时,甲、⼄两⼈合作⽣产4⼩时,结果⽐计划多⽣产100个零件.计划⽣产零件多少个?27.(6分)某出租车起步价(3公⾥内)是6元,超过3公⾥⽽在7公⾥以内每公⾥按1.2元计价;7公⾥以上部分每公⾥再加价50%.陈⽼师从英才学校乘出租车到距离约17公⾥的古雷PX化⼯⼚,试计算到达时应付车费多少元?28.(6分)张叔叔以每⽉1000元的租⾦租⽤了⼀个果品仓库,存进去5吨⽔果.按照惯例这些⽔果需要销售4个⽉.由于降低了销售价格,结果2个⽉就销售完了.由于节省了租⾦,结算下来,反⽽多赚了800元.销售时每千克⽔果⽐计划降低了多少元?29.(6分)有⼀装满8升⽔的甲桶,现分别有可装5升的空⼄桶和3升的空丙桶.(1)如何倒,可分出2升的⽔来?(2)如何倒,可分出1升⽔来?参考答案与试题解析⼀、思前想后,填补空⽩.(每⼩题2分,共24分)1.(2分)⼀个数由5个⼗,3个百分之⼀组成,这个数是50.03,这个数精确到⼗分位是50.0.【考点】⼩数的读写、意义及分类;近似数及其求法.【专题】⼩数的认识.【分析】(1)⼀个数由5个⼗,3个百分之⼀组成,这个的⼗位上就是5,百分位上就是3,其余数位上是0,(2)根据“四舍五⼊”法知要精确到⼗分位要看百分位,百位上是3⽐5⼩直接舍去.据此解答.【解答】解:根据以上分析知:⼀个数由5个⼗,3个百分之⼀组成,这个数是50.03,这个数精确到⼗分位是50.0.故答案为:50.03,50.0.【点评】本题主要考查了学⽣对⼩数写法和求近似值⽅法的掌握情况.2.(2分)如果某校获省级表彰的学⽣为1⼈.已知获省级表彰的学⽣⽐获市级表彰的学⽣少75%,那么获市级表彰的学⽣有4⼈.【考点】分数四则复合应⽤题.【专题】分数百分数应⽤题.【分析】【解答】解:1÷(1﹣75%)=1÷25%,=4(⼈).答:获市级表彰的学⽣有4⼈.故答案为:4.【点评】完成本题要注意单位“1”的确定,将获市级表彰的学⽣当作单位“1”.3.(2分)当X=0.6时,5X+3的值是6;当X=0.5时,8X+3=7.【考点】含字母式⼦的求值;⽅程的解和解⽅程.【专题】⽤字母表⽰数;简易⽅程.【分析】(1)把x=0.6代⼊式⼦中计算即可;(2)根据等式的性质解这个⽅程即可求出x的值.【解答】解:(1)当x=0.6时,5x+3=5×0.6+3=6;(2)8x+3=7,8x+3﹣3=7﹣3,8x=4,8x÷8=4÷8,x=0.5.故答案为:6;0.5.【点评】此题考查字母表⽰数的求值⽅法以及利⽤等式的性质解⽅程.4.(2分)如图中多边形的周长是14厘⽶.【考点】巧算周长.【专题】平⾯图形的认识与计算.【分析】观察图形可知,把这个图形的右上⽅的⼩线段分别向上向右平移,则这个图形的周长可以看做是长5厘⽶、宽2厘⽶的长⽅形的周长,据此利⽤长⽅形的周长公式计算即可解答.【解答】解:根据题⼲分析可得:(5+2)×2=14(厘⽶),答:这个图形的周长是14厘⽶.故答案为:14.【点评】不规则图形的周长⼀般可以利⽤线段平移的⽅法,把它们转化到规则图形中利⽤周长公式进⾏计算.5.(2分)分数,如果分母加上10,分⼦应加4才能使分数⼤⼩不变.【考点】分数的基本性质.【专题】运算顺序及法则.【分析】⾸先发现分母之间的变化,由5变为(5+10)=15,分母扩⼤了3倍,根据分数的基本性质,要使分数的⼤⼩相等,分⼦也应扩⼤3倍,由此通过计算就可以得出.【解答】解:原分数分母是5,现在分数的分⼦是5+10=15,分母扩⼤了3倍,原分数分⼦是2,要使前后分数相等,分⼦也应扩⼤3倍,变为6,即6=2+4;故答案为:4.【点评】此题主要利⽤分数的基本性质解答问题,先观察分⼦或分母之间的变化,发现规律,再进⼀步通过计算解答问题.6.(2分)⼀个圆锥体底⾯周长是6.28厘⽶,体积是6.28⽴⽅厘⽶,⾼是6厘⽶.【考点】圆锥的体积.【专题】⽴体图形的认识与计算.【分析】先根据圆的周长公式求出这个圆锥的底⾯半径是:6.28÷3.14÷2=1厘⽶,再利⽤圆的⾯积公式求出圆锥的底⾯积,⽤圆锥的体积×3÷底⾯积即可计算得出圆锥的⾼.【解答】解:圆锥的底⾯半径是:6.28÷3.14÷2=1(厘⽶),圆锥的底⾯积是:3.14×12=3.14(平⽅厘⽶),则圆锥的⾼是:6.28×3÷3.14=6(厘⽶),答:圆锥的⾼是6厘⽶.故答案为:6.【点评】此题考查了圆锥的计算公式的灵活应⽤.7.(2分)在4、6、3、0、2这五个数中选出四个数组成⼀个能同时被2、3、5整除的最⼩四位数2340.【考点】整除的性质及应⽤.【专题】数的整除.【分析】能同时被2和5整除的数是末尾为0的数,确定这个四位数的个位是0;能被3整除的数各个位上的数字和能被3整除,就从2、3、5、7中找出3个数字的和被3整除,为求最⼩就从最⼩的数字开始试算.【解答】解:能同时被2和5整除的数是末尾为0的数,所以这个数的个位是0;2+3+4=9,9能被3整除,符合题意,那么这三个数按照⾼位⼩的顺排列,即:234,再添上个位的0,就是2340;故答案为:2340.【点评】本题考查能被2、3、5整除数的特点,利⽤这些特点求解.8.(2分)有两个⾃然数相除,商是6,余数是2,已知被除数、除数、商与余数的和等于45,则被除数是32.【考点】有余数的除法.【专题】⽂字叙述题.【分析】设除数为x,根据“被除数=商×除数+余数”得:(6x+2)+x+6+2=45,解这个⽅程,求出除数,进⽽根据“被除数=商×除数+余数”解答即可.【解答】解:设除数为x,则:(6x+2)+x+6+2=45,7x=35,x=5;6×5+2,=30+2=32,答:被除数是32;故答案为:32.【点评】根据在有余数的除法中,被除数、除数、商和余数四者之间的关系,进⾏解答即可.9.(2分)12个朋友见⾯,每两个都互相赠送⼀张名⽚,共赠出132张名⽚.【考点】握⼿问题.【专题】传统应⽤题专题.【分析】每两⼈都互相赠送⼀张名⽚,则每⼈都要送出11张名⽚,则共送出11×12=132张名⽚;据此解答.【解答】解:共送出名⽚:11×12=132(张),答:共赠出132张名⽚.故答案为:132.【点评】此题类同于握⼿问题,但⼜有别于握⼿的求法,即赠名⽚的张数=⼈数×(⼈数﹣1).10.(2分)甲有132个玻璃球,⼄有84个同样的玻璃球.两⼈相互给球,16次后,甲有的个数是⼄的5倍,平均每次甲要少给⼄3个.【考点】和倍问题.【专题】和倍问题.【分析】根据题意,他们有玻璃球的和是132+84=216个,两⼈相互给球后,16次后,甲有的个数是⼄的5倍,由和倍公式求出甲现在有的个数,减去原来的有的个数,再除以16就是均每次甲要少给⼄的个数.【解答】解:根据题意可得:甲⼄有的玻璃球的和:132+84=216(个);由和倍公式可得:⼄现在的个数是:216÷(5+1)=36(个);甲现在的个数的:36×5=180(个);与原来的个数差是:180﹣132=48(个);平均每次少给的个数是:48÷16=3(个).答:平均每次甲要少给⼄3个.故答案为:3.【点评】本题的关键是根据和倍公式求出现在甲的个数,然后再根据题意进⼀步解答即可.11.(2分)⽣活中⽤扑克牌“算24点”是⼤家喜爱的⼀种游戏,现有10,10,4,4,四张牌,你能算出24点吗?请写出你的综合算式:(10×10﹣4)÷4=24.【考点】填符号组算式.【专题】填运算符号、字母等的竖式与横式问题.【分析】根据四个数字的特点,可以这样计算:10×10=100,100﹣4=96,96÷4=24,据此可得算式(10×10﹣4)÷4=24.【解答】解:根据题⼲分析可得:(10×10﹣4)÷4,=(100﹣4)÷4,=96÷4,=24.故答案为:(10×10﹣4)÷4=24.【点评】解答此题的关键认真审题,根据数的特点,进⾏试填运算符号,进⽽得出结论.12.(2分)如果×2014=+x成⽴,则x=2012.【考点】⽅程的解和解⽅程.【专题】简易⽅程.【分析】先化简⽅程,再依据等式的性质,⽅程两边同时减即可求解.【解答】解:×2014=+x,2012﹣=+x﹣,x=2012,故答案为:2012.【点评】等式的性质是解⽅程的依据,关键是对等式左边算式的计算,解⽅程时注意对齐等号.⼆、反复⽐较,慎重选择.(每⼩题2分,共10分)13.(2分)下⾯四个数中,最接近1的是()A.B.C.D.【考点】分数⼤⼩的⽐较.【专题】分数和百分数.【分析】分别求出各个分数与1的差,差最⼩的数就和1最接近.据此解答.【解答】解:A、﹣1=,B、1﹣=,C、,D、,因,所以接近1的数是.故选:D.【点评】本题的关键是求出各分数与1的差,再进⾏选择.14.(2分)在含盐量是20%的盐⽔中,盐⽐⽔少()A.52% B.80% C.75% D.60%【考点】百分数的实际应⽤.【专题】分数百分数应⽤题.【分析】含盐量是20%,是指盐占盐⽔总重量的20%,把盐⽔的总重量看成单位“1”,⽔就占盐⽔总重量的(1﹣20%),然后求出盐⽐⽔少占盐⽔的百分之⼏,再⽤这个少的百分数除以⽔占盐⽔的百分数即可.【解答】解:(1﹣20%﹣20%)÷(1﹣20%),=60%÷80%,=75%;答:盐⽐⽔少75%.故选:C.【点评】本题先找出单位“1”,把其它量⽤单位“1”表⽰出来,然后根据求⼀个数是另⼀个数百分之⼏的⽅法求解.15.(2分)今年⼩明的爸爸A岁,⼩明(A﹣26)岁,再过X年后,爸爸⽐⼩明⼤()岁.。
小升初重点中学招生考试数学试卷及详细答案解析(50题)

小升初重点中学招生考试数学试卷及详细答案解析(50题)一、选择题1、参加某次数学竞赛的女生和男生人数的比是1:3,这次竞赛的平均成绩是82分,其中男生的平均成绩是80分,女生的平均成绩是( )。
A.82 B.86 C.87 D.882、一种商品,原价98元,先提价10%后,再降价10%,现价与原价相比,价格( )。
A.相同B.高了C.低了D.无法确定3、甲数除以乙数的商是0.6,甲数是甲、乙两数和的( )%。
A.60 B.62.5 C.37.54、在下图中,平行四边形的面积是20平方厘米。
图中甲、乙面积比是( )。
A.3:2 B.5:2 C.3:1 D.5:15、一个口袋里装有红球3个,黄球1个(每次摸一个球再放回袋中),小明摸了三次摸到的都是红球,那么第四次摸到黄球的可能性是( )。
A.100% B.C.D.6、将直角三角形ABC的AB轴旋转一周,得到的圆锥体积是V,那么V=( )。
A.12兀B.25兀C.36兀D.48兀二、填空题7、一个盒子里装有大小、轻重完全一样的黄、红、白球共12个。
其中黄球6个,白球2个,红球4个。
从中任意摸出一个球,摸出白球的可能性是( )。
8、邹老师用一根28厘米长的铁丝围成了一个三角形,这个三角形的一边最长可能是( )厘米。
(取整厘米)9、一个数的小数点向左移动两位后。
得到的数比原数小11.88,原数是( )。
10、一条长1 200米的小路。
甲队单独修6小时修完,乙队单独修8小时修完,两队合作3小时后,还剩( )米没修完。
11、在做两位整数的乘法时。
小丁把被乘数的个位数字看镨了,所得结果是255;小东把被乘数的十位数字看错了。
所得结果365。
那么正确的乘积是( )。
12、实验小学在援助青海地震灾区捐款活动中,师生共捐款56000元。
教师的捐款是全校学生捐款的,教师捐款( )元。
13、有甲、乙两个两位数,甲数的等于乙数的。
这两个两位数的差最多是( )。
14、有83个玻璃球,其中有一个球比其他的球重一些。
2023年浙江宁波市重点中学小升初自主招生分班考数学试卷(全解全析)

绝密★启用前2023年浙江宁波市重点中学小升初自主招生分班考数学试卷(考试时间:90分钟试卷满分:100分)注意事项:1.答题前,务必将自己的姓名和准考证号填写在答题卡规定的位置上。
2.必须使用黑色墨水笔或黑色签字笔,将答案书写在答题卡规定的位置上。
3.所有题目必须在答题卡上作答,在试题卷上答题无效。
4.考试结束,将试题卷和答题卡一并交回。
一.耐心审题,巧思妙算(共3小题,满分28分)1.(8分)直接写出得数。
132+78= 6.2﹣2.6= 3.02×7==0.42÷0.6====【分析】根据整数、小数、分数加减乘除的计算方法依次口算结果。
【解答】解:132+78=210 6.2﹣2.6=3.6 3.02×7=21.14 =0.42÷0.6=0.7 ===【点评】本题解题的关键是熟练掌握整数、小数、分数加减乘除的计算方法。
2.(8分)解方程。
x÷=4x﹣x=(24+x)=30:27=【分析】(1)根据等式的性质,两边同时乘即可;(2)首先化简,然后根据等式的性质,两边同时乘即可;(3)首先根据等式的性质,两边同时乘3,然后两边再同时减去24即可;(4)首先根据比例的基本性质化简,然后根据等式的性质,两边同时除以54即可。
【解答】解:(1)x÷=4x÷×=4×x=(2)x﹣x=x=x×=×x=(3)(24+x)=30(24+x)×3=30×324+x=9024+x﹣24=90﹣24x=66(4):27=2x×27=×354x=54x÷54=÷54x=【点评】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去、同时乘或同时除以一个数(0除外),两边仍相等,以及解比例问题,注意比例的基本性质的应用。
3.(12分)脱式计算,能简便的用简便方法计算。
河南省郑州三中小升初数学试卷(含解析)

河南省郑州三中小升初数学试卷一.填空题(每题5分,共60分)1.(5分)(++)÷×=.2.(5分)设a.b为自然数,定义a※b如下:如果a≥b,定义a※b=a﹣b,如果a <b,则定义a※b=b﹣a.计算:(3※4)※9=.3.(5分)在所有的三位数中,能够被3整除的数共有个.4.(5分)三个连续自然数的积是2730,这三个数的和是.5.(5分)四个连续奇数,第一个数是第四个数的,那么四个数的和是.6.(5分)从A地到B地,甲车每5分钟行驶全程的10%,乙车每6分行驶全程的8%,乙车先出发,甲车后出发,但两车恰好同时到达B地.乙车比甲车早出发分.7.(5分)一段方钢,长2分米,横截面是正方形,把它锯成相等的两段后,表面积比原来增加8平方厘米,原来这个长方体方钢的表面积是平方厘米.8.(5分)一个等腰梯形中三条边的长分别是55厘米.25厘米.15厘米,并且它的下底是最长的一条边.那么,这个等腰梯形的一个腰长是厘米.9.(5分)a.b两数的和是11.5,如果把a的给b,那么b比a少2.9,原来b 比a少.10.(5分)长方形的长和宽的比是5:3,如果将长减少9厘米,宽增加7厘米,就变成一个正方形,原来长方形面积是平方厘米.11.(5分)去年光明小学的学生是红旗小学的,今年光明小学转入60名学生,红旗小学转出20名学生,现在光明小学的学生是红旗小学的,去年光明小学有学生人.二.应用题(写出主要的解答过程或推理过程,每题10分,共60分)12.(10分)果园里有苹果树.梨树一共800棵,其中苹果树占60%,后来又栽了一些苹果树,这样苹果树占总数的68%,后来又栽了多少棵苹果树?13.(10分)六年级学生120人在考试中语文.数学.外语三科及格百分比平均为85%,语文及格114人,外语及格100人,数学及格多少人?14.(10分)甲.乙共带86元钱,甲花去自己所带钱数的,乙花去16元,这时两人所剩钱数相等,求甲.乙原来各带了多少元钱?15.(10分)一辆车从甲地开往乙地.如果把车速减少10%,那么要比原定时间迟1小时到达,如果以原速行驶180千米,再把车速提高20%,那么可比原定时间早1小时到达.甲.乙两地之间的距离是多少千米?16.(10分)小明看一本故事书,小芳看一本科技书,故事书的页数是科技书的75%,小明每天看15页,小芳每天看18页.二人同时开始阅读,当小明看完故事书时,小芳还有24页没看.这两本书各有多少页?17.(10分)甲.乙两人分别从A.B两地同时出发,相向而行,乙的速度是甲的,两人相遇后继续前进,甲到达B地,乙到达A地立即返回,已知两人第二次相遇的地点距离第一次相遇的地点是3000米,求A.B两地的距离?参考答案与试题解析一.填空题(每题5分,共60分)1.(5分)(++)÷×=.【分析】根据数字特点,原式变为(++)××,进一步计算即可.【解答】解:(++)÷×,=(++)××,=(++)××,=×3××,=.故答案为:.2.(5分)设a.b为自然数,定义a※b如下:如果a≥b,定义a※b=a﹣b,如果a <b,则定义a※b=b﹣a.计算:(3※4)※9=8.【分析】根据“如果a≥b,定义a※b=a﹣b,如果a<b,则定义a※b=b﹣a,”得出新的运算方法,再利用新的运算方法计算(3※4)※9的值即可.【解答】解:(3※4)※9,=(4﹣3)※9,=1※9,=9﹣1,=8;故答案为:8.3.(5分)在所有的三位数中,能够被3整除的数共有300个.【分析】最大的三位数是999,最小的三位数是100,共有(999﹣100+1)=900个三位数,求所有的三位数中,能够被3整除的数共有多少个,即求900中能被3整除的数共有多少个,也就是求900里面有几个3即可.【解答】解:最大的三位数是999,最小的三位数是100,共有(999﹣100+1)=900个三位数,900÷3=300(个);答:在所有的三位数中,能够被3整除的数共有300个.故答案为:300.4.(5分)三个连续自然数的积是2730,这三个数的和是42.【分析】把2730分解质因数,从因数中找出3个连续的自然数,再把它们加起来即可.【解答】解:2730=2×3×5×7×13;2×7=14,3×5=15,所以这三个连续的自然数是13.14.15.13+14+15=42.答:这三个数的和是42.故答案为:42.5.(5分)四个连续奇数,第一个数是第四个数的,那么四个数的和是240.【分析】四个连续奇数第四个数比第一个要大6;把第四个数看成单位“1”,它的(1﹣)对应的数量是6,由此用除法求出这个数,进而求出其它的数,以及它们的和.【解答】解:6÷(1﹣),=6÷,=63;其它的三个数是:61,59,57;它们的和是:63+61+59+57,=(63+57)+(59+61),=120+120,=240;答:四个数的和是240.6.(5分)从A地到B地,甲车每5分钟行驶全程的10%,乙车每6分行驶全程的8%,乙车先出发,甲车后出发,但两车恰好同时到达B地.乙车比甲车早出发25分.【分析】已知甲每小时走全程的10%÷5=,乙每分钟走全程的8%÷6=.也就是说,甲走完全程要1÷=50(分),乙要1÷=75(分钟),乙想要与甲同时到达,要先走75﹣50=25(分钟).【解答】解:甲走完全程要:1÷(10%÷5),=1÷,=50(分);乙走完全程要:1÷(8%÷6),=1÷,=75(分钟);乙车比甲车早出发:75﹣50=25(分钟).答:乙车比甲车早出发25分钟.故答案为:25.7.(5分)一段方钢,长2分米,横截面是正方形,把它锯成相等的两段后,表面积比原来增加8平方厘米,原来这个长方体方钢的表面积是168平方厘米.【分析】根据题意可知,平均分成两段后表面积增加了两个底面积,那么每个底面积为(8÷2)平方厘米,再用分解因数的方法得到长方体方钢的底面正方形的边长,依此可求长方体方钢的侧面积,再用侧面积+2个底面积,即可得到这个长方体方钢的表面积.【解答】解:底面积为:8÷2=4(平方厘米),因为4=2×2,所以底面正方形的边长为2厘米,2分米=20厘米,这个长方体方钢的表面积为:2×4×20+4×2,=160+8,=168(平方厘米).答:原来这个长方体方钢的表面积是168平方厘米.故答案为:168.8.(5分)一个等腰梯形中三条边的长分别是55厘米.25厘米.15厘米,并且它的下底是最长的一条边.那么,这个等腰梯形的一个腰长是25厘米.【分析】首先确定下底是55厘米,再分腰长为25厘米或15厘米两种情况讨论即可求解.【解答】解:①腰长为25厘米时:55+25×2+15=55+50+15=120厘米;②腰长为15厘米时,两底是55厘米.25厘米,无法构成等腰梯形,不符合题意.故答案为:25.9.(5分)a.b两数的和是11.5,如果把a的给b,那么b比a少2.9,原来b 比a少 4.5.【分析】把a看成单位“1”,它的就是a;把a的给b后,a还剩下(1﹣)a,b就是b+a,那么根据题意可以得出如下两个方程:a+b=11.5;(1﹣)a﹣(a+b)=2.9;根据代换的方法求出原来的a和b,进而求出它们的差.【解答】解:根据题意可以得出如下两个方程:a+b=11.5①;(1﹣)a﹣(a+b)=2.9②;由①可得:b=11.5﹣a③;由②可得:a﹣a﹣b=2.9,a﹣b=2.9④;把③带入④得:a﹣(11.5﹣a)=2.9,0.8a﹣11.5+a=2.9,1.8a=14.4,a=8;b=11.5﹣a=11.5﹣8=3.5;8﹣3.5=4.5;答:原来b比a少4.5.故答案为:4.5.10.(5分)长方形的长和宽的比是5:3,如果将长减少9厘米,宽增加7厘米,就变成一个正方形,原来长方形面积是960平方厘米.【分析】如果长减少9厘米,宽增加7厘米,正好变成一个正方形,说明长与宽的差是16厘米,又因为长和宽的比是5:3,也就是说如果长占5份,宽占3份,它们的差占2份,则一份长度为16÷2=8厘米,那么长方形的长为:8×5=40厘米,宽为:8×3=24厘米.根据长方形的面积公式:s=ab,把数据代入公式解答即可.【解答】解:先求出一份的长:(9+7)÷(5﹣3),=16÷2,=8(厘米),长是:8×5=40(厘米),宽是:8×3=24(厘米),原来的面积是:40×24=960(平方厘米);答:原来长方形的面积是960平方厘米.故答案为:960.11.(5分)去年光明小学的学生是红旗小学的,今年光明小学转入60名学生,红旗小学转出20名学生,现在光明小学的学生是红旗小学的,去年光明小学有学生300人.【分析】我们运用方程进行解答,首先设去年光明小学有学生x人.由“今年光明小学转入60名学生,红旗小学转出20名学生,现在光明小学的学生是红旗小学的,”为等量关系列方程解答即可.【解答】解:设去年光明小学有学生x人.x+60=(x﹣20)×,x+60=x﹣15,x+60+15=x﹣15+15,x+75=x,x﹣x+75=x﹣x,x=75,x×4=75×4,x=300;答:去年光明小学有学生300人.故答案为:300.二.应用题(写出主要的解答过程或推理过程,每题10分,共60分)12.(10分)果园里有苹果树.梨树一共800棵,其中苹果树占60%,后来又栽了一些苹果树,这样苹果树占总数的68%,后来又栽了多少棵苹果树?【分析】苹果树.梨树一共800棵,其中苹果树占60%,则梨树占总数的1﹣60%,根据分数乘法的意义可知,梨树有800×(1﹣60%),又后来又栽了一些苹果树,这样苹果树占总数的68%,则此时梨树占总数的1﹣68%,根据分数除法的意义,此时共有果树800×(1﹣60%)÷(1﹣68%)棵,所以苹果树增加了800×(1﹣60%)÷(1﹣68%)﹣800棵.【解答】解:800×(1﹣60%)÷(1﹣68%)﹣800=800×40%÷32%﹣800,=1000﹣800,=200(棵).答:后来又栽了200棵苹果树.13.(10分)六年级学生120人在考试中语文.数学.外语三科及格百分比平均为85%,语文及格114人,外语及格100人,数学及格多少人?【分析】因为语文.数学.外语三科及格百分比平均为85%,所以85%×3等于三科及格率的和,和减去语文减去外语的及格率得出数学及格率,再用六年级学生120人乘数学及格率得出数学及格人数.【解答】解:数学及格人数:120×(85%×3﹣114÷120﹣100÷120),=120×(2.55﹣0.95﹣),=120×(1.6﹣),=120×1.6﹣120×,=192﹣100,=92(人).答:数学及格人92人.14.(10分)甲.乙共带86元钱,甲花去自己所带钱数的,乙花去16元,这时两人所剩钱数相等,求甲.乙原来各带了多少元钱?【分析】本题可列方程解答,设甲带了x元,则乙带了86﹣x元,甲花去自己所带钱数的,则还剩下(1﹣)x元,乙花去16元,则还剩下86﹣x﹣16元,此时这时两人所剩钱数相等,由此可是方程:(1﹣)x=86﹣x﹣16.【解答】解:设甲带了x元,则乙带了(86﹣x)元,可得方程:(1﹣)x=86﹣x﹣16.x=70﹣x,1x=70,x=45.86﹣45=41(元).答:甲带了45元,乙带了41元.15.(10分)一辆车从甲地开往乙地.如果把车速减少10%,那么要比原定时间迟1小时到达,如果以原速行驶180千米,再把车速提高20%,那么可比原定时间早1小时到达.甲.乙两地之间的距离是多少千米?【分析】由题意知,原定时间是1÷10%×(1﹣10%)=9小时;如果速度提高20%行完全程,时间就会提前9﹣9÷(1+20%)=;因为只比原定时间早1小时,所以,提高速度的路程是1÷=;所以甲乙两地之间的距离是180÷(1﹣)=540千米.【解答】解:①原定时间:1÷10%×(1﹣10%)=9(小时);②提高速度的路程:1÷[9﹣9÷(1+20%)]=;③180÷(1﹣)=540千米.答:甲.乙两地之间的距离是540千米.16.(10分)小明看一本故事书,小芳看一本科技书,故事书的页数是科技书的75%,小明每天看15页,小芳每天看18页.二人同时开始阅读,当小明看完故事书时,小芳还有24页没看.这两本书各有多少页?【分析】本题可列方程解答,设科技书有x页,则故事书有75%x页,小明每天看15页,小芳每天看18页,又当小明看完故事书时,小芳还有24页没看,由此可得方程=,解此方程后,即能求出两本书各有多少页.【解答】解:设科技书有x页,则故事书有75%x页,可得方程:=,(x﹣24)×5=6×75%x,5x﹣120=4.5x,0.5=120,x=240.240×75%=180(页)答:故事书有180页,科技书有240页.17.(10分)甲.乙两人分别从A.B 两地同时出发,相向而行,乙的速度是甲的,两人相遇后继续前进,甲到达B地,乙到达A地立即返回,已知两人第二次相遇的地点距离第一次相遇的地点是3000米,求A.B两地的距离?【分析】把两地间的路程看作单位“1”,当两人第二次相遇时,两人一共行驶了3个A.B 两地间的距离,根据时间一定路程和速度成正比,乙的速度是甲的,先求出两人行驶1个全程,甲和乙分别行驶的路程,进而求出行驶了3个A.B两地间的距离时,甲行驶的路程,再减去两地间的路程,也就是甲距B地的地点,最后求出3000米占总路程的分率,依据分数除法意义即可解答.【解答】解:2+3=5,3000÷[3﹣1﹣(1﹣)],=3000÷[﹣1﹣],=3000÷[],=3000,=7500(米),答:A.B两地的距离7500米.第11页(共11页)。
小升初重点中学招生考试数学模拟卷(三) l (通用版,含答案,双击可编辑 ) (共32张PPT)

2.有 3 个箱子,如果两箱两箱地称它们的质量,分别是 83 千克、85 千克和 86 千克,那么其中最轻的箱子重( A )千克。
A.41 B.42 C.43 D.40
[提示:(83+ 85+86)÷2- 86= 41(千克 )]
3.某人下午 6 点多外出时,看手表上两指针的夹角为 110°, 下午 7 点前回家时发现两指针夹角仍为 110°,他外出( C )分钟。
5.有两瓶相同质量的糖水,甲瓶的糖与水质量的比是 1∶5,
乙瓶的糖与水质量的比是 1∶7。如果将这两瓶糖水混合在一起,
混合后的糖水中糖与水质量的 C.7∶35 D.7∶41
[提示:从“甲瓶的糖与水质量的比是 1∶5”可知,甲瓶糖水
中,糖占糖水质量的1+1 5=16。从“乙瓶的糖与水重量的比是 1∶
A.30 B.35 C.40 D.42
[提示: 110× 2÷5.5= 40(分)]
4.如图,在三角形 ABC 中,∠B=70°,若沿图中的虚线剪 去∠B,则∠1+∠2 等于( A )。
A.250° B.270° C.225° D.290° [提示:三角形 BED 中∠B 以外的另两个内角和是 180°-70° = 110°,∠ 1+∠ 2= 180°× 2- 110°= 250° ]
二、选择。(把正确答案的序号填在括号里)(10 分)
1.小明买了 6 瓶饮料,共付款 7.8 元,喝完全部饮料退瓶时,
他了解到每个空瓶的价钱比瓶中饮料的价钱少 1.1 元,那么小明应
收到退款( B )元。
A.1.2 元
B.0.6 元
C.0.1 元
D.1.0 元
[提示:(7.8÷6-1.1)÷2×6=0.6(元)]
答案:5
小升初重点中学招生考试数学模拟试卷及答案(共三套)

45 个数是( 4064301 )。
4.三个分数22001167,22001165, 22001175中最大的是 (
2017 2015
),最小
的是 (
2016 2017
)。
5.甲、乙两种糖果混合后,平均每千克 18.5 元,其中甲种糖
果每千克 24.8 元,乙种糖果每千克 16.4 元,乙种糖果是甲种糖果
做对题数: 20-4= 16(道)] 6.小明 7:15 从家出发去学校,到学校的时间是 7:50,那
么这段时间分针走了( 210 )度,时针走了( 17.5 )度。[提示: 从 7:15 到 7:50 经过了 35 分,35÷60=172(时) 172×360°= 210° 172÷12×360°=17.5°]
筐的3,如果从 4
乙筐中取出
40
个放入甲筐,这时乙筐苹果的个数是甲筐的2。甲、 5
乙两筐原有苹果多少个?(7 分)
40÷3+4 4-5+2 2=40÷27=140(个)
140× 3 =60(个) 3+4
140- 60= 80(个 ) 答:甲筐原有苹果 60 个,乙筐原有苹果 80 个。
6.甲、乙两人同时从山脚开始爬山,到达山顶后立即下山, 甲、乙两人下山的速度都是各自上山速度的 2 倍,甲到山顶时乙 距山顶还有 500 米,甲回到山脚时乙刚好下到半山腰,求山脚到 山顶的路程。(7 分)
号。”孙飞说:“丁是 2 号,丙是 3 号。”李亮说:“丁是 1 号,
乙是 3 号。”又知道赵明、钱平、孙飞、李亮每人只说对了一半,
那么丙的号码是( A )。
A.4
B. 3
C.2
D.1
[提示:甲、Βιβλιοθήκη 、丙、丁分别是 1,3,4,2]三、计算。(20 分) 1.下面各题,能简算的要简算。(15 分) (1)4113×34+ 5114× 45+ 6115×56 =124×3+205×4+306×5
2023年江苏苏州市重点中学小升初自主招生分班考数学试卷附详细答案
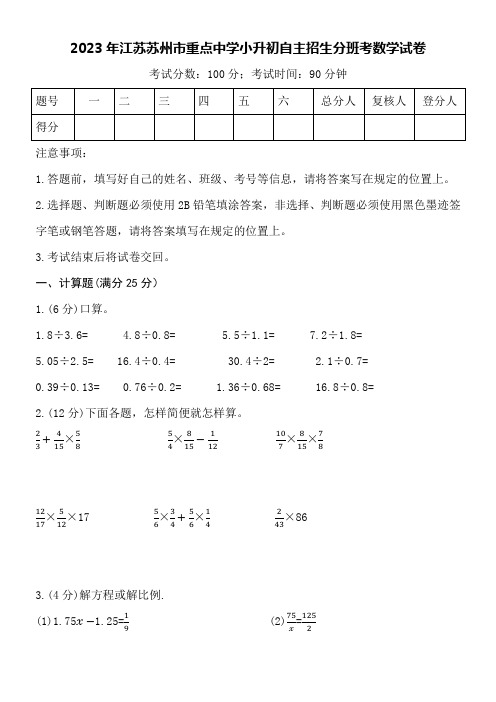
2023年江苏苏州市重点中学小升初自主招生分班考数学试卷考试分数:100分;考试时间:90分钟注意事项:1.答题前,填写好自己的姓名、班级、考号等信息,请将答案写在规定的位置上。
2.选择题、判断题必须使用2B 铅笔填涂答案,非选择、判断题必须使用黑色墨迹签字笔或钢笔答题,请将答案填写在规定的位置上。
3.考试结束后将试卷交回。
一、计算题(满分25分) 1.(6分)口算。
1.8÷3.6= 4.8÷0.8= 5.5÷1.1= 7.2÷1.8= 5.05÷2.5= 16.4÷0.4= 30.4÷2= 2.1÷0.7= 0.39÷0.13= 0.76÷0.2= 1.36÷0.68= 16.8÷0.8= 2.(12分)下面各题,怎样简便就怎样算。
23+415×5854×815−112107×815×781217×512×17 56×34+56×14243×863.(4分)解方程或解比例.(1)1.75x −1.25=19(2)75x=12524.(3分)计算下面图形中阴影部分的面积。
(单位:厘米)二、填空题(满分19分)5.5÷11的商用循环小数表示是( ),保留两位小数约是( )。
6.小刚把一个蛋糕平均分成6块,3块给奶奶,占这个蛋糕的( )( );2块给妈妈,占这个蛋糕的( )( )。
7.有一个正方形的池塘,四个角上都栽一棵树,如果每边栽9棵树,四边一共栽( )棵树。
8.分数2030的分子和分母的最大公因数是( );分数89和710的分母的最小公倍数是( )。
9.,这是( )比例尺,表示图上1cm 的距离相当于地面上( )km 的实际距离,改成数值比例尺就是( )。
10.一个圆形展台(如图)的半径是3m ,每平方米的租金是0.5万元,租这个圆形展台需要( )钱。
【精选精校】小升初数学名校招生分班考试试卷三(含答案)

小升初名校数学招生分班考试压轴精选试卷三考试时间:90分钟满分:100分姓名:__________ 班级:__________考号:__________第Ⅰ卷客观题第Ⅰ卷的注释一、单选题(共8题;共8分)1.王叔叔每月工资为6300元,如果按国家“超过5000元的那部分收入应缴纳3%的个人所得税”的规定,王叔叔应缴纳()元个人所得税.A. 189B. 39C. 150D. 902.瑶瑶看一本书,已经看了85%,还有51页没看,这本书一共有()页。
A. 60B. 170C. 240D. 3403.估算下面4个算式结果最大的是()。
A. 0.35×(1-13) B. 0.35×(1+13) C. 0.35÷(1+13) D. 0.35÷(1-13)4.在比例尺是1:4000000的地图上,量得A、B两港距离为9厘米,一艘货轮于上午6时以每小时24千米的速度从A开向B港,到达B港的时间是()A. 15点B. 17点C. 19点D. 21点5.下面公历年份中,不是闰年的是()A. 1996B. 2000C. 19006.两根同样长的绳子,第一根剪去它的13,第二根剪去13米,则剩下的绳子()。
A. 第一根长B. 第二根长C. 一样长D. 无法比较7.圆的半径扩大2倍,它的周长就()A. 扩大4倍B.扩大2倍 C. 扩大8倍8.如图,有一个无盖的正方体纸盒,下底标有字幕“M”,沿图中粗线将其剪开展成平面图形,想一想,这个平面图形是()。
A. B. C.D.阅卷人二、判断题(共8题;共8分)9.一种商品先提价20%,再降价20%,售价比原价降低了。
()10.5箱苹果重100kg,求3箱苹果的质量的算式可以是100× 35()11.1米的20%和2米的50%一样长.()12.一杯盐水,盐和水的比是1:9,则盐占盐水的19.()13.六年级3个班星期一的出勤率是(1)班出勤率98%,(2)班出勤率97%,(3)班出勤率100%,由此可以看出(3)班出勤的人数最多。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最新重点中学小升初自主招生数学备考试卷(含答案)
(考试时间60分钟,总分100分)
学校:_____________ 班级:_____________ 姓名:_____________ 电话:_____________
一、计算题(共20分)
1.计算下列各题,能简便的请用简便方法(12分)
1880×201.1−187.9×2011 25×5÷25×5 89×[34−(716−25%)] 7.2×61310+73.8×245
2.请用简便方法计算(8分)
(1+12+13+•••+12021)×(12+13+14+•••+12022)−(12+13+•••+12021)×(1+12+13
+•••+12022
)
二、填空题(每题3分,共27分)
3.20名乒乓球运动员参加单打比赛,两两配对进行淘汰赛,要决出冠军,一共要赛( )场.
4.下图中的阴影部分面积占长方形的( )。
5.某工厂,三月比二月产量高20%,二月比一月产量高20%,则三月比一月高( )%. 6.某次数学竞赛,试题共有10道,每做对一题得8分,每做错一题倒扣5分.小宇最终得41分,他做对( )题.
7.一个正方形的边长增加2厘米,面积增加了20平方厘米,扩大后正方形的面积是( )平方厘米;
8.一个长方形被内部一点分成4个不同的三角形(如图),若红色的三角形面积占长方形面积的18%,兰色的三角形面积是64cm2 则长方形面积是()。
9.一批苹果分装在33个筐内,如果每个筐多装110,可省()个筐。
10.将2022减去它的12,再减去余下的13,再减去余下的14,……最后减去余下的1
2022,差是()。
11.小明按照如图的方法用灰色和白色正方形摆图形.
当中间摆n个灰色的正方形时,四周共需要摆()个白色正方形.
三、解决问题(共53分)
12.甲仓有粮80吨,乙仓有粮120吨,如果把乙仓的一部分粮调到甲仓,使得乙仓存量是甲仓的60%,需要从乙仓调入甲仓多少吨粮食?(6分)
13.一个容器正好装满10升纯酒精,倒出3升后用水加满,再倒出4.5升后,再用水加满,这时容器中溶液的浓度是多少?(6分)
14.客车和货车分别从甲乙两站同时相向开出,5小时后相遇,相遇后两车仍按原速度
前进,当他们相距196千米时,客车行了全程的3
5,货车行了全程的80%。
(6分)
(1)全程是多少千米?
(2)货车行完全程需要多少个小时?
15.甲、乙人分别从A、B两地同时出发相向而行.他们的速度比是3:2.早上8时,甲到达途中C地,乙11时才到达C地.甲乙什么时候在途中相遇?(7分)
16.厂长把生产一批零件的任务交给甲车间,甲车间主任说:“我们20天内刚好可以完成任务”,甲车间生产了5天后厂长接到客户电话,要求6天后提货,厂长于是把剩下的生产任务交给乙车间,乙车间主任说:“这些任务我们需要12天才能完成”。
厂长决定上甲乙两个车间共同完成这些任务,请你算一算,他们能在6天内完成剩下的任务吗?(7分)
17.有甲、乙两个装满硫酸的容器,甲容器中装有浓度为16%的硫酸溶液300千克,乙容器中装有浓度为40%的硫酸溶液200千克。
问:从甲、乙两个容器各取多少千克硫酸溶液分别放入对方容器中,才能使这两个容器中硫酸溶液的浓度一样?(7分)
18.兄弟两人骑自行车同时从甲地到乙地,弟弟在前一半路程每小时行4千米,后一半
路程每小时行6千米。
哥哥按时间分段行驶,前1
3的时间每小时行4千米,中间
1
3的
时间每小时行5千米,最后1
3的时间每小时行6千米,结果哥哥比弟弟早到20分钟。
问:甲、乙两地相距多少千米?(7分)
19.某次大会安排代表住宿,若每间2人,则有12人没有床位;若每间3人,则多出2
个空床位.问宿舍共有几间?代表共有几人?(7分)
参考答案
1.201.1 25 12
648 2.解:令12+13+⋯+12021=A ,12+13+⋯+12022
=B ,所以原式=(1+A)×B-A×(1+B) =B+AB-A-AB =B-A =12022
3.19
4.14
5.44
6.7
7.36
8.200
9.3
10.1
11.2n+6
12.解:(80+120)÷(1+60%)=125 125−80=45(吨)
13.解:10−3−4.5×10−310
=7−3.15=3.85(升) 3.85÷10=38.5% 14.(1)解:196÷(35+80100⁄−1) =196÷(0.6+0.8−1) =490(千米)
(2)解:客货速度比为:35:80100⁄=3:4 则货车速度为:(490÷5)×43+4
=56(千米)
货车行完全程需要的时间是:490÷56=834
(小时) 15.解:假设甲到达C 时,乙还在D ,从D 到C 需要:11-8=3(小时),由他们的速度比是3:2则时间比是2:3;就将CD 的距离看作单位“1”,则甲的速度:12,乙的速度:13
; 则相遇时间:1÷(12+13)=1÷56
=1.2(小时) 1.2小时=1小时12分钟
最后甲乙的相遇时间:8时+1时12分=9时12分
16.解:1-120
×5 =1-14
=34
34÷12=116 34÷(120116)=34÷980=203(天) 203
>6 不能 17.解:两个容器中溶液混合后浓度为:
(300×16%+200×40%)÷(300+200)=(48+80)÷500=128÷500=25.6%所以应交换的硫酸溶液浓度的量为:(300×25.6%-300×16%)÷(40%-16%)=(76.8-48)÷0.24=28.8÷0.24=120(千克)答:从甲、乙两个容器各取120千克硫酸溶液分别放入对方容器中,才能使这两个容器中硫酸溶液的浓度一样.
18.解:设哥哥从甲地到乙地需要x 小时,
6:4=3:2,3+2=5
20分钟=13小时
13x×(4+5+6)=(x+13)×35×4+(x+13)×25×6
x=0.8 13×8×(4+5+6)=13×8×15=40(千米)
答:甲、乙两地相距40千米.
19.解:设宿舍共有x 间,
3x-2=2x+12
3x-2x=12+2
x=14
14×2+12
=28+12
=40(人)
答:宿舍有14间,代表共有40人.。
