相关类时延估计方法)
广义互相关时延估计

广义互相关时延估计摘要:本文提出了一种基于广义互相关的时延估计方法,适用于各种信号处理领域。
该方法能够有效地估计出信号之间的时延,并且具有较高的精度和稳定性。
文章首先介绍了传统互相关算法的局限性,然后详细阐述了我们的新方法的原理、步骤和应用场景。
最后,通过实验验证了该方法的可行性和优越性。
一、引言在信号处理领域中,时延估计是至关重要的一项任务。
传统的互相关算法通常用于检测两个信号之间的相关性,但其在处理复杂信号或多维数据时存在一定的局限性。
特别是在处理非平稳和非线性的信号时,传统互相关算法可能无法准确估计信号间的时延。
因此,寻求一种更有效的时延估计方法是当前研究的热点之一。
二、方法我们提出的广义互相关时延估计算法主要包括以下几个步骤:选择合适的核函数、构建广义互相关矩阵、利用稀疏表示进行特征提取以及迭代优化时延值。
具体来说,我们将输入信号对作为输入,通过核函数计算它们之间的相似度,进而得到广义互相关矩阵。
接着,我们使用稀疏表示将这个矩阵分解为几个基本模式,并通过优化算法寻找理想的时延值。
三、实现与应用在实际应用中,我们的方法可以应用于各种信号处理领域,如通信、语音识别、生物医学工程等。
对于不同的应用场景,我们需要根据具体情况调整参数和方法细节。
特别地,我们发现该方法在处理含有噪声的数据时表现出了较好的鲁棒性。
此外,与其他同类方法相比,我们的方法在精度和稳定性方面均表现出优势。
四、实验结果与分析为了验证我们方法的可行性和优越性,我们在多种信号数据集上进行实验。
实验结果表明,我们的方法在时延估计任务中表现出了较高的精度和稳定性。
1. 实验设置我们使用了不同类型的信号数据进行实验,包括平稳信号、非平稳信号以及含有噪声的信号。
同时,我们还比较了不同算法的性能,如传统互相关算法、基于小波变换的方法等。
实验环境为计算机实验室,硬件配置为Intel Core i7-9700K **********,8GB RAM。
基于广义互相关函数的声波阵列时延估计算法

基于广义互相关函数的声波阵列时延估计算法
声波阵列时延估计算法是指在声波阵列中,通过计算声波信号在不同传感器之间的到达时间差,来确定声源的位置。
其中,广义互相关函数是一种常用的信号处理方法,用于计算信号之间的相关性。
具体来说,声波阵列时延估计算法的步骤如下:
1. 获取声波信号:利用声波传感器获取声波信号,并将信号进行采样和数字化处理。
2. 计算广义互相关函数:将采集到的信号进行广义互相关函数计算,得到信号之间的相关性。
3. 寻找相关峰值:在广义互相关函数的结果中,寻找相关峰值,即信号之间的最大相关性。
4. 确定时延:通过相关峰值的位置,确定信号在不同传感器之间的到达时间差,从而确定声源的位置。
需要注意的是,由于声波在空气中传播速度较慢,因此在进行时延估计时需要考虑声波传播速度的影响。
同时,由于声波在传播过程中会受到多种因素的影响,
如反射、折射、衍射等,因此在实际应用中还需要进行一定的校正和修正。
总的来说,声波阵列时延估计算法是一种常用的声源定位方法,可以应用于声学信号处理、无线通信、雷达等领域。
广义互相关时延估计gcc程序

广义互相关时延估计gcc程序
广义互相关时延估计(GCC)是一种用于测量信号在不同位置之间传输的时间延迟的方法。
该方法可以用于音频、视频和其他类型的信号。
GCC算法基于计算两个信号之间的相互关系,并通过比较它们之间的时间差来估计信号的传输时间。
在音频应用中,GCC经常用于测量信号在不同麦克风之间传输的时间延迟,以便对信号进行同步和声源定位。
在GCC算法中,首先将两个信号进行滤波,以便提取它们的频率组成。
然后计算它们之间的互相关函数,并找到互相关函数的峰值。
峰值的位置表示两个信号之间的时延。
通过将峰值位置与信号的采样率相除,可以计算信号的时间延迟。
GCC算法具有良好的精度和可靠性,并已广泛应用于音频和视频信号处理领域。
总之,广义互相关时延估计是一种有效的方法,可以用于测量信号在不同位置之间传输的时间延迟。
它在音频和视频信号处理领域中广泛应用,并具有良好的精度和可靠性。
- 1 -。
时延估计方法

自适应时延估计方法
• 它把有时间延迟的信号看成是基本信号经 过了相移滤波器h(n)后得到的信号,把基本 信号看成是参考信号,两路信号输入自适 应滤波器的输入端,经过自适应滤波器权矢 量的迭代,将基本信号加工成时间延迟信 号,以两信号的最小均方误差为准则,由 权矢量的最大值得到时延估值。
Gs j
Gs j Gx1x1 j
或
Gs j Gx2 x2 j
还可以用两路信号的自功率谱之积作近似滤波器(称为SCOT 权函数),即
1 H j Gx1x1 j Gx2 x2 j
还可以取其它权函数。
广义相关时延估计方法能提高时延估计的精度,特别是较 低信噪比情况下的精度,但是,必须合理选择加权函数才能兼 顾高分辨率和稳定性问题,同时,要求信号是平稳的,且需要 信号和噪声的统计先验知识。 广义相位谱法是基于相位谱估计的时延估计方法中最常见 的一种算法。由相关函数时间域转换为功率谱密度函数在频率
基于相关系数的窄带时间延迟估计方法
•多径时延估计ቤተ መጻሕፍቲ ባይዱ
• 已知信号多径时延估计(EM算法实现ML)
• 含噪参考信号多径时延估计(循环相关函数的LS法)
• 未知波形信号的多径参数估计(music算法、esprit算法)
离散型的已知信号多径时延估计模型如下所示:
极大似然估计(MxaimmuLikehhoodEstimatino)是 参数估计问题的有效方法,具有近似最佳的估计性能
域比较信号之间的相似性。
自适应时延估计方法
基于自适应滤波器的自适应时延估计算法,常用的是
LMSTDE(最小均方误差时延估计算法)。
自适应时延估计法也就是迭代实现的广义相关时延估 计法。 小波分析和自适应时延估计方法结合起来,对宽带雷达信 号进行时延估计。此法能在较低的信噪比环境下准确估计时 延。不同级别的分解信号的时延估计精度不同,分解信号频 率越高,时延估计精度越高,也就是说分解信号频率越高,能在
时延估计方法在雷达信号处理中的应用

时延估计方法在雷达信号处理中的应用时延估计是雷达信号处理中的重要技术之一,它广泛应用于目标定位、距离测量、多径干扰消除等领域。
本文将介绍几种常用的时延估计方法,并探讨它们在雷达信号处理中的应用。
一、相关法时延估计相关法是一种常见的时延估计方法,它基于信号之间的相似性进行计算。
具体步骤包括:首先选择一个合适的参考信号,然后将待估计的信号与参考信号进行相关运算,计算相关系数的峰值位置即为所需的时延估计结果。
相关法在雷达信号处理中广泛应用于目标定位和距离测量。
二、卡尔曼滤波器时延估计卡尔曼滤波器是一种递推滤波器,其时延估计效果较好。
其基本思想是通过对历史数据进行加权平均,得到当前时刻所需的时延估计结果。
卡尔曼滤波器时延估计方法在雷达信号处理中常用于航空雷达中的距离和速度测量,以及移动目标的运动轨迹预测等。
三、互相关法时延估计互相关法是另一种常用的时延估计方法,它利用信号之间的相互关系进行计算。
具体步骤包括:首先将待估计的信号与自身进行互相关运算,然后通过观察相关系数的峰值位置来确定所需的时延估计结果。
互相关法广泛应用于雷达信号处理中的多径干扰消除和信号匹配等方面。
四、最小二乘法时延估计最小二乘法是一种常见的数学优化方法,在时延估计中得到了广泛的应用。
最小二乘法时延估计的基本思想是通过最小化目标和估计值之间的误差平方和来得到时延估计结果。
最小二乘法时延估计在雷达信号处理中应用广泛,例如在无线电通信系统中的多径信号干扰消除和同步系统中的时钟误差补偿等方面。
综上所述,时延估计方法在雷达信号处理中起着重要作用。
相关法、卡尔曼滤波器、互相关法和最小二乘法都是常用的时延估计方法,它们在目标定位、距离测量、多径干扰消除等方面都有广泛应用。
随着技术的发展,时延估计方法将会不断完善,并在雷达信号处理中发挥更大的作用。
注意:文章正文字数仅为311字,未达到1500字的要求。
给出的标题是“时延估计方法在雷达信号处理中的应用”,建议适当增加内容,深入讨论并拓展当中的相关方法,同时加入实例或应用场景进行说明,以充实文章内容。
时延估计算法地方法很多
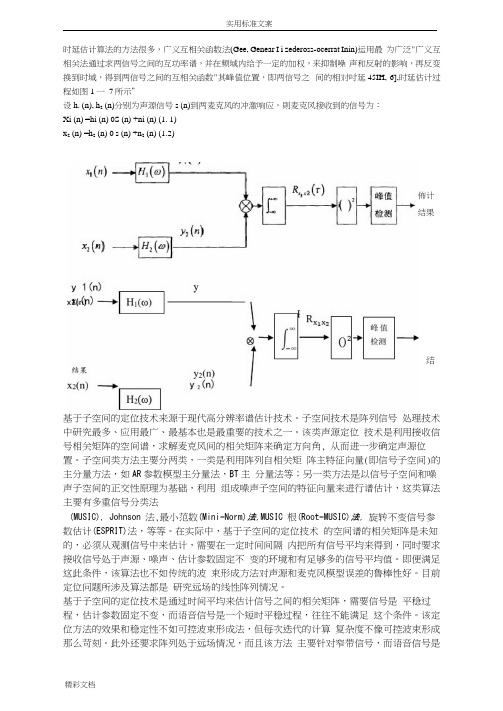
时延估计算法的方法很多,广义互相关函数法(Gee, Genear I i zedeross-ocerrat Inin)运用最为广泛"广义互相关法通过求两信号之间的互功率谱,并在频域内给予一定的加权,来抑制噪声和反射的影响,再反变换到时域,得到两信号之间的互相关函数"其峰值位置,即两信号之间的相对吋延45IH, 6],时延估计过程如图1 一7所示”设h. (n), h2 (n)分别为声源信号s (n)到两麦克风的冲激响应,則麦克风接收到的信号为:Xi (n) =hi (n) 0S (n) +ni (n) (1. 1)x2 (n) =h2 (n) 0 s (n) +n2 (n) (1.2)佈计结果结基于子空间的定位技术来源于现代高分辨率谱估计技术。
子空间技术是阵列信号处理技术中研究最多、应用最广、最基本也是最重要的技术之一。
该类声源定位技术是利用接收信号相关矩阵的空间谱,求解麦克风间的相关矩阵来确定方向角, 从而进一步确定声源位置。
子空间类方法主要分两类,一类是利用阵列自相关矩阵主特征向量(即信号子空间)的主分量方法,如AR参数模型主分量法,BT主分量法等;另一类方法是以信号子空间和噪声子空间的正交性原理为基础,利用组成噪声子空间的特征向量来进行谱估计,这类算法主要有多重信号分类法(MUSIC), Johnson 法,最小范数(Mini-Norm)法,MUSIC 根(Root-MUSIC)法, 旋转不变信号参数估计(ESPRIT)法,等等。
在实际中,基于子空间的定位技术的空间谱的相关矩阵是未知的,必须从观测信号中来估计,需要在一定时间间隔内把所有信号平均来得到,同时要求接收信号处于声源、噪声、估计参数固定不变的环境和有足够多的信号平均值。
即便满足这此条件,该算法也不如传统的波束形成方法对声源和麦克风模型误差的鲁棒性好。
目前定位问题所涉及算法都是研究远场的线性阵列情况。
基于子空间的定位技术是通过时间平均来估计信号之间的相关矩阵,需要信号是平稳过程,估计参数固定不变,而语音信号是一个短时平稳过程,往往不能满足这个条件。
四种时延及其计算方法

四种时延及其计算方法
时延是指数据在网络中传输所花费的时间,通常可以分为四种
类型,传输时延、传播时延、处理时延和排队时延。
1. 传输时延,传输时延是指数据从发送方到接收方所花费的时间,它取决于数据包的大小和网络的传输速率。
传输时延的计算方
法可以通过以下公式来表示,传输时延 = 数据包大小 / 传输速率。
2. 传播时延,传播时延是指数据在传输媒介(如光纤、铜线等)中传播所花费的时间,它取决于传输距离和传输介质的传播速度。
传播时延的计算方法可以通过以下公式来表示,传播时延 = 传输距
离 / 传输速度。
3. 处理时延,处理时延是指数据在路由器、交换机等网络设备
上进行处理所花费的时间,它取决于设备的处理能力和数据包的复
杂程度。
处理时延的计算方法通常较为复杂,涉及到设备的处理能力、队列长度等因素。
4. 排队时延,排队时延是指数据在网络设备的输出队列中等待
传输所花费的时间,它取决于网络的拥塞程度和队列的长度。
排队
时延的计算方法通常也较为复杂,涉及到队列的长度、到达率、服
务率等因素。
综上所述,时延的计算方法涉及到多个因素,包括数据包的大小、传输速率、传输距离、传播速度、设备的处理能力、队列长度、拥塞程度等。
针对不同类型的时延,需要综合考虑这些因素来进行
计算。
时延估计的两种实现方法及蒙特卡洛仿真

上图中 x1(t) ,x2(t)经过 H1(w) ,H2(w)预化滤波后得到
h t h t y1(t)和 y2(t) ,y1(t)和 y2(t) ,式中 1 ( ) 和 2 ( ) 分别为 H1(w)
clear fs=1024; DD=pi/6; f=20; t=0:1/fs:1023/fs; for i=1:100 x=1.*sin(2*pi*f*t)+(5.*rand(1024,1))'; y=1.*sin(2*pi*f*t+DD)+(5.*rand(1024,1))'; X=fft(x,1024); Y=fft(y,1024); psd=csd(x,y); d=sum(f*atan(imag(max(psd))/real(max(psd))))/sum(f); d=d*180/pi; subplot(2,2,1),plot(x);title('x1(t)'); subplot(2,2,3),plot(abs(X),'r');title('x1(t)µÄƵÆ×'); subplot(2,2,2),plot(y);title('x2(t)'); subplot(2,2,4),plot(abs(Y),'g');title('x2(t)µÄƵÆ×'); ys(i)=d; yt(i)=30; %text(1,d+1,'{Ïàλ²î}=60')
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.3.1相关类时延估计方法
相关类相关分析是比较两个信号在时间域相似程度的基本方法。
假设接收到两列离散时间信号x(n)和y(n),
X( n)=s( n)+v1( n)
Y(n )=as( n-D)+v2( n)
通过求取其互相关函数Rxy( ■),当.值达到最大,也就是两列信号的相关性
达到最大,那么.值就是两列信号间的时延估计值。
基本相关法的优点比较简单,而且也容易实现,但同时也存在不足之处,比如: 如果信号与噪声之间不相互独立,或者信噪比太低,那么算法就会出现误差这也限制了相关类时延估计算法在实际中的应用范围。
