微分方程总结
求微分方程的通解方法总结
求微分方程的通解方法总结微分方程是数学中的重要概念之一，广泛应用于物理、工程、经济等领域。
解微分方程可以帮助我们理解和预测自然界中的现象变化。
本文将总结几种常见的求微分方程通解的方法，帮助读者更好地掌握这一重要的数学技巧。
一、分离变量法分离变量法是求解一阶微分方程最常用的方法之一。
当微分方程可以写成dy/dx = f(x)g(y) 的形式时，我们可以通过分离变量的方式将方程化简为两个变量的乘积形式。
然后将两边同时积分，得到通解。
二、常数变易法常数变易法适用于齐次线性微分方程，形如 dy/dx + P(x)y = 0。
通过猜测一个解y = Ce^(∫P(x)dx)（C为常数），然后求导得到dy/dx 和 P(x)y，将其代入原方程，如果两边相等，则得到通解。
三、齐次方程法齐次方程法适用于一阶线性微分方程dy/dx + P(x)y = Q(x)，其中P(x) 和 Q(x) 都是已知函数。
首先解齐次方程 dy/dx + P(x)y = 0，得到通解y_h。
然后通过常数变易法，猜测一个特解y_p，将其代入原方程，得到Q(x) = y_p' + P(x)y_p。
最后通解为y = y_h + y_p。
四、二阶齐次线性微分方程法对于二阶齐次线性微分方程 d^2y/dx^2 + p(x)dy/dx + q(x)y = 0，可以通过特征方程 r^2 + p(x)r + q(x) = 0 求得特征根 r_1 和 r_2。
然后根据特征根的不同情况，得到通解y = C_1e^(r_1x) + C_2e^(r_2x)（C_1 和 C_2 为常数）。
五、常系数齐次线性微分方程法对于常系数齐次线性微分方程 d^2y/dx^2 + a dy/dx + by = 0，可以通过特征方程 r^2 + ar + b = 0 求得特征根 r_1 和 r_2。
然后根据特征根的不同情况，得到通解 y = C_1e^(r_1x) + C_2e^(r_2x)（C_1 和 C_2 为常数）。
微分方程通解总结
微分方程通解总结一、引言微分方程是数学中的一个重要分支，它在自然科学、工程技术等领域中具有广泛的应用。
微分方程通解是对微分方程的一种全面、详细、完整且深入的研究和总结。
本文将通过多个层次和多个级别的标题，对微分方程通解展开讨论。
二、微分方程的基本概念2.1 微分方程的定义微分方程是含有未知函数及其导数的方程。
通常用字母和导数符号表示。
2.2 微分方程的分类微分方程可分为常微分方程和偏微分方程两大类。
常微分方程中未知函数只有一个自变量，而偏微分方程中未知函数有多个自变量。
三、微分方程通解的基本理论3.1 齐次线性微分方程的通解齐次线性微分方程是形如f(x)y’’ + g(x)y’ + h(x)y = 0的方程，其中f(x)、g(x)、h(x)是已知的函数。
可以通过换元的方法得到齐次线性微分方程的通解。
3.2 非齐次线性微分方程的通解非齐次线性微分方程是形如f(x)y’’ + g(x)y’ + h(x)y = r(x)的方程，其中r(x)是已知的函数。
可以通过常数变易法得到非齐次线性微分方程的通解。
3.3 二阶常系数线性微分方程的通解二阶常系数线性微分方程是形如a y’’ + by’ + cy = 0的方程，其中a、b、c是已知的常数。
可以通过特征根法得到二阶常系数线性微分方程的通解。
3.4 高阶线性微分方程的通解高阶线性微分方程是形如anyn + an-1yn-1 + … + a1y’ + a0y = 0的方程，其中a0、a1、…、an是已知的常数。
可以通过特征根法得到高阶线性微分方程的通解。
四、微分方程通解的应用4.1 物理学中的应用微分方程通解在物理学中有着广泛的应用。
例如，通过对运动物体的运动方程建立微分方程并求解通解，可以得到物体的运动规律。
4.2 工程技术中的应用微分方程通解在工程技术中也有着重要的应用。
例如，在电路分析中，可以通过建立电路的微分方程并求解通解，得到电路中电流和电压的变化规律。
高数微分方程总结
５、二阶常系数齐次线性方程解法
形如 y(n) P1 y(n1) Pn1 y Pn y f ( x)
n阶常系数线性微分方程
y py qy 0 二阶常系数齐次线性方程 y py qy f ( x) 二阶常系数非齐次线性方程
解法 由常系数齐次线性方程的特征方程的根确 定其通解的方法称为特征方程法.
解 （１） 由题设可得：
2 p( x)2x 0,
2 x3
p( x)( 1 ) x2
f ( x),
解此方程组，得
p( x) 1 , x
f
(x)
3 x3
.
（２） 原方程为 y 1 y 3 .
x
x3
显见 y1 1, y2 x2 是原方程对应的齐次方 程 的两个线性无关的特解 ，
又 y* 1 是原方程的一个特解， x
dt 2
即 x g x g , 99
x(0) 0, x(0) 0.
10m
o x
解此方程得
x(t)
1
(e
1 3
gt
1
e3
gt
) 1,
2
整个链条滑过钉子 ,即 x 8,
代入上式得
t 3 ln(9 80). (秒) g
最好的，不一定是最合适的；最合适的，才是真正最好的。 最大的挑战和突破在于用人，而用人最大的突破在于信任人。——马云 快乐的人帮助别人，积极人的肯定自己。——王修强 对于每一个不利条件，都会存在与之相对应的有利条件。 人必须有自信，这是成功的秘密。 人一旦觉悟，就会放弃追寻身外之物，而开始追寻内心世界的真正财富。 这世间最可依赖的不是别人，而是你自己。不要指望他人，一定要坚强自立。 懂得感恩，感谢帮助你的每一个人。 不要因为小小的争执，远离了你至亲的好友，也不要因为小小的怨恨，忘记了别人的大恩。
微分方程的通解公式总结
微分方程的通解公式总结首先，我们来看一阶微分方程的通解公式。
一阶微分方程的一般形式为dy/dx=f(x,y)，其中f(x,y)为x和y的函数。
对于这种形式的微分方程，我们可以通过分离变量、齐次方程、恰当方程等方法求解，并得到通解公式y=F(x,C)，其中F(x,C)为x和常数C的函数。
这个通解公式中的C称为积分常数，它包含了微分方程的所有解。
在具体求解微分方程时，我们可以根据初值条件确定积分常数的值，从而得到微分方程的特解。
其次，我们来看高阶微分方程的通解公式。
高阶微分方程的一般形式为d^ny/dx^n=F(x)，其中F(x)为x的函数。
对于这种形式的微分方程，我们可以通过特征方程、常数变易法、待定系数法等方法求解，并得到通解公式y=y_0+y_h，其中y_0为特解，y_h为齐次方程的通解。
特解可以通过对非齐次方程进行积分得到，而齐次方程的通解可以通过求解对应的齐次方程得到。
最后，我们来看一些常见微分方程的通解公式。
常见的微分方程包括线性微分方程、非线性微分方程、常系数微分方程等。
对于这些常见的微分方程，我们可以通过不同的方法求解，并得到它们的通解公式。
例如，对于线性微分方程可以通过特征方程求解，对于非线性微分方程可以通过变量代换或者积分求解，对于常系数微分方程可以通过特征根的不同情况分类讨论。
通过总结这些微分方程的通解公式，我们可以更好地理解它们的特点和性质，为实际问题的求解提供指导。
总之，微分方程的通解公式总结是微分方程研究的重要内容，它对于理解微分方程的性质和特点，以及解决实际问题都具有重要意义。
通过对一阶微分方程、高阶微分方程以及常见微分方程的通解公式进行总结，我们可以更好地掌握微分方程的求解方法和技巧，为数学建模和实际问题的求解提供理论基础和数学工具。
希望本文的总结能够帮助读者更好地理解微分方程的通解公式，提高微分方程的解题能力。
高等数学微分方程总结ppt课件.pptx
y py qy f ( x)
代数法
求解二阶常系数线性方程
二阶常系数齐次线性微分方程求通解的一般步骤:
(1) 写出相应的特征方程 r 2 pr q 0;
(2) 求出特征方程的两个根 r1 与 r2；
(3) 根据特征方程的两个根的不同情况,按照下列规 则写出微分方程的通解
高阶常系数线性微分方程
P338
y(n) p1 y(n1) pn1 y pn y 0
代数特征方程 r n p1r n1 pn1r pn 0
1. 一阶标准类型方程求解 四个标准类型: 可分离变量方程, 齐次方程, 线性方程, 全微分方程
关键: 辨别方程类型 , 掌握求解步骤 2. 一阶非标准类型方程求解
所以F(x) 满足的一阶线性非齐次微分方程:
F (x) 2F (x) 4e2x
(2) 由一阶线性微分方程解的公式得
F (x) e 2d x 4e2x e 2d x d x C
e2x 4e4x d x C
e2x Ce2x 将 F (0) f (0)g(0) 0 代入上式，得 C 1
齐次通解
非齐特解
难点：如何求特解？
方法：待定系数法.
y py qy f ( x)
(1) f ( x) ex Pm ( x), (可以是复数）
y* xkexQm ( x);
0 不是根 k 1 是单根,
2 是重根
(2) f ( x) ex[Pl ( x)cosx Pn ( x)sinx],
令y=ut
可分离变量方程求解
(4) y2 (x 3y ) dx (1 3 xy2 ) dy 0 变方程为 y2 x dx dy 3 y2 ( ydx xdy) 0
微分方程公式总结
微分方程公式总结一、什么是微分方程微分方程是包含未知函数及其导数的方程，它描述了函数与其导数之间的关系。
一般形式的微分方程可以表示为：\[ F(x, y, \frac{{dy}}{{dx}}, \frac{{d^2y}}{{dx^2}}, ... , \frac{{d^ny}}{{dx^n}}) = 0 \]其中，\(y\) 是未知函数，\(x\) 是自变量，\(\frac{{dy}}{{dx}}\) 是\(y\) 对 \(x\) 的导数，\(n\) 是一个正整数，\(F\) 是一个给定的函数。
二、微分方程的分类根据微分方程中包含的未知函数的阶数，微分方程可分为常微分方程和偏微分方程两种。
1. 常微分方程：常微分方程是只包含未知函数的一阶或高阶导数的微分方程。
常微分方程的一般形式可以表示为：\[ F(x, y, \frac{{dy}}{{dx}}, \frac{{d^2y}}{{dx^2}}, ... , \frac{{d^ny}}{{dx^n}}) = 0 \]常微分方程的求解方法多种多样，其中常见的方法包括分离变量法、齐次方程法、一阶线性微分方程法等。
2. 偏微分方程：偏微分方程是包含多个未知函数及其偏导数的微分方程。
偏微分方程的一般形式可以表示为：\[ F(x, y_1, y_2, ..., \frac{{\partial y_1}}{{\partial x}}, \frac{{\partial y_2}}{{\partial x}}, ... , \frac{{\partial^2y_1}}{{\partial x^2}}, \frac{{\partial^2y_2}}{{\partial x^2}}, ... , \frac{{\partial^2y_1}}{{\partial x \partial y}}, \frac{{\partial^2y_2}}{{\partial x \partial y}}, ... ) = 0 \]偏微分方程的求解方法较为复杂，常用的方法包括分离变量法、特征线法、变量分离法等。
大一常微分方程一知识点总结
大一常微分方程一知识点总结本文档旨在总结大一常微分方程一课程中的主要知识点，帮助同学们复和回顾相关内容。
1. 什么是微分方程微分方程是一个含有未知函数及其导数的方程。
它通常用于描述自然现象中包含变化速率的问题，如物理、工程和经济等领域。
2. 常见的常微分方程类型常微分方程可以分为以下几类：- 一阶常微分方程：只涉及一阶导数的方程。
常见的一阶方程包括分离变量方程、线性方程和齐次方程等。
- 二阶常微分方程：涉及二阶导数的方程。
常见的二阶方程包括常系数二阶齐次方程和非齐次方程等。
3. 常微分方程的解法常微分方程的解法主要有以下几种：- 分离变量法：将方程的未知函数与其导数分开，将方程变为两个可积的方程，再进行求解。
- 变量替换法：通过合适的变量替换，将原方程转化为可以更容易求解的形式。
- 齐次方程的解法：通过适当的变量替换，使得方程变为可以分离变量的形式，然后利用分离变量法求解。
- 常系数二阶齐次方程的解法：通过对方程进行特征根分析，得到方程的通解。
- 非齐次方程的解法：通过求解对应的齐次方程的通解和非齐次方程的特解，得到非齐次方程的通解。
4. 常微分方程的应用常微分方程在各个领域都有广泛的应用，包括但不限于以下几个方面：- 物理学：常微分方程可以用于描述物理系统的运动规律，如牛顿运动定律、电路中的电流变化等。
- 工程学：常微分方程可以用于描述工程问题中的变化和变化率，如电路中的电压变化、机械系统的振动等。
- 经济学：常微分方程可以用于描述经济系统中的变化和变化率，如经济增长模型、人口增长模型等。
以上是对大一常微分方程一课程的主要知识点的简要总结，希望能够为同学们的学习提供一些帮助和参考。
微分方程解法总结
微分方程解法总结微分方程（DifferentialEquations）是数学中一类重要的运筹学问题，也是许多应用数学领域中最重要的数学工具之一。
微分方程可以应用在物理学、化学、工程学、生物学及经济学等学科中，在多学科领域中都发挥了重要作用。
一般来说，微分方程可以用一组方程来描述某种函数的变化，其中包括两个或更多的未知函数。
常用的微分方程解法包括，比如直接法、可积性法、积分变换法等。
1.接法直接法是指从微分方程的定义出发，直接寻找微分方程的解的方法。
一般来说，将定义域上的某个变量作为一个变量来代替原方程中的其它变量，从而将原方程变为一个关于这个变量的微分方程，再解此新的微分方程，最终得到需要的解。
2.积性法可积性法，即牛顿-拉夫逊定理，是指依据微分方程中的微分操作，运用积分学手段求出微分方程的解的方法。
牛顿-拉夫逊定理具有很强的通用性，几乎可以用于解决所有的不定积分问题，而且可以在多个变量之间进行推导。
3.分变换法积分变换法是一种特殊的可积性法，通过运用微积分中的奇偶变换，由傅里叶变换求出微分方程的解。
这种方法主要用于解决有限区间上的微分方程，既可以解决常规的微分方程，也可以解决非线性微分方程。
4.值方法数值方法是指用计算机从解析计算的角度进行微分方程的解法。
数值方法可分为两类，一类是有限差分的方法，另一类是可积性方法。
有限差分方法是在有限域上利用数值误差求解微分方程，它主要用于解决常微分方程组和椭圆型方程；可积性方法是指基于可积性定理，将微分方程转变为积分形式，再采用计算机数值解法，求出积分方程的解的方法。
总之，上述四类解法分别具有自己的优势和不足，因此要采取最适合的方式来解决某一类微分方程。
此外，在进行解微分方程的过程中，要进行精确的数学推导，以确保最终得到的解析解是准确可靠的。
通过上述分析，可以清楚地了解微分方程解法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第十章：微分方程总结姓名：刘桥
学号：40905237
班级：工商49班
小组：第八小组
组长：刘洪材
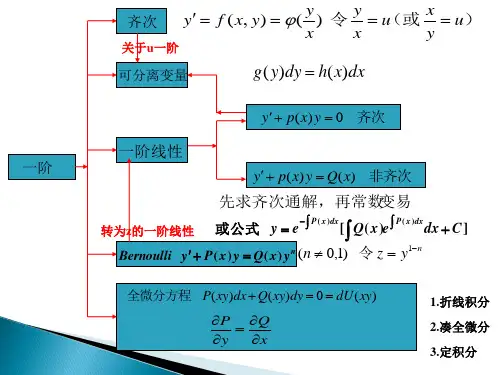
一、 微分方程的基本概念 1. 微分方程及其阶的定义
微分方程：凡含有未知函数的导数或微分的方程叫微分方程. 分类1：常微分方程（未知函数为一元函数的微分方程）
()()
,dy
axy a dx
dy p x y Q x dx
=+=为常数 偏微分方程（未知函数为多元函数，从而出现偏导数的微分方程）
()
22,2224
2
u u
f x y x y u u y x ∂∂+=∂∂∂∂=∂∂
微分方程的阶.：微分方程中出现的未知函数导数或微分的最高阶数. 分类2：一阶微分方程
(,,)0,(,);F x y y y f x y ''==
高阶(n )微分方程
()(,,,,)0,n F x y y y '=
()(1)(,,,
,).n n y f x y y y -'=
分类3：线性与非线性微分方程.
()(),y P x y Q x '+=2()20;x y yy x ''-+=
分类4：单个微分方程与微分方程组.
32,2,dy
y z dx
dz y z dx
⎧=-⎪⎪⎨
⎪=-⎪⎩ 2. 微风方程的解
微分方程的解：代入微分方程能使方程成为恒等式的函数.
微分方程解的分类：通解（微分方程的解中含有任意常数,且任意常数的个数与
微分方程的阶数相同.）
,y y '=例;x y ce =通解
0,y y ''+=12sin cos ;y c x c x =+通解
特解（ 确定了通解中任意常数以后的解.）
初始条件：用来确定任意常数的条件.
初值问题: 求微分方程满足初始条件的解的问题.
积分曲线：微分方程的任一特解的图形都是一条曲线,称为微分方程的积分曲线
二、 一阶微分方程 1. 可分离变量的方程
可分离变量的微分方程：形如： ()()g y dy f x dx =的一阶微分方程. 例题回味：求方程()290y
dy
x dy ye ++
=的通解 分离变量得，21
9
y ye dy dx x =
+ 两边同时积分得， 2
1
9y ye dy dx x =-
+⎰⎰ 于是得到通解为，()11arctan 33
y x
y e c -=+
2. 齐次方程
如果一阶微分方程可化为()dy y
f dx x
=形如的方程，那么久称之为齐次方程. 解法：作变量代换,y
u x
=
,y xu =或 两边分求微分得， ,dy udx xdu =+ 代入原式得，(),du u x
f u dx +=().du x f u u dx
=-即 ()0,f u u -≠若则对上式分离变量得，
()du dx
f u u x
=-.
两边分别积分得，
()du dx
f u u x
=-⎰
⎰
求出积分后，将y
u x
=
代入，就求得了原微分方程的通解. 例题回味：求解微分方程(cos )cos 0.y y
x y dx x dy x x
-+=
解，y
u x =令，dy xdu udx =+则，
(c o s )c o s ()x u x u d x x u u d x
x d u -+
+=
cos ,dx
udu x
=-
sin ln ,u x C =-+ 微分方程的解为sin ln .y
x C x
=-+
3. 一阶线性微分方程
形如
()()dy
p x y q x dx
+=的方程称为一阶线性微分方程 ()0,Q x ≠当称方程式为非齐次线性微分方程 ()0,Q x =当称方程
()()dy
p x y q x dx
+=为齐次线性微分方程 解法：1. 线性齐次方程（分离变量法） 2. 线性非齐次方程
例题回味：1sin .x
y y x x '+=
求方程的通解 解1(),P x x = sin (),x
Q x x
=
11sin dx dx x x
x y e e dx C x -
⎛⎫⎰⎰=⋅+ ⎪⎝⎭
⎰
l n l n
s i n x x x e e dx C x -⎛⎫=⋅+ ⎪⎝⎭⎰
(
)
1
s i n x d x
C x
=
+⎰ ()1
cos .x C x
=-+ 4. 伯努利方程
形如
()()n dy
P x y Q x y dx
+=（n 为常数）的方程称为伯努利方程. 三、 高阶微分方程
1. n 阶线性微分方程解的结构
n 阶线性微分方程的一般形式：()(1)11()()()().n n n n y a x y a x y a x y f x --'++++=
()0f x ≠当时，
称方程式为非齐次线性方程， ()0f x =当时，
称方程式为齐次线性方程。
定义：对于定义在区间（a,b ）上的函数组()()()12,,,k y x y x y x ⋅⋅⋅，如果存在不全
为0的常数12,,,k c c c ⋅⋅⋅，使得等式()()()11220k k c y x c y x c y x ++⋅⋅⋅+=在区间（a,b ）上恒成立，则称函数()()()12,,,k y x y x y x ⋅⋅⋅在区间（a,b ）上线性相关，否则，则称线性无关.
定理：①.如果函数()()()12,,,n y x y x y x ⋅⋅⋅都是其次线性方程式的解，则他们的线
性组合()()()()1122n n f x c y x c y x c y x =++⋅⋅⋅+也是齐次线性方程式的解，其中12,,,n c c c ⋅⋅⋅是n 个任意常数。
②. 如果()()()12,,,n y x y x y x ⋅⋅⋅是n 阶齐次线性方程式的两个线性无关的
特解, 则方程式的通解为()()()()1122c n n y x c y x c y x c y x =++⋅⋅⋅+.其中12,,,n c c c ⋅⋅⋅是n 个任意常数，而且方程式的任意解都可以表示成这个形式。
③. 设()y x 是n 阶非齐次线性方程
()(1)11()()()().n n n n y a x y a x y a x y f x --'++
++=的一个特解, ()c y x 是对
应的齐次方程式()()()11220k k c y x c y x c y x ++⋅⋅⋅+=的通解, 则非齐次线性微分方程的通解为()()()c y x y x y x =+. ④. 设非齐次方程(2)的右端 是几个函数之和, 如
12()()()()y P x y Q x y f x f x '''++=+而与分别是方程，
1()()()y P x y Q x y f x '''++=，2()()()y P x y Q x y f x '''++=的特解, 那么
**
12
y y +就是原方程的特解. 2. 二阶常系数线性方程
n 阶常系数线性微分方程的标准形式：()(1)
1
1()n n n n y Py P y P
y f x --'++++= 二阶常系数齐次线性方程的标准形式：0y py qy '''++= 二阶常系数非齐次线性方程的标准形式：()y py qy f x '''++=
特征根情况：(1)特征方程有两个不相等的实根(0)∆>
特征根为1r = 2r =
两个线性无关的特解11,r x y e = 22,r x y e =
得齐次方程的通解为1212;r x
r x
y C e C e =+ (2)特征方程有两个相等的实根(0)∆=
特征根为12,2
p
r r ==-
一特解为11,r x y e = 12(),r x y u x e =设另一特解为22
2y y y '''将，，代入原方程并化简， 2111(2)()0,u r p u r pr q u '''+++++= 0,u ''=知 (),u x x =取 12,r x y xe =则得齐次方程的通解为112();r x y C C x e =+ 3)特征方程有一对共轭复根(0)∆<
特征根为1,r i αβ=+ 2,r i αβ=- ()1,i x y e αβ+= ()2,i x y e αβ-=
重新组合1121()2y y y =+ cos ,x e x αβ= 2121
()2y y y i
=- sin ,x e x αβ=
得齐次方程的通解为12(cos sin ).x y e C x C x αββ=+
特征方程法步骤：(1) 写出所给方程的特征方程； (2) 求出特征根；
(3) 根据特征根的三种不同情况，写出对应的特解，并写出其
通解.
例题回味：250.y y y '''++=求方程的通解
特征方程为2250,r r ++= 解得1212,r i =-±，
其对应的两个线性无关的特解为y 1 = e-x cos2x ， y 2 = e-x sin2x 故所求通解为12(cos2sin 2).x y e C x C x -=+
四、 微分方程在经济中的应用（略）。