【第9章】 静电场[修正版]
大学物理课后习题答案

第九章 静电场 (Electrostatic Field)二、计算题9.7 电荷为+q 和-2q 的两个点电荷分别置于x =1 m 和x =-1 m 处.一试验电荷置于x 轴上何处,它受到的合力等于零?解:设试验电荷0q 置于x 处所受合力为零,根据电力叠加原理可得()()()()022220000(2)(2)ˆˆ0041414141q q q q q q i i x x x x εεεε⋅-⋅-+=⇒+=π-π+π-π+即:2610(3x x x m -+=⇒=±。
因23-=x 点处于q 、-2q 两点电荷之间,该处场强不可能为零.故舍去.得()223+=x m9.8 一个细玻璃棒被弯成半径为R 的半圆形,沿其上半部分均匀分布有电荷+Q ,沿其下半部分均匀分布有电荷-Q ,如题图9.4所示.试求圆心O 处的电场强度.解:把所有电荷都当作正电荷处理. 在θ 处取微小电荷d q = λd l = 2Q d θ / π它在O 处产生场强θεεd 24d d 20220R QR q E π=π=按θ 角变化,将d E 分解成二个分量:θθεθd sin 2sin d d 202R QE E x π==θθεθd cos 2cos d d 202RQE E y π-=-= 对各分量分别积分,积分时考虑到一半是负电荷⎥⎦⎤⎢⎣⎡-π=⎰⎰πππθθθθε2/2/0202d sin d sin 2R QE x =02022/2/0202d cos d cos 2R QR Q E y εθθθθεππππ-=⎥⎦⎤⎢⎣⎡-π-=⎰⎰ 所以j R Q j E i E E y x202επ-=+=9.9如图9.5所示,一电荷线密度为λ的无限长带电直导线垂直纸面通过A 点;附近有一电量为Q 的均匀带电球体,其球心位于O 点。
AOP ∆是边长为a 的等边三角形。
已知P 处场强方向垂直于OP ,求:λ和Q 间的关系。
大学物理下 第九章 静电场中的导体和电介质5
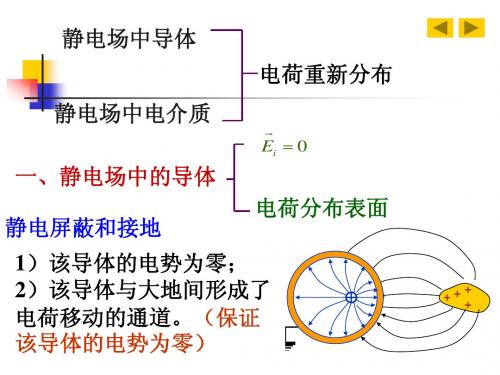
2
ε0S C= d
四,静电场的能量 (1)电容器的能量 )
1 Q2 W = CU 2 = 2 2C
(2)静电场的能量 有电场的地方就有能量 )
1 ωe = D E 2
W = ∫ ωe dV
(3)静电场的能量与功的关系 )
A 静 = W
已知 ε r1 : ε r 2 = 1 : 2 ,问 W1 : W2 = ?
λ o d a
λ λ U = ∫ + dr 2πε0r 2πε0 (d r ) a -λ λ λ d a λ d = Ln ≈ Ln πε0 a πε0 a
λ λ πε 0 ∴ C0 = = = d d λ U Ln Ln a a πε 0
r
d a
P79 99 讨论
1)通电后维持电压不变插入电介质 ) 2)通电后断开再插入电介质 ) 讨论插入前后的 E,D,U,Q. , , , 令插入前为E , , , (令插入前为 0,D0,U0,Q0) 2) Q = Q 0
4a
UBA = UB∞
场具有球对称性
a
3a
解(1)a < r < 3a
∫∫ D dS = ∫∫ DdS = D4πr = QA
2 S S
Q
4a
a
QA D= 2 4πr
D QA E= = 2 ε0εr 4πε0εr r
3a
r > 4a ∫∫ D dS = D 4 πr = Q + Q A
2 S
Q + QA D= 2 4 πr
∫∫ D dS = Q0
S
E = E0 + E'
9-6,8 ,
E0
讨论 p79
袁艳红主编大学物理学第九章课后习题答案

----------专业最好文档,专业为你服务,急你所急,供你所需-------------文档下载最佳的地方第9章 静电场习 题一 选择题9-1 两个带有电量为2q 等量异号电荷,形状相同的金属小球A 和B 相互作用力为f ,它们之间的距离R 远大于小球本身的直径,现在用一个带有绝缘柄的原来不带电的相同的金属小球C 去和小球A 接触,再和B 接触,然后移去,则球A 和球B 之间的作用力变为[ ](A)4f (B) 8f (C) 38f (D) 16f答案:B解析:经过碰撞后,球A 、B 带电量为2q,根据库伦定律12204q q F r πε=,可知球A 、B 间的作用力变为8f。
9-2关于电场强度定义式/F E =0q ,下列说法中哪个是正确的?[ ] (A) 电场场强E 的大小与试验电荷0q 的大小成反比 (B) 对场中某点,试验电荷受力F 与0q 的比值不因0q 而变 (C) 试验电荷受力F 的方向就是电场强度E 的方向 (D) 若场中某点不放试验电荷0q ,则0=F ,从而0=E 答案:B解析:根据电场强度的定义,E 的大小与试验电荷无关,方向为试验电荷为正电荷时的受力方向。
因而正确答案(B )习题9-3图(B) 穿过S 面的电场强度通量改变,O 点的场强大小改变 (C) 穿过S 面的电场强度通量不变,O 点的场强大小改变 (D) 穿过S 面的电场强度通量不变,O 点的场强大小不变 答案:D解析:根据高斯定理,穿过闭合曲面的电场强度通量正比于面内电荷量的代数和,曲面S 内电荷量没变,因而电场强度通量不变。
O 点电场强度大小与所有电荷有关,由点电荷电场强度大小的计算公式204q E rπε=,移动电荷后,由于OP =OT ,即r 没有变化,q 没有变化,因而电场强度大小不变。
因而正确答案(D )9-4 在边长为a 的正立方体中心有一个电量为q 的点电荷,则通过该立方体任一面的电场强度通量为 [ ](A) q /ε0 (B) q /2ε0 (C) q /4ε0 (D) q /6ε0 答案:D解析:根据电场的高斯定理,通过该立方体的电场强度通量为q /ε0,并且电荷位于正立方体中心,因此通过立方体六个面的电场强度通量大小相等。
第9章-静电场wzj

二 高斯定理
在真空中,通过任一闭合曲面的电场强度通量, 等于该曲面所包围的所有电荷的代数和除以 0 . (与面外电荷无关,闭合曲面称为高斯面)
1 ΦE E dS
S
0
q ( S内)
i 1 i
n
请思考:(1)高斯面上的 E 与那些电荷有关
(2)哪些电荷对闭合曲面
q dq (1) 体电荷密度 lim (C m 3 ) V dV q dq (2) 面电荷密度 lim (C m 2 ) S dS q dq 1 (3) 线电荷密度 lim (C m ) L dL
6. 点 电 荷(point charge): 7. 库仑定律(Coulomb law):
dΦ E
q 4 π 0 r
2
dS cos
q dS' 4 π 0 r 2
其中立体角
+
dS ' d S
dS' dΩ 2 r q q ΦE dΩ 0 4 π 0 S
r
dS '
dS
点电荷在封闭曲面之外
dΦ1 E1 dS1 0 dΦ2 E2 dS 2 0
E
?
s的 Φ 有贡献 ?
库仑定律
高斯定理的导出
电场强度叠加原理
高斯 定理
点电荷位于球面中心
4 π 0 r ΦE E dS Ecos0dS
2
S S
E
q
r
+
dS
ΦE E dS
S
q 4 π 0 r
4 πr 2 2
ΦE
q
0
点电荷在任意封闭曲面内
大学物理第9篇习题解答

第9章 真空中的静电场 习题解答9-1 精密的实验已表明,一个电子与一个质子的电量在实验误差为e 2110-±的范围内是相等的,而中子的电量在e 2110-±的范围内为零。
考虑这些误差综合的最坏情况,问一个氧原子(含8个电子、8个质子、8个中子)所带的最大可能净电荷是多少?若将原子看成质点,试比较两个氧原子间的电力和万有引力的大小,其净力是引力还是斥力?解:(1)一个氧原子所带的最大可能净电荷为 e q 21max 1024-⨯±=(2)两个氧原子间的电力和万有引力的大小之比为6222711221921122222max 0108.2)1067.116(1067.6)106.11024(1085.84141------⨯≈⨯⨯⨯⨯⨯⨯⨯⋅⨯⨯=≤r r r m G r q f f G e ππε氧其净力是引力。
9-2 如习题9-2图所示,在直角三角形ABC 的A 点处,有点电荷q 1 = ×10-9C ,B 点处有点电荷q 2 = -×10-9C ,AC = 3cm ,BC = 4cm ,试求C 点的场强。
解:根据点电荷场强大小的公式22014q qE kr r==πε, 点电荷q 1在C 点产生的场强大小为112014q E AC =πε 994-1221.810910 1.810(N C )(310)--⨯=⨯⨯=⨯⋅⨯ 方向向下。
点电荷q 2在C 点产生的场强大小为2220||14q E BC =πε E 2 EE 1q 2A C q 1B θ994-1224.810910 2.710(N C )(410)--⨯=⨯⨯=⨯⋅⨯, 方向向右。
C 处的总场强大小为E =44-110 3.24510(N C )==⨯⋅,总场强与分场强E 2的夹角为12arctan33.69E E ==︒θ.9-3 半径为R 的一段圆弧,圆心角为60°,一半均匀带正电,另一半均匀带负电,其电荷线密度分别为+λ和-λ,求圆心处的场强。
人教版高中物理必修第三册精品课件 第9章 静电场及其应用 二非点电荷电场强度的求解、电场线和轨迹问题

场线,虚线为某带电粒子只在静电力作用下的运动轨迹,a、b、c是轨迹上
的三个点,则( A C )
A.粒子一定带正电
B.粒子一定是从a点运动到b点
C.粒子在c点的加速度一定大于在b点的加速度
D.若粒子由a点运动到b点,则速度始终减小
解析 粒子做曲线运动时,合力的方向指向运动轨迹的凹侧,可知粒子受力方
向与电场方向一致,粒子带正电,故 A 正确。只知道曲线运动轨迹不能判断
运动方向,所以粒子运动方向无法确定,故 B 错误。由于 c 点电场线比 b 点电
场线密,则 c 点电场强度大于 b 点电场强度,在电场中根据
a=
=
可知,粒
子在 c 点的加速度大于在 b 点的加速度,故 C 正确。粒子由 a 点运动到 b 点
过程中,粒子所受静电力方向与速度方向所成的角由钝角逐渐减小为锐角,静
偿
为求解新模型与补充条件的差值问题。如采用补偿法将有缺口的带电
法
圆环补全为圆环,或将半球面补全为球面,从而将问题化难为易
应用体验
【例1】 (2023安徽安庆宿松中学校考)如图所示,空间存在水平向右的匀
强电场,电场强度大小为E,一个四分之一圆环形、粗细均匀的绝缘细棒AB
上均匀分布有正电荷,O为圆环的圆心,OB与电场线平行。将四分之一圆环
绕O点在圆环所在的平面内沿顺时针转过45°,这时O点的电场强度大小为
2E,则圆环上电荷在O点产生的电场强度大小为( D )
1
A. E
2
B.E
C.
3
E
2
D. 3E
解析 把圆环分割成无数段等长的小圆弧,每段小圆弧可以看作带相等电荷
量的点电荷,这些小圆弧关于 O 点和 AB 弧中点的连线对称, 根据电场的叠
大学物理第九章电荷与真空中的静电场详解

电荷相斥q1,异号r1电2 荷相吸。q2
F2 1
e12
F12
F1 2
k
q1q2 r122
e12
F2 1
k = 8.98755×109 N·m2 ·C-2 1
F
1
4 0
q1q2 r2
er
4 0
库仑定律是 全部静电学
的基础
0= 8.85×10-12C2 ·N-1·m-2 称为真空中的电容率。
9-2 电场和电场强度
1
4 0
2 2qr0 x3
1
2 0
p x3
1
q
E E 4 0 y 2 (r0 2)2
EB 2E cos i
2q
r0 / 2
i
4 0
(y2
r2 0
/
4) 3 /2
y2
当y r0时 :
EB
qr0
4 0 y3
p
4 0 y3
y
E
EB
B
E y
q
r0
q
x
3、连续分布任意带电体的场强
主要特点:研究对象不再是分离的实物,而是连
续分布的场,用空间函数
( 如E , U , B 等 )来描述。 静电场
电磁学
恒定磁场 变化中的电磁场
第九章 电荷与真空中的静电场
Electrostatic field
太阳风中高能离子沿着磁力 线侵入地球的极区在地球两 极的上层大气中放电而产生 的极光。
雷电
一、电场 Electric Field
1、超距作用不需要论时间
不需要介质
? 电荷
电荷
√ 2、法拉第提出近距作用, 并提出力线和场的概念
2025版高考物理一轮总复习知识梳理第9章静电场实验10观察电容器的充放电现象

试验十视察电容器的充、放电现象一、试验目的1.知道电容器的构造。
2.依据电路图正确连接实物图,细致视察电容器充放电的试验现象。
二、试验原理1.电容器的充电过程当S接1时,电容器接通电源,电容器上极板的自由电子在电场力的作用下将经过电源移到与电源负极相接的下极板,正极板由于失去负电荷而带正电,负极板由于获得负电荷而带负电,正、负极板所带电荷量大小相等,符号相反,如图甲所示。
电荷定向移动形成电流,由于同性电荷的排斥作用,所以起先电流最大,以后慢慢减小,在电荷移动过程中,电容器极板储存的电荷不断增加,电容器两极板间电压U等于电源电动势E时电荷停止移动,电流I=0。
2.电容器的放电过程当S接2时,电容器的两极板用导线连接起来,电容器C正极板上的正电荷与负极板上的负电荷中和,两极板的电荷量慢慢削减,表现为电流慢慢减小,电压也慢慢减小为零(如图乙所示)。
三、试验过程1.试验步骤(1)调整直流可调电源,输出为6 V,并用多用电表校准。
(2)关闭电源开关,正确连接实物图,电路图如图。
(3)打开电源,把单刀双掷开关S打到上面,使触点1和触点2连通,视察电容器的充电现象,并将结果记录在数据处理的表格中。
(4)把单刀双掷开关S打到下面,使触点3和触点2连通,视察电容器的放电现象,并将结果记录在数据处理的表格中。
(5)记录好试验结果,关闭电源。
2.数据处理当电容器极板上所储存的电荷发生变更时,电路中就有电流流过;若电容器极板上所储存的电荷量恒定不变时,则电路中就没有电流流过。
电路中的平均电流I =Δq Δt。
五、留意事项1.电流表要选用小量程的灵敏电流表。
2.要选择大容量的电容器。
3.试验过程中要在干燥的环境中进行。
4.在做放电试验时,在电路中串联一个电阻,避开烧坏电流表。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S Eds Nhomakorabea3. 闭合曲面电通量
e d e SE dS
dΦe E dS
n
E
dS 以曲面的外法线方向为正方向
π 0 ,从曲面穿出的电场线, 2
n
S
n
(2) 库仑定律适用于真空中的点电荷; (3) 库仑力满足牛顿第三定律; (4) 电荷之间距离小于10-10m时, 库仑定律仍保持有效.至于 大距离方面,虽然未作过实验验证,但也并没有特殊的理由 预料在大距离情况下库仑定律将失效.
例 氢原子中电子和质子的距离为 5.3 1011 m
求 此两粒子间的静电力和万有引力。 解 两粒子间的静电力大小为
3.7 10 47 N
讨论 (1) 库仑力和万有引力都是有心力和长程力 (2) 静电力既有引力也有斥力,而万有引力只是引力;两 种力的作用强度不同 F F
电 万
§9.2 电场 电场强度
9.2.1 电场 历史上的两种观点: 超距作用 场的作用 场的存在的客观依据 (1) 对位于其中的带电体有力的作用 (2) 带电体在电场中运动, 电场力要作功 场是物质存在的一种形态。一方面,它和实物有共性 的一面,即能量、质量和动量等物质的基本属性.另一方 面,电场又有其特殊性,它是无形的,弥漫在整个空间。
例 求电偶极子在中垂线上一点产生的电场强度。 E q 解 E E E E E B 2 2
E
B
4 0 (r l 4)
E
EBx 2E cos
cos
l 2 r2 l2 4
r
q
l
q
ql E 3 2 2 3/ 2 4 0r (1 l 4r )
E E ( x, y, z )
电场强度矢量是位置函数
Q
电场中某点的电场强度等于单位正电荷在该点的受力。
F E q0
9.2.3 场强叠加原理 点电荷产生的场强
1 qq0 0 F r 2 4 0 r
点电荷系的场强
F 1 q 0 E r 2 q0 4 0 r
相对于O点的力矩:
q
F
1 1 M F l sin F l sin 2 2 qlE sin M ql E p E
讨论
2 (2) 0
F
p
o l
q
E
(1)
力偶矩最大
力偶矩为零 (电偶极子处于稳定平衡) 力偶矩为零 (电偶极子处于非稳定平衡)
第4篇 电磁学
引言 第9章 静电场 第10章 稳恒磁场
第11章 电磁感应
电磁场是一个统一的整体 ,电、磁是一对孪生兄弟 。
电磁现象是自然界中极为普遍的现象
公元前600年 古希腊哲学家泰利斯就知道一块琥珀用木头摩擦之后 会吸引草屑等轻小物体;
春秋战国时期 《韩非子》和《吕氏春秋》都有天然磁石(Fe3O4) 的记载; 1785年 库仑定律提出,电磁学进入科学行列; 1820年 奥斯特发现电流的磁效应(电产生磁); 1831年 1865年 1887年 1905年 法拉第发现电磁感应现象 (磁产生电); 麦克斯韦建立了以麦克斯韦方程组为基础的完整 的电磁场理论; 赫兹利用振荡器在实验上证实了电磁波的存在; 爱因斯坦创立了相对论,解决了经典力学时空观与电磁 现象新的实验事实的矛盾。
q1
0 r 21
r
r
q2
F21
q1
F12
0 r 12
q2
q1q2 0 F k 2 r r
讨论 (1) 库仑定律中比率系数 k 为
1 k 4 0
0
真空中的介电常数
0 8.85418782 1012 C2 N 1 m 2)或(F m 1 ( )
1 xdq x rdr dE 2 2 3/ 2 4 0 (r x ) 2 0 (r 2 x 2 )3 / 2
dE
P
x
x R rdr E dE 2 0 0 (r 2 x 2 )3 / 2
x [1 2 2 1/ 2 ] 2 0 (R x )
(Coulomb)
在真空中两个静止点电荷之间的静电作用力与这两个
点电荷所带电量的乘积成正比,与它们之间距离的平方成 反比,作用力的方向沿着两个点电荷的连线。
电荷q1 对q2 的作用力F21 电荷q2对q1的作用力F12
q1q2 0 F21 k 2 r21 r q1q2 0 F12 k 2 r12 r
x
dE
求 圆环轴线上任一点P 的电场强度
解
dE x
dq dl 1 dq 0 dE r 2 4 0 r
P
dE
1 dq 0 E dE r 2 4 0 r
r
R
dq
O
dE dE sin
dEx dE cos
由于圆环上电荷分布关于x 轴对称
E dE
V
dE
dq
r
P
E E x i E y j EZ k
对于电荷连续分布的带电体,相应的元电荷为
dq 0 r 2 4 0 r
dl (线分布)
: 电荷线密度 : 电荷面密度 : 电荷体密度
dq
dS (面分布)
dV (体分布)
dq dx
a
O
L 2
1 dx dE 2 4 0(a x)
L 2
P
dq
x
dx E dE 40 a x) 2 ( L L
2 2
L q 2 2 0 4a L ( a 2 L2 ) 0 4
例 半径为R 的均匀带电细圆环,带电量为 q
E
Fk
k
q0
Fk 1 qk 0 Ek r 2 k k q0 k k 4 0 rk
点电荷系在某点P产生的电场强度等于各点电荷单独在 该点产生的电场强度的矢量和。这称为电场强度叠加原理。
连续分布带电体的场强
1 dq 0 dE r 2 4 0 r E
第9章
本章内容
静电场
§9.1 电荷 库仑定律
§9.2 电场 电场强度 §9.3 静电场中的高斯定律 §9.4 静电场中的环路定律 电势 §9.5 静电场中的导体 电容 §9.6 静电场中的介质 §9.7 静电场的能量
§9.1 电荷 库仑定律
9.1.1 电荷及其性质
1. 正负性: 同种电荷相斥;异种电荷相吸。 等量的正、负电荷相遇后,出现电中和。
r
R
O
x E [1 2 2 1/ 2 ]i 2 0 (R x )
已知带电系统的电荷分布时,根据电场强度的定义 求电场中任一点P的电场强度,其方法和步骤是:
根据给定的电荷分布,恰当的选择电荷元和坐标系; 应用点电荷电场强度的计算公式,在选定的坐标系中 写出某一电荷元dq在P点电场强度 dE ; 再应用电场强度叠加原理将每个电荷元产生的电场强度 相加,即可得到该点的电场强度;
由图上的几何关系
1 dx dE 2 4 0 r
y
dE y
dE
P
dEx
1
r
dq
a
O
2 2
2
x
2
x actan 2 dx a csc d
r a x a csc
2 2
y dE dE x cos d dE y 4 0 a P dEx dE y sin d 4 0 a r a 1 2 cos d Ex dEx dq O 4 0 a x (sin 2 sin 1 ) 4 0 a sin d (cos 1 cos 2 ) E y dE y 4 0 a 4 0 a
1 e 2 9.0 109 (1.6 1019 ) 2 8 Fe 8.1 10 N 2 11 2 4 0 r (5.3 10 )
两粒子间的万有引力为
me m p 6.7 1011 9.1 1031 1.7 1027 Fg G 2 r (5.3 1011 ) 2
注意:
要把 dE 向各坐标轴上投影,化矢量相加或矢量积分
为标量相加或标量积分,同时还要重视对称性的分析, 这样可省略一些不必要的计算;
例 已知圆环带电量为 q ,杆的电荷线密度为 ,长为 L 求 圆环对杆的作用力 解
dq dx 1 qx Ex 4 0 ( R 2 x 2 )3 / 2
dE
(1) 当 x = 0(即P点在圆环中心处)时,E 0
P
dE
(2) 当 x>>R 时
1 q E 4 0 x 2
r
R dq
可以把带电圆环视为一个点电荷 (3) 当 x
2 R 2
O
时 E 可取最大值。
例 求面密度为 的圆板轴线上任一点的电场强度 解
dq 2rdr
dF Ex dq Ex dx
R
q
O
dq
L
Ex
x
F 0
L
qxdx q 2 2 32 4 0 ( R x ) 40
1 R
2 2 R L 1
例 求电偶极子在均匀电场中受到的力偶矩。 (相对于O点的力矩)
解
F qE
F qE
E 0 1 q 1 cos 1 dq Ex r 2 cos 4 0 r 2 dq 4 0 r 2 cos 4 0
x cos r
r ( R 2 x 2 )1/ 2
